فیدبک (Feedback) در سیستم های کنترل — مفاهیم اصلی
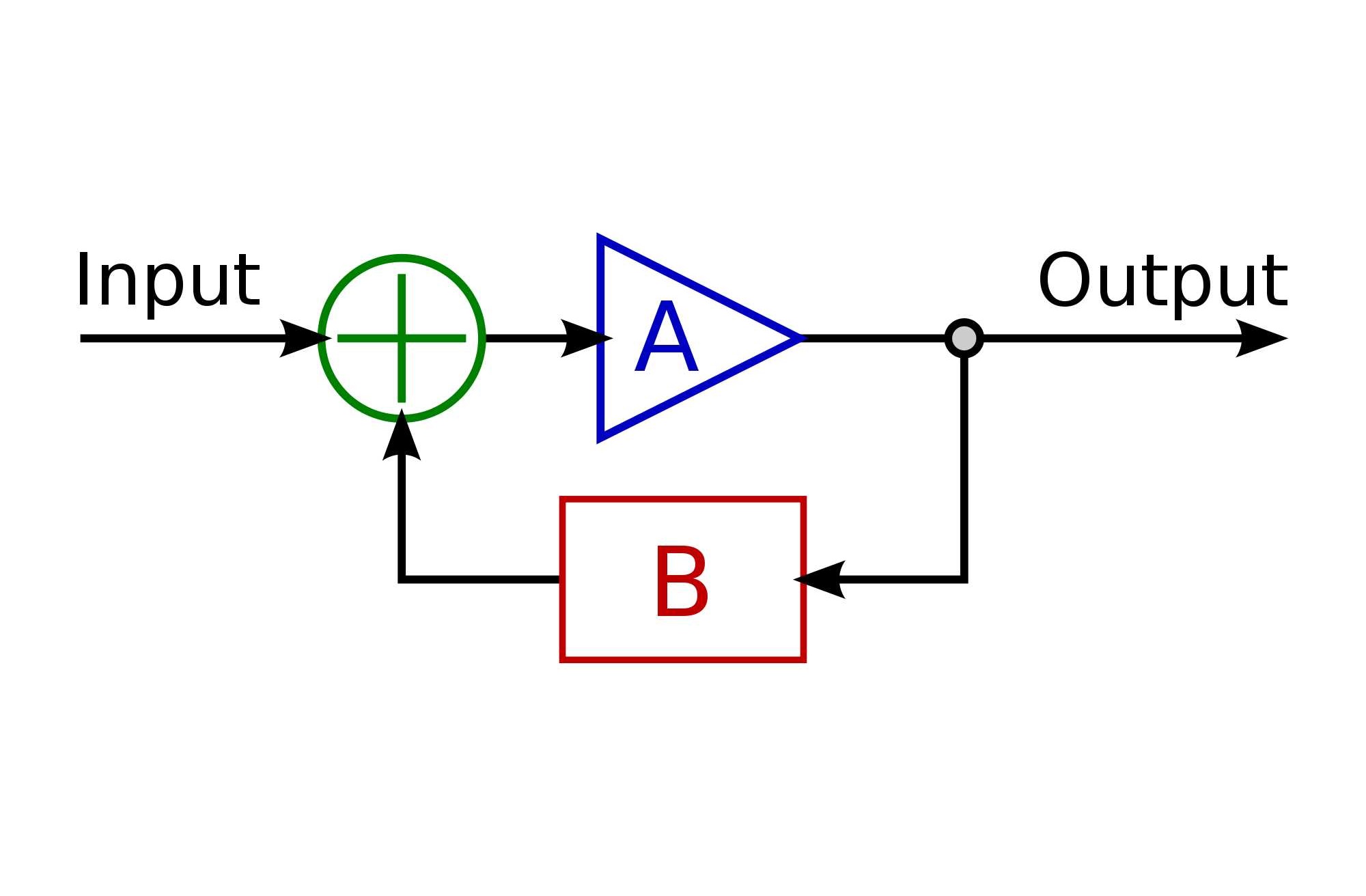
در حالت کلی، اگر خروجی یا بخشی از خروجی یک سیستم به ورودی برگردد و از آن استفاده شود، «فیدبک» (Feedback) یا پسخور نامیده میشود. فیدبک نقش مهمی در بهبود عملکرد سیستمهای کنترل ایفا میکند. در این آموزش، درباره انواع فیدبک و اثرات آن بحث خواهیم کرد.
انواع فیدبک
در حالت کلی، دو نوع فیدبک وجود دارد:
- فیدبک مثبت
- فیدبک منفی
در ادامه، در مورد هر یک از انواع فیدبکها به اختصار صحبت میکنیم.
فیدبک مثبت
در یک فیدبک مثبت، ورودی مرجع $$R(s)$$ و خروجی فیدبک با هم جمع میشوند.
شکل زیر، نمودار بلوکی سیستم کنترل فیدبک مثبت را نشان میدهد.
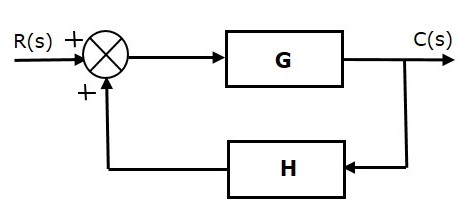
تابع تبدیل سیستم کنترل فیدبک مثبت به صورت زیر است:

که در آن:
- T تابع تبدیل یا بهره کلی سیستم،
- G بهره حلقه باز (تابعی از فرکانس)،
- و H بهره مسیر فیدبک (تابعی از فرکانس) است.
فیدبک منفی
فیدبک منفی، خطای بین ورودی مرجع $$R(s)$$ و خروجی سیستم را کاهش میدهد. شکل زیر، نمودار بلوکی سیستم کنترل فیدبک منفی را نشان میدهد.
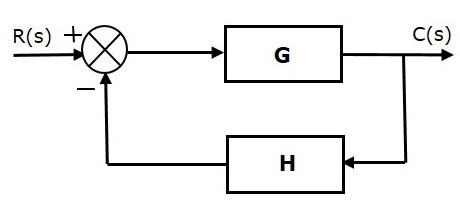
تابع تبدیل این سیستم، به صورت زیر است:
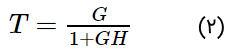
که در آن:
- T تابع تبدیل یا بهره کلی سیستم،
- G بهره حلقه باز (تابعی از فرکانس)،
- و H بهره مسیر فیدبک (تابعی از فرکانس) است.
اثرات فیدبک
اکنون و در ادامه این مطلب اثرات و مزایای فیدبک را بررسی میکنیم.
اثر فیدبک بر بهره کلی
- از معادله (2) مشخص است که بهره کلی سیستم کنترل حلقه بسته فیدبک منفی، برابر با نسبت $$G$$ و $$(1+GH)$$ است. بنابراین، بهره کلی را میتوان بسته به مقدار $$(1+GH)$$ افزایش یا کاهش داد.
- اگر مقدار $$(1+GH)$$ کمتر از 1 باشد، بهره افزایش خواهد یافت. در این حالت، مقدار GH منفی است
- اگر مقدار $$(1+GH)$$ بیشتر از 1 باشد، بهره کاهش خواهد یافت. در این حالت، مقدار GH مثبت است.
در حالت کلی، G و H توابعی از فرکانس هستند. بنابراین، فیدبک، بهره کلی سیستم را در فرکانسهایی افزایش خواهد داد و در فرکانسهای دیگر کم خواهد کرد.
اثر فیدبک بر حساسیت
حساسیت (T) بهره سیستم کنترل نسبت به تغییر بهره حلقه باز (G) به صورت زیر تعریف میشود:
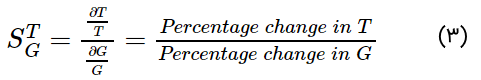
که در آن، $$\partial T$$ تغییر T نسبت به تغییر G است.
معادله (۳) را میتوانیم به صورت زیر بنویسیم:
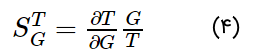
اگر از دو طرف معادله (۲) مشتق جزئی بگیریم، داریم:
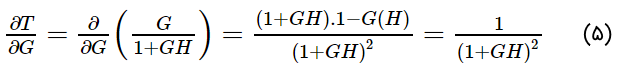
با توجه به رابطه (2)، میتوان نوشت:
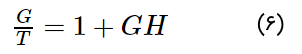
با جایگذاری معادلات (۵) و (۶) در رابطه (۴) به عبارت زیر میرسیم:
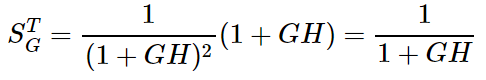
بنابراین، حساسیت بهره سیستم کنترل حلقه بسته، عکس $$(1+GH)$$ است و بسته به این مقدار میتواند افزایش یا کاهش یابد.
- اگر مقدار $$(1+GH)$$ کوچکتر از ۱ باشد، حساسیت افزایش خواهد یافت. این در صورتی اتفاق خواهد افتاد که $$GH$$ منفی باشد.
- اگر مقدار $$(1+GH)$$ بزرگتر از ۱ باشد، حساسیت کاهش مییابد. این موضوع در صورتی اتفاق خواهد افتاد که $$GH$$ مثبت باشد.
در حالت کلی، G و H توابعی از فرکانس هستند. بنابراین، فیدبک، حساسیت بهره سیستم را در فرکانسهایی افزایش خواهد داد و در فرکانسهای دیگر کم خواهد کرد. در نتیجه، باید GH را به گونهای انتخاب کنیم که سیستم نسبت به تغییرات پارامتر غیرحساس شود یا حساسیت کمی داشته باشد.
اثر فیدبک بر پایداری
- به سیستمی پایدار میگوییم که خروجی آن تحت کنترل باشد. در غیر این صورت، ناپایدار است.
- اگر مخرج معادله (۲) برابر صفر باشد (یعنی $$GH=-1$$)، خروجی سیستم کنترل بینهایت میشود. بنابراین، سیستم کنترل، ناپایدار خواهد شد.
در نتیجه، باید فیدبک را به گونهای انتخاب کنیم که سیستم کنترل پایدار باشد.
اثر فیدبک بر نویز
برای بررسی اثر فیدبک بر نویز، روابط تابع تبدیل سیستم را در حالت بدون فیدبک و با فیدبک بررسی میکنیم.
سیستم کنترل حلقه باز با یک سیگنال نویز در شکل زیر نشان داده شده است:
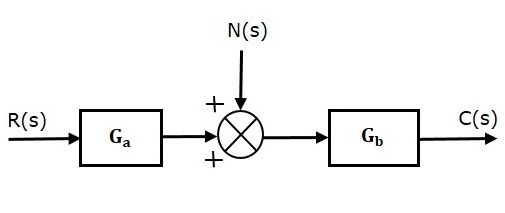
تابع تبدیل حلقه باز خروجی به سیگنال نویز، به صورت زیر است (این تابع تبدیل، با صفر قرار دادن ورودی $$R(s)$$ به دست میآید):
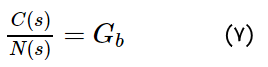
سیستم کنترل حلقه بسته زیر را در نظر بگیرید که نویز در آن وجود دارد:
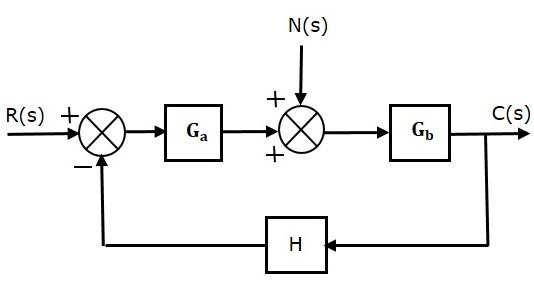
تابع تبدیل حلقه بسته نویز به خروجی با صفر قرار دادن ورودی $$R(s)$$ به شکل زیر به دست میآید:
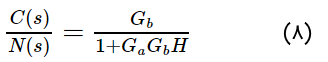
اگر دو تابع تبدیل رابطه (۷) و رابطه (۸) را مقایسه کنیم، میبینیم در سیستم حلقه بسته، بهره با ضریب $$(1+G_aG_bH)$$ کاهش یافته است، زیرا مقدار $$(1+G_aG_bH)$$ بزرگتر از ۱ است.
فیدبک منفی، معمولاً پرکاربردترین نوع فیدبک است. وقتی مقدار خروجی را از ورودی مطلوب کم میکنیم، سیگنال خطا تولید خواهد شد. این سیگنال به ما میگوید که چقدر با ورودی مطلوب اختلاف داریم. به این ترتیب میتوانیم برای کاهش خطا اقدام کنیم.
فیدبک مثبت، سیگنال ها را تقویت میکند. در یک سیستم فیدبک مثبت، اگر نویز به ورودی وارد شود، سیستم آن را تقویت و بزرگتر میکند. یک مثال برای سیستم فیدبک مثبت، وقتی است که میکروفن را به بلندگو نزدیک میکنید و به این ترتیب، میزان بزرگی صدا بیشتر و بیشتر میشود.
^^
 فرادرس
فرادرس