روش ضرایب نامعین — از صفر تا صد

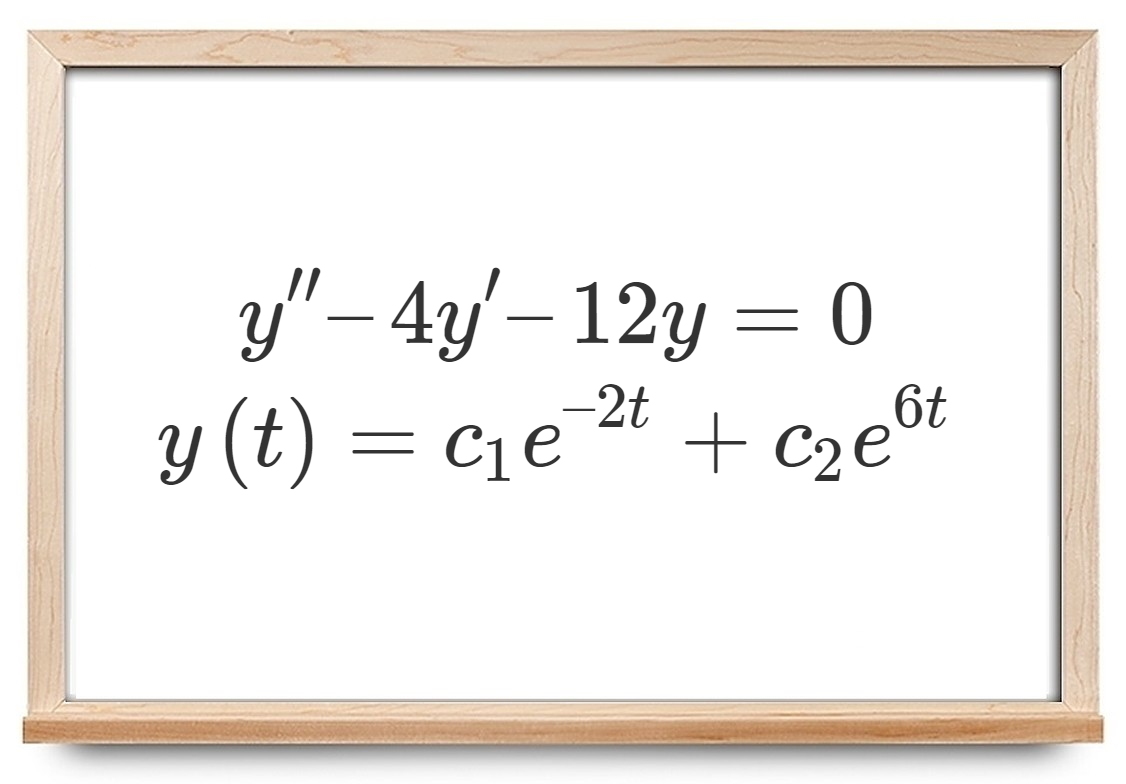
در این آموزش از مجموعه آموزش‌های ریاضیات مجله فرادرس، با روش ضرایب نامعین آشنا می‌شویم که در حل معادلات دیفرانسیل ناهمگن و همچنین دستگاه معادلات دیفرانسیل کاربرد دارد.

روش ضرایب نامعین در معادلات دیفرانسیل

در این بخش، روش ضرایب نامعین را برای یافتن جواب خصوصی یک معادله دیفرانسیل ناهمگن به شکل زیر بیان می‌کنیم:

$$\large y^{\prime \prime} + p \left ( t \right ) y' + q \left ( t \right ) y = g \left ( t \right )$$

یکی از مهم‌ترین مزیت‌های این روش این است که مسئله را به یک مسئله جبری کاهش می‌دهد. ممکن است جبر گاهی با دشواری روبه‌رو شود، اما برای اغلب مسائل مشکلی وجود نخواهد داشت. نکته خوب دیگر در مورد این روش این است که جواب عمومی به صورت صریح مورد نیاز نخواهد بود، اگرچه ما در بعضی موارد به دانستن جواب عمومی نیز نیاز خواهیم داشت.

البته این روش دو عیب نیز دارد. اول اینکه برای یک خانواده نسبتاً محدود از $$g ( t)$$ها کارساز است. $$g(t)$$هایی که این روش برای آن‌ها قابل اعمال است، شامل توابع متداول است، البته، توابعی نیز وجود دارند که روش ضرایب نامعین برای آن‌ها کارآمد نیست. دومین عیب این است که این روش تنها برای معادلات دیفرانسیل با ضرایب ثابت کاربرد دارد.

روش ضرایب نامعین بسیار ساده است. تمام چیزی که نیاز داریم، این است که $$g ( t)$$ را مشاهده کنیم و حدس بزنیم که $$Y _ P ( t)$$ چگونه خواهد بود، سپس ضرایب نامعین آن را به دست آوریم. نام ضرایب نامعین از همین‌جا آمده است. حدس خود را در معادله دیفرانسیل قرار داده و می‌بینیم که آیا می‌توانیم ضرایب نامعین را تعیین کنیم یا خیر. اگر بتوانیم این کار را انجام دهیم، حدس صحیح بوده، اما اگر نتوانیم مقادیر ضرایب را بیابیم، حدسمان اشتباه بوده است. معمولاً انجام این روش از توصیف چگونگی آن ساده‌تر است. بنابراین، در ادامه، چند مثال را بررسی می‌کنیم.

مثال‌های روش ضرایب نامعین در معادلات دیفرانسیل

مثال ۱: جواب خصوصی معادله دیفرانسیل زیر را به دست آورید:

$$\large y^{\prime\prime} - 4 y' - 1 2 y = 3 { { { e } } ^ { 5 t } }$$

حل: در اینجا باید یک جواب خصوصی را بیابیم، اما اولین کاری که می‌خواهیم انجام دهیم پیدا کردن جواب عمومی این معادله دیفرانسیل است. می‌دانیم که جواب عمومی از حل معادله زیر به دست می‌آید:

$$\large y ^ {\prime \prime} - 4 y' - 1 2 y = 0$$

معادله مشخصه این معادله دیفرانسیل به صورت زیر است:

$$\large { r ^ 2 } - 4 r - 1 2 = \left ( { r - 6 } \right ) \left ( { r + 2 } \right ) = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} \, \, { r _ 1 } = - 2 , \, \, \, \, { r _ 2 } = 6$$

در نتیجه، جواب عمومی به صورت زیر خواهد بود:

$$\large { y _ c } \left ( t \right ) = { c _ 1 } { { { e } } ^ { - 2 t } } + { c _ 2 } { { { e } } ^ { 6 t } }$$

همان‌طور که خواهیم دید، داشتن جواب عمومی مفید خواهد بود و بنابراین بهتر است قبل از اعمال روش ضرایب نامعین ، ابتدا جواب عمومی را داشته باشیم.

اکنون، یک جواب خصوصی را پیدا می‌کنیم. همان‌طور که قبل از شروع این مثال ذکر شد، باید شکل یک جواب خصوصی برای این معادله دیفرانسیل را حدس بزنیم. از آنجا که $$g ( t)$$ نمایی است و می‌دانیم که نماها در فرایند مشتق‌گیری از بین نمی‌روند، به نظر می‌رسد شکل احتمالی جواب خصوصی به صورت زیر باشد:

$$\large { Y _ P } \left ( t \right ) = A { { { e } } ^ { 5 t } }$$

اکنون باید دو بار از تابع بالا مشتق بگیریم و آن را در معادله دیفرانسیل قرار دهیم و ضریب $$A$$ را به دست آوریم.

با انجام این کار، خواهیم داشت:

$$\large \begin {align*} 2 5 A { { { e } } ^ { 5 t } } - 4 \left ( { 5 A { { { e } } ^ { 5 t } } } \right ) - 1 2 \left ( { A { { { e } } ^ { 5 t } } } \right ) & = 3 { { { e } } ^ { 5 t } } \\ - 7 A { { { e } } ^ { 5 t } } & = 3 { { { e } } ^ { 5 t } } \end {align*}$$

با برابر قرار دادن ضرایب دو طرف تساوی، خواهیم داشت:

$$\large - 7 A = 3 \hspace {0.25in} \Rightarrow \hspace {0.25in} A = - \frac { 3 } { 7 }$$

در نتیجه، جواب خصوصی معادله به شکل زیر خواهد بود:

$$\large { Y _ P } \left ( t \right ) = - \frac { 3 } { 7 }{ { { e } } ^ { 5 t } }$$

مثال ۲: جواب مسئله مقدار اولیه زیر را به دست آورید:

$$\large y ^ {\prime \prime} - 4 y' - 1 2 y = 3 { { { e } } ^ { 5 t } } \hspace {0.25in} \hspace {0.25in} y \left ( 0 \right ) = \frac { { 1 8 } } { 7 } \hspace {0.25in} y' \left ( 0 \right ) = - \frac { 1 } { 7 }$$

حل: جواب مسئله به فرم زیر است:

$$\large y \left ( t \right ) = { y _ c } \left ( t \right ) + { Y _ P } \left ( t \right )$$

با توجه به جواب عمومی معادله، می‌توان نوشت:

$$\large \begin {align*} y \left ( t \right ) & = { c _ 1 } { { { e } } ^ { - 2 t } } + { c _ 2 } { { { e } } ^ { 6 t } } - \frac { 3 } { 7 } { { { e } } ^ { 5 t } } \\ y' \left ( t \right ) & = - 2 { c _ 1 } { { { e } } ^ { - 2 t } } + 6 { c _ 2 } { { { e } } ^ { 6 t } } - \frac { { 1 5 } } { 7 } { { { e } } ^ { 5 t } } \end {align*}$$

اکنون شرایط اولیه را اعمال می‌کنیم:

$$\large \begin {align*} \frac { { 1 8 } } { 7 } = y \left ( 0 \right ) & = { c _ 1 } + { c _ 2 } - \frac { 3 } { 7 } \\ - \frac { 1 } { 7 } = y' \left ( 0 \right ) & = - 2 { c _ 1 } + 6 { c _ 2 } - \frac { { 1 5 } } { 7 } \end {align*}$$

در نتیجه، ضرایب $$c _ 1 = 2$$ و $$c _ 2 = 1$$ را خواهیم داشت و جواب نهایی به صورت زیر خواهد بود:

$$\large y \left ( t \right ) = 2 { { { e } } ^ { - 2 t } } + { { { e } } ^ { 6 t } } - \frac { 3 } { 7 } { { { e } } ^ { 5 t } }$$

مثال ۳: جواب خصوصی معادله زیر را بیابید.

$$\large y ^ {\prime \prime } - 4 y' - 1 2 y = \sin \left ( { 2 t } \right )$$

حل: حدس می‌زنیم جواب این معادله به شکل زیر باشد:

$$\large { Y _ P } \left ( t \right ) = A \sin \left ( { 2 t } \right )$$

با مشتق‌گیری از تابع بالا و قرار دادن آن در معادله اصلی، خواهیم داشت:

‌$$\large - 4 A \sin \left ( { 2 t } \right ) - 4 \left ( { 2 A \cos \left ( { 2 t } \right ) } \right ) - 1 2 \left ( { A \sin \left ( { 2 t } \right ) } \right ) = \sin \left ( { 2 t } \right )$$

$$\large - 1 6 A \sin \left ( { 2 t } \right ) - 8 A \cos \left ( { 2 t } \right ) = \sin \left ( { 2 t } \right )$$

اگر ضرایب دو طرف تساوی را برابر قرار دهیم، خواهیم داشت:

$$\large \begin {align*} & \cos \left ( { 2 t } \right ) \,: & - 8 A & = 0 \hspace{0.25in} \Rightarrow \hspace{0.25in} A = 0 \\ & \sin \left ( { 2 t } \right ) \,:& - 1 6 A & = 1 \hspace{0.25in} \Rightarrow \hspace{0.25in} A = - \frac { 1 } { { 16 } } \end {align*}$$

می‌بینیم که دو مقدار برای $$A$$ به دست می‌آید و این یک تناقض آشکار است که نشان می‌دهد حدس ما درست نبوده است. بنابراین، یک حدس دیگر می‌زنیم و با توجه به مسئله تابع کسینوس را نیز به آن اضافه می‌کنیم:

$$\large { Y _ P } \left ( t \right ) = A \cos \left ( { 2 t } \right ) + B \sin \left ( { 2 t } \right )$$

مانند  قبل، از جمله بالا مشتق گرفته و آن را در معادله اصلی قرار می‌دهیم:

$$\large \begin {align*} - 4 A \cos \left ( { 2 t } \right ) - 4 B \sin \left ( { 2 t } \right ) - 4 \left ( { - 2 A \sin \left ( { 2 t } \right ) + 2 B \cos \left ( { 2 t } \right ) } \right ) - \\ 1 2 \left ( { A \cos \left ( { 2 t } \right ) + B \sin \left ( { 2 t } \right ) } \right ) & = \sin \left ( { 2 t } \right ) \\ \left ( { - 4 A - 8 B - 1 2 A } \right ) \cos \left ( { 2 t } \right ) + \left ( { - 4 B + 8 A - 1 2 B } \right ) \sin \left ( { 2 t } \right ) & = \sin \left ( { 2 t } \right ) \\ \left ( { - 1 6 A - 8 B } \right ) \cos \left ( { 2 t } \right ) + \left ( { 8 A - 1 6 B } \right ) \sin \left ( { 2 t } \right ) & = \sin \left ( { 2 t } \right ) \end {align*}$$

با برابر قرار دادن ضرایب، داریم:

$$\large \begin {align*} & \cos \left ( { 2 t } \right ) \,: & - 1 6 A - 8 B & = 0 \\ & \sin \left ( { 2 t } \right ) \,: & 8 A - 1 6 B & = 1 \end {align*}$$

و ضرایب به صورت زیر به دست می‌آیند:

$$\large A = \frac { 1 } { { 4 0 } } \hspace {0.25in} \hspace {0.25in} B = - \frac { 1 } { { 2 0 } }$$

در نتیجه، جواب نهایی برابر خواهد بود با:

$$\large { Y _ P } \left ( t \right ) = \frac { 1 } { { 4 0 } } \cos \left ( { 2 t } \right ) - \frac { 1 } { { 2 0 } } \sin \left ( { 2 t } \right )$$

روش ضرایب نامعین در دستگاه معادلات دیفرانسیل

دستگاه معادلات خطی همگن با ضرایب ثابت زیر را در نظر بگیرید:

$$ \large { \mathbf { X }’ \left ( t \right ) = A \mathbf { X } \left ( t \right ) , \; \; } \kern-0.3pt<br /> { \mathbf { X } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { x _ 2 } \left ( t \right ) } \\<br /> \vdots \\<br /> { { x _ n } \left ( t \right ) }<br /> \end {array}} \right ] , \; \; } \kern-0.3pt<br /> { A = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & { { a _ { 1 2 } } } & \cdots &{ { a _ { 1 n } } } \\<br /> { { a _ { 2 1 } } } & { { a _ { 2 2 } } } & \cdots & { { a _ { 2 n } } } \\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> { { a _ { n 1 } } } & { { a _ { n 2 } } } & \cdots &{ { a _ { n n } } }<br /> \end {array} } \right ] . } $$

در اینجا، $$\mathbf{X}\left( t \right)$$ یک بردار با اندازه $$n$$ و $$A$$ یک ماتریس مربعی $$n \times n$$ شامل ضرایب ثابت است.

در ادامه، یک الگوریتم کلی برای حل این دستگاه ارائه می‌کنیم و موارد خاصی را در نظر می‌گیریم که جواب با روش ضرایب نامعین به دست می‌آید. ‌حل معادله داده شده را در قالب توابع برداری زیر بیان می‌کنیم:

$$\large \mathbf { X } \left ( t \right ) = { e ^ { \lambda t } } \mathbf { V } ,$$

که در آن، $$\lambda$$ مقدار ویژه $$A$$ و $$\mathbf{V}$$ بردار ویژه متناظر با مقدار ویژه است.

مقادیر ویژه $$\lambda _ i$$ از معادله کمکی زیر به دست می‌آیند:

$$\large \det \left( {A – \lambda I} \right) = 0$$

که در آن، $$I$$ ماتریس همانی است.

از آنجا که تعدادی از ریشه‌های $$\lambda _ i$$ می‌توانند مکرر باشند، در حالت کلیِ یک سیستم مرتبه $$n$$اُم، معادله کمکی به فرم زیر خواهد بود:

$$\large { { \left ( { – 1 } \right ) ^ n } { \left ( { \lambda – { \lambda _ 1 } } \right ) ^ { { k _ 1 } } } { \left ( { \lambda – { \lambda _ 2 } } \right ) ^ { { k _ 2 } } } \cdots } \kern0pt { { \left ( { \lambda – { \lambda _ m } } \right ) ^ { { k _ m } } } } = { 0 . }$$

در اینجا، شرط زیر برقرار است:

$$\large {k_1} + {k_2} + \cdots + {k_m} = n.$$

توان $$k_i$$ عامل $$(\lambda - \lambda _ i )$$ مرتبه تکرار جبری مقدار ویژه $$\lambda _ i$$ نامیده می‌شود.

برای هر مقدار ویژه $$\lambda _ i$$، می‌توانیم بردار ویژه (یا چند بردار ویژه را برای $$\lambda _ i$$ تکراری) با فرمول زیر محاسبه کنیم:

$$\large \left( {A – {\lambda _i}I} \right){\mathbf{V}_i} = \mathbf{0}.$$

تعداد بردار ویژه‌هایی که متناظر با مقدار ویژه $$\lambda _ i$$ هستند، مرتبه تکرار هندسی $$\lambda _ i$$ نامیده می‌شوند (آن را با $$s _ i$$ نشان می‌دهیم). بنابراین، مقدار ویژه $$\lambda _ i$$ با دو کمیت مشخص می‌شود: مرتبه تکرار جبری $$k_ i$$ و مرتبه تکرار هندسی $$s _ i$$. رابطه زیر را برای این دو پارامتر داریم:

$$\large 0 \lt {s_i} \le {k_i}$$

یعنی مرتبه تکرار هندسی $$s_ i$$ (یا تعداد بردار ویژه‌ها) از مرتبه تکرار جبری $$k_i$$ مقدار ویژه $$\lambda _ i$$ تجاوز نمی‌کند.

یک دستگاه پایه از جواب‌ها و در نتیجه، جواب عمومی دستگاه، شدیداً به مرتبه تکرار جبری و هندسی مقادیر ویژه $$\lambda _ i$$ بستگی دارد. در ساده‌ترین حالت $$s _ i = k _ i = 1$$، وقتی مقادیر ویژه $$\lambda _ i$$ ماتریس $$A$$ مجزا بوده و هر مقدار $$\lambda _ i$$ متناظر با یک بردار ویژه $$\mathbf{V}_i$$ باشند، دستگاه اساسی جواب‌ها شامل توابع زیر است:

$$\large {{e^{{\lambda _1}t}}{\mathbf{V}_1},\;}\kern-0.3pt{{e^{{\lambda _2}t}}{\mathbf{V}_2}, \;\ldots,\;}\kern-0.3pt{ {e^{{\lambda _n}t}}{\mathbf{V}_n}.}$$

در این حالت، جواب عمومی به صورت زیر نوشته می‌شود:

$$ \large { \mathbf { X } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { x _ 2 } \left ( t \right ) } \\<br /> \vdots \\<br /> { { x _ n } \left ( t \right ) }<br /> \end {array} } \right ] }<br /> = { { C _ 1 } { e ^ { { \lambda _ 1 } t } } { \mathbf { V } _ 1 } } + { { C _ 2 } { e ^ { { \lambda _ 2 } t } } { \mathbf { V } _ 2 } + \cdots }<br /> + { { C _ n } { e ^ { { \lambda _ n } t } } { \mathbf { V } _ n } }\\ \large<br /> = { \sum \limits _ { i = 1 } ^ n { { C _ i } { e ^ { { \lambda _ i } t } } { \mathbf { V } _ i } } , } $$

که در آن، $$C_i$$ها ثوابت دلخواهی هستند.

حالتی را در نظر بگیرید که ریشه‌های معادله مشخصه مختلط هستند. اگر همه ضرایب معادلات اعدادی حقیقی باشند، ریشه‌های مختلط به فرم مزدوج مختلط $$\alpha \pm i\beta$$ هستند. برای تشکیل یک جواب متناظر با این جفت ریشه، کافی است یک عدد، مثلاً $$\alpha + i\beta$$ را در نظر بگیریم و بردار ویژه $$\mathbf{V}$$ متناظر با آن را به دست آوریم که ممکن است مختصات مختلط داشته باشد. پس از آن، جواب با تابع برداری مختلط $${e^{\left( {\alpha + i\beta } \right)t}}\mathbf{V}\left( t \right)$$ نمایش داده می‌شود. تابع نمایی را می‌توان با فرمول اویلر گسترش داد:

$$\large { { e ^ { \left ( { \alpha + i \beta } \right ) t } } } = { { e ^ { \alpha t } } { e ^ { i \beta t } } } = { { e ^ { \alpha t } } \left ( { \cos \beta t + i \sin \beta t } \right ) . }$$

در نتیجه، بخشی از جواب عمومی که متناظر با مقادیر ویژه مزدوج $$\alpha \pm i\beta$$ است، به فرم زیر خواهد بود:

$$\large \begin {align*} \mathbf { X } \left ( t \right ) & = \kern0pt { { { e ^ { \alpha t } } \left ( { \cos \beta t + i \sin \beta t } \right ) \cdot } } \kern0pt { { \left ( { { \mathbf { V } _ \text {Re}} + i { \mathbf { V } _ \text {Im} } } \right ) } } \\ & = { { { e ^ { \alpha t } } \left [ { \cos \left ( { \beta t } \right ) { \mathbf { V } _ \text {Re}} } \right . } - { \left . { \sin \left ( { \beta t } \right ) { \mathbf { V } _ \text {Im} } } \right ] } } + { { i { e ^ { \alpha t } } \left [ { \cos \left ( { \beta t } \right ) { \mathbf { V } _ \text {Im}} } \right . } + { \left . { \sin \left ( { \beta t } \right ) { \mathbf { V } _ \text {Re} } } \right ] } } \\ & = { { \mathbf { X } ^ { \left ( 1 \right ) } } \left ( t \right ) + i { \mathbf { X } ^ { \left ( 2 \right ) } } \left ( t \right ) , } \end {align*}$$

که در آن، $${\mathbf{V}_\text{Re}} + i{\mathbf{V}_\text{Im}}$$ بردار ویژه مختلط است. توابع برداری $${\mathbf{X}^{\left( 1 \right)}}$$ و $${\mathbf{X}^{\left( 2 \right)}}$$ در بخش‌های حقیقی و موهومی عبارت حاصل، دو جواب حقیقی مستقل خطی را تشکیل می‌دهند.

همان‌طور که مشاهده می‌شود، جواب برای جفت مقدار ویژه مزدوج مختلط به شکل مشابه مقادیر ویژه حقیقی تشکیل شده است. تنها لازم است بین بخش‌های حقیقی و موهومی تابع برداری در انتهای تبدیلات کاملاً مجزا شوند.

اکنون، حالتی را در نظر می‌گیریم که ریشه‌های $$\lambda _ i$$ تکراری باشند. برای سادگی، فرض می‌کنیم در این حالت ریشه‌ها حقیقی باشند. مجدداً فرایند یافتن جواب به دو سناریو تقسیم می‌شود.

اگر مرتبه تکرار $$k _ i$$ و مرتبه تکرار هندسی $$s _ i$$ مقدار ویژه $$\lambda _ i$$ با هم برابر باشند ($${{k_i} = {s_i} \gt 1}$$)، تعداد $$k_ i$$ بردار ویژه برای این مقدار $$\lambda _ i$$ وجود دارد. در نتیجه، مقدار ویژه $$\lambda _ i$$ متناظر با $$k_i$$ جواب مستقل خطی به فرم زیر خواهد بود:

$$\large { { e ^ { { \lambda _ i } t } } \mathbf { V } _ i ^ { \left ( 1 \right ) } , \; } \kern-0.3pt { { e ^ { { \lambda _ i } t } } \mathbf { V } _ i ^ { \left ( 2 \right ) } , \; \ldots ,\;}\kern-0.3pt { { e ^ { { \lambda _ i } t } } \mathbf { V } _ i ^ { \left ( { { k _ i } } \right ) } . }$$

در این حالت، دستگاه $$n$$معادله‌ای در کل $$n$$ بردار ویژه خواهد داشت که یک دستگاه اساسی از جواب‌ها را تشکیل می‌دهد.

جذاب‌ترین حالت، $$\lambda _ i$$ تکراری است، وقتی که مرتبه تکرار هندسی $$s_ i$$ کمتر از مرتبه تکرار جبری $$k _ i$$ باشد. این یعنی تنها $$s_ i$$ بردار ویژه متناظر با $$\lambda _ i$$ وجود دارد. تعداد بردار ویژه‌های $$s _ i$$ با فرمول زیر تعیین می‌شود:

$$\large { { s _ i } } = { n – \text {rank} \left ( { A – { \lambda _ i } I } \right ) }$$

که در آن، $$\text{rank}\left( {A – {\lambda _i}I} \right)$$ رتبه ماتریس $${A – {\lambda _i}I}$$ را نشان می‌دهد.

جواب متناظر با $$\lambda _ i$$ را می‌توان به عنوان ضرب یک چندجمله‌ای درجه $${k_i} – {s_i}$$ با تابع نمایی $${e^{{\lambda _i}t}}$$ نوشت:

$$\large { { \mathbf { X } _ i } \left ( t \right ) = { \mathbf { P } _ { { k _ i } – { s _ i } } } \left ( t \right ) { e ^ { { \lambda _ i } t } } }$$

که در آن،

$$\large { { \mathbf { P } _ { { k _ i } – { s _ i } } } \left ( t \right ) } = { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t + \cdots } + { { \mathbf { A } _ { { k _ i } – { s _ i } } } { t ^ { { k _ i } – { s _ i } } } . }$$

در اینجا، $${\mathbf{P}_{{k_i} – {s_i}}}\left( t \right)$$ یک چندجمله‌ای برداری است، یعنی هریک از $$n$$ مختصات متناظر با یک چندجمله‌ای درجه $${{k_i} – {s_i}}$$ با تعدادی ضریب که باید تعیین شوند.

در واقع، استفاده از روش ضرایب نامعین تنها در حالتی لازم است که ریشه‌های تکراری $$\lambda _ i$$ را داشته باشیم و تعداد بردار ویژه‌های مستقل خطی کمتر از مرتبه تکرار جبری ریشه $$\lambda _ i$$ باشد.

برای یافتن بردارهای $${\mathbf{A}_0}$$، $${\mathbf{A}_1}$$، $$\ldots$$ و $${\mathbf{A}_{{k_i} – {s_i}}}$$ مربوط به هر مقدار ویژه $$\lambda _ i$$، باید تابع برداری $${\mathbf{X}_i}\left( t \right)$$ را در دستگاه اصلی معادلات جایگذاری کرد. با برابر قرار دادن ضرایب جملات با توان مشابه در سمت راست و چپ هر معادله، یک دستگاه معادلات جبری برای بردارهای مجهول $${\mathbf{A}_0}$$، $${\mathbf{A}_1}$$، $$\ldots$$ و $${\mathbf{A}_{{k_i} – {s_i}}}$$ به دست خواهد آمد.

این روش تشکیل جواب عمومی یک دستگاه معادلات دیفرانسیل گاهی روش اویلر نیز نامیده می‌شود.

مثال‌های روش ضرایب نامعین در دستگاه معادلات دیفرانسیل

در این بخش، چند مثال را از کاربرد روش ضرایب نامعین در حل دستگاه معادلات دیفرانسیل بیان می‌کنیم.

مثال ۱: جواب عمومی دستگاه معادلات خطی زیر را به دست آورید:

$$\large { \frac { { d x } } { { d t } } = x – y , \; \; }\kern-0.3pt { \frac { { d y } } { { d t} } = x + 3 y . }$$

حل: ابتدا مقادیر ویژه $$\lambda _ i$$ ماتریس $$A$$ را محاسبه می‌کنیم که از ضرایب معادلات به دست می‌آیند:

$$ \large \begin {align*} { { \det \left ( { A – \lambda I } \right ) } = { \left | { \begin {array} { * { 2 0 } { c } }<br /> { 1 – \lambda } & { – 1 } \\<br /> 1 & { 3 – \lambda }<br /> \end {array} } \right | = 0 , \; \; } } \Rightarrow<br /> { \left ( { 1 – \lambda } \right ) \left ( { 3 – \lambda } \right ) + 1 = 0 , \; \; } \\ \Rightarrow<br /> { { 3 – 3 \lambda – \lambda } + { { \lambda ^ 2 } + 1 = 0 , \; \; } } \Rightarrow<br /> { { \lambda ^ 2 } – 4 \lambda + 4 = 0 , \; \; } \Rightarrow<br /> { { \left ( { \lambda – 2 } \right ) ^ 2 } = 0 . } \end {align*} $$

بنابراین، مقادیر ویژه $$A$$، اعداد $$\lambda _ i = 2$$ با تکرار $$k _ 1 = 2$$ است. اکنون رتبه ماتریس $$A – {\lambda _1}I$$ را محاسبه می‌کنیم. با قرار دادن مقدار $${\lambda _1} = 2$$ در ماتریس و با استفاده از تبدیلات مقدماتی، خواهیم داشت:

$$ \large { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { 1 – 2 } & { – 1 } \\<br /> 1 & { 3 – 2 }<br /> \end {array} } \right ] } \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 1 } & { – 1 } \\<br /> 1 & 1<br /> \end {array} } \right ] }<br /> \sim { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 \\<br /> { – 1 } & { – 1 }<br /> \end {array} } \right ] } \right | \left . { \begin {array} { * { 20 } { c } }<br /> { } \\<br /> \small { { R _ 2 } + { R _ 1 } } \normalsize<br /> \end {array} } \right . } \\ \large<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> 0&0<br /> \end{array}} \right] }<br /> \sim {\left( {\begin{array}{*{20}{c}}<br /> 1&1<br /> \end{array}} \right).} $$

بنابراین، رتبه ماتریس $$A – {\lambda _1}I$$ برابر با $$1$$ است. در نتیجه، مرتبه تکرار هندسی $${s_1} = 1$$ را برای عدد $${\lambda _1} = 2$$ داریم، یعنی یک بردار ویژه به صورت زیر خواهیم داشت:

$$\large { { s _ 1 } } = { n – \text {rank} \left ( { A – { \lambda _ 1 } I } \right ) } = { 2 – 1 } = { 1 . }$$

جواب برداری عمومی به صورت زیر است:

$$ \large { \mathbf { X } \left ( t \right ) } = { \left [ { \begin {array} { * { 2 0 } { c } }<br /> x \\<br /> y<br /> \end {array} } \right ] + { \mathbf { P } _ { { k _ i } – { s _ i } } } \left ( t \right ) { e ^ { { \lambda _ i } t } } }<br /> = { { \mathbf { P } _ 1 } \left ( t \right ) { e ^ { { \lambda _ i } t } } }<br /> = { \left ( { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t } \right ) { e ^ { 2 t } } . } $$

اکنون از روش ضرایب نامعین استفاده می‌کنیم. عبارات زیر را در نظر بگیرید:

$$\large { x = \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } , \; \; } \kern-0.3pt { y = \left ( { { b _ 0 } + { b _ 1} t } \right ){ e ^ { 2 t } } . }$$

مشتقات برابرند با:

$$\large { \frac { { d x } } { { d t } } } = { { a _ 1 } { e^ { 2 t } } + 2 \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ { 2 t } } } = { \left ( { 2 { a _ 0 } + { a _ 1 } + 2 { a _ 1 } t } \right ) { e ^ { 2 t } } , }$$

$$\large { \frac { { d y } }{ { d t } } } = { { b _ 1 } { e ^ { 2 t } } + 2 \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ { 2 t } } } = { \left ( { 2 { b _ 0 } + { b _ 1 } + 2 { b _ 1 } t } \right ) { e ^ { 2 t } } . }$$

با جایگذاری توابع $$x$$ و $$y$$ و مشتق آن‌ها در دستگاه معادلات دیفرانسیل اصلی، داریم:

$$\large \left \{ \begin {array} { l } { \left ( { 2 { a _ 0 } + { a _ 1 } + 2 { a _ 1 } t } \right ){ e ^ { 2 t } } } = { \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } } - { \left ( { { b _ 0 } + { b _ 1 } t } \right ){ e ^ { 2 t } } } \\ { \left ( { 2 { b _ 0 } + { b _ 1 } + 2 { b _ 1 } t } \right ){ e ^ { 2 t } } } = { \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 2 t } } } + { 3 \left ( { { b _ 0 } + { b _ 1 } t } \right ){ e ^ { 2 t } } } \end {array} \right .$$

اکنون با تقسیم دو طرف تساوی بر $$e ^ { 2 t }$$ و برابر قرار دادن ضرایب جملات مشابه دو طرف، خواهیم داشت:

$$ \large { \left \{ \begin {array} { l }<br /> 2 { a _ 0 } + { a _ 1 } = { a _ 0 } – { b _ 0 } \\<br /> 2 { a _ 1 } = { a _ 1 } – { b _ 1 } \\<br /> 2 { b _ 0 } + { b _ 1 } = { a _ 0 } + 3 { b _ 0 } \\<br /> 2 { b _ 1 } = { a _ 1 } + 3 { b _ 1 }<br /> \end {array} \right . , \; \; } \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { a _ 0 } + { a _ 1 } + { b _ 0 } = 0 } \\<br /> { { a _ 1 } + { b _ 1 } = 0 } \\<br /> { { a _ 0 } + { b _ 0 } – { b _ 1 } = 0 } \\<br /> { { a _ 1 } + { b _ 1 } = 0 }<br /> \end {array} } \right . . } $$

در این دستگاه، فقط دو معادله مستقل وجود دارد. ضرایب مستقل $$a_ 0 = C _ 1$$ و $$a _ 1 = C _ 2$$ را در نظر می‌گیریم. دو مقدار باقیمانده $$b _ 0$$ و $$b_ 1$$ برحسب $$C_ 1$$ و $$C_ 2$$ قابل بیان هستند:

$$\large { { C _ 1 } + { C _ 2 } + { b _ 0 } = 0 , \; \; } \Rightarrow { { b _ 0 } = – { C _ 1 } – { C _ 2 } , } \\ \large { { C _ 2 } + { b _ 1 } = 0 , \; \; } \Rightarrow { { b _ 1 } = – { C _ 2 } . }$$

بنابراین، جواب عمومی به فرم زیر خواهد بود:

$$ \large { \mathbf { X } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> x \\<br /> y<br /> \end {array} } \right ] } = { { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 0 } + { a _ 1 } t } \\<br /> { { b _ 0 } + { b _ 1 } t }<br /> \end {array} } \right ] }<br /> = { { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { C _ 1 } + { C _ 2 } t } \\<br /> { – { C _ 1 } – { C _ 2 } – { C _ 2 } t }<br /> \end {array} } \right ] . } $$

و می‌توان آن را به سادگی به فرم برداری زیر نوشت:

$$ \large \begin {align*} \mathbf { X } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } { c } } x \\ y \end {array} } \right ] = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } + { { C _ 2 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } t \\ { – 1 – t } \end {array} } \right ] } \\ & = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } + { { C _ 2 } { e ^ { 2 t} } \left ( { \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ { – 1 } \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ { – 1 } \end {array} } \right ] } \right ) . } \end {align*} $$

مثال ۲: جواب عمومی دستگاه معادلات دیفرانسیل زیر را به دست آورید:

$$\large { \frac { { d x } } { { d t } } = – 2 x – 3 y – 5 z , \; \; } \kern-0.3pt { \frac { { d y } } { { d t } } = x + 4 y + z , \; \; } \kern-0.3pt { \frac { { d z } } { { d t } } = 2 x + 5 z . }$$

حل: ابتدا، مقادیر ویژه دستگاه را با حل معادله مشخصه متناظر آن محاسبه می‌کنیم:

$$ \large { \det \left ( { A – \lambda I } \right ) \text { = }} \kern0pt { \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 2 – \lambda } & { – 3 } & { – 5 } \\<br /> 1 & { 4 – \lambda } & 1 \\<br /> 2 & 0 & { 5 – \lambda }<br /> \end {array} } \right | } = { 0 . } $$

دترمینان را در طول سطر سوم بسط می‌دهیم:

$$ \large \begin {align*} &{ { 2 \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 3 } & { – 5 } \\<br /> { 4 – \lambda } & 1<br /> \end {array} } \right | } + { \left ( { 5 – \lambda } \right ) \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 2 – \lambda } & { – 3 } \\<br /> 1 & { 4 – \lambda }<br /> \end {array} } \right | } = { 0 , \; \; } } \\ & \Rightarrow<br /> { { 2 \left [ { – 3 + 5 \left ( { 4 – \lambda } \right ) } \right ] } + { \left ( { 5 – \lambda } \right ) \cdot } } \kern0pt { { \left [ { \left ( { – 2 – \lambda } \right ) \left ( { 4 – \lambda } \right ) + 3 } \right ] } = { 0 , \; \; } } \\ & \Rightarrow<br /> { { 2 \left ( { – 5 \lambda + 1 7 } \right ) } + { \left ( { 5 – \lambda } \right ) \left ( { { \lambda ^ 2 } – 2 \lambda – 5 } \right ) } } = { { 0 , \; \; } } \\ & \Rightarrow<br /> { { – \color {red} { 1 0 \lambda } + \color {green} { 3 4 } + \color {blue} { 5 { \lambda ^ 2 } } } - { \color {red}{ 1 0 \lambda } – \color {green} { 2 5 } – { \lambda ^ 3 } } } + { { \color {blue} { 2 { \lambda ^ 2 } } + \color {red} { 5 \lambda } = 0 , \; \; } } \\ & \Rightarrow<br /> { { \lambda ^ 3 } – \color {blue} { 7 { \lambda ^ 2 } } } + { \color {red} { 1 5 \lambda } } - { \color {green} 9 = 0 . } \end {align*} $$

یکی از ریشه‌های معادله درجه سه، عدد $$\lambda = 1$$ است. با فاکتور گرفتن از $$(\lambda - 1 )$$، خواهیم داشت:

$$\large \begin {align*} & { { { \lambda ^ 3 } – { \lambda ^ 2 } – 6 { \lambda ^ 2 } } + { 6 \lambda + 9 \lambda – 9 = 0 , \; \; } } \\ & \Rightarrow { { { \lambda ^ 2 } \left ( { \lambda – 1 } \right ) } - { 6 \lambda \left ( { \lambda – 1 } \right ) } } + { { 9 \left ( { \lambda – 1 } \right ) = 0 , \; \; } } \\ & \Rightarrow { { \left ( { \lambda – 1 } \right ) \cdot } \kern0pt { \left ( { { \lambda ^ 2 } – 6 \lambda + 9 } \right ) } = { 0 , \; \; } } \Rightarrow { \left ( { \lambda – 1 } \right ) { \left ( { \lambda – 3 } \right ) ^ 2 } = 0 . } \end {align*}$$

بنابراین، ماتریس دستگاه معادلات دو مقدار ویژه $$\lambda _ 1 = 1$$ با تکرار ۱ و $$\lambda _ 2 = 3$$ با تکرار ۲ خواهد داشت.

ریشه اول $$\lambda _ 1 = 1$$ را در نظر گرفته و جواب عمومی $${\mathbf{X}_1}$$ متناظر با این مقدار ویژه را به دست می‌آوریم. برای این کار، بردار ویژه متناظر $${\mathbf{V}_1}$$ را محاسبه می‌کنیم. دستگاه معادلات تعیین درایه‌های $${\mathbf{V}_1}$$ به صورت زیر است:

$$ \large { { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 2 – 1 } & { – 3 } & { – 5 } \\<br /> 1 & { 4 – 1 } & 1 \\<br /> 2 & 0 & { 5 – 1 }<br /> \end {array} } \right ] \cdot } \kern0pt { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 1 } } } \\<br /> { { V _ { 2 1 } } } \\<br /> { { V _ { 3 1 } } }<br /> \end {array} } \right ] = \mathbf { 0 } , \; \; } } \Rightarrow<br /> { { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 3 } & { – 3 } & { – 5 } \\<br /> 1 & 3 & 1 \\<br /> 2 & 0 & 4<br /> \end {array} } \right ] \cdot } \kern0pt { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 1 } } } \\<br /> { { V _ { 2 1 } } } \\<br /> { { V _ { 3 1 } } }<br /> \end {array} } \right ] = \mathbf { 0 } . } } $$

دستگاه را به شکل زیر ساده می‌کنیم:

$$ \large { \left \{ \begin {array} { l }<br /> – 3 { V _ { 1 1 } } – 3 { V _ { 2 1 } } – 5 { V _ { 3 1 } } = 0\\<br /> { V _ { 1 1 } } + 3 { V _ { 2 1 } } + { V _ { 3 1 } } = 0 \\<br /> 2 { V _ { 1 1 } } + 4 { V _ { 3 1 } } = 0<br /> \end {array} \right . , \; \; } \Rightarrow<br /> { { { \left \{ \begin {array} { l }<br /> { V _ { 1 1 } } + 3 { V _ { 2 1 } } + { V _ { 3 1 } } = 0 \\<br /> – 3 { V _ { 1 1 } } – 3 { V _ { 2 1 } } – 5 { V _ { 3 1 } } = 0 \\<br /> 2 { V _ { 1 1 } } + 4 { V _ { 3 1 } } = 0<br /> \end {array} \right . } , \; \; } } \\ \large \Rightarrow<br /> { \left \{ \begin {array} { l }<br /> { V _ { 1 1 } } + 3 { V _ { 2 1 } } + { V _ { 3 1 } } = 0 \\<br /> 0 + 6 { V _ { 2 1 } } – 2 { V _ { 3 1 } } = 0 \\<br /> 0 – 6 { V _ { 2 1 } } + 2 { V _ { 3 1 } } = 0<br /> \end {array} \right . , \; \; } \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { V _ { 1 1 } } + 3 { V _ { 2 1 } } + { V _ { 3 1 } } = 0 } \\<br /> { 3 { V _ { 2 1 } } – { V _ { 3 1 } } = 0 }<br /> \end {array} } \right . . } $$

متغیر مستقل $${V_{31}} = t$$ را در نظر می‌گیریم و مختصات باقیمانده را بر حسب $$t$$ به صورت زیر می‌نویسیم:

$$\large { 3 { V _ { 2 1 } } = { V _ { 3 1 } } = t , \; \; } \Rightarrow { { V _ { 2 1 } } = \frac { t } { 3 } , \; \; } \\ \large \Rightarrow { { V _ { 1 1 } } = – { V _ { 3 1 } } – 3 { V _ { 2 1 } } } = { – t – 3 \cdot \frac { t } { 3 } } = { – 2 t . }$$

بنابراین، بردار ویژه $${\mathbf{V}_1}$$ برابر است با:

$$ \large { { \mathbf { V } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ {1 1 } } } \\<br /> { { V _ { 2 1 } } } \\<br /> { { V _ { 3 1 } } }<br /> \end {array} } \right ] }<br /> = { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 2 t } \\<br /> { \frac { t } { 3 } } \\<br /> t<br /> \end {array} } \right ] }<br /> \sim { t \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 6 } \\<br /> 1 \\<br /> 3<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 6 } \\<br /> 1 \\<br /> 3<br /> \end {array} } \right ] . } $$

در نتیجه، مقدار ویژه $${\lambda _1} = 1$$، جواب عمومی زیر را می‌سازد:

$$ \large { { \mathbf { X } _ 1 } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> x \\<br /> y \\<br /> z<br /> \end {array} } \right ] }<br /> = { { C _ 1 } { e ^ { { \lambda _ 1 } t } } { \mathbf { V } _ 1 } }<br /> = { { C _ 1 } { e ^ { { \lambda _ 1 } t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 6 } \\<br /> 1 \\<br /> 3<br /> \end {array} } \right ] . } $$

اکنون مقدار ویژه $${\lambda _2} = 3$$ را با تکرار $${k_2} = 2$$ در نظر می‌گیریم. رتبه ماتریس را در $${\lambda _2} = 3$$ به دست می‌آوریم:

$$ \large { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 2 – 3 } & { – 3 } & { – 5 } \\<br /> 1 & { 4 – 3 } & 1 \\<br /> 2 & 0 & { 5 – 3 }<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 5 } & { – 3 } & { – 5 } \\<br /> 1 & 1 & 1 \\<br /> 2 & 0 & 2<br /> \end {array} } \right ] }<br /> \\ \large \sim { { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 & 1 \\<br /> 2 & 0 & 2 \\<br /> { – 5 } & { – 3 } & { – 5 }<br /> \end {array} } \right ] } }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 & 1 \\<br /> 0 & { – 2 } & 0 \\<br /> 0 & 2 & 0<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & 1 & 1 \\<br /> 0 & 2 & 0<br /> \end {array} } \right ] . } $$

می‌بینیم که $$\text{rank}\left( {A – {\lambda _2}I} \right) = 2$$. بنابراین، عدد $${\lambda _2} = 3$$ با مرتبه تکرار هندسی $${s_2} = 1$$ مشخص شده و یک بردار ویژه دارد:

$$\large { { s _ 2 } } = { n – \text {rank} \left ( { A – { \lambda _ 2 } I } \right ) } = { 3 – 2 = 1 . }$$

به دنبال جواب عمومی متناظر با مقدار ویژه $$\lambda _ 2$$ به صورت تابع زیر هستیم:

$$\large { { \mathbf { X } _ 2 } \left ( t \right ) } = { { \mathbf { P } _ { { k _ 2 } – { s _ 2 } } } \left ( t \right ) { e ^ { { \lambda _ 2 } t } } } = { \left ( { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t } \right ) { e ^ { 3 t } } , }$$

که در آن، چندجمله‌ای برداری $${\mathbf{P}_{{k_2} – {s_2}}}\left( t \right)$$ دارای مرتبه $${k_2} – {s_2} = 1$$ است. با قرار دادنِ

$$ \large { { \mathbf { A } _ 0 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 0 } } \\<br /> { { b _ 0 } } \\<br /> { { d _ 0 } }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { A } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } \\<br /> { { b _ 1 } } \\<br /> { { d _ 1 } }<br /> \end {array} } \right ] , } $$

فرمول‌های مختصات $${\mathbf{X}_2}$$ را می‌نویسیم:

$$\large { x = \left ( { { a _ 0 } + { a _ 1 } t } \right ){ e ^ { 3 t } } , \; \; } \kern-0.3pt { y = \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ { 3 t } } , \; \; } \kern-0.3pt { z = \left ( { { d _ 0 } + { d _ 1 } t } \right ) { e ^ { 3 t } } . }$$

مشتق این توابع به صورت زیر است:

$$\large \begin {align*} \frac { { d x } } { { d t } } = { { a _ 1 } { e ^ { 3 t } } + 3 \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ { 3 t } } , \; \; } \kern-0.3pt \\ { { \frac { { d y } } { { d t } } } = { b _ 1 } { e ^ { 3 t } } + 3 \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ { 3 t } } , \; \; } \kern-0.3pt \\{ { \frac { { d z } } { { d t } } } = { { d _ 1 } { e ^ { 3 t } } + 3 \left ( { { d _ 0 } + { d _ 1 } t } \right){ e ^ { 3 t } } . } } \end {align*}$$

با جایگذاری این عبارات در دستگاه اصلی و تقسیم بر $$e ^ { 3 t}$$، داریم:

$$\large \left \{ \begin {array} { l } { { a _ 1 } + 3 \left ( { { a _ 0 } + { a _ 1 } t } \right ) } = { – 2 \left ( { { a _ 0 } + { a _ 1 } t } \right ) } - { 3 \left ( { { b _ 0 } + { b _ 1 } t } \right ) } - { 5 \left ( { { d _ 0 } + { d _ 1 } t } \right ) } \\ { { b _ 1 } + 3 \left ( { { b _ 0 } + { b _ 1 } t } \right ) } = { { a _ 0 } + { a _ 1 } t } + { 4 \left ( { { b _ 0 } + { b _ 1 } t } \right ) } + { { d _ 0 } + { d _ 1 } t } \\ { { d _ 1 } + 3 \left ( { { d _ 0 } + { d _ 1 } t } \right ) } = { 2 \left ( { { a _ 0 } } + { { a _ 1 } t } \right ) } + { 5 \left ( { { d _ 0 } + { d _ 1 } t } \right ) } \end {array} \right .$$

با برابر قرار دادن ضرایب توان‌های مشابه $$t$$ در دو طرف تساوی، دستگاهی با شش معادله و شش مجهول $$a_0$$، $$a_1$$، $$b _ 0$$، $$b_1$$، $$d_0$$ و $$d_1$$ خواهیم داشت:

$$\large { \left \{ \begin {array} { l } { a _ 1 } + 3 { a _ 0 } = – 2 { a _ 0 } – 3 { b _ 0 } – 5 { d _ 0 } \\ 3 { a _ 1 } = – 2 { a _ 1 } – 3 { b _ 1 } – 5 { d _ 1 } \\ { b _ 1 } + 3 { b _ 0 } = { a _ 0 } + 4 { b _ 0 } + { d _ 0 } \\ 3 { b _ 1 } = { a _ 1 } + 4 { b _ 1 } + { d _ 1 } \\ { d _ 1 } + 3 { d _ 0 } = 2 { a _ 0 } + 5 { d _ 0 } \\ 3 { d _ 1 } = 2 { a _ 1 } + 5 { d _ 1 } \end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} { l } 5 { a _ 0 } + { a _ 1 } + 3 { b _ 0 } + 5 { d _ 0 } = 0 \\ 5 { a _ 1 } + 3 { b _ 1 } + 5 { d _ 1 } = 0 \\ { a _ 0 } + { b _ 0 } – { b _ 1 } + { d _ 0 } = 0 \\ { a _ 1 } + { b _ 1 } + { d _ 1 } = 0 \\ 2 { a _0 } + 2 { d _ 0 } – { d _ 1 } = 0 \\ { a _ 1 } + { d _ 1 } = 0 \end {array} \right . . }$$

در این دستگاه، تنها دو مورد از ضرایب مستقل هستند. این به این موضوع بر می‌گردد که $${\lambda_2} = 3$$ دارای مرتبه تکرار ۲ است و بنابراین، باید دو جواب مستقل خطی داشته باشیم. متغیرهای $$a_0$$ و $$a_ 1$$ را به صورت دلخواه انتخاب می‌کنیم:

$$\large { a _ 0 } = { C _ 2 } , \; \; { a _ 1 } = 2 { C _ 3 } .$$

که در آن، $$C_ 2$$ و $$C_ 3$$ اعداد دلخواهی هستند و ضریب ۲ برای خلاص شدن از کسرها است. ضرایب باقیمانده را به راحتی می‌توان به صورت زیر نوشت:

$$\large { { a _ 0 } = { _ 2 } , \; \; { b _0 } = { C _ 3 } , \; \; } \kern-0.3pt { { d _ 0 } = – { C _ 3 } – { C _ 2 } , \; \;} \kern-0.3pt { { a _ 1 } = 2 { C _ 3 } , \; \; } \kern-0.3pt { { b _ 1 } = 0 , \; \; } \kern-0.3pt { { d _ 1 } = – 2 { C _ 3 } . }$$

در نتیجه، بخش جواب عمومی متناظر با مقدار ویژه $$\lambda _ 2 = 3$$ را می‌توان به صورت زیر نوشت:

$$\large \left \{ \begin {array} { l } { x \left ( t \right ) } = { \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ { { \lambda _ 2 } t } } } = { \left ( { { C _ 2 } + 2 { C _ 3 } t } \right ) { e ^ { 3 t } } } \\ { y \left ( t \right ) } = { \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ { { \lambda _ 2 } t } } } = { { C _ 3 } { e ^ { 3 t } } } \\ { z \left ( t \right ) } = { \left ( { { d _ 0 } + { d _ 1 } t } \right) { e ^ { { \lambda _ 2 } t } } } = { \left ( { – {C_3} – { C _ 2 } – 2 { C _ 3 } t } \right ) { e ^ { 3 t } } } \end {array} \right . .$$

جواب را به فرم برداری زیر بازنویسی می‌کنیم:

$$ \large \begin {align*} { \mathbf { X } _ 2 } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } { c } } x \\ y \\ z \end {array} } \right ] = { { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 } { c } } { { C _ 2 } + 2 { C _ 3 } t } \\ { { C _ 3 } } \\ { – { C _ 3 } – { C _ 2 } – 2 { C _ 3 } t } \end {array} } \right ] } \\ & = { { C _ 2 } { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ 0 \\ { – 1 } \end {array} } \right ] } + { { C _ 3 } { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 } { c } } { 2 t } \\ 1 \\ { – 1 – 2 t } \end {array} } \right ] } \\ & = { { C _ 2 } { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ 0 \\ { – 1 } \end {array} } \right ] } + { { C _ 3 } { e ^ { 3 t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ 1 \\ { – 1 } \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 2 \\ 0 \\ { – 2 } \end {array} } \right ] } \right ) . } \end {align*} $$

در نهایت، جواب عمومی دستگاه به صورت زیر به دست می‌آید:

$$ \large \begin {align*} \mathbf { X } \left ( t \right ) = { \mathbf { X } _ 1 } \left ( t \right ) + { \mathbf { X } _ 2 } \left ( t \right ) = { { C _ 1 } { e ^ t } \left [ { \begin {array} { * { 2 0 } { c } } { – 6 } \\ 1 \\ 3 \end {array} } \right ] } + { { C _ 2 } { e ^ { 3 t } } \left [ { \begin {array}{ * { 2 0 } { c } } 1 \\ 0 \\ { – 1 } \end {array} } \right ] } + { { C _ 3 } { e ^ { 3 t } } \left ( { \left [ { \begin {array}{ * { 2 0 } { c } } 0 \\ 1 \\ { – 1 } \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 2 \\ 0 \\ { – 2 } \end {array} } \right ] } \right ) . } \end {align*} $$

مثال ۳: دستگاه معادلات زیر را حل کنید:

$$\large { \frac { { d x } } { { d t } } = – 6 x + 5 y , \; \; } \kern-0.3pt { \frac { { d y } } { { d t } } = – 2 x – y + 5 z , \; \; } \kern-0.3pt { \frac { { d z } } { { d t } } = x – 3 y + 4 z . }$$

حل: ابتدا مقادیر ویژه دستگاه را محاسبه می‌کنیم:

$$ \large { \det \left ( { A – \lambda I } \right ) \text { = }} \kern0pt{ \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 6 – \lambda } & 5 & 0 \\<br /> { – 2 } & { – 1 – \lambda } & 5 \\<br /> 1 & { – 3 } & { 4 – \lambda }<br /> \end {array} } \right | = 0 . } $$

دترمینان را در سطر اول گسترش می‌دهیم:

$$ \large { { \left ( { – 6 – \lambda } \right ) \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 1 – \lambda } & 5 \\<br /> { – 3 } & { 4 – \lambda }<br /> \end {array} } \right | } - { 5 \left | { \begin {array} { * { 2 0 } { c } }<br /> { – 2 } & 5 \\<br /> 1 & { 4 – \lambda }<br /> \end {array} } \right | = 0 , \; \; } } \\ \large \Rightarrow<br /> { { \left ( { – 6 – \lambda } \right ) \cdot } \kern0pt { \left [ { \left ( { – 1 – \lambda } \right ) \left ( { 4 – \lambda } \right ) + 1 5 } \right ] } }<br /> – { { 5 \left [ { – 2 \left ( { 4 – \lambda } \right ) – 5 } \right ] = 0 , \; \; } } \\ \large \Rightarrow<br /> { { \left ( { \lambda + 6 } \right ) \left ( { { \lambda ^ 2 } – 3 \lambda + 1 1 } \right ) } } + { { 5 \left ( { 2 \lambda – 1 3 } \right ) = 0 , \; \; } } \\ \large \Rightarrow<br /> { { { \lambda ^ 3 } + \color {blue} { 6 { \lambda ^ 2 } } – \color {blue} { 3 { \lambda ^ 2 } } } - { \color {red}{ 1 8 \lambda } + \color {red} { 1 1 \lambda } + \color {green} { 6 6 } } } + { { \color {red} { 1 0 \lambda } – \color {green}{ 6 5 } = 0 , \; \; } } \\ \large \Rightarrow<br /> { { \lambda ^ 3 } + \color {blue} { 3 { \lambda ^ 2 } } + \color {red} { 3 \lambda } + \color {green} 1 = 0 , \; \; } \Rightarrow<br /> { { \left ( { \lambda + 1 } \right ) ^ 3 } = 0 . } $$

بنابراین، ماتریس دارای مقدار ویژه $${\lambda _1} = – 1$$ با مرتبه تکرار $${k_1} = 3$$ است. اکنون رتبه ماتریس را در $${\lambda _1} = – 1$$ و مرتبه تکرار هندسی $$s_ 1$$ به دست می‌آوریم:

$$ \large { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 6 + 1 } & 5 & 0 \\<br /> { – 2 } & { – 1 + 1 } & 5 \\<br /> 1 & { – 3 } & { 4 + 1 }<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 5 } & 5 & 0 \\<br /> { – 2 } & 0 & 5 \\<br /> 1 & { – 3 } & 5<br /> \end {array} } \right ] } \\ \large<br /> \sim { { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 5 } & 5 & 0 \\<br /> { – 2 } & 0 & 5 \\<br /> 1 & { – 3 } & 5<br /> \end {array} } \right ] } }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & { – 3 } & 5 \\<br /> 0 & { – 2 } & 5 \\<br /> 0 & { – 6 } & { 1 5 }<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 & { – 3 } & 5 \\<br /> 0 & { – 2 } & 5<br /> \end {array} } \right ] . } $$

در نتیجه، $$\text{rank}\left( {A – {\lambda _1}I} \right) = 2$$ خواهد بود. بر این اساس، مرتبه تکرار هندسی (و تعداد بردار ویژه‌ها) برای مقدار ویژه $${\lambda _1} = – 1$$ برابر است با:

$$\large { { s _ 1 } } = { n – \text {rank} \left ( { A – { \lambda _ 1 } I } \right ) } = { 3 – 2 = 1 . }$$

با این حساب، ما به دنبال جواب عمومی $$\mathbf{X}$$ به فرم یک تابع برداری هستیم:

$$\large { \mathbf { X } \left ( t \right ) } = { { \mathbf { P } _ { { k _ 1 } – { s _ 1 } } } \left ( t \right ) { e ^ { { \lambda _ 1 } t } } } = { \left ( { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t + { \mathbf { A } _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } . }$$

بردارهای $${\mathbf{A}_0}$$، $${\mathbf{A}_1}$$ و $${\mathbf{A}_2}$$‌ دارای مختصات زیر هستند:

$$ \large { { \mathbf { A } _ 0 } = \left [ { \begin {array} { * { 2 0 } {c } }<br /> { { a _ 0 } } \\<br /> { { b _ 0 } } \\<br /> { { d _ 0 } }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { A } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } \\<br /> { { b _ 1 } } \\<br /> { { d _ 1 } }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { A } _ 2 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 2 } } \\<br /> { { b _ 2 } } \\<br /> { { d _ 2 } }<br /> \end {array} } \right ] . } $$

توابع مختصات را می‌نویسیم و مشتق آن‌ها را محاسبه می‌کنیم:

$$\large \begin {align*} x \left ( t \right ) & = { \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ y \left ( t \right ) & = { \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ z \left ( t \right ) & = { \left ( { { d _ 0 } + { d _ 1 } t + { d _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ { \frac { { d x } } { { d t } } } & = { \left ( { { a _ 1 } + 2 { a _ 2 } t } \right ) { e ^ { – t } } } – { \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ { \frac { { d y } } { { d t } } } & = { \left ( { { b _ 1 } + 2 { b _ 2 } t } \right ) { e ^ { – t } } } – { \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ { \frac { { d z } } { { d t } } } & = { \left ( { { d _ 1 } + 2 { d _ 2 } t } \right ) { e ^ { – t } } } – { \left ( { { d _ 0 } + { d _ 1 } t + { d _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } . } \end {align*}$$

با قرار دادن در دستگاه اصلی و تقسیم دو طرف معامله بر تابع نمایی $${e^{ – t}}$$، خواهیم داشت:

$$\large { { a _ 1 } + 2 { a _ 2 } t – { a _ 0 } } - { { a _ 1 } t – { a _ 2 } { t ^ 2 } } = { – 6 \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) } + { 5 \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) }$$

$$\large \begin {align*} { { b _ 1 } + 2 { b _ 2 } t – { b _ 0 } } - { { b _ 1 } t – { b _ 2 } { t ^ 2 } } = & { – 2 \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) } – { \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) } \\ & + { 5 \left ( { { d _ 0 } + { d _ 1 } t + { d _ 2 } { t ^ 2 } } \right ) } \end {align*}$$

$$\large \begin {align*} { { d _ 1 } + 2 { d _ 2 } t – { d _ 0 } } - { { d _ 1 } t – { d _ 2 } { t ^ 2 } } = & { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } – { 3 \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) } \\ & + { 4 \left ( { { d _ 0 } + { d _ 1 } t + { d _ 2 } { t ^ 2 } } \right ) . } \end {align*}$$

با برابر قرار دادن جملات مشابه توان‌های $$t$$ در دو طرف تساوی، دستگاه ۹ معادله‌ای زیر را خواهیم داشت:

$$\large { \left \{ \begin {array} { l } { a _ 1} – { a _ 0 } = – 6 { a _ 0 } + 5 { b _ 0 } \\ 2 { a _ 2 } – { a _ 1 } = – 6 { a _ 1 } + 5 { b _ 1 } \\ – { a _ 2 } = – 6 { a _ 2 } + 5 { b _ 2 } \\ { b _ 1 } – { b _ 0 } = – 2 { a _ 0 } – { b _ 0 } + 5 { d _ 0 } \\ 2 { b _ 2 } – { b _ 1 } = – 2 { a _ 1 } – { b _ 1 } + 5 { d _ 1 } \\ – { b _ 2 } = – 2 { a _ 2 } – { b _ 2 } + 5 { d _ 2 } \\ { d _ 1 } – { d _ 0 } = { a _ 0 } – 3 { b _ 0 } + 4 { d _ 0 } \\ 2 { d _ 2 } – { d _ 1 } = { a _ 1 } – 3 { b _ 1 } + 4 { d _ 1 } \\ – { d _ 2 } = { a _ 2 } – 3 { b _ 2 } + 4 { d _ 2 } \end {array} \right . , \; \; } \Rightarrow { \left \{ \begin {array} { l } 5 { a _ 0 } + { a _ 1 } – 5 { b _ 0 } = 0 \\ 5 { a _ 1 } + 2 { a _ 2 } – 5 { b _ 1 } = 0 \\ { a _ 2 } – { b _ 2 } = 0 \\ 2 { a _ 0 } + { b _ 1 } – 5 { d _ 0 } = 0 \\ 2 { a _ 1 } + 2 { b _ 2 } – 5 { d _ 1 } = 0 \\ 2 { a _ 2 } – 5 { d _ 2 } = 0 \\ { a _ 0 } – 3 { b _ 0 } + 5 { d _ 0 } – { d _ 1 } = 0 \\ { a _ 1 } – 3 { b _ 1 } + 5 { d _ 1 } – 2 { d _ 2 } = 0 \\ { a _ 2 } – 3 { b _ 2 } + 5 { d _ 2 } = 0 \end {array} \right . }$$

این دستگاه فقط سه متغیر مستقل دارد. این از این موضوع ناشی می‌شود که $$\mathbf{X}$$ باید شامل سه تابع مستقل خطی باشد. متغیرهای مستقل زیر را انتخاب می‌کنیم:

$$\large { { a _ 0 } = { C _ 1 } , \; \; } \kern-0.3pt { { a _ 1 } = { C _ 2 } , \; \; } \kern-0.3pt { { a _ 2 } = {C _ 3 } . }$$

سایر متغیرها را برحسب $$C_1$$، $$C_2$$ و $$C_3$$ می‌نویسیم:

$$\large { 5 { b _ 0 } = 5 { a _ 0 } + { a _ 1 } } = { 5 { C _ 1 } + { C _ 2 } , \; \; } \Rightarrow { { b _ 0 } = { C _ 1 } + \frac { 1 } { 5 } { C _ 2 } ; } \\ \large { 5 { b _ 1 } = 5 { a _ 1 } + 2 { a _ 2 } } = { 5 { C _ 2 } + 2 { C _ 3 } , \; \; } \Rightarrow { { b _ 1 } = { C _ 2 } + \frac { 2 } { 5 } { C _ 3 } ; } \\ \large { b _ 2 } = { a _ 2 } = { C _ 3 } ; \\ \large { 5 { d _ 0 } = 2 { a _ 0 } + { b _ 1 } } = { 2 { C _ 1 } + { C _ 2 } + \frac { 2 } { 5 } { C _ 3 } , \; \; } \Rightarrow { { d _ 0 } = \frac { 2 } { 5 } { C _ 1 } + \frac { 1 } { 5 }{ C _ 2 } + \frac { 2 } { { 2 5 } } { C _ 3 } ; } \\ \large { 5 { d _ 1 } = 2 { a _ 1 } + 2 { b _ 2 } } = { 2 { C _ 2 } + 2 { C _ 3 } , \; \; } \Rightarrow { { d _ 1 } = \frac { 2 } { 5 } { C _ 2 } + \frac { 2 } { 5 } { C _ 3 } ; } \\ \large { 5 { d _ 2 } = 2 { a _ 2 } = 2 { C _ 3 } , \; \; } \Rightarrow { { d _ 2 } = \frac { 2 } { 5 } { C _ 3 } . }$$

بنابراین، جواب عمومی را می‌توان به صورت زیر نوشت:

$$\large \begin {align*} { x \left ( t \right ) } & = { \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } } = { \left ( { { C _ 1 } + { C _ 2 } t + { C _ 3 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ { y \left ( t \right ) } & = { \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } } = { \left ( { { C _ 1 } + { \frac { 1 } { 5 } { C _ 2 } } } \right . } + { \left . { \left ( { { C _ 2 } + \frac { 2 } { 5 } { C _ 3 } } \right ) t } \right . } + { \left . { { C _ 3 } { t ^ 2 } } \right ) { e ^ { – t } } , } \\ { z \left ( t \right ) } & = { \left ( { { d _ 0 } + { d _ 1 } t + { d _ 2 } { t ^ 2 } } \right ) { e ^ { – t } } } = { \left ( { \frac { 2 } { 5 } { C _ 1 } + \frac { 1 } { 5 } { C _ 2 } + \frac { 2 } { { 2 5 } } { C _ 3 } }\right . } + { \left . { \left ( { \frac { 2 } { 5 } { C _ 2 } + \frac { 2 } { 5 } { C _ 3 } } \right ) t } \right . } + { \left . { \frac { 2 } { 5 } { C _ 3 } { t ^ 2 } } \right ) { e ^ { – t } } . } \end {align*}$$

جواب را با مشخص کردن بردارهای مستقل خطی صریح به صورت بردار نشان می‌دهیم:

$$ \large { \mathbf { X } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } } x \\ y \\ z \end {array} } \right ] } = { { C _ 1 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } 1 \\ 1 \\ { \frac { 2 } { 5 } } \end {array} } \right ] } + { { C _ 2 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } t \\\ { \frac { 1 } { 5 } + t } \\ { \frac { 1 } { 5 } + \frac { 2 } { 5 } t } \end {array} } \right ] } + { { C _ 3 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } { { t ^ 2 } } \\ { \frac { 2 } { 5 } t + { t ^ 2 } } \\ { \frac { 2 } { { 2 5 } } + \frac { 2 } { 5 } t + \frac { 2 } { 5 } { t ^ 2 } } \end{array} } \right ] . } $$

اعداد $$C_1$$، $$C_2$$ و $$C_ 3$$ را دوباره نرمالیزه می‌کنیم:

$$\large { { C _ 1 } \to 5 { C _ 1 } , \; \; } \kern-0.3pt { { C _ 2 } \to 5 { C _ 2 } , \; \; } \kern-0.3pt { { C _ 3 } \to 2 5 { C _ 3 } . }$$

در نتیجه، جواب به صورت زیر نوشته می‌شود:

$$ \large \begin {align*} \mathbf { X } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } { c } } x \\ y \\ z \end {array} } \right ] = { { C _ 1 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } 5 \\ 5 \\ 2 \end {array} } \right ] } + { { C _ 2 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } { 5 t } \\ { 1 + 5 t } \\ { 1 + 2 t } \end {array} } \right ] } + { { C _ 3 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } { 2 5 { t ^ 2 } } \\ { 1 0 t + 2 5 { t ^ 2 } } \\ { 2 + 1 0 t + 1 0 { t ^ 2 } } \end {array} } \right ] } \\ & = { { C _ 1 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } } 5 \\ 5 \\ 2 \end {array} } \right ] } + { { C _ 2 } { e ^ { – t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ 1 \\ 1 \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 5 \\ 5 \\ 2 \end {array} } \right ] } \right ) } + { { C _ 3 } { e ^ { – t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ 0 \\ 2 \end {array} } \right ] + t \left [ { \begin {array} { * { 2 0 } { c } } 0 \\ { 1 0 } \\ { 1 0 } \end {array} } \right ] } \right . } + { \left . { { t ^ 2 } \left [ { \begin {array} { * { 2 0 } { c } } { 2 5 } \\ { 2 5 } \\ { 1 0 } \end {array} } \right ] } \right ) . } \end {align*} $$

جواب عمومی شامل سه بردار مستقل خطی است:‌

$$ \large { { \mathbf { V } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } } 5 \\ 5 \\ 2<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { V } _ 2 } = \left [ { \begin {array} { * { 20 } { c } } 0 \\ 0 \\ 1<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { V } _ 3 } = \left [ { \begin {array} { * { 2 0 } {c } }<br /> 0 \\<br /> 1 \\<br /> 1<br /> \end {array} } \right ] . } $$

سایر بردارها نسبت‌ به بردارهای مشخص شده هم‌خطی هستند. از بین این سه بردار، $$\mathbf{V}_1$$ یک بردار ویژه معمولی است و بردارهای ویژه $${\mathbf{V}_2}$$ و $${\mathbf{V}_3}$$ بردارهای ویژه تعمیم‌یافته نامیده می‌شوند. فرم جواب عمومی با ساختاری موسوم به ماتریس جردن دستگاه مشخص می‌شود.