مزدوج مختلط – به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در مطالب گذشته وبلاگ فرادرس اعداد مختلط معرفی شدند. همان‌طور که در مطلب مذکور نیز بیان شد، اعداد مختلط دسته ویژه‌ای از اعداد هستند که از ترکیب یک عدد حقیقی و یک عدد موهومی تشکیل شده‌اند. در این مطلب قصد داریم تا مزدوج مختلط این اعداد را معرفی کنیم.

مزدوج مختلط

در ریاضیات، مزدوج مختلطِ یک عدد مختلط به عددی گفته می‌شود که بخش حقیقی آن برابر با عدد مختلط اصلی و بخش موهومی آن منفی بخش موهومیِ عدد مختلط است. برای نمونه عدد مختلط زیر را در نظر بگیرید.

$$3 + 4 i$$

بنابراین مزدوج مختلط عدد فوق برابر است با:

$$3 - 4 i$$

اما اعداد فوق در قالب مختصات کارتزینی توضیح داده شدند. حال عدد مختلط زیر را در نظر بگیرید که به صورت قطبی بیان شده است.

$$\large { \displaystyle r e ^ { i \varphi } }$$

با استفاده از فرمول اویلر عدد فوق را می‌توان به صورت زیر بیان کرد:

$$\large { \displaystyle r e ^ { i \varphi } = \cos \phi + i \sin \phi }$$

در این رابطه $$e$$ نشان‌دهنده پایه لگاریتم طبیعی بوده و $$i$$، بردار یکه مختلط است. با توجه به تعریف، مزدوج مختلط را می‌توان به صورت زیر بیان کرد:

$$\large \cos \phi - i \sin \phi$$

عبارت فوق نیز برابر است با:

$$\large { } {\displaystyle r e ^ { - i \varphi } }$$

مزدوج مختلط در یافتن ریشه‌های چندجمله‌‌ای‌هایِ با درجات بالا کاربرد دارند. توجه داشته باشید که همواره پاسخ‌های مختلط یک چند جمله‌‌ای به صورت مزدوج مختلط هستند.

$$\large x ^ 2 + 4 x + 5 = 0$$

ریشه‌های معادله زیر برابرند با:

$$\large x _ 1 = -2 + i$$
$$\large x _ 2 = -2 - i$$

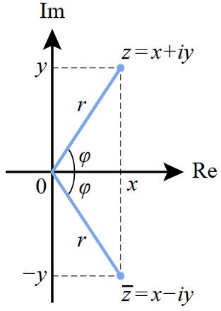
بنابراین با توجه به توضیحات متوجه شده‌اید که مزدوج مختلط دو بردار نسبت به محور حقیقی (یا همان $$x$$) قرینه یکدیگر هستند. برای نمونه در نمودار زیر یک جفت مزدوج مختلط نشان داده شده است.

نماد‌گذاری

مزدوج مختلطِ $$z$$ را معمولا با نماد‌های $$\bar { z }$$ یا $${ z } ^ { * }$$ نشان می‌دهند. معمولا از نماد دوم در فیزیک استفاده می‌شود. البته در برخی از موارد از $$c . c$$ نیز به منظور نشان دادن مزدوج مختلط استفاده می‌شود. برای نمونه:

$$\large e ^ { i \varphi } + c . c \ \equiv \ e ^ { i \varphi } + e ^ { - i \varphi }$$

فیلم آموزش ریاضی مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

ویژگی‌ها

ویژگی‌های زیر به ازای تمامی اعداد مختلطِ $$z , w$$ صادق هستند. توجه داشته باشید که این اعداد در قالب $$a + i b$$ قرار دارند. یک ویژگی منحصر به فرد در مورد اعداد مختلط این است که زمانی این عدد با مزدوج مختلطش برابر است که بخش موهومی آن برابر با صفر باشد. در ادامه مهم‌ترین ویژگی‌های اعداد مزدوج مختلط ارائه شده‌اند.

$$\large { \displaystyle { \begin {aligned} { \overline { z + w } } & = { \overline { z } } + { \overline { w } } \\ { \overline { z - w } } & = { \overline { z } } - { \overline { w } } \\ { \overline { z w } } & = { \overline { z } } \; { \overline { w } } \\ { \overline { \left ( { \frac { z } { w } } \right ) } } & = { \frac { \overline { z } }{ \overline { w } } } ,\quad {\text{if }}w\neq 0\\{\overline { z } } & = z ~ \Leftrightarrow ~z\in \mathbb {R} \\{\overline { z ^ { n } } } & = \left({\overline { z } } \right ) ^ { n } ,\quad \forall n\in \mathbb {Z} \\\left|{\overline { z } } \right|&=\left|z\right|\\{ \left|z\right|} ^ { 2 } & = z { \overline { z } } = { \overline {z}}z\\{ \overline {\overline { z } } } & = z \\ z ^ { - 1} & = { \frac { \overline { z } } { { \left|z\right|} ^ { 2 } } } ,\quad \forall z\neq 0\end {aligned} } }$$

اگر مزدوج مختلطِ یک عدد، توانِ تابعی نمایی یا پایه تابعی لگاریتمی باشد، در این صورت به منظور محاسبه مزدوج مختلط تابع، می‌توان مزدوج مختلط عدد را از تابع بیرون کشید. در حقیقت می‌توان گفت:

$$\large { \displaystyle \exp \left ( { \overline { z } } \right ) ={ \overline { \exp ( z ) } } \, \!}$$
$$\large { \displaystyle \log \left ( { \overline { z } } \right ) = { \overline { \log ( z ) } } \, \! }$$

اگر $$p$$ چندجمله‌ای با ضرایب حقیقی بوده و $$p ( z ) = 0$$، در این صورت $$p ( \bar z ) = 0$$ نیز برقرار است. در نتیجه ریشه‌های غیرحقیقی $$p$$، به صورت مختلط هستند. در حالتی کلی اگر $$\phi$$ تابعی تحلیلی و مختلط باشد، در این صورت می‌توان رابطه زیر را برای مختلط آن بیان کرد:

$$\large { \displaystyle \varphi \left ( { \overline { z } } \right ) = { \overline { \varphi ( z ) } } \,\! }$$

استفاده از متغیر

فرض کنید عدد مختلط $$z = x + i y$$ یا $$z = r e ^ { i \theta }$$ داده شده باشد. در این صورت بخش‌های مختلف این عدد را می‌توان با استفاده از مفهوم مزدوج مختلط به صورت زیر بیان کرد:

$$\large { \displaystyle x = \operatorname { R e } ( z ) = { \dfrac { z+ { \overline { z } } } { 2 } } }$$

$$\large { \displaystyle y = \operatorname { I m } ( z ) = { \dfrac { z - { \overline { z } } } { 2 i } } }$$

$$\large { \displaystyle r = \left| z \right| = { \sqrt { z { \overline { z } } } } }$$

$$\large { \displaystyle e ^ { i \theta } = e ^ { i \arg z } = { \sqrt { \dfrac { z }{ \overline { z } } } } }$$

$$\large { \displaystyle \theta = \arg z = { \dfrac { 1 } { i } } \ln { \sqrt { \frac { z } { \overline { z } } } } = { \dfrac { \ln z - \ln { \overline { z } } } {2 i } } }$$

علاوه بر موارد ارائه شده در بالا، می‌توان از مزدوج مختلط به منظور شناسایی خطوط نیز استفاده کرد. مجموعه زیر را در نظر بگیرید.

$$\large { \displaystyle \left \{ z \mid z {\overline { r } } +{ \overline { z } } r = 0 \right \} }$$

این مجموعه نشان‌دهنده خطی است که از مبدا عبور کرده و به $$\bar { r }$$ عمود است. دلیل این امر صفر بودن ضرب داخلی زیر است.

$$\large { \displaystyle z \cdot { \overline { r } } }$$

به طور مشابه، مجموعه نقاط زیر را در نظر بگیرید.

$$u = exp ( b i )$$

در این صورت معادله زیر نشان‌دهنده خط گذرنده از $$z _ 0$$، در راستای $$u$$ است.

$$\large { \displaystyle { \frac { z - z _ { 0 } } { { \overline { z } } - { \overline { z _ { 0 } } } } } = u }$$

در مطالب آینده در مورد فضای برداری مختلط نیز بحث خواهیم کرد. در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• توان و ریشه اعداد مختلط — از صفر تا صد
• فرم نمایی و قطبی اعداد مختلط — به زبان ساده
• اعداد مختلط – به زبان ساده

^^