آموزش اتحادهای مثلثاتی با فرمول اویلر — به زبان ساده
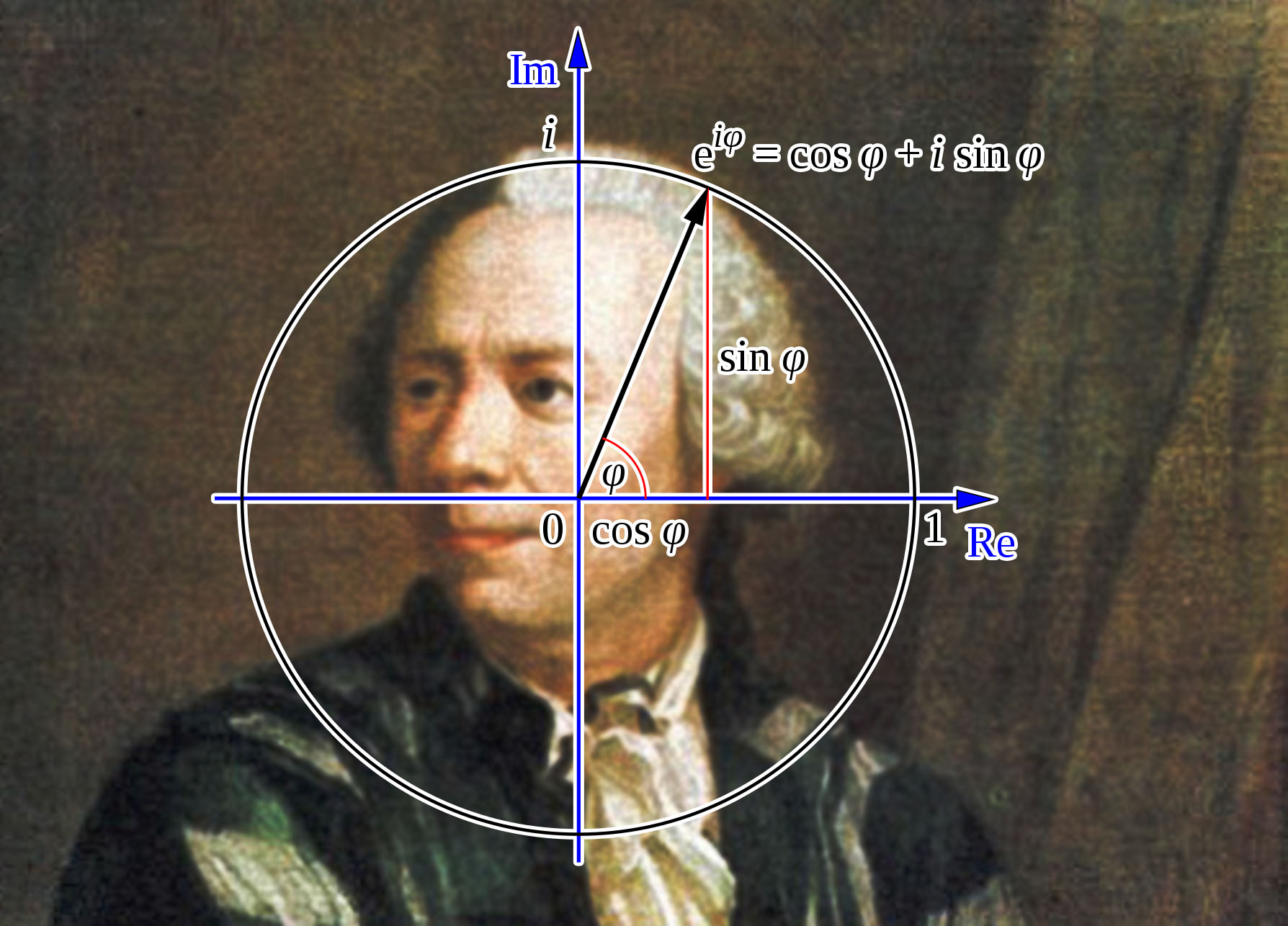
به خاطر سپردن اتحادهای مثلثاتی کار دشواری است. ما در این نوشته یک روش برای یادگیری اتحادهای مثلثاتی به روشی آسان ارائه میکنیم. اگر محاسبات خود را از قضیه فیثاغورس و فرمولهای مثلثاتی مشابه آغاز کنیم، میتوانیم ارتباطهای بین سینوس، کسینوس و موارد دیگر بیابیم.
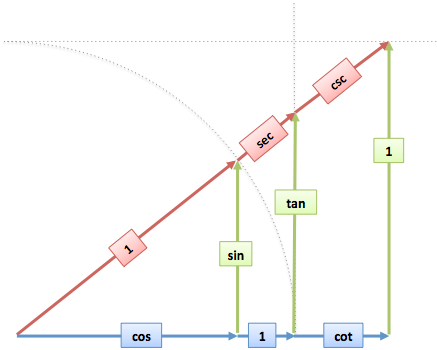
اما آیا میتوانیم عمیقتر بشویم؟ شاید بتوانیم سینوس را به خودش مرتبط کنیم. بر اساس عبارتهای ریاضی ما به دنبال فرمولهایی مانند زیر هستیم:
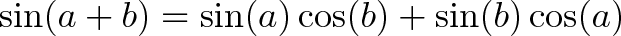
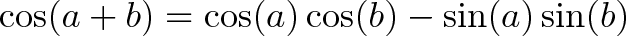
به جای این که این فرمولهای دشوار را به خاطر بسپارید میتوانید روش به دست آوردن فرمولها را بیاموزید. به این منظور میتوانیم از فرمول اویلر کمک بگیریم.
ارتباطها در جبر
در زمینه محاسبات جبری، روابط مختلف چیزی مانند زیر هستند:
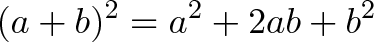
برای مثال محاسبه $$17^2$$ به صورت مستقیم دشوار است؛ اما میتوان آن را به صورت زیر ساده کرد:

در زمینه محاسبات کامپیوتری میتوان $$17^2$$ را به صورت مستقیم محاسبه کرد. جنبه مهم این محاسبه آن است که درک کنیم $$(a+b)^2$$ را میتوان به واحدهای سادهتری تجزیه کرد که شامل $$a^2, b^2,a,b$$ هستند. این حالت در زمینه فاکتورگیری، سادهسازی معادلات و موارد دیگر بسیار مفید است.
ارتباطها در مثلثات
اگر بخواهیم مثلثات را به زبان ساده توضیح دهیم، معنی عبارت زیر چه خواهد بود؟
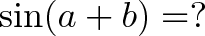
اگر به خاطر بیاورید که سینوس همان ارتفاع (به صورت درصدی از بیشینه) است، در این صورت معادله گویا خواهد بود: اگر دو زاویه را با هم جمع کنیم، مجموع ارتفاع آنها چه قدر میشود؟
یک حدس سریع این است که میتوانیم ارتفاعها را با هم ترکیب کنیم:
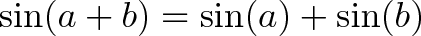
با این که ساده به نظر میرسد؛ اما کاملاً درست نیست. اگر به جمع کردن زوایا ادامه بدهیم، مقدار آنها آن قدر افزایش مییابد که از بیشینه (100%) تجاوز میکند و سپس شروع به کاهش میکند.

رابطه بین زاویه و ارتفاع نمیتواند یک جمع زدن ساده باشد. نکته عجیب همین جا است. ما میتوانیم زاویه جدید را پیدا کنیم؛ اما نمیتوانیم آن را به یک معادله تبدیل کنیم. البته به کمک فرمول اویلر شاید بتوانیم.
ترسیم به وسیله فرمول اویلر
فرمول اویلر امکان ایجاد مسیرهای دایرهای با استفاده از اعداد مختلط را میدهد:
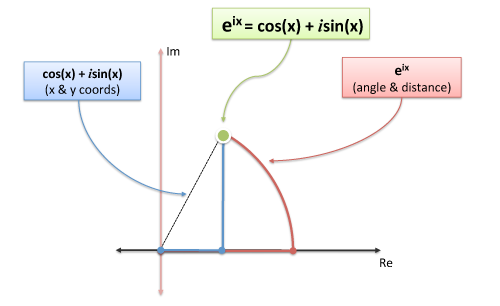
به طور اساسی ضرب کردن اعداد مختلط باعث ایجاد یک چرخش میشود. بدین ترتیب میتوانیم از فرمول اویلر برای به دست آوردن چرخش مورد نیاز خود استفاده کنیم:
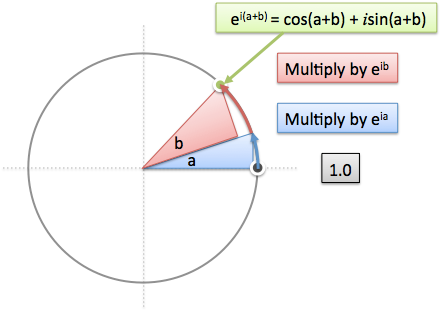
مراحل کار به صورت زیر است:
- از مقدار 1.0 که معادل 0 درجه است، شروع کنید.
- آن را در $${e^{ia}}$$ که چرخش به میزان a است، ضرب کنید.
- آن را در $${e^{ib}}$$ که چرخش به میزان b است، ضرب کنید.
- موقعیت نهایی به صورت $$1.0 × e^{ia} × e^{ib} = e^{i(a+b)} $$ یا همان 1.0 در زاویه (a+b) است.
$$ e^{i(a+b)} $$ یک عدد نمایی مختلط است که ظاهر پیچیدهای دارد. همان طور که $$17^2$$ را میتوانیم به اجزای سادهتر تقسیم کنیم، این عبارت را نیز سادهسازی خواهیم کرد:
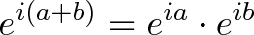

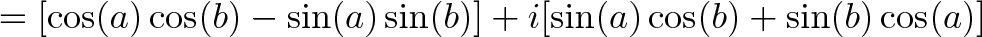
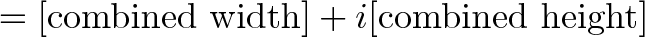
بدین ترتیب چرخش افقی (بخش حقیقی) به طور کامل از چرخش عمودی (بخش موهومی) مجزا میشود:
- ارتفاع ترکیبی: (sin(a+b)=sin(a)cos(b)+sin(b)cos(a
- عرض ترکیبی: (cos(a+b)=cos(a)cos(b)−sin(a)sin(b
همچنان که میبینید برای یک محاسبه ساده با دو اتحاد مثلثاتی مواجه هستیم که بهخاطرسپاری آنها واقعاً دشوار است.
درک معادله
اینک که برای مسئله خود معادلهای یافتهایم، باید به دنبال درک معنای آن باشیم. زمانی که دو ارتفاع را با هم جمع میکنیم، وقایع زیر رخ میدهند:
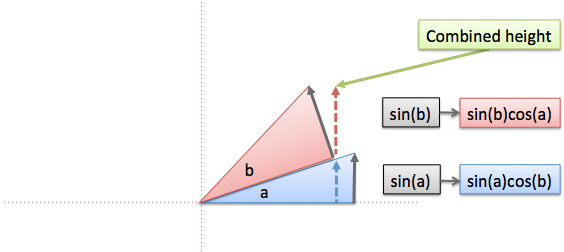
ارتفاع کامل مثلث آبی رنگ برابر با (sin(a قابل استفاده نیست، چون ارتفاع مثلث قرمز رنگ در راستای آن امتداد نیافته است. در واقع زمانی که زاویه b را اضافه میکنیم با زاویهای تندتر با همان وتر حرکت میکنیم. بدین ترتیب به صورت عمودی حرکت میکنیم و مسافت افقی را از دست میدهیم. در واقع ما در عمل (sin(a را به عقب میلغزانیم و آن را به میزان (cos(b کاهش میدهیم.
ارتفاع کامل مثلث قرمز یعنی (sin(b نیز قابل استفاده نیست، چون یک زاویه محسوب میشود و باید (sin(b را چرخش داده و آن را به میزان عامل (cos(a کاهش دهیم.
به خاطر داشته باشید که سینوس و کسینوس درصد هستند. در این مورد:
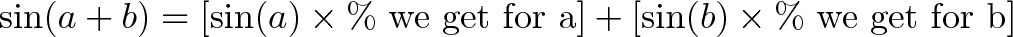
یا
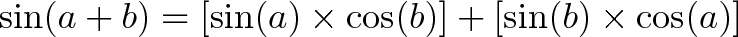
بدیهی است که ما دوست داریم ارتفاع کامل هر مثلث را به دست آوریم. اما از روی نمودار میبینیم که a به سمت عقب لغزیده است و b نیز چرخیده است، بنابراین ارتفاع در عمل کاهش یافته است. اگر هر کسینوس را مانند مالیاتی برای ارتفاع در نظر بگیریم، مقدار کاهش یافته، همان پولی است که به دست میآید.
اکنون شاید بپرسید چه اتفاقی برای زوایای کوچک مانند (sin(.01+.02 میافتد؟
میتوان آن را محاسبه کرد، اما تصور اولیه ما این است که چیزی در حدود زیر خواهد بود:
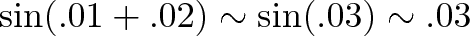
نمودار ذهنی ما چیزی مانند زیر است:

اختلاف ملموسی بین ارتفاعهای (sin(a و (sin(b و نسخههای «متنی» (sin(a)cos(b و (sin(b)cos(a وجود ندارد.
- برای زاویههای خیلی کوچک، (sin(a+b یک خط عمودی است و به ندرت به دلیل لغزش یا پیچش ارتفاعی را از دست میدهد.
- در مورد زوایای کوچک، کسینوس (درصدی که میماند) نزدیک به 100% است و بخش بسیار عمدهای از ارتفاع حفظ میشود.
- sin(x)∼x در مورد زوایای کوچک تقریب نسبتاً خوبی است و در اغلب موارد محاسبات استفاده میشود. اساساً (sin(x خطی برای دوره زمانی کوتاه است. در مورد زاویههای کوچک sin(a+b)∼sin(a)+sin(b)∼a+b است.
در مورد کسینوس نمودار مشابهی داریم:
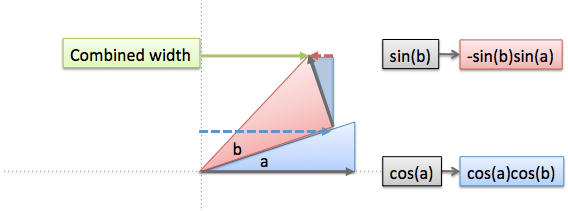
این بار عامل تبدیل، مطابقت مییابد. (کسینوس با کسینوس، سینوس با سینوس)
- عرض کامل مثلث اول (cos(a کاهش مقیاس مییابد تا با عرض مثلث دوم مطابقت داشته باشد.
- عبارت سینوس منفی است چون به سمت بالا انتقال مییابد و ارتفاع را کاهش میدهد. میتوان از مثلثهای مشابهی برای محاسبه این بخش استفاده کرد.
مشاهده طرز عملکرد این بخشهای مختلف در نمودار بسیار آموزنده است. اما اگر فقط به اتحاد مثلثاتی نیاز دارید میتوانید از طریق فرمول اویلر به صورت جبری آن را محاسبه کنید.
اتحادهای مثلثاتی چه اهمیتی دارند؟
برای سؤال فوق پاسخهای مختلفی میتوان ارائه کرد که برخی از آنها را در ادامه فهرست کردهایم:
1. ما مجبور به استفاده از اتحادهای مثلثاتی هستیم. بسیاری از شما شاید مقدار زیادی از وقت گرانبهای خود را صرف حفظ کردن اتحادهای مثلثاتی کردهاید؛ اما واقعاً به این کار نیازی نیست، چون میتوان این اتحادها را به سادگی از طریق فرمول به دست آورد.
2. به وسیله اتحادهای مثلثاتی میتوان معادلات مثلثاتی را سادهسازی کرد. با استفاده از اتحادهای مثلثاتی، میتوان معادلهها را به بخشهای کوچکتری تقسیم نمود که در حسابان بسیار مفید است.
برای نمونه برای یافتن مشتق سینوس باید به روش زیر عمل کنیم:
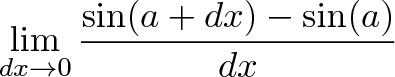
و اجازه میدهیم dx به صفر میل کند. این روش محاسبه مستقیم است؛ اما اگر از (sin(a + b استفاده کنیم رابطه زیر به دست میآید:
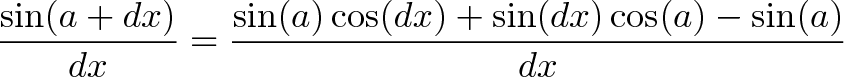
و زمانی که dx به صفر میل میکند، cos(dx) = 1 خواهد بود، یعنی در زاویه صفر عرض کامل است و از این رو داریم:
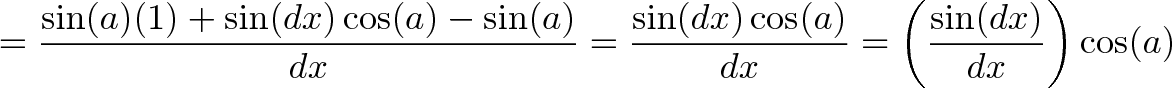
و زمانی که dx به سمت صفر میل میکند، (sin(dx و dx برابر میشوند:

با استفاده از این واقعیت (cos(a را به عنوان مشتق (sin(a به دست میآوریم. میبینید که کار کردن با تابعهای مثلثاتی گرچه همیشه آسان نیست؛ اما دست کم قابل مدیریت است.
3. از نظر محاسباتی کارآمد است. اگر مشغول کارهای گرافیک کامپیوتری باشید و به طور متناوب سینوس و کسینوس را (برای مثال جهت ضرب داخلی) محاسبه کنید، اتحادهای مثلثاتی بسیار به کار شما میآیند. در گذشته این اتحادها به روشی مشابه برای محاسبه جدولهای لگاریتمی و سادهتر ساختن محاسبات دستی مورد استفاده قرار میگرفتند.
4. ریاضیات برای مشاهده ارتباطها است. از آنجا که اتحادهای مثلثاتی از دایرهها و تابعهای نمایی مشتق میشوند از این رو در همه جا میتوان آنها را مشاهده کرد. برخی اوقات میتوان یک سناریو را با تبدیل محاسبات نمایی به مثلثاتی و یا برعکس ساده ساخت.
5. دانش شما از فرمول اویلر را عمیقتر میسازد. اگر فرمول اویلر را به خوبی بیاموزید، دایرهها را به طور کامل یاد گرفتهاید و بدین ترتیب دنیا را شناختهاید. برای نمونه فرمول اویلر به ما کمک میکند که یک دایره رسم کرده و نقطهای را روی آن مشخص کنیم. این شگفتانگیز است. در واقع با کمی ضرب و تقسیم میتوانیم از محاسبات هندسی زیاد خلاص شویم. اگر به ریاضیات پیشرفته علاقهمند هستید، باید به طور کامل با فرمول اویلر آشنا باشید.
سخن پایانی
در این بخش برخی از فرمولهای بیشتری را که در متن نیامدهاند، ارائه کردهایم.
فرمول تفریق: جایگزینی b با b-
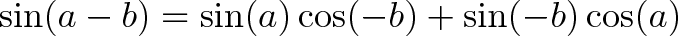
فرمول دو برابر زاویه: جایگزین b با a
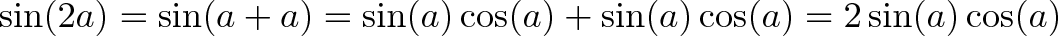
پس از محاسبه عامل تبدیل، ارتفاع را به خودش اضافه میکنیم.
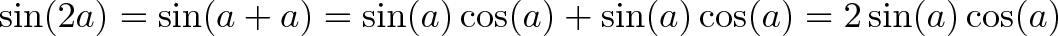
فرمول نصف زاویه: جایگزینی و حل
اگر این فرمول را بخواهیم از دو برابر زاویه به دست آوریم میتوانیم آن را برای (sin(a حل کنیم که نیمی از زاویه مورد استفاده برای (sin(2a است. بدین ترتیب فرمول نیم زاویه به دست میآید.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- درک موج های سینوسی — به زبان ساده
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- انتگرال توابع مثلثاتی — از صفر تا صد
- نمونه سوال مثلثات — همراه با جواب
- قضیه فیثاغورس و کاربردهای شگفت انگیز آن — به زبان ساده
- سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده
==











فقط می تونم بگم معرکه س.
اگر منبع داخلی یا خارجی که بیشتر راجع به این دست مسایل ریاضی به صورت گرافیکی بحث می کنه در اختیار دارید لطفا به اشتراک بزارید. تشکر فراوان