دستگاه معادلات خطی و حل آن – به زبان ساده

در این آموزش از سلسله آموزش‌های ریاضیات مجله فرادرس، روش‌های حل دستگاه معادلات خطی را بررسی می‌کنیم. دستگاه یا سیستم معادلات، مجموعه‌ای از معادلات است که هریک شامل یک یا چند متغیر مجهول هستند. در ادامه، روش حل دستگاه‌های معادلات با دو معادله و دو مجهول، سپس دستگاه معادلات سه مجهولی را معرفی خواهیم کرد.

دستگاه معادلات خطی با دو متغیر

یک دستگاه معادلات با دو متغیر را به‌صورت زیر نمایش می‌دهیم:

$$\begin{align*}ax + by & = p\\ cx + dy & = q\end{align*}$$

که در آن، $$x$$ و $$y$$ متغیرهای مجهول بوده و همه ثوابت می‌توانند صفر باشند، اما هر معادله باید حداقل یک متغیر داشته باشد. معادله، «خطی» نامیده می‌شود، اگر تنها توان اول متغیرها در آن وجود داشته باشد و متغیرها در هم ضرب نشوند.

برای مثال، دستگاه زیر را در نظر بگیرید:

$$\begin{align*}3x - y & = 7\\ 2x + 3y & = 1\end{align*}$$

قبل از آنکه درباره حل دستگاه معادلات بحث کنیم، ابتدا باید جواب دستگاه معادلات را تعریف کنیم. تعیین جواب دستگاه معادلات، همان تعیین مقدار $$x$$ و مقدار $$y$$ است، به‌طوری که اگر هر دو را در معادلات قرار دهیم، در آن صدق کنند.

برای مثال بالا، $$x=2$$ و $$y=-1$$ یک جواب برای دستگاه معادلات است. صحت این جواب را می‌توان به‌سادگی تحقیق کرد:

$$\begin{align*}3\left( 2 \right) - \left( { - 1} \right) & = 7\\ 2\left( 2 \right) + 3\left( { - 1} \right) & = 1\end{align*}$$

دقت کنید که جواب‌ها باید در هر دو معادله صدق کنند. برای مثال $$x=1$$ و $$y=-4$$ در معادله اول دستگاه صدق می‌کنند اما در معادله دوم، خیر. بنابراین، این دو عدد حل دستگاه معادلات نیستند.

اما جواب دستگاه معادلات دقیقاً چه چیزی را نشان می‌دهد؟ یا به عبارت بهتر، چه تعبیری برای آن وجود دارد؟ همان طور که می‌دانیم، معادله‌های دستگاه، هر کدام یک خط راست را نشان می‌دهند (شکل زیر را ببینید).

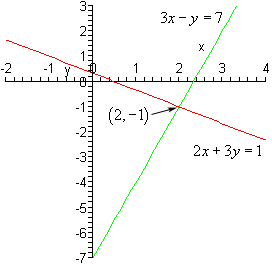
همان‌طور که می‌بینیم، جواب دستگاه، متناظر با نقطه‌ای است که دو خط یک‌دیگر را قطع می‌کنند. در ادامه، دو روش حل دستگاه معادلات خطی با دو متغیر را معرفی می‌کنیم.

روش اول، روش جایگذاری یا جانشینی نامیده می‌شود. در این روش،‌ یکی از معادلات را برای یکی از متغیرها حل کرده و مقدار به دست آمده را در معادله دیگر جایگذاری می‌کنیم. نتیجه این کار، یک معادله و یک متغیر مجهول خواهد بود. پس از آنکه این معادله را حل کردیم، مقدار به‌دست آمده را در یکی از معادلات قرار داده و متغیر مجهول دیگر را به‌دست می‌آوریم. برای درک بهتر، دو مثال زیر را بررسی کنید.

مثال ۱

معادلات زیر را حل کنید.

(الف) $$\begin{align*}3x - y & = 7\\ 2x + 3y & = 1\end{align*}$$

(ب) $$\begin{align*}5x + 4y & = 1\\ 3x - 6y & = 2\end{align*}$$

حل (الف): مطابق آن‌چه که گفته شد، ابتدا با استفاده از معادله اول، مقدار $$y$$ را به‌دست می‌آوریم:

$$3x - 7 = y$$

اکنون، رابطه اخیر را در معادله دوم جایگذاری می‌کنیم:

$$2x + 3\left( {3x - 7} \right) = 1$$

معادله فوق بر حسب متغیر $$x$$ است و به‌صورت زیر حل می‌شود:

$$\begin{align*}2x + 9x - 21 & = 1\\ 11x & = 22\\ x & = 2\end{align*}$$

حال که مقدار $$x$$ را به‌دست آورده‌ایم، آن را در یکی از دو معادله قرار داده و مقدار $$y$$ را محاسبه می‌کنیم:

$$y = 3x - 7 = 3\left( 2 \right) - 7 = - 1$$

در نتیجه، جواب دستگاه معادلات، $$x = 2$$ و $$y=-1$$ است.

حل (ب): برای حل این دستگاه معادلات، ابتدا از معادله دوم، $$x$$ را بر حسب $$y$$ به‌دست می‌آوریم:

$$\begin{align*}3x & = 6y + 2\\ x & = 2y + \frac{2}{3}\end{align*}$$

مقدار به‌دست آمده را در معادله نخست جایگذاری کرده و از معادله یک‌مجهولی حاصل، مقدار $$y$$ را محاسبه می‌کنیم:

$$\begin{align*}5\left( {2y + \frac{2}{3}} \right) + 4y & = 1\\ 10y + \frac{{10}}{3} + 4y & = 1\end{align*}$$

$$\begin{align*} 14y & = 1 - \frac{{10}}{3} = - \frac{7}{3}\\ y & = - \left( {\frac{7}{3}} \right)\left( {\frac{1}{{14}}} \right)\\ y & = - \frac{1}{6}\end{align*}$$

در نهایت، مقدار متغیر مجهول $$x$$ را به‌دست می‌آوریم:

$$x = 2\left( { - \frac{1}{6}} \right) + \frac{2}{3} = - \frac{1}{3} + \frac{2}{3} = \frac{1}{3}$$

بنابراین، جواب دستگاه معادلات، $$x = \frac{1}{3}$$ و $$y = - \frac{1}{6}$$ است.

برای تأیید صحت پاسخ می‌توانیم مقادیر محاسبه‌شده را در دو معادله جایگذاری کنیم.

در ادامه، روش دیگر به‌دست آوردن جواب دستگاه معادلات را معرفی می‌کنیم. این روش، روش حذف نام دارد. در این روش، یکی از معادلات یا هر دو آن‌ها را در در عددی ضرب می‌کنیم، به‌گونه‌ای که ضریب نهایی یکی از متغیرها در دو معادله، قرینه هم شوند. سپس دو معادله را با هم جمع می‌کنیم. از آن‌جایی که ضرایب یکی از متغیرهای مجهول در دو معادله قرینه هم است، مجهول مذکور حذف خواهد شد و به معادله‌ای با یک مجهول خواهیم رسید. با به‌دست آوردن این مجهول و جایگذاری مقدار آن در یکی از معادله‌ها، مجهول دیگر نیز به‌دست می‌آید.

مثال زیر، روند حل با استفاده از این روش را به‌خوبی نشان می‌دهد.

مثال ۲

دستگاه معادلات زیر را حل کنید:

(الف) $$\begin{align*}5x + 4y & = 1\\ 3x - 6y & = 2\end{align*}$$

(ب) $$\begin{align*}2x + 4y & = - 10\\ 6x + 3y & = 6\end{align*}$$

حل (الف): در این دستگاه، به‌صورت کاملاً اختیاری ضرایب $$y$$ را به‌گونه‌ای تغییر می‌دهیم که بتوان آن را حذف کرد. برای این کار، معادله اول را در $$3$$ و معادله دوم را در $$2$$ ضرب می‌کنیم که ضریب جدید $$y$$ در دو معادله به‌ترتیب $$12$$ و $$-12$$ شود.

$$\begin{align*} 5x+4y & = 1 & \underrightarrow{\times \,\,3} \hspace{0.5in} & 15x+12y=3 \\ 3x-6y & = 2 & \underrightarrow{\times \,\,2} \hspace{0.5in} & \underline{\,\,6x-12y=4} \\ & & & 21x \hspace{0.5in} =7 \\ \end{align*}$$

اکنون به‌راحتی می‌توانیم مقدار $$x = \frac{1}{3}$$ را به‌دست آوریم. حال از معادله دوم استفاده کرده و با کمک آن، مقدار $$y$$ را محاسبه می‌کنیم:

$$\begin{align*}3\left( {\frac{1}{3}} \right) - 6y & = 2\\ 1 - 6y & = 2\\ - 6y & = 1\\ y & = - \frac{1}{6}\end{align*}$$

حل (ب): مانند قبل عمل کرده و برای این مثال، ضریب $$x$$ در دو معادله را به‌گونه‌ای تغییر می‌دهیم که $$x$$ از دو معادله حذف شود. با مشاهده معادلات می‌بینیم اگر معادله اول را در $$-3$$ ضرب کنیم به هدف موردنظر خواهیم رسید:

$$\begin{align*} 2x+4y & =-10 & \underrightarrow{\times \,\,-3} \hspace{0.5in} & -6x-12y=30 \\ 6x+3y & =6 & \underrightarrow{\times 1} \hspace{0.5in} &\underline{\hspace{0.35in}6x+3y=6} \\ & & & \hspace{0.5in} -9y=36 \\ & & & \hspace{0.85in} y=-4 \\ \end{align*}$$

در نهایت، مقدار به‌دست آمده را در یکی از معادلات جایگذرای کرده و $$x$$ را به‌دست می‌آوریم:

$$\begin{align*}2x + 4\left( { - 4} \right) & = - 10\\ 2x - 16 & = - 10\\ 2x & = 6\\ x & = 3\end{align*}$$

در ادامه، دو حالت خاص از دستگاه معادلات خطی را بیان می‌کنیم.

مثال ۳

دستگاه معادلات خطی زیر را حل کنید:

$$\begin{align*}x - y & = 6\\ - 2x + 2y & = 1\end{align*}$$

حل: برای یافتن پاسخ این دو معادله می‌توانیم از دو روشی که بیان شد استفاده کنیم. ابتدا مقدار $$x$$ را از معادله اول به‌دست می‌آوریم:

$$\begin{align*}x & = 6 + y\\ & \\ - 2\left( {6 + y} \right) + 2y & = 1\\ - 12 - 2y + 2y & = 1\\ - 12 & = 1\,\,\,??\end{align*}$$

واضح است که تساوی اخیر متناقض است، در حالی که ما اشتباهی نکرده‌ایم. اما مشکل کجاست؟ برای پیدا کردن مشکل، نمودار زیر را در نظر بگیرید که در آن، دو معادله رسم شده‌اند.

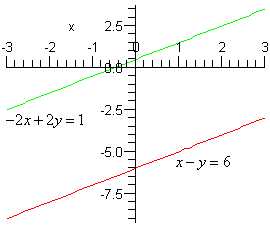
از نمودار بالا مشخص است که دو خط موازی هستند و می‌دانیم که دو خط موازی هیچ‌گاه یک‌دیگر را قطع نمی‌کنند. بنابراین، دستگاه معادلات فوق، جوابی ندارد.

اما یک حالت دیگر نیز داریم. مثال زیر، این مورد را به‌وضوح بیان می‌کند.

مثال ۴

دستگاه معادله زیر را حل کنید.

$$\begin{align*}2x + 5y & = - 1\\ - 10x - 25y & = 5\end{align*}$$

حل: به‌نظر می‌رسد روش حذف، راحت‌ترین کار برای حل دستگاه فوق باشد. بنابراین، داریم:

$$\begin{align*} 2x+5y & =-1 & \underrightarrow{\times \,\,5} \hspace{0.5in} & \,\,\,\,10x+25y=-5 \\ -10x-25y & =5 & \underrightarrow{\times 1} \hspace{0.5in} & \underline{-10x-25y=5} \\ & & & \hspace{0.9in} 0=0 \\ \end{align*}$$

تساوی منتجه از حل دستگاه معادلات ($$0=0$$)، بدیهی است. اما نمی‌دانیم این تساوی چه مفهومی دارد. البته تا این‌جا می‌توانیم بگوییم که این تساوی برخلاف مثال قبل، تناقضی ندارد.

اگر برای دو معادله، $$y$$ را برحسب $$x$$ بنویسیم، با دو معادله خط مواجه خواهیم بود که شیب و عرض از مبدأ یکسانی دارند. در واقع، دو خط یکی هستند. در این حالت، هر نقطه‌ای را که برای یک معادله در نظر بگیریم، در معادله دیگر نیز صدق می‌کند. بنابراین، می‌توان گفت دستگاه معادلات فوق، بی‌نهایت جواب دارد.

حال می‌خواهیم بدانیم مجموعه جواب دستگاه معادلات فوق چگونه خواهد بود. فرض می‌کنیم مقدار متغیر $$x$$ برابر با $$t$$ باشد، بنابراین، حل نهایی به‌صورت زیر خواهد بود:

$$\begin{array}{*{20}{c}}\begin{aligned}x & = t\\ y & = - \frac{2}{5}t - \frac{1}{5}\end{aligned}&{\hspace{0.25in}}\end{array}$$

برای مثال اگر فرض کنیم $$t=0$$ آن‌گاه جواب به‌ازای آن برابر است با:

$$x = 0\hspace{0.25in}y = - \frac{1}{5}$$

دستگاه معادلات سه مجهولی

حل دستگاه معادلات سه مجهولی را در قالب دو مثال بیان می‌کنیم.

مثال ۵

دستگاه معادلات زیر را حل کنید:

$$\begin{align*}x - 2y + 3z & = 7\\ 2x + y + z & = 4\\ - 3x + 2y - 2z & = - 10\end{align*}$$

حل: باید مقادیر $$x$$، $$y$$ و $$z$$ را به‌گونه‌ای پیدا کنیم که در هر سه معادله صدق کنند. برای حل دستگاه معادلات، یکی از متغیرهای مجهول را از دو معادله حذف کرده و دو مجهول دیگر را به‌دست می‌آوریم. با به‌دست آوردن این دو متغیر مجهول، متغیر مجهول سوم را نیز می‌توانیم محاسبه کنیم.

بنابراین، $$y$$ را از دو معادله آخر حذف می‌کنیم:

$$\begin{align*} x-2y+3z & =7 & \underrightarrow{\times \, 1}\hspace{0.1in} & & x-2y+3z & =7 \\ 2x+y+z & =4 & \underrightarrow{\times \,\,2}\hspace{0.1in} & & 4x+2y+2z & =8 \\ -3x+2y-2z & =-10 & \underrightarrow{\times \, 1}\hspace{0.1in} & & -3x+2y-2z & =-10 \\ \end{align*}$$

نتیجه به‌صورت زیر خواهد بود:

$$\begin{align*}x - 2y + 3z & = 7\\ 5x\,\,\,\,\,\,\,\,\,\,\,\, + 5z & = 15\\ - 2x\,\,\,\,\,\,\,\,\,\,\,\,\,\, + z & = - 3\end{align*}$$

در ادامه، متغیر $$z$$ را حذف می‌کنیم:

$$\begin{align*} x-2y+3z & =7 & \underrightarrow{\times \, 1} \hspace{0.1in} & & x-2y+3z & =7 \\ 5x\,\,\,\,\,\,\,\,\,\,\,\,+5z & =15 & \underrightarrow{\times \, 1 } \hspace{0.1in} & & 5x\,\,\,\,\,\,\,\,\,\,\,\,+5z & =15 \\ -2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,+z & =-3 & \underrightarrow{\times \,\,-5} \hspace{0.1in} & & 10x\,\,\,\,\,\,\,\,\,\,\,\,-5z & =15 \\ \end{align*}$$

نتیجه حاصل، سه معادله زیر خواهد بود:

$$\begin{align*}x - 2y + 3z & = 7\\ 5x\,\,\,\,\,\,\,\,\,\,\,\, + 5z & = 15\\ 15x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & = 30\end{align*}$$

از معادله آخر، به‌راحتی می‌توان $$x=2$$ را به‌دست آورد. با قرار دادن این مقدار در معادله دوم، مقدار $$z$$ محاسبه می‌شود:

$$\begin{align*}5\left( 2 \right) + 5z & = 15\\ 10 + 5z & = 15\\ 5z & = 5\\ z & = 1\end{align*}$$

در نهایت، با استفاده از مقادیر معین $$x$$ و $$z$$ می‌توانیم مقدار $$y$$ را حساب کنیم.:

$$\begin{align*}2 - 2y + 3\left( 1 \right) & = 7\\ - 2y + 5 & = 7\\- 2y & = 2\\ y & = - 1\end{align*}$$

مثال ۶

دستگاه معادلات زیر را حل کنید:

$$\begin{align*}2x - 4y + 5z & = - 33\\ 4x - y & = - 5\\ - 2x + 2y - 3z & = 19\end{align*}$$

حل: اگر به معادلات فوق دقت کنیم، می‌بینیم که معادله دوم، فقط دو متغیر دارد. می‌توانیم از این معادله استفاده کرده و با قرار دادن آن در دو معادله دیگر، به دو معادله و دو مججهول برسیم. بنابراین، معادلات مذکور را به‌صورت زیر می‌نویسیم:

$$\begin{align*}2x - 4\left( {4x + 5} \right) + 5z & = - 33\\- 2x + 2\left( {4x + 5} \right) - 3z & = 19\end{align*}$$

اکنون معادله اخیر را در دو معادله دیگر جایگذاری می‌کنیم:

$$\begin{align*}2x - 4\left( {4x + 5} \right) + 5z & = - 33\\- 2x + 2\left( {4x + 5} \right) - 3z & = 19\end{align*}$$

با ساده کردن این دو معادله داریم:

$$\begin{array}{*{20}{c}}{2x - 16x - 20 + 5z = - 33}\\{ - 2x + 8x + 10 - 3z = 19}\end{array}\hspace{0.25in} \to \hspace{0.25in}\begin{array}{*{20}{c}}{ - 14x + 5z = - 13}\\{6x - 3z = 9}\end{array}$$

دو معادله بالا را می‌توانیم به‌سادگی حل کنیم:

$$\begin{align*} -14x+5z & =-13 & \underrightarrow{\times \,\,3}\hspace{0.5in} & -42x+15z=-39 \\ 6x-3z & =9 & \underrightarrow{\times \,\,5}\hspace{0.5in} & \underline{\hspace{0.25in}30x-15z=45} \\ & & & \hspace{0.5in} -12x=6 \\ \end{align*}$$

اکنون که مقدار $$x = - \frac{1}{2}$$ به‌دست آمده است، می‌توانیم مقدار $$z$$ را محاسبه کنیم:

$$\begin{align*}6\left( { - \frac{1}{2}} \right) - 3z & = 9\\ - 3 - 3z & = 9\\ - 3z & = 12\\ z & = - 4\end{align*}$$

در نهایت، مقدار $$y$$ را با استفاده از معادله دو مجهولی $$y = 4x + 5$$ به‌دست می‌آوریم:

$$y = 4\left( { - \frac{1}{2}} \right) + 5 = 3$$

ماتریس افزوده

در این بخش، حل دستگاه معادلات خطی را با استفاده از ماتریس افزوده معرفی می‌کنیم. این روش، نسبت به روش‌هایی که برای حل دستگاه دو معادله و دو مجهولی بیان کردیم، کمی پیچیده‌‌تر به‌نظر می‌رسد. اما برای دستگاه معادلاتی با بیش از دو معادله و دو مجهول، استفاده از این روش می‌تواند کارساز باشد.

ماتریس افزوده یک دستگاه معادلات، ماتریسی عددی است که هر سطر آن، ضرایب و ثوابت هر دو سمت معادله را نشان می‌دهد و هر ستون، نماینده ضرایب مربوط به یک متغیر است.

برای آشنایی بیشتر، یکی از مثال‌هایی را بررسی می‌کنیم که قبلاً ارائه کردیم:

$$\begin{align*}x - 2y + 3z & = 7\\ 2x + y + z & = 4\\ - 3x + 2y - 2z & = - 10\end{align*}$$

ماتریس افزوده دستگاه معادلات بالا به‌صورت زیر است:

$$\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{ - 3}&2&{ - 2}&{ - 10}\end{array}} \right]$$

سطر نخست، متشکل از اعدادی است که ستون اول آن ضریب $$x$$، ستون دوم ضریب $$y$$ و ستون سوم، ضریب $$z$$ است. ستون چهارم سطر اول نیز مقدار ثابت سمت راست معادله اول را نشان می‌دهد. سایر درایه‌های این ماتریس نیز مربوط به دو معادله دیگر هستند.

برای حل معادلات با استفاده از ماتریس افزوده، ابتدا باید درباره عملیات سطری مقدماتی بحث کنیم. در این‌جا، سه عمل سطری مقدماتی را بیان می‌کنیم. برای بیان این عملیات، از ماتریس افزوده بالا استفاده می‌کنیم.

1. تعویض دو سطر: با این عمل، درایه‌های سطر $$i$$ و سطر $$j$$ را با هم تعویض می‌کنیم. این کار را با نماد $${R_i} \leftrightarrow {R_j}$$ نشان می‌دهیم. در ماتریس مورد نظر داریم:

$$\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{ - 3}&2&{ - 2}&{ - 10}\end{array}} \right]\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}{ - 3}&2&{ - 2}&{ - 10}\\2&1&1&4\\1&{ - 2}&3&7\end{array}} \right]$$

دقت کنید که همه چهار درایه دو سطر تعویض شده‌اند.

2. ضرب عدد ثابت در یک سطر: در این عمل، هریک از درایه‌های سطر $$i$$ را در عدد ثابت $$c$$ ضرب می‌کنیم و آن را به‌صورت $$c{R_i}$$ می‌نویسیم. همچنین می‌توانیم یک سطر را بر عدد ثابتی تقسیم کنیم و آن را با $$\frac{1}{c}{R_i}$$ نمایش دهیم. برای مثال، داریم:

$$\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{ - 3}&2&{ - 2}&{ - 10}\end{array}} \right]\begin{array}{*{20}{c}}{ - 4{R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{12}&{ - 8}&8&{40}\end{array}} \right]$$

بنابراین، وقتی از ضرب یک سطر در یک عدد ثابت یا تقسیم بر آن سخن می‌گوییم، بدین معنی است که تک تک درایه‌های آن سطر را در عدد ثابت ضرب یا بر آن تقسیم می‌کنیم.

3. جمع چند سطر با هم:‌ با این عمل می‌توانیم سطر $$i$$ را با حاصل جمع «سطر $$i$$» و «$$c$$ برابر سطر $$j$$» تعویض کنیم. این کار را با $${R_i} + c{R_j} \to {R_i}$$ نشان می‌دهیم. برای مثال:

$$\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{ - 3}&2&{ - 2}&{ - 10}\end{array}} \right]\begin{array}{*{20}{c}}{{R_3} - 4{R_1} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&3&7\\2&1&1&4\\{ - 7}&{10}&{ - 14}&{ - 38}\end{array}} \right]$$

جزئیات محاسبه سطر سوم به‌صورت زیر است:

$$\begin{align*} - 3 - 4\left( 1 \right) & = - 7\hspace{0.25in}\\ 2 - 4\left( { - 2} \right) & = 10\\ - 2 - 4\left( 3 \right) & = - 14\\ - 10 - 4\left( 7 \right) & = - 38\end{align*}$$

اکنون که عملیات سطری مقدماتی را معرفی کردیم، شیوه حل دستگاه معادلات با روش ماتریس افزوده را با اعمال آن بر یک دستگاه معادله دو مجهولی بیان می‌کنیم. بدین منظور، دستگاه معادلات زیر را در نظر بگیرید:

$$\begin{align*}ax + by & = p\\ cx + dy & = q\end{align*}$$

ابتدا ماتریس افزوده را تشکیل می‌دهیم:

$$\left[ {\begin{array}{rr|r}a&b&p\\c&d&q\end{array}} \right]$$

با استفاده از عملیات سطری مقدماتی می‌توانیم ماتریس بالا را به‌صورت زیر بنویسیم:

$$\left[ {\begin{array}{rr|r}1&0&h\\0&1&k\end{array}} \right]$$

با توجه به ماتریس اخیر، مقادیر $$x=h$$ و $$y=k$$ به‌دست می‌آیند. این روش، حذف گوس-جردن یا حذف گوسی نامیده می‌شود.

مثال 7

دستگاه معادلات زیر را حل کنید:

$$\begin{align*}3x - 2y & = 14\\ x + 3y & = 1\end{align*}$$

حل: اولین گام، نوشتن ماتریس افزوده معادلات است:

$$\require{color}\left[ {\begin{array}{rr|r} {\color{Red} 3}&{ - 2}&{14}\\1&3&1\end{array}} \right]$$

برای تبدیل ماتریس بالا به ماتریس مورد نظر که بتوان از آن، معادلات را حل کرد، از درایه بالای سمت چپ شروع می‌کنیم و در خلاف جهت عقربه‌های ساعت پیش می‌رویم تا به هدف مورد نظر برسیم.

ابتدا جای دو سطر را با هم تعویض می‌کنیم:

$$\require{color}\left[ {\begin{array}{rr|r}3&{ - 2}&{14}\\1&3&1\end{array}} \right]\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&3&1\\{\color{Red} 3}&{ - 2}&{14}\end{array}} \right]$$

گام بعدی، صفر کردن درایه پایین‌تر از عدد $$1$$ است؛ این بدین معنی است که باید عدد $$3$$ قرمز را به صفر تبدیل کنیم. برای این کار، $$-3$$ برابرِ سطر اول را با سطر دوم جمع کرده و آن را در سطر دوم قرار می‌دهیم.

$$\require{color}\left[ {\begin{array}{rr|r}1&3&1\\3&{ - 2}&{14}\end{array}} \right]\begin{array}{*{20}{c}}{{R_2} - 3{R_1} \to {R_2}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&3&1\\0&{\color{Red} - 11}&{11}\end{array}} \right]$$

در ادامه، باید عدد $$-11$$ را به $$1$$ تبدیل کنیم. برای این کار، عمل سطری مقدماتی زیر را انجام می‌دهیم:

$$\require{color}\left[ {\begin{array}{rr|r}1&3&1\\0&{ - 11}&{11}\end{array}} \right]\begin{array}{*{20}{c}}{ - \frac{1}{{11}}{R_2}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&{\color{Red} 3}&1\\0&1&{ - 1}\end{array}} \right]$$

تا این‌جا بیشتر راه را رفته‌ایم. گام آخر، تبدیل عدد $$3$$ قرمز بالا به عدد $$0$$ است. با استفاده از عملیات سطری مقدماتی داریم:

$$\require{color}\left[ {\begin{array}{rr|r}1&3&1\\0&1&{ - 1}\end{array}} \right]\begin{array}{*{20}{c}}{{R_1} - 3{R_2} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rr|r}1&0&4\\0&1&{ - 1}\end{array}} \right]$$

در نتیجه، حل دستگاه معادلات، $$x=4$$ و $$y=-1$$ است.

لازم به ذکر است عملیات سطری که انجام دادیم، منحصر به فرد نیست و می‌توان آن را به شیوه‌های مختلف انجام داد. نکته مهم این است که باید راهی را انتخاب کنیم که کم‌ترین محاسبات را در پی داشته باشد.

برای دستگاه دو معادله‌ای، ممکن استفاده از ماتریس افزوده نسبت به روش‌های دیگری که بیان کردیم، پیچیده‌تر باشد. اما برای دستگاه‌هایی با معادلات بیشتر، این روش بسیار مفید است.

مثلاً، برای یک دستگاه با سه معادله، باید ماتریس افزوده را به‌فرم زیر درآوریم:

$$\left[ {\begin{array}{rrr|r}1&0&0&p\\0&1&0&q\\0&0&1&r\end{array}} \right]$$

که پاسخ $$x=p$$، $$y=q$$ و $$z=r$$‌ را نتیجه خواهد داد.

مثال ۸

دستگاه معادلات زیر را حل کنید:

$$\begin{align*}3x + y - 2z & = 2\\ x - 2y + z & = 3\\ 2x - y - 3z & = 3\end{align*}$$

حل: ابتدا ماتریس افزوده سیستم را به‌صورت زیر می‌نویسیم:

$$\require{color}\left[ {\begin{array}{rrr|r} {\color{Red} 3}&1&{ - 2}&2\\1&{ - 2}&1&3\\2&{ - 1}&{ - 3}&3\end{array}} \right]$$

در ادامه، سطر اول و دوم را تعویض می‌کنیم:

$$\require{color}\left[ {\begin{array}{rrr|r}{\color{Red} 3}&1&{ - 2}&2\\1&{ - 2}&1&3\\2&{ - 1}&{ - 3}&3\end{array}} \right]\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\{\color{Red} 3}&1&{ - 2}&2\\{\color{Red} 2}&{ - 1}&{ - 3}&3\end{array}} \right]$$

سپس، درایه‌های پایین‌تر از عدد $$1$$ را در ستون دوم و سوم،‌ صفر می‌کنیم:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\{\color{Red} 3}&1&{ - 2}&2\\{\color{Red} 2}&{ - 1}&{ - 3}&3\end{array}} \right]\begin{array}{*{20}{c}}{{R_2} - 3{R_1} \to {R_2}}\\{{R_3} - 2{R_1} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&{\color{Red} 7}&{ - 5}&{ - 7}\\0&3&{ - 5}&{ - 3}\end{array}} \right]$$

اکنون درایه مشترک سطر دوم و ستون دوم را به $$1$$ تغییر می‌دهیم:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&{\color{Red} 7}&{ - 5}&{ - 7}\\0&3&{ - 5}&{ - 3}\end{array}} \right]\begin{array}{*{20}{c}}{\frac{1}{7}{R_2}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&1&{ - \frac{5}{7}}&{ - 1}\\0&{\color{Red} 3}&{ - 5}&{ - 3}\end{array}} \right]$$

حال باید عدد $$3$$ قرمز را در ماتریس بالا، به $$0$$ تبدیل کنیم:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&1&{ - \frac{5}{7}}&{ - 1}\\0&{\color{Red} 3}&{ - 5}&{ - 3}\end{array}} \right]\begin{array}{*{20}{c}}{{R_3} - 3{R_2} \to {R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&1&{ - \frac{5}{7}}&{ - 1}\\0&0&{\color{Red} - \frac{{20}}{7}}&0\end{array}} \right]$$

در این‌جا نوبت به درایه مشترک سطر سوم و ستون سوم می‌رسد که باید آن را به $$1$$ تبدیل کنیم:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{ - 2}&1&3\\0&1&{ - \frac{5}{7}}&{ - 1}\\0&0&{\color{Red} - \frac{{20}}{7}}&0\end{array}} \right]\begin{array}{*{20}{c}}{ - \frac{7}{{20}}{R_3}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{ - 2}&{\color{Red} 1}&3\\0&1&{\color{Red} - \frac{5}{7}}&{ - 1}\\0&0&1&0\end{array}} \right]$$

در مرحله بعد، باید عدد $$-\frac{5}{7}$$ را به $$0$$ تبدیل کنیم:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{ - 2}&{\color{Red} 1}&3\\0&1&{\color{Red} - \frac{5}{7}}&{ - 1}\\0&0&1&0\end{array}} \right]\begin{array}{*{20}{c}}{{R_2} + \frac{5}{7}{R_3} \to {R_2}}\\{{R_1} - {R_3} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&{\color{Red} - 2}&0&3\\0&1&0&{ - 1}\\0&0&1&0\end{array}} \right]$$

گام آخر، تغییر $$-2$$ قرمز ماتریس اخیر به $$0$$ است:

$$\require{color}\left[ {\begin{array}{rrr|r}1&{\color{Red} - 2}&0&3\\0&1&0&{ - 1}\\0&0&1&0\end{array}} \right]\begin{array}{*{20}{c}}{{R_1} + 2{R_2} \to {R_1}}\\ \to \end{array}\left[ {\begin{array}{rrr|r}1&0&0&1\\0&1&0&{ - 1}\\0&0&1&0\end{array}} \right]$$

در نهایت، جواب دستگاه معادلات را به‌صورت زیر به‌دست می‌آوریم:

$$x = 1,\,\,\,y = - 1,\,\,\,z = 0$$

شاید حل دستگاه سه معادله و سه مجهول با استفاده از روش حذف گوسی، کمی‌ زمان‌بر باشد،‌ اما به‌اندازه روش مستقیم وقت‌گیر نیست.