معادله دیفرانسیل بسل — به زبان ساده
در آموزشهای پیشین مجله فرادرس، درباره معادلات دیفرانسیل بحث و روشهای حل معادلات دیفرانسیل مرتبه دوم را بررسی کردیم. «معادله دیفرانسیل بسل» (Bessel Differential Equation) نوع خاصی از معادلات دیفرانسیل مرتبه دوم است که در این آموزش به آن میپردازیم.
معادله دیفرانسیل زیر را معادله بسل مینامند:
$${{x^2}y^{\prime\prime} + xy’ }+{ \left( {{x^2} – {v^2}} \right)y }={ 0}$$
عدد $$v$$، مرتبه معادله بسل نامیده میشود.
نام این معادله برگرفته از اسم ریاضیدان و ستارهشناش آلمانی «فریدریش ویلهلم بسل» (Friedrich Wilhelm Bessel) است. بسل جزئیات این معادله را بررسی کرد و در سال 1824 نشان داد که حل آن را میتوان با کلاس خاصی از توابع بهنام «توابع استوانهای» (cylinder functions) یا «توابع بسل» بیان کرد.
جواب عمومی به عدد $$v$$ بستگی دارد. برای $$v$$ دو حالت داریم:
- مرتبه $$v$$ غیرصحیح باشد
- مرتبه $$v$$ صحیح باشد
حالت اول: مرتبه $$v$$ غیرصحیح است
فرض کنید عدد $$v$$، مثبت و غیرصحیح باشد. در این صورت، جواب معادله بسل را میتوان بهصورت زیر نوشت:
$${y\left( x \right) }={ {C_1}{J_v}\left( x \right) + {C_2}{J_{ – v}}\left( x \right)}$$
که در آن، $$C_1$$ و $$C_2$$ اعداد ثابت اختیاری و $${J_v}\left( x \right)$$ و $${J_{ – v}}\left( x \right)$$ توابع بسل نوع اول هستند.
تابع بسل را میتوان با یک سری بر اساس «تابع گاما» نشان داد:
$${{J_v}\left( x \right) \text{=}}\kern0pt{ \sum\limits_{p = 0}^\infty {\frac{{{{\left( { – 1} \right)}^p}}}{{\Gamma \left( {p + 1} \right)\Gamma \left( {p + v + 1} \right)}} \cdot}\kern0pt{ {{\left( {\frac{x}{2}} \right)}^{2p + v}}} }$$
تابع گاما، تعمیمی از تابع فاکتوریل اعداد صحیح است. این تابع، بهصورت زیر تعریف میشود:
$${\Gamma \left( {p + 1} \right) = p!,\;\;}\kern-0.3pt
{\Gamma \left( {p + v + 1} \right) }={ \left( {v + 1} \right)\left( {v + 2} \right) \cdots }\kern0pt{ \left( {v + p} \right)\Gamma \left( {v + 1} \right).}$$
توابع بسل مرتبه منفی ($$-v$$) (با فرض $$v>0$$) بهصورت زیر نوشته میشوند:
$${{J_{ – v}}\left( x \right) \text{=}}\kern0pt{ \sum\limits_{p = 0}^\infty {\frac{{{{\left( { – 1} \right)}^p}}}{{\Gamma \left( {p + 1} \right)\Gamma \left( {p – v + 1} \right)}} \cdot}\kern0pt{ {{\left( {\frac{x}{2}} \right)}^{2p – v}}} }$$
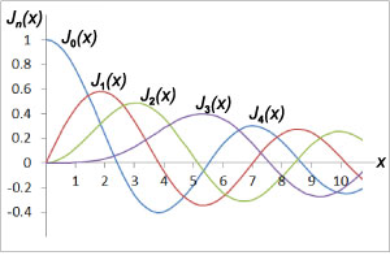
این توابع را میتوان با بسیاری از بستههای نرمافزاری ریاضی محاسبه کرد. برای مثال، توابع بسل نوع اول مرتبه $$v=0$$ تا $$v=4$$ در شکل ۱ نشان داده شدهاند. توابع متناظر با این منحنیها، در نرمافزار اکسل موجود است.
حالت دوم: مرتبه $$v$$ عددی صحیح است
اگر مرتبه $$v$$ معادله دیفرانسیل بسل، یک عدد صحیح باشد، توابع بسل $${J_v}\left( x \right)$$ و $${J_{ – v}}\left( x \right)$$ وابسته خواهند بود. در این حالت، جواب عمومی با فرمول زیر توصیف میشود:
$${y\left( x \right) }={ {C_1}{J_v}\left( x \right) + {C_2}{Y_v}\left( x \right)}$$
که در آن، $${Y_v}\left( x \right)$$ تابع بسل نوع دوم است. گاهی این خانواده توابع بسل را توابع نویمان (Neumann functions) یا توابع وبر (Weber functions) مینامند.
تابع بسل نوع دوم $${Y_v}\left( x \right)$$ را میتوان براساس توابع بسل نوع اول $${J_v}\left( x \right)$$ و $${J_{ – v}}\left( x \right)$$ بیان کرد:
$${{Y_v}\left( x \right) }={ \frac{{{J_v}\left( x \right)\cos \pi v – {J_{ – v}}\left( x \right)}}{{\sin \pi v}}.}$$
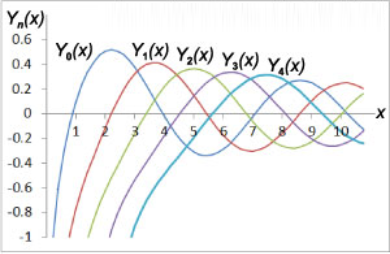
منحنیهای توابع $${Y_v}\left( x \right)$$ بهازی چند $$v$$ مرتبه اول در شکل 2 نشان داده شدهاند.
نکته: جواب عمومی معادله دیفرانسیل برحسب توابع بسل نوع اول و دوم، برای مرتبههای غیرصحیح نیز قابل بیان است.
معادلات قابل تبدیل به معادله دیفرانسیل بسل
(۱) یکی از معادلات شناختهشده که به معادله دیفرانسیل بسل قابل تبدیل است، «معادله بسل اصلاحشده» نام دارد. این معادله، از جایگزینی $$x$$ با $$-ix$$ بهدست میآید:
$${{x^2}y^{\prime\prime} + xy’ }-{ \left( {{x^2} + {v^2}} \right)y }={ 0.}$$
جواب معادله فوق را میتوان با توابع موسوم به بسل اصلاحشده نوع اول و دوم بهصورت زیر نوشت:
$${y\left( x \right) }={ {C_1}{J_v}\left( { – ix} \right) + {C_2}{Y_v}\left( { – ix} \right) }
= {{C_1}{I_v}\left( x \right) + {C_2}{K_v}\left( x \right)}$$
که در آن، $${I_v}\left( x \right)$$ و $${K_v}\left( x \right)$$ بهترتیب، توابع بسل نوع اول و دوم هستند.
(۲) «معادله دیفرانسیل ایری» (Airy) که در ستاره شناسی و فیزیک کاربرد دارد، بهفرم زیر است:
$$y^{\prime\prime} – xy = 0.$$
معادله فوق را میتوان به معادله بسل کاهش داد. جواب را نیز میتوان براساس توابع بسل مرتبه کسری $$\pm {\large\frac{1}{3}\normalsize}$$ بیان کرد:
$${y\left( x \right) }
= {{C_1}\sqrt x {J_{\large\frac{1}{3}\normalsize}}\left( {\frac{2}{3}i{x^{\large\frac{3}{2}\normalsize}}} \right) }
+ {{C_2}\sqrt x {J_{ – \large\frac{1}{3}\normalsize}}\left( {\frac{2}{3}i{x^{\large\frac{3}{2}\normalsize}}} \right).}$$
(۳) معادله دیفرانسیل بهفرمِ
$${{x^2}y^{\prime\prime} + xy’ }+{ \left( {{a^2}{x^2} – {v^2}} \right)y }={ 0}$$
فقط در ضریب $$a^2$$ قبل از $$x^2$$ با معادله بسل تفاوت دارد و جواب عمومی آن بهفرم زیر است:
$${y\left( x \right) }={ {C_1}{J_v}\left( {ax} \right) + {C_2}{Y_v}\left( {ax} \right).}$$
(۴) معادله دیفرانسیل بهشکلِ
$${{x^2}y^{\prime\prime} + axy’ }+{ \left( {{x^2} – {v^2}} \right)y }={ 0}$$
را میتوان به معادله بسل کاهش داد:
$${{x^2}z^{\prime\prime} + xz’ }+{ \left( {{x^2} – {n^2}} \right)z }={ 0}$$
که در آن، از تبدیل زیر استفاده میکنیم:
$$y\left( x \right) = {x^{\large\frac{{1 – a}}{2}\normalsize}}z\left( x \right)$$
پارامتر $$n^2$$ نیز بهصورت زیر تعریف میشود:
$${n^2} = {v^2} + \frac{1}{4}{\left( {a – 1} \right)^2}.$$
در نتیجه، جواب عمومی معادله دیفرانسیل را میتوان بهصورت زیر بیان کرد:
$${y\left( x \right) }={ {x^{\large\frac{{1 – a}}{2}\normalsize}}\left[ {{C_1}{J_n}\left( x \right) }\right.}+{\left.{ {C_2}{Y_n}\left( x \right)} \right].}$$
توابع بسل خاص، کاربرد گستردهای در حل مسائل فیزیک نظری دارند. برای مثال، در بررسی انتشار امواج، انتقال حرارت و ارتعاشات صفحه در سیستمهایی با تقارن استوانهای یا کروی.
مثال ۱
معادله دیفرانسیل زیر را حل کنید:
$${x^2}y^{\prime\prime} + xy’+ \left( {3{x^2} – 2} \right)y=0$$
حل: این معادله، با معادله بسل تعمیمیافته در ضریب $$3$$ مربوط به $$x^2$$ تفاوت دارد. مرتبه معادله نیز $$\sqrt 2$$ است. در نتیجه، جواب عمومی را میتوان بهشکل توابع بسل اصلاحشده نوشت:
$${y\left( x \right) }={ {C_1}{J_{\sqrt 2 }}\left( {\sqrt 3 x} \right) }+{ {C_2}{Y_{\sqrt 2 }}\left( {\sqrt 3 x} \right)}$$
که در آن، $$C_1$$ و $$C_2$$ ثابتها و $${J_{\sqrt 2 }}\left( {\sqrt 3 x} \right)$$ و $${Y_{\sqrt 2 }}\left( {\sqrt 3 x} \right)$$ بهترتیب، توابع بسل نوع اول و دوم هستند.
مثال ۲
معادله دیفرانسیل زیر را حل کنید:
$${x^2}y^{\prime\prime} + xy’- \left( {4{x^2} + {\large\frac{1}{2}\normalsize}} \right)y= 0.$$
حل: این معادله، با معادله بسل تعمیمیافته در ضریب $$4$$ مربوط به $$x^2$$ تفاوت دارد. مرتبه معادله نیز $$v = {\large\frac{1}{{\sqrt 2 }}\normalsize}$$ است. در نتیجه، جواب عمومی را میتوان بهشکل توابع بسل اصلاحشده نوشت:
$${y\left( x \right) }={ {C_1}{I_{\large\frac{1}{{\sqrt 2 }}\normalsize}}\left( {2x} \right) }+{ {C_2}{K_{\large\frac{1}{{\sqrt 2 }}\normalsize}}\left( {2x} \right)}$$
که در آن، $$C_1$$ و $$C_2$$ ثابتهای دلخواهی هستند.
مثال ۳
جواب عمومی معادله دیفرانسیل زیر را بهدست آورید:
$${x^2}y^{\prime\prime} + 2xy’+ \left( {{x^2} – 1} \right)y= 0.$$
حل: از جانشینی زیر استفاده میکنیم:
$${y = {x^{\large\frac{{1 – 2}}{2}\normalsize}}z = {x^{ – \large\frac{1}{2}\normalsize}}z,\;\;}\\
\Rightarrow
{ y’ = – \frac{1}{2}{x^{ – \large\frac{3}{2}\normalsize}}z + {x^{ – \large\frac{1}{2}\normalsize}}z’,\;\;}\\
\Rightarrow
{y^{\prime\prime} = \frac{3}{4}{x^{ – \large\frac{5}{2}\normalsize}}z
– \frac{1}{2}{x^{ – \large\frac{3}{2}\normalsize}}z’ – \frac{1}{2}{x^{ – \large\frac{3}{2}\normalsize}}z’ }+{ {x^{ – \large\frac{1}{2}\normalsize}}z^{\prime\prime} } \\
= {\frac{3}{4}{x^{ – \large\frac{5}{2}\normalsize}}z – {x^{ – \large\frac{3}{2}\normalsize}}z’ }+{ {x^{ – \large\frac{1}{2}\normalsize}}z^{\prime\prime}.}$$
با قرار دادن عبارت فوق در معادله، داریم:
$${x^2}y^{\prime\prime} + 2xy’ + \left( {{x^2} – 1} \right)y = 0,\;\Rightarrow \\
{{x^2}\left( {\frac{3}{4}{x^{ – \large\frac{5}{2}\normalsize}}z – {x^{ – \large\frac{3}{2}\normalsize}}z’ }+{ {x^{ – \large\frac{1}{2}\normalsize}}z^{\prime\prime}} \right) }
+ {2x\left( { – \frac{1}{2}{x^{ – \large\frac{3}{2}\normalsize}}z }+{ {x^{ – \large\frac{1}{2}\normalsize}}z’} \right) } + {\left( {{x^2} – 1} \right){x^{ – \large\frac{1}{2}\normalsize}}z = 0,} \\
{\Rightarrow \color{blue}{\frac{3}{4}{x^{ – \large\frac{1}{2}\normalsize}}z} }
– {\color{red}{{x^{ – \large\frac{1}{2}\normalsize}}z’} + {x^{\large\frac{3}{2}\normalsize}}z^{\prime\prime} }
– {\color{blue}{{x^{ – \large\frac{1}{2}\normalsize}}z} + \color{red}{2{x^{\large\frac{1}{2}\normalsize}}z’} }
+ {\color{blue}{{x^{\large\frac{3}{2}\normalsize}}z} – \color{blue}{{x^{ – \large\frac{1}{2}\normalsize}}z} = 0,} \\
\Rightarrow {{x^{\large\frac{3}{2}\normalsize}}z^{\prime\prime} + \color{red}{{x^{ – \large\frac{1}{2}\normalsize}}z’} }+{\color{blue}{\left( { – \frac{5}{4}{x^{ – \large\frac{1}{2}\normalsize}} + {x^{\large\frac{3}{2}\normalsize}}} \right)z} }={ 0}, \\
\Rightarrow {{x^2}z^{\prime\prime} + xz’ }+{ \left( {{x^2} – \frac{5}{4}} \right)z }={ 0.}$$
در واقع، مشاهده میکنیم:
$${{n^2} = {v^2} + \frac{1}{4}{\left( {a – 1} \right)^2} }
= {1 + \frac{1}{4}{\left( {2 – 1} \right)^2} }
= {1 + \frac{1}{4} }
= {\frac{5}{4}.}$$
بنابراین، حل عمومی تابع $$z\left( x \right)$$ را میتوان بهفرم زیر نوشت:
$${y\left( x \right) = {x^{ – \large\frac{1}{2}\normalsize}}z\left( x \right) }
= {\frac{1}{{\sqrt x }}\left[ {{C_1}{J_{\large\frac{{\sqrt 5 }}{2}\normalsize}}\left( x \right) }\right.}+{\left.{ {C_2}{Y_{\large\frac{{\sqrt 5 }}{2}\normalsize}}\left( x \right)} \right],}$$
که در آن، $$C_1$$ و $$C_2$$ ثابتهای اختیاری هستند.











خط اول حالت دوم رو اشتباه نوشتید! در واقع
اگه مرتبه معادله دیفرانسیل بسل عدد صحیح باشه، توابع مستقل از هم نخواهند بود و وابسته ی خطی میشن، برای همینه که باید جواب عمومی رو برحسب تابع بسل نوع دوم بنویسیم
سلام.
بله، کاملاً صحیح است. مطلب تصحیح شد.
سپاس از همراهی و بازخورد دقیقتان.
چرا هر مبحثی که برای من مشکله اینجا فیلم ازش نیست
دقیقا