ترموشیمی چیست؟ – آشنایی با گرماشیمی به زبان ساده

ترموشیمی یکی از شاخههای مهم در دنیای شیمی است که به بررسی ماهیت انرژی در قالب کار و گرما میپردازد و مفاهیم مرتبط با آنها مانند آنتالپی و قانون اول ترمودینامیک را بررسی میکند. آشنایی با این مفهوم از آنجایی حائز اهمیت است که اطلاعات فراوانی در مورد نحوه انتقال انرژی بهصورت گرما در سیستمهای مختلف شیمیایی به دست میدهد. از همین رو دانشجویان و شاغلان در این حوزه برای درک و امکان طراحی سیستمهای شیمیایی مورد نیاز باید با مفاهیم ترموشیمی و نحوه استفاده از روابط مسلط بر آن آشنایی داشته باشند.
در این مطلب مجله فرادرس برای بررسی مفهوم ترموشیمی ابتدا به ماهیت انرژی میپردازیم و انواع سیستمهای موجود در شیمی را معرفی میکنیم. سپس با بررسی قانون ترمودینامیک به مفهوم آنتالپی بهعنوان یک تابع حالت خواهیم پرداخت. در ادامه با آنتالپی در واکنش و قانون هس آشنا میشویم و روشهای موجود برای کالریمتری را بررسی خواهیم کرد. در هر مورد روابط موجود آورده شده است و مثالهایی برای درک بهتر آنها نیز ارائه دادهایم. در نهایت نیز برای عمق بخشیدن به درک خود از این مفهوم تعدادی مثال و تمرین چندگزینهای را مرور کردهایم.
ترموشیمی چیست؟
«ترموشیمی» (Thermochemistry) دانشی از شیمی است که شامل مطالعه گرما و انرژی میشود. این پدیدهها طی تبدیلات و واکنشهای شیمیایی متفاوت به وجود میآيند. برای مثال در واکنشی شیمیایی ممکن است انرژی جذب شود که به آن «واکنش گرماگیر» (Endothermic Reaction) گفته میشود. همچنین «واکنش گرماده» (Exothermic Reaction) واکنشی است که طی واکنش از خود انرژی آزاد میکند.
ترموشیمی به تغییرات در انرژی به ویژه توسط سیستمها با محیط اطراف آنها میپردازد، بنابراین در ادامه به هر یک از این مفاهیم میپردازیم. با توجه به قوانین ترمودینامیک، انرژی یک سیستم ایزوله در طول زمان ثابت باقی میماند و در صورتی که سیستم ایزوله نباشد، شاهد تغییراتی در سطح انرژی آن هستیم. برای درک تغییرات انرژی، تغییرات گرمایی و خودبهخودی بودن واکنش میتوان از ترموشیمی کمک گرفت.
در تمامی واکنشها روابطی برای گرما، کار و گرما-کار وجود دارد. در طی یک واکنش ممکن است روی سیستم کار انجام شود. همچنین خود سیستم نیز میتواند انجامدهنده کار باشد. این مورد را با گرماده و گرماگیر بودن واکنش مقایسه کنید. برای مطالعه این موارد پیش از هر چیزی باید درکی از ماهیت انرژی و انواع روشهای انتقال آن داشته باشیم.
ماهیت انرژی
انرژی انواع مختلفی دارد که از این بین میتوان به «انرژی گرمایی» (Thermal Energy)، «انرژی تابشی» (Radiant Energy)، «انرژی الکتریکی» (Electrical Energy)، «انرژی هستهای» (Nuclear Energy) و «انرژی شیمیایی» (Chemical Energy) اشاره کرد. انرژی گرمایی از حرکت اتمها و مولکولها ناشی میشود و هرچه سرعت حرکت آنها بیشتر باشد، مقدار این انرژی نیز بیشتر خواهد بود.
همانطور که میدانید انواع انرژی میتوانند از نوعی به نوع دیگر تبدیل شوند. در ادامه میخواهیم به رابطه انرژی و کار بپردازیم و معادلات مسلط بر آنها را مورد مطالعه قرار دهیم.
رابطه انرژی، گرما و کار
انرژی در واقع همان ظرفیت و توانایی انجام «کار» (Work) است. سادهترین نوع کاری که میتوان در ترموشیمی برای مثال از آن استفاده کرد کار مکانیکی است که برابر با مقدار انرژی مورد نیاز برای جابهجا کردن یک شیء در فاصله $$d$$ توسط نیروی $$F$$ است. بنابراین میتوان کار را حاصلضرب نیرو در فاصله دانست که آن را با رابطه زیر نمایش میدهیم.
$$w=F\,d $$
طبق تعریف، نیرو برابر با جرم یک شیء $$(m)$$ ضرب در شتاب $$(a)$$ آن است، بنابراین میتوان رابطه بالا را بهصورت زیر بازنویسی کرد.
$$w = m\,a\,d $$
برای مثال به کار مکانیکی توجه کنید که برای رفتن از طبقه اول یک ساختمان به طبقه دوم آن نیاز دارید. در این صورت برای پیمایش آن به مقدار انرژی نیاز است که توسط کار مکانیکی تعریف میشود.
گرما چیست؟
«گرما» (Heat) در ترموشیمی نوعی از انرژی است که از جسم ۱ با دمای ۱ به جسم ۲ با دمای ۲ منتقل میشود. انتقال این انرژی در صورتی که دمای دو جسم با یکدیگر برابر شود، به حالت توقف میرسد.
انرژی کمیتی مقداری است زیرا مقدار انرژی گرمایی انتقالی از یک جسم به جسم دیگر به دما و جرم آن بستگی دارد. برای مثال گرمکنی که حاوی ۱۵۰ لیتر از آب در دمای ۵۰ درجه سانتیگراد است، نسبت به کتری حاوی ۱ لیتر از آب در دمای ۵۰ درجه سانتیگراد، انرژی گرمایی بیشتری دارد.
توجه داشته باشید که مفهوم انرژی بسیار وسیعتر از مواردی است که در اینجا به آن پرداختیم اما برای بررسی ترموشیمی به همین نکات بسنده خواهیم کرد.
واحد انرژی
واحد انرژی برای تمامی انواع آن یکسان است. یکی از واحدهایی که برای بیان انرژی از آن استفاده میشود، «کالری» (Calorie) است که طبق تعریف ۱ کالری مقدار انرژی است که برای افزایش دمای ۱ گرم آب به میزان ۱ درجه سانتیگراد مورد نیاز است. واحد دیگری که برای بیان انرژی از آن استفاده میشود، «ژول» (Joule) نامیده میشود و میتوان رابطه این دو کمیت را بهصورت زیر نشان داد.
$$1 \;cal = 4.184 \;J $$
$$1 \;J = 0.2390\; cal $$
انواع سیستم
برای مطالعه جریان انرژی در طول واکنشی شیمیایی، باید بتوانیم بین سیستم و محیط اطراف آن تمایز قائل شویم و برای این کار باید با انواع سیستمهایی که در ترموشیمی با آن روبرو میشویم، آشنایی پیدا کنیم. طبق تعریف، ترکیبی از مواد شیمیایی که وارد واکنش میشود، «سیستم» (System) نام دارد.
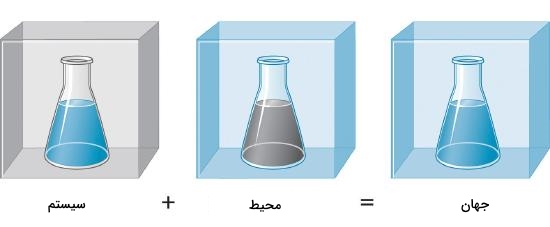
همچنین جریان انرژی از سیستم به بیرون یا برعکس را به نام «محیط» (Surronding) میشناسیم. سیستم و محیط با یکدیگر جهان را تشکیل میدهند. این را میتوانید در تصویر زیر بهصورت بسیار ساده مشاهده کنید.
سه نوع سیستم وجود دارند که از اهمیت بالایی برخوردارند و باید با آنها و ویژگیهایی که از خود نشان میدهند برای درک ترموشیمی آشنایی داشته باشیم. در ادامه به این سه نوع سیستم ترمودینامیکی خواهیم پرداخت.
سیستم باز چیست؟
«سیستم باز» (Open System) سیستمی است که میتواند با محیط پیرامون خود تبادل انرژی و ماده داشته باشد. برای مثال کتری در حال جوش نمونهای از یک سیستم باز است که در آن انرژی بهصورت گرما و ماده بهصورت بخار آب تبادل میشود.
سیستم بسته چیست؟
«سیستم بسته» (Closed System) نوعی از سیستم است که با محیط پیرامون خود تبادل انرژی دارد اما تبادل ماده انجام نخواهد داد. در صورتی که آب در کتری در حال جوش باشد و در کتری بسته باشد، انتقال انرژی صورت میگیرد اما بخار آب نمیتواند به محیط پیرامون وارد شود و این سیستم از نوع بسته خواهد بود.
سیستم ایزوله چیست؟
«سیستم ایزوله» (Isolated System) در ترموشیمی سیستمی است که با محیط پیرامون خود نه تبادل ماده، نه تبادل انرژی انجام نمیدهد. توجه داشته باشید که در واقع همیشه سیستمها با محیط اطراف خود تبادل انرژی انجام میدهند اما در صورتی که این تبادل بسیار کند باشد آن را سیستم ایزوله میدانیم. مثالی از این سیستم، فلاسک نگهداری چای است. در این فلاسک تبادل جرم و انرژی انجام نمیشود اما در نهایت چای داخل فلاسک سرد خواهد شد.

در تمام سیستمهایی که بررسی کردیم، مقدار گرمایی که سیستم از دست میدهد برابر با مقدار گرمایی است که محیط پیرامون آن دریافت میکند. عکس این نکته نیز صادق است، یعنی اگر سیستم از محیط پیرامون خود گرما دریافت کند، مقدار آن برابر با مقدار گرمایی است که از محیط پیرامون از دست رفته است.
انتقال گرما
در این بخش میخواهیم کمی بیشتر در مورد نحوه انتقال گرما در واکنشهای شیمیایی بدانیم. برای مثال واکنش پودر عنصر آلومینیوم با آهن (II) اکسید را در نظر بگیرید که به نام «واکنش ترمیت» (Thermite Reaction) شناخته میشود. طی این واکنش مقادیر بسیار زیادی گرما تولید میشود. این گرما آنقدر زیاد است که میتوان از آن برای ذوب کردن استیل استفاده کرد. واکنش موزانه شده ترمیت را در زیر مشاهده میکنید.
$${ 2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s)} $$
میتوان گرما را نیز به عنوان یکی از محصولات واکنش در سمت راست آن یادداشت کرد که در این صورت به آن «معادله ترموشیمیایی» (Thermochemical Equation) گفته میشود. این واکنش نمونهای از واکنش گرماده است که در آن انرژی بهصورت گرما به محیط انتقال مییابد و معادله زیر برای آن صادق است.
$$ q<0 $$
همچنین واکنش گرماگیر واکنشی است که طی آن انرژی بهصورت گرما از محیط به سیستم وارد میشود. مثالی از این نوع واکنش آب شدن یخ است. اگر قطعه یخی را در دست خود نگه دارید، گرما از دست و محیط به یخ منتقل میشود و شاهد آب شدن آن هستیم. این واکنش ترموشیمیایی را میتوان بهصورت زیر نمایش داد.
$${heat + H_2O(s) \rightarrow H_2O(l)} $$
توجه داشته باشید که در واکنش گرماگیر، مولفه گرما در سمت چپ واکنش قرار داده میشود و انتقال گرما در این سیستم را میتوان بهصورت زیر نمایش داد.
$$ q>0 $$
قانون اول ترمودینامیک
رابطه بین تغییرات انرژی یک سیستم و محیط پیرامون آن را میتوان توسط «قانون اول ترمودینامیک» (First Law of Thermodynamic) بیان کرد. طبق این قانون انرژی جهان همواره ثابت است و میتوان آن را بهصورت زیر نشان داد.
$$ U_{univ}=ΔU_{sys}+ΔU_{surr}=0 $$
$$ \Delta{U_{sys}}=−ΔU_{surr} $$
مولفههای موجود در این رابطه بهصورت زیر تعریف میشوند.
- $$ \Delta{U_{sys}}$$: انرژی پتانسیلی سیستم
- $$ \Delta{U_{univ}}$$: انرژی پتانسیلی جهان
- $$ \Delta{U_{surr}}$$: انرژی پتانسیلی محیط
طبق این رابطه مقدار تغییر انرژی سیستم و محیط با یکدیگر برابر و دارای علامت مخالف است. توجه داشته باشید که انرژی در یک سیستم در دو حالت میتواند منتقل شود که گرما و کار هستند. بنابراین مجموع انرژی یک سیستم برابر با گرمای منتقل شده به علاوه کار انجام شده است که آن را توسط رابطه زیر نشان میدهیم.
$$ ΔU_{sys} = q + w $$
- $$ ΔU_{sys} $$: تغییرات انرژی
- $$ q $$: گرمای منتقل شده
- $$ w $$: کار انجا شده
کار و گرما خود «تابع حالت» (State Function) نیستند اما مجموع آنها یعنی انرژی، مستقل از مسیر پیموده شده و بنابراین تابع حالت است. یکی از مهمترین کارهایی که طراحان برای ماشینهای مبدل انرژی به کار، انجام میدهند، افزایش مقدار کار به دست آمده و کاهش مقدار انرژی منتقل شده به محیط در قالب گرما است.
طبق قانون اول ترمودینامیک، در صورتی که مقدار کار و گرمای سیستمی را داشته باشیم، میتوانیم مقدار انرژی آن را به دست آوریم. مقدار گرما را میتوان با تغییر مقدار دمای محیط به دست آورد. همچنین میتوان از رابطه زیر برای به دست آوردن کار انجام شده توسط سیستم یا بر روی آن استفاده کرد.
$$ w = −PΔV $$
علامت منفی در این معادله نشاندهنده این است که با افزایش حجم، سیستم انرژی از دست میدهد. بنابراین گازی که منبسط میشود روی محیط اطراف خود کار انجام میدهد و روی گازی که منقبض میشود، توسط سیستم کار انجام میشود.
آنتالپی
در این بخش میخواهیم به مفهوم مهم دیگری در ترموشیمی به نام «آنتالپی» (Enthalpy) بپردازیم و برای بیان آن نیاز به مقدمهای داریم که در ادامه مشاهده میکنید.
برای محاسبه مقدار کار، میتوان دو فرض را پیش گرفت. به این صورت که در یکی از آنها فشار و در دیگری حجم سیستم ثابت باشد. برای سادگی در اینجا فرض بر این است که تنها کاری که انجام میشود، گونهای است که مقدار آن با معادله بالا قابل دستیابی است و در این صورت میتوان آن را در معادله قانون اول ترمودینامیک جایگذاری کرد که نتیجه بهصورت زیر خواهد بود.
$$ ΔU = q − PΔV $$
اگر واکنش مورد نظر در ظرفی با حجم مشخص و غیرقابل تغییر انجام شود، میتوان مقدار $$ΔV $$ را برابر با صفر در نظر گرفت. در این حالت مقدار گرما در فشار ثابت با تغییر انرژی برابر خواهد بود که آن را در معادله زیر نمایش دادهایم. توجه داشته باشید که زیروند $$v$$ برای گرما، نشاندهنده این است که حجم سیستم ثابت میماند.
$$ {q_{\textrm v}=\Delta U} $$
با این حال توجه داشته باشید که اغلب واکنشهای شیمیایی در ظرفهای دربسته و با حجم ثابت انجام نمیشوند. بسیاری از آنها در ظرفهایی باز انجام میشوند اما فشار آنها در گذر زمان به نسبت ثابت باقی میماند و برابر با ۱ اتمسفر خواهد بود. در این حالت برای نشان دادن گرما در فشار ثابت به آن زیروند $$p$$ افزوده میشود. رابطه قانون اول ترمودینامیک را تحت چنین شرایطی بهصورت زیر نمایش میدهیم.
$$ {q_{\textrm p}=\Delta U+P\Delta V} $$
بنابراین همانطور که مشاهده میکنید تحت این شرایط مقدار کار انجام شده نیز در معادله حضور دارد. واکنشهایی که در این شرایط انجام میشوند در شیمی از اهمیت بسیار زیادی برخوردارند و به همین دلیل مولفهای به نام آنتالپی که تابع حالت است برای بیان آن در نظر گرفته شده است که معادله آن بهصورت زیر است.
$$ H =U + PV $$
در فشار ثابت تغییرات آنتالپی یک سیستم را با فرمول زیر نشان میدهیم.
$$ΔH = ΔU + Δ(PV) = ΔU + PΔV$$
بنابراین در فشار ثابت، تغییرات آنتالپی یک سیستم برابر با گرمای آن است.
$$ ΔH = q_p $$
در نهایت میتوان تعریف جامع و سادهای برای آنتالپی به دست آورد. آنتالپی مقدار گرمای جذب شده یا تولید شده طی فرآیندی است که فشار ثابتی دارد. برای درک بهتر این مفهوم و نحوه استفاده از روابط آن در بخش بعد مثالی از آن را مورد بررسی قرار میدهیم.
مثال از آنتالپی
آنتالپی مولی ذوب یخ در دمای ۰ درجه سانتیگراد و فشار ۱ اتمسفر برابر با ۶٫۰۱ کیلوژول است. همچنین حجم مولی یخ و آب در همان دما برابر با ۰٫۰۱۹۷ لیتر و ۰٫۰۱۸ لیتر است. مقدار $$ΔH $$ و $$ΔU $$ ذوب شدن یخ را به دست آورید.
پاسخ
از آنجا که در ذوب شدن ۱ مول از یخ، ۶٫۰۱ کیلوژول گرما توسط محیط اطراف جذب میشود و فرآیند نیز در فشار ثابت است، میتوان رابطه زیر را نوشت.
$$ q = q_p = ΔH = 6.01 kJ $$
سپس باید مقدار $$ΔU $$ را بیابیم و برای این کار باید مقدار $$ Δ(PV)$$ را در دست داشته باشیم. همانطور که پیشتر گفتیم این واکنش در فشار ثابت انجام میشود و میتوان محاسبات زیر را برای آن انجام داد.
$$ \begin{align}\Delta(PV)&=P\Delta V=P(V_{\textrm f}-V)=(1.00\textrm{ atm})(\textrm{0.0180 L}-\textrm{0.0197 L})
\\ &=(-1.7\times10^{-3}\;\mathrm{L\cdot atm})(101.3\;\mathrm{J/L\cdot atm})=-0.0017\textrm{ J}\end{align} \nonumber$$
در مرحله بعد با جایگذاری مقادیر به دست آمده میتوانیم $$ΔU $$ را داشته باشیم.
$$ ΔU = ΔH − PΔV = 6010 J − (−0.0017 J) = 6010 J = 6.01 kJ$$
رابطه بین $$ ΔH$$ و $$ ΔU$$
در این بخش میخواهیم به بررسی رابطه بین این دو مولفه مهم در ترموشیمی بپردازیم. در صورتی که در واکنشی مقدار $$ ΔH$$ در دست باشد، میتوان از رابطه زیر برای به دست آوردن تغییرات انرژی استفاده کرد.
$$ ΔH = ΔU + Δ(PV) = ΔU + PΔV$$
در صورتی که در واکنش تنها ترکیبات مایع و جامد یا مخلوطی از آنها دخیل باشد، تفاوت زیادی در مقدار حجم ایجاد نمیشود و میتوان متغیر حجم را برابر با صفر در نظر گرفت. تحت چنین شرایطی رابطه بالا را بهصورت زیر ساده میکنیم.
$$ ΔH = ΔU $$
در صورتی که در واکنش ترکیبات گازی حضور داشته باشند، مقدار این دو میتواند متفاوت باشد. برای به دست آوردن این دو مقدار میتوان از رابطه زیر استفاده کرد.
$$ PV = nRT $$
سپس با جایگذاری این مقدار در رابطه آنتالپی، خواهیم داشت:
$$ ΔH = ΔU + Δ(PV) = ΔU + Δ(nRT) $$
در شرایطی که دما ثابت باشد، تساوی زیر برقرار است.
$$ Δ(nRT) = RTΔn $$
منظور از $$Δn$$ در این رابطه، تفاوت بین تعداد مولهای اولیه و نهایی گاز مورد نظر در واکنش است. با جایگذاری رابطه بالا در رابطه اصلی به معادله زیر میرسیم.
$$ΔU = ΔH − RTΔn $$
برای واکنشهای گرماده که در آن تعداد مولها افزایش پیدا میکند، میتوان اینطور نوشت:
$$ Δn > 0 $$
$$ ΔU < ΔH $$
همچنین برای واکنشهای گرماگیر که در آن مقدار تغییرات آنتالپی بزرگتر از صفر است، تعدادی مول گازی مصرف میشوند، بنابراین مولها در پایان واکنش از ابتدای واکنش کمتر خواهد بود و میتوان روابط زیر را برای آنها نوشت.
$$ Δn < 0 $$
$$ ΔU > ΔH $$
در ادامه مثالی را مورد بررسی قرار میدهیم که در آن از روابط بالا استفاده میشود.
مثال از رابطه انرژی و آنتالپی
واکنش سوختن گرافیت برای تولید کربن دیاکسید را بهصورت زیر نشان میدهیم.
$$C_{(graphite, s)} + O_{2(g)} → CO_{2(g)} \nonumber$$
در دمای ۲۹۸ کلوین و فشار ۱ اتمسفر، مقدار تغییرات آنتالپی آن برابر با ۳۹۳٫۵- کیلوژول بر مول است. همچنین حجم مولی گرافیت برابر با ۰٫۰۰۵۳ لیتر است. مقدار $$ ΔU$$ را برای این واکنش به دست آورید.
پاسخ
در این واکنش ۱ مول از گاز کربن دیاکسید تولید و ۱ مول از گاز اکسیژن مصرف میشود، بنابراین تغییرات آنتالپی مانند زیر برابر با صفر است.
$$ Δn = 1 − 1 = 0$$
با جایگذاری مقادیر داده شده در رابطه، میتوانیم مقدار انرژی را به دست آوریم.
$$ ΔU=ΔH−RTΔn=(−393.5 kJ/mol)−[8.314 J/(mol⋅K)](298 K)(0)
=(−393.5 kJ/mol)−(0 J/mol)=−393.5 kJ/mol $$
توجه داشته باشید که حجم مولی گرافیت برابر با ۰٫۰۰۵۳ لیتر است، بنابراین تغییران آن نیز نسبت به گاز با حجم مولی ۲۲٫۴ لیتر بر مول بسیار ناچیز خواهد بود. این حجم مربوط به فشار و دما در شرایط استاندارد است.
آنتالپی واکنش چیست؟
در این بخش میخواهیم بررسی دقیقتری بر مفهوم ترموشیمی آنتالپی در واکنشهای شیمیایی داشته باشیم. واکنشی را در نظر بگیرید که در آن گاز تولید میشود، برای مثال واکنش حل شدن تکهای مس در نیتریک اسید غلیظ. معادله شیمیایی این واکنش را بهصورت زیر نمایش میدهیم.
$$ {Cu(s) + 4HNO_3(aq) \rightarrow Cu(NO_3)_2(aq) + 2H_2O(l) + 2NO_2(g)} \nonumber $$
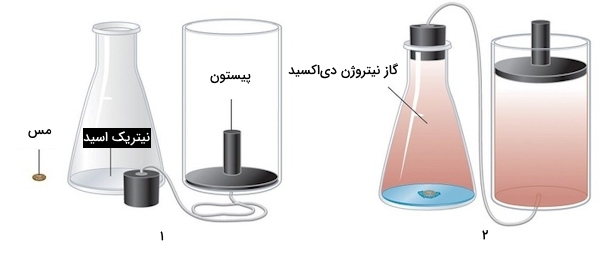
در صورتی که این واکنش در سیستم بستهای انجام شود که فشار آن توسط پیستونی قابل حرکت کنترل میشود، با تولید گاز نیتروژن دیاکسید، پیستون به سمت بالا حرکت میکند. در این صورت در سیستم کار انجام میشود که مقدار آن را میتوان بهراحتی از رابطه کار، محاسبه کرد. در تصویر شماره ۲ زیر شاهد حرکت پیستون به سمت بالا هستید که نشاندهنده انجام واکنش و تولید گاز در محیط است.
طبق رابطه آنتالپی میدانیم که تمامی مولفههای آن مانند انرژی، فشار و حجم توابع حالت هستند، بنابراین آنتالپی نیز تابع حالت است و میتوان در یک واکنش رابطه زیرا را برای آن نوشت.
$$ ΔH = H_{final} − H_{initial} \nonumber $$
در مطالعه تغییرات انرژی در یک واکنش شیمیایی، مهم ترین کمیتی که به آن میپردازیم، آنتالپی آن است. در صورتی که گرما از سیستم به محیط پیرامون آن منتقل شود، آنتالپی سیستم کاهش پیدا میکند و مقدار آن را با علامت منفی نشان میدهیم. در حالت دیگر اگر گرما از محیط پیرامون به سیستم منتقل شود، آنتالپی سیستم افزایش پیدا میکند و مقدار آن نیز مثبت خواهد بود.
بهطور کلی میتوان اینطور بیان کرد که در واکنشهایی که در آنها پیوندی شیمیایی میشکند، نیاز به ورود انرژی داریم و واکنش از نوع گرماگیر خواهد بود. برعکس این مورد نیز صدق میکند. یعنی در واکنشهایی که شامل تشکیل پیوند شیمیایی جدید هستند، انرژی آزاد میشود و واکنش از نوع گرماده است.
در صورتی که مقدار آنتالپی یک واکنش در ترموشیمی عددی منفی باشد به این معناست که آنتالپی محصولات کمتر از آنتالپی واکنشدهندههای اولیه خواهد بود و این واکنش گرماده است. همچنین اگر مقدار آنتالپی یک واکنش عددی مثبت باشد، آنتالپی محصولات بزرگتر از آنتالپی واکنشدهنده اولیه و واکنش گرماگیر است. این گفتهها را میتوانید بهصورت بسیار ساده در تصویر زیر مشاهده کنید. در ادامه میخواهیم به تعدادی از ویژگیهای این کمیت بپردازیم.
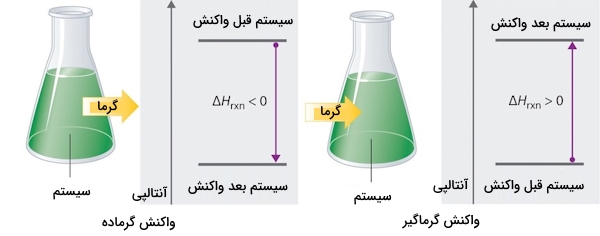
در صورتی که واکنشی در جهت عکس خود انجام شود، علامت $$ΔH$$ آن نیز تغییر خواهد کرد. برای مثال میتوان به یخ اشاره کرد که در ذوب شدن به خود گرما جذب میکند و در آن برهمکنشهای الکتروستاتیک میشکنند. در این صورت آب مایع در فرآيند منجمد شدن از خود گرما آزاد میکند که در آن برهمکنشهایی الکتروستاتیک به وجود میآیند. این را میتوانید در دو واکنش زیر مشاهده کنید.
$$\begin{matrix}
heat+ H_{2}O(s) \rightarrow H_{2}O(l) & \Delta H > 0
\end{matrix}$$
$$\begin{matrix}
H_{2}O(l) \rightarrow H_{2}O(s) + heat & \Delta H < 0
\end{matrix} $$
توجه داشته باشید که مقدار دو آنتالپی با یکدیگر برابر است و تنها علامت آنها متفاوت خواهد بود.
آنتالپی مانند جرم «خاصیت مقداری» (Extensive Property) است، یعنی بزرگی آن متناسب با مقدار مواد اولیهای است که در واکنش شرکت میکنند. برای مثال آتشی بزرگ گرمای بسیار بیشتری نسبت به یک چوب کبریت ایجاد میکند، گرچه واکنش سوختن چوب در هر دو مورد یکسان است. به همین دلیل در بیشتر موارد تغییرات آنتالپی یک واکنش را در واحد کیلوژول بر مول واکنشدهنده یا محصولی خاص گزارش میدهند.
به معادله زیر توجه کنید که مربوط به واکنش بین آلومینیوم با آهن(III) اکسید با فرمول شیمیایی $$Fe_2O_3$$ است. با در نظر گرفتن استوکیومتری این واکنش، ۲ مول از $$Fe$$ و ۱ مول از $$Al_2O_3$$ و ۸۵۱٫۵ کیلوژول گرما، تولید میشود و ۲ مول از $$Al$$ و ۱ مول از $$Fe_2O_3$$ مورد استفاده قرار میگیرد.
$${2Al(s) + Fe2O3(s) \rightarrow 2Fe (s) + Al2O3 (s) } + 815.5 \; kJ $$
بنابراین میتوان مقدار آنتالپی را بهصورت زیر نمایش داد.
$$ ΔH = −851.5 \;kJ/mol \;of \;Fe_2O_3 $$
در صورتی که بخواهیم مقدار آنتالپی را با توجه به واکنشدهنده آلومینیوم بیان کنیم، آن را بهصورت زیر نشان میدهیم.
$$ ΔH = −425.8 \;kJ/mol \;of \;Al $$
توجه داشته باشید که در این واکنش ۲ مول از آلومینیوم مصرف میشود، بنابراین مقدار ۸۵۱٫۵ کیلوژول را تقسیم بر عدد ۲ میکنیم. بهصورت کلی رابطه بین مقدار هر واکنشدهنده و تغییرات آنتالپی را میتوان با تساوی زیر بیان کرد.
$$ - \dfrac{851.5 \; kJ}{2 \; mol \;Al} = - \dfrac{425.8 \; kJ}{1 \; mol \;Al} = - \dfrac{1703 \; kJ}{4 \; mol \; Al} $$
انواع آنتالپی
برای تعیین مقدار تغییر آنتالپی یک واکنش تنها نیاز داریم آنتالپی ابتدا و انتهایی آن را داشته باشیم زیرا آنتالپی تابع حالت است. با توجه به واکنشی که در ترموشیمی انجام میشود، آنتالپی نامهای مختلف خواهد داشت که در ادامه به برخی از آنها اشاره میکنیم.
آنتالپی سوختن
«آنتالپی سوختن» (Enthalpy of Combustion) که آن را با نماد $$ ΔH_{comb} $$ نمایش میدهیم، تغییر آنتالپی است که در واکنش سوختن رخ میدهد. مقدار آنتالپی سوختن برای هر مادهای که میتواند در واکنش با اکسیژن بسوزد را اندازهگیری کردهاند. مقادیر آنتالپی سوختن معمولا به ازای ۱ مول از ماده اولیه گزارش میشود.
آنتالپی ذوب
«آنتالپی ذوب» (Enthalpy of Fusion)، آنتالپی است که در آن ۱ مول از مادهای ذوب میشود و آن را با نماد $$ ΔH_{fus} $$ نشان میدهند. در منابع میتوان مقدار آنتالپی ذوب را برای بیشتر عنصرها و همچنین بسیاری از ترکیبات شیمیایی ساده پیدا کرد.

آنتالپی تبخیر
«آنتالپی تبخیر» (Enthalpy of Vaporization)، آنتالپی تغییری است که طی آن ۱ مول از مادهای تبخیر میشود و با نماد $$ ΔH_{vap} $$ مشخص میشود. مقدار این آنتالپی نیز برای بیشتر عنصرها و بساری از ترکیبات فرار اندازهگیری و گزارش شده است.
آنتالپی انحلال
«آنتالپی انحلال» (Enthalpy of Solution) را با نماد $$ ΔH_{soln} $$ نمایش میدهیم و برابر تغییر آنتالپی است که در انحلال مقدار مشخصی از یک حلشونده در مقدار مشخصی از یک حلال رخ میدهد.
مقادیر زیر مربوط به آنتالپی تبخیر و آنتالپی ذوب تعدادی از ترکیبات پرکاربرد در دنیای شیمی هستند.
| نام ماده | $$ΔH_{vap} (kJ/mol)$$ | $$ΔH_{fus} (kJ/mol)$$ |
| آرگون | ۶٫۳ | ۱٫۳ |
| متان | ۹٫۲ | ۰٫۸۴ |
| اتانول | ۳۹٫۳ | ۷٫۶ |
| آب | ۴۰٫۷ | ۶٫۰ |
| جیوه | ۵۹٫۰ | ۲٫۲۹ |
قانون هس چیست؟
همانطور که پیشتر گفتیم، آنتالپی تابع حالت است و تنها به حالت اولیه و نهایی یک واکنش بستگی دارد که توسط «قانون هس» (Hess's Law) بیان میشود.
مثال از قانون هس
آنتالپی واکنش زیر را با توجه به قانون هس محاسبه کنید.
$$ 2C(s) + H_2(g) \rightarrow C_2H_2(g)$$
معادلات ترموشیمیایی این واکنش بهصورن زیر است:
$$ C_2H_2(g) + \frac{5}{2}O_2(g) \rightarrow 2CO_2(g) + H_2O(ℓ) \;\;\;\;\;\;\;\;ΔH° = −1299.5\; kJ$$
$$ C(s) + O_2(g) \rightarrow CO_2(g) \;\;\;\;\;\;\;ΔH° = −393.5\; kJ$$
$$H_2(g) + \frac{1}{2}O_2(g) \rightarrow H2O(ℓ) \;\;\;\;\;ΔH° = −285.8 \;kJ$$
پاسخ
ابتدا باید معادلات ترموشیمیایی را بهصورتی بنویسیم که با واکنش اصلی مطابقت داشته باشند. برای این کار واکنش اول را برعکس میکنیم تا $$C_2H_2$$ در محصولات باشد و علامت آنتالپی آن نیز تغییر میکند. سپس واکنش دوم را در عدد ۲ ضرب میکنیم و مقدار آنتالپی آن نیز دو برابر میشود. توجه داشته باشید که واکنش سوم نیازی به تغییر ندارد.
$$2CO_2(g) + H_2O(ℓ) \rightarrow C_2H_2(g) + \frac{5}{2}O_2(g) \;\;\;\;\;ΔH° = +1299.5\; kJ$$
$$2 C(s) +2 O_2(g) \rightarrow 2CO_2(g) \;\;\;\;\;\;\;ΔH° = −787\; kJ$$
واکنشدهندههای یکسان را در دو طرف واکنشها با یکدیگر حذف میکنیم. واکنشدهنده $$2CO_2$$ از وکنش اول و دوم، واکنشدهنده $$H_2O$$ از واکنش اول و سوم و واکنشدهنده $$\frac{5}{2}O_2$$ از واکنش اول و مجموع دوم و سوم حذف خواهد شد تا واکنش اصلی به دست بیاید. سپس از روش زیر مقدار آنتالپی واکنش به دست میآيد.
$$+1299.5\; kJ + (−787 \;kJ) + (−285.8 \;kJ) = +226.7 \;kJ
$$
کالریمتری چیست؟
اندازهگیری انرژی گرمایی به راحتی قابل انجام نیست اما میتوان تغییر دمای حاصل از انتقال این انرژی بین اشیا و ترکیبات را به دست آورد. در «کالریمتری» یا «گرماسنجی» (Calorimetry) با روشهایی آشنایی میشویم که در آن تغییر آنتالپی طی یک واکنش شیمیایی توسط یک کالریمتر مورد اندازهگیری قرار میگیرد.
برای این کار باید با مفاهیم مربوط به آن آشنا شویم که در ادامه به برخی از آنها خواهیم پرداخت.
ظرفیت گرمایی
بزرگی و مقدار تغییر دما بستگی به دو عامل مقدار انرژی منتقل شده و «ظرفیت گرمایی» (Heat Capacity) جسم دارد. ظرفیت گرمایی را در ترموشیمی با نماد $$C$$ نمایش میدهند و مقدار انرژی است که برای افزایش دمای یک جسم به میزان ۱ درجه سانتیگراد مورد نیاز است.
واحد ظرفیت گرمایی برابر با ژول بر درجه سانتیگراد است. توجه داشته باشید که ۱ درجه سانتیگراد با ۱ کلوین برابر است و میتوان ظرفیت گرمایی را با واحد ژول بر کلوین نیز بیان کرد. از رابطه زیر برای نشان دادن مقدار تغییر دما استفاده میکنیم.
$$\Delta T = \dfrac{q}{C} $$
در این رابطه منظور از $$q$$ مقدار گرما بر حسب ژول است و مقدار $$\Delta T $$ از اختلاف بین دمای انتهایی و دمای ابتدایی به دست میآید. مقدار ظرفیت گرمایی برابر با عددی مثبت است اما دو مولفه دیگر این رابطه میتوانند دارای علامت مثبت یا منفی باشند، اما علامت هر دو باید از یک نوع باشد.
در صورتی که علامت تغییرات دما و گرما مثبت باشد به این معناست که گرما از محیط پیرامون به سیستم وارد میشود. همچنین اگر علامت این دو منفی باشد، متوجه میشویم که گرما از سیستم به محیط پیرامون جریان پیدا میکند.
ظرفیت گرمایی یک جسم هم به جرم آن، هم به ترکیبات سازنده آن بستگی دارد. برای مثال با دو برابر شدن جرم یک جسم، مقدار ظرفیت گرمایی آن نیز دو برابر خواهد شد. بنابراین در هنگام گزارش ظرفیت گرمایی یک جسم باید جرم آن نیز مشخص باشد. همنین میتوان از زیرشاخههای این کمیت نیز بهصورت زیر استفاده کرد.
- «ظرفیت گرمایی مولی» (Molar Heat Capacity): این کمیت را با نماد $$C_p$$ نمایش میدهند و برابر با مقدار انرژی مورد نیاز برای افزایش دمای ۱ مول از یک ماده به اندازه ۱ درجه سانتیگراد است. واحد این کمیت بهصورت ژول بر مول در درجه سانتیگراد است. وجود زیروند $$p$$ به این معناست که مقدار به دست آمده در فشار ثابت اندازهگیری شده است.
- «ظرفیت گرمایی ویژه» (Specific Heat Capacity): این کمیت را با نماد $$C_s$$ نشان میدهند و برابر با انرژی مورد نیاز برای افزایش دمای ۱ گرم از یک ماده به اندازه ۱ درجه سانتیگراد است. واحد این کمیت برابر با ژول بر گرم در درجه سانتیگراد است.
در زیر ارتباط بین مقدار گرمای منتقل شده، طرفیت گرمایی آن و تغییرات دمایی را مشاهده میکنید. توجه داشته باشید که در این رابطه منظور از $$n$$ تعداد مولهای ماده است.
$$q = nC_pΔT $$
همچنین در صورتی که به جای ظرفیت گرمایی مولی، ظرفیت گرمایی ویژه را قرار دهیم، مقدار مول با جرم ماده جایگزین خواهد شد.
$$q = mC_sΔT $$
در جدول زیر مقادیر ظرفیت گرمایی ویژه را برای برخی از ترکیبات متداول در شیمی مشاهده میکنید. همانطور که مشاهده میکنید این مقدار برای بیشتر جامدها کمتر از ۱ ژول بر گرم در درجه سانتیگراد اما برای بیشتر مایعات حدود ۲ ژول بر گرم در درجه سانتیگراد است. همچنین ظرفیت گرمایی یخ دو برابر مقدار ظرفیت گرمایی برای بیشتر جامدات است و ظرفیت گرمایی آب بهصورت مایع نیز برابر با ۴٫۱۸۴ ژول بر گرم در درجه سانتیگراد است و مقدار بزرگی به حساب میآید.
| نام ماده | ظرفیت گرمایی ویژه بر حسب ژول بر گرم در درجه سانتیگراد |
| یخ | ۲/۱۰۸ |
| آب | ۴٫۱۸۴ |
| بخار آب | ۲٫۰۶۲ |
| متانول | ۲٫۵۳۱ |
| گرافیت | ۹٫۷۰۹ |
| الماس | ۰٫۵۰۹ |
| اتانول | ۲٫۴۳۸ |
| مس | ۰٫۳۸۵ |
| آلومینیوم | ۰٫۸۹۷ |
مقدار بالای ظرفیت گرمایی ویژه آب مایع برای حیات روی سیاره زمین از اهمیت بهسزایی برخوردار است. مقدار مشخصی آب در تغییر دما به اندازه ۱ درجه سانتیگراد بیش از ۵ برابر مادهای مانند سنگ آهک با همان جرم، گرما آزاد میکند. به همین دلیل مناطق ساحلی شاهد تغییرات آب و هوایی کمتری نسبت به مناطقی هستند که در میانه یک قاره واقع شدهاند. آبهای موجود در سطح کره زمین مقدار زیادی از انرژی گرمایی خورشید را در تابستان به خود جذب میکنند و آن را در زمستان بهصورت تدریجی آزاد خواهند کرد. در این صورت سرمای هوای این مناطق در زمستان کمتر از مقدار مورد انتظار است.
مورد دیگری که میتوان به آن اشاره کرد بدن انسان است که حدود ۷۰٪ آن از آب تشکیل شده است و برای تغییر دمای آن به مقدار ۱ درجه سانتیگراد به گرمای بسیار زیادی نیاز است. به همین دلیل در صورتی که بدن ما از مادهای غیر از آب تشکیل شده بود، نگهداری دمای آن در حدود ۳۷ درجه سانتیگراد با مشکلات فراوانی روبرو میشد.

مثال از ظرفیت گرمایی ویژه
یک سیستم انرژی خورشیدی خانگی از ۴۰۰ لیتر آب برای ذخیره انرژی گرمایی استفاده میکند. در یک روز آفتابی تابستانی، دمای اولیه آب برابر با ۲۲ درجه سانتیگراد است و به ۳۸ درجه سانتیگراد میرسد. در این صورت چه مقدار انرژی در آب ذخیره شده است. (چگالی آب با ۲۲ درجه سانتیگراد برابر با ۰٫۹۹۸ گرم بر میلیلیتر است.)
پاسخ
برای پاسخ به این سوال ابتدا جرم آب را از چگالی و حجم آن به دست میآوریم.
$$\begin{align*} \text{mass of }{H_2O} &= 400 \; {L}\left ( \dfrac{1000 \; {mL}}{1 \; {L}} \right ) \left ( \dfrac{0.998 \; g}{1 \;{mL}} \right ) \\[4pt] &= 3.99\times 10^{5}g\; {H_2O} \end{align*} \nonumber $$
همچنین مقدار تغییرات دمایی را از تفاضل دمای نهایی و دمای اولیه محاسبه میکنیم.
$$38.0 ^oC − 22.0 ^oC = +16.0^oC. \nonumber $$
از جدول بالا میدانیم که ظرفیت گرمایی ویژه آب برابر با ۴٫۱۸۴ ژول بر گرم در درجه سانتیگراد است، بنابراین مقدار گرمای جذب شده توسط آب را از رابطه زیر به دست میآوریم.
$$\begin{align*} q &=mC_{s}\Delta T \\[4pt] &= \left ( 3.99 \times 10^{5} \;{g} \right )\left ( \dfrac{4.184 \; J}{{g}\cdot {^{o}C}} \right ) \left ( 16.0 \;{^{o}C} \right ) \\[4pt] &= 2.67 \times 10^{7}\,J = 2.67 \times 10^{4}\,kJ \end{align*} \nonumber$$
همانطور که مشاهده میکنید مقادیر گرما و تغییرات دما دارای علامت مثبت هستند و این نشاندهنده این است که در این فرآيند گرما توسط آب جذب و ذخیره شده است.
جریان گرما
زمانی که دو جسم دارای دمای متفاوت در تماس با یکدیگر قرار بگیرند، گرما از جسم گرمتر به جسم سردتر منتقل میشود. این فرآیند تا جایی ادامه مییابد که دمای دو جسم با یکدیگر برابر شود. طبق قانون پایستگی انرژی در ترموشیمی، مقدار انرژی کل در طول فرآيند ثابت است که میتوان آن را بهصورت زیر نمایش داد.
$$q_{cold} + q_{hot} = 0 $$
طبق این معادله مقدار گرمایی که جسم گرمتر از دست میدهد برابر با مقدار گرمایی است که جسم سردتر دریافت میکند. از آنجا که جهت انتقال گرما در این دو مورد عکس یکدیگر است، مانند رابطه زیر دارای علامت مخالف هم خواهند بود.
$$q_{cold} = −q_{hot} $$
میتوان مقدار این گرما را با توجه به رابطه ظرفیت گرمایی ویژه نوشت و آن را بازآرایی کرد که نتیجه بهصورت زیر خواهد بود.
$$\left [ mC_{s} \Delta T \right ] _{cold} + \left [ mC_{s} \Delta T \right ] _{hot}=0 $$
$$\left [ mC_{s} \Delta T \right ] _{cold} = - \left [ mC_{s} \Delta T \right ] _{hot} $$
از این رابطه میتوان برای به دست آوردن پاسخ مثالهای مرتبط استفاده کرد.
مثال و حل تمرین
تا اینجا با مفهوم ترموشیمی و مطالعه آن در سیستمهای مختلف شیمیایی آشنا شدیم. در این بخش میخواهیم تعدادی مثال را به همراه پاسخ تشریحی آنها بررسی کنیم و سپس چند تمرین چند گزینهای را مرور خواهیم کرد.
مثال از ترموشیمی
در این بخش به بررسی تعدادی مثال میپردازیم. توجه به پاسخهای تشریحی آنها کمک میکند تا توانایی پاسخگویی به سوالهای مشابه را داشته باشیم.
مثال اول
برخی از نقاط دنیا با کمبود آب شیرین مواجه هستند و یک راهحل برای برطرف کردن این مشکل، انتقال کوههای یخ به آن مناطق و ذوب کردن آن است. اگر آنتالپی این واکنش در دمای ۰ درجه سانتیگراد و فشار ثابت برابر با ۶٫۰۱ کیلوژول بر مول باشد، برای ذوب کردن تکه یخی به جرم ۱ میلیون تن متریک، به چه مقدار انرژی نیاز داریم؟ (هر ۱ تن متریک برابر با ۱۰۰۰ کیلوگرم است.)
$$ {H2O(s) → H_2O(l)} \nonumber $$
پاسخ
از آنجا که آنتالپی خاصیتی مقداری است، مقدار انرژی مورد نیاز برای ذوب کردن یخ به مقدار آن بستگی دارد. در این مورد مقدار تغییر آنتالپی فرآیند داده شده است که برابر با مقدار انرژی مورد نیاز برای ذوب کردن ۱ مول یا ۱۸٫۰۱۵ گرم از یخ است. بنابراین باید تعداد مولهای یخ را محاسبه کنیم و در مقدار آنتالپی داده شده ضرب کنیم. برای این کار ابتدا رابطه استوکیومتری زیر را پیاده میکنیم.
$$ \begin{align*} moles \; H_{2}O & = 1.00\times 10^{6} \; {\text{metric ton }} {H2O} \left ( \dfrac{1000 \; {kg}}{1 \; {\text{metric ton}}} \right ) \left ( \dfrac{1000 \; {g}}{1 \; {kg}} \right ) \left ( \dfrac{1 \; mol \; H_{2}O}{18.015 \; {g \; H_{2}O}} \right ) \\[4pt] & = 5.55\times 10^{10} \; mol \,{H2O} \end{align*} \nonumber$$
بنابراین میتوان مقدار انرژی مورد نیاز برای آب کردن این کوه یخ را به شکل زیر به دست آورد.
$$ \left ( \dfrac{6.01 \; kJ}{{mol \; H_{2}O}} \right )\left ( 5.55 \times 10^{10} \; {mol \; H_{2}O} \right )= 3.34 \times 10^{11} \; kJ \nonumber$$
همانطور که مشاهده میکنید انجام این روش برای تهیه آب شیرین نیازمند انرژی بسیار بالایی است و به همین دلیل روش مقرون بهصرفهای به حساب نمیآید.
مثال دوم
اگر قطعهای ۳۰ گرمی از لوله مسی با دمای ۸۰ درجه سانتیگراد در ۱۰۰ گرم آب با دمای ۲۷ درجه سانتیگراد قرار گیرد، دمای نهایی چه مقدار خواهد بود. فرض بر این است که انتقال گرمای دیگری در محیط پیرامون صورت نمیگیرد.
پاسخ
برای رسیدن به پاسخ این مثال، از رابطه زیر استفاده میکنیم.
$$\left [ mC_{s} \left (T_{final} - T_{initial} \right ) \right ] _{Cu} + \left [ mC_{s} \left (T_{final} - T_{initial} \right ) \right ] _{H_{2}O} =0 \nonumber $$
با توجه به اطلاعات صورت سوال و استخراج ثابتها از منابع و جایگذاری آنها در رابطه بالا، خواهیم داشت:
$$\newcommand{\celsius}{\,^\circ\text{C}} \begin{align*} \left [ \left (30 \; g \right ) \left (0.385 \; J \right ) \left (T_{final} - 80.0 \celsius \right ) \right ] _{Cu} + \left [ (100\,g) (4.18\, J/\celsius) \left (T_{final} - 27.0 \celsius \right ) \right ] _{{H_2O}} &=0 \\[4pt] \left[T_{final}\left ( 11.6 \; J/ \celsius \right ) -924 \; J \right] + \left[ T_{final}\left ( 418.4 \; J/\celsius \right ) -11,300 \; J \right]&= 0 \\[4pt] T_{final}\left ( 430 \; J/\left ( g \cdot \celsius \right ) \right ) &= 12,224 \; J \\[4pt] T_{final} &= 28.4 \; \celsius \end{align*} \nonumber $$
در این مثال با توجه به دمای بالای لوله مسی، انتظار افزایش دمای بالایی در آب داشتیم، اما همانطور که مشاهده میکنید این افزایش دما مقدار اندکی است. دلیل این امر این است که جرم آب بسیار زیادتر است، همچنین ظرفیت گرمایی ویژه آن در مقایسه با مس عدد بزرگتری است.
حل تمرین از ترموشیمی
در این بخش تعدادی تمرین چندگزینهای را مرور خواهیم کرد.
تمرین اول
در دمای ۲۹۸ کلوین و فشار ۱ اتمسفر، تبدیل گرافیت به الماس نیازمند ۱٫۸۵ کیلوژول گرما به ازاری هر ۱ مول از کربن است. حجم مولی گرافیت و الماس به ترتیب برابر با ۰٫۰۰۵۳۴ لیتر و ۰٫۰۰۳۴۲ لیتر است. مقدار $$ ΔH$$ و $$ ΔU$$ را برای این تبدیل محاسبه کنید.
$$ ΔH$$ برابر با ۱٫۸۵ کیلوژول بر مول و $$ ΔU$$ برابر با ۱٫۸۵ کیلوژول بر مول است.
$$ ΔH$$ برابر با ۱ کیلوژول بر مول و $$ ΔU$$ برابر با ۱٫۸۵ کیلوژول بر مول است.
$$ ΔH$$ برابر با ۲٫۸۵ کیلوژول بر مول و $$ ΔU$$ برابر با ۰٫۸۵ کیلوژول بر مول است.
$$ ΔH$$ برابر با ۳٫۴۵ کیلوژول بر مول و $$ ΔU$$ برابر با ۱٫۸۵ کیلوژول بر مول است.
تمرین دوم
مقدار $$ ΔU $$ برای تبدیل گاز اکسیژن به اوزون در دمای ۲۹۸ کلوین در کدام یک از گزینههای زیر بهصورت صحیح آورده شده است؟ (مقدار آنتالپی این واکنش برابر با ۲۸۵٫۴ کیلوژول است.)
$$3O_2(g) \rightarrow 2O_3(g)\nonumber $$
۲۸۵ کیلوژول
۲۴۳ کیلوژول
۲۸۸ کیلوژول
۲۰۹ کیلوژول
تمرین سوم
در صورتی که ۱۷٫۳ گرم از پودر آلومینیوم با مقدار مازادی از $$Fe_2O_3$$ واکنش دهد، چه مقدار گرمایی تولید خواهد کرد؟
۲۷۳ کیلوژول
۲۳۸ کیلوژول
۷۴۳ کیلوژول
۴۳۱ کیلوژول
تمرین چهارم
اگر قطعهای ۱۴ گرمی از طلا با دمای ۲۰ درجه سانتیگراد در ۲۵ گرم آب با دمای ۸۰ درجه سانتیگراد انداخته شود، دمای نهایی به چه مقداری خواهد رسید؟ فرض بر این است که در محیط پیرامون شاهد انتقال گرمای دیگر نیستیم.
۳۰ درجه سانتیگراد
۸۰ درجه سانتیگراد
۴۰ درجه سانتیگراد
۶۰ درجه سانتیگراد
سوالات متدوال ترموشیمی
حال که میدانیم ترموشیمی چیست و پدیدههای مرتبط با آن را نیز مورد بررسی قرار دادیم، میخواهیم به تعدادی از مهمترین و پرتکرارترین پرسشهای موجود پیرامون آن پاسخ دهیم.
آنتالپی در ترموشیمی چیست؟
آنتالپی مقدار گرمای جذب شده یا تولید شده طی فرآیندی است که مقدار فشار ثابتی دارد.
سیستم ایزوله چیست؟
سیستم ایزوله سیستمی است که با محیط پیرامون خود نه تبادل ماده و نه تبادل انرژی انجام نمیدهد.
ظرفیت گرمایی مولی چیست؟
ظرفیت گرمایی مولی کمیتی است که آن را با نماد $$C_p$$ نمایش میدهند و برابر با مقدار انرژی مورد نیاز برای افزایش دمای ۱ مول از یک ماده به اندازه ۱ درجه سانتیگراد است.
سیستم بسته چیست؟
سیستم بسته نوعی از سیستم است که با محیط پیرامون خود تبادل انرژی دارد اما تبادل ماده انجام نخواهد داد.
قانون هس چیست؟
آنتالپی تابع حالت است و تنها به حالت اولیه و نهایی یک واکنش بستگی دارد که توسط قانون هس بیان میشود.
گرما چیست؟
گرما نوعی از انرژی است که از جسم ۱ با دمای ۱ به جسم ۲ با دمای ۲ منتقل میشود. انتقال این انرژی در صورتی که دمای دو جسم با یکدیگر برابر شود، به حالت توقف میرسد.
ظرفیت گرمایی ویژه در ترموشیمی چیست؟
ظرفیت گرمایی ویژه کمیتی است که آن را با نماد $$C_s$$ نشان میدهند و برابر با انرژی مورد نیاز برای افزایش دمای ۱ گرم از یک ماده به اندازه ۱ درجه سانتیگراد است.
سیستم باز چیست؟
سیستم باز سیستمی است که میتوان با محیط پیرامون خود تبادل انرژی و ماده داشته باشد.
جمعبندی
هدف از این مطلب مجله فرادرس آشنایی با مفهوم ترموشیمی و مولفههایی است که آن را تشکیل میدهند. در ترموشیمی به مطالعهای مفاهیمی مانند ماهیت انرژی و انتقال گرما، آنتالپی و قانون هس وکالریمتری میپردازیم که در اینجا بهتفضیل در مورد هر یک از آنها صحبت کردهایم.
همچنین برای درک بهتر مفاهیم و روابط مسلط بر ترموشیمی، تلاش شده است تا در پایان هر موضوع، مثالی مرتبط آورده شود تا نحوه استفاده از روابط بهصورت عملی آموزش داده شود. در نهایت نیز به بررسی تعدادی مثال به همراه پاسخ تشریحی و چند تمرین چندگزینهای پیرامون ترموشیمی پرداختهایم.