روش های انتخاب ویژگی در پایتون — راهنمای جامع

همه کسانی که در حوزه «هوش مصنوعی» (Artificial Intelligence) و «یادگیری ماشین» (Machine Learning) فعالیت دارند، با مسأله انتخاب «ویژگی‌های مرتبط» (Relevant Features) در یک مجموعه داده و حذف یا نادیده گرفتن ویژگی‌های «نامرتبط» (Irrelevant) یا کم اهمیت (که سهم چندانی در پیش بینی درست برچسب کلاس نمونه‌های جدید و به تبع آن، عملکرد مدل‌های یادگیری ندارند) دست و پنجه نرم کرده‌اند. «انتخاب ویژگی» (Feature Selection)، یکی از مفاهیم کلیدی در یادگیری ماشین است. روش های انتخاب ویژگی نقش مهمی در عملکرد بهینه مدل‌های یادگیری دارند.

ویژگی‌هایی که یک مهندس یادگیری ماشین یا دانشمند داده برای آموزش مدل یادگیری ماشین استفاده می‌کنند، تاثیر شگرفی بر عملکرد، دقت و کارایی مطلوب سیستم پیاده‌سازی شده خواهند داشت. همچنین، ویژگی‌های نامرتبط یا تا حدودی مرتبط می‌توانند تاثیر منفی بر عملکرد سیستم داشته باشند. پیاده‌سازی روش های انتخاب ویژگی و «پاک‌سازی داده‌ها» (Data Cleaning)، اولین و مهم‌ترین گام در طراحی مدل‌های هوشمند یادگیری قلمداد می‌شوند. در این مطلب، مهم‌ترین و شایع‌ترین روش های انتخاب ویژگی شرح داده خواهند شد. همچنین، در این مطلب سعی شده است تا کدهای پیاده‌سازی شده در زبان برنامه‌نویسی پایتون، برای بیشتر روش‌های ارائه شده نمایش داده شوند.

اهمیت مرحله انتخاب ویژگی در طراحی مدل‌های یادگیری

تحقیقات انجام شده در زمینه تاثیر انتخاب ویژگی‌های مناسب در عملکرد روش‌های یادگیری ماشین، نشان داده است که انتخاب مجموعه مناسب از ویژگی‌ها در هنگام طراحی مدل‌های یادگیری ماشین، عملکرد، دقت و کارایی روش‌های یادگیری «نظارت شده» (Supervised) و «نظارت نشده» (Unsupervised) را بهبود می‌بخشد.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

همچنین، وقتی که ابعاد فضای ویژگی داده‌ها بسیار زیاد است و با معضل «نفرین ابعاد بالا» (Curse of Dimensionality) مواجه هستیم، استفاده از مجموعه ویژگی‌های مناسب، «هزینه‌های محاسباتی» (نظیر زمان آموزش و یا منابع) لازم برای آموزش بهینه سیستم را به شدت کاهش می‌دهد. محاسبه درجه اهمیت ویژگی‌ها و استفاده از آن‌ها در مرحله انتخاب ویژگی، گام مهمی در جهت «تفسیرپذیری» (Interpretability) مدل‌های یادگیری ماشین خواهد بود.

روش های انتخاب ویژگی نظارت شده و نظارت نشده

برای انتخاب بهترین ویژگی‌ها برای یک مدل یادگیری نظارت شده، «روش های انتخاب ویژگی نظارت شده» (Supervised Feature Selection) ارائه شده‌اند. هدف این دسته از الگوریتم‌ها، انتخاب بهترین زیر مجموعه از ویژگی‌ها برای تضمین عملکرد بهینه یک مدل نظارت شده (به عنوان نمونه، مسائل دسته‌بندی (Classification) و «رگرسیون» (Regression)) است. این الگوریتم‌ها برای انتخاب بهترین ویژگی‌ها، از «داده‌های برچسب زده» (Labelled Data) استفاده می‌کنند. با این حال، در شرایطی که داده‌های برچسب زده در دسترس نیستند (یادگیری نظارت نشده)، روش‌هایی به نام «روش های انتخاب ویژگی نظارت نشده» (Unsupervised Feature Selection) پیاده‌سازی شده‌اند که ویژگی‌ها را براساس معیارهای مختلفی نظیر «واریانس» (Variance)، آنتروپی (Entropy)، قابلیت ویژگی‌ها در حفظ اطلاعات مرتبط با مشابهت‌های محلی (Local Similarity) و سایر موارد امتیازبندی می‌کنند.

فیلم آموزش انتخاب ویژگی با استفاده از الگوریتم های فراابتکاری و تکاملی در فرادرس

کلیک کنید

ویژگی‌های مرتبطی که از طریق «فرایندهای مکاشفه‌ای نظارت نشده» (Unsupervised Heuristics) شناسایی شده‌اند، می‌توانند در مدل‌های یادگیری نظارت شده نیز مورد استفاده قرار بگیرند. چنین کاربردهایی از ویژگی‌های شناسایی شده، به سیستم یادگیری نظارت شده اجازه می‌دهد تا علاوه بر شناسایی میزان «همبستگی» (Correlation) ویژگی‌ها با برچسب کلاس داده‌ها، الگوهای دیگری نیز در داده‌های یادگیری شناسایی کنند. از دیدگاه طبقه‌بندی، روش های انتخاب ویژگی را می‌توان در چهار دسته زیر طبقه‌بندی کرد:

• روش‌های «فیلتر» (Filter)
• روش‌های «بسته‌بند» (Wrapper)
• روش‌های «تعبیه شده» (Embedded)
• روش‌های «ترکیبی» (Hybrid)

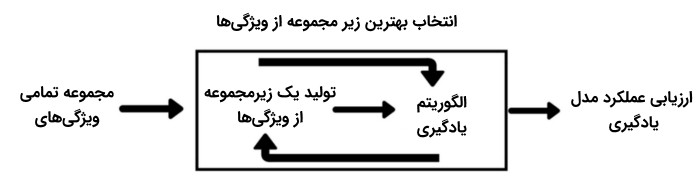
روش‌های انتخاب ویژگی بسته‌بند

این دسته از روش های انتخاب ویژگی، در هر مرحله، زیرمجموعه‌ای از ویژگی‌ها در فضای ویژگی را انتخاب می‌کند و عملکرد الگوریتم یادگیری ماشین روی این زیر مجموعه سنجیده می‌شود. از نتیجه عملکرد الگوریتم یادگیری ماشین، برای ارزیابی زیرمجموعه انتخاب شده از فضای ویژگی استفاده می‌شود.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

به عنوان نمونه، مشخص می‌شود که کدام یک از زیر مجموعه‌های انتخاب شده، بیشترین تاثیر را در افزایش دقت یک مسأله دسته‌بندی خواهند داشت. از این روش مدل‌سازی و جستجوی ویژگی برای انتخاب ویژگی جهت آموزش انواع روش‌های یادگیری ماشین استفاده می‌شود.

انتخاب ویژگی مستقیم

در «روش های انتخاب ویژگی مستقیم» (Forward Feature Selection)، ابتدا یک زیر مجموعه تهی از ویژگی‌ها ساخته می‌شود. سپس در هر مرحله، ویژگی‌هایی که بهترین عملکرد را برای مدل یادگیری به ارمغان می‌آورند، به این زیر مجموعه اضافه می‌شوند. در زبان برنامه نویسی پایتون، از بسته نرم‌افزاری mlxtend برای پیاده‌سازی روش های انتخاب ویژگی مستقیم استفاده می‌شود. در کد زیر، از این روش انتخاب ویژگی جهت آموزش یک «دسته‌بند جنگل تصادفی» (Random Forest) استفاده شده است.

1from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
2from sklearn.metrics import roc_auc_score
3
4from mlxtend.feature_selection import SequentialFeatureSelector
5
6feature_selector = SequentialFeatureSelector(RandomForestClassifier(n_jobs=-1),
7           k_features=15,
8           forward=True,
9           verbose=2,
10           scoring='roc_auc',
11           cv=4)
12
13features = feature_selector.fit(np.array(train_features.fillna(0)), train_labels)
14
15filtered_features= train_features.columns[list(features.k_feature_idx_)]
16filtered_features
17
18filtered_features= train_features.columns[list(features.k_feature_idx_)]
19
20clf = RandomForestClassifier(n_estimators=100, random_state=41, max_depth=3)
21clf.fit(train_features[filtered_features].fillna(0), train_labels)
22
23train_pred = clf.predict_proba(train_features[filtered_features].fillna(0))
24print('Accuracy on training set: {}'.format(roc_auc_score(train_labels, train_pred[:,1])))
25
26test_pred = clf.predict_proba(test_features[filtered_features].fillna(0))
27print('Accuracy on test set: {}'.format(roc_auc_score(test_labels, test_pred [:,1])))

در این قطعه کد، متغیر (k_features) تعداد ویژگی‌های انتخابی را نشان می‌دهد. پارامتر (forward) در صورتی که True باشد، برای سیستم مشخص می‌کند که باید از روش مستقیم برای انتخاب ویژگی استفاده شود.

انتخاب ویژگی معکوس

در «روش های انتخاب ویژگی معکوس» (Backward Feature Selection)، ابتدا تمامی ویژگی‌ها در زیر مجموعه حضور دارند. سپس در هر مرحله، بدترین ویژگی‌ها از زیر مجموعه حذف می‌شوند (ویژگی‌هایی که حذف آن‌ها، باعث ایجاد کمترین کاهش در عملکرد، دقت و کارایی روش یادگیری ماشین می‌شوند).

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

در زبان برنامه نویسی پایتون، از بسته نرم‌افزاری mlxtend برای پیاده‌سازی روش های انتخاب ویژگی معکوس استفاده می‌شود. در کد زیر، از این روش انتخاب ویژگی جهت آموزش یک «دسته‌بند جنگل تصادفی» (Random Forest) استفاده شده است.

1from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
2from sklearn.metrics import roc_auc_score
3from mlxtend.feature_selection import SequentialFeatureSelector
4
5feature_selector = SequentialFeatureSelector(RandomForestClassifier(n_jobs=-1),
6           k_features=15,
7           forward=False,
8           verbose=2,
9           scoring='roc_auc',
10           cv=4)
11
12features = feature_selector.fit(np.array(train_features.fillna(0)), train_labels)
13
14filtered_features= train_features.columns[list(features.k_feature_idx_)]
15filtered_features
16
17clf = RandomForestClassifier(n_estimators=100, random_state=41, max_depth=3)
18clf.fit(train_features[filtered_features].fillna(0), train_labels)
19
20train_pred = clf.predict_proba(train_features[filtered_features].fillna(0))
21print('Accuracy on training set: {}'.format(roc_auc_score(train_labels, train_pred[:,1])))
22
23test_pred = clf.predict_proba(test_features[filtered_features].fillna(0))
24print('Accuracy on test set: {}'.format(roc_auc_score(test_labels, test_pred [:,1])))

در این قطعه کد، متغیر (k_features) تعداد ویژگی‌های انتخابی را نشان می‌دهد. پارامتر (forward) در صورتی که False باشد، برای سیستم مشخص می‌کند که باید از روش معکوس برای انتخاب ویژگی استفاده شود.

روش حذف بازگشتی ویژگی

روش «حذف بازگشتی ویژگی» (Recursive Feature Elimination)، یک روش «حریصانه» (Greedy) برای انتخاب ویژگی است. در این روش، ویژگی‌ها به طور بازگشتی و با در نظر گرفتن مجموعه‌های کوچک و کوچک‌تر از ویژگی‌ها (در هر مرحله) انتخاب می‌شوند.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

در این روش، ویژگی‌ها بر اساس مرتبه حذف شدن آن‌ها از فضای ویژگی رتبه‌بندی می‌شوند. در زبان برنامه برنامه‌نویسی پایتون، از بسته نرم‌افزاری SciKit-Learn برای حذف بازگشتی ویژگی‌های نامرتبط و انتخاب بهترین ویژگی‌ها استفاده می‌شود. در قطعه کد زیر، از این دسته از روش های انتخاب ویژگی برای انتخاب بهترین ویژگی‌های ممکن جهت «دسته‌بندی ارقام» (Digit Classification) استفاده می‌شود.

1from sklearn.svm import SVC
2from sklearn.datasets import load_digits
3from sklearn.feature_selection import RFE
4import matplotlib.pyplot as plt
5
6# Load the digits dataset
7digits = load_digits()
8X = digits.images.reshape((len(digits.images), -1))
9y = digits.target
10
11# Create the RFE object and rank each pixel
12svc = SVC(kernel="linear", C=1)
13rfe = RFE(estimator=svc, n_features_to_select=1, step=1)
14rfe.fit(X, y)
15ranking = rfe.ranking_.reshape(digits.images[0].shape)
16
17# Plot pixel ranking
18plt.matshow(ranking, cmap=plt.cm.Blues)
19plt.colorbar()
20plt.title("Ranking of pixels with RFE")
21plt.show()

روش های انتخاب ویژگی تعبیه شده

از «روش‌های تعبیه شده» (Embedded Methods)، برای انتخاب ویژگی در الگوریتم‌های یادگیری ماشینی استفاده می‌شود که عملیات انتخاب ویژگی و «برازش مدل» (Model Fitting) در آن‌ها، به صورت همزمان انجام می‌شوند. چنین کاری معمولا از طریق یک روش «تنظیم‌گر پراکندگی» (Sparsity Regularizer) و یا تعریف «قید» (Constraint) قابل انجام است که سبب صفر شدن وزن برخی از ویژگی‌ها می‌شود.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

روش رگرسیون لجستیکی چند جمله‌ای اسپارس

در روش «رگرسیون لجستیکی چند جمله‌ای اسپارس» (Sparse Multinomial Logistic Regression)، مکانیزم تنظیم‌گر پراکندگی از طریق تعریف «توزیع احتمال پیشین جهت تعیین خودکار مرتبط بودن» (Automatic Relevance Determination Prior)، برای یک روش رگرسیون لجستیکی چند جمله‌ای کلاسیک پیاده‌سازی می‌شود. مکانیزم تنظیم‌گر پراکندگی، اهمیت هر کدام از ویژگی‌ها را تخمین می‌زند و ویژگی‌هایی که برای پیش‌بینی مفید نیستند را هرس می‌کند. پیاده‌سازی کامل این دسته از روش های انتخاب ویژگی در زبان برنامه‌نویسی پایتون، از طریق [+] قابل دسترس است.

روش رگرسیون تعیین خودکار مرتبط بودن

روش «رگرسیون تعیین خودکار مرتبط بودن» (Automatic Relevance Determination Regression)، یک روش مبتنی بر «رگرسیون ستیغی بیزی» (Bayesian Ridge Regression) است. این مدل انتخاب ویژگی، وزن‌های ویژگی‌ها را بیش از دیگر مدل‌های رگرسیونی دیگر نظیر «رگرسیون کمترین توان‌های دوم عادی» (Ordinary Least Square Regression)، به سمت صفر سوق می‌دهد (به شکل‌های زیر دقت کنید).

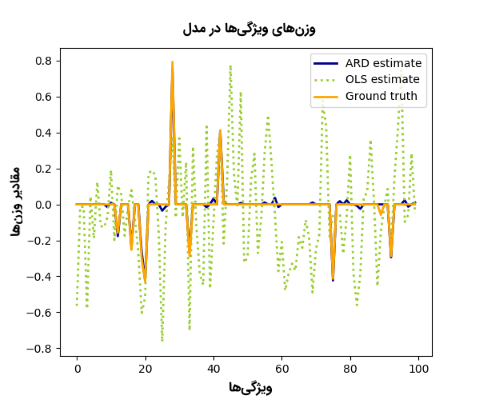
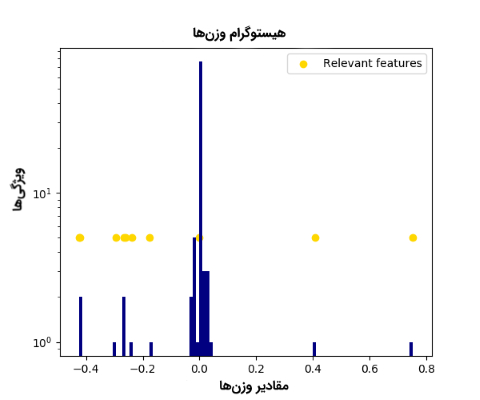
همانطور که در شکل بالا مشاهده می‌شود، «قید پراکندگی» (Sparsity Constraint) روش رگرسیون تعیین خودکار مرتبط بودن، وزن برخی از ویژگی‌ها را صفر می‌کند و از این طریق، ویژگی‌های مرتبط در فضای ویژگی را تعیین می‌کند. در قطعه کد زیر، روش های انتخاب ویژگی «رگرسیون تعیین خودکار مرتبط بودن»، با روش های انتخاب ویژگی «رگرسیون کمترین توان‌های دوم عادی» مقایسه شده‌اند. در این قطعه کد، ابتدا یک فضای ویژگی (100x100) به‌طور تصادفی و از طریق توزیع گوسی تولید می‌شود. هدف پیدا کردن زیر مجموعه‌ای از 10 ویژگی مهم و مرتبط از فضای ویژگی مسأله است. برای پیاده‌سازی این قطعه کد، از  بسته نرم‌افزاری SciKit-Learn پایتون استفاده شده است.

1import numpy as np
2import matplotlib.pyplot as plt
3from scipy import stats
4
5from sklearn.linear_model import ARDRegression, LinearRegression
6
7# #############################################################################
8# Generating simulated data with Gaussian weights
9
10# Parameters of the example
11np.random.seed(0)
12n_samples, n_features = 100, 100
13# Create Gaussian data
14X = np.random.randn(n_samples, n_features)
15# Create weights with a precision lambda_ of 4.
16lambda_ = 4.
17w = np.zeros(n_features)
18# Only keep 10 weights of interest
19relevant_features = np.random.randint(0, n_features, 10)
20for i in relevant_features:
21    w[i] = stats.norm.rvs(loc=0, scale=1. / np.sqrt(lambda_))
22# Create noise with a precision alpha of 50.
23alpha_ = 50.
24noise = stats.norm.rvs(loc=0, scale=1. / np.sqrt(alpha_), size=n_samples)
25# Create the target
26y = np.dot(X, w) + noise
27
28# #############################################################################
29# Fit the ARD Regression
30clf = ARDRegression(compute_score=True)
31clf.fit(X, y)
32
33ols = LinearRegression()
34ols.fit(X, y)
35
36# #############################################################################
37# Plot the true weights, the estimated weights, the histogram of the
38# weights, and predictions with standard deviations
39plt.figure(figsize=(6, 5))
40plt.title("Weights of the model")
41plt.plot(clf.coef_, color='darkblue', linestyle='-', linewidth=2,
42         label="ARD estimate")
43plt.plot(ols.coef_, color='yellowgreen', linestyle=':', linewidth=2,
44         label="OLS estimate")
45plt.plot(w, color='orange', linestyle='-', linewidth=2, label="Ground truth")
46plt.xlabel("Features")
47plt.ylabel("Values of the weights")
48plt.legend(loc=1)
49
50plt.figure(figsize=(6, 5))
51plt.title("Histogram of the weights")
52plt.hist(clf.coef_, bins=n_features, color='navy', log=True)
53plt.scatter(clf.coef_[relevant_features], np.full(len(relevant_features), 5.),
54            color='gold', marker='o', label="Relevant features")
55plt.ylabel("Features")
56plt.xlabel("Values of the weights")
57plt.legend(loc=1)
58
59plt.figure(figsize=(6, 5))
60plt.title("Marginal log-likelihood")
61plt.plot(clf.scores_, color='navy', linewidth=2)
62plt.ylabel("Score")
63plt.xlabel("Iterations")
64
65
66# Plotting some predictions for polynomial regression
67def f(x, noise_amount):
68    y = np.sqrt(x) * np.sin(x)
69    noise = np.random.normal(0, 1, len(x))
70    return y + noise_amount * noise
71
72
73degree = 10
74X = np.linspace(0, 10, 100)
75y = f(X, noise_amount=1)
76clf_poly = ARDRegression(threshold_lambda=1e5)
77clf_poly.fit(np.vander(X, degree), y)
78
79X_plot = np.linspace(0, 11, 25)
80y_plot = f(X_plot, noise_amount=0)
81y_mean, y_std = clf_poly.predict(np.vander(X_plot, degree), return_std=True)
82plt.figure(figsize=(6, 5))
83plt.errorbar(X_plot, y_mean, y_std, color='navy',
84             label="Polynomial ARD", linewidth=2)
85plt.plot(X_plot, y_plot, color='gold', linewidth=2,
86         label="Ground Truth")
87plt.ylabel("Output y")
88plt.xlabel("Feature X")
89plt.legend(loc="lower left")
90plt.show()

روش‌های انتخاب ویژگی فیلتر

در این دسته از روش های انتخاب ویژگی، اهمیت ویژگی‌ها بر اساس مشخصات ذاتی آن‌ها و بدون استفاده از الگوریتم‌های یادگیری (جهت سنجش کیفیت ویژگی‌های انتخابی) ارزیابی می‌شوند. چنین الگوریتم‌هایی نسبت به روش‌های بسته‌بند سریعتر هستند و بار محاسباتی کمتری را به سیستم تحمیل می‌کنند.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

اگر داده کافی برای مدل‌سازی «همبستگی آماری» (Statistical Correlation) میان ویژگی‌ها وجود نداشته باشد، روش‌های فیلتر نتایج به مراتب بدتری نسبت به روش‌های بسته‌بند ارائه می‌کنند. برخلاف روش‌های بسته‌بند، روش های انتخاب ویژگی فیلتر در معرض «بیش برازش» (Overfitting) قرار نمی‌گیرند. این دسته روش‌ها بیشتر زمانی به کار گرفته می‌شوند که استفاده از روش‌های بسته‌بند برای انتخاب ویژگی، بار محاسباتی فوق‌العاده زیادی به سیستم تحمیل می‌کنند. به ویژه زمانی که ابعاد فضای ویژگی بسیار زیاد باشد (داده‌ها با ابعاد بالا) و استفاده از روش‌های بسته‌بند از لحاظ محاسباتی مقرون به صرفه نباشد، از روش‌های فیلتر به‌وفور استفاده می‌شود.

روش‌های انتخاب ویژگی نظارت شده

در این بخش، مهم‌ترین روش‌های فیلتر نظارت شده برای انتخاب ویژگی مورد بحث و بررسی قرار می‌گیرند.

روش انتخاب ویژگی Relief

در این روش، در هر مرحله و به طور تصادفی، یک نمونه از میان نمونه‌های موجود در مجموعه داده انتخاب می‌شود. سپس، میزان مرتبط بودن هر کدام از ویژگی‌ها، بر اساس اختلاف میان نمونه انتخاب شده و دو نمونه همسایه نزدیک (کلاس نمونه‌ اول، مشابه کلاس نمونه انتخابی و کلاس نمونه دوم، مخالف کلاس نمونه انتخابی است) به روز رسانی می‌شود. اگر یکی از ویژگی‌های نمونه انتخاب شده با ویژگی‌ مشابه در نمونه همسایه از کلاس مشابه (نمونه Hit) اختلاف داشته باشد، امتیاز این ویژگی کاهش می‌یابد. از سوی دیگر، اگر همان ویژگی در نمونه انتخاب شده با ویژگی‌ مشابه در نمونه همسایه از کلاس مخالف (نمونه Miss) اختلاف داشته باشد، امتیاز این ویژگی افزایش می‌یابد.

$$W _ { i } = W _ { i } - ( x _ { i } - nearHit _ { i }) ^ { 2 } + ( x _ { i } - nearMiss _ { i }) ^ { 2 }$$

همان طور که در رابطه بالا مشخص است، در صورتی اختلاف میان یک ویژگی در نمونه انتخاب شده و ویژگی مشابه در نمونه کلاس مشابه، بیشتر از اختلاف میان همان ویژگی در نمونه انتخاب شده با ویژگی مشابه در نمونه کلاس مخالف باشد، وزن (درجه اهمیت) این ویژگی کاهش می‌یابد و برعکس. در الگوریتم ReleifF، که گسترشی از الگوریتم Relief محسوب می‌شود، نمونه‌های همسایه بیشتری برای به روز رسانی وزن‌ها جستجو می‌شوند. پیاده‌سازی کامل این دسته از روش های انتخاب ویژگی در زبان برنامه‌نویسی پایتون، از طریق [+] قابل دسترس است.

روش انتخاب ویژگی امتیاز فیشر (Fisher)

از این روش انتخاب ویژگی، بیشتر برای مقاصد «دسته‌بندی باینری» (Binary Classification) استفاده می‌شود. در این دسته از روش های انتخاب ویژگی، «نسبت فیشر» (FiR) در قالب «فاصله میان میانگین نمونه کلاس‌ها (مثبت و منفی) به ازای یک ویژگی خاص» تقسیم بر «واریانس کلاس‌ها (مثبت و منفی) به ازای همان ویژگی» تعریف می‌شود. از طریق این روش، میزان اهمیت (وزن) هر ویژگی مشخص می‌شود.

$$FiR _ { i } = \frac { \mid \overline { X _ i ^ { (0) } } - \overline { X _ i ^ { (1) } } \mid } { \sqrt { Var ( X_{i} ) ^ { (0) } + Var ( X _ { i } )^{ (1) } } }$$

روش انتخاب ویژگی امتیاز کای 2 (Chi-squared)

این روش انتخاب ویژگی، اختلاف معنادار میان «تناوب مشاهده شده» (Observed Frequency) و «تناوب مورد انتظار» (Expected Frequency) دو ویژگی «دسته‌ای» (Categorical) را می‌سنجد. «فرض صفر» (Null Hypothesis) در این روش بیان می‌کند که هیچ‌گونه همبستگی (تناظری) میان این دو متغیر وجود ندارد. این روش، به «آزمون مستقل بودن کای 2» (Chi-square Test of Independence) نیز مشهور است.

$$X ^ { 2 } = \frac { (Observed \; Frequency - Expected \; Frequency ) ^ { 2 } } { Expected \; Frequency }$$

برای اینکه بتوان به درستی از این رابطه، برای سنجش رابطه میان ویژگی‌های مختلف موجود در یک مجموعه داده و ویژگی هدف (که به آن، متغیر کلاس یا Target نیز گفته می‌شود) استفاده کرد، باید دو شرط زیر برقرار باشد:

• ویژگی‌ها باید دسته‌ای باشند.
• ویژگی‌ها باید مستقل از یکدیگر نمونه‌گیری شده باشند.
• تناوب مورد انتظار متغیرها بزرگتر از پنج باشد.

شرط آخر تضمین می‌کند که «تابع توزیع تجمعی» (Cumulative Distribution Function) آماره‌های آزمون کای 2، از طریق توزیع کای 2 (Chi-square Distribution) «قابل تقریب زدن» (Approximation) خواهد بود. در زبان برنامه برنامه‌نویسی پایتون، از بسته نرم‌افزاری SciKit-Learn برای انتخاب بهترین ویژگی‌ها به روش امتیاز کای 2 استفاده می‌شود. در قطعه کد زیر، از این روش انتخاب ویژگی‌های برای انتخاب 2 ویژگی برتر در مجموعه داده iris استفاده شده است.

1from sklearn.datasets import load_iris
2from sklearn.feature_selection import SelectKBest
3from sklearn.feature_selection import chi2
4iris = load_iris()
5X, y = iris.data, iris.target
6X.shape
7
8X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
9X_new.shape

روش انتخاب ویژگی مبتنی بر همبستگی (Correlation-based)

در این روش انتخاب ویژگی، به زیرمجموعه‌ای از ویژگی‌ها، یک زیرمجموعه خوب گفته می‌شود که ویژگی‌های موجود در آن، از یک سو، همبستگی بالایی با «دسته‌بندی» (Classification) یا ویژگی هدف داشته باشند و از سوی دیگر، با یکدیگر «ناهمبسته» (Uncorrelated) باشند. میزان «شایستگی» (Merit) یا خوب بودن یک زیرمجموعه از ویژگی‌ها، از طریق رابطه زیر محاسبه می‌شود:

$$Merit _ { S _ { k }}= \frac { k \overline {r} _ {cf} } { \sqrt {k+k(k-1) \overline{r} _ {ff} } }$$

در این رابطه، $$\overline {r} _ {cf}$$ مقدار میانگین همبستگی محاسبه شده میان ویژگی هدف و تمامی ویژگی‌های موجود در مجموعه داده و $$\overline{r} _ {ff}$$ مقدار میانگین همبستگی یک به یک محاسبه شده میان ویژگی‌ها است. در نهایت، روش مبتنی بر همبستگی به شکل زیر فرموله می‌شود:

$$CFS = max _ {S _ { k } } \left [ \frac { r_ { cf_ {1} }+ r_{ cf_ {2} }+ ...... + r_ { cf_{k} } }{ \sqrt {k + 2 (r_ {f_ {2} f_ {1} }+ .... +r_ {f_ {i} f_ {j} }+ ..... +r_ {f_ {k} f_ {1} } ) } } \right]$$

در این رابطه، به متغیرهای $$r_ { cf_ {i}}$$ و $$r_ {f_ {i} f_ {j} }$$، مقدار همبستگی گفته می‌شود. در زبان برنامه برنامه‌نویسی پایتون، از بسته نرم‌افزاری scikit-learn برای انتخاب بهترین ویژگی‌ها به روش مبتنی بر همبستگی استفاده می‌شود. در قطعه کد زیر، از روش مبتنی بر همبستگی برای انتخاب 5 ویژگی برتر از یک مجموعه داده استفاده شده است. در مرحله بعد، از ویژگی‌های انتخاب شده برای آموزش و تست یک مدل «ماشین بردار پشتیبان» (Support Vector Machine) استفاده می‌شود.

1from sklearn import svm
2from sklearn.metrics import accuracy_score
3import numpy as np
4from skfeature.function.similarity_based import fisher_score
5score = fisher_score.fisher_score(X_train, y_train)
6idx = fisher_score.feature_ranking(score)
7num_fea = 5
8selected_features_train = X_train[:, idx[0:num_fea]]
9selected_features_test = X_test[:, idx[0:num_fea]]
10clf.fit(selected_features_train, y_train)
11y_predict = clf.predict(selected_features_test)
12acc = accuracy_score(y_test, y_predict)

روش انتخاب ویژگی فیلتر مبتنی بر همبستگی سریع

روش فیلتر مبتنی بر همبستگی سریع (Fast Correlation-based Filter)، سرعت و کارایی بهتری نسبت به روش‌های انتخاب ویژگی ReliefF و «مبتنی بر همبستگی» از خود نشان می‌دهد. در نتیجه، به شکل بهتری می‌تواند خود را با داده‌های با ابعاد بالا منطبق و ویژگی‌های به مراتب بهتری را از داده‌های ورودی انتخاب کند. در این روش، ابتدا مقدار «عدم حتمیت نامتقارن» (Symmetrical Uncertainty) برای تمامی ویژگی‌ها محاسبه می‌شود.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

این مقدار، از طریق محاسبه «بهره اطلاعاتی x به شرط y» تقسیم بر «مجموع کل آنتروپی تمامی ویژگی‌ها» به دست می‌آید. سپس، مقادیر عدم حتمیت نامتقارن، مرتب‌سازی و ویژگی‌های «زائد» (Redundant) حذف می‌شوند. در زبان برنامه برنامه‌نویسی پایتون، می‌توان از بسته نرم‌افزاری skfeature برای پیاده‌سازی فیلتر مبتنی بر همبستگی سریع استفاده کرد.

1import numpy as np
2from skfeature.utility.mutual_information import su_calculation
3
4
5def fcbf(X, y, **kwargs):
6    """
7    This function implements Fast Correlation Based Filter algorithm
8    Input
9    -----
10    X: {numpy array}, shape (n_samples, n_features)
11        input data, guaranteed to be discrete
12    y: {numpy array}, shape (n_samples,)
13        input class labels
14    kwargs: {dictionary}
15        delta: {float}
16            delta is a threshold parameter, the default value of delta is 0
17    Output
18    ------
19    F: {numpy array}, shape (n_features,)
20        index of selected features, F[0] is the most important feature
21    SU: {numpy array}, shape (n_features,)
22        symmetrical uncertainty of selected features
23    Reference
24    ---------
25        Yu, Lei and Liu, Huan. "Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution." ICML 2003.
26    """
27
28    n_samples, n_features = X.shape
29    if 'delta' in kwargs.keys():
30        delta = kwargs['delta']
31    else:
32        # the default value of delta is 0
33        delta = 0
34
35    # t1[:,0] stores index of features, t1[:,1] stores symmetrical uncertainty of features
36    t1 = np.zeros((n_features, 2), dtypes='object')
37    for i in range(n_features):
38        f = X[:, i]
39        t1[i, 0] = i
40        t1[i, 1] = su_calculation(f, y)
41    s_list = t1[t1[:, 1] > delta, :]
42    # index of selected features, initialized to be empty
43    F = []
44    # Symmetrical uncertainty of selected features
45    SU = []
46    while len(s_list) != 0:
47        # select the largest su inside s_list
48        idx = np.argmax(s_list[:, 1])
49        # record the index of the feature with the largest su
50        fp = X[:, s_list[idx, 0]]
51        np.delete(s_list, idx, 0)
52        F.append(s_list[idx, 0])
53        SU.append(s_list[idx, 1])
54        for i in s_list[:, 0]:
55            fi = X[:, i]
56            if su_calculation(fp, fi) >= t1[i, 1]:
57                # construct the mask for feature whose su is larger than su(fp,y)
58                idx = s_list[:, 0] != i
59                idx = np.array([idx, idx])
60                idx = np.transpose(idx)
61                # delete the feature by using the mask
62                s_list = s_list[idx]
63                length = len(s_list)//2
64                s_list = s_list.reshape((length, 2))
65    return np.array(F, dtype=int), np.array(SU)

روش‌های انتخاب ویژگی نظارت نشده

در این بخش، مهم‌ترین روش‌های فیلتر نظارت نشده برای انتخاب ویژگی مورد بحث و بررسی قرار می‌گیرند.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

روش انتخاب ویژگی واریانس

روش «واریانس» (Variance)، یکی از روش‌های فیلتر نظارت نشده برای انتخاب ویژگی است. این روش، یکی از بهترین و موثرترین روش‌ها برای انتخاب ویژگی‌های مرتبطی است که معمولا امتیاز واریانس بالاتری دارند. در زبان برنامه برنامه‌نویسی پایتون، می‌توان از بسته نرم‌افزاری scikit-feature برای پیاده‌سازی فیلتر واریانس استفاده کرد. به عنوان نمونه، در کد زیر، یک مجموعه داده حاوی مقادیر ویژگی صحیح تعریف شده است. در هر نمونه از این مجموعه داده، دو ویژگی یکسان وجود دارد. روش واریانس به راحتی قادر خواهد بود تا ویژگی‌های یکسان در نمونه‌ها را حذف کند.

1X = [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]]
2selector = VarianceThreshold()
3selector.fit_transform(X)

روش انتخاب ویژگی میانگین قدر مطلق تفاضل‌ها

در این روش، «میانگین قدر مطلق تفاضل‌ها» (Mean Absolute Difference) برای ویژگی‌های موجود در مجموعه داده، با استفاده «مقدار میانگین» (Mean Value) ویژگی‌ها محاسبه می‌‌شوند. ویژگی‌هایی که میانگین قدر مطلق تفاضل بالاتری داشته باشند، «قدرت متمایز کنندگی» (Discriminative Power) بالاتری خواهند داشت؛ در نتیجه، ویژگی‌های مرتبط‌تری هستند.

$$MAD _ { i } = \frac { 1 } { n } \sum _ { j = 1 } ^ n \mid X _ { ij } - \overline { X_ { i } } \mid$$

از طریق کد زیر در برنامه‌نویسی پایتون، می‌توان درجه اهمیت یا مرتبط بودن ویژگی‌ها را با استفاده از میانگین قدر مطلق تفاضل‌ها محاسبه کرد.

1mad = np.sum(np.abs(data -np.mean(data, axis =0 )), axis = 0)/data.shape[0]

روش انتخاب ویژگی نسبت پراکندگی

روش «نسبت پراکندگی» (Dispersion Ratio)، از طریق محاسبه میانگین ریاضی (Arithmetic Mean)، تقسیم بر، «میانگین هندسی» (Geometric Mean) هر ویژگی، درجه اهمیت یا مرتبط بودن یک ویژگی را مشخص می‌کند. نسبت پراکندگی بالاتر برای یک ویژگی، به معنای مرتبط‌تر بودن آن ویژگی نسبت به دیگر ویژگی‌های موجود در مجموعه داده است.

$$AM_{i}= \overline{X}_{i}=\frac{1}{n}\sum_{j=1}^n X_{ij}, \;\;\;\; GM_{i}=\left( \prod_{j=1}^n X_{ij}\right)^{\frac{1}{\pi}}$$

$$R _ { i }= \frac { AM _ { i }} { GM { i } } \in \left [ 1, \infty \right]$$

از طریق کد زیر در برنامه‌نویسی پایتون، می‌توان درجه اهمیت یا مرتبط بودن ویژگی‌ها را با استفاده از روش نسبت پراکندگی محاسبه کرد.

1def dispersion(data):
2    data = data +1 #avoid 0 division
3    aritmeticMean = np.mean(data, axis =0 )
4    geometricMean = np.power(np.prod(data, axis =0 ),1/data.shape[0])
5    R = aritmeticMean/geometricMean
6    return R
7
8R = dispersion(data)

روش انتخاب ویژگی امتیاز لاپلاسین

روش «امتیاز لاپلاسین» (Laplacian Score)، بر پایه این مشاهده بنا نهاده شده است که داده‌های یک کلاس یکسان، معمولا در همسایگی یکدیگر در فضای ویژگی قرار دارند؛ در نتیجه اهمیت (مرتبط بودن) یک ویژگی را می‌توان از طریق محاسبه قدرت این ویژگی در حفظ اطلاعات «محلیت» (Locality) نمونه‌ها سنجید. در این روش، ابتدا نمونه‌ها با استفاده از یک معیار فاصله دلخواه به یک «گراف نزدیک‌ترین همسایه» (Nearest Neighbor Graph) نگاشت می‌شوند.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

سپس، ماتریس وزن محاسبه می‌شود. در مرحله بعد، امتیاز لاپلاسین برای هر کدام از ویژگی‌ها محاسبه می‌شود. ویژگی‌هایی که اهمیت بیشتری (مرتبط‌تر) نسبت به دیگر ویژگی‌ها داشته باشند، امتیاز لاپلاسین کمتری نسبت به دیگر ویژگی‌ها خواهند داشت و برعکس. با این حال در پایان، برای مشخص کردن بهترین زیر مجموعه از ویژگی‌ها، از یک روش «خوشه‌بندی» (Clustering) نظیر K-Means استفاده می‌شود. در زبان برنامه برنامه‌نویسی پایتون، می‌توان از بسته نرم‌افزاری skfeature، برای پیاده‌سازی فیلتر امتیاز لاپلاسین استفاده کرد.

1import numpy as np
2from scipy.sparse import *
3from skfeature.utility.construct_W import construct_W
4
5
6def lap_score(X, **kwargs):
7    """
8    This function implements the laplacian score feature selection, steps are as follows:
9    1. Construct the affinity matrix W if it is not specified
10    2. For the r-th feature, we define fr = X(:,r), D = diag(W*ones), ones = [1,...,1]', L = D - W
11    3. Let fr_hat = fr - (fr'*D*ones)*ones/(ones'*D*ones)
12    4. Laplacian score for the r-th feature is score = (fr_hat'*L*fr_hat)/(fr_hat'*D*fr_hat)
13    Input
14    -----
15    X: {numpy array}, shape (n_samples, n_features)
16        input data
17    kwargs: {dictionary}
18        W: {sparse matrix}, shape (n_samples, n_samples)
19            input affinity matrix
20    Output
21    ------
22    score: {numpy array}, shape (n_features,)
23        laplacian score for each feature
24    Reference
25    ---------
26    He, Xiaofei et al. "Laplacian Score for Feature Selection." NIPS 2005.
27    """
28
29    # if 'W' is not specified, use the default W
30    if 'W' not in kwargs.keys():
31        W = construct_W(X)
32    # construct the affinity matrix W
33    W = kwargs['W']
34    # build the diagonal D matrix from affinity matrix W
35    D = np.array(W.sum(axis=1))
36    L = W
37    tmp = np.dot(np.transpose(D), X)
38    D = diags(np.transpose(D), [0])
39    Xt = np.transpose(X)
40    t1 = np.transpose(np.dot(Xt, D.todense()))
41    t2 = np.transpose(np.dot(Xt, L.todense()))
42    # compute the numerator of Lr
43    D_prime = np.sum(np.multiply(t1, X), 0) - np.multiply(tmp, tmp)/D.sum()
44    # compute the denominator of Lr
45    L_prime = np.sum(np.multiply(t2, X), 0) - np.multiply(tmp, tmp)/D.sum()
46    # avoid the denominator of Lr to be 0
47    D_prime[D_prime < 1e-12] = 10000
48
49    # compute laplacian score for all features
50    score = 1 - np.array(np.multiply(L_prime, 1/D_prime))[0, :]
51    return np.transpose(score)
52
53
54def feature_ranking(score):
55    """
56    Rank features in ascending order according to their laplacian scores, the smaller the laplacian score is, the more
57    important the feature is
58    """
59    idx = np.argsort(score, 0)
60    return idx

ترکیب روش امتیاز لاپلاسین با روش آنتروپی مبتنی بر فاصله برای انتخاب ویژگی

این روش انتخاب ویژگی، بر پایه روش امتیاز لاپلاسین بنا نهاده شده است. با این تفاوت که در پایان، برای مشخص کردن بهترین زیر مجموعه از ویژگی‌ها، از روش «آنتروپی مبتنی بر فاصله» (Distance-based Entropy) به جای روش خوشه‌بندی K-Means استفاده می‌شود. این روش، عملکرد و پایداری بهتری در انتخاب بهترین ویژگی‌ها در مجموعه داده‌های با ابعاد بالا (High-Dimensional Datasets) از خود نشان داده است.

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

در زبان برنامه برنامه‌نویسی پایتون، می‌توان از بسته نرم‌افزاری skfeature برای پیاده‌سازی فیلتر امتیاز لاپلاسین استفاده کرد. شایان توجه است که در این قطعه کد، از توابع پیاده‌سازی برای روش امتیاز لاپلاسین (کدهای روش امتیاز لاپلاسین) جهت محاسبه درجه اهمیت (مرتبط بودن) ویژگی‌ها استفاده می‌شود.

1def distanceEntropy(d, mu = 0.5, beta=10):
2    """
3    As per: An Unsupervised Feature Selection Algorithm: Laplacian Score Combined with
4    Distance-based Entropy Measure, Rongye Liu 
5    """
6    if d<=mu:
7        result = (np.exp(beta * d) - np.exp(0))/(np.exp(beta * mu) - np.exp(0))
8    else:
9        result = (np.exp(beta * (1-d) )- np.exp(0))/(np.exp(beta *(1- mu)) - np.exp(0))              
10    return result
11
12def lse(data, ls):
13    """
14    This method takes as input a dataset, its laplacian scores for all features
15    and applies distance based entropy feature selection in order to identify
16    the best subset of features in the laplacian sense.
17    """
18    orderedFeatures = np.argsort(ls)
19    scores = {}
20    for i in range (2,len(ls)):
21        selectedFeatures = orderedFeatures[:i]
22        selectedFeaturesDataset = data[:, selectedFeatures]
23        d =sklearn.metrics.pairwise_distances(selectedFeaturesDataset, metric = 'euclidean' )
24        beta =10
25        mu = 0.5
26
27        d = preprocessing.MinMaxScaler().fit_transform(d)
28        e = np.vectorize(distanceEntropy)(d) 
29        e = preprocessing.MinMaxScaler().fit_transform(e)
30        totalEntropy= np.sum(e)
31        scores[i] = totalEntropy
32    bestFeatures = orderedFeatures[:list(scores.keys())[np.argmin(scores.values())]]
33    return bestFeatures
34
35selectedFeatures = lse(data, ls)

روش انتخاب ویژگی چند خوشه‌ای

در روش «انتخاب ویژگی چند خوشه‌ای» (Multi-Cluster Feature selection)، یک «تحلیل طیفی» (Spectral Analysis) با هدف اندازه‌گیری همبستگی میان ویژگی‌های مختلف انجام می‌شود. بهترین «بردارهای ویژه» تولید شده از ماتریس لاپلاسین، برای خوشه‌بندی داده‌ها و محاسبه امتیاز برای هر کدام از ویژگی‌ها مورد استفاده قرار می‌گیرند. ویژگی مهم این روش، انتخاب بهترین ویژگی‌ها برای حفظ ساختار چند کلاستری داده‌ها در یادگیری نظارت نشده است. پیاده‌سازی کامل این روش انتخاب ویژگی در زبان برنامه‌نویسی پایتون، از طریق [+] قابل دسترس است.

1import numpy as np
2from fsfc.generic import NormalizedCut
3from sklearn.pipeline import Pipeline
4from sklearn.cluster import KMeans
5
6data = np.array([...])
7
8pipeline = Pipeline([
9    ('select', NormalizedCut(3)),
10    ('cluster', KMeans())
11])
12pipeline.fit_predict(data)

روش‌های انتخاب ویژگی ترکیبی

گزینه دیگر برای انتخاب بهترین ویژگی‌ها، ترکیب روش‌های فیلتر و بسته‌بند است. در چنین روش‌هایی از یک فرآیند دو مرحله‌ای برای ترکیب دو روش فیلتر و بسته‌بند استفاده می‌شود. در مرحله اول، ویژگی‌ها بر اساس مشخصه‌های آماری فیلتر می‌شوند. در مرحله بعد، با استفاده از یک روش انتخاب ویژگی بسته‌بند، بهترین ویژگی‌ها برای آموزش یک مدل یادگیری انتخاب می‌شوند.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های داده‌کاوی و یادگیری ماشین
• آموزش ​اصول و روش‌های داده‌کاوی (Data Mining)
• مجموعه آموزش‌‌های هوش مصنوعی
• انتخاب ویژگی (Feature Selection) در داده‌های ابعاد بالا — خودآموز ساده
• یادگیری ویژگی (Feature Learning) نظارت نشده — به زبان ساده
• یادگیری ماشین (Machine Learning) چیست؟ — راهنمای کامل

^^