رگرسیون ستیغی (Ridge Regression) در پایتون — راهنمای کاربردی

در مباحث مربوط به رگرسیون چند گانه، تعیین تعداد متغیرهای مستقلی که باید در مدل به کار گرفته شوند، یک مشکل محسوب می‌شود. با افزایش تعداد متغیرها، بیش‌برازش (Overfitting) رخ داده و با کاهش آن‌ها نیز ممکن است با مسئله کم‌برازش (Underfitting) مواجه شویم. در صورتی که مدل رگرسیونی دچار بیش‌برازش شود، خطای آن برای برآورد مقدارهای جدید متغیر وابسته زیاد خواهد بود در حالیکه وجود متغیرهای کمتر از حد لازم در مدل (کم‌برازش) واریانس مدل را افزایش می‌دهد. بنابراین با افزایش تعداد متغیرها مشکل همخطی و بیش‌برازش ظاهر شده و با کاهش آن‌ها، واریانس مدل افزایش خواهد یافت. یکی از روش‌های غلبه بر این مسائل در رگرسیون چندگانه، استفاده از مدل «رگرسیون ستیغی» (Ridge Regression) است. از آنجایی که در زمانی که متغیرهای مدل، زیاد و یا همخطی چندگانه وجود داشته باشد، واریانس برآوردگرها متورم شده و به شکل قله (ستیغ) در می‌آید، از همین روی، این روش رگرسیونی که بر این مشکل غلبه می‌کند، رگرسیون ستیغی نام‌گذاری شده است.

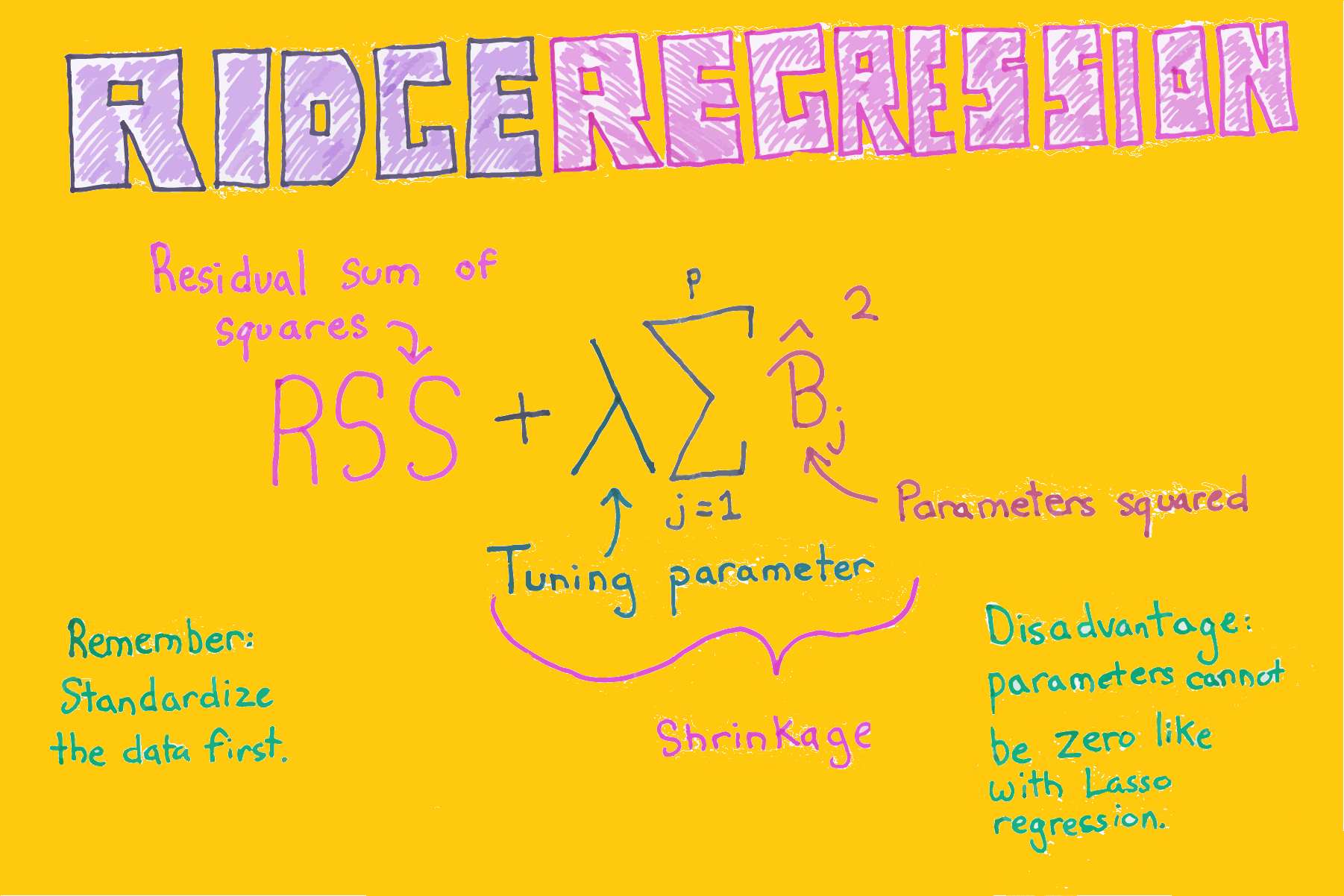
در مسئله رگرسیون خطی، از یک تابع خطا استفاده شده و سعی بر آن است که «مجموع مربعات خطا» (Sum of Square Error) را کمینه کنند. در رگرسیون ستیغی به کمک ترکیب تابع مجموع مربعات خطا و مقدار جریمه مرتبط با تعداد پارامترها، تابع جدیدی ساخته می‌شود که برای برآورد پارامترهای مدل رگرسیونی به کار می‌رود. حالت کلی‌تر این روش را به نام «قاعده‌سازی تیکانوف» (Tikhonov Regularization) می‌شناسند. در این نوشتار به بررسی رگرسیون ستیغی پرداخته و شیوه محاسبه پارامترها را مرور خواهیم کرد. همچنین در انتها نیز با استفاده از زبان برنامه نویسی پایتون، با شیوه اجرای این روش رگرسیونی بیشتر آشنا خواهیم شد.

به منظور آگاهی بیشتر با شیوه‌های مختلف اجرای رگرسیون به مطلب آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس مراجعه کنید. همچنین خواندن نوشتارهای رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده و هم خطی در مدل رگرسیونی — به زبان ساده ضروری به نظر می‌رسد. در عین حال خواندن مطلب رگرسیون لاسو (Lasso Regression) — به زبان ساده نیز خالی از لطف نیست.

رگرسیون ستیغی (Ridge Regression)

قبل از آنکه به مبحث رگرسیون ستیغی بپردازیم، باید چند اصطلاح را در حوزه مربوط به رگرسیون خطی معرفی کنیم.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

• متغیر مستقل: متغیری که به صورت مستقل (Independent) قابل اندازه‌گیری است و در مدل رگرسیونی به عنوان متغیر پیشگو، ویژگی و یا صفت به کار می‌رود.
• متغیر وابسته: متغیری که تغییرات آن وابسته (Dependent) به متغیرهای مستقل است. هدف از ایجاد مدل رگرسیونی، پیدا کردن رابطه‌ای بین متغیرهای مستقل و وابسته است.
• مدل رگرسیونی: شکل رابطه ریاضی بین متغیرهای مستقل و وابسته را با توجه به الگوی احتمالی، مدل رگرسیونی می‌نامند.
• پارامترهای مدل رگرسیونی: در رابطه یا مدل رگرسیونی، برای هر متغیر مستقل، ضرایبی در نظر گرفته می‌شود که در تحلیل رگرسیونی باید برآورد شوند. معمولا این پارامترها را به صورت بردار $$\beta$$ نشان می‌دهند.
• همخطی: زمانی که متغیرهای مستقل با یکدیگر دارای ارتباط باشند بطوریکه ضریب همبستگی بین آن‌ها از لحاظ آماری معنی‌دار باشد، مشکل یا مسئله همخطی (Colinearity) بوجود آمده‌ است. در نتیجه اثر هر یک از متغیرها ممکن است در مدل رگرسیونی توسط متغیرهای دیگر برآورد شود. به این ترتیب برآوردگرها بسیار حساس شده و واریانس آن‌ها نیز بزرگ خواهد شد.
• مجموع مربعات خطا (باقی‌مانده‌ها)، RSS: مجموع اختلاف مقدارهای واقعی و پیش‌بینی‌ شده توسط مدل رگرسیونی متغیر وابسته Residual Sum of Squares می‌نامند. مدلی که دارای کمترین میزان RSS باشد، مدل مناسب‌تری است.
• اریبی (Bais) برآوردگر: این شاخص نشان می‌دهد که پارامترهای مدل رگرسیونی چقدر به مقدار واقعی نزدیک یا دورند. اگر میزان اریبی زیاد باشد، نشان می‌دهد که به طور متوسط برآوردگرها از مقداری واقعی دور هستند و در صورت وجود نااریبی می‌توان گفت که به طور متوسط برآورد پارامترها با مقدارهای واقعی مطابقت دارند. بنابراین نااریبی برای برآوردگرها از اهمیت زیادی برخوردار است.
• واریانس برآوردگر: ممکن است که متوسط برآوردگر به مقدار واقعی نزدیک باشد (نااریب باشد) ولی میزان پراکندگی آن نسبت به مقدار واقعی زیاد باشد. در این حالت واریانس برآوردگر زیاد است. واریانس را توسط میانگین مربعات خطا (MSE) اندازه‌گیری می‌کنند.

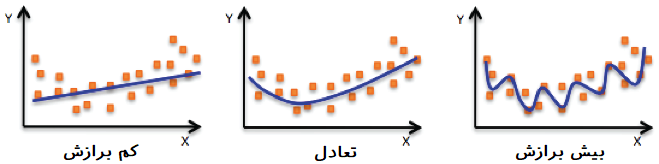
وجود اریبی یا واریانس زیاد برای برآوردگرهای مدل رگرسیونی از معایب آن مدل محسوب می‌شود که هر یک ممکن است به بیش‌برازش یا کم‌برازش منجر شوند. برای مشخص شدن این مفاهیم به تصویر زیر توجه کنید.

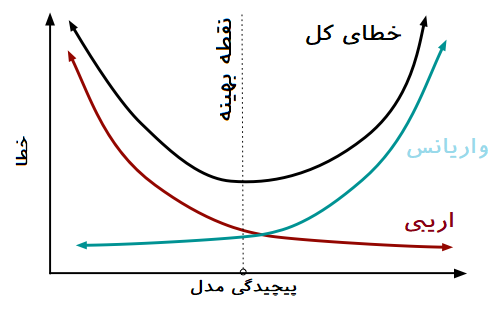
ساختار یک مدل رگرسیون خطی چندگانه به صورت زیر نوشته می‌شود.

$$\large y_{i}=\beta _{0}1+\beta _{1}x_{i1}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i},\qquad i=1,\ldots ,n$$

همانطور که می‌دانید $$x_{ip}$$ مقدار متغیر مستقل pام برای مشاهده iام است. از طرفی $$\varepsilon_{i}$$ نیز باقی‌مانده برای مشاهده iام را نشان می‌دهد. در صورتی که بخواهیم مدل را به صورت برداری و ماتریسی نمایش دهیم، از شکل زیر استفاده خواهیم کرد.

$$\large y=X\beta+\epsilon$$

مشخص است که در اینجا $$X$$ ماتریس متغیرهای مستقل و $$\beta$$‌ نیز بردار پارامترهای مدل رگرسیونی است. همچنین $$\epsilon$$ بیانگر بردار خطا یا همان باقی‌مانده‌ها است. به این ترتیب می‌توان مجموع مربعات خطا (یا مربع فاصله اقلیدسی) را به صورت زیر نشان داد.

$$\large ||\epsilon||_2^2 =  ||y-X\beta||_2^2$$

در اینجا منظور از  $$||.||_2$$ فاصله اقلیدسی است. در نتیجه $$||.||_2^2$$ مربع فاصله اقلیدسی را نشان می‌دهد.

همانطور که در دیگر نوشتارهای فرادرس با موضوع رگرسیون چندگانه و همخطی مطالعه کرده‌اید، می‌دانید که یکی از روش‌های برآورد پارامترهای رگرسیون خطی، «کمینه‌سازی مجموع مربعات خطا» (Ordinary least Square) است که گاهی به اختصار OLS نامیده می‌شود. متاسفانه در این روش هر چه تعداد متغیرهای به کار رفته در رگرسیون چندگانه افزایش یابد، میزان خطا کاهش پیدا می‌کند ولی این امر منجر به بیش‌برازش خواهد شد. از طرفی به کارگیری همه متغیرها در مدل مشکل همخطی را افزایش می‌دهد. بنابراین باید به دنبال روشی برای برآورد پارامترهای رگرسیونی بود که از بوجود آمدن چنین مشکلاتی جلوگیری کند.

برآورد پارامترها در روش OLS

اگر ملاک بهینه‌سازی در مدل رگرسیونی، کمترین مجموع مربعات خطا (RSS) باشد، مدل OLS بهترین برآوردها را ارائه خواهد داد. همانطور که در قبل اشاره شد، روش رگرسیون OLS، پارامترهای به شکلی برآورد می‌شوند که مربع فاصله اقلیدسی مقدار مشاهده شده از مقدار برآورده شده توسط مدل رگرسیونی حداقل ممکن شود. در این حالت برآورد پارامترها در مدل OLS بر اساس محاسبات زیر خواهد بود.

$$\large \operatorname{argmin} ||y-\widehat{y}||_2^2= \operatorname{argmin} \sum [y_i-(\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_px_p)]^2$$

توجه داشته باشید که منظور از  $$\operatorname{argmin}$$ مقدارهایی از $$\beta$$ است که تابع مورد نظر را کمینه می‌کند.

ولی سوال این است که آیا مدل حاصل از روش OLS بهترین مدل است؟ مشخص است که مقدار RSS برای چنین مدلی کمتر از هر مدل دیگر است. ولی نمی‌توان مطمئن بود که برای داده‌هایی حاصل از یک نمونه دیگر، مدل به خوبی عمل برازش را انجام دهد. لزوما مدل بدست آمده توسط OLS بهترین مدل برای پیش‌بینی مقدارهای متغیر وابسته که در ایجاد مدل به کار نرفته‌اند، نخواهد بود. به این معنی که نمی‌توان انتظار داشت که مدل با کمترین مجموع مربعات خطا، کمترین واریانس برای برآوردگرها را نیز داشته باشد. بنابراین باید راهی برای انتخاب تعداد مناسب برآوردگرها (متغیرهای مستقل) در نظر گرفت. در چنین حالتی است که روش رگرسیون ستیغی به کار می‌رود. مشخص است که برآوردگرهای حاصل از رگرسیون ستیغی نااریب نبوده ولی واریانس کوچکترین نسبت به روش OLS دارند.

برآورد پارامترها در روش ستیغی

برای برآورد کردن پارامترهای رگرسیونی در روش ستیغی، قیدی روی پارامترها گذاشته شده است. این قید به صورت زیر نوشته می‌شود.

$$\large \beta_0^2+\beta_1^2+\cdots+\beta_p^2\leq C^2$$

این محدودیت، مشخص می‌کند که باید مجموع مربعات پارامترها از مقدار ثابت یا آستانه‌ای کمتر باشند. این شرط را به صورت ماتریسی به صورت زیر نشان می‌دهیم.

$$\large ||\beta||_2^2 \leq C^2$$

حال این قید را نیز به روش OLS اضافه کرده و تابع هدف حاصل را ملاک برآورد پارامترهای مدل رگرسیون خطی قرار خواهیم داد. در نتیجه شیوه برآورد پارامترها به صورت زیر در خواهد آمد.

$$\large \operatorname{argmin}||y-X\beta||_2^2+\lambda||\beta||_2^2$$

پارامتر $$\lambda$$ در اینجا میزان جریمه (Penalty) نامیده می‌شود زیرا با توجه به افزایش تعداد پارامترها، مقدار RSS را افزایش می‌دهد. با تغییر مقدار $$\lambda$$ و برآورد پارامترهای مدل، مدلی که کمترین مقدار مربع خطا (Mean Square Error) را داشته باشد، به عنوان مدل مناسب در نظر گرفته می‌شود.

پارامترهای حاصل از این روش، معمولا از روش OLS مناسب‌تر هستند بخصوص در هنگامی که هدف پیش‌بینی برای داده‌هایی باشد که در ایجاد مدل به کار نرفته‌اند. برآورد پارامترهای مدل رگرسیون ستیغی به صورت زیر حاصل می‌شود.

$$\large \widehat{\beta}^{ridge} =(X^TX+\lambda I)^{-1}X^Ty$$

نکته: مشخص است که اگر هیچ جریمه‌ای برای مدل در نظر نگیریم و مقدار $$\lambda$$ را صفر انتخاب کنیم، روش برآورد به شیوه OLS تبدیل خواهد شد. در نتیجه می‌توان روش OLS را حالت خاصی از روش ستیغی در نظر گرفت.

در تعریف پارامترها در مدل ستیغی، می‌توان دید که مقدار $$\lambda$$ در مخرج کسر مربوط به پارامتر ظاهر می‌شود. به این ترتیب با افزایش میزان جریمه، مقدار پارامترها به صفر نزدیک می‌شوند ولی هرگز به صفر نمی‌رسند. به این ترتیب در روش ستیغی برای متغیرها کم اهمیت ضریب $$\beta$$ کوچک شده ولی هیچگاه صفر نمی‌شوند. به این شکل می‌توان متغیرهای پراهمیت را در مدل حفظ و بقیه را نادیده گرفت.

تفسیر هندسی روش ستیغی

شاید نمایش روش ستیغی برای برآورد پارامترهای مدل رگرسیونی در درک کارایی آن کمک کند. فرض کنید در مدل رگرسیونی دو متغیر $$X_1$$ و $$X_2$$ حضور دارند که ضرایب (پارامترهای) هر یک $$\beta_1$$ و $$\beta_2$$ نام‌گذاری شده‌اند. از آنجایی که در روش OLS با مربع فاصله اقلیدسی سروکار داریم، انتظار داریم که فضای پارامتری، نقاط هندسی را ایجاد کند که میزان RSS یا همان مجموع مربعات خطای آن ثابت باشد. پارامترهای $$\beta_1$$ و $$\beta_2$$ مکان هندسی نقاطی را روی یک دایره یا بیضی ایجاد می‌کنند که RSS یکسانی دارند. مشخص است که کمترین مقدار RSS در مرکز این دایره یا بیضی قرار می‌گیرد. در نتیجه مختصات این نقطه، حاصل برآوردگر OLS محسوب می‌شود.

فیلم آموزش رگرسیون غیرخطی و لجستیک در تحلیل اطلاعات با SAS (رایگان) در فرادرس

کلیک کنید

حال جمله مربوط به جریمه را نیز در نظر بگیرد. این جمله به صورت مربع فاصله اقلیدسی برای پارامترهای $$\beta_1$$ و $$\beta_2$$ نوشته شده است که از نظر نقاط هندسی تشکیل یک دایره در مرکز مختصات را می‌دهد. هر چه مقدار $$\lambda$$ تغییر کند اندازه این دایره نیز تغییر خواهد کرد.

از محل برخورد دایره آبی رنگ با بیضی‌های سبز رنگ حاصل از روش OLS، برآوردگر ستیغی حاصل می‌شود. این محل برخورد نشان می‌دهد که برای مدل حاصل از رگرسیون ستیغی مقدار RSS ممکن است بزرگتر از مقدار حاصل از مدل OLS باشد. با تغییر پارامتر $$\beta$$ که اندازه دایره آبی را مشخص می‌کند، می‌توان به نقطه‌ای رسید که دارای کمترین میزان RSS روی دایره سبز باشد. به این ترتیب جواب بهینه به دست خواهد آمد.

البته برای پیدا کردن مقدار بهینه برای $$\lambda$$ نیز می‌توان از روش‌های مختلف مانند اعتبار سنجی متقابل استفاده کرد. هرچه مقدار $$\lambda$$ افزایش پیدا کند تعداد پارامترها کاهش پیدا خواهد کرد. با کاهش این مقدار نیز برآوردگرها به مقدار مشابه در روش OLS نزدیک می‌شوند ولی با افزایش میزان جریمه این ضرایب کاهش یافته می‌توان آن‌ها را نادیده گرفت. به این ترتیب بزرگی یا کوچکی مقدار $$\lambda$$ می‌تواند روی تعداد پارامترها و مقدار آن‌ها تاثیر گذار باشد. در ادامه به کمک زبان برنامه نویسی پایتون به بررسی مدل رگرسیونی ستیغی برای داده‌های واقعی پرداخته و مقدار $$\lambda$$ را مشخص می‌کنیم.

اجرای رگرسیون ستیغی در پایتون

در ادامه به بررسی رگرسیون ستیغی در پایتون خواهیم پرداخت. در این میان از بانک اطلاعاتی قیمت خانه‌ها (Boston House Price) در کتابخانه $$sklearn$$ استفاده خواهیم کرد.

فیلم آموزش کاربرد رگرسیون و همبستگی در آمار استنباطی برای مدیریت و علوم انسانی (رایگان) در فرادرس

کلیک کنید

کد زیر به منظور آماده سازی محیط برای اجرای رگرسیون ستیغی نوشته شده است.

1# dataframe and plot
2import numpy as np
3import pandas as pd
4import matplotlib.pyplot as plt
5import matplotlib.ticker as ticker
6
7# dataset
8from sklearn.datasets import load_boston
9# scaling and dataset split
10from sklearn import preprocessing
11from sklearn.model_selection import train_test_split
12# OLS, Ridge
13from sklearn.linear_model import LinearRegression, Ridge
14# model evaluation
15from sklearn.metrics import r2_score, mean_squared_error

حال که داده‌های بارگذاری شده‌اند، باید آن‌ها را استاندارد کرد. از آنجایی که در رگرسیون ستیغی ضرایب مدل رگرسیونی براساس میزان جریمه تعیین می‌شوند، باید داده‌ها را استاندارد کرد تا جریمه‌ها عادلانه باشند. به کد زیر دقت کنید. پس از استاندارد سازی بوسیله تابع scale، داده‌ها به دو بخش آموزشی (Train) و آزمایشی (Test) تفکیک شده‌اند.

1# load dataset
2house_price = load_boston()
3df = pd.DataFrame(house_price.data, columns=house_price.feature_names)
4df['PRICE'] = house_price.target
5
6# standardize and train/test split
7house_price.data = preprocessing.scale(house_price.data)
8X_train, X_test, y_train, y_test = train_test_split(
9    house_price.data, house_price.target, test_size=0.3, random_state=10)

در اینجا برای تعیین $$\lambda$$ مقدار آن را از ۰ تا ۱۹۹ تغییر داده و برآورد پارامترها را مشخص می‌کنیم.

1# initialize
2ridge_reg = Ridge(alpha=0)
3ridge_reg.fit(X_train, y_train)
4ridge_df = pd.DataFrame({'variable': house_price.feature_names, 'estimate': ridge_reg.coef_})
5ridge_train_pred = []
6ridge_test_pred = []
7
8# iterate lambdas
9for alpha in np.arange(0, 200, 1):
10    # training
11    ridge_reg = Ridge(alpha=alpha)
12    ridge_reg.fit(X_train, y_train)
13    var_name = 'estimate' + str(alpha)
14    ridge_df[var_name] = ridge_reg.coef_
15    # prediction
16    ridge_train_pred.append(ridge_reg.predict(X_train))
17    ridge_test_pred.append(ridge_reg.predict(X_test))
18
19# organize dataframe
20ridge_df = ridge_df.set_index('variable').T.rename_axis('estimate').rename_axis(None, 1).reset_index()

حال مقدار پارامترها را با توجه به میزان $$\lambda$$ برای متغیرهای مختلف ترسیم می‌کنیم. کد زیر به این منظور تهیه شده است. مشخص است که این نمودار براساس ridge_df که یک چهارچوب (DataFrame) متشکل از نتایج اجرای رگرسیون ستیغی است ترسیم شده است. البته توجه داشته باشید که در این نمودار فقط پنچ مشخصه یا متغیر مستقل (تعداد اتاق خواب (Room)، ناحیه مسکونی (Resident Zone)، دسترسی به بزرگراه (Highway Access)، نرخ جرم و جنایت (Crime Rate)، و مالیات (Tax)) که بیشترین ارتباط با متغیر وابسته را داشته‌اند ترسیم شده‌‌اند.

1# plot betas by lambda
2fig, ax = plt.subplots(figsize=(10, 5))
3ax.plot(ridge_df.RM, 'r', ridge_df.ZN, 'g', ridge_df.RAD, 'b', ridge_df.CRIM, 'c', ridge_df.TAX, 'y')
4ax.axhline(y=0, color='black', linestyle='--')
5ax.set_xlabel("Lambda")
6ax.set_ylabel("Beta Estimate")
7ax.set_title("Ridge Regression Trace", fontsize=16)
8ax.legend(labels=['Room','Residential Zone','Highway Access','Crime Rate','Tax'])
9ax.grid(True)

همانطور که در نمودار مشخص است، متغیر Room که تعداد اتاق خواب‌ها را نشان می‌دهد بیشترین تاثیر را در تعیین قیمت خانه دارد. به همین دلیل خط قرمز که مربوط به این پارامتر است، به سمت صفر میل نمی‌کند. در مقابل متغیر Highway Access یا دسترسی به بزرگراه که با خط آبی مشخص شده، به سرعت به سمت صفر میل کرده است که نشان دهنده کم اهمیت بودن این متغیر در برآورد متغیر وابسته (قیمت خانه) است.

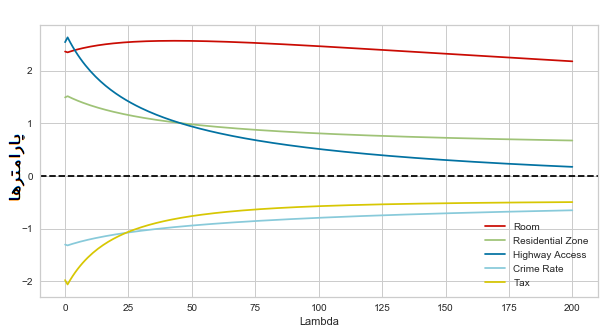
بقیه متغیرها نیز با توجه به خط‌چین سیاه رنگ که مقدار صفر را نشان می‌دهد، دارای اهمیت‌های مختلف خواهند بود. به این ترتیب مشخص است که اگر بخواهیم کمترین واریانس را داشته باشیم (در حقیقت با بیشترین اریبی) باید مقدار $$\lambda$$ افزایش یابد. در این حالت فقط متغیر Room در مدل رگرسیون ستیغی باقی می‌ماند.

برای بررسی میزان MSE مدل نیز از کد زیر استفاده کرده‌ایم، به این ترتیب با توجه به تعداد پارامترها یا در حقیقت مقدار $$\lambda$$، کمترین MSE‌ تعیین می‌شود. به خوبی دیده می‌شود که این میزان با توجه به مدل OLS که با خط سبز در نمودار مشخص است، کاملا تفاوت دارد.

1# MSE of Ridge and OLS
2ridge_mse_test = [mean_squared_error(y_test, p) for p in ridge_test_pred]
3ols_mse = mean_squared_error(y_test, ols_pred)
4
5# plot mse
6plt.plot(ridge_mse_test[:25], 'ro')
7plt.axhline(y=ols_mse, color='g', linestyle='--')
8plt.title("Ridge Test Set MSE", fontsize=16)
9plt.xlabel("Model Simplicity$\longrightarrow$")
10plt.ylabel("MSE")

نمودار حاصل از اجرای کد بالا به صورت زیر است. هر چه میزان $$\lambda$$ افزایش یابد، مقدارهای روی محور افقی که نشان دهنده سادگی مدل است افزایش می‌یابد زیرا متغیرهای کمتری در مدل وجود خواهند داشت.

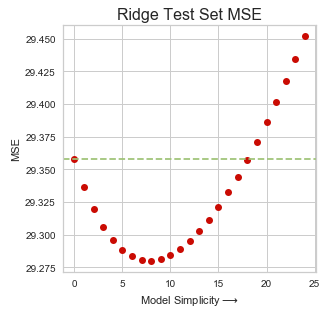
ابتدا با افزایش مقدار $$\lambda$$ میزان MSE نیز کاهش می‌یابد ولی پس از رسیدن مقدار $$\lambda$$ به مقدار مشخصی، مقدار MSE شروع به افزایش می‌کند. این امر نشان می‌دهد که در این نقطه، باید مقدار $$\lambda$$ را انتخاب کرد.

نکته: همانطور که گفته شد، مدل OLS دارای برآوردگرهای نااریب است در حالیکه می‌بینیم خطای مدل با پارامترهای حاصل از رگرسیون ستیغی کمتر از مدل OLS‌ نااریب است.

خلاصه و جمع‌بندی

در این نوشتار به بررسی رگرسیون ستیغی از جنبه‌های مختلف از جمله ریاضیاتی، هندسی و البته برنامه نویسی پرداختیم. مشخص شد که روش برآورد رگرسیون OLS می‌تواند حالت خاصی از رگرسیون ستیغی در نظر گرفته شود. همانطور که دیدید، تعیین مقدار مناسب برای پارامتر $$\lambda$$ به راحتی میسر نیست و باید با سعی و خطا مقدار آن را جستجو کرد. در اینجا به کمک ترسیم نمودار MSE برحسب مقدار $$\lambda$$ به جواب مناسب برای این مقدار رسیدیم. از ویژگی‌هایی مدل رگرسیون ستیغی و OLS می‌توان به موارد زیر اشاره کرد.

• مدل رگرسیون OLS بهترین پیش‌بینی را برای داده‌هایی خواهد داشت که در ایجاد مدل سهیم هستند.
• مدل رگرسیون ستیغی به ویژگی‌هایی که مهم‌تر هستند وزن بیشتری می‌دهد.
• از مقدار $$R^2$$ یا MSE برای تعیین مقدار مناسب $$\lambda$$ می‌توان استفاده کرد.
• نقش هر یک از متغیرها در تعیین مقدار RSS متفاوت است. بنابراین هنگام استفاده از رگرسیون ستیغی ابتدا باید داده‌ها را استاندارد کرد.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش یادگیری ماشین
• مجموعه آموزش‌های نرم‌افزارهای آماری
• بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی
• ماشین بردار پشتیبان — به همراه کدنویسی پایتون و R
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده
• آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس

^^