آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن

الگوریتمهای متنوع و زیادی برای انجام عملیات خوشهبندی در دادهکاوی به کار میرود. آگاهی از الگوریتمهای خوشهبندی و آشنایی با نحوه اجرای آنها کمک میکند تا مناسبترین روش را برای خوشهبندی دادههای خود به کار ببرید.
«تحلیل خوشهبندی» (Cluster Analysis) نیز مانند «تحلیل طبقهبندی» (Classification Analysis) در «یادگیری ماشین» (Machine Learning) به کار میرود. هر چند که تحلیل طبقهبندی یک روش «با ناظر» (Supervised) محسوب شده ولی خوشهبندی روشی «بدون ناظر» (Unsupervised) است.
در این متن، ابتدا خوشهبندی را تعریف میکنیم و سپس به معرفی گونههای مختلف الگوریتمهای خوشهبندی میپردازیم.
خوشهبندی (Clustering)
«تحلیل خوشهبندی» (Cluster Analysis) یا بطور خلاصه خوشهبندی، فرآیندی است که به کمک آن میتوان مجموعهای از اشیاء را به گروههای مجزا افراز کرد. هر افراز یک خوشه نامیده میشود. اعضاء هر خوشه با توجه به ویژگیهایی که دارند به یکدیگر بسیار شبیه هستند و در عوض میزان شباهت بین خوشهها کمترین مقدار است. در چنین حالتی هدف از خوشهبندی، نسبت دادن برچسبهایی به اشیاء است که نشان دهنده عضویت هر شیء به خوشه است.
به این ترتیب تفاوت اصلی که بین تحلیل خوشهبندی و «تحلیل طبقهبندی» (Classification Analysis) وجود دارد، نداشتن برچسبهای اولیه برای مشاهدات است. در نتیجه براساس ویژگیهای مشترک و روشهای اندازهگیری فاصله یا شباهت بین اشیاء، باید برچسبهایی بطور خودکار نسبت داده شوند. در حالیکه در طبقهبندی برچسبهای اولیه موجود است و باید با استفاده از الگویهای پیشبینی قادر به برچسب گذاری برای مشاهدات جدید باشیم.

با توجه به روشهای مختلف اندازهگیری شباهت یا الگوریتمهای تشکیل خوشه، ممکن است نتایج خوشهبندی برای مجموعه داده ثابت متفاوت باشند. شایان ذکر است که تکنیکهای خوشهبندی در علوم مختلف مانند، گیاهشناسی، هوش مصنوعی، تشخیص الگوهای مالی و ... کاربرد دارند.
روشهای خوشهبندی
اگر چه بیشتر الگوریتمها یا روشهای خوشهبندی مبنای یکسانی دارند ولی تفاوتهایی در شیوه اندازهگیری شباهت یا فاصله و همچنین انتخاب برچسب برای اشیاء هر خوشه در این روشها وجود دارد. برای آشنایی بیشتر با شیوه محاسبه فاصله در الگوریتمهای خوشهبندی بهتر است مطلب فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی را مطالعه کنید.

هر چند ممکن است امکان دستهبندی روشها و الگوریتمها خوشهبندی به راحتی میسر نباشد، ولی طبقهبندی کردن آنها درک صحیحی از روش خوشهبندی بکار گرفته شده در الگوریتمها به ما میدهد. معمولا ۴ گروه اصلی برای الگوریتمهای خوشهبندی وجود دارد. الگوریتمهای خوشهبندی تفکیکی، الگوریتمهای خوشهبندی سلسله مراتبی، الگوریتمهای خوشهبندی برمبنای چگالی و الگوریتمهای خوشهبندی برمبنای مدل. در ادامه به معرفی هر یک از این گروهها میپردازیم.
خوشهبندی تفکیکی (Partitional Clustering)
در این روش، براساس n مشاهده و k گروه، عملیات خوشهبندی انجام میشود. به این ترتیب تعداد خوشهها یا گروهها از قبل در این الگوریتم مشخص است. با طی مراحل خوشهبندی تفکیکی، هر شیء فقط و فقط به یک خوشه تعلق خواهد داشت و هیچ خوشهای بدون عضو باقی نمیماند. اگر $$l_{ij}$$ نشانگر وضعیت تعلق $$x_i$$ به خوشه $$c_j$$ باشد تنها مقدارهای ۰ یا ۱ را میپذیرد. در این حالت مینویسند:
$$l_{ij}=1,\;\;\ x_i \in c_j \;\;or\;\;\;l_{ij}=0,\;\;\ x_i \notin c_j $$
هر چند این قانونها زمانی که از روش «خوشهبندی فازی» (Fuzzy Clustering) استفاده میشود، تغییر کرده و برای نشان دادن تعلق هر شئی به هر خوشه از درجه عضویت استفاده میشود. به این ترتیب میزان عضویت $$x_i$$ به خوشه $$c_j$$ مقداری بین ۰ و ۱ است. در این حالت مینویسند:
$$l_{ij} \in [0,1]$$
معمولا الگوریتمهای تفکیکی بر مبنای بهینهسازی یک تابع هدف عمل میکنند. این کار براساس تکرار مراحلی از الگوریتمهای بهینهسازی انجام میشود. در نتیجه الگوریتمهای مختلفی بر این مبنا ایجاد شدهاند. برای مثال الگوریتم «k-میانگین» (K-means) با تعیین تابع هدف براساس میانگین فاصله اعضای هر خوشه نسبت به میانگینشان، عمل میکند و به شکلی اشیاء را در خوشهها قرار میدهد تا میانگین مجموع مربعات فاصلهها در خوشهها، کمترین مقدار را داشته باشد. اگر مشاهدات را با x نشان دهیم، تابع هدف الگوریتم «k-میانگین» را میتوان به صورت زیر نوشت:
$$E=\sum_{j=1}^k\sum_{x\in c_j}dist(x,\mu_{c_j})$$
که در آن $$\mu_{cj}$$ میانگین خوشه $$c_j$$ و dist نیز مربع فاصله اقلیدسی است.
به این ترتیب با استفاده از روشهای مختلف بهینهسازی میتوان به جواب مناسب برای خوشهبندی تفکیکی رسید. ولی از آنجایی که تعداد خوشهها یا مراکز اولیه باید به الگوریتم داده شود، ممکن است با تغییر نقاط اولیه نتایج متفاوتی در خوشهبندی بدست آید. در میان الگوریتمهای خوشهبندی تفکیکی، الگوریتم k-میانگین که توسط «مککوئین» (McQueen) جامعه شناس و ریاضیدان در سال ۱۹۶۵ ابداع شد از محبوبیت خاصی برخوردار است.

نکته: در شیوه خوشهبندی تفکیکی با طی مراحل خوشهبندی، برچسب عضویت اشیاء به هر خوشه براساس خوشههای جدیدی که ایجاد میشوند قابل تغییر است. به این ترتیب میتوان گفت که الگوریتمهای خوشهبندی تفکیکی جزء الگوریتمهای «یادگیری ماشین بدون ناظر» (Unsupervised Machine Learning) محسوب میشوند.
در تصویر ۱ نتایج ایجاد ۴ خوشه روی دادههای دو بعدی به کمک الگوریتم k-میانگین نمایش داده شده است. داشتن حالت کروی برای دادهها به ایجاد خوشههای مناسب در الگوریتم k-میانگین کمک میکند.
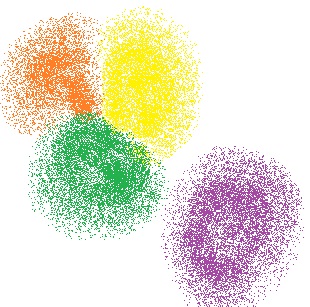
خوشهبندی سلسله مراتبی (Hierarchical Clustering)
برعکس خوشهبندی تفکیکی که اشیاء را در گروههای مجزا تقسیم میکند، «خوشهبندی سلسله مراتبی» (Hierarchical Clustering)، در هر سطح از فاصله، نتیجه خوشهبندی را نشان میدهد. این سطوح به صورت سلسله مراتبی (Hierarchy) هستند.
برای نمایش نتایج خوشهبندی به صورت سلسله مراتبی از «درختواره» (Dendrogram) استفاده میشود. این شیوه، روشی موثر برای نمایش نتایج خوشهبندی سلسله مراتبی است. در تصویر ۲ نتایج خوشهبندی سلسله مراتبی روی دادههای $$s={1,3,6,2,8,10}$$ با استفاده از درختواره را میبینید.
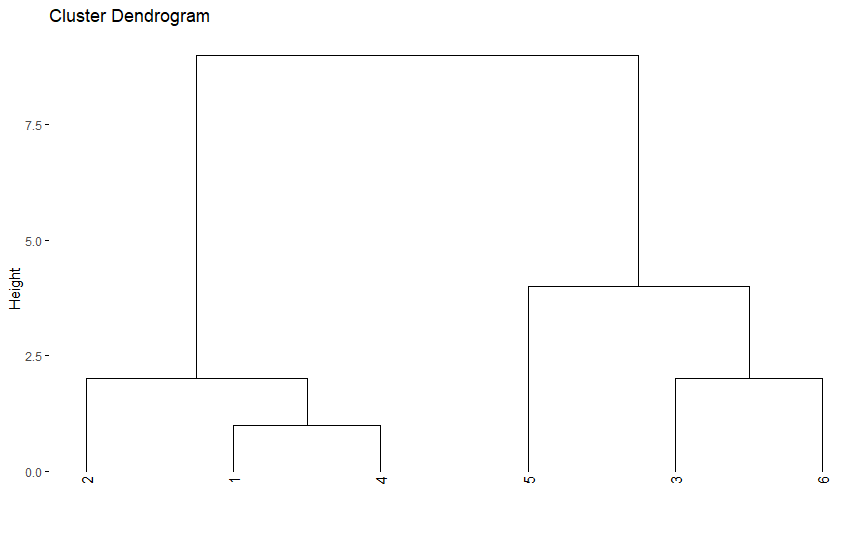
همانطور که در تصویر ۲ قابل رویت است، ابتدا هر مقدار یک خوشه محسوب میشود. در طی مراحل خوشهبندی، نزدیکترین مقدارها (براساس تابع فاصله تعریف شده) با یکدیگر ادغام شده و خوشه جدیدی میسازند.
در نتیجه براساس تصویر ۲ ابتدا در مرحله اول مقدار اول و چهارم تشکیل اولین خوشه را میدهند، زیرا کمترین فاصله را دارند. سپس در مرحله دو، مقدار دوم با خوشه تشکیل شده در مرحله اول ترکیب میشود. در مرحله سوم مقدارهای سوم و ششم با هم تشکیل یک خوشه میدهند که در مرحله چهارم با مقدار پنجم ترکیب شده و خوشه جدیدی میسازند.
در انتها نیز خوشه تشکیل شده در مرحله دوم با خوشه تشکیل شده در مرحله چهارم ادغام شده و خوشه نهایی را ایجاد میکنند. همانطور که دیده میشود با داشتن شش مقدار خوشهبندی سلسله مراتبی، پنچ مرحله خواهد داشت زیرا در هر مرحله فقط یک عمل ادغام انجام میشود.
نکته: توجه داشته باشید که مقدارهایی که روی محور افقی دیده میشوند، بیانگر موقعیت مقدارها در لیست دادهها است و نه خود مقادیر. همچنین محور عمودی نیز فاصله یا ارتفاع بین خوشهها را نشان میدهد.
در الگوریتم خوشهبندی سلسله مراتبی معمولا با کوچکترین خوشهها شروع میکنیم. به این معنی که در ابتدا هر مقدار بیانگر یک خوشه است. سپس دو مقداری که بیشترین شباهت (کمترین فاصله) را دارند با یکدیگر ادغام شده و یک خوشه جدید میسازند. بعد از این مرحله، ممکن است دو مقدار یا یک مقدار با یک خوشه یا حتی دو خوشه با یکدیگر ادغام شده و خوشه جدیدی ایجاد کنند.
این عملیات با رسیدن به بزرگترین خوشه که از همه مقدارها تشکیل یافته پایان مییابد. به این ترتیب اگر n مقدار داشته باشیم در مرحله اول تعداد خوشهها برابر با n است و در آخرین مرحله یک خوشه باقی خواهد ماند.
برای اندازهگیری فاصله بین دو خوشه یا یک مقدار با یک خوشه از روشهای «پیوند» (Linkage) استفاده میشود. از انواع روشهای پیوند میتوان به «نزدیکترین همسایه» (Nearest Neighbor) یا «پیوند تکی» (Single Linkage)، «دورترین همسایه» (Furthest Neighbor) یا «پیوند کامل» (Complete Linkage) و همچنین «پیوند میانگین» (Average Linkage) اشاره کرد.
معمولا به این شیوه خوشهبندی سلسله مراتبی، روش «تجمیعی» (Agglomerative) میگویند.
برعکس اگر عمل خوشهبندی سلسله مراتبی به شکلی باشد که با بزرگترین خوشه، عملیات خوشهبندی شروع شده و با تقسیم هر خوشه به خوشههای کوچکتر ادامه پیدا کند، به آن «خوشهبندی سلسله مراتبی تقسیمی» (Divisive Hierarchical Clustering) میگویند. در آخرین مرحله این روش، هر مقدار تشکیل یک خوشه را میدهد پس n خوشه خواهیم داشت.
هر چند شیوه نمایش خوشهبندی سلسله مراتبی تقسیمی نیز توسط درختواره انجام میشود ولی از آنجایی که محدودیتهایی برای تقسیم یک خوشه به زیر خوشههای دیگر وجود دارد، روش تقسیمی کمتر به کار میرود.
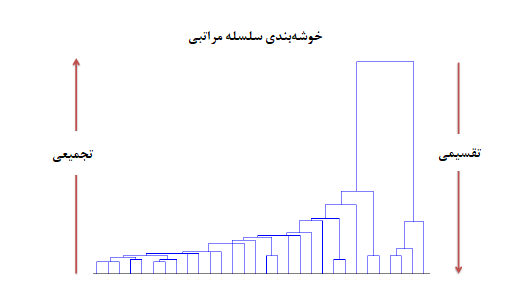
نکته: در شیوه خوشهبندی سلسله مراتبی، عمل برچسب گذاری در طی مراحل خوشهبندی اصلاح پذیر نیست. به این معنی که وقتی عضوی درون یک خوشه قرار گرفت هرگز از آن خوشه خارج نمیشود.
از الگوریتمهای معروف برای خوشهبندی سلسله مراتبی تجمیعی میتوان به AGNES و برای تقسیمی به DIANA اشاره کرد.
خوشهبندی برمبنای چگالی (Density-Bases Clustering)
روشهای خوشهبندی تفکیکی قادر به تشخیص خوشههایی کروی شکل هستند. به این معنی که برای تشخیص خوشهها از مجموعه دادههایی به شکلهای «کوژ» (Convex) یا محدب خوب عمل میکنند. در عوض برای تشخیص خوشهها برای مجموعه دادههای «کاو» (Concave) یا مقعر دچار خطا میشوند. به تصویر ۳ توجه کنید که بیانگر شکلهای کاو است.
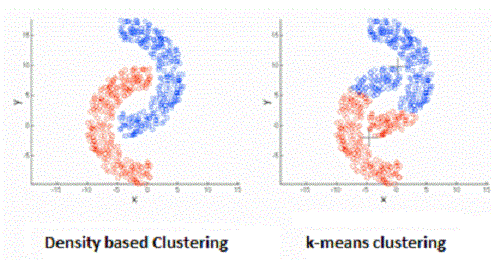
همانطور که دیده میشود میانگین هر دو خوشه در روش k-means در محلی قرار گرفته است که مربوط به خوشه دیگر است. در حالی که خوشهبندی برمبنای چگالی به خوبی نقاط را در خوشههای درست قرار داده است.
در الگوریتمها خوشهبندی برمبنای چگالی، نقاط با تراکم زیاد شناسایی شده و در یک خوشه قرار میگیرند. از الگوریتمهای معروف در این زمینه میتوان به DBSCAN اشاره کرد که در سال ۱۹۹۶ توسط «استر» (Ester) معرفی شد.
این الگوریتم توانایی شناسایی نقاط دورافتاده را داشته و میتواند تاثیر آنها را در نتایج خوشهبندی از بین ببرد. شیوه کارکرد این الگوریتم بنا به تعریفهای زیر قابل درک است:
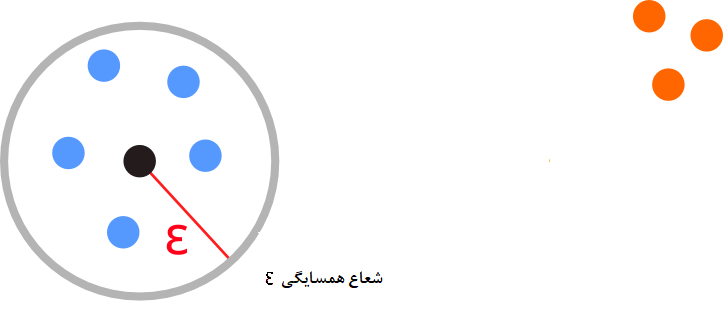
- همسایگی به شعاع $$\epsilon$$: اگر فضای با شعاع $$\epsilon$$ را حول نقطهای x در نظر بگیریم، یک همسایگی ایجاد کردهایم که به شکل $$N_{\epsilon}(x)$$ نشان داده میشود. شکل ریاضی این همسایگی به صورت زیر است.
$$N_{\epsilon}(x)=\{y \in D ; d(x,y)\leq \epsilon\}$$
بطوری که D مجموعه داده و d تابع فاصله است. تصویر 4 مفهوم همسایگی را نشان میدهد.
- قابل دسترسی مستقیم (Directly density-reachable): نقطه x را قابل دسترسی مستقیم از y مینامند اگر براساس دو پارامتر $$N_{min}$$ و $$\epsilon$$ داشته باشیم:
$$x\in N_{\epsilon}(y) $$
$$|N_{\epsilon}(y)|\geq N_{min} $$
در اینجا $$|N_{\epsilon}(y)|$$ نشانگر تعداد اعضای همسایگی به شعاع $$\epsilon$$ از نقطه y است.
پس شرط اول به معنی این است که x در همسایگی از y قرار دارد و شرط دوم نیز بیان میکند که باید تعداد اعضای همسایگی y از حداقل تعداد اعضای همسایگی بیشتر باشد.
- نقطه قابل دسترسی (Density-Reachable): نقطه x را از طرق y قابل دسترس مینامند، اگر دنبالهای از نقاط مثل $$x_1, x_2,\ldots,x_i$$ موجود باشند که نقطه x را به y برسانند. یعنی:
$$x=x_1,x_2,\ldots,x_i=y$$
در این حالت برای مثال $$x_1$$ «قابل دسترسی مستقیم» (Direct Reachable) به $$x_2$$ نامیده میشود.
- نقاط متصل (Density-Connected): دو نقطه x و y را متصل گویند اگر براساس پارامترهای $$\epsilon$$ و $$N_{min}$$ نقطهای مانند z وجود داشته باشد که هر دو نقطه x و y از طریق آن قابل دسترسی باشند.
- خوشه (Cluster): فرض کنید مجموعه داده D موجود باشد. همچنین C یک زیر مجموعه غیر تهی از D باشد. C را یک خوشه مینامند اگر براساس پارمترهای $$\epsilon$$ و $$N_{min}$$ در شرایط زیر صدق کند:
۱- اگر x درون C باشد و y نیز قابل دسترسی به x با پارامترهای $$\epsilon$$ و $$N_{min}$$ باشد، آنگاه y نیز در C است.
۲- اگر دو نقطه x و y در C باشند آنگاه این نقاط براساس پارامترهای $$\epsilon$$ و $$N_{min}$$ نقاط متصل محسوب شوند.
به این ترتیب خوشهها شکل گرفته و براساس میزان تراکمشان تشکیل میشوند. نویز یا نوفه (Noise) نیز نقاطی خواهند بود که در هیچ خوشهای جای نگیرند. برای روشن شدن این تعریفها به تصویر 5 توجه کنید.
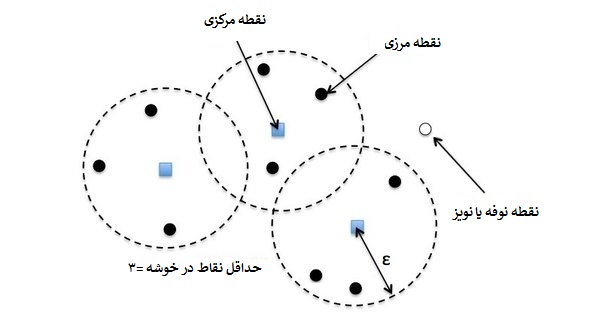
نکته: با توجه به تعریف خوشه، مشخص است که اندازه هر خوشه از $$N_{min}$$ بیشتر است.
مراحل خوشهبندی برمبنای چگالی به این ترتیب است که ابتدا یک نقطه را به صورت اختیاری انتخاب کرده و نقاط قابل دسترس برای آن پیدا میشود. اگر x یک نقطه مرکزی باشد (نقطهای که درون خوشه قرار داشته باشد)، خوشه را تشکیل میدهد ولی اگر x نقطهای مرزی باشد (نقطهای که در لبههای خوشه قرار داشته باشد) آنگاه هیچ نقطه قابل دسترسی برای x وجود نخواهد داشت و الگوریتم از نقطهای دیگری ادامه پیدا میکند.
در مراحل خوشهبندی ممکن است دو خوشه که به یکدیگر نزدیک باشند، ادغام شوند. فاصله بین دو خوشه برحسب حداقل فاصله بین اعضای دو خوشه (پیوند تکی) سنجیده میشود.
نکته: انتخاب مقدار برای پارامترهای $$\epsilon$$ و $$N_{min}$$ مسئله مهمی است که براساس نظر محقق باید به الگوریتم داده شوند. ترسیم نمودار دادهها در انتخاب این پارامترها میتواند موثر باشد. هرچه دادهها در دستههای متراکمتر دیده شوند بهتر است مقدار $$\epsilon$$ را کوچک در نظر گرفت و اگر لازم است که تعداد خوشهها کم باشند بهتر است مقدار $$N_{min}$$ را بزرگ انتخاب کرد.
خوشهبندی برمبنای مدل (Model-Based Clustering)
در روشهای پیشین، فرضیاتی مبنی بر وجود یک توزیع آماری برای دادهها وجود نداشت. در روش «خوشهبندی برمبنای مدل» (Model-Based Clustering) یک توزیع آماری برای دادهها فرض میشود. هدف در اجرای خوشهبندی برمبنای مدل، برآورد پارامترهای توزیع آماری به همراه متغیر پنهانی است که به عنوان برچسب خوشهها در مدل معرفی شده.
با توجه به تعداد خوشههایی که در نظر گرفته شده است، مثلا k، تابع درستنمایی را برای پیدا کردن خوشهها به صورت زیر مینویسند:
$$L_M(\Theta_1,\Theta_2,\Theta_3,\ldots,\Theta_k;t_1,t_2,\ldots,t_k)=\prod_{i=1}^n\sum_{j=1}^kt_jf_j(x_i,\Theta_j)$$
در رابطه بالا $$t_j$$ بیانگر احتمال تعلق نقطه به خوشه jام و $$f_j$$ نیز توزیع آمیخته با پارامترهای $$\Theta_j$$ است.
در اکثر مواقع برای دادهها توزیع نرمال آمیخته در نظر گرفته میشود. در چنین حالتی توزیع آمیخته را به فرمی مینویسند که درصد آمیختگی (درصدی از دادهها که متعلق به هر توزیع هستند) نیز به عنوان پارامتر در مدل حضور دارد.
$$f(x)=\sum_{j=1}^k p_j\Phi(X;\mu_j,\Sigma_{i})$$
در رابطه بالا $$\Phi$$ توزیع نرمال با پارامترهای $$\mu_j$$ و $$\Sigma_j$$ برای توزیع jام هستند و $$p_j$$ نیز درصد آمیختگی برای توزیع jام محسوب میشود. در تصویر 6 یک نمونه از توزیع آمیخته نرمال دو متغیره نمایش داده شده است.
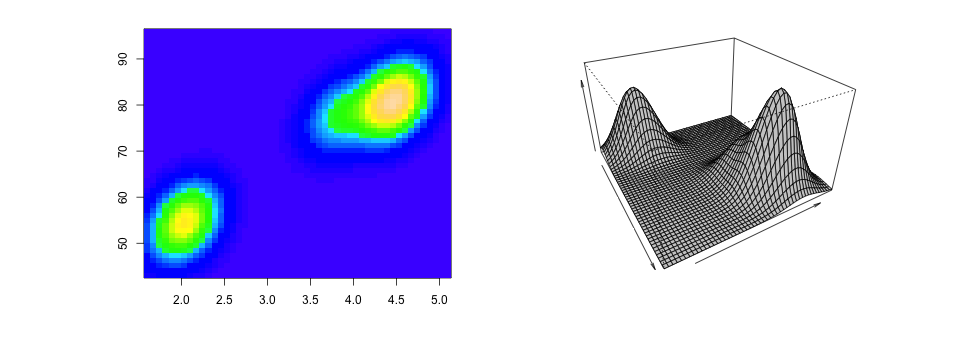
انتخابهای مختلفی برای ماتریس واریانس-کوواریانس یا $$\Sigma$$ وجود دارد. یکی از این حالتها در نظر گرفتن استقلال و یکسان بودن واریانس برای همه توزیعها است. همچنین میتوان واریانس هر توزیع را متفاوت از توزیعهای دیگر در نظر گرفت و بدون شرط استقلال عمل کرد. در حالت اول پیچیدگی مدل و تعداد پارامترهای برآورد شده کم و در حالت دوم پیچیدگی مدل و تعداد پارامترهای برآورده شده زیاد خواهد بود.
برای برآورد پارامترهای چنین مدلی باید از تابع درستنمایی استفاده کرد و به کمک مشتق مقدار حداکثر را برای این تابع بدست آورد. با این کار پارامترهای مدل نیز برآورد میشوند. ولی با توجه به پیچیدگی تابع درستنمایی میتوان از روشهایی ساده و سریعتری نیز کمک گرفت. یکی از این روشها استفاده از الگوریتم EM (مخفف Expectation Maximization) است. در الگوریتم EM که براساس متغیر پنهان عمل میکند، میتوان به حداکثر مقدار تابع درستنمایی همراه با برآورد پارامترها دست یافت.
در چنین حالتی میتوان برچسب تعلق هر مقدار به خوشه را به عنوان متغیر پنهان در نظر گرفت. اگر متغیر پنهان را $$z_{ij}$$ در نظر بگیریم مقداری برابر با ۱ دارد اگر مشاهده iام در خوشه jام باشد و در غیر اینصورت مقدار آن 0 خواهد بود.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
- آموزش خوشه بندی تفکیکی با نرم افزار R
- آموزش خوشه بندی سلسله مراتبی با SPSS
- فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی
^^











سلام عالی بود.
داده های مربوط به خوشه بندی غیر کروی رو میتونین ارسال کنین؟
سلام و وقت بخیر
خیلی مفید و کاربردی بود. ممنون از شما
سلام لطفا در خصوص خوشه ریزشبکه ها و فیلم آموزشی مدیرت انرژی در این خوشه و یا لینک مربوط به تهیه موارد فوق را ارسال بفرمایید ممنون می شوم اگر سریعتر باشد با احترام
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم.
این مطلب با محوریت خوشهبندی در یادگیری ماشین ارائه شده است. برای یادگیری این مبحث میتوانید از دورههای آموزشی زیر استفاده کنید:
برای شما آرزوی سلامتی و موفقیت داریم.
راجع به خوشه بندی affinity Propagation هم اگر مطلب بگذارید ممنون می شوم
سلام وقتتون بخیر
من منطق ترکیب خوشه بندی و دسته بندی رو توی بعضی از مقاله ها نمیفهمم! دقیقا منطقش چی هستش در برنامه ای مثل رپیدماینر؟
سلام وقتتون بخیر
ببخشید من پایان نامه ام درمورد خوشه بندی داده های دودویی(باینری) هستش میخوام سه روش خوشه بندی رو برای داده ها باینری بیان کنم میشه راهنمایی کنید یااینکه کتابی مقاله ای چیزی میشناسید بهم معرفی کنم هرچی سرچ میزنم هیچی پیدا نمیکنم
سلام وقتتون بخیر…میشه منو در زمینه خوشه بندی ENCEMBLE یا تجمیعی راهنمایی کنید؟
مرسی از مطلبتون
خیلی جالبه من مبحث Clustering and Classification رو در درس پایگاه داده پیشرفته در فصلی مربوط به انلایز داده و Data mining در یه دانشگاه خارج از کشور می خونم. البته وارد جزئیات مفاهیم ریاضی آن نمی شن.
مرسی
سلام آقای دکتر
وقت شما به خیر
آیا میتونم در مورد integrated Laplace approximation (INLA) methodology
برای آنالیز بیزین از شما کمک و راهنمایی بگیرم؟
با تشکر
کوروش
سلام و وقت بخیر
از اینکه همراه مجله فرادرس هستید بر خود میبالیم.
برای آشنایی با INLA بهتر است مطلبی که در اینجا اشاره شده را بخوانید. البته به زودی توضیح و ترجمه آن نیز در مجله فرادرس منتشر خواهد شد.
تندرست و شاد و موفق باشید.