بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی

در تحلیل‌های مدل‌های رگرسیونی، مسئله «بیش‌برازش» (Overfitting) و کم‌برازش (Underfitting) موضوعات با اهمیتی هستند. این مسئله باعث می‌شود که «ضرایب رگرسیونی» (Regression coefficients) به درستی برآورد نشوند. در داده‌کاوی و مبحث آموزش ماشین، معمولا به بیش‌برازش، بیش‌آموزش (OverTraining) و به کم‌برازش، کم‌آموزش (UnderTraining) می‌گویند.

در این مطلب،‌ به بررسی مدل‌های بیش‌برازش و کم‌برازش می‌پردازیم و شیوه‌های شناسایی آن‌ها را بررسی می‌کنیم. برای آگاهی بیشتر در مورد برآورد به روش رگرسیون بهتر است مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده مطالعه شود.

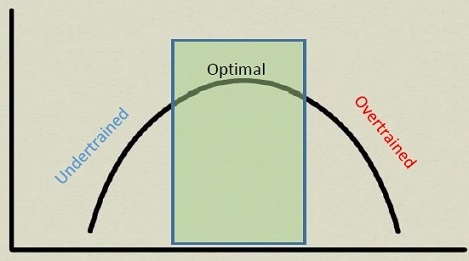
بیش‌برازش، کم برازش و برازش مناسب

مدل بیش‌برازش، مدلی بسیار پیچیده برای داده‌ها است. به این معنی که در تحلیل رگرسیونی، مدلی با بیشترین پارامترها ایجاد می‌شود. در چنین حالتی،‌ مدل با تغییرات جهشی سعی در پوشش داده‌های حاصل از نمونه و حتی مقدارهای نویز می‌کند. در حالیکه چنین مدلی باید منعکس کننده رفتار جامعه باشد. در این گونه موارد، اگر مدل رگرسیون بدست آمده، برای پیش‌بینی نمونه دیگری به کار رود، مقدارهای پیش‌بینی شده اصلا مناسب به نظر نخواهند رسید.

فیلم آموزش آزمون های نیکویی برازش با نرم افزار EasyFit در فرادرس

کلیک کنید

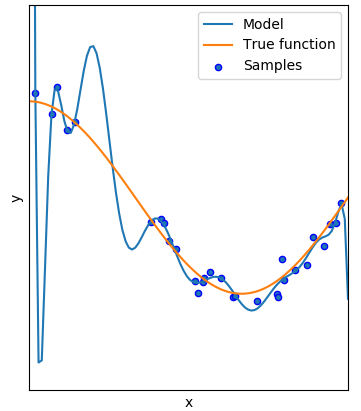
در تصویر 1، نمودار حاصل از بیش‌برازش روی داده‌های حاصل از نمونه دیده می‌شود. خط آبی، نشان دهنده منحنی برازش شده روی داده‌ها است و خط نارنجی تابعی است که مدل واقعی جامعه آماری را نشان می‌دهد. نقاط آبی رنگ نیز نمونه‌های تصادفی از جامعه آماری را نشان می‌دهند. در مدل بیش‌برازش، نقطه‌های حاصل از نمونه‌ بهترین برازش را دارند و خط آبی تقریباً از همه آن‌ها عبور کرده است.

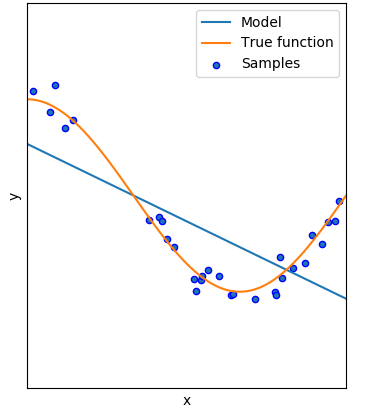
همچنین در زمانی که پارامترهای مدل رگرسیونی به صورت کم برازش برآورد می‌شوند، جانب احتیاط حفظ شده و مدل سعی می‌کند با کمترین پارامترها، عمل برازش را انجام دهد. در نتیجه خطای حاصل از این مدل حتی براساس نمونه‌های به کار رفته نیز بسیار زیاد است. در تصویر ۲، یک نمونه از مدل رگرسیونی کم‌برازش دیده می‌شود. درجه منحنی به کار رفته در این حالت ۱ است که معادله خط محسوب می‌شود.

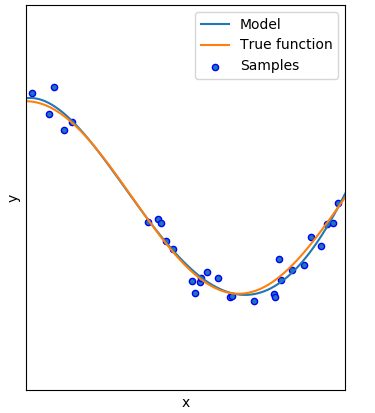
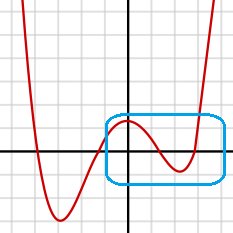
انتظار ما از یک تحلیل رگرسیون مناسب، ایجاد مدلی است که نه تنها بتواند برای داده‌های مربوط به نمونه برازش مناسب را انجام دهد، بلکه برای داده‌هایی جدید نیز امکان برآورد مناسب وجود داشته باشد. همانطور که در تصویر ۳ دیده می‌شود مدل مناسب دارای خطای کوچکی است و قابلیت پیش‌بینی برای داده‌های جدید را دارد.

علت بروز بیش‌برازش یا کم‌برازش

معمولا در برازش مدل روی داده‌ها، با یک نمونه از جامعه آماری مواجه هستیم و سعی داریم براساس اطلاعاتی که نمونه جمع‌آوری شده از جامعه آماری به همراه دارد، در مورد پارامترهای آن تصمیم‌گیری کنیم. ولی مشکلی که در این میان وجود دارد، کمبود اطلاعاتی است که از جامعه آماری بدست ما رسیده است. زیرا نمونه گرفته شده از جامعه آماری همه اطلاعات آن را منعکس نمی‌کند و نمونه فقط می‌تواند بخشی از اطلاعات را به ما نشان دهد.

هرچه اندازه نمونه بزرگتر باشد، اطلاعات بیشتری نیز از جامعه آماری به همراه دارد ولی انتخاب نمونه‌های بزرگ از جامعه آماری، هزینه و زمان زیادی می‌برند. در همین راستا انتخاب تعداد نمونه مناسب قبل از انجام تحلیل، ضروری است.

اگر امکان دسترسی به نمونه بزرگتر وجود ندارد، ممکن است برازش مدل دچار مشکل شود. فرض کنید براساس یک نمونه کوچک می‌خواهید برآورد رگرسیونی با پارامترهای متعدد ایجاد کنید. در چنین حالتی مدل دچار بیش‌برازش می‌شود. در نتیجه براساس تعداد پارامترهای زیادی که در نظر گرفته شده است، مدل فقط برای نمونه به کار رفته به خوبی عمل می‌کند ولی برای بیش‌بینی داده‌هایی غیر از نمونه گرفته شده، قابل اتکا نیست.

برعکس، اگر براساس تعداد پارامترهای کم، عمل برازش را انجام دهیم، مدل دچار کم‌برازش خواهد شد و قدرت پیش‌بینی برای جامعه آماری را از دست خواهد داد. حتی برای داده‌های موجود نیز به علت کمبود پارامترهای به کار رفته، خطای زیادی در مدل بوجود می‌آید.

همانطور که در تصاویر ۱ تا ۳ دیده می‌شود،‌ سه مدل متفاوت با استفاده از یک نمونه ۲۸ تایی، برازش شده است. در تصویر ۱ به علت کمبود داده‌های موجود در نمونه، مدلی با 16 پارامتر (چند جمله‌ای مرتبه ۱۵) دچار بیش‌برازش شده است. در تصویر ۲ نیز با همان تعداد نمونه، دو پارامتر برای مدل به کار رفته است و یک چند جمله‌ای مرتبه ۱ (معادله خط) برای برازش در نظر گرفته شده. در این حالت، مدل با مشکل کم‌برازشی مواجه شده است.

اگر براساس این حجم نمونه، مدل را یک چند جمله‌ای مرتبه ۴ در نظر بگیریم، مناسب‌ترین مدل با خطای کمینه حاصل می‌شود. همانطور که در تصویر ۴ می‌بینید، داده‌های نمونه، قسمتی از چند جمله‌ای مرتبه چهار به نظر می‌رسند.

نکته: مدل خطی یا چند جمله‌ای مرتبه n به صورت زیر نوشته می‌شود:

$$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_nx^n$$

همانطور که قابل مشاهد است مدل چند جمله‌ای مرتبه ۱، دارای دو پارامتر $$a_0,a_1$$ است. پس تعداد پارامترهای مدل، یکی بیشتر از مرتبه چند جمله‌ای است.

تشخیص مدل بیش‌برازش و کم‌برازش

معمولا روش برآورد پارامترهای یک مدل برازشی برای داده‌ها، کمینه سازی یک «تابع خطا» (Error Function) یا «تابع هزینه» (Cost Function) است. در نتیجه مطمئن هستیم که برای داده‌های حاصل از نمونه، مدل بهترین برازش را براساس تابع خطای انتخابی خواهد داشت. البته انتخاب تابع خطای مناسب برای مدل، احتیاج به مهارت و بررسی عمیق داده‌ها دارد. ولی به هر حال با توجه به تابع خطای انتخابی، لازم است که وجود مشکل بیش‌برازش برای مدل مورد کاوش قرار گیرد.

فیلم آموزش طراحی و آنالیز داده ها با نرم افزار اوریجین پرو OriginPro در فرادرس

کلیک کنید

البته رفع مشکل کم‌برازش با افزایش تعداد پارامترهای مدل قابل رفع است، ولی نکته‌ای که باید رعایت کرد، انتخاب تعداد پارامترهای مناسب در مدل است که آن را دچار بیش‌برازش نکند. روش‌های متعددی برای تشخیص مدل‌های بیش‌برازش وجود دارد. در ادامه به بررسی دو روش تشخیصی «اعتبارسنجی متقاطع» (Cross-Validation) و «ضریب تعیین پیش‌بینی شده» (Predicted R-squared)، می‌پردازیم.

اعتبارسنجی متقاطع

برای تشخیص بیش‌برازش در مدل می‌توان از «اعتبارسنجی متقاطع» استفاده کرد. در این حالت داده‌های نمونه به دو یا چند بخش تفکیک شده و در هر مرحله یکی از بخش‌ها برای برآورد پارامترهای مدل به کار می‌رود. این بخش از نمونه را «مجموعه داده‌های آموزشی» (Training Set) می‌نامند.

بخش‌های دیگر نمونه که به آن «مجموعه داده‌های آزمایشی» (Test Set) می‌گویند برای سنجش میزان خطای پیش‌بینی مدل به کار می‌روند. روند اعتبار سنجی متقاطع به صورت زیر است:

1. داده‌ها را به دو بخش آموزشی و آزمایشی تفکیک می‌کنیم.
2. برای داده‌های آموزشی پارامترهای مدل مناسب را براساس کمینه سازی تابع خطا، برآورد می‌کنیم.
3. خطای برازش مدل ایجاد شده را روی داده‌های آزمایشی اندازه‌گیری می‌کنیم.
4. نسبت خطای بدست آمده از مدل، برای داده‌های آزمایشی و آموزشی نباید خیلی بزرگ باشد.
5. مراحل ۱ تا ۴ را با توجه به همگرا شدن نسبت حاصل از مرحله ۴ ادامه می‌دهیم در غیر این صورت به تعداد تکرار مشخص، عملیات پایان می‌یابد (هر کدام زودتر به وقوع بپیوندد). با توجه به میزان نسبت خطاهای ذکر شده بهترین مدل در این مرحله حاصل می‌شود.

ضریب تعیین پیش‌بینی شده

با توجه به اینکه در مدل رگرسیونی نیاز داریم بیشترین «تغییرات در داده‌ها» (Data Variation) توسط مدل، قابل پوشش باشد، به شاخصی احتیاج است که میزان تغییرات پوشش داده شده را نشان دهد.

«ضریب تعیین» (Coefficient of determination) بیانگر درصدی از تغییرات کلی داده‌ها است که توسط مدل رگرسیونی قابل محاسبه است. مقدار ضریب تعیین بین ۰ و ۱ قرار دارد و هرچه به ۱ نزدیک‌تر باشد نشان می‌دهد که درصد بیشتری از تغییرات داده‌ها، توسط مدل رگرسیونی و درصد کمتری توسط خطا‌های تصادفی (نویز) قابل پیش‌بینی است.

فیلم مجموعه آموزش مدل سازی، برازش و تخمین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

انتظار داریم که از بین چندین مدل رگرسیونی، مدلی با ضریب تعیین بزرگتر بهتر باشد. ولی در این حالت به دو مسئله برخورد می‌کنیم:

مسئله اول: با اضافه کردن یک پارامتر بیشتر به مدل (حتی یک پارامتر شانسی) مقدار ضریب تعیین افزایش می‌یابد. یعنی با اضافه کردن پارامترهای مدل، ضریب تعیین بهبود می‌یابد.

مسئله دوم: مدل با تعداد پارامترهای زیاد (مثلا مرتبه بزرگ برای چند جمله‌ای)، ممکن است، مقادیر نویز (Noise) را نیز پیش‌بینی کند. در این حالت مدلی با ضریب تعیین بزرگ بدست آمده که قادر به پیش‌بینی داده‌های آینده نیست.

در چنین مواقعی، از «ضریب تعیین پیش‌بینی شده» استفاده می‌شود. این شاخص نوع خاصی از حالت اعتبار سنجی متقاطع است.

شاخص یاد شده بیان می‌کند که مدل چقدر قدرت پیش‌بینی برای داده‌های جدید را دارد. در نتیجه از ضریب تعیین پیش‌بینی شده، برای تشخیص بیش‌برازش استفاده می‌شود. در بیشتر نرم‌افزارهای آماری در بخش مدل‌های رگرسیونی، این شاخص با حذف سیستماتیک یک مشاهده و برآورد پارامترهای مدل و محاسبه ضریب تعیین برای مدل‌های بدست آمده، محاسبه می‌شود.

اگر مدل با تعداد پارامترهای مناسب ایجاد شده باشد، اختلاف زیادی بین ضریب تعیین و ضریب تعیین پیش‌بینی شده وجود نخواهد داشت. ولی اگر اختلاف محسوسی بین این دو شاخص قابل مشاهده باشد، مشخص است که مدل دچار بیش‌برازش شده است.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های SPSS
• آموزش همبستگی و رگرسیون خطی در SPSS
• مهم‌ترین الگوریتم‌های یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده 
• آموزش یادگیری ماشین
• مجموعه آموزش‌های نرم‌افزارهای آماری