در آموزشهای قبلی از مجموعه مطالب ریاضیات مجله فرادرس ، درباره انتگرال و روشهای محاسبه آن بحث کردیم. در این آموزشها، مباحثی مانند انتگرال توابع مثلثاتی و انتگرالگیری جزء به جزء را بیان کردیم. همچنین با انتگرال دوگانه و محاسبه آن در مختصات قطبی آشنا شدیم و به روشهایی مانند حل انتگرال دوگانه با استفاده از تغییر متغیر پرداختیم. کاربرد انتگرال دوگانه در فیزیک ، یکی دیگر از مباحثی بود که آن را بررسی کردیم. در این آموزش، برخی از کاربردهای انتگرال دوگانه را در محاسبه مساحت و حجم معرفی میکنیم.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
محاسبه مساحت
اگر f ( x , y ) = 1 f\left( {x,y} \right) = 1 f ( x , y ) = 1 ∬ R f ( x , y ) d x d y \iint\limits_R {f\left( {x,y} \right)dxdy} R ∬ f ( x , y ) d x d y R R R
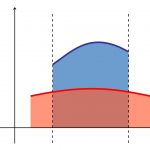
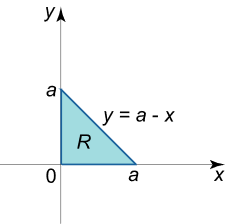
شکل ۱ مساحت یک ناحیه نوع I I I
A = ∫ a b ∫ g ( x ) h ( x ) d y d x . \large A = \int \limits _ a ^ b { \int \limits _ { g \left ( x \right ) } ^ { h \left ( x \right ) } { d y d x } } . A = a ∫ b g ( x ) ∫ h ( x ) d y d x .
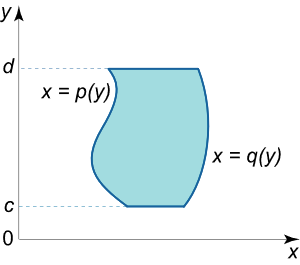
به طریق مشابه، مساحت یک ناحیه نوع I I II II
A = ∫ c d ∫ p ( y ) q ( y ) d x d y . \large A = \int \limits _ c ^ d { \int \limits _ { p \left ( y \right ) } ^ { q \left ( y \right ) } { d x d y } } . A = c ∫ d p ( y ) ∫ q ( y ) d x d y .
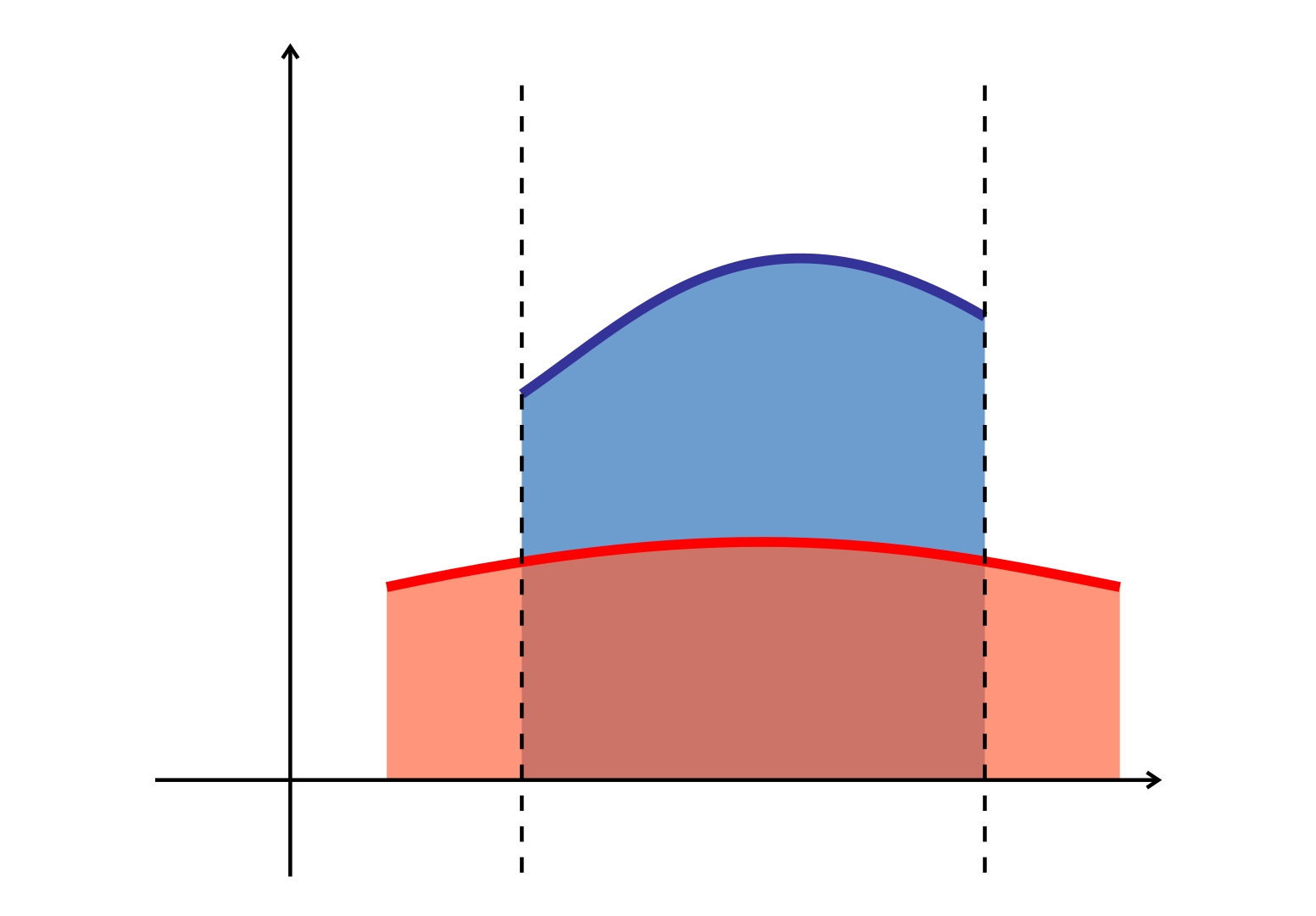
شکل ۲ محاسبه حجم
اگر در ناحیه R R R f ( x , y ) > 0 {f\left( {x,y} \right)} \gt 0 f ( x , y ) > 0 z = f ( x , y ) z = {f\left( {x,y} \right)} z = f ( x , y ) R R R
V = ∬ R f ( x , y ) d A . \large V = \iint \limits _ R { f \left ( { x , y } \right ) d A } . V = R ∬ f ( x , y ) d A .
اگر R R R I I I x = a x = a x = a x = b x=b x = b y = g ( x ) y=g (x) y = g ( x ) y = h ( x ) y = h (x ) y = h ( x )
V = ∬ R f ( x , y ) d A = ∫ a b ∫ g ( x ) h ( x ) f ( x , y ) d y d x . \large { V } = { \iint \limits _ R { f \left ( { x , y } \right ) d A } } = { \int \limits _ a ^ b { \int \limits _ { g \left ( x \right ) } ^ { h \left ( x \right ) } { f \left ( { x , y } \right ) d y d x } } . } V = R ∬ f ( x , y ) d A = a ∫ b g ( x ) ∫ h ( x ) f ( x , y ) d y d x .
به طریق مشابه، اگر R R R I I II II y = c y =c y = c y = d y = d y = d x = p ( y ) x = p(y) x = p ( y ) x = q ( y ) x = q (y) x = q ( y )
V = ∬ R f ( x , y ) d A = ∫ c d ∫ p ( y ) q ( y ) f ( x , y ) d x d y . \large { V } = { \iint \limits _ R { f \left ( { x , y } \right ) d A } } = { \int \limits _ c ^ d { \int \limits _ { p \left ( y \right ) } ^ { q \left ( y \right ) } { f \left ( { x , y } \right ) d x d y } } . } V = R ∬ f ( x , y ) d A = c ∫ d p ( y ) ∫ q ( y ) f ( x , y ) d x d y .
اگر در ناحیه R R R f ( x , y ) ≥ g ( x , y ) f\left( {x,y} \right) \ge g\left( {x,y} \right) f ( x , y ) ≥ g ( x , y ) z 1 = g ( x , y ) {z_1} = g\left( {x,y} \right) z 1 = g ( x , y ) z 2 = f ( x , y ) {z_2} = f\left( {x,y} \right) z 2 = f ( x , y ) R R R
V = ∬ R [ f ( x , y ) – g ( x , y ) ] d A . \large { V } = { \iint \limits _ R { \left [ { f \left ( { x , y } \right ) – g \left ( { x , y } \right ) } \right ] d A } . } V = R ∬ [ f ( x , y ) – g ( x , y ) ] d A .
مساحت سطح
فرض کنید سطحی با تابع z = g ( x , y ) z = g\left( {x,y} \right) z = g ( x , y ) R R R R R R
S = ∬ R 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d x d y \large { S \text { = } } \kern-0.3pt { \iint \limits _ R { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } d x d y } } S = R ∬ 1 + ( ∂ x ∂ z ) 2 + ( ∂ y ∂ z ) 2 d x d y
که در آن، مشتقهای ∂ z ∂ x {\large\frac{{\partial z}}{{\partial x}}\normalsize} ∂ x ∂ z ∂ z ∂ y {\large\frac{{\partial z}}{{\partial y}}\normalsize} ∂ y ∂ z R R R پیوسته هستند.
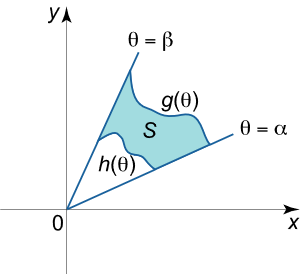
مساحت و حجم در مختصات قطبی
اگر S S S x y xy x y θ = α \theta = \alpha θ = α θ = β \theta = \beta θ = β r = h ( θ ) r = h\left( \theta \right) r = h ( θ ) r = g ( θ ) r = g\left( \theta \right) r = g ( θ )
A = ∬ R d A = ∫ α β ∫ h ( θ ) g ( θ ) r d r d θ . \large { A = \iint \limits _ R { d A } } = { \int \limits _ \alpha ^ \beta { \int \limits _ { h \left ( \theta \right ) } ^ { g \left ( \theta \right ) } { r d r d \theta } } . } A = R ∬ d A = α ∫ β h ( θ ) ∫ g ( θ ) r d r d θ .
شکل ۳ حجم فضای زیر z = f ( r , θ ) z = f\left( {r,\theta } \right) z = f ( r , θ ) S S S مختصات قطبی به صورت زیر قابل محاسبه است:
V = ∬ S f ( r , θ ) r d r d θ . \large { V } = { \iint \limits _ S { f \left ( { r , \theta } \right ) r d r d \theta } . } V = S ∬ f ( r , θ ) r d r d θ .
مثالها
در ادامه، مثالهایی را از کاربردهای انتگرال دوگانه بیان میکنیم.
مثال ۱
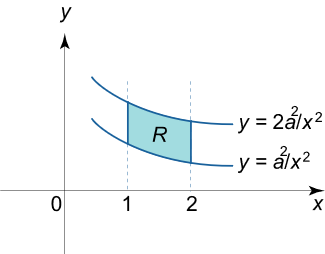
مساحت ناحیه R R R هذلولویهای y = a 2 x y = {\large\frac{{{a^2}}}{x}\normalsize} y = x a 2 y = 2 a 2 x y = {\large\frac{{2{a^2}}}{x}\normalsize} y = x 2 a 2 a > 0 a>0 a > 0 خطوط عمودی x = 1 x=1 x = 1 x = 2 x= 2 x = 2
حل: ناحیه R R R
شکل ۴ با استفاده از فرمول مساحت برای یک ناحیه نوع I I I
A = ∬ R d x d y = ∫ a b ∫ g ( x ) h ( x ) d y d x \large { A = \iint \limits _ R { d x d y } } = { \int \limits _ a ^ b { \int \limits _ { g \left ( x \right ) } ^ { h \left ( x \right ) } { d y d x } } } A = R ∬ d x d y = a ∫ b g ( x ) ∫ h ( x ) d y d x
بنابراین، مساحت ناحیه مورد نظر برابر است با:
A = ∬ R d x d y = ∫ 1 2 [ ∫ a 2 x 2 a 2 x d y ] d x = ∫ 1 2 [ y ∣ a 2 x 2 a 2 x ] d x = ∫ 1 2 ( 2 a 2 x – a 2 x ) d x = a 2 ∫ 1 2 d x x = a 2 ( ln 2 – ln 1 ) = a 2 ln 2. \large \begin {align*} A & = \iint \limits _ R { d x d y } = { \int \limits _ 1 ^ 2 { \left [ { \int \limits _ { \frac { { { a ^ 2 } } } { x } } ^ { \frac { { 2 { a ^ 2 } } } { x } } { d y } } \right ] d x } } = { \int \limits _ 1 ^ 2 { \left [ { \left . y \right | _ { \frac { { { a ^ 2 } } } { x } } ^ { \frac { { 2 { a ^ 2 } } } { x } } } \right ] d x } } \\ & = { \int \limits _ 1 ^ 2 { \left ( { \frac { { 2 { a ^ 2 } } } { x } – \frac { { { a ^ 2 } } } { x } } \right ) d x } } = { { a ^ 2 } \int \limits _ 1 ^ 2 { \frac { { d x } } { x } } } = { { a ^ 2 } \left ( { \ln 2 – \ln 1 } \right ) } = { { a ^ 2 } \ln 2 . } \end {align*} A = R ∬ d x d y = 1 ∫ 2 x a 2 ∫ x 2 a 2 d y d x = 1 ∫ 2 [ y ∣ x a 2 x 2 a 2 ] d x = 1 ∫ 2 ( x 2 a 2 – x a 2 ) d x = a 2 1 ∫ 2 x d x = a 2 ( ln 2– ln 1 ) = a 2 ln 2.
مثال ۲
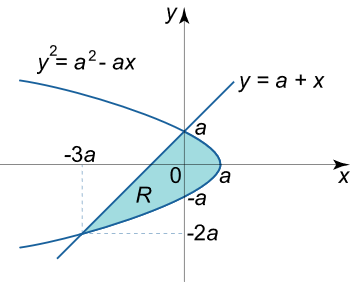
مساحت ناحیه R R R y = a + x y = a + x y = a + x y 2 = a 2 – a x {y^2} = {a^2} – ax y 2 = a 2 – a x
حل: ابتدا نقاط تقاطع دو منحنی را پیدا میکنیم:
{ y 2 = a 2 – a x y = a + x , ⇒ ( a + x ) 2 = a 2 – a x , ⇒ a 2 + 2 a x + x 2 = a 2 – a x , ⇒ x 2 + 3 a x = 0 , ⇒ x ( x + 3 a ) = 0 , ⇒ x 1 , 2 = 0 ; – 3 a . \large \begin {align*} \left\{ \begin {array} {l} { y ^ 2 } = { a ^ 2 } – a x \\ y = a + x \end {array} \right . , \; \; & \Rightarrow { { \left ( { a + x } \right ) ^ 2 } = { a ^ 2 } – a x , \; \; } \\ & \Rightarrow { { a ^ 2 } + 2 a x + { x ^ 2 } = { a ^ 2 } – a x , \; \; } \\ & \Rightarrow { { x ^ 2 } + 3 a x = 0 , \; \; } \\ & \Rightarrow { x \left ( { x + 3 a } \right ) = 0 , \; \; } \Rightarrow { { x _ { 1 , 2 } } = 0 ; \; – 3 a . } \end {align*} { y 2 = a 2 – a x y = a + x , ⇒ ( a + x ) 2 = a 2 – a x , ⇒ a 2 + 2 a x + x 2 = a 2 – a x , ⇒ x 2 + 3 a x = 0 , ⇒ x ( x + 3 a ) = 0 , ⇒ x 1 , 2 = 0 ; –3 a .
بنابراین، مختصات نقاط تقاطع به صورت زیر به دست میآیند:
x 1 = 0 , y 1 = a + 0 = a , x 2 = – 3 a , y 2 = a – 3 a = – 2 a . \large { { x _ 1 } = 0 , \; \; } \kern-0.3pt { { y _ 1 } = a + 0 = a , } \\ \large { { x _ 2 } = – 3 a , \; \; } \kern-0.3pt { { y _ 2 } = a – 3 a = – 2 a . } x 1 = 0 , y 1 = a + 0 = a , x 2 = –3 a , y 2 = a –3 a = –2 a .
اگر ناحیه R R R I I II II
شکل ۵ برای محاسبه مساحت ناحیه مورد نظر، معادلات مرزها را به فرم استاندارد تبدیل میکنیم:
y 2 = a 2 – a x , ⇒ a x = a 2 – y 2 , ⇒ x = a – y 2 a , y = a + x , ⇒ x = y – a . \large { { y ^ 2 } = { a ^ 2 } – a x , \; \; } \Rightarrow { a x = { a ^ 2 } – { y ^ 2 } , \; \; } \Rightarrow { x = a – \frac { { { y ^ 2 } } } { a } , } \\ \large { y = a + x , \; \; } \Rightarrow { x = y – a . } y 2 = a 2 – a x , ⇒ a x = a 2 – y 2 , ⇒ x = a – a y 2 , y = a + x , ⇒ x = y – a .
در نتیجه، داریم:
A = ∬ R d x d y = ∫ – 2 a a [ ∫ y – a a – y 2 a d x ] d y = ∫ – 2 a a [ ∫ y – a a – y 2 a d x ] d y = ∫ – 2 a a [ x ∣ y – a a – y 2 a ] d y = ∫ – 2 a a [ a – y 2 a – ( y – a ) ] d y = ∫ – 2 a a ( 2 a – y 2 a – y ) d y = ( 2 a y – y 3 3 a – y 2 2 ) ∣ – 2 a a = ( 2 a 2 – a 3 3 a – a 2 2 ) − ( – 4 a 2 + 8 a 3 3 a – 4 a 2 2 ) = 9 a 2 2 . \large \begin {align*} A & = \iint \limits _ R { d x d y } = { \int \limits _ { – 2 a } ^ a { \left [ { \int \limits _ { y – a } ^ { a – \frac { { { y ^ 2 } } } { a } } { d x } } \right ] d y } } = { \int \limits _ { – 2 a } ^ a { \left [ { \int \limits _ { y – a } ^ { a – \frac { { { y ^ 2 } } } { a } } { d x } } \right ] d y } } \\ & = { \int \limits _ { – 2 a } ^ a { \left [ { \left . x \right | _ { y – a } ^ { a – \frac { { { y ^ 2 } } } { a } } } \right ] d y } } = { \int \limits _ { – 2 a } ^ a { \left [ { a – \frac { { { y ^ 2 } } } { a } – \left ( { y – a } \right ) } \right ] d y } } \\ & = { \int \limits _ { – 2 a } ^ a { \left ( { 2 a – \frac { { { y ^ 2 } } } { a } – y } \right ) d y } } = { \left . { \left ( { 2 a y – \frac { { { y ^ 3 } } } { { 3 a } } – \frac { { { y ^ 2 } } } { 2 } } \right ) } \right | _ { – 2 a } ^ a } \\ & = { \left ( { 2 { a ^ 2 } – \frac {{ { a ^ 3 } } } { { 3 a } } – \frac { { { a ^ 2 } } } { 2 } } \right ) } - { \left ( { – 4 { a ^ 2 } + \frac { { 8 { a ^ 3 } } } { { 3 a } } – \frac { { 4{ a ^ 2 }} } { 2 } } \right ) } = { \frac { { 9 { a ^ 2 } } } { 2 } . } \end {align*} A = R ∬ d x d y = –2 a ∫ a y – a ∫ a – a y 2 d x d y = –2 a ∫ a y – a ∫ a – a y 2 d x d y = –2 a ∫ a [ x ∣ y – a a – a y 2 ] d y = –2 a ∫ a [ a – a y 2 – ( y – a ) ] d y = –2 a ∫ a ( 2 a – a y 2 – y ) d y = ( 2 a y – 3 a y 3 – 2 y 2 ) –2 a a = ( 2 a 2 – 3 a a 3 – 2 a 2 ) − ( –4 a 2 + 3 a 8 a 3 – 2 4 a 2 ) = 2 9 a 2 .
مثال ۳
حجمی از فضای سه بعدی را بیابید که در یکهشتم اول دستگاه مختصات محدود به صفحات y = 0 y = 0 y = 0 z = 0 z = 0 z = 0 z = x z = x z = x z + x = 4 z+x = 4 z + x = 4
حل: فضای مورد نظر در شکل ۶ نشان داده شده است.
شکل ۶ همانطور که در شکل بالا میبینیم، R R R مربعی در ربع اول است. مقدار z z z z = x z =x z = x z = 4 − x z = 4 - x z = 4 − x
V = ∬ R [ ( 4 – x ) – x ] d x d y = ∫ 0 2 [ ∫ 0 2 ( 4 – 2 x ) d y ] d x = ∫ 0 2 [ ( 4 y – 2 x y ) ∣ y = 0 2 ] d x = ∫ 0 2 ( 8 – 4 x ) d x = ( 8 x – 2 x 2 ) ∣ 0 2 = 16 – 8 = 8. \large \begin {align*} V & = \iint \limits _ R { \left [ { \left ( { 4 – x } \right ) – x } \right ] d x d y } = { \int \limits _ 0 ^ 2 { \left [ { \int \limits _ 0 ^ 2 { \left ( { 4 – 2 x } \right ) d y } } \right ] d x } } \\ & = { \int \limits _ 0 ^ 2 { \left [ { \left . { \left ( { 4 y – 2 x y } \right ) } \right | _ { y = 0 } ^ 2 } \right ] d x } } = { \int \limits _ 0 ^ 2 { \left ( { 8 – 4 x } \right ) d x } } = { \left . { \left ( { 8 x – 2 { x ^ 2 } } \right ) } \right | _ 0 ^ 2 } \\ & = { 1 6 – 8 } = { 8 . } \end {align*} V = R ∬ [ ( 4– x ) – x ] d x d y = 0 ∫ 2 0 ∫ 2 ( 4–2 x ) d y d x = 0 ∫ 2 [ ( 4 y –2 x y ) ∣ y = 0 2 ] d x = 0 ∫ 2 ( 8–4 x ) d x = ( 8 x –2 x 2 ) 0 2 = 16–8 = 8.
مثال ۴
فضایی را توصیف کنید که حجم آن با رابطه زیر محاسبه میشود:
V = ∫ 0 1 d x ∫ 0 1 – x ( x 2 + y 2 ) d y . \large V = \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ { 1 – x } { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d y } . V = 0 ∫ 1 d x 0 ∫ 1– x ( x 2 + y 2 ) d y .
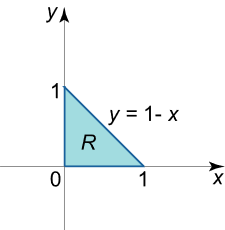
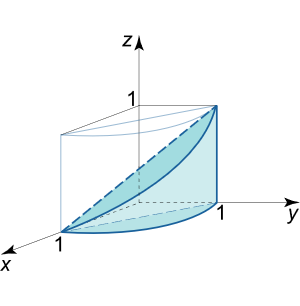
حل: تصویر زیرین جسم داده شده (شکلهای ۷ و ۸)، در مثلث R R R x y xy x y O x Ox O x O y Oy O y y = 1 − x y =1-x y = 1 − x R R R سهمیوار z = x 2 + y 2 z = {x^2} + {y^2} z = x 2 + y 2
شکل ۷ شکل ۸ حجم این جسم، برابر است با:
V = ∫ 0 1 d x ∫ 0 1 – x ( x 2 + y 2 ) d y = ∫ 0 1 [ ( x 2 y + y 3 3 ) ∣ y = 0 1 – x ] d x = ∫ 0 1 [ x 2 ( 1 – x ) + ( 1 – x ) 3 3 ] d x = ∫ 0 1 ( 2 x 2 – 4 x 3 3 – x + 1 3 ) d x = ( 2 x 3 3 – 4 3 ⋅ x 4 4 – x 2 2 + x 3 ) ∣ 0 1 = 2 3 – 1 3 – 1 2 + 1 3 = 1 6 . \large \begin {align*} { V } & = { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ { 1 – x } { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d y } } = { \int \limits _ 0 ^ 1 { \left [ { \left . { \left ( { { x ^ 2 } y + \frac { { { y ^ 3 } } } { 3 } } \right ) } \right | _ { y = 0 } ^ { 1 – x } } \right ] d x } } \\ & = { \int \limits _ 0 ^1 { \left [ { { x ^ 2 } \left ( { 1 – x } \right ) + \frac { { { { \left ( { 1 – x } \right ) } ^ 3 } } } { 3 } } \right ] d x } } = { \int \limits _ 0 ^ 1 { \left ( { 2 { x ^ 2 } – \frac { { 4 { x ^ 3 } } } { 3} – x + \frac { 1 } { 3 } } \right ) d x } } \\ & = { \left . { \left ( { \frac { { 2 { x ^ 3 } } } { 3 } – \frac { 4 } { 3 } \cdot \frac { { { x ^ 4 } } } { 4 } – \frac { { { x ^ 2 } } } { 2 } + \frac { x } { 3 } } \right ) } \right | _ 0 ^ 1 } = { \frac { 2 } { 3 } – \frac { 1} { 3 } – \frac { 1 } { 2 } + \frac { 1 } { 3 } } = { \frac { 1 }{ 6 } . } \end {align*} V = 0 ∫ 1 d x 0 ∫ 1– x ( x 2 + y 2 ) d y = 0 ∫ 1 ( x 2 y + 3 y 3 ) y = 0 1– x d x = 0 ∫ 1 [ x 2 ( 1– x ) + 3 ( 1– x ) 3 ] d x = 0 ∫ 1 ( 2 x 2 – 3 4 x 3 – x + 3 1 ) d x = ( 3 2 x 3 – 3 4 ⋅ 4 x 4 – 2 x 2 + 3 x ) 0 1 = 3 2 – 3 1 – 2 1 + 3 1 = 6 1 .
مثال ۵
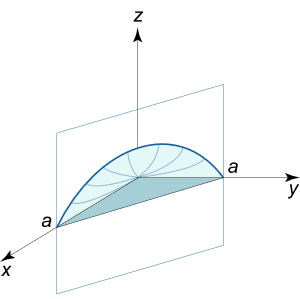
حجم جسم محدود به z = x y z = xy z = x y x + y = a x + y = a x + y = a z = 0 z = 0 z = 0
حل: جسم مورد نظر، فضای بالای مثلث R R R x y x y x y z = x y z = xy z = x y
شکل ۹ شکل ۱۰ حجم این جسم برابر است با:
V = ∬ R x y d x d y = ∫ 0 a [ ∫ 0 a – x x y d y ] d x = ∫ 0 a [ ( f r a c x y 2 2 ) ∣ y = 0 a – x ] d x = 1 2 ∫ 0 a x ( a – x ) 2 d x = 1 2 ∫ 0 a x ( a 2 – 2 a x + x 2 ) d x = 1 2 ∫ 0 a ( a 2 x – 2 a x 2 + x 3 ) d x = 1 2 ( a 2 ⋅ x 2 2 – 2 a ⋅ x 3 3 + x 4 4 ) ∣ 0 a = 1 2 ( a 2 2 – 2 a 4 3 + a 4 4 ) = a 4 24 . \large \begin {align*} V = \iint \limits _ R { x y d x d y } & = { \int \limits _ 0 ^ a { \left [ { \int \limits _ 0 ^ { a – x } { x y d y } } \right ] d x } } = { \int \limits _ 0 ^ a { \left [ { \left . { \left ( {\ frac { { x { y ^ 2 } } } { 2 } } \right ) } \right | _ { y = 0 } ^ { a – x } } \right ] d x } } \\ & = { \frac { 1 } { 2 } \int \limits _ 0 ^ a { x { { \left ( { a – x } \right ) } ^ 2 } d x } } = { \frac { 1 }{ 2 } \int \limits _ 0 ^ a { x \left ( { { a ^ 2 } – 2 a x + { x ^ 2 } } \right ) d x } } \\ & = { \frac { 1 } { 2 } \int \limits _ 0 ^ a { \left ( { { a ^ 2 } x – 2 a { x ^ 2 } + { x ^ 3 } } \right ) d x } } \\ & = { \frac { 1 } { 2 } \left . { \left ( { { a ^ 2 } \cdot \frac { { { x ^ 2 } } } { 2 } – 2 a \cdot \frac { { { x ^ 3 } } } { 3 } + \frac { { { x ^ 4 } } } { 4 } } \right ) } \right | _ 0 ^ a } \\ & = { \frac { 1 } { 2 }\left ( { \frac { { { a ^ 2 } } } { 2 } – \frac { { 2 { a ^ 4 } } } { 3 } + \frac { { { a ^ 4 } } } { 4 } } \right ) } = { \frac { { { a ^ 4 } } } { { 2 4 } } . } \end {align*} V = R ∬ x y d x d y = 0 ∫ a 0 ∫ a – x x y d y d x = 0 ∫ a [ ( f r a c x y 2 2 ) y = 0 a – x ] d x = 2 1 0 ∫ a x ( a – x ) 2 d x = 2 1 0 ∫ a x ( a 2 –2 a x + x 2 ) d x = 2 1 0 ∫ a ( a 2 x –2 a x 2 + x 3 ) d x = 2 1 ( a 2 ⋅ 2 x 2 –2 a ⋅ 3 x 3 + 4 x 4 ) 0 a = 2 1 ( 2 a 2 – 3 2 a 4 + 4 a 4 ) = 24 a 4 .
مثال ۶
حجم جسم محدود به سطوح z = 0 z = 0 z = 0 x + y = 1 x + y = 1 x + y = 1 x 2 + y 2 = 1 {x^2} + {y^2} = 1 x 2 + y 2 = 1 z = 1 – x z = 1 – x z = 1– x
حل: همانطور که در شکلهای ۱۱ و ۱۲ نشان داده شده است، ناحیه انتگرالگیری R R R y y y 0 ≤ x ≤ 1 0 \le x \le 1 0 ≤ x ≤ 1 1 − x 1- x 1 − x 1 – x 2 \sqrt {1 – {x^2}} 1– x 2
شکل ۱۱ شکل ۱۲ بنابراین، حجم مورد نظر برابر است با:
V = ∬ R ( 1 – x ) d x d y = ∫ 0 1 [ ∫ 1 – x 1 – x 2 ( 1 – x ) d y ] d x = ∫ 0 1 [ ( 1 – x ) y ∣ 1 – x 1 – x 2 ] d x = ∫ 0 1 ( 1 – x ) ( 1 – x 2 – 1 + x ) d x = ∫ 0 1 1 – x 2 d x – ∫ 0 1 x 1 – x 2 d x – ∫ 0 1 ( 1 + 2 x – x 2 ) d x . \large \begin {align*} {V } & ={ \iint \limits _ R { \left ( { 1 – x } \right ) d x d y } } = { \int \limits _ 0 ^ 1 { \left [ { \int \limits _ { 1 – x } ^ { \sqrt { 1 – { x ^ 2 } } } { \left ( { 1 – x } \right ) d y } } \right ] d x } } \\ & = { \int \limits _ 0 ^ 1 { \left [ { \left ( { 1 – x } \right ) \left . y \right | _ { 1 – x } ^ { \sqrt { 1 – { x ^ 2 } } } } \right ] d x } } = { \int \limits _ 0 ^ 1 { \left ( { 1 – x } \right ) \left ( { \sqrt { 1 – { x ^ 2 } } – 1 + x } \right ) d x } } \\ & = { \int \limits _ 0 ^ 1 { \sqrt { 1 – { x ^ 2 } } d x } } – { \int \limits _ 0 ^ 1 { x \sqrt { 1 – { x ^ 2 } } d x } } – { \int \limits _ 0 ^ 1 { \left ( { 1 + 2 x – { x ^ 2 } } \right ) d x } . } \end {align*} V = R ∬ ( 1– x ) d x d y = 0 ∫ 1 1– x ∫ 1– x 2 ( 1– x ) d y d x = 0 ∫ 1 [ ( 1– x ) y ∣ 1– x 1– x 2 ] d x = 0 ∫ 1 ( 1– x ) ( 1– x 2 –1 + x ) d x = 0 ∫ 1 1– x 2 d x – 0 ∫ 1 x 1– x 2 d x – 0 ∫ 1 ( 1 + 2 x – x 2 ) d x .
سه انتگرال بالا را به صورت جداگانه محاسبه میکنیم. انتگرال نخست، برابر است با:
I 1 = ∫ 0 1 1 – x 2 d x . \large { I _ 1 } = \int \limits _ 0 ^ 1 { \sqrt { 1 – { x ^ 2 } } d x } . I 1 = 0 ∫ 1 1– x 2 d x .
برای حل این انتگرال، از تغییر متغیر x = sin t x = \sin t x = sin t d x = cos t d t dx = \cos tdt d x = cos t d t x = 0 x =0 x = 0 t = 0 t = 0 t = 0 x = 1 x = 1 x = 1 t = π 2 t = {\large\frac{\pi }{2}\normalsize} t = 2 π
I 1 = ∫ 0 1 1 – x 2 d x = ∫ 0 π 2 1 – sin 2 t cos t d t = ∫ 0 π 2 cos 2 t d t = ∫ 0 π 2 1 + cos 2 t 2 d t = 1 2 ∫ 0 π 2 ( 1 + cos 2 t ) d t = 1 2 ( t + sin 2 t 2 ) ∣ 0 π 2 = 1 2 ( π 2 + sin π 2 ) = π 4 . \large \begin {align*} { I _ 1 } & = \int \limits _ 0 ^ 1 { \sqrt { 1 – { x ^ 2 } } d x } = { \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \sqrt { 1 – { { \sin } ^ 2 } t } \cos t d t } } = { \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { { \cos } ^ 2 } t d t } } \\ & = { \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \frac { { 1 + \cos 2 t } } { 2 } d t } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \left ( { 1 + \cos 2 t } \right ) d t } } \\ & = { \frac { 1 } { 2 } \left . { \left ( { t + \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } = { \frac { 1 } { 2 } \left ( { \frac { \pi } { 2 } + \frac { { \sin \pi } } { 2 } } \right ) } = { \frac { \pi } { 4 } . } \end {align*} I 1 = 0 ∫ 1 1– x 2 d x = 0 ∫ 2 π 1– sin 2 t cos t d t = 0 ∫ 2 π cos 2 t d t = 0 ∫ 2 π 2 1 + cos 2 t d t = 2 1 0 ∫ 2 π ( 1 + cos 2 t ) d t = 2 1 ( t + 2 sin 2 t ) 0 2 π = 2 1 ( 2 π + 2 sin π ) = 4 π .
انتگرال دوم I 2 = ∫ 0 1 x 1 – x 2 d x {I_2} = \int\limits_0^1 {x\sqrt {1 – {x^2}} dx} I 2 = 0 ∫ 1 x 1– x 2 d x 1 – x 2 = w 1 – {x^2} = w 1– x 2 = w − 2 x d x = d w -2xdx = dw − 2 x d x = d w x d x = – d w 2 xdx = {\large\frac{{ – dw}}{2}\normalsize} x d x = 2 – d w x = 0 x =0 x = 0 w = 1 w = 1 w = 1 x = 1 x = 1 x = 1 w = 0 w = 0 w = 0
I 2 = ∫ 0 1 x 1 – x 2 d x = ∫ 1 0 w ( – d w 2 ) = – 1 2 ∫ 1 0 w d w = 1 2 ∫ 0 1 w d w = 1 2 ∫ 0 1 w 1 2 d w = 1 2 ( 2 w 3 2 3 ) ∣ 0 1 = 1 3 . \large \begin {align*} { I _ 2 } & = \int \limits _ 0 ^ 1 { x \sqrt { 1 – { x ^ 2 } } d x } = { \int \limits _ 1 ^ 0 { \sqrt w \left ( { – \frac { { d w } } { 2 } } \right ) } } \\ & = { – \frac { 1 } { 2 } \int \limits _ 1 ^ 0 { \sqrt w d w } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ 1 { \sqrt w d w } } \\ & = { \frac { 1 } { 2 } \int \limits _ 0 ^ 1 { { w ^ { \large \frac { 1 } { 2 } \normalsize } } d w } } = { \frac { 1 } { 2 } \left . { \left ( { \frac { { 2 { w ^ { \large \frac { 3 } { 2 } \normalsize } } } } { 3 } } \right ) } \right | _ 0 ^ 1 } = { \frac { 1 } { 3 } . } \end {align*} I 2 = 0 ∫ 1 x 1– x 2 d x = 1 ∫ 0 w ( – 2 d w ) = – 2 1 1 ∫ 0 w d w = 2 1 0 ∫ 1 w d w = 2 1 0 ∫ 1 w 2 1 d w = 2 1 3 2 w 2 3 0 1 = 3 1 .
انتگرال سوم نیز به صورت زیر محاسبه میشود:
$$ \large \begin {align*}<br />
\require {cancel} { I _ 3 } & = \int \limits _ 0 ^ 1 { \left ( { 1 – 2 x + { x ^ 2 } } \right ) d x } \\ & = { \left . { \left ( { x – { x ^ 2 } + \frac { { { x ^ 3 } } } { 3 } } \right ) } \right | _ 0 ^ 1 } = { \cancel { 1 } – \cancel { 1 } + \frac { 1 } { 3 } } = { \frac { 1 } { 3 } . }<br />
\end {align*} $$
در نهایت، حجم مورد نظر برابر است با:
V = I 1 – I 2 – I 3 = π 4 – 1 3 – 1 3 = π 4 – 2 3 ≈ 0 , 12. \large { V = { I _ 1 } – { I _ 2 } – { I _ 3 } } = { \frac { \pi } { 4 } – \frac { 1 } { 3 } – \frac { 1 } { 3 } } = { \frac { \pi } { 4 } – \frac { 2 } { 3 } }\approx { 0,12 . } V = I 1 – I 2 – I 3 = 4 π – 3 1 – 3 1 = 4 π – 3 2 ≈ 0 , 12.
مثال ۷
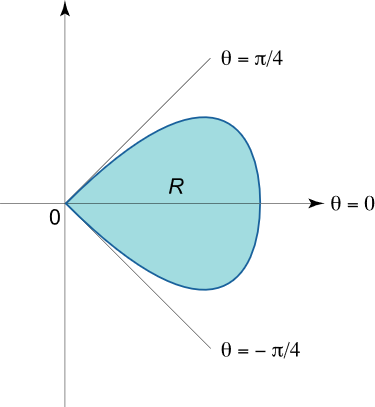
مساحت یک حلقه از گلدیسی را بیابید که با معادله r = cos 2 θ r = \cos 2\theta r = cos 2 θ
حل: حلقه ناحیه – π 4 ≤ θ ≤ π 4 – {\large\frac{\pi }{4}\normalsize} \le \theta \le {\large\frac{\pi }{4}\normalsize} – 4 π ≤ θ ≤ 4 π
شکل ۱۳ ناحیه انتگرالگیری R R R
R = { ( r , θ ) ∣ 0 ≤ r ≤ cos 2 θ , – π 4 ≤ θ ≤ π 4 } . \large { R } = { \left\{ { \left ( { r , \theta } \right) | \; 0 \le r \le \cos 2 \theta , \; } \right . }\left.{ – {\large\frac{\pi }{4}\normalsize } \le \theta \le { \large \frac { \pi }{ 4 } \normalsize } } \right\} . R = { ( r , θ ) ∣ 0 ≤ r ≤ cos 2 θ , – 4 π ≤ θ ≤ 4 π } .
بنابراین، مساحت ناحیه در مختصات قطبی برابر است با:
A = ∬ R r d r d θ = ∫ – π 4 π 4 [ ∫ 0 cos 2 θ r d r ] d θ = ∫ – π 4 π 4 [ ( r 2 2 ) ∣ 0 cos 2 θ ] d θ = 1 2 ∫ – π 4 π 4 cos 2 ( 2 θ ) d θ = 1 2 ∫ – π 4 π 4 1 + cos 4 θ 2 d θ = 1 4 ∫ – π 4 π 4 ( 1 + cos 4 θ ) d θ = 1 4 ( θ + sin 4 θ 4 ) ∣ – π 4 π 4 = 1 4 [ ( π 4 + sin π 4 ) − ( – π 4 + sin ( – π ) 4 ) ] = π 8 . \large \begin {align*} A & = \iint \limits _ R { r d r d \theta } = { \int \limits _ { – \large \frac { \pi } { 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } { \left [ { \int \limits _ 0 ^ { \cos 2 \theta } { r d r } } \right ] d \theta } } = { \int \limits _ { – \large \frac { \pi }{ 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } { \left [ { \left . { \left ( { \frac { { { r ^ 2 } } } { 2 } } \right ) } \right | _ 0 ^ { \cos 2 \theta } } \right ] d \theta } } \\ & = { \frac { 1 } { 2 } \int \limits _ { – \large \frac { \pi } { 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } { { { \cos } ^ 2 } \left ( { 2 \theta } \right ) d \theta } } = { \frac { 1 } { 2 } \int \limits _ { – \large \frac { \pi }{ 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } { \frac { { 1 + \cos 4 \theta } } { 2 } d \theta } } \\ & = { \frac { 1 } { 4 } \int \limits _ { – \large \frac { \pi } { 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } { \left ( { 1 + \cos 4 \theta } \right ) d \theta } } = { \frac { 1 } { 4 } \left . { \left ( { \theta + \frac { { \sin 4 \theta } } { 4 } } \right ) } \right | _ { – \large \frac { \pi }{ 4 } \normalsize } ^ { \large \frac { \pi } { 4 } \normalsize } } \\ & = { \frac { 1 } { 4 } \left [ { \left ( { \frac { \pi } { 4 } + \frac { { \sin \pi } } { 4 } } \right ) } \right . } - { \left . { \left ( { – \frac { \pi } { 4 } + \frac { { \sin \left ( { – \pi } \right ) } } { 4 } } \right ) } \right ] } = { \frac { \pi } { 8 } . } \end {align*} A = R ∬ r d r d θ = – 4 π ∫ 4 π 0 ∫ c o s 2 θ r d r d θ = – 4 π ∫ 4 π ( 2 r 2 ) 0 c o s 2 θ d θ = 2 1 – 4 π ∫ 4 π cos 2 ( 2 θ ) d θ = 2 1 – 4 π ∫ 4 π 2 1 + cos 4 θ d θ = 4 1 – 4 π ∫ 4 π ( 1 + cos 4 θ ) d θ = 4 1 ( θ + 4 sin 4 θ ) – 4 π 4 π = 4 1 [ ( 4 π + 4 sin π ) − ( – 4 π + 4 sin ( – π ) ) ] = 8 π .
مثال ۸
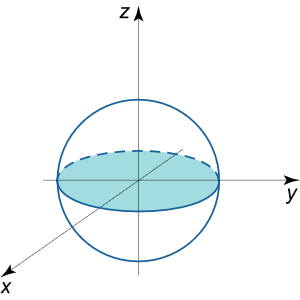
حجم یک کره واحد را به دست آورید.
حل: معادله کرهای به شعاع یک، x 2 + y 2 + z 2 = 1 {x^2} + {y^2} + {z^2} = 1 x 2 + y 2 + z 2 = 1
شکل ۱۴ به دلیل تقارن کره، نیمکره بالایی را در نظر گرفته و حجم آن را در 2 2 2
z = 1 – ( x 2 + y 2 ) . \large z = \sqrt { 1 – \left ( { { x ^ 2 } + { y ^ 2 } } \right ) } . z = 1– ( x 2 + y 2 ) .
معادله بالا را به مختصات قطبی تبدیل میکنیم:
z ( r , θ ) = 1 – r 2 . \large z \left ( { r , \theta } \right ) = \sqrt { 1 – { r ^ 2 } } . z ( r , θ ) = 1– r 2 .
در مختصات قطبی، ناحیه انتگرالگیری R R R
R = { ( r , θ ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π } . \large { R } = { \left\{ { \left ( { r , \theta } \right ) | \; 0 \le r \le 1 , \; } \right . } { \left . { 0 \le \theta \le 2 \pi } \right \} . } R = { ( r , θ ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π } .
بنابراین، حجم نیمکره بالایی برابر است با:
V 1 2 = ∬ R 1 – r 2 r d r d θ = ∫ 0 2 π d θ ∫ 0 1 1 – r 2 r d r = 2 π ∫ 0 1 1 – r 2 r d r . \large \begin {align*} { { V _ { \large \frac { 1 } { 2 } \normalsize } } } & = { \iint \limits _ R { \sqrt { 1 – { r ^ 2 } } r d r d \theta } } = { \int \limits _ 0 ^ { 2 \pi } { d \theta } \int \limits _ 0 ^ 1 { \sqrt { 1 – { r ^ 2 } } r d r } } \\ & = { 2 \pi \int \limits _ 0 ^ 1 { \sqrt { 1 – { r ^ 2 } } r d r } . } \end {align*} V 2 1 = R ∬ 1– r 2 r d r d θ = 0 ∫ 2 π d θ 0 ∫ 1 1– r 2 r d r = 2 π 0 ∫ 1 1– r 2 r d r .
برای محاسبه انتگرال اخیر، از تغییر متغیر 1 – r 2 = t 1 – {r^2} = t 1– r 2 = t − 2 r d r = d t -2rdr = dt − 2 r d r = d t r d r = – d t 2 rdr = – {\large\frac{{dt}}{2}\normalsize} r d r = – 2 d t r = 0 r=0 r = 0 t = 1 t = 1 t = 1 r = 1 r = 1 r = 1 t = 0 t = 0 t = 0
V 1 2 = 2 π ∫ 0 1 1 – r 2 r d r = 2 π ∫ 1 0 t ( – d t 2 ) = – π ∫ 1 0 t d t = π ∫ 0 1 t 1 2 d t = π ( t 3 2 3 2 ) ∣ 0 1 = 2 π 3 . \large \begin {align*} { { V _ { \large \frac { 1 } { 2 } \normalsize } } } & = { 2 \pi \int \limits _ 0 ^ 1 { \sqrt { 1 – { r ^ 2 } } r d r } } = { 2 \pi \int \limits _ 1 ^ 0 { \sqrt t \left ( { – \frac { { d t } } { 2 } } \right ) } } \\ & = { – \pi \int \limits _ 1 ^ 0 { \sqrt t d t } } = { \pi \int \limits _ 0 ^ 1 { { t ^ { \large \frac { 1 } { 2 } \normalsize } } d t } } = { \pi \left . { \left ( { \frac { { { t ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 3 } { 2 } } } } \right ) } \right | _ 0 ^ 1 } = { \frac { { 2 \pi } } { 3 } . } \end {align*} V 2 1 = 2 π 0 ∫ 1 1– r 2 r d r = 2 π 1 ∫ 0 t ( – 2 d t ) = – π 1 ∫ 0 t d t = π 0 ∫ 1 t 2 1 d t = π 2 3 t 2 3 0 1 = 3 2 π .
در نهایت، حجم کره برابر است با:
V = 2 V 1 2 = 4 π 3 . \large { V = 2 { V _ { \large \frac { 1 } { 2 } \normalsize } } } = { \frac { { 4 \pi } } { 3 } . } V = 2 V 2 1 = 3 4 π .
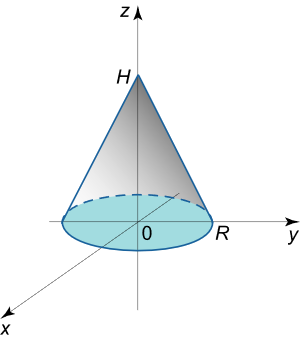
مثال ۹
از مختصات قطبی استفاده کرده و حجم یک مخروط قائم را با ارتفاع H H H دایرهای به شعاع R R R
شکل ۱۵ حل: ابتدا معادله مخروط را به دست میآوریم. با توجه به مثلثهای شکل ۱۶، میتوانیم رابطه زیر را بنویسیم:
r R = H – z H , r = x 2 + y 2 . \large { \frac { r } { R } = \frac { { H – z } } { H } , \; \; } \kern-0.3pt { \text { } \; \; r = \sqrt { { x ^ 2 } + { y ^ 2 } } . } R r = H H – z , r = x 2 + y 2 .
شکل ۱۶ بنابراین، حجم مخروط برابر است با:
V = ∬ R z ( x , y ) d x d y = ∬ R H R ( R – x 2 + y 2 ) d x d y = H R ∬ R ( R – r ) r d r d θ = H R ∫ 0 2 π [ ∫ 0 R ( R – r ) d r d ] d θ = H R ∫ 0 2 π d θ ∫ 0 R ( R r – r 2 ) d r = 2 π H R ∫ 0 R ( R r – r 2 ) d r = 2 π H R ( R r 2 2 – r 3 3 ) ∣ r = 0 R = 2 π H R ( R 3 2 – R 3 3 ) = 2 π H R ⋅ R 3 6 = π R 2 H 3 . \large \begin {align*} V & = \iint \limits _ R { z \left ( { x , y } \right ) d x d y } = { \iint \limits _ R { \frac { H } { R } \left ( { R – \sqrt { { x ^ 2 } + { y ^ 2 } } } \right ) d x d y } } \\ & = { \frac { H } { R } \iint \limits _ R { \left ( { R – r } \right ) r d r d \theta } } = { \frac { H } { R } \int \limits _ 0 ^ { 2 \pi } { \left [ { \int \limits _ 0 ^ R { \left ( { R – r } \right ) d r d } } \right ] d \theta } } \\ & = { \frac { H } { R } \int \limits _ 0 ^ { 2 \pi } { d \theta } \int \limits _ 0 ^ R { \left ( { R r – { r ^ 2 } } \right ) d r } } = { \frac { { 2 \pi H } } { R } \int \limits _ 0 ^ R { \left ( { R r – { r ^ 2 } } \right ) d r } } \\ & = { \frac { { 2 \pi H } } { R } \left . { \left ( { \frac { { R { r ^2 } } } { 2 } – \frac { { { r ^ 3 } } } { 3 } } \right ) } \right | _ { r = 0 } ^ R } = { \frac { { 2 \pi H } } { R } \left ( { \frac { { { R ^ 3 } } } { 2 } – \frac { { { R ^ 3 } } } { 3 } } \right ) } \\ & = { \frac { { 2 \pi H } } { R } \cdot \frac { { { R ^ 3 } } } { 6 } } = { \frac { { \pi { R ^ 2 } H } } { 3 } . } \end {align*} V = R ∬ z ( x , y ) d x d y = R ∬ R H ( R – x 2 + y 2 ) d x d y = R H R ∬ ( R – r ) r d r d θ = R H 0 ∫ 2 π 0 ∫ R ( R – r ) d r d d θ = R H 0 ∫ 2 π d θ 0 ∫ R ( R r – r 2 ) d r = R 2 π H 0 ∫ R ( R r – r 2 ) d r = R 2 π H ( 2 R r 2 – 3 r 3 ) r = 0 R = R 2 π H ( 2 R 3 – 3 R 3 ) = R 2 π H ⋅ 6 R 3 = 3 π R 2 H .
مثال ۱۰
مساحت سطح کرهای به شعاع a a a
حل: نیمکره بالایی را در نظر میگیریم. معادله آن به صورت زیر است:
x 2 + y 2 + z 2 = a 2 \large { x ^ 2 } + { y ^ 2 } + { z ^ 2 } = { a ^ 2 } x 2 + y 2 + z 2 = a 2
یا
z = a 2 – x 2 – y 2 \large z = \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } z = a 2 – x 2 – y 2
واضح است که ناحیه انتگرالگیری R R R a a a
S 1 2 = ∬ R 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d x d y \large { { S _ { \large \frac { 1 } { 2 } \normalsize } } \; \text { = } } \kern0pt { \iint \limits _ R { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } d x d y } } S 2 1 = R ∬ 1 + ( ∂ x ∂ z ) 2 + ( ∂ y ∂ z ) 2 d x d y
اکنون مشتقات جزئی را محاسبه میکنیم:
∂ z ∂ x = ∂ ∂ x a 2 – x 2 – y 2 = – 2 x 2 a 2 – x 2 – y 2 = – x z , ∂ z ∂ y = ∂ ∂ y a 2 – x 2 – y 2 = – 2 y 2 a 2 – x 2 – y 2 = – y z . \large \begin {align*} { \frac { { \partial z } } { { \partial x } } } & = { \frac { \partial } { { \partial x } } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } = { \frac { { – \cancel { 2 } x } } { { \cancel { 2 } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } } } = { – \frac { x } { z } , } \\ { \frac { { \partial z } } { { \partial y } } } & = { \frac { \partial } { { \partial y } } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } = { \frac { { – \cancel { 2 } y } } { { \cancel { 2 } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } } } = { – \frac { y } { z } . } \end {align*} ∂ x ∂ z ∂ y ∂ z = ∂ x ∂ a 2 – x 2 – y 2 = 2 a 2 – x 2 – y 2 – 2 x = – z x , = ∂ y ∂ a 2 – x 2 – y 2 = 2 a 2 – x 2 – y 2 – 2 y = – z y .
با جایگزینی مشتقات بالا در معادله سطح نیمکره، داریم:
S 1 2 = ∬ R 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d x d y = ∬ R 1 + x 2 z 2 + y 2 z 2 d x d y = ∬ R z 2 + x 2 + y 2 z 2 d x d y = ∬ R a z d x d y . \large \begin {align*} { S _ { \large \frac { 1 } { 2 } \normalsize } } \; & = \kern0pt { \iint \limits _ R { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } d x d y } } \\ & = { \iint \limits _ R { \sqrt { 1 + \frac { { { x ^ 2 } } }{ { { z ^ 2 } } } + \frac { { { y ^ 2 } } } { { { z ^ 2 } } } } d x d y } } \\ & = { \iint \limits _ R { \sqrt { \frac { { { z ^ 2 } + { x ^ 2 } + { y ^ 2 } } } { { { z ^ 2 } } } } d x d y } } \\ & = { \iint \limits _ R { \frac { a } { z } d x d y } . } \end {align*} S 2 1 = R ∬ 1 + ( ∂ x ∂ z ) 2 + ( ∂ y ∂ z ) 2 d x d y = R ∬ 1 + z 2 x 2 + z 2 y 2 d x d y = R ∬ z 2 z 2 + x 2 + y 2 d x d y = R ∬ z a d x d y .
انتگرال دوگانه را با استفاده از مختصات قطبی محاسبه میکنیم:
S 1 2 = ∬ R a z d x d y = ∫ 0 2 π ∫ 0 a a a 2 – r 2 r d r d θ = a ∫ 0 2 π d θ ∫ 0 a r d r a 2 – r 2 = – 2 π a ∫ 0 a d ( a 2 – r 2 ) 2 a 2 – r 2 = – 2 π a ( a 2 – r 2 ) ∣ r = 0 a = – 2 π a ( 0 – a ) = 2 π a 2 . \large \begin {align*} { { S _ { \large \frac { 1 } { 2 } \normalsize } } } & = { \iint \limits _ R { \frac { a } { z } d x d y } } = { \int \limits_ 0 ^ { 2 \pi } { \int \limits _ 0 ^ a { \frac { a } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } r d r d \theta } } } \\ & = { a \int \limits _ 0 ^ { 2 \pi } { d \theta } \int \limits _ 0 ^ a { \frac { { r d r } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } } } = { – 2 \pi a \int \limits _ 0 ^ a { \frac { { d \left ( { { a ^ 2 } – { r ^ 2} } \right)}} { { 2 \sqrt {{a^2} – {r^2}} }}} } \\ &= { – 2\pi a\left. {\left( {\sqrt {{a^2} – {r^2}} } \right)} \right|_{r = 0}^a } = { – 2\pi a \left ( {0 – a} \right ) } = { 2 \pi { a ^ 2 } .} \end {align*} S 2 1 = R ∬ z a d x d y = 0 ∫ 2 π 0 ∫ a a 2 – r 2 a r d r d θ = a 0 ∫ 2 π d θ 0 ∫ a a 2 – r 2 r d r = –2 πa 0 ∫ a 2 a 2 – r 2 d ( a 2 – r 2 ) = –2 πa ( a 2 – r 2 ) r = 0 a = –2 πa ( 0– a ) = 2 π a 2 .
بنابراین، مساحت رویه کل کره برابر است با:
S = 2 S 1 2 = 4 π a 2 . \large { S = 2 { S _ { \large \frac { 1 } { 2 } \normalsize } } } = { 4 \pi { a ^ 2 } . } S = 2 S 2 1 = 4 π a 2 .
اگر مطلب بالای برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش کاربردهای انتگرال دوگانه – همراه با مثال (+ دانلود فیلم آموزش رایگان) فیلم آموزشی محاسبه مساحت دوبعدی با انتگرال دوگانه فیلم آموزشی محاسبه مساحت سهبعدی با انتگرال دوگانه فیلم آموزشی محاسبه حجم با انتگرال دوگانه فیلم آموزشی حل مثال از محاسبه حجم با انتگرال دوگانه فیلم آموزشی مساحت در مختصات قطبی فیلم آموزشی حجم در مختصات قطبی