انتگرال دوگانه و محاسبه آن – به زبان ساده

در مطالب قبلی وبلاگ، مفاهیم انتگرال و نحوه محاسبه آن‌ توضیح داده شد. در مطالب مذکور عنوان شد که با انتگرال‌گیری از تابع $$\large f ( x , y )$$ در بازه‌ای از $$x$$، مساحت سطح زیر تابع $$\large f ( x , y )$$ در آن بازه محاسبه می‌شود. حال تابع دومتغیره‌ی $$\large f ( x , y )$$ را در نظر بگیرید؛ اگر بخواهیم از این تابع انتگرال بگیریم، x ،y یا هردوی آن‌ها متغیر هستند؟ این جا است که مفهوم انتگرال دوگانه مطرح می‌شود. البته انتگرال دوگانه در مسائل فیزیک و مهندسی نیز کاربرد بسیاری دارد.

تعریف انتگرال دوگانه

ناحیه‌ای را مطابق با شکل زیر به‌ نام R تصور کنید. هم‌چنین تابعی دومتغیره تحت عنوان (f(x,y را در نظر بگیرید.

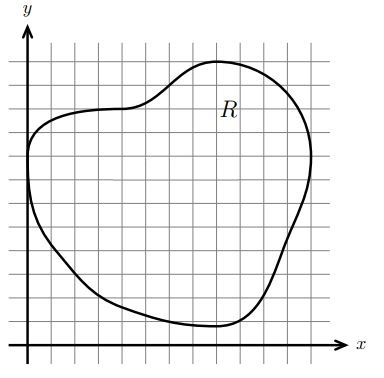
با این فرضیات انتگرال دوگانه تابع f روی ناحیه‌ی R مطابق با رابطه زیر نشان داده می‌شود.

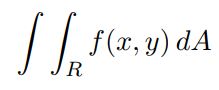
جهت درک مفهوم انتگرالِ فوق، در ابتدا ناحیه‌ی R را مطابق با شکل زیر تقسیم‌بندی و هرکدام از سلول‌ها را با اعداد $$i=1,2,3,...,n$$ نام‌گذاری می‌کنیم. مساحت آن‌ها نیز برابر با $$\Delta A_i$$ در نظر گرفته می‌شوند. توجه داشته باشید که مرکز سلول iام در نقطه (x_i,y_i) قرار گرفته است.

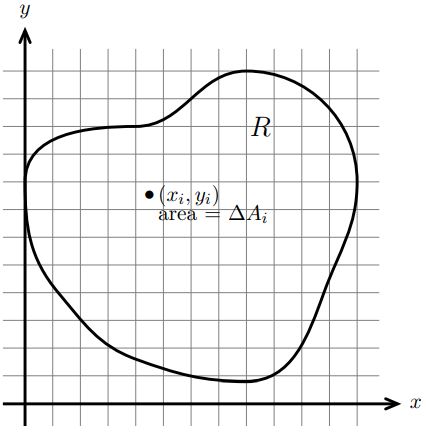
همان‌طور که می‌دانید تابع f نشان دهنده سطحی سه‌بعدی است که در بالای ناحیه R قرار گرفته است. در شکل زیر تابع f و ناحیه‌ی R نشان داده شده‌اند.

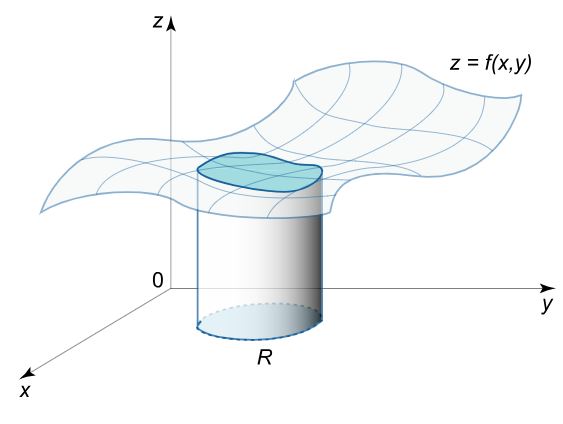
اگر ناحیه R را بخش‌های کوچک تقسیم کنیم و مساحت‌ها بخش‌ها را در مقدار تابع f ضرب کنیم، حجم ناحیه‌ی محصور بدست می‌آید. حال مقدار (f(x_i,y_i را در مساحت $$\Delta A_i$$ ضرب می‌کنیم. هریک از این ضرب‌ها،‌ نشان دهنده حجم اندکی است که بین ناحیه R و سطح f بوجود آمده است. این حجم‌ها را به عنوان «حجم‌های دیفرانسیلی» می‌شناسیم. نهایتا با جمع زدن تمامی عبارت‌ها، خواهیم داشت:

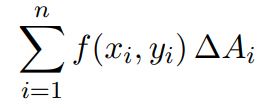
حاصل جمع بالا در صورتی که مساحت‌های $$\Delta A_i$$ را به سمت صفر میل دهیم، همان مفهوم انتگرال دوگانه تابع f روی ناحیه R بدست می‌آید. به این ترتیب می‌توان تساوی زیر را نوشت:

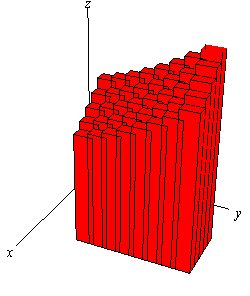
در حقیقت رابطه بالا حجم محصور شده بین ناحیه R و تابع f را نشان می‌دهد. در شکل زیر حجم‌های دیفرانسیلی، به خوبی نشان داده شده‌اند.

محاسبه انتگرال دوگانه

به‌منظور محاسبه انتگرال دوگانه بایستی:

1. ناحیه‌ای که روی آن‌ انتگرال گرفته می‌شود، مشخص شود.
2. تابع f که هدف محاسبه انتگرال آن است، نیز معلوم باشد.
3. متناسب با ناحیه، بازه‌‌های انتگرال معلوم شوند.

فیلم آموزش ریاضیات مهندسی – حل سوالات کنکور ارشد و دکتری در فرادرس

کلیک کنید

در شکل زیر ناحیه تحت انتگرال و تابع f نشان داده شده‌اند.

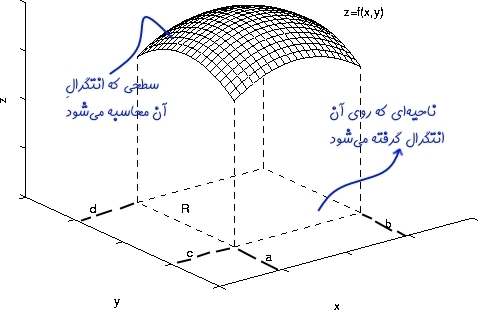
اما چگونه باید ناحیه‌ی تحت انتگرال را مشخص کرد؟ این ناحیه به صورت بازه‌هایی در انتگرال اول و دوم تعریف می‌شود. برای نمونه در شکل فوق ناحیه R در بازه‌ی c<y<d و a<x<b قرار گرفته؛‌ بنابراین انتگرال تابع f را می‌توان به‌صورت زیر بیان کرد:

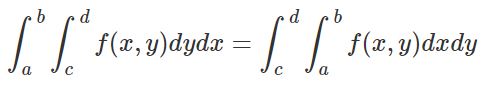
در برخی از موارد ناحیه توصیف شده دقیقا به‌صورت مربع یا مستطیل نیست. برای نمونه فرض کنید ناحیه تحت انتگرال به‌صورت زیر باشد.

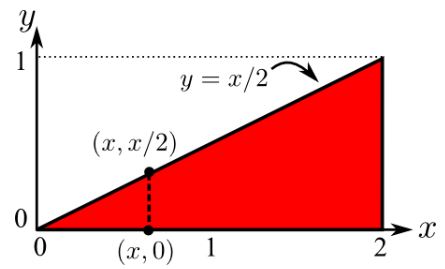
ناحیه فوق را می‌توان به دو صورت بیان کرد:

1. ناحیه x از صفر تا ۲ تغییر می‌کند. از طرفی متغیر y بین ۰ تا x/2 تغییر می‌کند. بنابراین در این حالت $$0$$ و $$0$$ فرض می‌شوند.
2. متغیرِ y از صفر تا ۱ تغییر کرده و x از 2y تا ۲ تغییر می‌کند. بنابراین در این حالت $$0$$ و $$2y$$ است.

در مثال ۲ نحوه بیان کران‌های این انتگرال توضیح داده شده است. جهت محاسبه انتگرال، در ابتدا نسبت به متغیر داخلی انتگرال گرفته و سپس نسبت به متغیر خارجی انتگرال بگیرید. به‌منظور درک بهتر مفاهیم بیان شده، مطالعه مثال‌های زیر توصیه می‌شود. همچنین، برای درک بهتر انتگرال دوگانه و چگونگی حل مسائل مرتبط با آن می‌توانید به مجموعه آموزش ریاضی دانشگاهی (ریاضی پایه و عمومی) فرادرس مراجعه کنید و با تماشای فیلم‌های آموزشی مرتبط، درک بهتری از انتگرال دوگانه و در ادامه، انتگرال سه‌گانه داشته باشید.

مثال ۱: کران‌های مستقل

حاصل انتگرال زیر را روی سطح نشان داده شده بدست آورید.

هم‌چنین سطحی که روی آن‌ انتگرال گرفته می‌شود، مستطیلی با ابعاد نشان داده شده است.

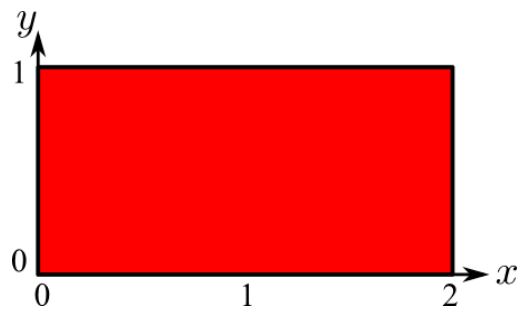
توجه داشته باشید که تفاوتی نمی‌کند dA را به‌صورت dxdy یا dydx در نظر بگیرید. در این جا dA را به ‌شکل dxdy در نظر می‌گیریم. در این صورت انتگرال به‌شکل زیر در خواهد آمد.

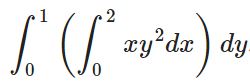
متغیر dx در داخل قرار گرفته، بنابراین در ابتدا نسبت به x انتگرال گرفته و y را هم‌چون یک ثابت در نظر بگیرید. با انتگرال‌گیری از تابع f نسبت به متغیر x داریم:

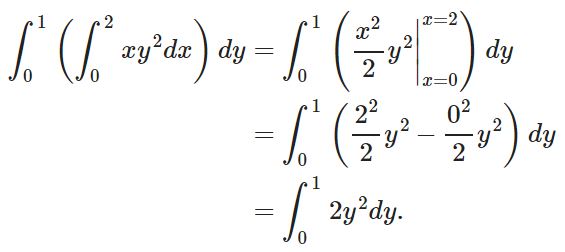
توجه داشته باشید که در هر مرحله از انتگرال‌گیری، متغیری که نسبت به آن انتگرال گرفته شده،‌ بایستی حذف شود. در رابطه بالا نیز می‌بینید که در 2y² متغیر xای وجود ندارد. در مرحله بعد، از عبارت باقیمانده نسبت به y انتگرال گرفته می‌شود. نهایتا پاسخ انتگرال برابر است با:

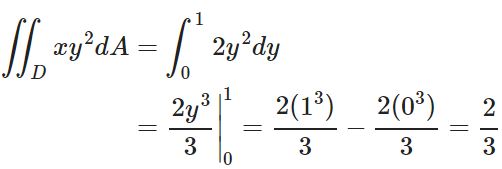
حال dA را به‌صورت dydx در نظر گرفته و انتگرال می‌گیریم. در این حالت پاسخ زیر بدست می‌آید.

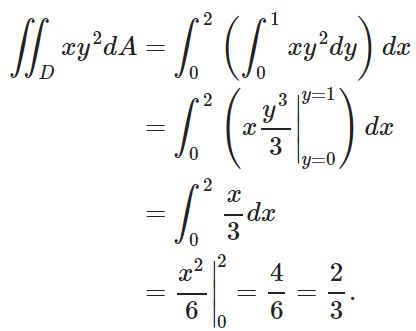
هما‌ن‌طور که می‌بینید در این حالت نیز پاسخ مشابه با روش قبلی است. انتگرال‌گیری دوگانه روی سطوح مستطیلی بسیار آسان است، چراکه در آن‌ها متغیر‌های x و y به هم‌ وابسته نیستند.

مثال ۲: کران‌های وابسته

حاصل انتگرال تابع دوگانه‌ی xy² را روی سطح زیر بیابید.

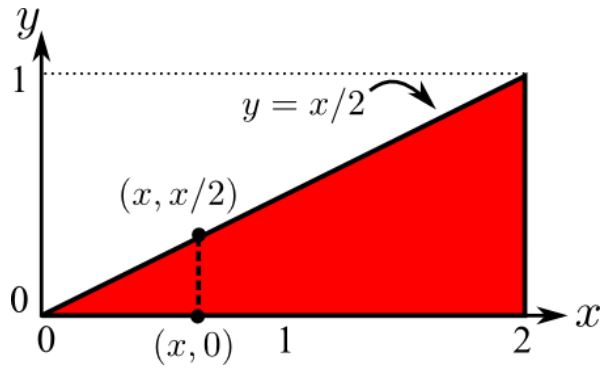
در سطوحی هم‌چون شکل فوق، تغییرات یکی از متغیرها به تغییرات متغیر دوم وابسته است. در این مثال تغییرات x را به‌صورت $$0$$ و تغییرات y را به‌صورت $$0$$ در نظر می‌گیریم. با توجه به این‌که y به‌صورت متغیر در نظر گرفته شده بنابراین dy بایستی داخل قرار گیرد. بایستی توجه داشته باشید که همواره بازه مربوط به متغیر خارجی بایستی به‌صورت عدد ثابت باشد.

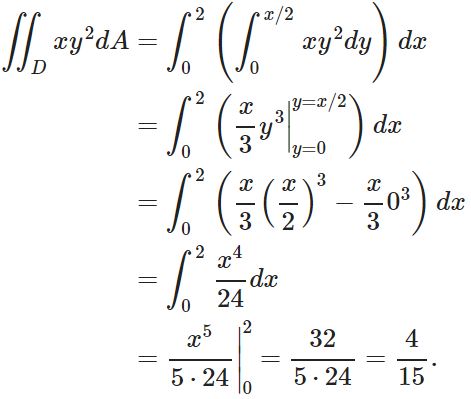
البته همین مسئله را می‌توانستیم به‌صورتی حل کنیم که در آن متغیر داخلی برابر با x و متغیر خارجی برابر با y باشد. در این حالت بازه‌ی x نیز بایستی وابسته به y بیان شود. جهت محاسبه انتگرالِ مذکور، بازه‌ها را بایستی به‌صورت $$0≤y≤1$$ و $$2y \le x \le 2$$ تعریف کرد. در این حالت، حاصل انتگرال برابر است با:

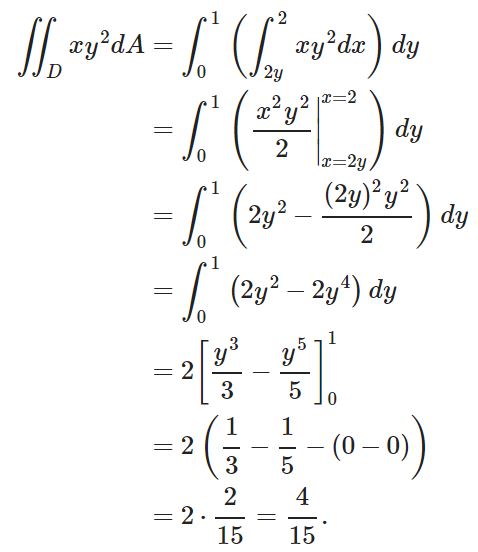
همان‌طور که می‌بینید پاسخِ‌ انتگرال در این حالت برابر با روش اول است.

مثال ۳

انتگرال دوگانه زیر را در نظر بگیرید.

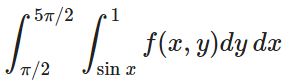
انتگرال فوق را به شکلی بیان کنید که در آن متغیر x داخل قرار گرفته و متغیر y بیرون قرار گرفته باشد.

فیلم آموزش ریاضی عمومی ۱ + مرور و حل تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

همان‌طور که در رابطه فوق نیز نشان داده شده، باز‌ه‌های انتگرال‌گیری به‌صورت زیر تعریف شده‌اند.

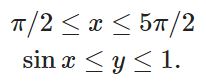
در ابتدا نمودار‌های y=sin x و y=1 را رسم کرده و ناحیه‌ی بین آن‌ها را برابر با ناحیه انتگرال‌گیری در نظر می‌گیریم. بازه‌ی x نیز بین x=π/2 تا x=5π/2 در نظر گرفته می‌شود. در نتیجه ناحیه‌ی انتگرال‌گیری به‌صورت زیر است.

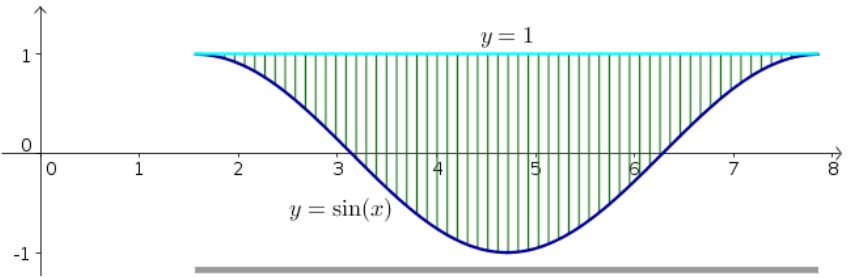
در حالتی که بخواهیم بازه انتگرال‌ را عوض کنیم، بایستی مقادیر ماکزیمم و مینیمم y را مشخص کنیم. نقاط مینیمم و ماکزیمم به‌ترتیب برابر با ۱- و ۱ هستند. بنابراین بازه y به‌صورت $$-1$$ است.

به‌منظور بدست آوردن بازه‌ی x، منحنی پایین را مطابق با شکل زیر به دو بخش تقسیم‌ می‌کنیم.

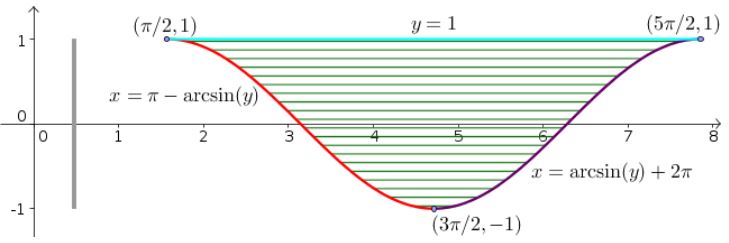
با توجه به مفاهیم تابع معکوس، منحنی سمت چپ برابر با (x=π-arcsin(y و منحنی سمت راست برابر با (x=۲π+arcsin(y است. در نتیجه بازه‌ی x نیز به‌صورت زیر بدست می‌آید.

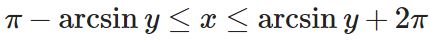
در نتیجه انتگرال را می‌توان به‌صورت زیر بازنویسی کرد.

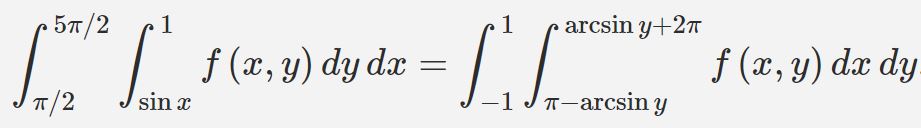
تغییر متغیر‌های داخلی و خارجی انتگرال، زمانی مورد نیاز می‌شود که محاسبه انتگرالِ یک تابع نسبت به یک متغیر مشکل باشد. از این رو با تغییر بازه‌های انتگرال، می‌توان محاسبه را آسان‌تر کرد. در آینده در مورد کاربرد انتگرال دوگانه در فیزیک و دیگر کاربرد‌های آن صحبت خواهیم کرد.