انتگرال دوگانه در فیزیک — به زبان ساده (+ دانلود فیلم آموزش رایگان)

پیش‌تر در وبلاگ فرادرس مفاهیم انتگرال دوگانه توضیح داده شد. از این رو در این مطلب قصد داریم تا تعدادی از کاربرد‌های انتگرال دوگانه در فیزیک را بیان کنیم. البته پیشنهاد می‌شود قبل از مطالعه، مطالب انتگرال دوگانه، انتگرال دوگانه در مختصات قطبی و انتگرال سطحی را مطالعه فرمایید.

جرم و گشتاور استاتیکی

ورقه‌ای با توزیع جرمی ناهمگن را در نظر بگیرید که ناحیه R را در صفحه x-y اشغال کرده است. فرض کنید چگالی جرمی این ورقه در نقطه (x,y) برابر با $$ \large \rho ( x , y ) $$ باشد. جرم کل ورقه را می‌توان با استفاده از انتگرال دوگانه و به صورت زیر محاسبه کرد.

$$ \Large m = \iint \limits _ R { \rho \left ( { x , y } \right) d A } $$

به همین صورت گشتاور استاتیکی یا همان گشتاور اول سطحِ ورقه حول محور‌های x و y را نیز می‌توان به صورت زیر بدست آورد.

$$ \Large { M _ x } = \iint \limits _ R { y \rho \left ( { x , y } \right ) d A } $$

$$ \Large { M _ y } = \iint \limits _ R { x \rho \left ( { x , y } \right ) d A } $$

در نتیجه روابط فوق، مختصات‌های مرکز جرم نیز به شکل زیر قابل بیان هستند.

$$ \Large { \bar x = \frac { { { M _y }} } {m } }
= {\frac { 1 } { m } \iint \limits _ R { x \rho \left ( { x , y } \right ) d A } }
= {\frac { { \iint\limits_R {x\rho \left( {x,y} \right)dA} }}{{\iint\limits_R {\rho \left( {x,y} \right)dA} } } } $$

$$ \Large {\bar y = \frac{{{M_x}}}{m} }
= {\frac { 1 } { m } \iint \limits _ R { y \rho \left ( { x , y } \right) d A } }
= { \frac { { \iint\limits_R {y\rho \left( {x,y} \right)dA} }}{{\iint\limits_R {\rho \left( {x,y} \right ) d A } } } }$$

زمانی که چگالی جرمی در تمامی نقاط صفحه برابر با $$ \large \rho \left ( { x , y } \right) = 1 $$ باشد، مرکز جرمی، تنها وابسته به شکل ناحیه R خواهد بود. در چنین مواردی از اصطلاح مرکز سطح نیز استفاده می‌شود. البته در مواردی که چگالی جرمی در تمامی نقاط یک صفحه برابر باشد نیز مرکز سطح و مرکز جرم در یک نقطه قرار خواهند داشت.

لختی دورانی

لختی دورانی یا گشتاور اینرسی یک سیستم حول محور‌های x و y را می‌توان با استفاده از رابطه زیر محاسبه کرد.

$$ \Large { { I _ x } } = { \iint \limits _ R { { y ^ 2 } \rho \left ( { x , y } \right ) d A } } $$

$$ \Large { { I _ y } } = { \iint \limits _ R { { x ^ 2 } \rho \left ( { x , y } \right ) d A } } $$

با توجه به دو رابطه فوق، ممان اینرسی قطبی نیز به صورت زیر قابل محاسبه خواهد بود.

$$ \Large { { I_ 0 } } = { \iint \limits _ R { \left ( { { x ^2 } + { y ^ 2 } } \right ) \rho \left ( { x , y } \right ) d A} } $$

بار الکتریکی صفحه

فرض کنید بار الکتریکی با چگالی $$ \large { \sigma \left( { x , y } \right ) } $$ روی ناحیه R توزیع شده باشد. در این صورت کل بار Q قرار گرفته روی سطح، برابر است با:

$$ \large Q = \iint \limits _ R { \sigma \left ( { x , y } \right ) d A } $$

احتمالا متوجه همانندی فرمول محاسبه بار الکتریکی و جرم شده‌اید. این شباهت در به خاطر سپردن فرمول‌ها و یادگیری مفاهیم بسیار کمک کننده خواهند بود.

میانگین یک تابع

تابعی هم‌چون $$ \large f ( x , y ) $$ را در نظر بگیرید که توصیف کننده ناحیه R است. توجه داشته باشید که این تابع روی این صفحه به صورت پیوسته در نظر گرفته شده. در این صورت میانگین تابع روی ناحیه R را می‌توان در قالب انتگرال دوگانه،‌ به صورت زیر محاسبه کرد.

$$ \large \mu = \frac{ 1 } { S } \iint \limits _ R { f \left ( { x , y } \right ) d A } $$

توجه داشته باشید که در ابتدا باید مساحت ناحیه R مطابق با رابطه زیر محاسبه شود.

$$ \large S = \iint \limits _ R { d A } $$

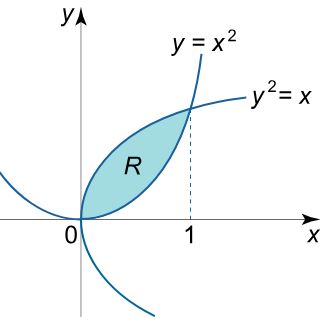
مثال ۱

مرکز سطح ناحیه‌ای را بیابید که بین دو نمودار $$ \large { y ^ 2 } = x $$ و $$ \large y = { x ^ 2 } $$ محصور شده است.

شکل ناحیه توصیف شده در ادامه نشان داده شده است.

ما به دنبال مرکز سطح هستیم. بنابراین از فرمول مرکز جرم در حالتی استفاده می‌کنیم که $$ \rho ( x , y ) = 1 $$ است. در نهایت جرم صفحه برابر می‌شود با:

$$ \large \begin {align*} { m = \iint \limits _ R { d A } }
& = { \int \limits _ 0 ^ 1 {\left[ {\int\limits_{{x^2}}^{\sqrt x } {dy} } \right]dx} }
\\ & = {\int\limits_0^1 {\left[ {\left. y \right|_{{x^2}}^{\sqrt x }} \right]dx} }
\\ & = {\int\limits_0^1 {\left( {\sqrt x – {x^2}} \right)dx} }
\\ & = { \int \limits _ 0 ^ 1 { \left ( { { x ^ { \large \frac { 1 } {2 }\normalsize}} – { x ^ 2 } } \right)dx} }
\\ & = { \left. {\left( {\frac{{2{x^{\large\frac{3}{2}\normalsize}}}}{3} – \frac { { { x ^ 3 } } } { 3 } } \right)} \right| _ 0 ^ 1 }
\\ & = { \frac { 2 } { 3 } – \frac{1}{3} }={ \frac{1}{3}} \end {align*} $$

با بدست آمدن جرم صفحه، گشتاور استاتیکی حول محور‌ x به صورت زیر بدست می‌آید.

$$ \large \begin {align*} { { M _ x } = \iint \limits _ R { y d A } }
& = {\int \limits _ 0 ^ 1 { \left [ { \int \limits _ { { x ^ 2 } } ^ { \sqrt x } {ydy} } \right]dx} }
\\ & = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^2}}}{2}} \right ) } \right | _ { { x ^ 2 } } ^ { \sqrt x } } \right] d x } } \\ & = {\frac{1}{2}\int\limits_0^1 {\left( {x – {x^4}} \right)dx} }
\\ & = {\frac{1}{2}\left. {\left( {\frac{ { { x ^ 2 } } } { 2} – \frac{{{x^5}}}{5}} \right)} \right|_0^1 }
\\ & = {\frac{1}{2}\left( {\frac{1}{2} – \frac{1}{5}} \right) }={ \frac { 3 } { { 2 0 } } } \end {align*} $$

به همین صورت گشتاور استاتیکی حول محور y نیز برابر است با:

$$ \large \begin {align*} {{M_y} = \iint\limits_R { x d A } }
& = {\int\limits_0^1 {\left[ {\int\limits_{{x^2}}^{\sqrt x } {dy} } \right]xdx} }
\\ & = {\int\limits_0^1 {\left( {\sqrt x – {x^2}} \right)xdx} }
\\ & = {\int\limits_0^1 {\left( {{x^{\large\frac{3}{2}\normalsize}} – {x^3}} \right)dx} }
\\ & = {\left. {\left( { \frac { { 2 { x ^ { \large\frac{5}{2}\normalsize } } } } { 5} – \frac{{{x^4}}}{4}} \right)} \right|_0^1 }
\\ & = {\frac{2}{5} – \frac{1}{4} }={ \frac{3}{{20 } } } \end {align*} $$

در نهایت مختصات x و y مرکز جرم به صورت زیر بدست می‌آید.

$$ \large \begin {align*} {{\bar x = \frac{{{M_y}}}{m} = \frac{{\frac{3}{{20}}}}{{\frac{1}{3}}} }={ \frac{9}{{20}} ,\;\;}}\kern-0.3pt
{{\bar y = \frac { { { M _ x } } } { m } = \frac{{\frac{3}{{20}}}}{{\frac{1}{3}}} }={ \frac { 9 } { { 2 0}} } } \end {align*} $$

مثال ۲

لختی دورانی جرمی مثلثی شکل را بیابید که به خطوط $$ \large x + y = 1 \ , \ x=0 \ , \ y=0 $$ محدود شده است. هم‌چنین چگالی جرمی سطح را به صورتِ $$ \large \rho \left ( { x , y } \right ) = x y $$ در نظر بگیرید.

همان‌طور که در مثال ۱ نیز بیان شد در ابتدا باید تصویری درست از ناحیه توصیف شده را در ذهن داشته باشید. ناحیه R در ادامه نشان داده شده است.

لختی دورانی یا گشتاور اینرسی حول محور x برابر است با:

$$ \large \begin {align*} { { I _ x } } = & { \iint\limits_R {{y^2}\rho \left( {x,y} \right)dxdy} }
\\ & = {\int\limits_0^1 {\left[ {\int\limits_0^{1 – x} {{ y ^ 2 } x y d y } } \right]d x } }
\\ & = {\int\limits_0^1 {\left[ {\int\limits_0^{1 – x} { { y ^3 } d y } } \right]xdx} } = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^4}}}{4}} \right)} \right|_0^{1 – x}} \right] x d x } }
\\ & = {\frac { 1 } { 4} \int\limits_0^1 {{{\left( {1 – x} \right ) } ^4 } x d x } }
\\ & = {\frac { 1 } { 4 }\int\limits_0^1 {\left( {1 – 4x + 6 { x ^ 2 } }\right.}-{\left.{ 4{x^3} + {x^4}} \right) x d x } } \\ & = {\frac { 1 } { 4 }\int\limits_0^1 {\left( {x – 4{x^2} + 6{x^3} }\right.}-{\left.{ 4{x^4} + {x^5}} \right)dx} } \\ & = {\frac{1}{4}\left. {\left( {\frac{{{x^2}}}{2} – \frac{{4{x^3}}}{3} + \frac{{6{x^4}}}{4} }\right.}\right. – \left.{\left.{ \frac{ { 4 { x^ 5 } } } { 5} + \frac{{{x^6}}}{6}} \right)} \right|_0^1 }
\\ & = {\frac{1}{4}\left( {\frac{1}{2} – \frac{4}{3} + \frac{3}{2} – \frac{4}{5} + \frac{1}{6}} \right) }
\\ & = { \frac { {1 } } {{ 1 2 0 } }} \end {align*} $$

به طور مشابه لختی دورانی حول محور y نیز به صورت زیر بدست می‌آید.

$$ \large \begin {align*} { { I _ y } } = & { \iint\limits _ R { { x ^ 2 } \rho \left ( { x , y } \right) d x d y } }
\\ & = {\int\limits_0^1 {\left[ {\int\limits_0^{1 – x} {{x^2}xydy} } \right]dx} }
\\ & = {\int\limits_0^1 {\left[ {\int\limits_0^{1 – x} {ydy} } \right]{x^3}dx} }
\\ & = {\int\limits_0^1 {\left[ {\left. {\left( {\frac{{{y^2}}}{2}} \right)} \right|_0^{1 – x}} \right]{x^3}dx} }
\\ & = {\frac{1}{2}\int\limits_0^1 {{{\left( {1 – x} \right)}^2}{x^3}dx} }
\\ & = {\frac{1}{2}\int\limits_0^1 {\left( {1 – 2x + {x^2}} \right){x^3}dx} }
\\ & = {\frac{1}{2} \int \limits _ 0 ^1 {\left( {{ x ^ 3 } – 2 { x ^ 4} + { x ^5}} \right) d x } }
\\ & = {\frac{1}{2}\left. {\left( {\frac{{{x^4 } } }{4} – \frac{{2{x^5}}}{5} + \frac{{{x^6}}}{6}} \right)} \right|_0^1 }
\\ & = {\frac{1}{2}\left( {\frac{1}{4} – \frac{2}{5} + \frac{1}{6}} \right) }
\\ & = {\frac{1}{{120}} } \end {align*} $$

مثال ۳

فرض کنید بار الکتریکی روی دیسکِ $$ \large { x ^2 } + { y ^ 2 } = 1 $$ توزیع شده باشد. هم‌چنین چگالی بار الکتریکی را مطابق با رابطه $$ \large \sigma ( x , y ) = 1 + { x ^ 2 } + { y ^ 2} $$ فرض کنید. با این فرضیات کل بار موجود در صفحه را بدست آورید.

$$ \large \begin {align*} Q = & \iint\limits_R {\sigma \left( {x,y} \right)dxdy}
\\ & = {\int\limits_0^{2\pi } {d\theta } \int\limits_0^1 {\left( {1 + {r^2}} \right)rdr} }
\\ & = {2\pi \int\limits_0^1 {\left( {r + {r^3}} \right)dr} }
\\ & = {2\pi \left. {\left( {\frac{{{r^2}}}{2} + \frac{{{r^4}}}{4}} \right)} \right|_0^1 }
\\ & = {2\pi \left( {\frac{1}{2} + \frac{1}{4}} \right) }
\\ & = {\frac{{3\pi }}{2}\;\left( {\text{coulomb}} \right ) } \end {align*} $$

در این مطلب کاربرد‌های اولیه انتگرال دوگانه در فیزیک توضیح داده شدند. با این حال گفتنی است که این مفهوم در دیگر مفاهیم پیشرفته‌تر ریاضیات و فیزیک مدرن نیز کاربرد بسیاری دارد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های فیزیک
• لختی دورانی — به زبان ساده
• انتگرال دوگانه — به زبان ساده
• مرکز جرم — به زبان ساده

^^

فیلم‌ های آموزش انتگرال دوگانه در فیزیک — به زبان ساده (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی انتگرال دوگانه در فیزیک – جرم و گشتاور استاتیکی

فیلم آموزشی انتگرال دوگانه در فیزیک – لختی دورانی

فیلم آموزشی انتگرال دوگانه در فیزیک – بار الکتریکی صفحه

فیلم آموزشی انتگرال دوگانه در فیزیک – میانگین یک تابع