حل انتگرال دوگانه با استفاده از تغییر متغیر — به زبان ساده
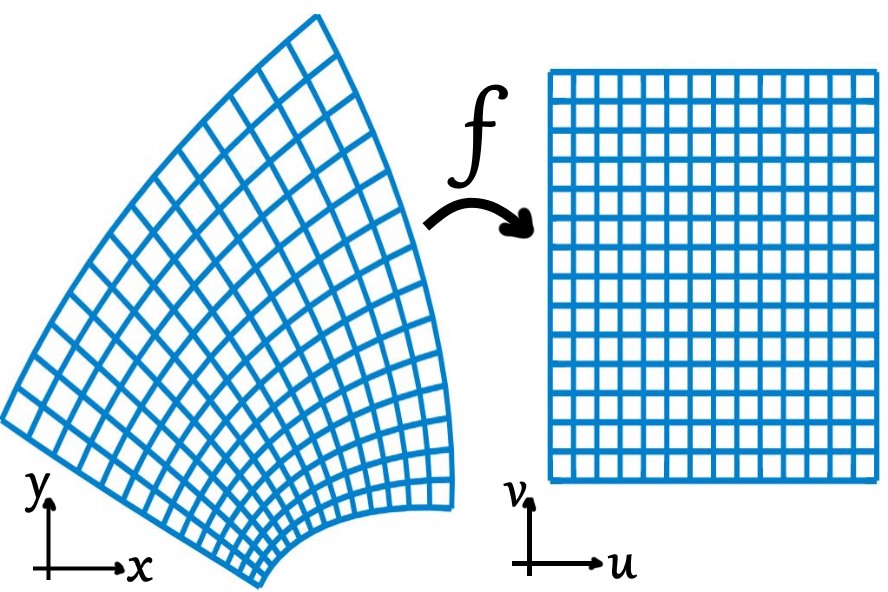
پیشتر در وبلاگ فرادرس در مورد مفاهیم و نحوه محاسبه انتگرال صحبت کردیم. بنابراین در این مطلب قصد داریم تا نحوه بکارگیری تغییر متغیر در حل انتگرال دوگانه را توضیح دهیم. از این رو پیشنهاد میشود مطالبِ انتگرال دوگانه و انتگرال سطحی را مطالعه فرمایید.
مقدمه
در ریاضیات از دستگاههای مختصات متفاوتی استفاده میشود. در حل انتگرال دوگانه نیز گاهی بهتر است که انتگرالِ $$ \large \iint \limits _ R { f \left( { x , y } \right ) d x d y } $$ در دستگاه مختصاتی غیر از کارتزین محاسبه شود.
برای نمونه در شکل زیر با استفاده از تغییر متغیرِ $$ (x,y) \Rightarrow (u,v) $$، ناحیه انتگرالگیری به صورت یک مستطیل در آمده که انتگرالگیری از آن نیز راحتتر میشود.
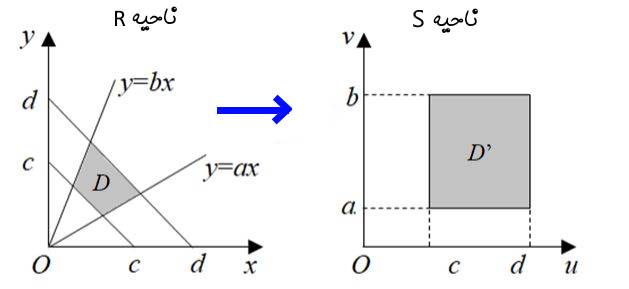
فرض کنید با استفاده از یک تغییر متغیر، مختصات $$ \large ( x , y ) $$ به $$ \large ( u , v ) $$ تبدیل شده است. در این صورت حاصل انتگرال را در مختصات جدید میتوان به صورت زیر محاسبه کرد.
$$ \Large { \iint \limits _ R { f \left ( { x , y } \right ) d x d y } }
= { \iint \limits _ S { f \left [ { x \left ( { u , v } \right ) , y \left ( { u , v } \right ) } \right ] } \kern0pt { \left | { \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left ( { u , v } \right ) } } } \right|d x d y} , } $$
توجه داشته باشید که در رابطه فوق، $$ \large \left| { \large \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left ( { u , v } \right ) } } \normalsize} \right| = \left| {\begin{array}{*{20}{ c } } {\frac{{\partial x}}{{\partial u} } } & { \frac { { \partial x } } { { \partial v}}}\\{\frac{{\partial y}}{{\partial u } } } & { \frac { { \partial y } } { { \partial v } } } \end {array}} \right| $$ ژاکوبین نامیده میشود. در نتیجه این تغییر متغیر، ناحیه R به ناحیه S تبدیل میشود. برای بدست آوردن ژاکوبین نیز از رابطه زیر استفاده میشود.
$$ \Large { \left| { \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left ( { u , v } \right ) } } } \right| } = { \left| { { { \left ( { \frac { { \partial \left( { u , v } \right ) } } { { \partial \left( { x , y } \right ) } } } \right ) } ^ { – 1} } } \right| } $$
بنابراین به منظور استفاده از تغییر متغیر در حل انتگرال دوگانه به ترتیب زیر عمل کنید:
- ناحیه R را با استفاده از تغییر متغیر، به ناحیه S تبدیل کنید. توجه داشته باشید که ناحیه S در مختصات (u,v) بیان میشود.
- ژاکوبین تغییر متغیرِ $$ \large \left ( { x , y } \right ) \to \left ( { u , v } \right ) $$ را نوشته و دیفرانسیل dxdy را به صورت $$ \large d x d y = \left| { \large\frac{{\partial \left( {x,y} \right)}}{{\partial \left ( { u , v } \right ) } } \normalsize} \right|dudv $$ بنویسید.
- عبارت تحت انتگرال را با استفاده از دو عبارتِ $$ \large x = x\left( { u , v } \right) $$ و $$ \large y = y \left( { u , v } \right) $$ بر حسب u و v نوشته و نهایتا حاصل انتگرال را محاسبه کنید.
در ادامه مثالهایی ارائه شده که مطالعه آنها را توصیه میکنیم.
مثال ۱
حاصل انتگرال دوگانه $$ \large \iint \limits _ R { \left ( { y – x } \right ) d x d y } $$ را در ناحیه R بدست آورید.
فرض کنید R ناحیه محدود شده بین توابع $$ \large y = x + 1 , y = x - 3 , y = – { \large \frac { x } { 3 } \normalsize } + 2 , y = – { \large \frac { x } { 3 } \normalsize} + 4 $$ است.
برای استفاده از تغییر متغیر در ابتدا باید تصویری از ناحیه انتگرالگیری در ذهن داشته باشید. با توجه به توابع مطرح شده، ناحیه R به صورت زیر است.
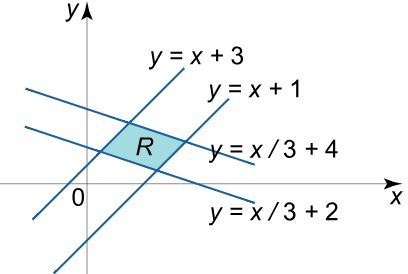
هدف اصلی از تغییر متغیر در حل انتگرال دوگانه سادهتر کردن ناحیه انتگرالگیری است. با فرض توابع u و v به صورت $$ \large u = y – x , v = y + { \large \frac { x } { 3 } \normalsize} $$ داریم:
$$ \Large \begin {align*} { y = x + 1 \; \; } \Rightarrow { y – x = 1 \; \; } \Rightarrow {u = 1} \\~\\ {y = x – 3 \;\;}\Rightarrow {y – x = -3 \; \;}\Rightarrow {u = -3 } \\~\\ {y = – \frac { x } { 3 } + 2 \;\;}\Rightarrow
{ y + \frac { x } { 3 } = 2 \;\;}\Rightarrow
{ v = 2} \\~\\ { y = – \frac { x } { 3 } + 4 \; \; } \Rightarrow
{ y + \frac { x } { 3 } = 4 \;\;}\Rightarrow
{ v = 4 } \end {align*} $$
با توجه به توابع u و v بدست آمده شکل ناحیه S به صورت زیر در میآید.
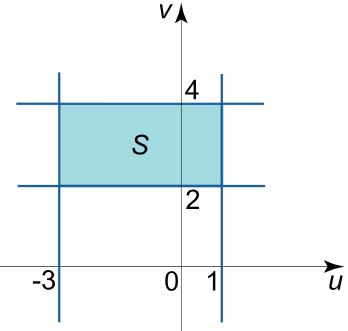
در مرحله بعد ژاکوبین این تغییر متغیر به صورت زیر قابل محاسبه است.
$$ \Large \begin {align*} {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}}
= \left| { \begin {array} {*{20} { c } } {\frac{{\partial u}}{{\partial x}}}&{\frac{{\partial u}}{{\partial y}}}\\
{\frac{{\partial v}}{{\partial x}}}&{\frac{{\partial v}}{{\partial y}}}
\end{array}} \right| } & = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( { y – x } \right)}}{{\partial x}}}&{\frac{{\partial \left( {y – x} \right ) } } { { \partial y } } } \\ { \frac { { \partial \left( {y + \frac { x } { 3} } \right)}}{{\partial x}}}&{\frac{{\partial \left( {y + \frac{x}{3}} \right)}}{{\partial y}}} \end{array}} \right| } = \\ & {\left| {\begin{array}{*{20}{c}} { – 1}&1 \\ {\frac{1}{3}} & 1 \end{array}} \right| } ={ – \frac{4}{3}} \end {align*} $$
در نتیجه مقدار مطلق ژاکوبین برابر با عدد زیر بدست میآید.
$$ \Large {\left| { \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left( {u,v} \right)}}} \right| }
= {\left| {{{\left( {\frac{{\partial \left( {u,v} \right)}}{{\partial \left ( { x , y } \right ) } } } \right)}^{ – 1}}} \right| }
= {\left| {\frac{1}{{ – \frac{4}{3}}}} \right| }={ \frac{3}{4} } $$
با بدست آمدن ژاکوبین، دیفرانسیلها را نیز میتوان به شکل زیر، بر حسب u و v بیان کرد.
$$ \Large { d x d y } = { \left| { \frac { { \partial \left ( { x , y } \right ) } }{ { \partial \left( { u , v } \right ) }} } \right|dudv } = { \frac { 3 } { 4 } d u d v } $$
همانطور که میبینید حل انتگرال دوگانه در مختصات (u,v) بسیار راحتتر شده. نهایتا حاصل انتگرال برابر است با:
$$ \Large \begin {align*} \Large { \iint \limits_R {\left( {y – x} \right) d x d y } }
& = { \iint \limits _ S {\left( u \cdot \frac{3}{4}dudv \right)} }
\\ & = {\frac{ 3 } { 4 } \int\limits _ { – 3 } ^ 1 { u d u } \int \limits_2^4 { d v } }
\\ & = {\frac{3}{4}\left. {\left( {\frac{ { { u ^ 2 } } }{2 } } \right)} \right|_{ – 3}^1 \cdot \left. v \right|_2^4 }
= {\frac{ 3 } { 4 } \left( {\frac { 1 } { 2 } – \frac { 9 } { 2 } } \right) \cdot \left ( { 4 – 2} \right) } \\ & = { – 6 } \end {align*} $$
مثال ۲
حاصل انتگرالِ $$ \large \iint \limits _ R { \left ( { x + y } \right ) d x d y } $$ را روی ناحیه R بدست آورید. فرض کنید ناحیه R محصور شده بین توابع $$ \large y = x , \ \ y = 2 x , \ \ x + y = 2 $$ است.
با توجه به توابع ارائه شده در صورت سوال، ناحیه R را میتوان به صورت زیر تصور کرد.
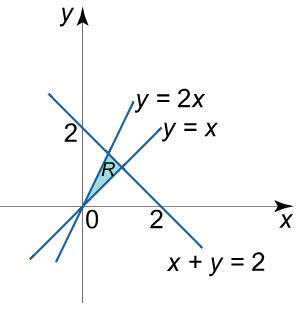
به منظور سادهتر کردن ناحیه انتگرالگیری از تغییر متغیرهای $$ \large y – x = u \ , \ y – 2 x = v $$ استفاده میکنیم. در مرحله بعد باید x,y را بر حسب توابعی از u و v بدست آورد. دو تابع y=x و y=۲x را میتوان در صفحه (u,v) به صورت زیر بیان کرد.
$$ \Large {y = x \;\;}\Rightarrow
{y – x = 0 \;\; } \Rightarrow {u = 0 } $$
$$ \Large {y = 2x \;\;}\Rightarrow
{y – 2x = 0 \;\;}\Rightarrow
{v = 0} $$
از طرفی با استفاده از تبدیل در نظر گرفته شده میتوان گفت:
$$ \Large { u – v } = { \left ( { y – x } \right ) } - { \left ( { y – 2 x } \right ) }={ x } $$
در نتیجه داریم:
$$ \Large {y = x + u }
= {u – v + u }
= {2u – v} $$
نهایتا تابع x+y=2 در صفحهی (u,v)، به صورت زیر قابل محاسبه خواهد بود.
$$ \Large { x + y = 2 \; \; } \Rightarrow
{ u – v + 2 u – v = 2 \; \; }\Rightarrow
{ 3 u – 2 v = 2 } $$
حال سه تابع در نظر گرفته شده در مختصات (u,v) توصیف شدند. بنابراین صفحه جدید به صورت زیر خواهد بود.
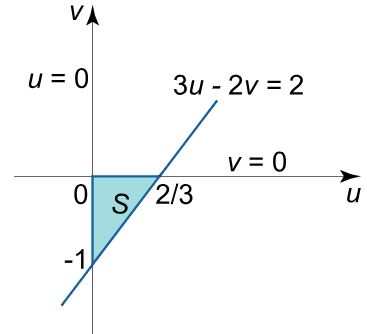
با استفاده از تغییر متغیر انجام شده، ژاکوبین برابر با عدد زیر بدست میآید.
$$ \Large { \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left ( { u , v } \right ) } } }
= { \left| {\begin {array} {*{20} { c } }
{ \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial x } } { { \partial v } } } \\
{\frac { { \partial y } } { { \partial u } } } & { \frac{{\partial y}}{{\partial v}}}
\end{array}} \right| }
= {\left| {\begin{array}{*{20}{c}}
{\frac{{\partial \left( { u – v } \right)}}{{\partial u}}}&{\frac{{\partial \left( {u – v} \right)}}{{\partial v}}}\\
{\frac{{\partial \left( {2 u – v} \right)}}{{\partial u}}}&{\frac{{\partial \left( {2 u – v } \right)}}{{\partial v}}}
\end{array}} \right| }
= {\left| {\begin{array}{*{20}{c}}
1&{ – 1}\\
2&{ – 1}
\end{array}} \right| }
= {1 \cdot \left( { – 1} \right) – \left( { – 1} \right) \cdot 2 }={ 1 } $$
با توجه به تغییر متغیرهای در نظر گرفته شده، دیفرانسیلهای dx و dy با du و dv تفاوتی ندارند. بنابراین میتوان گفت دیفرانسیلهای $$ \Large d x d y = d u d v $$ برابر هستند. نهایتا حاصل انتگرال دوگانه با استفاده از تغییر متغیر به صورت زیر بدست میآید.
$$ \Large \begin {align*} { \iint \limits _ R { \left ( { x + y } \right ) d x d y } }
= & { \iint \limits _ S { \left ( { u – v + 2 u – v } \right ) d u d v } }
\\ & = { \iint \limits _ S { \left ( { 3 u – 2 v } \right ) d u d v } }
\\ & = {\int \limits _ 0 ^ { \frac { 2 } { 3} } {\left[ {\int\limits_{\frac { 3 } { 2 } u – 1 } ^ 0 { \left ( { 3 u – 2 v } \right ) d v } } \right] d u } } \\ & = { \int \limits _ 0 ^ { \frac {2 } { 3 } } { \left [ {\left. {\left( {3uv – {v^2}} \right)} \right|_{v = \frac{3}{2}u – 1}^0} \right]du} }
\\ & = { – \int \limits _ 0 ^ { \frac{2}{3}} {\left[ {3u\left( {\frac{3}{2}u – 1} \right) }\right.}-{\left.{ {{\left( {\frac{3}{ 2 } u – 1 } \right ) } ^ 2 } } \right] d u } }
\\ & = { – \int\limits_0^{\frac{2}{3}} {\left( {\frac { { 9 {u ^ 2 } } } {2} – 3u }\right.}-{\left.{ \frac{{9{ u ^ 2 } } }{4} + 3 u – 1} \right) d u} } \\ & = { – \int\limits_0^{\frac{2}{3}} {\left( {\frac{{9{u^2}}}{4} – 1} \right) d u} }
\\ & = {\left. {\left( {u – \frac{9}{4}\frac{{{u^3}}}{3}} \right)} \right|_0^{\frac{2}{3}} }
= {\frac{2}{3} – \frac{3}{4} \cdot {\left( {\frac{2}{3}} \right)^3} } = { \frac{4}{9 } } \end {align*} $$
مثال ۳
حاصل انتگرال $$ \large \iint \limits _ R { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d x d y } $$ را روی ناحیه R بدست آورید. فرض کنید R ناحیه محدود شده به خطوط $$ \large y = x $$ و $$ \large y = a $$ و $$ \large y = 2a $$ است. مقادیر a را مثبت فرض کنید.
در شکل زیر ناحیه محدود به توابع نشان داده شده است.
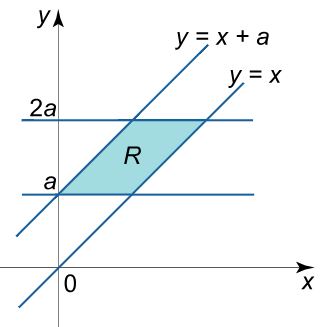
همانطور که در شکل بالا نیز نشان داده شده، ناحیه به صورت یک متوازیالاضلاع است. با استفاده از تغییر متغیر زیر این ناحیه به صورت یک مربع در خواهد آمد.
$$ \Large { \left \{ \begin {array} { l }
u = y – x \\
v = y
\end {array} \right.\; \;} \kern-0.3pt
{\text{or}\;\;\left\{ \begin{array}{l}
x = y – u = v – u\\
y = v
\end{array} \right. } $$
در شکل زیر ناحیه S در صفحه (u,v) نشان داده شده است. با استفاده از توابع تعریف شده، توابع توصیف کننده ناحیه R را به صورت زیر بر حسب u و v بیان میکنیم.
$$ \Large {y = x,\;\;}\Rightarrow
{y – x = 0 \;\;}\Rightarrow
{u = 0 } $$
$$ \Large {y = x + a \;\;}\Rightarrow {y – x = a \;\;}\Rightarrow {u = a} $$
$$ \Large y = a \; \; \Rightarrow v = a $$
$$ \Large y = 2a \; \; \Rightarrow v = 2a $$
در مرحله بعد باید ژاکوبین تغییر متغیر در نظر گرفته شده را محاسبه کنیم. بدین منظور داریم:
$$ \Large { \frac { { \partial \left ( { x , y } \right ) } } { { \partial \left( { u , v } \right)}} }
= {\left| {\begin{array}{*{20}{c}}
{\frac{{\partial x } } {{\partial u } } } & {\frac{{\partial x } } {{\partial v}}}\\
{\frac{{\partial y } } { {\partial u } } } & {\frac{{\partial y } } {{\partial v}}}
\end{array}} \right| }
= {\left| {\begin{array}{*{20}{ c } }
{\frac { { \partial \left ( { v – u } \right)} } { { \partial u}}}&{\frac{{\partial \left( {v – u} \right)}}{{\partial v } } } \\ {\frac{{\partial v } } { { \partial u}}}&{\frac{{\partial v } } {{\partial v}}}
\end{array}} \right| } = {\left| {\begin{array}{*{20}{ c } }
{ – 1}&1 \\ 0&1 \end{array}} \right| }
= { – 1 \cdot 1 – 1 \cdot 0 }={ – 1 } $$
در مرحله آخر دیفرانسیل مساحت را در ناحیه R به دیفرانسیل مساحت در ناحیه S تبدیل میکنیم.
$$ \Large { d x d y }={ \left| {\frac{{\partial \left( { x , y } \right ) } } { { \partial \left ( { u , v } \right ) } } } \right|d u d v } = { \left| { – 1} \right| \cdot d u d v } = { d u d v . } $$
حال میتوان حاصل انتگرال دوگانه را به صورت زیر محاسبه کرد.
$$ \large \begin {align*} {\iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} }
= & {\iint\limits_S {\left[ {{{\left( {v – u} \right)}^2} + {v^2}} \right]dudv} }
\\ & = {\iint\limits_S {\left( {{v^2} – 2uv }\right.}+{\left.{ { u ^2} + { v ^2}} \right)dudv} }
\\ & = {\int\limits_a ^{2 a} {\left[ {\int\limits_0^a {\left( {2{v^2} – 2 u v + {u^2}} \right)du} } \right]dv} }
\\ & = {\int\limits_a^{2 a} {\left[ {\left. {\left( {2{v^2}u – v { u ^2} + \frac{{{u^3}}}{3}} \right)} \right|_{u = 0}^a} \right]dv} }
\\ & = {\int\limits_a^{2a} {\left( {2a{v^2} – {a^2}v + \frac{{{a^3}}}{3}} \right) d v} }
\\ & = {\left. {\left( {2a \cdot \frac{{{ v ^ 3 }}}{3} – { a ^ 2} \cdot \frac{{{ v ^ 2 }}}{2} + \frac { { { a ^ 3 } } } { 3} \cdot v} \right)} \right|_a ^ { 2 a} }
\\ & = {\left( {\frac { { 2 a } } { 3 } \cdot 8 { a ^ 3} – \frac{{{ a ^ 2 }} } {2} \cdot 4 {a ^ 2} }\kern0pt{+ \frac{{{ a ^3 } } }{ 3 } \cdot 2 a} \right ) }\kern0pt – {\left ( { \frac{{ 2 a } }{ 3 } \cdot { a ^ 3} – \frac{{{ a ^ 2 } } } { 2} \cdot { a ^ 2 } + \frac { { { a ^ 3} } } { 3 } \cdot a } \right) }
\\ & = {\frac {{ 7 { a ^ 4 } } } { 2 } } \end {align*} $$
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضی
- مجموعه آموزشهای ریاضی و فیزیک
- انتگرال سه گانه -- از صفر تا صد
- انتگرال دوگانه — به زبان ساده
- انتگرال و روش های محاسبه — به زبان ساده
^^












خیلی از قسمتاشو نمی شه به راحتی فهمید و خیلی خلاصه و مختصر توضیح داده
معرکه بووود خیلی ممنون