مشبکه در ریاضیات | تعریف در نظریه گروه — به زبان ساده

در ریاضیات و به‌ویژه در هندسه و «نظریه هندسی اعداد» (Geometry of numbers)، به یک «گروه گسسته» (Discrete Group) در فضای اعداد حقیقی (چند بُعدی)، «مشبکه» (Lattice) یا «توری» گفته می‌شود. یک مشبکه می‌تواند با ترکیبات خطی (با ضرایب صحیح) از چندین بردار ایجاد شود که در نتیجه به چنین مجموعه‌‌ای با کمترین تعداد از بردارها، «پایه مشبکه» (Lattice Basis) می‌گویند. در این متن از مجله فرادرس، به این نوع مشبکه در ریاضیات پرداخته و با مبانی و تعاریف ارائه شده در این حوزه آشنا خواهیم شد.

به عنوان پیش‌نیاز و مقدمه برای این بحث، بهتر است مطالب دیگری از مجله فرادرس مانند بردار و اسکالر — به زبان ساده و ضرب داخلی بردارها — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای فضای اقلیدسی و خصوصیات آن — به زبان ساده و فضای هیلبرت و خصوصیات آن نیز خالی از لطف نیست.

مشبکه در ریاضیات و نظریه گروه

در هندسه و «نظریه گروه» (Group Theory)، یک مشبکه در فضای $${\displaystyle \mathbb {R} ^ {n}}$$، یک «زیر گروه» (Subgroup) از گروه جمع‌پذیر $${\displaystyle \mathbb {R} ^ {n} }$$ است که «هم‌ریخت» (Isomprphic) نسبت به گروه جمع‌پذیر $${\displaystyle \mathbb {Z} ^ {n} }$$ محسوب می‌شود که «فضای برداری» (Vector Space) حاصل از اعداد حقیقی $${\displaystyle \mathbb {R} ^ {n} }$$ را پوشانده یا «فرش» (Span) می‌کند.

فیلم آموزش جبر ۱ – گام به گام و با مثال های عملی در فرادرس

کلیک کنید

نکته: توجه دارید که $${\displaystyle \mathbb {R} ^ {n} }$$ و $${\displaystyle \mathbb {Z} ^ {n} }$$‌، به ترتیب فضاهای $$n$$ بُعدی از اعداد حقیقی و صحیح هستند.

مشبکه در ریاضی محض، خصوصاً در ارتباط با «جبر لی» (Lie Algebra)، «نظریه اعداد» (Number Theory) و «نظریه گروه» (Group Theory) کاربردهای قابل توجهی دارد. مشبکه‌ها همچنین در ریاضیات کاربردی و در حوزه‌های مرتبط با «نظریه کدگذاری» (Coding Theory)، و «رمزنگاری» (Cryptography) به دلیل مشخص کردن سختی محاسباتی برای مسائل مبتنی بر چندین مشبکه، حضور دارند. حتی در علوم دیگر مانند فیزیک حضور مشبکه‌ها پر رنگ است.

به عنوان مثال، در علم مواد و «فیزیک حالت جامد» (Solid-state Physics)، یک مشبکه مترادف برای «قاب کاری» (Frame Work) در یک ساختار بلوری (Crystal) است. به این ترتیب یک آرایه 3 بعدی از نقاط که دارای نظم و فاصله یکسانی از یکدیگر هستند، یک مشبکه یا بلور را مشخص کرده و بر این اساس موقعیت اتم یا مولکول‌های یک کریستال مورد بررسی قرار می‌گیرند.

به طور کلی، بسیاری از مدل‌های فیزیکی می‌توانند به صورت مشبکه تصور شده و اغلب با استفاده از تکنیک‌های فیزیک محاسباتی، تجزیه و تحلیل می‌شوند.

خاصیت تقارن مشبکه در ریاضیات

یک توصیف مناسب برای مشبکه در ریاضیات به این صورت است: «مشبکه یک گروه متقارن از یک مجموعه گسسته در $$n$$ جهت متفاوت است». الگوی تصویری که توسط مشبکه تولید می‌شود، ممکن است دارای زیر مجموعه‌های متقارنی نیز باشد. اگر مشبکه را یک گروه در نظر بگیریم، می‌توان آن را یک «گروه آبلی (جابجایی) آزاد متناهی» ( finitely-generated free abelian group) در نظر گرفت. این موضوع نشان می‌دهد که مشبکه‌ها، با فضای اعداد صحیح ($$Z^n$$) «هم‌ریخت» (Isomorphic) هستند.

اگر یک مشبکه را به معنای یک آرایه 3 بُعدی از نقاط منظم و با فاصله‌های مشخص در نظر بگیریم، می‌توانیم برای بیان موقعیت اتم یا مولکول‌ها در یک کریستال، یا به طور کلی، «مدار» (Orbit)، از آن بهره ببریم.

یک مثال ساده از مشبکه در $${\displaystyle \mathbb {R} ^ {n}}$$ زیر گروه $${\displaystyle \mathbb {Z} ^ {n}}$$ است. نمونه‌های پیچیده‌تر شامل مشبکه E8 است که در یک فضای $${\displaystyle \mathbb {R} ^ {8}}$$ تعریف می‌شود. همچنین «مشبکه زالو» (Leech lattice) در $${\displaystyle \mathbb {R} ^ {24}}$$ مثال دیگری در یک فضای چند بُعدی است.

در سال‌های انتهای قرن نوزدهم، ریاضی‌دان‌ها، مفاهیم مربوط به مشبکه متناوب در فضای دو بعدی ($$R^2$$) را با مرکزیت «توابع بیضوی» (Elliptic Functions) توسعه داده و نظریه توابع آبلی را در ابعاد بزرگ، به حالت عمومی بیان کردند. به عنوان مثال، می‌توان به مشبکه E8 اشاره کرد که با «جبری لی» (Lie Algebra) در ارتباط است.

در تصویر ۱، نمونه‌ای از مشبکه در «صفحه اقلیدسی» (Euclidean Plane) در فضای دو بُعدی را مشاهده می‌کنید.

تقسیم فضا بر اساس مشبکه در ریاضیات

یک مشبکه معمولی با نام $${\displaystyle \Lambda}$$ در $${\displaystyle \mathbb {R} ^ {n}}$$ را به صورت زیر با ترکیب خطی از بردارهای پایه نمایش می‌دهند.

$$\large {\displaystyle \Lambda = \left\{ \sum_ {i = 1} ^ {n} a_{i} v_{i} \, \vert \, a_{i} \in \mathbb {Z} \right\} }$$

رابطه ۱: تعریف مشبکه در ریاضیات

به طوری که $$v_1, \ldots , v_n$$ بردارهای پایه برای $${\displaystyle \mathbb {R} ^ {n}}$$ هستند. پایه‌های متفاوت ممکن است مشبکه یکسانی تولید کنند، اما مقدار قدرمطلق دترمینان بردارهای $$v_i$$ که با نماد $$d(\Lambda)$$ مشخص می‌شود، به طور منحصر به فردی مشبکه $$\lambda$$ را تعیین می‌نماید.

همانطور که می‌بینید، رابطه ۱، نمایانگر یک ترکیب خطی از بردارها است که با ضرایبی صحیح به کار رفته‌اند. گاهی برای نامیدن مشبکه $$d(\Lambda)$$ از عبارت covolume نیز استفاده می‌کنند. اگر این دترمینان برابر با ۱ باشد، مشبکه را «تک مادول» (Unimodular) می‌نامند. مشبکه‌های «E8» و «مشبکه زالو»، از مشبکه‌های «تک مادول» معروف هستند.

فیلم آموزش ساختمان گسسته با رویکرد حل مساله در فرادرس

کلیک کنید

فضای دو بعدی و مشبکه در ریاضیات

در این قسمت پنج مشبکه در صفحه اقلیدسی را معرفی کرده و خصوصیات آن‌ها را تعیین می‌کنیم.

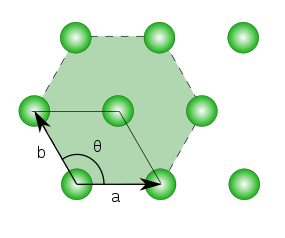
به طور کلی پنج نوع مشبکه دو بُعدی وجود دارد که توسط «قضیه محدودیت بلورنگاری» (Crystallographic Restriction Theorem) بیان می‌شوند. در زیر، تصویرهایی از این پنج مشبکه را مشاهده می‌کنید. رابطه بین طول اضلاع و زاویه بین آن‌ها به خوبی مشخص شده است. به بردارهایی که این مشبکه‌ها را تولید کرده‌ و نقاط فضای اقلیدسی توجه کنید.

توجه داشته باشید که در اینجا منظور از بردارهای برابر، طول آن‌ها است که با علامت $$| \cdot |$$ مشخص شده است. به خوبی مشخص است که بردارها برای آنکه بتوانند کل فضای دو بُعدی را اسپن کنند، نباید یکسان باشند. یکسان نبودن، به معنی اختلاف در اندازه و زاویه است.

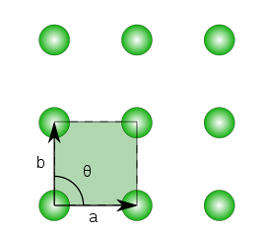
همانطور که در تصویر ۲ مشاهده می‌کنید، یک مشبکه با ویژگی‌های خاصی ایجاد می‌شود. مشبکه مربوط به تصویر ۲ را می‌توان مشابه با «مختصات دکارتی» (Cartesian Coordination) در فضای دو بعدی در نظر گرفت. زیرا بردارهای حاصل، کل فضای اقلیدسی را فرش کرده و به عنوان پایه محسوب می‌شوند. از طرفی بردارها نیز بر هم عمودند و فاصله نقاط روی محور افقی و عمودی یکسان است. این خصوصیات، ویژگی‌های اصلی مختصات دکارتی است.

$$\large | a |  =  | b | , \;\;\; \theta = 90^{\circ}$$

در تصویر ۳، یک مشبکه را مشابه با مشبکه تصویر ۲ می‌بینید که به یک طرف کشیده شده است. واضح است زاویه بین بردارها، ۹۰ درجه نیست و در نتیجه طول بردارها نیز متفاوت خواهد بود.

$$\large | a |  \neq  | b | , \;\;\; \theta \neq 90^{\circ}$$

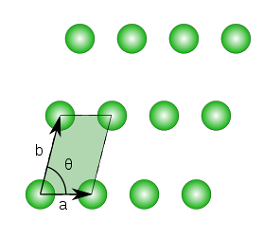
تصویر ۴، به معرفی یک مشبکه چهار ضلعی می‌پردازد که می‌تواند به شکل یک مستطیل یا لوزی نمایش داده شود.

شرط و محدودیت‌هایی که برای این مشبکه در نظر گرفته می‌شود به صورت زیر است. البته زاویه $$\phi$$، یک زاویه باز در نظر گرفته شده. همچنین اندازه بردار $$b$$ بزرگتر از بردار $$a$$ است.

$$\large | a |  \neq  | b | , \;\;\; \theta =90^{\circ} \\ \large |c| = |d| , \; \phi \neq 90^{\circ}$$

عدم یکسان بودن فاصله عمودی و افقی بین نقطه‌ها، مشبکه تصویر ۴ را از مشبکه تصویر ۳ و ۲، متمایز می‌کند.

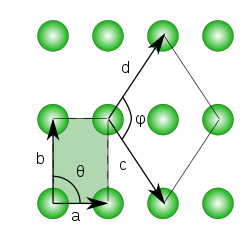
در تصویر ۵، یک مشبکه مانند تصویر ۴ را مشاهده می‌کنید که برای زاویه $$\phi$$، فرض تند بودن را محسوب کرده است. ولی بقیه خصوصیات یکسان در نظر گرفته شده است. توجه داشته باشید که اگر $$|a|$$ بزرگتر از $$|b|$$ باشد چنین اتفاقی خواهد افتاد.

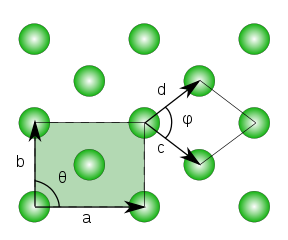
برعکس تصاویر قبلی که بردارها یک فضای چهار ضلعی را «اسپن» (Span) می‌کردند، در تصویر ۶، یک مشبکه به صورت شش وجهی را مشاهده می‌کنید. در این حالت، زاویه بین بردارها، ۱۲۰ درجه بوده و طول بردارها نیز برابر است.

$$\large | a |  = | b | , \;\;\; \theta =120^{\circ}$$

نکته: هر یک از این مشبکه‌ها می‌توانند پایه‌ای برای فضای اقلیدسی دو بعُدی باشند.

مشخصات یک مشبکه در ریاضیات

برای طبقه بندی یا شناخت بهتر یک مشبکه از مشبکه‌های دیگر و ایجاد آن، به ترتیبی که در ادامه آمده، عمل می‌کنیم.

1. یک نقطه را به عنوان محل شروع مشبکه در نظر می‌گیریم.
2. نزدیکترین نقطه (نقطه دوم) را در مشبکه پیدا می‌کنیم. اگر مشبکه در فضای اقلیدسی دو بُعدی باشد، واضح است که تابع فاصله، همان «فاصله اقلیدسی» (Euclidean Distance Function) است.
3. برای نقطه سوم، نقطه‌ای را در نظر می‌گیریم که در راستای نقطه اول و دوم نبوده و کمترین فاصله را از نقطه اول داشته باشد. واضح است که این فاصله بزرگتر یا مساوی با فاصله نقطه اول و دوم است.

همانطور که می‌بینید این سه نقطه در رابطه «نامساوی مثلثی» (Triangle Inequality) صدق خواهند کرد. پنج حالتی که در شکل‌های مربوط به تصاویر ۲ تا ۶ دیده شد، این خصوصیات را دارند. به این ترتیب ممکن است مشبکه‌ها، ساختاری شبیه مثلث (Triangle) (مثلث متساوی‌الضلاع- Equilateral triangle، متساوی‌الساقین- Isosceles triangle یا مثلث قائم‌الزاویه- Right triangle) داشته باشند.

در یک مشبکه لوزی شکل (مانند شکل‌های کناری تصویرهای 4 و 5)، کمترین فاصله ممکن است یک ضلع لوزی باشد، به عنوان مثال، قطعه خط اتصال دو نقطه اول و دوم ممکن است یکی از ساق‌ها باشد. این موضوع به زاویه کوچکتر لوزی بستگی دارد که آیا کمتر از 60 درجه است یا بین 60 و 90 تغییر می‌کند.

حالت کلی مشبکه را به عنوان «مشبکه دوری» (Period Lattice) یا مشبکه دوردار می‌شناسیم. به این ترتیب، اگر بردارهای p و q مشبکه تولید کنند، می‌توانیم به جای این بردارها از بردارهای p و p -q نیز برای تعریف مشبکه استفاده کنیم. عموماً در حالت دو بُعدی، می‌توانیم از ضرایبی مثل $$a,b,c,d$$ به شکلی استفاده کنیم که برای بردارهای $$p$$ و $$q$$، روابط زیر برقرار باشند.

$$\large a p + bq , \;\;\; cp + d p ,\;\;\;\; ad -bc =\pm 1$$

رابطه ۲: رابطه بین ضرایب یک مشبکه در ریاضیات

این امر تضمین می‌کند که دو بردار پایه مشبکه، خود ترکیب‌های خطی صحیح از بردارهای $$p$$ و $$q$$ هستند. هر جفت بردار $$p ، q$$ طبق رابطه ۲، یک «متوازی الاضلاع» (Parallelogram) را تشکیل می‌دهند که در تصویرهای ۲ تا ۶ به خوبی مشخص است. به این ترتیب ضرب داخلی آن‌ها، مساحت شکل مورد نظر را تعیین می‌کند. چنین شکلی را «پایه متوازی‌الاضلاع» (Fundamental Parallelogram) می‌نامند.‌

بردارهای $$p$$ و $$q$$ را می‌توان با اعداد مختلط نیز نشان داد که البته بستگی به اندازه و جهت بردارها دارد. حتی این کار به کمک نمایش ضرایب نیز امکان‌پذیر است. بیان هندسی یک مشبکه را توسط دو نقطه صفر و یک در نظر گرفته و نقطه سوم را براساس روندی که در بالا گفته شد، تعیین می‌کنیم. به این ترتیب، مشبکه از لحاظ هندسی مشخص می‌شود.

مشبکه در ریاضیات برای فضای مختلط

مشبکه‌ای در $${\displaystyle \mathbb {C} ^ {n}}$$، یک زیر گروه مجزا از $${\displaystyle \mathbb {C} ^ {n}}$$ است که فضای برداری مختلط با دو بُعد یا مولفه حقیقی را اسپن کند. به عنوان مثال، «اعداد صحیح گاوسی» (Gaussian integers) یک مشبکه در $${\displaystyle \mathbb {C} ^ {1}}$$ تشکیل می‌دهند.

هر مشبکه در $${\displaystyle \mathbb {R} ^ {n}}$$ یک گروه آبلی آزاد با رتبه $$n$$ است. از طرفی هر مشبکه در $${\displaystyle \mathbb {C} ^ {n}}$$ یک گروه آبلی (جابجایی) آزاد با رتبه $$2n$$ خواهد بود.

نکته: در نظریه اعداد، یک عدد صحیح گاوسی، مقدار یا «عددی مختلط» (Complex Number) است که هر دو بخش حقیقی و موهومی آن، مقادیری متعلق به مجموعه «اعداد صحیح» (Whole Number) هستند.

مشبکه در ریاضیات در فضای بردار عمومی

به طور معمول مشبکه در ریاضیات مربوط به فضای حقیقی یعنی $${\displaystyle \mathbb {R} ^ {n}}$$ هستند در حالیکه می‌توان آن‌ها را به فضای عمومی نیز تعمیم داد.

فرض کنید که $$K$$ یک «میدان» (Field) باشد، از طرفی $$V$$ را یک فضای $$K$$-بردار $$n$$ بُعدی در نظر بگیرید و بطوری که مجموعه $${\displaystyle B = \{ \mathbf {v}_{1}, \ldots, \mathbf{v}_ {n} \} }$$ یک $$K$$-پایه برای $$V$$ باشد. همچنین $$R$$ را یک «حلقه» (Ring) شامل $$K$$ محسوب کنید.

در نتیجه مشبکه حلقه $$R$$ تولید شده توسط $$B$$ به نام $${\displaystyle {\mathcal {L}}}$$ در $$V$$ به صورت زیر تعریف می‌شود.

$$\large {\displaystyle {\mathcal {L} }= \left\{ \sum_{i =1}^{n} a_{i} \mathbf {v}_{i} \mid a_{i}\ in R \right\} }$$

رابطه ۳

کاملا مشخص است که تعریف ارائه شده در رابطه ۱ و ۳، شبیه یکدیگر هستند و فقط در تعیین ضرایب و فضای برداری تفاوت دارند. واضح است که در رابطه ۳، ضرایب، متعلق به یک حلقه (مثل $$R$$) هستند و بردارهای $$V$$ لزومی به داشتن پایه حقیقی نیز ندارند.

به طور کلی، پایه‌های مختلف $$B$$، مشبکه‌های مختلفی را تولید می‌کنند. با این حال، اگر ماتریس انتقال $$T$$ بین پایه‌ها در گروه تبدیلات خطی عمومی (General Linear Group) با نماد $$GL_n(R)$$ قرار گرفته باشد، می‌توان نتیجه گرفت که مشبکه‌های تولید شده توسط این پایه‌ها، «یک ریخت» (Isomorphic) هستند، زیرا $$T$$ باعث ایجاد یک هم‌ریختی بین دو مشبکه می‌شود.

موارد مهم ظهور چنین مشبکه‌هایی در نظریه اعداد با در نظر گرفتن $$K$$ به عنوان یک میدان $$p-adic$$ دیده می‌شود. منظور از $$p$$ در اینجا، یک «عدد اول» (Prime Number) است.

برای یک فضای برداری که یک فضای ضرب داخلی نیز هست، «مشبکه دوگان» (Double Lattice) را می‌توان بطور مشخص، توسط مجموعه زیر توصیف کرد:

$$\large {\displaystyle {\mathcal {L}}^{*} =\{ \mathbf{v} \in V \mid \langle \mathbf {v} ,\mathbf {x} \rangle \in R\,, \;\;\;  \forall  \,\mathbf {x} \in { \mathcal {L}} \} }$$

 یا از رابطه معادل آن به صورت زیر استفاده نمود.

$$\large {\displaystyle {\mathcal {L}}^{*} =\{ \mathbf{v} \in V \mid \langle \mathbf {v} ,\mathbf {v}_{i} \rangle \in R,\, i=1, \ldots , n\} }$$

معرفی فیلم آموزش ساختمان گسسته با رویکرد حل مساله

در این فیلم آموزشی، سرفصل‌های کنکورهای کارشناسی ارشد و وزارت علوم برای درس ساختمان گسسته مورد بحث قرار می‌گیرد. با توجه به اینکه درس ساختمان گسسته یکی از دروس اصلی در رشته کامپیوتر محسوب می‌شود، مفاهیم اصلی ارائه شده در این آموزش، راهگشای ورود به دوره کارشناسی ارشد است. سرفصل‌ و عنوان‌های مطرح شده در این فرادرس طبق فهرست زیر ارائه شده.

• درس یکم: منطق و جبر گزاره‌های بولی
• درس دوم: تعریف مجموعه - رابطه و تابع
• درس سوم: ترتیب جزیی، مشبکه، جبر بول
• درس چهارم: گراف و انواع آن
• درس پنجم: درخت و انواع آن
• درس ششم: مبانی و اصول شمارش، جایگشت، ترکیب و ترتیب
• درس هفتم: روابط بازگشتی – معرفی توابع مولد و کاربردهای آن

این فیلم با ۱۶ ساعت و ۳۳ دقیقه، به طور مفصل به آموزش مباحث ساختمان گسسته پرداخته که بخصوص برای دانشجویان کارشناسی کامپیوتر و داوطلبان کارشناسی ارشد، توصیه می‌شود.

• برای مشاهده فیلم آموزش ساختمان گسسته با رویکرد حل مساله + اینجا کلیک کنید.

خلاصه و جمع‌بندی

در این نوشتار، با مفهوم مشبکه در نظریه گروه آشنا شدید. البته مشبکه در نظریه ترتیب (ترتیب جزئی یا ترتیب کلی) نیز استفاده می‌شود که در مطلب جداگانه‌ای به آن خواهیم پرداخت. مشبکه در ریاضیات ریشه عمیقی در ریاضیات گسسته دارد. به همین دلیل در اکثر حوزه‌هایی که مباحث اعداد صحیح به کار می‌روند، از نظریه مشبکه می‌توان استفاده کرد. ساختمان‌های گسسته رشته کامپیوتر یکی از مواردی است که مباحث مربوط به مشبکه در آن پرداخته و مورد بررسی قرار می‌گیرد.