میدان، حلقه و گروه در ریاضی – مفاهیم اولیه

ساختارهای (Structure) مختلفی در ریاضیات و بخصوص در حوزه نظریه مجموعه‌ها (Set Theory) به کار می‌روند که مهم‌ترین آن‌ها، گروه (Groups)، حلقه (Rings) و میدان (Fields) هستند. هر چند ممکن است با این اصطلاحات از قبل آشنایی نداشته باشیم ولی قبلاً در بسیاری از محاسبات و جنبه‌های مختلف ریاضیات با آن‌ها برخورد کرده‌اید. هدف از این نوشتار آشنایی با میدان، حلقه و گروه در ریاضی به عنوان ساختارهایی هستند که در مباحث دیگر ریاضی مدرن مانند «آنالیز حقیقی» (Real Analysis) به کار برده می‌شوند.

از آنجایی که ساختارهای میدان، حلقه و گروه در ریاضی به موضوع مجموعه و اعمال جبری روی اعضای آن‌ها باز می‌گردد، مطالعه نوشتارهای دیگر مجله فرادرس با عنوان اعداد صحیح — به زبان ساده و مجموعه ها در ریاضیات – مفاهیم پایه و اطلاع از اصطلاحات آن‌ها ضروری است. همچنین خواندن مطالب نظریه اعداد و کاربردهای آن — به زبان ساده و عدد مرکب و خواص آن — به زبان ساده نیز خالی از لطف نیست.

میدان، حلقه و گروه در ریاضی

یک مجموعه (Set) و اعضای آن (Elements) را در نظر بگیرید. عملگرهایی (Operators) که قادر به استفاده از این اعضا بوده و اعضای دیگری از این مجموعه را بسازند، انگیزه‌‌های اصلی برای معرفی مفاهیمی مانند میدان، حلقه و گروه در ریاضی شده است. بنابراین هر چند ممکن است قبلاً از این اصطلاحات آگاهی نداشته باشید، ولی هنگام جمع‌کردن دو عدد صحیح یا تقسیم دو عدد طبیعی از میدان، حلقه و گروه در ریاضی استفاده کرده‌اید.

فیلم آموزش مقدماتی نظریه اعداد در فرادرس

کلیک کنید

مطالعه و آگاهی از این گونه ساختارها ما را به مفاهیم و قضیه‌های مهم مربوط به نظریه اعداد رهنمون خواهد کرد. واضح است که اغلب عملگرها و ساختارهای مربوط به آن‌ها در مجموعه‌های اعداد صحیح (Integer Numbers) شکل گرفته‌اند ولی بعدا در مجموعه اعداد حقیقی (Real Numbers) و حتی اعداد مختلط (Complex Numbers) نیز قابل استفاده بوده و شاخه جدیدی از ریاضیات را ایجاد کرده‌اند.

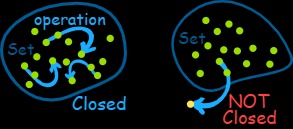
به طور غیر رسمی می‌توانیم اصطلاح «گروه» (Groups) را به مجموعه‌ای نسبت بدهیم که تحت یک عمل خاص «بسته» (Closed) باشد. اغلب این مجموعه را اعداد صحیح فرض کرده و عملگرهای جمع یا ضرب را برای این مجموعه از اعداد در نظر می‌گیریم. خصوصیات جابجایی و شرکت‌پذیری این عملگرها در چنین مجموعه‌ای از خصوصیات مربوط به ساختار گروه است.

از طرفی «حلقه» (Ring) درست به مانند گروه بوده ولی از دو عملگر همزمان پشتیبانی می‌کند. خصوصیاتی که حلقه را از گروه جدا می‌سازد در ادامه و طی تعریف دقیق آن، مشخص خواهد شد.

«میدان» (Field) نیز یک گروه محسوب شده که خواص بیشتری دارد. در نتیجه این ساختار از لحاظ عملکرد، محدودتر بوده و مجموعه‌ها و عملگرهای کمتری را شامل می‌شود زیرا شرط‌های بیشتری نسبت به ساختارهای قبلی دارد.

بسته بودن یک مجموعه نسبت به یک عملگر

برای آغاز بحث مربوط به ساختارهای ریاضی، بهتر است ابتدا یکی از خصوصیات جالب مربوط به مجموعه و عملگر تعریف شده روی آن ارائه دهیم. خاصیت مورد بحث ما در اینجا «بسته بودن» (Closure) نامیده می‌شود. ابتدا به طور خلاصه با مجموعه و عملگرهای مربوطه آشنا شده و خاصیت بسته بودن را معرفی می‌کنیم، سپس اصطلاحات مربوط به میدان، حلقه و گروه در ریاضی را مطرح خواهیم کرد.

مجموعه: در نظریه اعداد، تعریف و مفهوم علمی مجموعه (Set) بسیار پیچیده است، ولی می‌دانیم اغلب، یک مجموعه را به کمک مشخص کردن اعضای آن یا قانون عضویت، معرفی می‌کنند. البته با مجموعه اعداد طبیعی (Natural Numbers)، صحیح (Integer Numbers)، حقیقی (Real Numbers) و مختلط (Complex Number) به عنوان مبنای عملیات ریاضی در دیگر نوشتارهای فرادرس آشنا شده‌اید.

عملگر: روی یک مجموعه، می‌توان یک عملگر (Operator) تعریف کرد، بطوری که امکان تغییر یک یا چند عضو از این مجموعه به کمک عملگر وجود داشته باشد. یک عملگر ممکن است فقط به یک عضو، دو عضو یا چندین عضو از مجموعه برای انجام محاسبات احتیاج داشته باشد. نتیجه یا حاصل اجرای عملیات یک عملگر روی اعضای مجموعه، می‌تواند عضوی از آن مجموعه یا اعضای از مجموعه‌های دیگر باشد.

خاصیت بسته بودن: مجموعه $$ A $$ و عملگر دو تایی مانند $$ * $$ روی آن را در نظر بگیرید. توجه دارید که در اینجا از علامت $$ * $$ به عنوان یک عملگر روی این مجموعه استفاده کرده‌ایم و در اینجا، همیشه علامت ستاره، نشانگر عملگر ضرب (Multiplication) نخواهد بود.

منظور از عملگر دو تایی، محاسباتی است که برای انجام آن به دو عضو از مجموعه $$ A $$‌ احتیاج باشد. برای مثال عملگر ضرب حسابی، یک عملگر دو تایی است زیرا عملگر ضرب بین دو عدد تعریف شده است. مجموعه $$ A $$ را تحت عمل $$ * $$، بسته (Closed) گویند اگر نتیجه این عملگر روی این مجموعه، عضوی از آن را ایجاد کند. به بیان ریاضی خواهیم داشت.

$$ \large \forall x , y \in A ,\; \; (x * y) \in A $$

برای مثال می‌دانیم که مجموعه اعداد طبیعی نسبت به عمل جمع (+) یا (Addition) بسته است،‌ زیرا مجموعه دو عدد طبیعی حتما یک عدد طبیعی است. ولی همین مجموعه نسبت به عمل تفریق (-) یا (Subtraction) روی مجموعه اعداد طبیعی بسته نیست، زیرا

$$ \large 3 , 7 \in N , \; \; 3 - 7 = -4  \notin N $$

ساختار گروه

مجموعه $$ G $$، تحت عملگر (*) را یک گروه می‌نامیم، اگر تحت این عملگر بسته بوده و خواص زیرا را داشته باشد.

• خاصیت همانی (Identity): مجموعه $$ G $$ دارای عضو خنثی باشد به این معنی که برای هر عضوی از $$ G $$ رابطه زیر برقرار باشد.

$$ \large \exists e \in G, \forall x \in G,  \;\; e * x = x * e = x $$

رابطه ۱

به این ترتیب اجرای عملگر * روی $$ e $$ و $$ x $$، عنصر $$ x $$ را تغییر نمی‌دهد.

• خاصیت وارون (Inverse): با توجه به وجود عضو خنثی در مجموعه $$ G $$، هر عضو از این مجموعه یک عضو معکوس یا وارون (Inverse) دارد. به بیان ریاضی این ویژگی را به صورت زیر نشان می‌‌دهیم:

$$ \large  \forall x \in G,\; \exists y \in G, \;\; x * y = y * x = e $$

رابطه ۲

مشخص است که در اینجا منظور از $$ e $$، همان عضو خنثی عمل * است. در این شرایط به عنصر $$ y $$‌، عضو معکوس $$ x $$ تحت عملگر * گفته می‌شود. برای مثال در مجموعه اعداد حقیقی، وارون هر عدد $$ x $$ نسبت به عمل ضرب، به شکل $$ \frac{1}{x} $$ نشان داده می‌شود به شرطی که مقدار $$x$$ صفر نباشد یعنی $$ x \neq 0 $$.

• خاصیت شرکت‌پذیری (Associativity): خاصیت شرکت‌پذیری بیان می‌کند که اجرای عملگر * روی این مجموعه دارای اولویت نیست. به این ترتیب اگر سه عضو دلخواه $$ x, y , z $$ را از مجموعه $$ G $$‌ در نظر بگیرید، رابطه زیر برقرار خواهد بود.

$$ \large x * ( y * z ) = (x * y ) * z $$

رابطه ۳

اگر $$ A $$ یک مجموعه با اعضای $$ \{0 , 1 , -1 \} $$ باشد، آنگاه تحت عملگر جمع حسابی ( + ) یک گروه خواهد بود. مشخص است که این مجموعه فقط دارای عضو خنثی عمل جمع و وارون عمل جمع است. همچنین مجموعه $$ \{ 0 \} $$ کوچکترین مجموعه‌ای است که با عمل جمع، یک گروه تشکیل می‌دهد.

مثال‌هایی از ساختار گروه

همانطور که گفته شد، مجموعه‌ها و عملگرهایی که دارای خصوصیات ذکر شده در بندهای ۱ تا ۳ باشند، یک «گروه» (Group) نامیده می‌شوند. در این قسمت با ذکر مثال‌هایی از مجموعه‌ها و عملگرهای مربوطه، گروه بودن آن‌ها را مورد بررسی قرار می‌دهیم.

فیلم آموزش جبر خطی در فرادرس

کلیک کنید

مثال ۱

مجموعه اعداد صحیح، با عملگر جمع، یک گروه ایجاد می‌کند. زیرا:

$$ \large   \forall x \in Z, \;\;  x + 0 = 0 + x = x $$

$$ \large \forall x \in Z , x + (-x) = 0 $$

$$ \large \forall x,y, x \in Z , x + (y + z) = (x + y) + z $$

در عین حال، مجموعه اعداد صحیح با عملگر ضرب، یک گروه نخواهد بود. به روابط زیر توجه کنید.

$$ \large \forall x \in Z, \;\;  x \times 1 = 1 \times  x = x $$

پس این مجموعه تحت عملگر ضرب، دارای عضو خنثی است، ولی عضو وارون ندارد.

$$ \large \forall x \in Z , x \times \frac{1}{x} = 1,\;\; \frac{1}{x} \notin Z $$

مشخص است که به جز یک و قرینه یک هیچ عضوی از مجموعه اعداد صحیح را نمی‌توان معکوس کرده و مقدار حاصل، عضوی از مجموعه اعداد صحیح باشد. برای مثال عدد ۲ را در نظر بگیرید. وارون آن که برابر با $$ \frac{1}{2} $$ است، در مجموعه اعداد صحیح جای ندارد.

از طرفی مقدار صفر را در نظر بگیرید که وارون ضربی آن وجود ندارد. پس عضوی مثل صفر در مجموعه اعداد صحیح قرار دارد که دارای عضو وارون برای عملگر ضرب نیست یا عضو وارون ضربی آن در مجموعه اعداد صحیح قرار ندارد.

مثال ۲

عاد کردن تحت جمع دو عدد صحیح را به عنوان عملگر * در نظر بگیرید. به این معنی که اگر $$ a $$ و $$ b $$‌ به همراه $$ n $$ سه عدد صحیح باشند، عملگر * به صورت زیر خواهد بود:

$$ \large a * b: n | a + b $$

به این معنی که عملگر * ابتدا دو عدد $$ a $$‌ و $$ b $$ را با یکدیگر جمع کرده، سپس باقی مانده تقسیم آن‌ها را بر $$ n $$ بدست می‌آورد. در ادامه ویژگی‌های زیر را برای مجموعه اعداد صحیح و این عملگر مورد بررسی قرار می‌دهیم.

• مجموعه اعداد صحیح تحت عملگر * بسته است. با توجه به تعریف عاد کردن یا شمارنده بودن $$ n $$، می‌دانیم نتیجه اجرای عملگر * مقداری صحیح خواهد بود.
• خاصیت همانی برای مجموعه اعداد صحیح و عملگر * وجود دارد، زیرا تحت این عملگر، عنصر ۰، عضو خنثی است. واضح است که رابطه زیر برای هر عدد صحیح مثل $$ a $$ و $$ n $$ برقرار است.

$$ \large a * 0 = (a+0) \mod n \equiv a \mod n \equiv (0 + a)  \mod n \equiv a \mod n $$

• خاصیت وارون برای عملگر * در مجموعه اعداد صحیح، برقرار است. به این معنی که برای هر $$ a $$ باید $$ b $$ در مجموعه اعداد صحیح وجود داشته باشد که نتیجه رابطه $$a * b $$ برابر با عضو خنثی (یعنی صفر) باشد.

$$ \large a * b = \Big( a + b \equiv 0 \; ( \text{ mod } n) \Big) $$

با توجه به رابطه یا خاصیت قبل می‌توان $$ b $$ را به صورت $$ n - a $$‌ در نظر گرفت. زیرا:

$$ \large a * (n-a) : \Big (a + (n-a) \equiv 0\; (\text{ mod } n) \Big) = n ( \text{ mod } n ) = 0 $$

• طبق ویژگی‌های و قواعد بخش پذیری و خاصیت جمع، عملگر * نیز دارای خاصیت شرکت‌پذیری است. به این ترتیب داریم:

$$ \large a + (b + c) = a + (b + c) \; \rightarrow \; a * (b * c ) = ( a * b ) * c $$

یعنی همیشه رابطه زیر برقرار است.

$$ \large a + (b + c) \equiv  a + (b + c) \big ( \text{ mod } n \big) $$

گروه آبلی

گروه $$ G $$ را یک «گروه آبلی» (Abelian Group) می‌نامیم اگر علاوه بر خصوصیات مربوط به روابط ۱ تا ۳، خاصیت جابجایی نیز وجود داشته باشد. گاهی به گروه آبلی، گروه جابجایی نیز می‌گویند. به این ترتیب رابطه ۴ نیز برای گروه آبلی برقرار است.

$$ \large \forall x ,\; y  \in G,\;\; x * y = y * x $$

مجموعه‌ها و عملگرهای مطرح شده در مثال‌های ۱ و ۲، گروه‌های آبلی محسوب می‌شوند.

نام گذاری گروه آبلی به افتخار دانشمند و ریاضیدان نروژی «نیلز هنریک آبل» (Niels Henrik Abel) و بواسطه فعالیت‌های او در شناخت چنین مجموعه‌هایی انتخاب شده است.

ساختار حلقه

یک حلقه (Ring) مجموعه‌ای مثل $$ R $$ است که تحت دو عملگر + و × بسته بوده و خواص زیر را داشته باشد.

• مجموعه $$ R $$ با عملگر +، یک گروه آبلی تشکیل دهد.
• مجموعه $$ R $$ تحت عملگر ×، شرکت‌پذیر باشد.
• توزیع پذیری ضرب نسبت به جمع

$$ \large a , b, c \in\; R, \;\; a \times ( b  \times c ) = ( a \times b ) \times c $$

رابطه ۵

• مجموعه $$ R $$ تحت عمل پخشی (توزیع‌پذیری یا Distributive)  × نسبت به جمع، بسته باشد. به این ترتیب برای هر سه عضو از مجموعه $$ R $$ داریم:

$$ \large \forall a,b,c \in R, \;\; a \times (b + c) = (a \times b ) + (a \times c) $$

رابطه ۶

و همچنین

$$ \large \forall a,b,c \in R, \;\; (b + c) \times a = (b \times a ) + ( c \times a) $$

رابطه ۷

نکته: در اینجا برای نمایش عملگر اول و دوم از نمادهای + و × استفاده کرده‌ایم ولی مشخص است که منظورمان می‌تواند هر عملگر با خواص ذکر شده باشد. خوشبختانه عملگرهای جمع و ضرب حسابی، روی اعداد صحیح، یک حلقه ایجاد می‌کنند.

همانطور که می‌بینید، حلقه به مجموعه‌هایی که با دو عملگر به کار گرفته می‌شوند، ارتباط دارد. طبق اولین مشخصه حلقه، واضح است که چنین مجموعه‌ای باید یک گروه باشد و حتی نسبت به مجموعه اول نیز یک گروه آبلی محسوب شود. رابطه ۵ مشخص است که تحت عملگر دوم هم خاصیت شرکت‌پذیری وجود خواهد داشت.

مثال‌هایی از ساختار حلقه

در این قسمت به معرفی بعضی از مجموعه‌ها و بررسی حلقه بودن آن‌ها خواهیم پرداخت. در این قسمت علاوه بر مجموعه اعداد صحیح، به مجموعه اعداد حقیقی هم خواهیم پرداخت.

مثال ۳

همانطور که گفتیم، مجموعه اعداد صحیح، تحت جمع، یک گروه آبلی بوده، پس خواص زیر را خواهیم داشت. قبلاً نشان دادیم که مجموعه اعداد صحیح تحت جمع، یک گروه آبلی است.

• اعداد عضو مجموعه اعداد صحیح، دارای خاصیت شرکت‌پذیری در عملگر ضرب هستند.
• اعداد صحیح، دارای خاصیت پخشی ضرب نسبت به جمع هستند.

به این ترتیب مجموعه اعداد صحیح تحت جمع و ضرب حسابی، یک حلقه خواهند بود.

نکته: به ترتیبی که عملگرها در تعریف حلقه دارند، توجه کنید. همانطور که دیدید، ابتدا عملگر جمع و سپس عملگر ضرب مطرح شد.

مثال ۴

مجموعه اعداد صحیح تحت ضرب و جمع، یک حلقه نخواهد بود. زیرا از ابتدا مشخص است که مجموعه اعداد صحیح، براساس عملگر ضرب یک گروه نیست، زیرا:

• اعداد صحیح تحت عملگر ضرب، دارای عضو وارون نیست.
• اعداد صحیح تحت عملگر ضرب، یک گروه آبلی نیست.
• عملگر جمع نسبت به ضرب، خاصیت پخشی یا توزیع‌پذیری ندارد.

$$ \large a + ( b \times c )  \neq ( a + b ) \times (a + c ) $$

نکته: همانطور که دیده شد، با جابجایی عملگرها در رابطه با مجموعه، ممکن است خصوصیات آن تغییر کرده و دیگر یک حلقه محسوب نشود.

تا اینجا می‌دانیم ساختار حلقه و گروه چیست. در ادامه، در مورد انواع حلقه و ساختار میدان صحبت می‌کنیم. اگر بخواهید با این مباحث به طور کامل و عمیق آشنا شوید می‌توانید به مجموعه آموزش جبر درس، تمرین، حل مثال و تست فرادرس مراجعه کنید.

نیم حلقه

یکی دیگر از ساختارهای جبر و ریاضی، «نیم حلقه» (Semiring) است که یکی از خصوصیات حلقه را ندارد. مجموعه $$ R $$ با عملگرهای + و × را در نظر بگیرید. اگر این مجموعه به همراه عملگرهایش، همه خواص حلقه را داشته و فقط عضو وارون عملگر + وجود نداشته باشد، آن را «نیم حلقه» می‌نامیم. به این ترتیب می‌توان هر حلقه را یک نیم حلقه هم در نظر گرفت.

فیلم آموزش جبر جابجایی در فرادرس

کلیک کنید

به عنوان مثال مجموعه اعداد طبیعی ($$ N $$) یک نیم حلقه با عملگرهای + و × می‌سازد. همچنین اعداد صحیح مثبت، و اعداد حقیقی مثبت نیز تحت جمع و ضرب حسابی، نیم حلقه محسوب می‌شوند.

ساختار میدان

مجموعه $$ F $$ که تحت دو عملگر + و × بسته است را یک میدان (Field) می‌نامیم، اگر دو خاصیت زیر برای آن برقرار باشد.

• مجموعه $$ F $$ تحت عملگر +، یک گروه آبلی باشد.
• مجموعه $$ F $$ بدون در نظر گرفتن عضو خنثی عملگر +، یک گروه آبلی تحت عملگر × باشد.

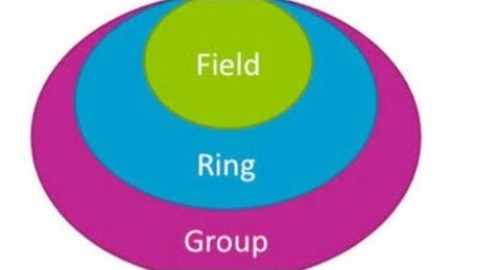
همانطور که دیده می‌شود، میدان یک حلقه است که تحت عملگر دوم نیز یک گروه آبلی خواهد بود، به شرطی که عضو خنثی عملگر اول را از مجموعه، حذف کرده باشیم.

به روشنی دیده می‌شود، ساده‌ترین ساختار توسط «گروه» ایجاد شده و به ترتیب شرط‌های مربوط به «حلقه» و «میدان» سخت‌تر می‌شوند.

مثال‌هایی از ساختار میدان

به یاد دارید که مجموعه اعداد صحیح به کمک عملگر جمع، یک گروه تشکیل داد ولی متاسفانه عملگر ضرب باعث گروه شدن مجموعه اعداد صحیح نمی‌شود. از طرفی مجموعه اعداد صحیح با عملگرهای جمع و ضرب (به ترتیب) یک حلقه محسوب شده ولی یک میدان ایجاد نمی‌کند زیرا نسبت به عملگر ضرب، معکوس‌پذیر نیست.

مثال 5

مجموعه اعداد گویا (Rational Numbers)، که به صورت نسبت دو عدد صحیح ($$ a , b \in Z , \frac{a}{b} , \; b \neq 0 $$) نوشته می‌شوند، تحت عملگرهای (+) و (×) یک میدان محسوب می‌شوند. زیرا:

• مجموعه اعداد گویا (Q) نسبت به عمل جمع بسته هستند.
• مجموعه اعداد گویا (Q) نسبت به عمل ضرب بسته هستند.
• مجموعه اعداد گویا (Q) دارای عضو خنثی عمل جمع (یعنی صفر) است.
• مجموعه اعداد گویا (Q) دارای عضو خنثی عمل ضرب (یعنی یک) است.
• مجموعه اعداد گویا (Q) دارای عضو معکوس عمل جمع (قرینه) است.
• مجموعه اعداد گویا (Q) دارای عضو معکوس عمل ضرب (معکوس) است. بدون در نظر گرفتن صفر که عضو خنثی عمل جمع است.
• مجموعه اعداد گویا (Q) دارای خاصیت جابجایی تحت عمل جمع است.
• مجموعه اعداد گویا (Q) دارای خاصیت جابجایی تحت عمل ضرب است.
• مجموعه اعداد گویا (Q) دارای خاصیت شرکت‌پذیری تحت عمل جمع است.
• مجموعه اعداد گویا (Q) دارای خاصیت شرکت‌پذیری تحت عمل ضرب است.
• مجموعه اعداد گویا (Q) دارای خاصیت پخشی (توزیع‌پذیری) ضرب نسبت به جمع است.

خاصیت پخشی ضرب نسبت به جمع در ادامه مشخص شده است. در اینجا فرض شده است که $$ a , b, c, d, e, f $$ همگی اعداد صحیح هستند.

$$ \large { \displaystyle { \begin{aligned} & { \frac {a}{b}} \cdot \left( { \frac {c}{d} } + {\frac {e}{f}} \right) \\[6pt] = {} & { \frac {a}{b}} \cdot \left( { \frac {c}{d}} \cdot { \frac {f}{f} } + { \frac {e}{f} } \cdot { \frac {d}{d} } \right) \\[6pt] = {} & { \frac {a}{b}} \cdot \left( { \frac {cf}{df} } + { \frac {ed}{fd} } \right) = { \frac {a}{b} } \cdot { \frac {cf + ed}{df} } \\[6pt] = {} & { \frac { a (cf + ed) }{ bdf } } = { \frac {acf} {bdf}} + { \frac {aed} {bdf}} = {\frac {ac} {bd}} + {\frac {ae} {bf}} \\[6pt] = {} & { \frac {a}{b} } \cdot { \frac {c}{d}} + { \frac {a}{b} } \cdot { \frac {e}{f}} \end{aligned}} } $$

• اگر صفر را از مجموعه اعداد گویا خارج کنیم، این مجموعه نسبت به عملگر ضرب یک گروه آبلی خواهد بود.

در نتیجه مجموعه اعداد گویا با دو عملگر + و ×، تشکیل یک میدان (Field) می‌دهد.

مثال ۶

مجموعه اعداد حقیقی تحت عملگرهای جمع (+) و ضرب (×)، یک میدان محسوب می‌شود، زیرا با توجه به خصوصیات اعداد حقیقی، بسته بودن این مجموعه تحت عملگر جمع مشخص است و همچنین با توجه به خصوصیات گروه‌ها، این مجموعه تحت عملگر (+) یک گروه آبلی است.

$$ \large  \forall x, y, z \in R , \;\; x + y \in R $$

$$ \large  x + 0 = 0 + x = x , 0 \in R $$

$$ \large x + ( -x ) = -x +x = 0 ,\; \; 0 , -x \in R $$

$$ \large x + ( y + z ) = ( x + y ) + z $$

از طرفی مجموعه اعداد حقیقی تحت عملگر ضرب نیز بسته بوده و بدون در نظر گرفتن صفر از این مجموعه، تشکیل یک گروه آبلی را می‌دهد.

$$ \large \forall x, y, z \in R ,\;\; x \times y \in R\ $$

$$\large x  \times 1 = 1 \times x = x, \;\; 1 \in R $$

$$ \large  x \times \frac{1}{x} = \frac{1}{x} \times x = 1 ,\; x \neq 0 , \;\;\frac{1}{x} \in R $$

$$\large x \times (y \times z) = (x \times y)  \times z $$

از طرفی وجود خاصیت شرکت‌پذیری و جابجایی و همچنین پخشی ضرب نسبت به جمع نیز در این مجموعه برقرار است. در نتیجه مجموعه اعداد حقیقی و عملگرهای + و ×، تشکیل یک میدان می‌دهند.

آموزش ویدیویی مبانی آنالیز حقیقی

همانطور که دیدید، بسیاری از مفاهیم به کار رفته در این نوشتار مربوط به اعداد حقیقی و حتی اعداد مختلط می‌شد. اگر می‌خواهید موضوعات گسترده و پیشرفته‌تر در این مجموعه اعداد را مورد بررسی قرار دهید، آموزش ویدیویی مبانی آنالیز حقیقی از سری آموزش‌های ریاضیات فرادرس به شما پیشنهاد می‌شود. این مجموعه ویدیویی آموزشی در حدود ۵ ساعت، به مباحث مختلف آنالیز حقیقی طی چهار درس پرداخته و موضوعات مرتبط با مبانی آنالیز حقیقی را مرور کرده است.

فیلم آموزش مبانی آنالیز حقیقی در فرادرس

کلیک کنید

درس اول به مجموعه‌ها و روابط بین آن‌ها اختصاص دارد. همچنین فضاهای متریک و دنباله‌های اعداد حقیقی در این قسمت مورد بحث قرار گرفته است. در درس دوم، «نظریه اندازه‌» (Measure Theory) و جبر مجموعه‌ها پرداخته شده است. میدان‌های سیگمایی و توابع اندازه‌پذیر از مباحثی هستند که در این قسمت، آموزش داده می‌شود.

درس سوم و چهار نیز به انتگرال و قضیه همگرایی و «لم فاتو» (Fatu Lemma) همچنین فضاهای نرم‌دار می‌پردازد. فضای باناخ، ضرب داخلی و فضای هیلبرت نیز موضوعات مورد بحث در این قسمت‌ها محسوب می‌شوند.

خلاصه و جمع‌بندی

در این نوشتار با مفهوم و اصطلاحات میدان، حلقه و گروه در ریاضی آشنا شدیم که هر یک از آن‌ها خصوصیاتی را برای توصیف رابطه بین عملگرها و اعضای مجموعه‌ها را بیان می‌کنند. قضیه‌ها و گزاره‌های زیادی بخصوص در حوزه نظریه اعداد برای میدان، حلقه و گروه در ریاضی وجود دارد که البته اثبات و یا به کارگیری آن‌ها در بسیاری از شاخه‌های دیگر ریاضی به کار می‌روند.

کاربردهای زیادی برای مفاهیم میدان، حلقه و گروه در ریاضی جدید و مدرن وجود دارد که در بخصوص در بحث «آنالیز حقیقی» (Real Analysis) و «توابع» (Functions) و محاسبه «انتگرال‌های ریمان» (Reimmanian Integrals) به کار می‌رود.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• آموزش ریاضیات مهندسی
• تقسیم عدد صحیح — به زبان ساده
• قضایای همنهشتی در اعداد صحیح — به زبان ساده
• قواعد بخش پذیری یا عاد کردن — به زبان ساده

^^