نمایش ماتریسی گراف — به زبان ساده
در آموزشهای قبلی مجله فرادرس درباره گراف و تعاریف مربوط به آن بحث کردیم. در این آموزش قصد داریم نمایش ماتریسی گراف و یکریختی دو گراف را بیان کنیم.
نمایش ماتریسی گراف
همانطور که در تعریف گراف دیدیم، معمول است گراف را به صورت مجموعهای از یالها و گرهها نمایش دهیم. اما اگر بخواهیم یک گراف را در کامپیوتر ذخیره کنیم، چنین نمایشی مناسب نخواهد بود.
یک روش ساده برای ذخیره گراف، لیست کردن رئوس مجاور هم در گراف است. در شکل زیر، لیستی از رئوس مجاور هم نشان داده شده است:
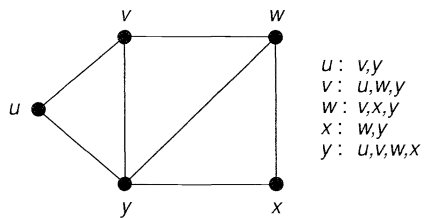
یک نمایش پرکاربرد دیگر برای گراف، استفاده از ماتریس است. فرض کنید $$G$$ یک گراف با رئوس برچسبدار (Labelled Vertices) باشد. تعداد رئوس این ماتریس $$n$$ و تعداد یالهای آن $$m$$ است.
«ماتریس مجاورت» (Adjatency Matrix) برای یک گراف را با نماد $$A$$ نشان میدهند. ماتریس مجاورت، یک ماتریس $$n\times n$$ است و به رئوس گراف مربوط میشود. مقدار درایه $$ij$$ام ماتریس مجاورت، برابر با تعداد یالهای بین رأس $$i$$ و رأس $$j$$ است.
«ماتریس تلاقی» (Incidence Matrix) برای یک گرف را با نماد $$M$$ نشان میدهند. ماتریس تلاقی یا وقوع، یک ماتریس $$n\times m$$ است که به یالهای گراف مربوط میشود. فرض کنید که همه یالها نیز برچسبدار شوند. در این حالت، اگر رأس $$i$$ با یال $$j$$ تلاقی داشته باشد، مقدار درایه $$ij$$ام ماتریس تلاقی، عدد ۱ است و اگر رأس $$i$$ با یال $$j$$ تلاقی نداشته باشد، مقدار درایه $$ij$$ام آن، صفر خواهد بود. در یک گراف بدون حلقه، درجه یک رأس با تلاقی آن رأس با یالهایش برابر است.
شکل زیر، گراف برچسب دار $$G$$ به همراه ماتریس مجاورت ($$A$$) و ماتریس تلاقی آن ($$M$$) را نشان میدهد:
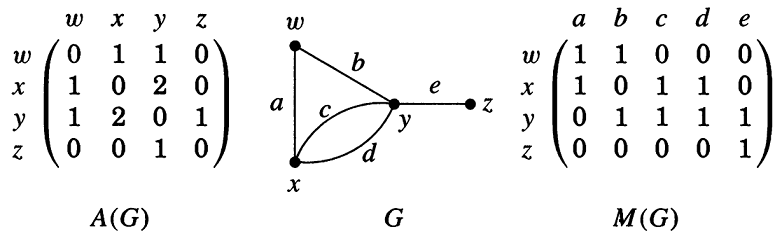
برای نوشتن ماتریس مجاورت و ماتریس تلاقی، مانند شکل بالا، ابتدا ترتیب نوشتن رئوس برای سطرها و ستونها را مشخص میکنیم، سپس به نمایش ماتریسی گراف میپردازیم.
در شکل بالا، روی رأس $$w$$، حلقه وجود ندارد، پس درایه اول ماتریس مجاورت صفر است. از رأس $$w$$ به رأس $$x$$ یک یال وجود دارد که با $$a$$ نشان داده شده است، پس درایه سطر اول، ستون دوم ماتریس مجاورت برابر ۱ است، زیرا یک یال بین این دو رأس وجود دارد. بین رئوس $$x$$ و $$y$$ دو یال وجود دارد که یک حلقه تشکیل میدهند. همانطور که در ماتریس نیز مشخص است، اعداد ماتریس برای این دو درایه برابر ۲ است.
به همین ترتیب میتوان همه درایههای ماتریس مجاورت و ماتریس تلاقی را مشخص کرد.
اگر برای سطر و ستونهای ماتریسهای مجاورت و تلاقی، از نامگذاری درست استفاده شود، این دو ماتریس قابل تبدیل به هم هستند.
به عنوان مثالی دیگر، در شکل زیر، یک گراف به همراه ماتریس مجاورت و ماتریس تلاقی آن نشان داده شده است:
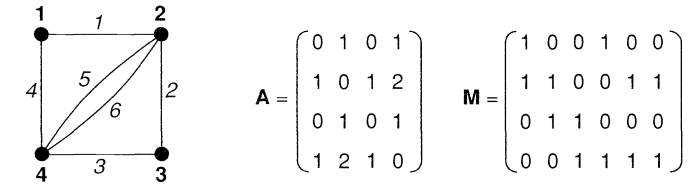
نکته
یک ماتریس مجاورت با مرتبسازی رئوسِ گراف مربوط به آن مشخص میشود. همه ماتریسهای مجاورت، متقارن هستند. به عبارت دیگر در همه سطر و ستونهای ماتریس مجاورت رابطه زیر برقرار است:
$$\large a_{i,j} = a_{j,i}$$
ماتریس مجاورت برای یک گراف ساده $$G$$، تنها اعداد صفر و یک دارد. اعداد روی قطر ماتریس مجاورت در یک گراف ساده برابر صفر است. درجه رأس $$v$$، جمع همه اعداد روی سطر $$v$$ام از ماتریس مجاورت ($$A$$) یا ماتریس تلاقی ($$M$$) است.
مثال
ماتریس مجاروت و ماتریس تلاقی گراف شکل زیر را بنویسید.
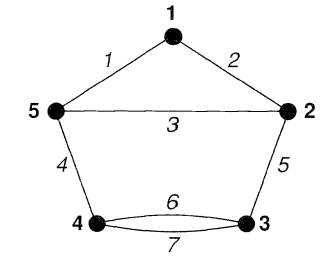
حل: نمایش ماتریسی گراف داده شده به صورت زیر است:
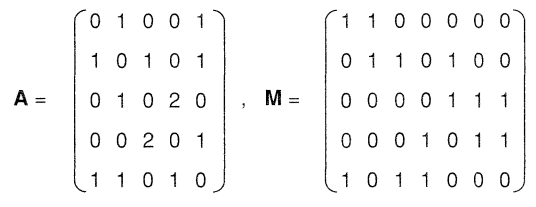
درجه رأس چهارم برابر سه است. این عدد، با جمع سطر چهارم در ماتریس مجاورت یا ماتریس تلاقی، برابر است.
تساوی ماتریس مجاورت دو گراف
همانطور که بیان شد، رأس $$i$$ام یک گراف، به سطر و ستون $$i$$ام در ماتریس مجاورت آن ارتباط دارد. ذخیره یک گراف در کامپیوتر به نامگذاری رئوس ماتریس وابسته است. با این حال، ما به دنبال مطالعه خواصی هستیم که به این نامگذاریها وابسته نباشد (مانند همبندی).
دو گراف $$G$$ و $$H$$ را در نظر بگیرید. اگر با تغییر نامگذاری رئوس $$G$$ با استفاده از رئوس $$H$$، بتوان از گراف $$G$$ به گراف $$H$$ رسید، میتوان به طور شهودی گفت مشخصات ساختاری دو گراف $$G$$ و $$H$$ یکسان است. پس میتوان برای گرافهای ساده، یک تعریف دقیق بیان کرد. یک تابعِ تغییر نام، مانند $$f$$ را در نظر بگیرید:
$$f: V(G)\to V(H)$$
این تابع، هر المان $$V(H)$$ را به یک المان از $$V(G)$$ نسبت میدهد و یک تناظر یک به یک بین $$V(G)$$ و $$V(H)$$ برقرار میکند. بنابراین تابع $$f$$ یک تابع یک به یک و پوشا است. اگر با تغییر نام رئوس، گراف $$G$$ به گراف $$H$$ تبدیل شود، ماتریس مجاورت این دو گراف با یکدیگر برابر هستند.
تعریف یکریختی
یکریختی، از گراف ساده $$G$$ به گراف ساده $$H$$، یک نگاشت دو سویه از تابع $$f:V(G)\to V(H)$$ است. $$f$$ یک تابع تغییر نام رئوس گراف $$G$$ به گراف $$H$$ است. اگر $$uv$$ یک یال در گراف $$G$$ باشد، یال متناظر آن در گراف $$H$$، عبارت است از $$f(u)f(v)$$. به عبارت دیگر، اگر دو رأس متناظر با هم در گرافهای $$G$$ و $$H$$ وجود داشته باشد، یالهای مربوط به این دو رأس نیز متناظر هستند.
تعریف یکریختی دو گراف با استفاده از ماتریس مجاورت
گرافهای $$G$$ و $$H$$ شکل زیر را در نظر بگیرید:
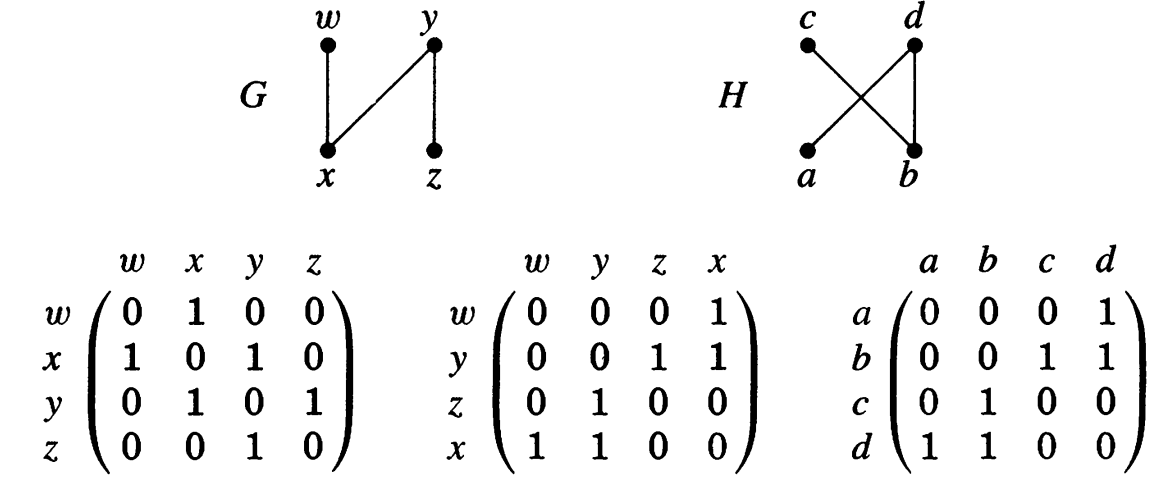
این دو گراف ۴ رأس دارند. با تعریف تابع $$f: V(G) \to V(H)$$ به صورت زیر داریم:
$$f(w)=a, \, f(x)=d, \, f(y)=b, \, f(z)=c.$$
تابع $$f$$ یک تابع یکریخت است، اگر و فقط اگر این تابع، یالها و غیریالها را در خود نگهداری کند.
توجه به این نکته ضروری است که میتوان ماتریس $$A(G)$$ را با تغییر در ترتیب رئوس ماتریس، به ماتریس $$A(H)$$ تبدیل کرد. این مسئله در شکل نشان داده شده است. پس $$f$$، یک تابعِ یکریخت است.
یک نگاشت دیگر برای نشان دادن یکریختی دو گراف شکل بالا، به صورت زیر است:
$$f(w)=c, \, f(x)=b, \, f(y)=d, \, f(z)=a.$$
یافتن یکریختی
همانطور که در مثال بالا نشان داده شد، یکی از روشهای اثبات همریختی دو گراف، مرتب کردن رئوس در ماتریسهای مجاورت و رسیدن به ماتریسهای مشابه است. یکی دیگر از روشهای یافتن همریختی بین دو گراف، ایجاد تناظر بین رئوس دو گراف است. رئوس متناظر باید رفتارهای مشابهی داشته باشند (مثلا درجه رئوس یکسان باشد). در حالت کلی توجه به نکتههای زیر برای یافتن یکریختی دو ماتریس ضروری است:
- تعداد رئوس دو گراف
- تعداد یالهای دو گراف
- درجه هر یک از رئوس
- ماتریس مجاورت دو گراف
تعریف یکریختی دو گراف با استفاده از رئوس متناظر
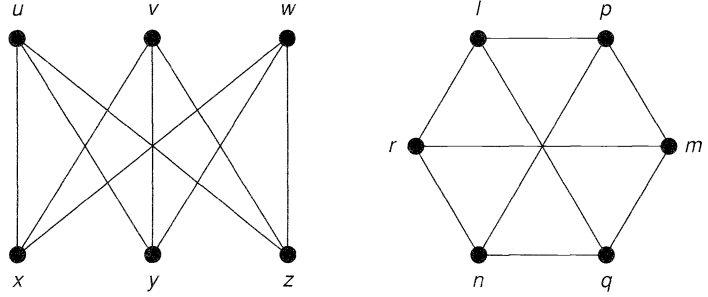
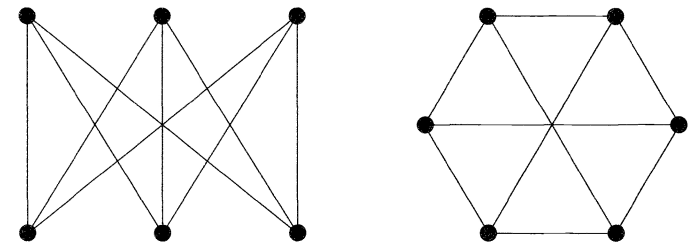
دو گراف $$G_1$$ و $$G_2$$ یکریخت نامیده میشوند اگر یک رابطه یک به یک بین همه رأسهای $$G_1$$ و $$G_2$$ وجود داشته باشد. به طوری که تعداد یالهایی که هر دو رأس از $$G_1$$ را به هم وصل میکند با تعداد یالهایی که دو رأس متناظر آن در $$G_2$$ به هم متصل میکند، برابر باشند. بنابراین، دو گراف $$G_1$$ و $$G_2$$ شکل زیر یکریخت هستند.
رأسهای متناظر این دو گراف عبارت است از:
$$ \large u \leftrightarrow l, \, v \leftrightarrow m \, , w \leftrightarrow n, \, x \leftrightarrow p , \, y \leftrightarrow q, \, z \leftrightarrow r \,$$
برای بسیاری از مسائل به برچسب روی رأسها نیازی نیست و آن را حذف میکنیم. بنابراین میتوان گفت دو «گراف بدون برچسب» (Unlaballed Graphs) یکریخت هستند، اگر بتوان با تعیین برچسب برای هریک از رئوس دو گراف و تبدیل آنها به «گراف برچسب دار» (Labelled Graph) یکریختی آنها را ثابت کرد. برای مثال، دو گراف بدون برچسب شکل زیر یکریخت هستند، زیرا میتوان مانند حالت قبل، دو گراف را برچسب دار کرد.
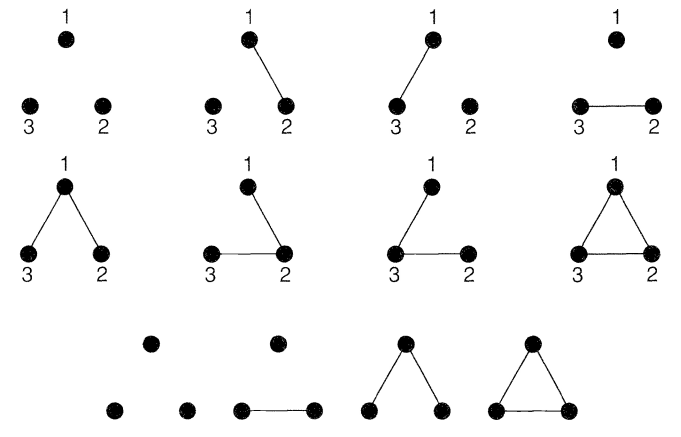
تفاوت دو گراف برچسب دار و بدون برچسب، هنگام شمردن دو گراف مشخص میشود. مثلا اگر یک گراف با سه رأس در نظر گرفته شود، هشت گراف برچسب دار متفاوت حاصل میشود. در حالیکه فقط ۴ گراف بدون برچسب متفاوت وجود خواهد داشت.
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره سایر موضوعات مربوط به ریاضیات، مطالب بیشتری یاد بگیرید، آموزشهای زیر به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- مجموعه آموزشی جامع ریاضی دبیرستان – علوم تجربی
- گزاره ها و سورهای منطقی — به زبان ساده
- ترکیب گزاره های منطقی — به زبان ساده
- گراف — تعاریف و انواع به زبان ساده
- درخت در گراف — به زبان ساده
^^










ویدیو آموزشی نداره؟?