انتگرال بیضوی — از صفر تا صد

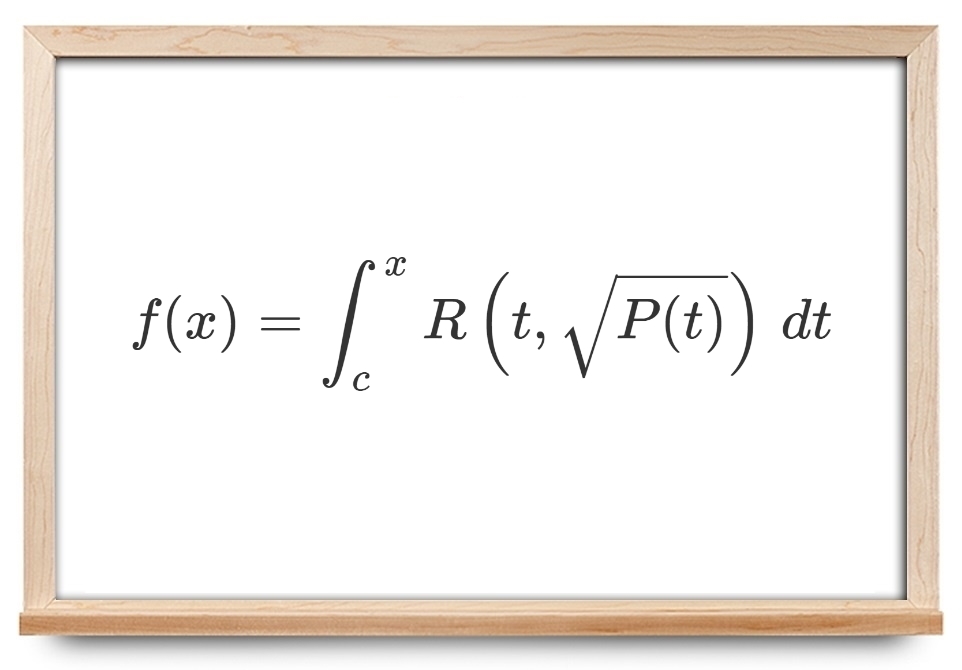
در این آموزش با انتگرال بیضوی (Elliptic Integral) و انتگرال‌های بیضوی لژاندر، توابع تتا و توابع بیضوی ژاکوبی آشنا می‌شویم. این انتگرال‌ها و توابع بیضوی در نظریه اعداد، جبر، هندسه، معادلات دیفرانسیل معمولی و جزئی خطی و غیرخطی، دینامیک، مکانیک، الکترواستاتیک، رسانش و نظریه میدان‌ها کاربرد دارند.

تاریخچه

اولین مطالعات در زمینه انتگرال‌های بیضوی در سال 1655 منتشر شد که در آن هنگام، «جان والیس» (John Wallis) طول قوس یک بیضی را بررسی کرد. جان والیس و «آیزاک نیوتن» (Isaac Newton)، هر دو، یک بسط سری بینهایت برای طول قوس بیضی ارائه کردند. اما در اواخر سال 1700 بود که لژاندر از توابع بیضوی برای مسائلی مانند حرکت یک آونگ ساده و تغییر شکل یک نوار الاستیک نازک استفاده کرد. این مسائل را می‌توان با توابع ساده تعریف کرد.

«آدریان-ماری لژاندر» (Adrien-Marie Legendre)، ریاضیدان فرانسوی، که برای نماد لژاندر و توابع لژاندر معروف است، بیش از چهل سال از زندگی خود را صرف کار بر روی توابع بیضوی، از جمله دسته‌بندی انتگرال‌های بیضوی کرد. اولین نوشته‌های منتشر شده او در مورد انتگرال‌های بیضوی شامل دو مقاله در Memoires de l’Acadmie Francaise در سال 1786 برای قوس بیضوی است.

کار اصلی لژاندر روی توابع بیضوی در سه مجلد در سال‌های ۱۸۱۱ تا ۱۸۱۶ منتشر شد. در جلد اول، لژاندر ویژگی‌های اساسی انتگرال‌های بیضوی و توابع بتا و گاما را معرفی کرد. نتایج بیشتر در مورد توابع بتا و گاما و کاربردهای آن‌ها در مکانیک، گردش زمین، جذب بیضی‌ها و سایر مسائل در جلد دوم منتشر شد. جلد سوم شامل همان جدول‌های مفصلی بود که امروزه به نام جداول انتگرال‌های بیضوی شناخته می‌شوند و لژاندر خودش آن‌ها را محاسبه کرده بود. او در ادامه، دوباره در سه مجلد، در سال‌های ۱۸۲۵ تا ۱۸۳۰ کارهایش را تکرار کرد.

علی‌رغم آنکه لژاندر چهل سال از عمر خود را صرف مطالعه توابع بیضوی کرد، کارهای او اساساً تا سال ۱۸۲۷ مورد توجه عم‌عصرانش قرار نگرفت. در این سال، دو دانشمند جوان و ناشناخته به نام «نیلس هنریک آبل» (Niels Henrik Abel) و «کارل گوستاو ژاکوب ژاکوبی» (Carl Gustav Jacob Jacobi) موضوع را بر مبنای جدیدی قرار دادند و آن را متحول کردند.

در سال ۱۸۲۵، دولت نروژ به آبل یک کمک‌هزینه تحقیقاتی برای سفر به فرانسه و آلمان اعطا کرد. آبل به پاریس رفت و در آنجا مقاله مهمی را درباره تناوب مضاعف توابع بیضوی ارائه کرد. آبل در کنار سایر کارهای مهمش، کار مهمی را در زمینه توابع بیضوی انجام داد که متأسفانه تا بعد از مرگش کشف نشد.

ژاکوبی یک مقاله کلاسیک در مورد اهمیت توابع بیضوی در فیزیک ریاضی به دلیل لزوم انتگرال‌گیری از معادلات انرژی جنبشی مرتبه دوم نوشت. بر این اساس، معادلات حرکت به فرم چرخشی فقط برای سه مورد آونگ، قله متقارن در یک میدان گرانشی و یک جسم-فنر آزاد انتگرال‌پذیر هستند که جواب‌ها برحسب توابع بیضوی ارائه می‌شوند.

ژاکوبی اولین ریاضی‌دانی بود که توابع بیضوی را در نظریه اعداد، برای مثال، اثبات قضیه اعداد چندضلعی فرما (Fermat Polygonal Number Theorem) به کار برد. توابع تتای ژاکوبی نیز در مطالعه سری‌های فوق‌هندسی، بسیار مورد استفاده قرار گرفته‌اند.

مقدمه

یک انتگرال بیضوی به فرم عمومی زیر است:

$$ \large f ( x ) = \int \frac { A ( x ) + B ( x ) } { C ( x ) + D ( x ) \sqrt { S ( x ) } } d x $$

که در آن، $$ A ( x )$$، $$ B ( x )$$، $$ C ( x ) $$ و $$ D ( x ) $$ چندجمله‌ای‌هایی برحسب $$ x $$ هستند و $$ S ( x ) $$ یک چندجمله‌ای مرتبه سه یا چهار است. در ادامه، انتگرال‌های بیضوی نوع اول و دوم را معرفی می‌کنیم.

انتگرال بیضوی نوع اول

فرض می‌کنیم ضریب $$ k $$ در $$ 0 \le k ^ 2 < 1 $$ صدق می‌کند (این موضوع گاهی برحسب پارامتر $$ m = k ^ 2 $$ یا ضریب زاویه‌ای $$ \alpha \equiv \sin ^ { - 1 } k $$ نوشته می‌شود). «انتگرال بیضوی ناقص نوع اول» (Incomplete Elliptic Integral of the First Kind) به صورت زیر نوشته می‌شود:

$$ \large  { F } ( \phi , k ) = \int _ { 0 } ^ { \sin \phi } \frac { d t } { \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } , \quad 0 \leq k ^ { 2 } \leq 1 \quad \text { , } \quad 0 \leq \sin \phi \leq 1 $$

اگر $$ t = \sin \theta $$ و $$ d t = \cos \theta d \theta = \sqrt {1-t ^ 2 } d \theta $$ را در نظر بگیریم، خواهیم داشت:

$$ \large F ( \phi , k ) = \int _ { 0 } ^ { \phi } \frac { d \theta }{ \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \theta } } , \quad 0 \leq k ^ { 2 } \leq 1 \quad \text {, } \quad 0 \leq \phi \leq \pi / 2 $$

انتگرال اخیر، به عنوان «انتگرال بیضوی لژاندر ناقص» (Incomplete Legendre Elliptic Integral) شناخته می‌شود. انتگرال بیضوی کامل را می‌توان با قرار دادن حداکثر مقدار بازه در کران بالای انتگرال، یعنی $$ \sin \phi = 1 $$ یا $$ \phi = \pi / 2 $$، به دست آورد:

$$ \large \begin {aligned}
{ K } ( { k } ) & = \int _ { 0 } ^ { 1 } \frac { d t } { \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } \\
& = \int _ { 0 } ^ { \pi / 2 } \frac { d \theta } { \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \theta } } \end{aligned} $$

انتگرال بیضوی نوع دوم

انتگرال بیضوی نوع دوم به فرم زیر است:

$$ \large \begin {aligned}
{ E } ( \phi , k ) & = \int _ { 0 } ^ { \sin \phi } \frac { \sqrt { 1 - k ^ { 2 } t ^ { 2 } } } { \sqrt { 1 - t ^ { 2 } } } d t \\
& = \int _ { 0 } ^ { \phi } \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \theta } d \theta
\end {aligned} $$

به طور مشابه، انتگرال بیضوی کامل را می‌توان با برابر قرار دادن کران بالای انتگرال با حداکثر مقدار  آن به دست آورد:

$$ \large \begin {aligned}
{ E } ( { k } ) & = \int _ { 0 } ^ { 1 } \frac { \sqrt { 1 - k^ { 2 } t ^ { 2 } } } { \sqrt { 1 - t ^ { 2 } } } d t \\
& = \int _ { 0 } ^ { \pi / 2 } \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } t } d t
\end {aligned} $$

یک دسته بسیار مفید دیگر از توابع را می‌توان با معکوس کردن انتگرال‌های بیضوی به دست آورد. به عنوان مثال، تابع بیضوی ژاکوبی $$sn$$ را می‌توان از عبارت زیر به دست آورد:

$$ \large u ( x = \sin \phi , k ) = F ( \phi , k ) = \int _{ 0 } ^ { \sin \phi } \frac { d t } { \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } $$

اگر بخواهیم معکوس انتگرال بیضوی را بنویسیم، داریم:

$$ \large x = \sin \phi = sn ( u , k ) $$

یا

$$ \large u = \int _ { 0 } ^ { s n } \frac { d t } { \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } $$

با توجه به قطب‌ها و کران بالای انتگرال بیضوی، دوازده نوع مختلف تابع بیضوی ژاکوبی وجود دارد، اما سه مورد محبوب این توابع عبارتند از: دامنه سینوسی $$ s n ( u , k )$$، دامنه کسینوسی $$ c n ( u , k ) $$ و تابع بیضوی دامنه دلتا $$ d n ( u , k ) $$ که روبط زیر بین آن‌ها برقرار است:

$$ \large s n ^ 2 + c n ^ 2 = 1 $$   و   $$ k ^ 2 s n ^ 2 + d n ^ 2 = 1 $$

انتگرال بیضوی

سه فرم اساسی از انتگرال‌های بیضوی لژاندر وجود دارد که در اینجا درباره آن‌ها بحث می‌کنیم. این انتگرال‌ها، نوع اول، نوع دوم و نوع سوم نام دارند. در معروف‌ترین فرم عمومی، انتگرال‌های بیضوی در فرمی نمایش داده می‌شوند که انتگرال ناقص نام دارد و حدود انتگرال، محدوده زیر را شامل می‌شود:

$$ 0 \le \sin \phi \le 1 $$ یا $$ 0 \le \phi \le \pi / 2 $$

نوع اول

انتگرال بیضوی ناقص را می‌توان به صورت زیر نوشت:

$$ \large \begin {aligned}
\mathrm { F } ( \sin \phi , k ) = \int _ { 0 } ^ { \sin \phi } \frac { d t } { \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } , & \;\;\;\;\;\;\;0 \leq k ^ { 2 } \leq 1 \\
& \;\;\;\;\;\;\;0 \leq \sin \phi \leq 1
\end {aligned} \;\;\; ( 1 ) $$

با قرار دادن $$ t = \sin \theta $$، معادله (۱) به صورت زیر در می‌آید:

$$ \large \begin {aligned}
\mathrm { F } ( \phi , k ) = \int _ { 0 } ^ { \phi } \frac { d \theta } { \sqrt { \left ( 1 - k ^ { 2 } \sin ^ { 2 } \theta \right ) } } , & \;\;\;\;\;\; 0 \leq k ^ { 2 } < 1 \\
& \;\;\;\;\;\; 0 \leq \phi < \frac { \pi } { 2 }
\end {aligned} \;\;\;\; ( 2 ) $$

پارامتر $$k$$ مشخصه (Modulus) انتگرال بیضوی و $$ \phi $$ زاویه دامنه (Amplitude Angle) است.

انتگرال بیضوی کامل با قرار دادن دامنه $$ \phi = \pi / 2 $$ یا $$ \sin \phi = 1 $$، که حداکثر محدوده در کران بالای انتگرال‌گیری برای انتگرال بیضوی است، به دست می‌آید:

$$ \large \mathrm { F } \left ( \phi = \frac { \pi } { 2 } , k \right ) = \mathrm { F } ( \sin \phi = 1 , k ) = \mathrm{ K } ( k ) = \ \mathrm {K} \;\;\;\;\; \; (3) $$

یک فرم مکمل برای انتگرال بیضوی را می‌توان با قرار دادن مشخصه زیر به دست آورد:

$$ \large ( k' ) ^ 2 = 1 - k ^ 2 \;\;\;\; ( 4 ) $$

اگر $$ v = \tan \theta $$ و در نتیجه $$ d v = \sec ^ 2 \theta d \theta = ( 1 + v ^ 2 ) d \theta $$ را در نظر بگیریم، آنگاه داریم:‌

$$ \large \begin {aligned}
\mathrm { F } ( \phi , k ) & = \int _ { 0 } ^ { \tan \phi } \frac { d v } { \left ( 1 + v ^ { 2 } \right ) \sqrt { \left ( 1 -k ^ { 2 } \left ( \frac { v ^ { 2 } } { 1 + v ^ { 2 } } \right ) \right ) } } \\
& = \int _ { 0 } ^ { \tan \phi } \frac { d v } { \sqrt { 1 + v ^ { 2 } } \sqrt { \left ( 1 + v ^ { 2 } - k ^ { 2 } v ^ { 2 } \right . } } \\
& = \int _ { 0 } ^ { \tan \phi } \frac { d v }{ \sqrt { \left ( 1 + v ^ { 2 } \right ) \left ( 1 + k ^ { \prime } v ^ { 2 } \right ) } } \end {aligned} \;\;\;\;\; \; ( 5 ) $$

مکمل انتگرال بیضوی کامل به صورت زیر است:

$$ \large \mathrm { F } \left ( \phi = \frac { \pi } { 2 } , k ^ { \prime } \right ) = \mathrm { F } \left ( \sin \phi = 1 , k ^ { \prime } \right ) = \mathrm { K } \left ( k ^ { \prime } \right ) = \mathrm { K } ^ { \prime } \;\;\;\;\; ( 6 )$$

نوع دوم

انتگرال بیضوی نوع دوم به فرم زیر است:

$$ \large \mathrm { E } ( \phi , k ) = \int _ { 0 } ^{ \sin \phi } \sqrt { \frac { 1 - k ^ { 2 } t ^ { 2 } } { 1 - t ^ { 2 } } } d t , \quad 0 \leq k ^ { 2 } \leq 1 \;\;\;\;\; ( 7 ) $$

یا معادل آن:

$$ \large \begin {aligned}
\mathrm { E } ( \phi , k ) = \int _ { 0 } ^ { \phi } \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \theta } d \theta , & \;\;\;\;\;\;\;\;0 \leq k ^ { 2 } \leq 1 \\ & \;\;\;\;\;\;\;\;0 \leq \phi \leq \frac { \pi } { 2 } \end {aligned} \;\;\;\;\; ( 8 ) $$

و به طور مشابه، انتگرال بیضوی کامل نوع دوم را می‌توان به صورت زیر نوشت:

$$ \large \mathrm { E } \left ( \phi = \frac { \pi } { 2 } , k \right ) = \mathrm { E } ( \sin \phi = 1 , k ) = \mathrm { E } ( k ) = \mathrm { E } \;\;\;\;\; ( 9 ) $$

مکمل انتگرال کامل نوع دوم نیز به شکل زیر است:

$$ \large \mathrm { E } \left ( \phi = \frac { \pi } { 2 } , k ^ { \prime } \right ) = \mathrm { E } \left ( \sin \phi = 1 , k ^ { \prime } \right ) = \mathrm { E } \left ( k ^ { \prime } \right ) = \mathrm { E } ^ { \prime } \;\;\;\;\; ( 1 0) $$

نوع سوم

انتگرال بیضوی نوع سوم به شکل زیر است:

$$ \large \Pi ( \phi , n , k ) = \int _ { 0 } ^ { \sin \phi } \frac { d t } { ( 1 + n t ) ^ { 2 } \sqrt { \left ( 1 - t ^ { 2 } \right ) \left ( 1 - k ^ { 2 } t ^ { 2 } \right ) } } , \quad 0 \leq k ^ { 2 } \leq 1 \;\;\;\;\; (11 ) $$

یا معادل آن:

$$ \large \begin {aligned}
\Pi ( \phi , n , k ) = \int _ { 0 } ^ { \phi } \frac { d \theta }{ \left (1 + n \sin ^ { 2 } \theta \right ) \sqrt { \left ( 1 - k ^ { 2 } \sin ^ { 2 } \theta \right ) } } , & \;\;\;\;\;\;\; 0 \leq k ^ { 2 } \leq 1 \\
& \;\;\;\;\;\;\;0 \leq \phi \leq \frac { \pi } { 2 }
\end {aligned} \;\;\;\; ( 12 ) $$

کاربردهای انتگرال بیضوی

تعیین طول قوس یک دایره به سادگی و با استفاده از توابع مثلثاتی قابل انجام است. این در صورتی است که برای محاسبه طول قوس یک بیضی از انتگرال‌های بیضوی استفاده می‌شود. همچنین، طول مسیر طی شده یک آونگ را می‌توان برای زاویه‌های کوچک با استفاده از توابع مثلثاتی به دست آورد، اما برای تعیین کل مسیر آونگ باید از انتگرال‌های بیضوی استفاده کرد.

روابط بین انتگرال‌های بیضوی و مقادیر منتخب آن‌ها

در این بخش، روابط بین انتگرال‌های بیضوی را بررسی می‌کنیم.

انتگرال‌های بیضوی کامل نوع اول و دوم $$ \Large \mathrm { K } $$، $$\Large \mathrm {K}'$$، $$\Large \mathrm { E}  $$ و $$\Large \mathrm { E}' $$

چهار انتگرال بیضوی $$ \mathrm { K } $$، $$ \mathrm {K }' $$، $$ \mathrm { E } $$ و $$ \mathrm { E}' $$ در اتحاد زیر صدق می‌کنند (این اتحاد را لژاندر معرفی کرد):

$$ \large \mathrm { K E } ^ { \prime } + \mathrm { K } ^ { \prime } \mathrm { E } - \mathrm { K } \mathrm { K } ^ { \prime } = \frac { \pi } { 2 } \;\;\;\;\; ( 13 ) $$

انتگرال‌های بیضوی $$ \mathrm { K } $$ و $$ \mathrm { E} $$ به عنوان توابعی از مشخصه $$ k$$ با معادلات زیر به هم مربوط می‌شوند:

$$ \large \begin {aligned}
\frac { d \mathrm { E } } { d k } & = \frac { 1 } { k }( \mathrm { E } - \mathrm { K } ) \quad \quad \quad \quad \quad \quad (14)\\
\frac { d \mathrm { K } } { d k } & = \frac { 1 }{ k \left ( k ^ { \prime } \right ) ^ { 2 } } \left [ \mathrm { E } -\left ( k ^ { \prime } \right ) ^ { 2 } \mathrm { K } \right ] \;\;\;\;\; ( 15 )
\end {aligned} $$

انتگرال‌های بیضوی ناقص نوع اول و دوم $$ \Large \mathrm { F } ( \phi , k ) $$ و $$ \Large \mathrm { E} ( \phi , k ) $$

به سادگی می‌توان یک انتگرال بیضوی را که مکرراً با آن سر و کار داریم و $$ \mathrm { E } $$ و $$ \mathrm { F } $$ را به هم مربوط می‌کند معرفی کرد.

$$ \large \mathrm { D } ( \phi , k ) = \int _ { 0 } ^ { \phi } \frac { \sin ^ { 2 } \theta } { \Delta } d \theta = \frac { \mathrm { F } - \mathrm { E } } { k ^ { 2 } } \;\;\;\;\; ( 16 )$$

که در آن:

$$ \large \Delta = \sqrt { 1 - k ^ 2 \sin ^ 2 \theta } \;\;\;\;\; ( 17 ) $$

بنابراین:

$$ \large \mathrm { F } = \mathrm { E} + k ^ 2 \mathrm { D}  \;\;\;\;\; ( 18 ) $$

سایر انتگرال‌های ناقصی که با $$ \mathrm { D}$$، $$\mathrm { E}$$ و $$ \mathrm { F}$$ توصیف می‌شوند، به صورت زیر هستند:

$$ \large \begin {aligned}
\int _ { 0 } ^ { \phi } \frac { \cos ^ { 2 } \theta } { \Delta } d \theta & = \mathrm { F } - \mathrm { D } \quad \quad (19) \\
\int _ { 0 } ^ { \phi } \frac { \tan ^ { 2 } \theta } { \Delta } d \theta & = \frac { \Delta \tan \phi - \mathrm { E } }{ \left ( k ^ { \prime } \right ) ^ { 2 } } \quad \quad (20) \\
\int _ { 0 } ^ { \phi } \frac { d \theta } { \Delta \cos ^ { 2 } \theta } & = \frac { \Delta \tan \phi + k ^ { 2 } ( \mathrm { D } - \mathrm {F } ) } { \left ( k ^ { \prime } \right ) ^ { 2 } } \quad \quad (21) \\
\int _ { 0 } ^ { \phi } \frac { \sin ^ { 2 } \theta } { \Delta \cos ^ { 2 } \theta } & = \frac { \mathrm { F } - \mathrm { D } } { \left ( k ^ { \prime } \right ) ^ { 2 } } - \frac { \sin \phi \cos \phi } { \left ( k ^ { \prime } \right ) ^ { 2 } \Delta } \quad \quad (22) \\
\int _ { 0 } ^ { \phi } \frac { \cos ^ { 2 } \theta }{ \Delta ^ { 2 } } d \theta & = \mathrm { D } + \frac { \sin \phi \cos \phi } { \Delta } \quad \quad (23) \\
\int _ { 0 } ^ { \phi } \Delta \tan ^ { 2 } \theta d \theta & = \Delta \tan \phi + \mathrm { F } - 2 \mathrm { E } \quad \quad (24) \end {aligned} $$

مقادیر خاص انتگرال‌های بیضوی

برخی از مقادیر خاص و عددی انتگرال‌های بیضوی به صورت زیر هستند:

$$ \large \begin {aligned}
\mathrm { E } ( 0 , k ) & = 0 \quad \quad (25) \\
\mathrm { F } ( 0 , k ) & = 0 \quad \quad (26) \\
\pi \left ( 0 , \alpha ^ { 2 } , k \right ) & = 0 \quad \quad (-\alpha ^ 2 = n ) \quad \quad (27) \\
\mathrm { E } ( \phi , k ) & = \phi \quad \quad (28) \\
\mathrm { F } ( \phi , k ) & = \phi \quad \quad (29) \\
\end {aligned} $$

$$ \large \begin {aligned}
\pi \left ( \phi , \alpha ^ { 2 } , 0 \right ) & = \phi \quad ( \text { if } n = 0 ) \quad \quad (30) \\
& = \frac { \arctan ( \sqrt { \left ( 1 - \alpha ^ { 2 } \right ) } \tan \phi ) } { \sqrt { 1 - \alpha ^ { 2 } } } , \quad \text { if } \alpha ^ { 2 } < 1 \quad \quad (31) \\
& = \frac { \operatorname {arctanh}( \sqrt { \left ( \alpha ^ { 2 } - 1 \right ) } \tan \phi ) } { \sqrt { \alpha ^ { 2 } - 1 } } , \quad \text { if } \alpha ^ { 2 } > 1 \quad \quad (32)
\end {aligned} $$

$$ \large \begin {aligned}
\mathrm { K } ( 0 ) & = \mathrm { K } ^ { \prime } ( 1 ) = \pi / 2 \qquad (33)\\
\mathrm { E } ( 0 ) & = \mathrm { E } ^ { \prime } ( 1 ) = \pi / 2 \qquad (34) \\
\mathrm { E } ( \phi , 1 ) & = \sin \phi \qquad (35)\\
\mathrm { F } ( \phi , 1) & = \ln ( \tan \phi + \sec \phi ) \qquad (36) \end {aligned} $$

$$ \large \begin {aligned}
\mathrm { F } \left ( \phi , \mathrm { \alpha } ^ { 2 } , 1 \right ) & = \frac { 1 } { 1 - \alpha ^ { 2 } } [ \ln ( \tan \phi + \sec \phi ) - \alpha \ln \sqrt { \frac { 1 + \alpha \sin \phi } { 1 -\alpha \sin \phi } } ] \qquad (37) \\
& \quad \quad \quad \quad \quad \quad \quad \begin {array} {l}
{ \quad } & { \quad \text { if } \alpha ^ { 2 } > 0 }, \; \alpha ^ 2 \neq 1
\end {array} \\
& = \frac { 1 } { 1 - \alpha ^ { 2 } } [ \ln ( \tan \phi+\sec \phi ) + | \alpha | \arctan ( | \alpha | \sin \phi ) ] \\
& \quad \quad \quad \quad \quad \quad \quad \begin {array} {l}
{ \quad } & { \quad \text { if } \alpha ^ { 2 } < 0 }
\end {array}
\end{aligned} $$

مشتق و انتگرال نسبت به مشخصه $$ \LARGE k $$

مشتق و انتگرال انتگرال‌ بیضوی نسبت به مشخصه $$k$$ به صورت زیر است:

$$ \large \begin {aligned}
\frac { \partial \mathrm { F } } { \partial k } & = \frac { k }{ \left ( k ^ { \prime } \right ) ^ { 2 } } \left [ \mathrm { F } -\mathrm { D } - \frac { \sin \phi \cos \phi } { \Delta } \right ] \quad \quad ( 38 ) \\
\frac { \partial \mathrm { E } } { \partial k } & = - k \mathrm { D } \quad \quad ( 39 ) \\
\frac { \partial \mathrm { D } } { \partial k } & = \frac { 1 }{ k \left ( k ^ { \prime } \right ) ^ { 2 } } \left [ \mathrm { F }( \phi , k ) - \mathrm { D } ( \phi , k ) - \frac { \sin \phi \cos \phi } { \Delta } - \frac { \mathrm { D } ( \phi , k ) } { k } \right ] \quad \quad ( 40 ) \\
\int \mathrm { F } k d k & = \mathrm { E } ( \phi , k ) - \left ( k ^ { \prime } \right ) \mathrm { F } ( \phi , k ) - ( 1 - \Delta ) \operatorname {cotan} \phi \quad \quad ( 41 ) \\
\int \mathrm { D } k d k & = - \mathrm { E } ( \phi , k ) \quad \quad ( 42 ) \\
\int \mathrm { E } k d k & = \frac { 1 } { 3 } \left ( 1 + k ^ { 2 } \right ) \mathbf { E } ( \phi , k ) -\left ( k ^ { \prime } \right ) ^ { 2 } \mathrm { F } ( \phi , k ) - ( 1 - \Delta ) \operatorname {cotan} \phi \quad \quad ( 43 )
\end {aligned} $$

توابع بیضوی

چندین نوع تابع بیضوی شامل توابع بیضوی «وایرشتراس» (Weierstrass) و توابع تتا وجود دارند، اما رایج‌ترین توابع بیضوی توابع بیضوی ژاکوبی، مبتنی بر معکوس سه نوع انتگرال بیضوی هستند.

توابع بیضوی ژاکوبی

سه فرم استاندارد انتگرال‌های بیضوی ژاکوبی با $$ s n ( u , k ) $$، $$ c n ( u , k ) $$ و $$ d n ( u , k ) $$ مشخص می‌شوند و به ترتیب، توابع بیضوی دامنه سینوس، کسینوس و دلتا هستند. این توابع با معکوس کردن انتگرال بیضوی نوع اول به دست می‌آیند:

$$ \large u = F ( \phi , k ) = \int _ { 0 } ^ { \phi } \frac { d \theta } { \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \theta } } \quad \quad (44)$$

که در آن، $$ 0 < k ^ 2 < 1 $$ است و $$ k $$ به مشخصه بیضوی $$ u$$ اطلاق می‌شود. همچنین، $$ \phi $$ کران بالای انتگرال بیضوی است و دامنه ژاکوبی ($$ amp$$) نام دارد.

معکوس انتگرال بیضوی منجر به رابطه زیر می‌شود:‌

$$ \large \phi = \mathrm { F } ^ { - 1 } ( \mathrm { u } , \mathrm { k } ) = amp ( \mathrm { u } , \mathrm { k } ) \;\;\;\;\; ( 45) $$

و با استفاده از این رابطه، می‌توان نوشت:

$$ \large \begin {aligned}
\sin \phi & = \sin ( a m p ( u , k ) ) = s n ( u , k ) \quad \quad (46) \\
\cos \phi & = \cos ( { a m p } ( u , k ) ) = c n ( u , k ) \quad \quad (47) \\
\sqrt { 1 - k ^ { 2 } \sin ^ { 2 } \phi } & = \sqrt { 1 - k ^ { 2 } \sin ^ { 2 } ( a m p ( u , k ) ) } = d n ( u , k ) \quad \quad (48) \end {aligned} $$

این توابع تعمیم‌های دوره‌ای مضاعف از توابع مثلثاتی هستند که در روابط زیر صدق می‌کنند:

$$ \large \begin {array} { l }
{ s n ( u , 0 ) = \sin u } \quad \quad (49) \\
{ { c n } ( u , 0 ) = \cos u } \quad \quad (50) \\
{ d n ( u , 0 ) = 1 } \quad \quad (51)
\end {array} $$

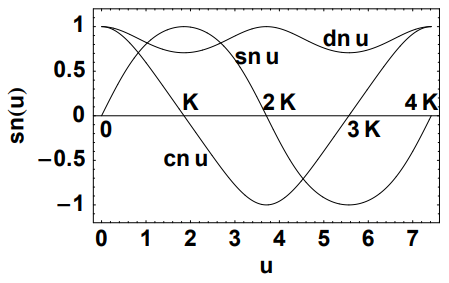
در کل، ۱۲ تابع بیضوی ژاکوبی وجود دارد که ۹ تای باقیمانده را می‌توان به سه تایی که داریم، مرتبط کرد:

$$ \large \begin {aligned}
\operatorname { cd } ( u ) & = \frac { \operatorname { cn }( u ) } { \operatorname { dn } ( u ) } & \operatorname { dc }( u ) & = \frac { \operatorname { dn } ( u ) } { \operatorname { cn } ( u ) } & \operatorname { ns } ( u ) & = \frac { 1 }{ \operatorname { sn } ( u ) } \\
\operatorname { sd } ( u ) & = \frac { \operatorname { sn } ( u ) } { \operatorname { dn } ( u ) } & \operatorname { nc } ( u ) & = \frac { 1 } { \operatorname { cn } ( u ) } & \operatorname { ds } ( u ) & = \frac { \operatorname { dn } ( u ) } { \operatorname { sn } ( u ) } \\
\operatorname { nd } ( u ) & = \frac { 1 } { \operatorname { dn } ( u) } & \operatorname { sc } ( u ) & = \frac { \operatorname { sn } ( u ) } { \operatorname { cn } ( u ) } & \operatorname { cs } (u ) & = \frac { \operatorname { cn } ( u ) } { \operatorname { sn } ( u ) }
\end {aligned} $$

توابع بیضوی وایرشتراس

تفاوت اصلی بین انتگرال‌های بیضوی ژاکوبی و وایرشتراس، در تعداد قطب‌های هر سلول پایه است. در حالی که تابع بیضوی ژاکوبی دو قطب ساده در هر سلول دارد، و می‌توان آن را به عنوان یک جواب برای معادله دیفرانسیل زیر در نظر گرفت:

$$ \large \frac { d ^ { 2 } x } { d t ^ { 2 } } = A + B x + C x ^ { 2 } + D x ^ { 3 } $$

تابع بیضوی وایرشتراس یک قطب دوگانه دارد و جواب معادله زیر است:‌

$$ \large \frac { d ^ { 2 } x } { d t ^ { 2 } } = A + B x + C x ^ { 2 } $$

توابع تتا

توابع تتا مشابه‌هایی برای تابع نمایی هستند و معمولاً به صورت $$ \theta _ a ( u , q ) $$ نوشته می‌شوند که در آن، $$ a $$ از $$ 1 $$ تا $$ 4 $$ تغییر می‌کند. در نمایش چهار تابع تتا، $$ u$$ نیز آرگومان تابع است و $$ q $$ نوم (Nome) است که به صورت زیر تعریف می‌شود:

$$ \large q = e ^ { i \pi t } = e ^ { \pi \mathrm {K}' / \mathrm { K } } \;\;\;\;\;\; ( 52)$$

که در آن:

$$ \large t = - i \frac { \mathrm {K}' ( k ) }{\mathrm {K} ( k )} $$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضی عمومی ۲
• مجموعه آموزش‌های محاسبات عددی
• آموزش روش‌های عددی کامپیوتری در مهندسی به همراه پیاده‌سازی عملی در میپل
• مانده تابع — به زبان ساده
• رسم تابع چگالی احتمال دو بعدی با پایتون — راهنمای کاربردی
• انتگرال توابع گنگ — از صفر تا صد

^^