الگوریتم کد گذاری هافمن (Huffman Coding) — به زبان ساده

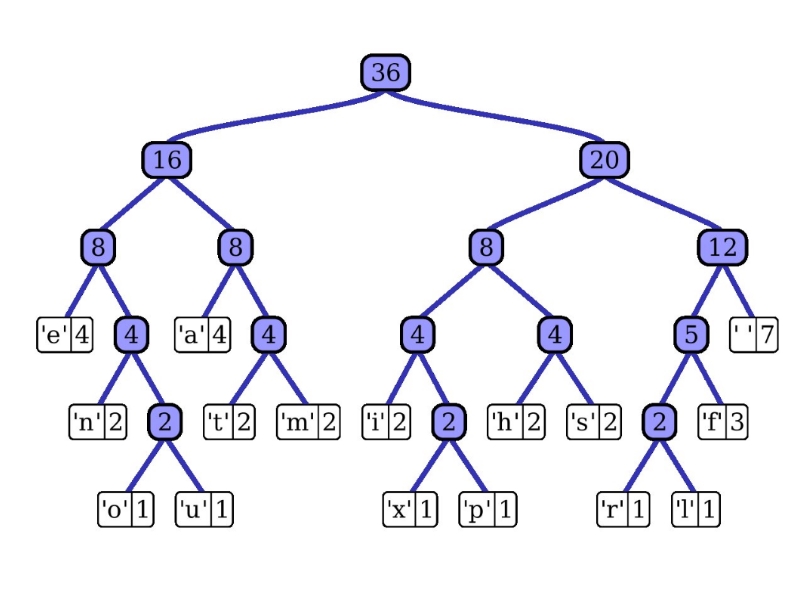
در این مطلب، الگوریتم هافمن (Huffman Algorithm) مورد بررسی قرار خواهد گرفت. همچنین، پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C و «جاوا» (Java) ارائه شده است. «کد هافمن» (Huffman Code) نوع خاصی از «کدهای پیشوندی» (Prefix Codes) بهینه است که اغلب برای فشرده‌سازی بی‌اتلاف اطلاعات مورد استفاده قرار می‌گیرد. فرایند پیدا کردن یا استفاده از این کد به وسیله کدگذاری هافمن (Huffman coding)، با بهره‌گیری از الگوریتمی انجام می‌شود که توسط «دیوید آ هافمن» (David A. Huffman) توسعه داده شده است.

کدهای پیشوندی نوعی از کدها (توالی بیت‌ها) هستند که در آن‌ها کد اختصاص داده شده به یک کاراکتر پیشوند کد تخصیص داده شده به هیچ کاراکتر دیگری نیست. این، روشی است که کدگذاری هافمن با استفاده از آن اطمینان حاصل می‌کند که هیچ ابهامی هنگام رمزگشایی توالی بیت‌های (جریان بیت) تولید شده وجود نخواهد داشت. در ادامه، برای درک بهتر موضوع، مثالی ارائه شده است. فرض می‌شود که چهار کاراکتر c ،b ،a و d موجود هستند و کدهای طول متغیر متناظر با آن‌ها به ترتیب ۰۰، ۰۱، ۰ و ۱ است. این کدگذاری موجب ابهام می‌شود زیرا کد تخصیص یافته به c، پیشوند کدهای تخصیص یافته به a و b است. اگر جریان رشته فشرده شده ۰۰۰۱ است، خروجی که از حالت فشرده خارج شود امکان دارد cccd یا ccb یا acd یا ab باشد. دو بخش اصلی مهم در کدگذاری هافمن وجود دارد:

1. ساخت درخت هافمن از کاراکترهای ورودی
2. پیمایش درخت هافمن و تخصیص کد به کاراکترها

مراحل ساخت درخت هافمن

در اینجا، ورودی آرایه‌ای از کاراکترهای یکتا با تکرار وقوع هر یک و خروجی یک «درخت هافمن» (درخت هافمن) است:

فیلم آموزش طراحی الگوریتم در فرادرس

کلیک کنید

1. یک گره برگ برای هر کاراکتر یکتا بساز و همچنین، «هرم کمینه» (Min Heap) از همه گره‌های برگ را بساز (هرم کمینه به عنوان صف اولویت استفاده می‌شود. مقدار فیلد تکرار برای مقایسه دو گره در هرم کمینه مورد استفاده قرار می‌گیرد. به طور اولیه، کاراکتری با کمترین تکرار در ریشه است).
2. دو گره با حداقل تکرار از هرم کمینه را استخراج کن.
3. یک گره داخلی با فرکانسی برابر با مجموع تکرارهای دو گره را بساز. اولین گره استخراج شده را به عنوان فرزند سمت چپ و دیگر گره استخراج شده را به عنوان گره سمت راست قرار بده. این گره را به هرم کمینه اضافه کن.
4. گام‌های ۲ و ۳ را تا هنگامی که هرم تنها حاوی یک گره باشد تکرار کن. گره باقی‌مانده، گره ریشه و درخت کامل است.

در ادامه، برای درک بهتر موضوع، یک مثال بیان شده است.

character   Frequency
    a            5
    b           9
    c           12
    d           13
    e           16
    f           45

گام ۱: یک هرم کمینه بساز که شامل ۶ گره است و هر گره، نشانگر ریشه درخت با یک گره یکتا است.

گام ۲: دو گره با کمترین تکرار را از درخت کمینه استخراج کن. گره داخلی جدید با تکرار ۱۴ = ۹ + ۵ را اضافه کن.

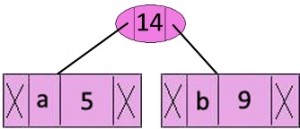
اکنون، هرم کمینه حاوی ۵ گره است که ۴ گره، هر یک با یک عنصر مجرد، ریشه‌های درخت‌ها هستند و یک گره هرم نیز ریشه درخت با ۳ عنصر است.

character           Frequency
       c               12
       d               13
 Internal Node         14
       e               16
       f                45

گام ۳: دو گره کمینه را از هرم استخراج کن. یک گره داخلی جدید با تکرار ۲۵ = ۱۲ + ۱۳ را اضافه کن.

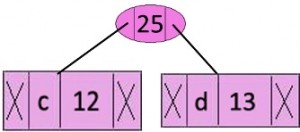
اکنون، هرم کمینه حاوی ۴ گره است که دو گره هر یک با تنها یک عنصر ریشه‌های درخت‌ها هستند و دو گره هرم با بیش از یک گره، ریشه درخت هستند.

character           Frequency
Internal Node          14
       e               16
Internal Node          25
       f               45

گام ۴: دو گره با کمترین تکرار را از هرم استخراج کن. یک گره داخلی جدید با تکرار ۳۰ = ۱۶ + ۱۴ اضافه کن.

اکنون، هرم اصلی حاوی ۳ گره است.

character          Frequency
Internal Node         25
Internal Node         30
      f               45

گام ۵: دو گره با تکرار کمتر را استخراج کن. یک گره داخلی با تکرار ۵۵ = ۳۰ + ۲۵ را اضافه کن.

اکنون، هرم اصلی حاوی دو گره است.

character     Frequency
       f         45
Internal Node    55

گام ۶: دو گره با کمترین تکرار را استخراج کن. یک گره داخلی جدید با تکرار ۱۰۰ = ۵۵ + ۴۵ را اضافه کن.

اکنون، هرم کمینه تنها حاوی یک گره است.

character      Frequency
Internal Node    100

به دلیل آنکه هرم تنها حاوی یک گره است، الگوریتم در این مرحله متوقف می‌شود.

چاپ کدها از درخت هافمن

پیمایش درخت ساخته شده، از ریشه آغاز می‌شود. برای این کار، باید از یک آرایه کمکی استفاده شود. در این راستا، هنگامی که به فرزند سمت چپ حرکت می‌شود، ۰ باید در آرایه نوشته شود و در حالیکه به سمت فرزند سمت راست حرکت می‌شود، ۱ را باید در آرایه نوشت.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

آرایه را هنگامی که یک گره برگ مشاهده شد، چاپ کن.

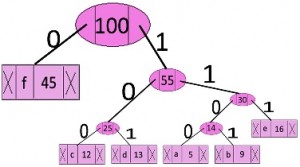
کدها به صورت زیر هستند:

character   code-word
    f          0
    c          100
    d          101
    a          1100
    b          1101
    e          111

در ادامه، پیاده‌سازی رویکرد بالا انجام شده است.

پیاده‌سازی الگوریتم هافمن در C

// C program for Huffman Coding 
#include <stdio.h> 
#include <stdlib.h> 
  
// This constant can be avoided by explicitly 
// calculating height of Huffman Tree 
#define MAX_TREE_HT 100 
  
// A Huffman tree node 
struct MinHeapNode { 
  
    // One of the input characters 
    char data; 
  
    // Frequency of the character 
    unsigned freq; 
  
    // Left and right child of this node 
    struct MinHeapNode *left, *right; 
}; 
  
// A Min Heap:  Collection of 
// min-heap (or Huffman tree) nodes 
struct MinHeap { 
  
    // Current size of min heap 
    unsigned size; 
  
    // capacity of min heap 
    unsigned capacity; 
  
    // Array of minheap node pointers 
    struct MinHeapNode** array; 
}; 
  
// A utility function allocate a new 
// min heap node with given character 
// and frequency of the character 
struct MinHeapNode* newNode(char data, unsigned freq) 
{ 
    struct MinHeapNode* temp 
        = (struct MinHeapNode*)malloc
(sizeof(struct MinHeapNode)); 
  
    temp->left = temp->right = NULL; 
    temp->data = data; 
    temp->freq = freq; 
  
    return temp; 
} 
  
// A utility function to create 
// a min heap of given capacity 
struct MinHeap* createMinHeap(unsigned capacity) 
  
{ 
  
    struct MinHeap* minHeap 
        = (struct MinHeap*)malloc(sizeof(struct MinHeap)); 
  
    // current size is 0 
    minHeap->size = 0; 
  
    minHeap->capacity = capacity; 
  
    minHeap->array 
        = (struct MinHeapNode**)malloc(minHeap-> 
capacity * sizeof(struct MinHeapNode*)); 
    return minHeap; 
} 
  
// A utility function to 
// swap two min heap nodes 
void swapMinHeapNode(struct MinHeapNode** a, 
                     struct MinHeapNode** b) 
  
{ 
  
    struct MinHeapNode* t = *a; 
    *a = *b; 
    *b = t; 
} 
  
// The standard minHeapify function. 
void minHeapify(struct MinHeap* minHeap, int idx) 
  
{ 
  
    int smallest = idx; 
    int left = 2 * idx + 1; 
    int right = 2 * idx + 2; 
  
    if (left < minHeap->size && minHeap->array[left]-> 
freq < minHeap->array[smallest]->freq) 
        smallest = left; 
  
    if (right < minHeap->size && minHeap->array[right]-> 
freq < minHeap->array[smallest]->freq) 
        smallest = right; 
  
    if (smallest != idx) { 
        swapMinHeapNode(&minHeap->array[smallest], 
                        &minHeap->array[idx]); 
        minHeapify(minHeap, smallest); 
    } 
} 
  
// A utility function to check 
// if size of heap is 1 or not 
int isSizeOne(struct MinHeap* minHeap) 
{ 
  
    return (minHeap->size == 1); 
} 
  
// A standard function to extract 
// minimum value node from heap 
struct MinHeapNode* extractMin(struct MinHeap* minHeap) 
  
{ 
  
    struct MinHeapNode* temp = minHeap->array[0]; 
    minHeap->array[0] 
        = minHeap->array[minHeap->size - 1]; 
  
    --minHeap->size; 
    minHeapify(minHeap, 0); 
  
    return temp; 
} 
  
// A utility function to insert 
// a new node to Min Heap 
void insertMinHeap(struct MinHeap* minHeap, 
                   struct MinHeapNode* minHeapNode) 
  
{ 
  
    ++minHeap->size; 
    int i = minHeap->size - 1; 
  
    while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) { 
  
        minHeap->array[i] = minHeap->array[(i - 1) / 2]; 
        i = (i - 1) / 2; 
    } 
  
    minHeap->array[i] = minHeapNode; 
} 
  
// A standard function to build min heap 
void buildMinHeap(struct MinHeap* minHeap) 
  
{ 
  
    int n = minHeap->size - 1; 
    int i; 
  
    for (i = (n - 1) / 2; i >= 0; --i) 
        minHeapify(minHeap, i); 
} 
  
// A utility function to print an array of size n 
void printArr(int arr[], int n) 
{ 
    int i; 
    for (i = 0; i < n; ++i) 
        printf("%d", arr[i]); 
  
    printf("\n"); 
} 
  
// Utility function to check if this node is leaf 
int isLeaf(struct MinHeapNode* root) 
  
{ 
  
    return !(root->left) && !(root->right); 
} 
  
// Creates a min heap of capacity 
// equal to size and inserts all character of 
// data[] in min heap. Initially size of 
// min heap is equal to capacity 
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) 
  
{ 
  
    struct MinHeap* minHeap = createMinHeap(size); 
  
    for (int i = 0; i < size; ++i) 
        minHeap->array[i] = newNode(data[i], freq[i]); 
  
    minHeap->size = size; 
    buildMinHeap(minHeap); 
  
    return minHeap; 
} 
  
// The main function that builds Huffman tree 
struct MinHeapNode* buildHuffmanTree(char data[], int freq[], int size) 
  
{ 
    struct MinHeapNode *left, *right, *top; 
  
    // Step 1: Create a min heap of capacity 
    // equal to size.  Initially, there are 
    // modes equal to size. 
    struct MinHeap* minHeap = createAndBuildMinHeap(data, freq, size); 
  
    // Iterate while size of heap doesn't become 1 
    while (!isSizeOne(minHeap)) { 
  
        // Step 2: Extract the two minimum 
        // freq items from min heap 
        left = extractMin(minHeap); 
        right = extractMin(minHeap); 
  
        // Step 3:  Create a new internal 
        // node with frequency equal to the 
        // sum of the two nodes frequencies. 
        // Make the two extracted node as 
        // left and right children of this new node. 
        // Add this node to the min heap 
        // '$' is a special value for internal nodes, not used 
        top = newNode('$', left->freq + right->freq); 
  
        top->left = left; 
        top->right = right; 
  
        insertMinHeap(minHeap, top); 
    } 
  
    // Step 4: The remaining node is the 
    // root node and the tree is complete. 
    return extractMin(minHeap); 
} 
  
// Prints huffman codes from the root of Huffman Tree. 
// It uses arr[] to store codes 
void printCodes(struct MinHeapNode* root, int arr[], int top) 
  
{ 
  
    // Assign 0 to left edge and recur 
    if (root->left) { 
  
        arr[top] = 0; 
        printCodes(root->left, arr, top + 1); 
    } 
  
    // Assign 1 to right edge and recur 
    if (root->right) { 
  
        arr[top] = 1; 
        printCodes(root->right, arr, top + 1); 
    } 
  
    // If this is a leaf node, then 
    // it contains one of the input 
    // characters, print the character 
    // and its code from arr[] 
    if (isLeaf(root)) { 
  
        printf("%c: ", root->data); 
        printArr(arr, top); 
    } 
} 
  
// The main function that builds a 
// Huffman Tree and print codes by traversing 
// the built Huffman Tree 
void HuffmanCodes(char data[], int freq[], int size) 
  
{ 
    // Construct Huffman Tree 
    struct MinHeapNode* root 
        = buildHuffmanTree(data, freq, size); 
  
    // Print Huffman codes using 
    // the Huffman tree built above 
    int arr[MAX_TREE_HT], top = 0; 
  
    printCodes(root, arr, top); 
} 
  
// Driver program to test above functions 
int main() 
{ 
  
    char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' }; 
    int freq[] = { 5, 9, 12, 13, 16, 45 }; 
  
    int size = sizeof(arr) / sizeof(arr[0]); 
  
    HuffmanCodes(arr, freq, size); 
  
    return 0; 
}

پیاده‌سازی الگوریتم هافمن در ++C

// C++ program for Huffman Coding 
#include <iostream> 
#include <cstdlib> 
using namespace std; 
  
// This constant can be avoided by explicitly 
// calculating height of Huffman Tree 
#define MAX_TREE_HT 100 
  
// A Huffman tree node 
struct MinHeapNode { 
  
    // One of the input characters 
    char data; 
  
    // Frequency of the character 
    unsigned freq; 
  
    // Left and right child of this node 
    struct MinHeapNode *left, *right; 
}; 
  
// A Min Heap: Collection of 
// min-heap (or Huffman tree) nodes 
struct MinHeap { 
  
    // Current size of min heap 
    unsigned size; 
  
    // capacity of min heap 
    unsigned capacity; 
  
    // Attay of minheap node pointers 
    struct MinHeapNode** array; 
}; 
  
// A utility function allocate a new 
// min heap node with given character 
// and frequency of the character 
struct MinHeapNode* newNode(char data, unsigned freq) 
{ 
    struct MinHeapNode* temp 
        = (struct MinHeapNode*)malloc
(sizeof(struct MinHeapNode)); 
  
    temp->left = temp->right = NULL; 
    temp->data = data; 
    temp->freq = freq; 
  
    return temp; 
} 
  
// A utility function to create 
// a min heap of given capacity 
struct MinHeap* createMinHeap(unsigned capacity) 
  
{ 
  
    struct MinHeap* minHeap 
        = (struct MinHeap*)malloc(sizeof(struct MinHeap)); 
  
    // current size is 0 
    minHeap->size = 0; 
  
    minHeap->capacity = capacity; 
  
    minHeap->array 
        = (struct MinHeapNode**)malloc(minHeap-> 
capacity * sizeof(struct MinHeapNode*)); 
    return minHeap; 
} 
  
// A utility function to 
// swap two min heap nodes 
void swapMinHeapNode(struct MinHeapNode** a, 
                    struct MinHeapNode** b) 
  
{ 
  
    struct MinHeapNode* t = *a; 
    *a = *b; 
    *b = t; 
} 
  
// The standard minHeapify function. 
void minHeapify(struct MinHeap* minHeap, int idx) 
  
{ 
  
    int smallest = idx; 
    int left = 2 * idx + 1; 
    int right = 2 * idx + 2; 
  
    if (left < minHeap->size && minHeap->array[left]-> 
freq < minHeap->array[smallest]->freq) 
        smallest = left; 
  
    if (right < minHeap->size && minHeap->array[right]-> 
freq < minHeap->array[smallest]->freq) 
        smallest = right; 
  
    if (smallest != idx) { 
        swapMinHeapNode(&minHeap->array[smallest], 
                        &minHeap->array[idx]); 
        minHeapify(minHeap, smallest); 
    } 
} 
  
// A utility function to check 
// if size of heap is 1 or not 
int isSizeOne(struct MinHeap* minHeap) 
{ 
  
    return (minHeap->size == 1); 
} 
  
// A standard function to extract 
// minimum value node from heap 
struct MinHeapNode* extractMin(struct MinHeap* minHeap) 
  
{ 
  
    struct MinHeapNode* temp = minHeap->array[0]; 
    minHeap->array[0] 
        = minHeap->array[minHeap->size - 1]; 
  
    --minHeap->size; 
    minHeapify(minHeap, 0); 
  
    return temp; 
} 
  
// A utility function to insert 
// a new node to Min Heap 
void insertMinHeap(struct MinHeap* minHeap, 
                struct MinHeapNode* minHeapNode) 
  
{ 
  
    ++minHeap->size; 
    int i = minHeap->size - 1; 
  
    while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) { 
  
        minHeap->array[i] = minHeap->array[(i - 1) / 2]; 
        i = (i - 1) / 2; 
    } 
  
    minHeap->array[i] = minHeapNode; 
} 
  
// A standard function to build min heap 
void buildMinHeap(struct MinHeap* minHeap) 
  
{ 
  
    int n = minHeap->size - 1; 
    int i; 
  
    for (i = (n - 1) / 2; i >= 0; --i) 
        minHeapify(minHeap, i); 
} 
  
// A utility function to print an array of size n 
void printArr(int arr[], int n) 
{ 
    int i; 
    for (i = 0; i < n; ++i) 
        cout<< arr[i]; 
  
    cout<<"\n"; 
} 
  
// Utility function to check if this node is leaf 
int isLeaf(struct MinHeapNode* root) 
  
{ 
  
    return !(root->left) && !(root->right); 
} 
  
// Creates a min heap of capacity 
// equal to size and inserts all character of 
// data[] in min heap. Initially size of 
// min heap is equal to capacity 
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) 
  
{ 
  
    struct MinHeap* minHeap = createMinHeap(size); 
  
    for (int i = 0; i < size; ++i) 
        minHeap->array[i] = newNode(data[i], freq[i]); 
  
    minHeap->size = size; 
    buildMinHeap(minHeap); 
  
    return minHeap; 
} 
  
// The main function that builds Huffman tree 
struct MinHeapNode* buildHuffmanTree(char data[], int freq[], int size) 
  
{ 
    struct MinHeapNode *left, *right, *top; 
  
    // Step 1: Create a min heap of capacity 
    // equal to size. Initially, there are 
    // modes equal to size. 
    struct MinHeap* minHeap = createAndBuildMinHeap(data, freq, size); 
  
    // Iterate while size of heap doesn't become 1 
    while (!isSizeOne(minHeap)) { 
  
        // Step 2: Extract the two minimum 
        // freq items from min heap 
        left = extractMin(minHeap); 
        right = extractMin(minHeap); 
  
        // Step 3: Create a new internal 
        // node with frequency equal to the 
        // sum of the two nodes frequencies. 
        // Make the two extracted node as 
        // left and right children of this new node. 
        // Add this node to the min heap 
        // '$' is a special value for internal nodes, not used 
        top = newNode('$', left->freq + right->freq); 
  
        top->left = left; 
        top->right = right; 
  
        insertMinHeap(minHeap, top); 
    } 
  
    // Step 4: The remaining node is the 
    // root node and the tree is complete. 
    return extractMin(minHeap); 
} 
  
// Prints huffman codes from the root of Huffman Tree. 
// It uses arr[] to store codes 
void printCodes(struct MinHeapNode* root, int arr[], int top) 
  
{ 
  
    // Assign 0 to left edge and recur 
    if (root->left) { 
  
        arr[top] = 0; 
        printCodes(root->left, arr, top + 1); 
    } 
  
    // Assign 1 to right edge and recur 
    if (root->right) { 
  
        arr[top] = 1; 
        printCodes(root->right, arr, top + 1); 
    } 
  
    // If this is a leaf node, then 
    // it contains one of the input 
    // characters, print the character 
    // and its code from arr[] 
    if (isLeaf(root)) { 
  
        cout<< root->data <<": "; 
        printArr(arr, top); 
    } 
} 
  
// The main function that builds a 
// Huffman Tree and print codes by traversing 
// the built Huffman Tree 
void HuffmanCodes(char data[], int freq[], int size) 
  
{ 
    // Construct Huffman Tree 
    struct MinHeapNode* root 
        = buildHuffmanTree(data, freq, size); 
  
    // Print Huffman codes using 
    // the Huffman tree built above 
    int arr[MAX_TREE_HT], top = 0; 
  
    printCodes(root, arr, top); 
} 
  
// Driver program to test above functions 
int main() 
{ 
  
    char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' }; 
    int freq[] = { 5, 9, 12, 13, 16, 45 }; 
  
    int size = sizeof(arr) / sizeof(arr[0]); 
  
    HuffmanCodes(arr, freq, size); 
  
    return 0; 
}

پیاده‌سازی الگوریتم هافمن در ++C با استفاده از STL

// C++ program for Huffman Coding 
#include <bits/stdc++.h> 
using namespace std; 
  
// A Huffman tree node 
struct MinHeapNode { 
  
    // One of the input characters 
    char data; 
  
    // Frequency of the character 
    unsigned freq; 
  
    // Left and right child 
    MinHeapNode *left, *right; 
  
    MinHeapNode(char data, unsigned freq) 
  
    { 
  
        left = right = NULL; 
        this->data = data; 
        this->freq = freq; 
    } 
}; 
  
// For comparison of 
// two heap nodes (needed in min heap) 
struct compare { 
  
    bool operator()(MinHeapNode* l, MinHeapNode* r) 
  
    { 
        return (l->freq > r->freq); 
    } 
}; 
  
// Prints huffman codes from 
// the root of Huffman Tree. 
void printCodes(struct MinHeapNode* root, string str) 
{ 
  
    if (!root) 
        return; 
  
    if (root->data != '$') 
        cout << root->data << ": " << str << "\n"; 
  
    printCodes(root->left, str + "0"); 
    printCodes(root->right, str + "1"); 
} 
  
// The main function that builds a Huffman Tree and 
// print codes by traversing the built Huffman Tree 
void HuffmanCodes(char data[], int freq[], int size) 
{ 
    struct MinHeapNode *left, *right, *top; 
  
    // Create a min heap & inserts all characters of data[] 
    priority_queue<MinHeapNode*, vector<MinHeapNode*>, compare> minHeap; 
  
    for (int i = 0; i < size; ++i) 
        minHeap.push(new MinHeapNode(data[i], freq[i])); 
  
    // Iterate while size of heap doesn't become 1 
    while (minHeap.size() != 1) { 
  
        // Extract the two minimum 
        // freq items from min heap 
        left = minHeap.top(); 
        minHeap.pop(); 
  
        right = minHeap.top(); 
        minHeap.pop(); 
  
        // Create a new internal node with 
        // frequency equal to the sum of the 
        // two nodes frequencies. Make the 
        // two extracted node as left and right children 
        // of this new node. Add this node 
        // to the min heap '$' is a special value 
        // for internal nodes, not used 
        top = new MinHeapNode('$', left->freq + right->freq); 
  
        top->left = left; 
        top->right = right; 
  
        minHeap.push(top); 
    } 
  
    // Print Huffman codes using 
    // the Huffman tree built above 
    printCodes(minHeap.top(), ""); 
} 
  
// Driver program to test above functions 
int main() 
{ 
  
    char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' }; 
    int freq[] = { 5, 9, 12, 13, 16, 45 }; 
  
    int size = sizeof(arr) / sizeof(arr[0]); 
  
    HuffmanCodes(arr, freq, size); 
  
    return 0; 
} 
  
// This code is contributed by Aditya Goel

پیاده‌سازی الگوریتم هافمن در جاوا

edit
play_arrow

brightness_4
import java.util.PriorityQueue; 
import java.util.Scanner; 
import java.util.Comparator; 
  
// node class is the basic structure 
// of each node present in the Huffman - tree. 
class HuffmanNode { 
  
    int data; 
    char c; 
  
    HuffmanNode left; 
    HuffmanNode right; 
} 
  
// comparator class helps to compare the node 
// on the basis of one of its attribute. 
// Here we will be compared 
// on the basis of data values of the nodes. 
class MyComparator implements Comparator<HuffmanNode> { 
    public int compare(HuffmanNode x, HuffmanNode y) 
    { 
  
        return x.data - y.data; 
    } 
} 
  
public class Huffman { 
  
    // recursive function to print the 
    // huffman-code through the tree traversal. 
    // Here s is the huffman - code generated. 
    public static void printCode(HuffmanNode root, String s) 
    { 
  
        // base case; if the left and right are null 
        // then its a leaf node and we print 
        // the code s generated by traversing the tree. 
        if (root.left 
                == null
            && root.right 
                   == null
            && Character.isLetter(root.c)) { 
  
            // c is the character in the node 
            System.out.println(root.c + ":" + s); 
  
            return; 
        } 
  
        // if we go to left then add "0" to the code. 
        // if we go to the right add"1" to the code. 
  
        // recursive calls for left and 
        // right sub-tree of the generated tree. 
        printCode(root.left, s + "0"); 
        printCode(root.right, s + "1"); 
    } 
  
    // main function 
    public static void main(String[] args) 
    { 
  
        Scanner s = new Scanner(System.in); 
  
        // number of characters. 
        int n = 6; 
        char[] charArray = { 'a', 'b', 'c', 'd', 'e', 'f' }; 
        int[] charfreq = { 5, 9, 12, 13, 16, 45 }; 
  
        // creating a priority queue q. 
        // makes a min-priority queue(min-heap). 
        PriorityQueue<HuffmanNode> q 
            = new PriorityQueue<HuffmanNode>(n, new MyComparator()); 
  
        for (int i = 0; i < n; i++) { 
  
            // creating a Huffman node object 
            // and add it to the priority queue. 
            HuffmanNode hn = new HuffmanNode(); 
  
            hn.c = charArray[i]; 
            hn.data = charfreq[i]; 
  
            hn.left = null; 
            hn.right = null; 
  
            // add functions adds 
            // the huffman node to the queue. 
            q.add(hn); 
        } 
  
        // create a root node 
        HuffmanNode root = null; 
  
        // Here we will extract the two minimum value 
        // from the heap each time until 
        // its size reduces to 1, extract until 
        // all the nodes are extracted. 
        while (q.size() > 1) { 
  
            // first min extract. 
            HuffmanNode x = q.peek(); 
            q.poll(); 
  
            // second min extarct. 
            HuffmanNode y = q.peek(); 
            q.poll(); 
  
            // new node f which is equal 
            HuffmanNode f = new HuffmanNode(); 
  
            // to the sum of the frequency of the two nodes 
            // assigning values to the f node. 
            f.data = x.data + y.data; 
            f.c = '-'; 
  
            // first extracted node as left child. 
            f.left = x; 
  
            // second extracted node as the right child. 
            f.right = y; 
  
            // marking the f node as the root node. 
            root = f; 
  
            // add this node to the priority-queue. 
            q.add(f); 
        } 
  
        // print the codes by traversing the tree 
        printCode(root, ""); 
    } 
} 
  
// This code is contributed by Kunwar Desh Deepak Singh

خروجی قطعه کدهای بالا به صورت زیر است.

f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111

پیچیدگی زمانی روش ارائه شده از درجه (O(nlogn است که در آن، n تعداد کاراکترهای یکتا محسوب می‌شود. اگر n گره وجود داشته باشد، ()extractMin به تعداد $$2*(n – 1)$$ مرتبه فراخوانی می‌شود.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم در فرادرس

کلیک کنید

()extractMin از درجه (O(logn است، زیرا ()minHeapify را فراخوانی می‌کند. بنابراین، پیچیدگی کلی از درجه (O(nlogn خواهد بود. اگر آرایه ورودی مرتب شده باشد، الگوریتم دارای پیچیدگی زمانی خطی می‌شود.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• برنامه تجزیه عدد به عوامل اول آن — به زبان ساده

^^