مجموعه باز و بسته در ریاضیات – به زبان ساده

مفهوم مجموعه‌ (Set) و خواص آن یکی از مباحث پایه در ریاضیات محسوب می‌شود. در ریاضیات جدید، همه چیز با مجموعه آغاز شده و مفاهیم و اصول به همراه قضیه‌های ریاضی، مرتبط با مجموعه‌ها هستند. در این نوشتار به نوع خاصی از مجموعه‌ها به نام مجموعه باز و بسته در ریاضیات خواهیم پرداخت. البته هر کجا احتیاج به توضیحات مقدماتی باشد، آن را شرح داده سپس ارتباطش را با مجموعه باز و بسته بیان خواهیم کرد.

برای درک بعضی از اصطلاحات مطرح شده در این متن بهتر است نوشتارهای فضای متریک و نامساوی مثلثی — به زبان ساده و مجموعه ها در ریاضیات – مفاهیم پایه را مطالعه کنید. همچنین خواندن فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی  نیز خالی از لطف نیست.

مجموعه باز و بسته در ریاضیات

مجموعه‌ها به عنوان رکن اصلی در ریاضیات جدید محسوب می‌شوند. با توجه به تعداد اعضای یک مجموعه، آن‌ها را به مجموعه‌های متناهی و نامتناهی تقسیم‌بندی می‌کنند. زمانی که با مجموعه‌های نامتناهی سروکار داریم، لازم است رفتار و خصوصیات آن‌ها را بهتر بشناسیم زیرا به همه اعضای آن دسترسی نداریم.

فیلم آموزش مبانی آنالیز ریاضی در فرادرس

کلیک کنید

دنباله‌ها (Series) می‌توانند یک مجموعه نامتناهی ایجاد کنند. برای مثال مقادیر مربوط به دنباله یا تصاعد حسابی زیر، یک مجموعه نامتناهی می‌سازند که با جمله عمومی آن دنباله مشخص می‌شود.

$$\large a_{n+1}=a_1+n\times d$$

که در آن با در نظر گرفتن $$a_1=3$$ و $$d=2$$ خواهیم داشت.

$$\large \{3,5,7,9,\ldots\}$$

مشخص است که این دنباله مربوط به مجموعه اعداد فرد است. در مبحث مجموعه باز و بسته، بیشتر از آنکه به اعضای مجموعه‌ها توجه کنیم، به فاصله و ارتباط بین اعضای یک مجموعه تمرکز خواهیم داشت. در دنباله بالا، فاصله هر دو عضو دنباله هم، برابر با $$d=2$$ است. بنابراین بهتر است تعریف و معرفی عناصر مجموعه و همچنین شیوه اندازه‌گیری فاصله بین اعضای مجموعه را مرور کنیم.

مجموعه و تعریف آن

برای مشخص کردن یک مجموعه می‌توان اعضای آن را معرفی کرد. به طور رسمی مجموعه به صورت زیر تعریف می‌شود.

مجموعه: گردایه‌ای از اشیاء که اعضای آن قابل تعیین باشد، یک مجموعه نامیده می‌شود. مجموعه‌ها با حروف بزرگ لاتین مانند A, B مشخص می‌شوند.

معرفی یک مجموعه متناهی به کمک اعضای آن ممکن است به سادگی صورت گیرد ولی زمانی که تعداد اعضای یک مجموعه نامتناهی (شمارش‌پذیر یا شمارش‌ناپذیر) باشد، دیگر معرفی آن به کمک مشخص کردن اعضای آن کار ساز نیست. به همین دلیل قاعده یا قانون عضویت برای تعریف چنین مجموعه‌هایی به کار می‌رود. در مثالی که برای اعداد دنباله یا تصاعد حسابی آوردیم، قانون عضویت را برای نشان دادن اعضای این مجموع معرفی کرده و براساس آن اعضا را ایجاد کردیم. از آنجایی که مجموعه باز و بسته نیز ممکن است دارای بی‌شمار عضو باشند، تعیین قاعده عضویت برای آن‌ها لازم است.

برای مجموعه‌ها، عملیاتی نظیر اجتماع، اشتراک و تفاضل، همچنین متمم‌گیری نسبت به مجموعه مرجع وجود دارد که برای آشنایی با آن‌ها بهتر است نوشتار اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده را مطالعه کنید.

فضای متریک و خصوصیات آن

مجموعه $$S$$ را در نظر بگیرید. اگر تابع $$d$$ روی این مجموعه به شکلی تعیین شود که روابط زیر برقرار باشد، آنگاه تابع $$d$$ را یک تابع فاصله روی مجموعه $$S$$ می‌نامند.

$$\large d(x,x)=0, \;\;\; d(x,y)=d(x,y), \;\;\; d(x,y)+d(x,z)\geq d(x,z), \;\;\;\forall x,y,z \in S$$

رابطه ۱

به دو تایی $$(S,f)$$ در این حالت فضای متریک (Metric Space) گفته می‌شود.

برای مثال مجموعه اعداد حقیقی (Real Numbers Set) و تابع قدرمطلق (Absolute Value Function) یک فضای متریک می‌سازد.

همچنین مجموعه $$n$$ بعدی از اعداد حقیقی $$R^n$$ و فاصله اقلیدسی (Euclidean Distance) نیز یک فضای متریک ایجاد می‌کنند. به این ترتیب می‌توان علاوه بر جایگاه هر یک از نقاط در این مجموعه، فاصله هر دو نقطه از آن را نیز اندازه‌گیری کرد.

آخرین قسمت در رابطه ۱، مربوط به نامساوی مثلثی است. اگر تابع فاصله $$f$$ در این رابطه صدق نکند، به آن تابع شبه متر و فضای حاصل را شبه متریک (SemiMetric) می‌گویند.

فاصله باز و بسته

برای هر دو عدد $$a, b \in R$$ با شرط $$a<b$$ فاصله بسته را به صورت زیر تعریف می‌کنند.

$$\large [a,b] = \{x \in R, a\leq x \leq b\}$$

همانطور که می‌بینید، فاصله بسته به صورت یک مجموعه معرفی شده است. واضح است که دو مقدار ابتدایی و انتهایی این فاصله یعنی $$a$$ و $$b$$ در فاصله بسته قرار دارند.

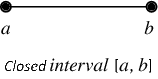
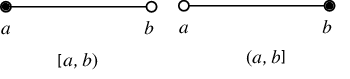
اگر نقاط ابتدا و انتهایی (نقاط مرزی یا Boundary Points) این فاصله را از آن حذف کنیم، فاصله باز $$a$$ تا $$b$$ حاصل خواهد شد که آن را به صورت زیر نمایش می‌دهند.

$$\large (a,b) = \{x \in R, a< x < b\}$$

برای مثال فاصله بسته از ۰ تا ۱ بوسیله $$[0,1]$$ و فاصله باز به شکل $$(0,1)$$‌ مشخص می‌شود. توجه داشته باشید که گاهی برای نمایش فاصله باز از نماد $$]a,b[$$ نیز کمک می‌گیرند.

نکته: ممکن است فاصله‌ها به صورت باز-بسته یا بسته-باز هم معرفی شوند. در این حالت داریم:

$$\large (a,b] = \{x \in R, a< x \leq b\}$$

و

$$\large [a,b) = \{x \in R, a\leq x < b\}$$

برای مثال فاصله $$[0,1)$$ و $$[0,1)$$ به این صورت نوشته می‌شوند.

همسایگی و شعاع همسایگی

یک نقطه یا عضوی از مجموعه $$S$$ را با نام $$x$$ در نظر بگیرد. نقاطی از مجموعه $$S$$ که حول نقطه $$x$$ قرار دارند، یک همسایگی از آن محسوب می‌شوند.

فیلم آموزش مبانی توپولوژی عمومی در فرادرس

کلیک کنید

فرض کنید حداکثر فاصله نقاط همسایگی حول نقطه $$x$$ برابر با $$\delta$$ باشد. در این صورت می‌توانیم مجموعه نقاط همسایگی حول نقطه $$x$$ را به صورت زیر معرفی کنیم.

$$\large N_{\delta}(x)=\{y \in S, d(x,y)< \delta\}$$

در این حالت $$\delta>0$$ را شعاع همسایگی و $$x$$ را مرکز همسایگی می‌نامند.

مثال

قبلا اشاره کردیم که مجموعه اعداد حقیقی و فاصله قدرمطلق (اقلیدسی) یک فضای متریک تشکیل می‌دهند. همسایگی حول نقطه $$x$$ از اعداد حقیقی با شعاع همسایگی $$\delta=0.001$$ به صورت زیر نمایش داده می‌شود.

$$\large N_{\delta}(x)=\{y \in R, |x-y|)< 0.001\}$$

که می‌توان آن را به صورت زیر مشخص کرد.

$$\large N_{0.001}(x)=(x-0.001, x+0.001)$$

با در نظر گرفتن $$x=0$$ خواهیم داشت:

$$\large N_{0.001}(0)=(-0.001, 0.001)$$

که آن را فاصله باز از 0٫001- تا 0٫001 می‌شناسیم.

همانطور که مشاهده کردید، فاصله باز در مجموعه اعداد حقیقی را می‌توان به صورت یک همسایگی در نظر گرفت که مرکز آن $$x$$ و با شعاع $$\delta$$ تشکیل دهیم. واضح است که در اینجا تابع فاصله، قدر مطلق یا تابع فاصله اقلیدسی است. از طرفی نقاط مرزی یا حدی یعنی $$x+\delta$$ و $$x-\delta$$ در فاصله باز، قرار ندارند.

$$\large N_{\delta}(x)=\{y \in R, |x-y|<\delta\}\equiv (x-\delta,x+\delta) $$

رابطه ۲

پس با توجه به رابطه ۲ فاصله (a,b) را می‌توان به شکل یک همسایگی به مرکز x و به شعاع $$\delta$$ نوشت. این نحوه نمایش را در ادامه شرح می‌دهیم.

برای تبدیل فاصله به همسایگی، شعاع همسایگی به صورت زیر محاسبه می‌شود.

$$\large \delta = \frac{b-a}{2}$$

از طرفی برای بدست آوردن مرکز همسایگی نیز از رابطه ۲ کمک گرفته و می‌نویسیم:

$$\large x = \frac{(a+b)}{2}$$

حال بازه را می‌توانیم به صورت یک همسایگی بیان کنیم.

$$\large (x-\delta,x+\delta)\equiv N_{\delta}(x)=\{y \in R, |x-y|<\delta\} $$

مثال: فاصله (1,5) را به صورت یک همسایگی نشان می‌دهیم. از آنجایی که فاصله نقطه ابتدایی و انتهایی برابر با 4 است، شعاع همسایگی را نصف این فاصله در نظر می‌گیریم. یعنی $$\delta=\frac{4}{2}=2$$ خواهد بود. همچنین نقطه مرکزی هم به شکل $$x=\frac{1+5}{2}=3$$ حاصل می‌شود. در نتیجه خواهیم داشت:

$$\large (1,5)\equiv N_{2}(3)=\{y \in R, |3-y|<2\} $$

به این ترتیب فاصله‌های باز $$(-\infty,a)$$ و $$(a,+\infty)$$ فاصله‌های باز تلقی می‌شوند. واضح است که در این حالت $$\delta$$ بی‌نهایت است.

نکته: مفهوم همسایگی نه تنها برای مجموعه اعداد حقیقی و ابعاد بالاتر آن به کار می‌رود بلکه برای مجموعه‌های متناهی و گسسته نیز کاربرد دارد. در نظریه شبکه‌ و گراف نیز مفهوم همسایگی یا مجاورت برای گره یا راس با این مفهوم قابل مقایسه است.

مجموعه باز و بسته

با توجه به تعریفی که برای فاصله باز و بسته روی مجموعه اعداد حقیقی گفتیم، می‌توانیم مجموعه‌های باز و بسته را هم معرفی کنیم. کافی است که تابع فاصله مناسب و همسایگی دلخواهی برای اعضای مجموعه‌ها را مشخص کرده باشیم.

تعریف مجموعه باز:  مجموعه $$A$$ که زیر مجموعه $$S$$ از فضای متریک $$(S,d)$$ محسوب می‌شود، یک مجموعه باز است اگر برای هر نقطه‌ای مثل $$x$$ در آن، رابطه زیر برقرار باشد:

$$\large \forall x \in A: \exists \delta>0; N_{\delta}(x) \subseteq A$$

رابطه ۳

به مجموعه‌های باز در فضاهای $$n$$ بُعدی، «گوی باز» (Open Ball) نیز می‌گویند. در تصویر زیر یک گوی باز یا دیسک باز را در فضای دو بعُدی مشاهده می‌کنید.

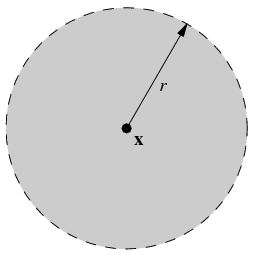
به این ترتیب می‌توانیم در مجموعه اعداد حقیقی و متر فاصله اقلیدسی، فاصله‌های باز را به صورت مجموعه باز در نظر بگیریم.

مثال: مجموعه یا بازه $$(-3,3)$$ یک مجموعه باز خواهد بود زیرا در این حالت برای هر $$x\in (-3,3)$$ داریم:

$$\large -3<x<3, \;\;\;x\in N_{3}(0)\subseteq (-3,3)$$

بطور کلی می‌توان تمامی فاصله‌های باز در مجموعه اعداد حقیقی را یک مجموعه باز در نظر گرفت.

$$\large (a,b)=\{x\in R, a<x<b\}, \text{ are open set.}$$

نکته: می‌توان نشان داد که قضیه‌های زیر برای مجموعه‌های باز برقرار است:

• اجتماع مجموعه‌های باز، یک مجموعه باز خواهد بود.
• اشتراک متناهی از مجموعه‌های باز، باز خواهد بود.

اگر گفته شود مجموعه $$A$$ باز نیست به این معنی است که نقطه‌ای در $$A$$ وجود دارد که هیچکدام از همسایگی‌های آن، زیر مجموعه $$A$$ نیست. این عبارت به بیان ریاضی به صورت زیر نوشته می‌شود.

$$\large \text{A is not open set}: \sim \left( \forall x \in A, \;\exists \delta >0;\;\;N_{\delta}(a) \subseteq A\right)$$

اگر نقیض ($$\sim$$) را به این عبارت اثر دهیم، خواهیم داشت:

$$\large \text{A is not open set}: \exists a^* \in A, \;\forall \delta >0;\;\;N_{\delta}(a^*) \not\subseteq A$$

مثال: مجموعه یا فاصله بسته $$[-3,3]$$ یک مجموعه باز نیست. زیرا برای نقطه‌ای مثل ۳ در این فاصله، می‌توان یک همسایگی هر چند کوچک در نظر گرفت که نقاط همسایگی مربوط به آن، در مجموعه $$A$$‌ نباشد.

بطور کلی می‌توان گفت، تمامی مجموعه‌هایی از اعداد حقیقی که به شکل فاصله‌های باز-بسته یا بسته-باز هستند، یک مجموعه باز نخواهند بود. به این ترتیب مشخص است که اعضای یک مجموعه باز، همگی نقاط داخلی (Interior) هستند و شامل نقاط مرزی نیستند.

تعریف مجموعه بسته: مجموعه‌ای که متمم آن باز باشد، یک مجموعه بسته نامیده می‌شود. بنابراین مجموعه $$A$$ را بسته گویند اگر $$\bar{A}$$ باز باشد.

مثال: مجموعه یا فاصله بسته $$[-3,3]$$ یک مجموعه بسته است، زیرا متمم‌ این مجموعه به صورت فاصله‌های $$(-\infty,3)\cup(3,\infty)$$ خواهد بود.

با توجه به اینکه اجتماع دو مجموعه باز، یک مجموعه باز است، پس نتیجه می‌گیریم که متمم آن یعنی $$[-3,3]$$ یک مجموعه بسته است. پس می‌توان گفت که اعضای مجموعه بسته، شامل نقاط مرزی نیز هست.

نکته: می‌توان نشان داد که قضیه‌های زیر برای مجموعه‌های بسته برقرار است:

• اشتراک مجموعه‌های بسته، یک مجموعه بسته خواهد بود.
• اجتماع متناهی از مجموعه‌های بسته، یک مجموعه بسته می‌سازد.

نکته: مجموعه تهی $$\varnothing$$ در فضای متریک اعداد حقیقی، هم بسته و هم باز است. باز است زیرا دارای هیچ عضوی نیست که بتوانیم همسایگی اطراف آن در نظر بگیریم. در نتیجه مقدم گزاره شرطی در رابطه ۳، غلط بوده، در نتیجه کل رابطه شرطی صحیح خواهد بود. از طرفی متمم مجموعه تهی نیز در این فضا، مجموعه اعداد حقیقی است. که یک مجموعه باز است. ولی از آنجایی که متمم آن نیز باز است، می‌توان آن را یک مجموعه بسته در نظر گرفت. همچنین چون متمم مجموعه اعداد حقیقی که یک مجموعه باز است، تشکیل مجموعه تهی را می‌دهد، نتیجه می‌گیریم که تهی یک مجموعه بسته است. این رابطه‌ها نشان می‌دهد که مجموعه تهی و اعداد حقیقی در فضای متریک اعداد حقیقی، هم باز و هم بسته هستند. چنین مجموعه‌هایی را بازبسته (Clopen) می‌نامند. در تصویر زیر گرافی را مشاهده می‌کنید که هر یک از بخش‌های سه تایی از آن بازبسته (Clopen) هستند.

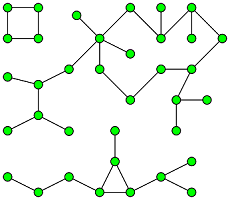
مجموعه نه بسته و نه باز: با توجه به تعریفی که برای مجموعه‌های بسته و باز ارائه شد، می‌توان مجموعه‌هایی مثال زد که نه بسته هستند و نه باز.

مثال: فاصله $$[0,3)$$ نه مجموعه باز است و نه مجموعه بسته. واضح است که این مجموعه باز نیست، زیرا نقطه صفر در این مجموعه است ولی همسایگی‌های نقطه صفر در این بازه قرار ندارد.

ولی برای بسته بودن آن باید نشان دهیم که متمم آن یک مجموعه باز است. می‌دانیم که متمم این بازه به صورت $$(-\infty,0)\cup [3,\infty)$$ است. نقطه ۳ را در نظر بگیرید، حداقل یک همسایگی حول نقطه ۳ وجود دارد که در این مجموعه نیست. برای مثال همسایگی از نقطه ۳ به شعاع ۲، شامل نقطه ۱٫۵ است که در این بازه قرار ندارد. پس متمم فاصله $$[0,3)$$ باز نیست، در نتیجه، این بازه بسته هم نخواهد بود.

نکته: با توجه به این مثال می‌توان دید که یک مجموعه ممکن است نه باز باشد و نه بسته. در نتیجه مجموعه‌های باز و بسته، فضای متریک را افراز نمی‌کنند.

مثال: فاصله‌های $$(0,\infty)$$ و $$(-\infty,0)$$ هر دو باز هستند. زیرا هر همسایگی از نقاط درون این فاصله‌ها، درون این مجموعه قرار دارد. از طرفی فاصله‌های $$[0,\infty)$$ و $$(-\infty,0]$$ بسته هستند زیرا متمم آن‌ها باز خواهند بود.

خواص مجموعه باز و بسته

همانطور که در قبل نیز اشاره شد، قضیه‌های مربوط به اجتماع و اشتراک مجموعه‌های باز و بسته وجود دارد در این قسمت می‌خواهیم به اثبات آن‌ها بپردازیم.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل تست کنکور ارشد – بخش دوم در فرادرس

کلیک کنید

قضیه ۱: اجتماع مجموعه‌های باز، باز خواهد بود.

اثبات: فرض کنید کلاس مجموعه‌های $$\{U_n\}$$ از مجموعه‌های باز تشکیل شده است. $$U$$ را اجتماع چنین مجموعه‌هایی بنامید.

$$\large U=\cup U_n$$

عضوی از مجموعه $$U$$ مثل $$x$$ را در نظر بگیرید. مطمئن هستیم که این عضو باید در یکی از مجموعه‌های $$U_n$$ باشد. از آنجایی که $$U_n$$ها، مجموعه‌های باز هستند، همسایگی حول $$x$$ وجود دارد که زیر مجموعه $$U_n$$ است.

از آنجای که $$U$$ از اجتماع $$U_n$$ها تشکیل شده، واضح است که $$x$$ در $$U$$ بوده و هر همسایگی از آن چون در $$U_n$$ قرار دارد، پس در $$U$$ نیز قرار خواهد داشت. در نتیجه $$U$$ یا اجتماع مجموعه‌های باز، باز خواهد بود.

قضیه ۲: اشتراک مجموعه‌های بسته، بسته است.

اثبات: $$I$$ را اشتراک مجموعه‌های بسته $$I_n$$ در نظر بگیرید. در نتیجه داریم:

$$\large I = \cap I_n$$

باید نشان دهیم که متمم مجموعه $$I$$، یک مجموعه باز است.

$$\large \bar{I}= \cup \bar{I}_n$$

از آنجایی که $$I_n$$ها، مجموعه‌های بسته هستند، متمم آن‌ها یعنی $$\bar{I}$$ها هم باز خواهند بود. طبق قضیه قبل اجتماع مجموعه‌های باز، باز است. در نتیجه اشتراک مجموعه‌های بسته نیز بسته می‌باشد. توجه داشته باشید که در این میان از قضیه دمورگان برای متمم اشتراک مجموعه‌ها استفاده کرده‌ایم.

قضیه ۳:اشتراک متناهی از مجموعه‌های باز، باز است.

اثبات: $$U_n$$ها را دنباله‌ای متناهی از مجموعه‌های باز در نظر بگیرید که در آن $$n=1,2,\ldots,N$$ است. اشتراک آن‌ها به صورت زیر خواهد بود.

$$U^*=\cap_{i=1}^N U_n$$

یکی از اعضای مجموعه $$U^*$$ مثلا $$x$$ را در نظر بگیرید. از آنجایی که $$x$$‌ در اشتراک این مجموعه‌ها قرار دارد، پس در همه آن‌ها نیز خواهد بود.

$$x$$ در مجموعه $$U_1$$ است در نتیجه یک $$\delta_1>0$$ همسایگی حول $$x$$ وجود دارد که زیر مجموعه $$U_1$$‌ است.

$$x$$ در مجموعه $$U_2$$ است در نتیجه یک $$\delta_2>0$$ همسایگی حول $$x$$  وجود دارد که زیر مجموعه $$U_2$$‌ است.

...

$$x$$ در مجموعه $$U_N$$ است در نتیجه یک $$\delta_N>0$$ همسایگی حول $$x$$ وجود دارد که زیر مجموعه $$U_N$$‌ است.

پس اگر $$\delta^*$$ را برابر با کمینه مقادیر $$\delta_n, n=1,2,\ldots,N$$ در نظر بگیریم، می‌توانیم همسایگی حول $$x$$ با شعاع $$\delta^*$$ پیدا بکنیم که در هر یک از $$U_n$$ باشد.

$$\large \delta^*=\min(\delta_1,\delta_2,\ldots,\delta_N)$$

از آنجایی که $$x$$ را اختیاری انتخاب کردیم، پس می‌توانیم برای هر عضوی از اشتراک متناهی از مجموعه‌های باز، با مقدار شعاع همسایگی $$\delta^*$$، زیر مجموعه‌ای از $$U^*$$ پیدا کنیم. پس اشتراک متناهی از مجموعه‌های باز، باز خواهد بود.

قضیه ۴: اجتماع متناهی از مجموعه‌های بسته، بسته است.

اثبات: با توجه به قانون دمورگان، توسط قضیه ۳، اثبات کامل می‌شود.

خلاصه و جمع‌بندی

در این نوشتار با همسایگی و فاصله‌های باز و بسته آشنا شدیم. این موضوعات به درک مفهوم مجموعه باز و بسته کمک می‌کند. همانطور که مشاهده کردید، مجموعه باز و بسته می‌توانند یک دنباله یا سری را نشان دهند. در ادامه این سلسله مباحث به توپولوژی و مجموعه‌های کامل (Perfect Set) و فشرده (Compact Set) خواهیم پرداخت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش مبانی آنالیز حقیقی
• مجموعه آموزش های نگارش مقاله، پایان نامه و نشریه علمی
• تقسیم عدد صحیح — به زبان ساده
• الگوریتم تقسیم اعداد — از صفر تا صد
• قواعد بخش پذیری یا عاد کردن — به زبان ساده

^^