فضای هیلبرت و خصوصیات آن – به زبان ساده

فضای هیلبرت (Hilbert Space) در حقیقت، حالت تعمیم یافته‌ای از «فضای اقلیدسی» (Euclidean Space) است. به این ترتیب جبر بردارها (Vector Algebra) از فضای دو و سه بعُدی به ابعاد متناهی و حتی نامتناهی سوق داده می‌شوند. در این نوشتار به فضای هیلبرت و خصوصیات آن پرداخته، ویژگی و کاربردهای آن را مورد بررسی قرار خواهیم داد.

به عنوان مقدمه موضوع مورد بحث، بهتر است با خواندن نوشتارهای فضای توپولوژیک در ریاضیات — به زبان ساده و فضای متریک و نامساوی مثلثی — به زبان ساده با اصطلاحات به کار رفته در این مطلب آشنا شوید. همچنین مطالعه تانسور چیست؟ — مفاهیم اصلی و دستگاه مختصات دکارتی — به زبان ساده نیز خالی از لطف نیست.

فضای هیلبرت و خصوصیات آن

در ریاضیات و فیزیک، «فضای هیلبرت» (Hilbert Space) کاربردهای فراوانی دارد، بخصوص در «فضاهای تابعی بی‌نهایت-بُعد» (Infinite-dimensional Function Spaces) فضای هیلبرت نقش اساسی ایفا می‌کند.

مشخص است که ابتدایی‌ترین فضاهای هیلبرت، توسط «دیوید هیلبرت» (David Hilbert) و «ارهارد اشمیت» (Erhard Schmidt) در اوایل قرن بیستم مطرح شدند. این فضاها، به عنوان ابزارهایی برای انجام محاسبات در حوزه‌های «معادلات دیفرانسیل جزئی» (Partial Differential Equations)، «مکانیک کوانتمی» (Quantum Mechanics)، «تحلیل فوریه» (Fourier Analysis) و «نظریه ارگودیک» (Ergodic Theory) به کار رفتند.

توصیف و شواهد هندسی در تئوری فضای هیلبرت نقش اساسی ایفا می‌کند. همچنین مشخص است که «قضیه فیثاغورث» (Pythagorean Theorem) و «قاعده متوازی الاضلاع» (Parallelogram Law) در فضای هیلبرت نیز صادق است.

از طرفی هر عنصر از فضای هیلبرت را می‌توان بر اساس مختصات آن روی محورها (پایه‌های متعامد نرمال- Orthonormal Basis) نشان داد. این موضوع درست شبیه «مختصات دکارتی» (Cartesian Coordinate) در فضای اقلیدسی است.

تعمیم فضای اقلیدسی

قبل از آنکه به فضای هیلبرت بپردازیم، ابتدا کمی در مورد فضای اقلیدسی صحبت می‌کنیم سپس تعریف ارائه شده را به فضای هیلبرت تعمیم می‌دهیم.

فضای برداری $$R^3$$ و ضرب داخلی (Inner Product) بردارها را در نظر بگیرید. فرض کنید $$\text{X}$$ و $$\text{Y}$$ دو بردار در این فضای سه بُعدی باشند. در این صورت ضرب داخلی یا همان ضرب نقطه‌ای (Dot Product) آن‌ها به صورت زیر نمایش داده می‌شود.

$$\large { \displaystyle { \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}} \cdot { \begin{pmatrix} y_{1} \\ y_{2} \\ y_{3} \end{pmatrix} } = x_{1} y_{1} + x_{2} y_{2} + x_{3} y_{3} \, }$$

واضح است که نتیجه ضرب نقطه‌ای دو بردار در چنین فضایی، یک عدد حقیقی است. ضرب داخلی یا نقطه‌ای دارای خصوصیات زیر است:

• ضرب نقطه‌ای، متقارن است. در نتیجه داریم:

$$\large \text{X} \cdot \text{Y} = \text{Y} \cdot \text{X}$$

• ضرب داخلی نسبت به پارامتر اول آن یک رابطه خطی است. به این معنی که

$$\large (ax_1 + bx_2) \cdot \text{Y} = ax_1 \cdot \text{Y} + bx_2 \cdot \text{Y}$$

• ضرب داخلی، «معین مثبت» (Positive Definite) است. به این ترتیب خواهیم داشت:

$$\large \text{X} \cdot \text{X} \geq 0 , \text{ with equality } , \text{X}=0$$

بردارها و ضرب داخلی (ضرب نقطه‌ای) به این ترتیب یک فضای ضرب داخلی ایجاد می‌کنند. نکته‌ای که هندسه اقلیدسی و فضای ضرب داخلی را به یکدیگر پیوند می‌دهد، استفاده از طول (نرم) هر بردار است که به وسیله $$||X||$$ نشان داده می‌شود. به این ترتیب رابطه بین ضرب داخلی و اندازه هر بردار به صورت زیر خواهد بود.

$$\large {\displaystyle \mathbf {X} \cdot \mathbf {Y} =\|\mathbf {X} \|\,\|\mathbf {Y} \|\,\cos \theta \,.}$$

برای اطلاعات بیشتر در زمینه ضرب داخلی نوشتار ضرب داخلی بردارها — به زبان ساده را مطالعه کنید.

تعریف فضای هیلبرت

حسابان چند متغیره در فضای اقلیدسی برمبنای محاسبه حد (Limit) پایه‌ریزی شده است. دنباله ریاضی که براساس بردارهای $$X_n$$ ایجاد شده را در نظر بگیرید. برای نمایش این دنباله از رابطه زیر استفاده کرده ایم.

$$\large \sum _{n = 0}^{ \infty } \mathbf {x} _{n}$$

چنین دنباله‌ای را مطلقاً همگرا (Absolute Convergent) گوییم، اگر مجموع طول بردارها به صورت یک دنباله از اعداد حقیقی، همگرا باشد. به این معنی که رابطه زیر برای اندازه بردارها بررسی شود.

$$\large { \displaystyle \sum _{k=0}^{\infty } \| \mathbf {x} _{k} \|<\infty \,}$$

درست به مانند دنباله‌های عددی، یک دنباله از بردارها در صورتی که مطلقاً همگرا (Absolute Convergence) به یک بردار ثابت مثل $$L$$ باشد، همگرا خواهد بود. به این ترتیب طبق تعریف حد در فضای اقلیدسی خواهیم داشت:

$$\large { \displaystyle \left\| \mathbf {L} -\sum _{k=0}^{N} \mathbf {x} _{k} \right\| \to 0 \quad { \text{ as }} N \to \infty \,}$$

چنین ویژگی، نشانگر کامل بودن (Completeness) فضای اقلیدسی است. به این معنی که یک دنباله مطقا همگرا، به صورت عادی نیز همگرا است.

فضای هیلبرت معمولا روی مجموعه اعداد مختلط (Complex Numbers) و صفحات مختلط (Complex Plane) تعریف می‌شود. فرض کنید یک صفحه مختلط با نماد $$C$$ با تابع اندازه $$|z|$$ به صورت زیر تعریف شده است. در نظر داشته باشید که $$z$$ به صورت $$z = x + iy$$ یک عدد یا بردار مختلط است.

$$\large { \displaystyle | z |^{2} = z { \overline { z }} \,}$$

در اینجا منظور از $$\bar{z}$$ مزدوج مختلط عدد $$z$$ است.

با توجه به فضای اقلیدسی دو بُعدی می‌توانیم اندازه چنین برداری را به صورت زیر محاسبه کنیم.

$$\large { \displaystyle | z | = { \sqrt {x^{2} + y^{2}}}\ ,}$$

ضرب داخلی برای $$z$$ و $$w$$ که مقادیر یا بردارهای مختلط هستند، به صوت زیر حاصل می‌شود.

$$\large { \displaystyle \langle z, w \rangle = z { \overline {w} }\, }$$

واضح است که منظور از $$\overline{ w}$$‌، مزدوج مختلط $$w$$ است. به این ترتیب نتیجه ضرب داخلی این دو بردار یک عدد مختلط خواهد بود.

نکته: قسمت حقیقی این عدد مختلط، همان ضرب داخلی در فضای اقلیدسی دو بردار است که مربوط به قسمت حقیقی بردارهای مختلط هستند.

حال زمان آن رسیده است که فضای هیلبرت را تعریف کنیم. الگوی معرفی این فضا درست به مانند فضای اقلیدسی است.

تعریف فضای هیلبرت: با توجه به توضیحات داده شده، «فضای هیلبرت» (Hilbert Space)  که با نماد $$H$$ نشان داده می‌شود، یک فضای ضرب داخلی روی مجموعه اعداد حقیقی یا مختلط است که نسبت به تابع فاصله ایجاد شده از ضرب داخلی، یک فضای متریک کامل (Complete Metric Space) نیز هست.

در تعریف فضای هیلبرت دو نکته مشخص است. اول آن که این فضا حاصل از یک فضای ضرب داخلی است و دوم فضای هیلبرت یک فضای متریک کامل خواهد بود. در ادامه هر یک از ویژگی‌ها را بیشتر مورد تجزیه و تحلیل قرار می‌دهیم.

فضای ضرب داخلی و فضای هیلبرت

فضای هیلبرت، یک فضای ضرب داخلی است. به این ترتیب مشخص است که $$H$$ یک فضای برداری مختلط است که ضرب داخلی روی آن برای هر زوج از بردارها دارای خواص زیر است.

• ضرب داخلی یک عمل متقارن نسبت به مزدوج مختلط است. به این معنی که رابطه زیر بین دو بردار مختلط $$x$$ و $$y$$ و ضرب داخلی بین آن‌ها وجود دارد.

$$\large { \displaystyle \langle y , x \rangle = { \overline { \langle x,y \rangle } } \, }$$

• ضرب داخلی نسبت به اولین مولفه، دارای خاصیت خطی است. به این ترتیب برای دو عدد مختلط مثل $$a$$ و $$b$$ خواهیم داشت:

$$\large {\displaystyle \langle ax_{1} + bx_{2},y\rangle = a \langle x_{1},y \rangle + b \langle x_{2}, y \rangle \,}$$

• ضرب داخلی هر عنصر در خودش، معین مثبت (Positive Definite) است. به این معنی که رابطه زیر برقرار است.

$$\large { \displaystyle { \begin{cases} \langle x , x \rangle > 0 & x \neq 0 \\ \langle x , x \rangle = 0 & x = 0 \, \end{cases} } }$$

نکته: با در نظر گرفتن این ویژگی‌ها باز هم مشخص است که ضرب داخلی مختلط، یک ترکیب خطی مزدوج نسبت به مولفه دوم نیز هست.

$$\large { \displaystyle \langle x , ay_{1} + by_{2} \rangle = { \bar {a}} \langle x, y_{1} \rangle + { \bar {b}} \langle x,y_{2} \rangle \, }$$

باید توجه داشته باشید که فضای هیلبرت در مجموعه اعداد حقیقی یا بردارهای حقیقی نیز به همین شکل و ترتیب تعریف می‌شود. با این تفاوت که ضرب داخلی بردارها، مقادیر حقیقی و ترکیب خطی از هر دو مولفه اول و دوم است.

از طرفی تابع فاصله در این فضا بر حسب ضرب داخلی به صورت زیر تعریف می‌شود.

$$\large { \displaystyle d(x,y) = \|x - y \| = { \sqrt { \langle x - y ,x - y \rangle }} \,}$$

واضح است که چنین تابعی در نامساوی مثلثی صدق خواهد کرد در نتیجه، ضرب داخلی به این شکل، یک متر و فضای حاصل یک فضای متریک خواهد بود.

$$\large { \displaystyle d( x , z ) \leq d( x , y ) + d( y , z ) \,}$$

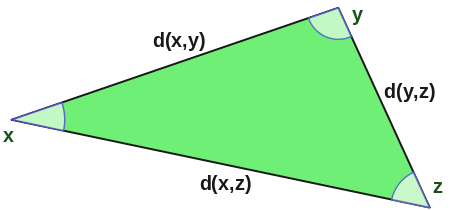
نکته: نامساوی مثلثی (Triangle Inequality) در فضای ضرب برداری ناشی از «نامساوی کوشی- شوارتز» (Cauchy-Schwarz Inequality) است که به صورت زیر بیان می‌شود. نامساوی کوشی- شوارتز  به شرط وجود وابستگی خطی بین $$x$$‌ و $$y$$ حاصل می‌شود.

$$\large { \displaystyle { \bigl | } \langle x , y \rangle { \bigr |}\leq \| x\ | \, \|y \| }$$

به توجه به تعریفی که از تابع فاصله (Distance Function) داریم، می‌توان هر فضای ضرب داخلی (Inner Product Space) را یک فضای متریک (Metric Space) نیز در نظر گرفت.

فضای کامل و فضای هیلبرت

کامل بودن فضای هیلبرت به کمک دنباله‌های کوشی (Cauchy Sequence) در این فضا مشخص می‌شود. دنباله‌ای از بردارهایی $$u_k$$ را در نظر بگیرید. دنباله کوشی حاصل از آن‌ها به شکل زیر است.

$$\large { \displaystyle \sum _{k = 0}^{ \infty } u_{k}}$$

کامل بودن در چنین فضای منجر به همگرایی مطلق (مطلقا همگرا) رابطه زیر است.

$$\large { \displaystyle \sum_{k = 0}^{ \infty } \| u_{k} \| < \infty \, }$$

نکته: در اینجا منظور از $$||u_k||$$، وابسته به ضرب داخلی بردار در مزدوج مختلطش یا نرم بردار $$u_k$$ است.

برای مثال فضای دنباله‌ای (Sequence Space) به صورت $$l^2$$ که شامل دنباله‌ای نامتناهی از اعداد مختلط است را به صورت $$z = (z_1 , z_2 ,\ldots )$$ در نظر بگیرید. دنباله‌ $$\sum _{n = 1}^{\infty }|z_{n}|^{2}$$ همگرا است.

ضرب داخلی در چنین فضایی به صورت زیر تعریف می‌شود.

$$\large { \displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle = \sum_{n = 1}^{\infty } z_{n}{ \overline {w_{n}}} \, }$$

با توجه به نامساوی کوشی-شوارتز، طرف راست تساوی بالا همگرا است. در نتیجه فضای $$l^2$$ حتی برای بردارهای مختلط نیز مطلقا همگرا بوده و به یکی از عناصر این فضا میل خواهد کرد. در نتیجه طبق تعریف فضای کامل، فضای $$l^2$$، یک فضای هیلبرت خواهد بود.

خصوصیات فضای هیلبرت

فضای برداری هیلبرت دارای خصوصیاتی است که در مجموعه اعداد حقیقی نیز وجود دارند. در ادامه به بعضی از این خصوصیات خواهیم پرداخت.

رابطه فیثاغورث در فضای هیلبرت

همانطور که می‌دانید رابطه فیثاغورث (Pythagorean identity) برای مثلث‌ها در فضای اعداد حقیقی به صورت زیر نوشته می‌شود:

$$\large a^2 + b^2 = c^2$$

حال دو بردار $$u$$ و $$v$$ را در فضای هیلبرت $$H$$ در نظر بگیرید که در آن $$\langle u , v \rangle = 0$$ است. به این معنی که این دو بردار در این فضا بر یکدیگر عمودند. در این حالت از نماد $$u \bot v$$ استفاده می‌کنیم.

در حالت عمومی‌تر زمانی که $$S$$ یک زیر فضای از $$H$$ باشد، نماد $$u \bot S$$ بیانگر آن است که بردار $$u$$ بر هر برداری از زیرفضای $$S$$ عمود است.

زمانی که دو بردار $$u$$ و $$v$$ بر هم عمودند، رابطه زیر برقرار خواهد بود.

$$\large { \displaystyle \|u + v\|^{2} = \langle u + v , u + v \rangle = \langle u , u \rangle + 2 \, \operatorname {Re} \langle u , v \rangle + \langle v , v \rangle =\|u\|^{2} + \|v\|^{2} }$$

می‌توان به کمک استقرا برای خانواده‌ای از $$n$$ بردار به صورت $$u_1 , \ldots , u_n$$ که بر یکدیگر عمودند، رابطه زیر را نوشت:

$$\large { \displaystyle \| u_{1} + \cdots + u_{n}\|^{2}=\|u_{1}\|^{2} + \cdots + \|u_{n}\|^{2}\,.} { \displaystyle \|u_{1 }+ \cdots +u_{n}\|^{2}}$$

ارتباط فضای هیلبرت و فضای باناخ

براساس تعریف، هر فضای هیلبرت، یک «فضای باناخ» (Banach Space) محسوب می‌شود. به این ترتیب تساوی مربوط به «قانون متوازی‌الاضلاع» (Parallelogram identity) نیز برقرار است. در هندسه اقلیدسی بین قطرهای یک متوازی‌الاضلاع رابطه زیر برقرار است.

$$\large AC^2 + BD^2 = 2(AB^2 + AD^2 )$$

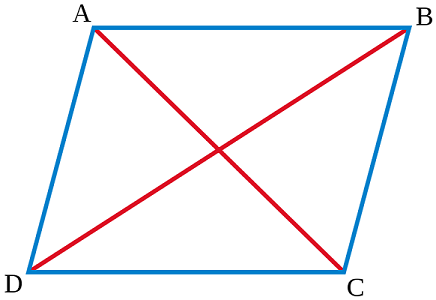
به بیان دیگر مجموع مربعات قطرهای یک متوازی الاصلاع با دو برابر مجموع مربعات دو ضلع مجاور برابر است.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

چنین رابطه‌ای نیز در فضای هیلبرت برقرار خواهد بود. به این ترتیب برای هر دو بردار $$u$$ و $$v$$ از فضای هیلبرت داریم:

$$\large { \displaystyle \|u+v\|^{2} + \|u-v\|^{2}=2\left(\|u\|^{2} + \|v\|^{2} \right)\,.}$$

و برعکس هر فضای باناخ که در نامساوی متوازی‌الاضلاع صدق کند، یک فضای هیلبرت خواهد بود و ضرب داخلی به شکل منحصر به فردی براساس نرم یک بردار نشان داده می‌شود.

در این حالت در فضاهای حقیقی هیلبرت رابطه زیر برای محاسبه ضرب داخلی دو بردار براساس اندازه یا نرم آن‌ها نوشته می‌شود.

$$\large { \displaystyle \langle u,v \rangle = { \frac {1}{4}} \left( \| u + v \|^{2 } - \|u - v\|^{2} \right)\,.}$$

و در فضاهای مختلط هیلبرت نیز این تساوی به صورت زیر خواهد بود.

$$\large { \displaystyle \langle u , v \rangle = { \tfrac {1}{4}} \left( \| u + v \|^{2}- \| u - v \|^{2} + i \| u + iv \|^{2} - i \| u - iv \|^{2}\right) \,.}$$

قانون متوازی الاضلاع نشان می‌دهد که هر فضای هیلبرت یک «فضای محدب یکنواخت باناخ» (Uniformly Convex Banach space) است.

کاربردهای فضای هیلبرت

بسیاری از کاربردهای فضای هیلبرت برگرفته از تعمیم خواص هندسی ساده در فضای اقلیدسی است. برای مثال «تصویر کردن» (Projection) و «تغییر پایه» (Change of Basis) در فضاهای با ابعاد متناهی به فضای هیلبرت از مواردی است که وسعت کاربردهای فضای هیلبرت را نشان می‌دهد.

چنین وضعیتی در سری یا «دنباله‌های هارمونیک» (Harmonic Series) و همچنین حل «معادلات دیفرانسیل معمولی»(Ordinary Differential Equations)  مورد توجه است. نظریه ارگودیک (Ergodic Theory) و تحلیل فوریه (Fourier Analysis) از دیگر مسائلی هستند که در آن‌ها از فضای هیلبرت استفاده می‌شود.

خلاصه و جمع‌بندی

در این نوشتار با تعریف فضای هیلبرت و خصوصیات آن آشنا شدید. همچنین ویژگی‌های این فضا و مقایسه آن با فضای اقلیدسی مورد بحث قرار گرفت. به این ترتیب مشخص است که فضای هیلبرت (با توجه به تعمیم فضای اقلیدسی) کاربردهای زیادی در ریاضیات و حتی زندگی روزمره خواهد داشت.