فیزیک ۱ – مفاهیم پایه به زبان ساده
فیزیک ۱ دانشگاه که با عنوان فیزیک پایه ۱ یا مکانیک کلاسیک نیز شناخته میشود، یکی از دروسی است که در اغلب رشتههای علوم پایه و مهندسی و در ترمهای اول یا دوم تدریس خواهد شد. همین مسئله نشان میدهد که یادگیری مفاهیم این درس تا چه اندازه در ادامه روند تحصیلی دانشجویان این رشتهها حائز اهمیت است. در این مطلب از مجله فرادرس تمام مفاهیم و سرفصلهای این درس را به زبانی ساده توضیح میدهیم.
- کلیات مباحث مطرح شده در فیزیک ۱ را خواهید شناخت.
- یاد میگیرید که سینماتیک خطی و دورانی چیست.
- با قوانین دینامیک در مکانیک کلاسیک آشنا خواهید شد.
- مفاهیمی مانند تکانه و انواع برخورد را خواهید آموخت.
- با سیستم ذرات و نحوه ارزیابی حرکت در چنین سیستمهایی آشنا خواهید شد.
- میآموزید که تعادل در استاتیک با چه شرطهایی ایجاد میشود.


مفاهیم پایه مطرح شده در فیزیک ۱ چه هستند؟
سرفصلهای فیزیک ۱ در اغلب کتابهای مرجع برای این درس بهصورت زیر فهرست میشوند:
- اندازهگیری و قوانین برداری
- سینماتیک
- دینامیک
- کار و انرژی
- تکانه و برخورد
- مرکز جرم و سیستم ذرات
- حرکت دورانی
- تعادل و استاتیک
- نوسان
در ادامه این مطلب به معرفی کمیتها، فرمولها و توضیح مهمترین مفاهیم مطرح شده در مورد هر کدام خواهیم پرداخت.
مرجع فیزیک ۱ چه کتابی است؟
کتابی که بهعنوان مرجع اصلی درس فیزیک ۱ در تمام دانشگاهها تدریس میشود، جلد اول از مجموعه کتابهای «مبانی فیزیک» نوشته «دیوید هالیدی» (David Halliday)، «رابرت رزنیک» (Robert Resnick) و «جرل واکر» (Jearl Walker) است. ویرایشها و ترجمههای مختلفی از این کتاب در بازار موجود است که در اغلب آنها موضوعات اشاره شده مشترک هستند.
دقت کنید کتابهای هالیدی چند جلد هستند و تنها جلد اول بهعنوان فیزیک ۱ در نظر گرفته میشود. تصویری از جلد آخرین ویرایش (ویرایش دوازدهم) کتاب فیزیک ۱ را در ادامه مشاهده میکنید:

اندازه گیری و قوانین برداری
اولین مرحله یادگیری شاخههای مختلف فیزیک آشنایی با انواع کمیتهای فیزیکی، روش اندازهگیری هر کدام و تشخیص واحدها یا یکاهای استاندارد آنها است. به همین دلیل فصل اول فیزیک ۱ که شروع آموزش فیزیک در دانشگاه محسوب میشود، با این مباحث آغاز شده است. گام بعدی، تعیین کمیتهای اسکالر و برداری در فیزیک و یادگیری قوانین بردارها است که تشخیص آنها در حل مسائل فیزیکی بسیار مهم است. از حرکت و نیرو گرفته تا انرژی و تکانه، تمام این مفاهیم بهصورت عددی یا برداری توصیف میشوند. به این ترتیب تسلط به این اصول، پیشنیاز موضوعات بعدی در فیزیک ۱، فیزیک ۲ و ... است.
کمیت های فیزیکی و اندازه گیری
علم فیزیک بر مبنای مشاهدات دقیق، اندازهگیری و مدلسازی ریاضی پدیدههای طبیعی توسعه پیدا کرد. به همین دلیل در ابتدای مسیر یادگیری فیزیک ۱، آشنایی با مفاهیمی مانند کمیتهای فیزیکی و واحدهای اندازهگیری آنها بسیار مهم است. توصیف هر کمیت فیزیکی با دو فاکتور کامل میشود: یک عدد بهعنوان مقدار آن کمیت و یک واحد اندازهگیری. برای مثال، زمانی که میگوییم سرعت جسمی است، عدد مقدار سرعت و واحد آن است.
در صورت تمایل به استفاده از آموزشهای بصری، پیشنهاد میکنیم فیلم آموزشی رایگان زیر را مشاهده کنید. در فیلم زیر درس فیزیک ۱ را به شکل خلاصه و سریع بررسی کردهایم. از آشنایی با کمیتهای فیزیکی و قوانین برداری گرفته تا معرفی نوسان و حرکت هماهنگ ساده در فیلم زیر، توضیح داده شدهاند.
بر اساس یکا یا واحد میتوانیم تمام کمیتها در فیزیک را به دو گروه اساسی تقسیمبندی کنیم:
- کمیتهای اصلی: طول، جرم، زمان، مقدار ماده، شدت روشنایی، دما و بار الکتریکی.
- کمیتهای فرعی: هر کمیتی که در گروه کمیتهای اصلی نباشد، مانند سرعت، میدان الکتریکی، فشار، انرژی و ...
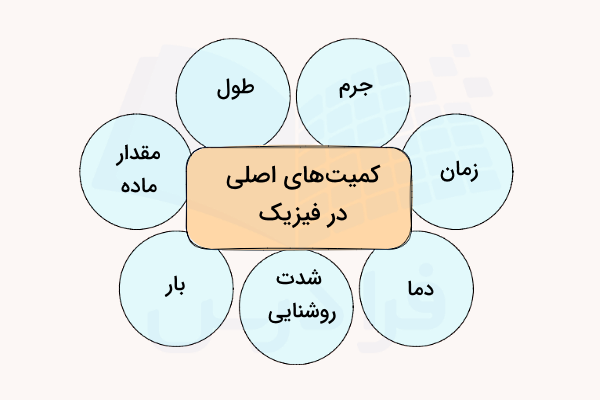
تعداد کمیتهای اصلی مشخص است (هفت مورد بالا)، اما بهجز این هفت کمیت، سایر کمیتها در فیزیک از نوع فرعی محسوب میشوند. در حقیقت، کمیت فرعی به کمیتی گفته میشود که واحد آن از ترکیب واحدهای کمیتهای اصلی ساخته میشود. همچنین برای اینکه در مورد واحد تمام کمیتها یک توافق جهانی وجود داشته باشد، اغلب از سیستم بینالمللی واحدها یا SI بهعنوان یک استاندارد جهانی برای اندازهگیری پیروی میشود. واحدهای اصلی طبق سیستم SI به شکل زیر تعریف میشوند:
- متر یا برای طول
- کیلوگرم یا برای جرم
- ثانیه یا برای زمان
- مول یا برای مقدار ماده
- شمع یا برای شدت روشنایی
- کلوین یا برای دما
- کولن یا برای بار الکتریکی
دقت کنید اندازهگیری هیچگاه بهصورت دقیقی انجام نمیشود و همیشه دارای نوعی عدمقطعیت است که میتواند ناشی از خطای ابزار یا روش اندازهگیری باشد. به همین علت مهم است که در گزارش نتایج خود همیشه تعداد ارقام معنادار و تخمینی از خطای اندازهگیری خود را نیز ذکر کنیم.
قوانین بردارها
برای توصیف دقیق بسیاری از کمیتها در فیزیک فقط داشتن عدد یا مقدار آن کمیت کافی نیست، بلکه مشخص کردن جهت آن نیز مهم است. این کمیتها را کمیت برداری مینامیم. نمونههایی از کمیتهای برداری در فیزیک ۱ عبارتاند از نیرو، شتاب و جابجایی. اما کمیتهایی مانند دما، جرم و انرژی جهت ندارند و برای توصیف دقیق آنها کافی است بدانیم مقدار هر یک چقدر است. این کمیتها را کمیت نردهای (عددی یا اسکالر) مینامیم. تفاوت مهم دیگر بین این دو نوع کمیت در این است که برای جمع و تفریق یا ضرب کمیتهای برداری باید از قوانین بردارها استفاده کنیم.
جمع و تفریق بردارها
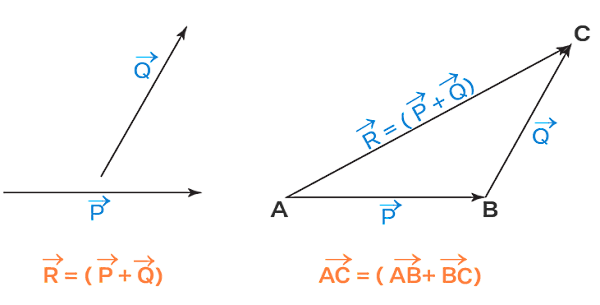
ابتدا باید ببینیم یک بردار چیست و چگونه تعریف میشود. بردارها توسط پیکانهایی نمایش داده میشوند که طول پیکان نشاندهنده اندازه بردار و جهت آن بیانگر جهت بردار است. جمع بردارها به دو روش انجام میشود:
- روش گرافیکی یا مثلثی: ابتدا بردار اول را رسم کرده و سپس بردار دوم را از انتهای بردار اول رسم میکنیم. خطی که ابتدای بردار اول را به انتهای بردار دوم وصل میکند، بردار حاصلجمع است.
- روش مولفهای یا تجزیه کردن: ابتدا هر بردار را به دو مولفه افقی و عمودی (در دو بعد) یا به سه مولفه (در سه بعد) تجزیه میکنیم. سپس مولفههای همجهت را با هم جمع میکنیم تا بردار حاصلجمع بهدست آید.
دقت کنید در روش تجزیه اندازه و جهت بردار نهایی را میتوان توسط قضیه فیثاغورث و تانژانت معکوس محاسبه کرد. برای مثال، اگر بردار حاصلجمع شامل دو مولفه و باشد، اندازه و جهت آن به شکل زیر محاسبه خواهد شد:
ضرب بردارها
در فیزیک ۱ دو نوع ضرب برای بردارها تعریف شده است که عبارتاند از:
- ضرب نقطهای، عددی یا اسکالر (ضرب داخلی): حاصل همیشه یک عدد است.
- ضرب برداری (ضرب خارجی): حاصل همیشه برداری است عمود بر دو بردار دیگر.
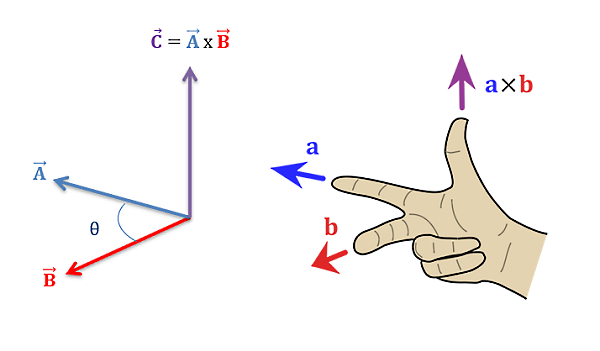
جهت بردار حاصل از ضرب خارجی را میتوان توسط قانون دست راست تعیین کرد. همچنین فرمول این دو نوع ضرب به شکل زیر است:
| فرمول ضرب داخلی دو بردار و با زاویه | |
| فرمول ضرب خارجی دو بردار و با زاویه |
یادگیری فیزیک ۱ دانشگاهی با فرادرس
یکی از مهمترین مباحث فیزیک دانشگاهی در اغلب رشتههای مهندسی و علوم پایه، فیزیک مکانیک یا فیزیک ۱ است. به همین دلیل در این بخش قصد داریم چند فیلم آموزشی مرتبط با این درس را به شما معرفی کنیم. مشاهده این دورههای فرادرس به شما کمک میکند تا با حل مثالها و تمرینهای متنوع درک بسیار عمیقتری نسبت به این مبحث کسب کنید:
- فیلم آموزش فیزیک پایه ۱ فرادرس
- فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله فرادرس
- فیلم آموزش فیزیک پایه ۱ مرور و حل مساله فرادرس
- فیلم آموزش فیزیک پایه ۱ مرور و حل تست فرادرس
- فیلم آموزش رایگان فیزیک پایه ۱ حرکت دورانی فرادرس
- فیلم آموزش رایگان حرکت ذره در سه بعد در مکانیک تحلیلی فرادرس
سینماتیک
اولین قدم در یادگیری حرکتشناسی یا سینماتیک آشنایی با کمیتهایی مانند سرعت، شتاب، مسافت و جابجایی است. سپس بر این اساس که سرعت و شتاب در حرکت مورد بررسی ما چگونه با زمان تغییر میکنند، میتوانیم نوع حرکت را تعیین کنیم. انواع حرکت در سینماتیک عبارتاند از:
- حرکت با سرعت ثابت (حرکت یکنواخت)
- حرکت با شتاب ثابت
- حرکت با شتاب متغیر
جابجایی برداری است که تغییر مکان یک جسم را نسبت به نقطه شروع حرکت آن نشان میدهد. برخلاف مسافت، جابجایی یک کمیت برداری است، یعنی هم مقدار آن مهم است و هم جهت آن. برای مثال، اگر شخصی به سمت شرق و سپس به سمت شمال حرکت کند، جابجایی او برداری مستقیم بین نقطه شروع و پایان است که میتوان آن را با استفاده از قضیه فیثاغورث محاسبه کرد:
در نتیجه جابجایی همیشه برابر است با کوتاهترین مسیر بین دو نقطه و ممکن است از مسافت طی شده کمتر باشد. کمیتهای مهم بعدی در فیزیک ۱ تندی و سرعت هستند. سرعت معادل است با آهنگ تغییرات جابجایی در واحد زمان یا مشتق تغییرات مکانی نسبت به زمان. بنابراین اگر مکان را با و زمان را با نشان دهیم، فرمول سرعت یا به شکل زیر خواهد شد:
اگر سرعت جسمی با گذر زمان تغییر کند، حرکت آن جسم شتابدار خواهد شد و این شتاب به شکل زیر محاسبه میشود:
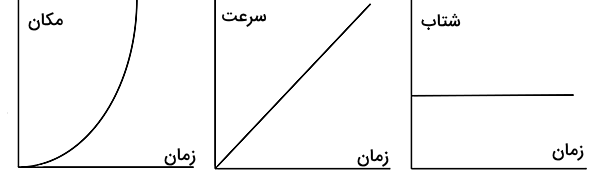
تصویر بالا نشان میدهد بین این سه پارامتر چه ارتباطی برقرار است. اگر تغییرات مکان با زمان به شکل یک معادله درجه دو باشد، در این صورت نمودار مکان - زمان به شکل یک سهمی خواهد شد. مشتقگیری از معادله مکان، همان پیدا کردن شیب خط مماس بر نمودار مکان - زمان است که در اینجا نتیجه به شکل یک خط مستقیم با شیب ثابت خواهد شد. مشتقگیری مجدد از معادله مکان، شتاب حرکت را به ما میدهد که نمودار آن همان شیب خط مماس بر نمودار سرعت - زمان است. پس اگر معادله مکان از درجه دوم باشد، شتاب ایجاد شده همواره مقدار ثابتی با گذر زمان خواهد داشت.
حرکت در یک بعد
در بخش قبل یاد گرفتیم سه کمیت مهم سینماتیک در فیزیک ۱ چه هستند. حرکت اجسام ممکن است تنها روی یک خط راست باشد (حرکت در یک بعد) یا در دو یا سه بعد صورت بگیرد. در این بخش و بخش بعد چند مثال از انواع حرکت را با هم بررسی میکنیم. سقوط آزاد یک حرکت یک بعدی و با شتاب ثابت است که در آن تنها نیروی موثر وارد بر جسم، نیروی گرانش زمین است. اگر مقاومت هوا را نادیده بگیریم، تمام اجسام صرفنظر از مقدار جرمی که دارند، با شتابی یکسان به سمت زمین سقوط میکنند. این شتاب را مینامیم.
حرکت در دو و سه بعد
گسترش حرکت یک بعدی ما را به حرکت در دو و سه بعد میرساند که در آن موقعیت یک جسم در صفحه یا فضای سه بعدی تعریف میشود. این نوع حرکتها با استفاده از بردار مکان در دستگاه مختصات دو بعدی یا سه بعدی توصیف میشود و به ما این امکان را میدهد تا مسیر حرکت، سرعت و شتاب جسم را بهصورت دقیقی تحلیل کنیم. در ادامه این بخش به بررسی دو حرکت دو بعدی معروف در فیزیک ۱ و معادلات آنها خواهیم پرداخت.
حرکت پرتابی
حرکت پرتابی یکی از مهمترین مثالهای حرکت در دو بعد است و زمانی رخ میدهد که جسمی با یک سرعت اولیه مشخص نسبت به سطح افق پرتاب شود. این حرکت ترکیبی از دو حرکت است، حرکت یکنواخت در راستای افقی و حرکت با شتاب ثابت به سمت پایین و در راستای عمودی ناشی از نیروی گرانش. در چنین وضعیتی سرعت افقی جسم ثابت باقی میماند، چون شتاب افقی آن صفر است (البته در شرایط ایدهآل بدون مقاومت هوا). اما در راستای عمودی سرعت جسم تحت تاثیر شتاب گرانشی تغییر میکند.
به این ترتیب پارامترهای اصلی در حرکت پرتابهای که با سرعت اولیه و زاویه نسبت به سطح افق پرتاب میشود، عبارتاند از:
- برد پرتابه (مسافت افقی):
- ارتفاع بیشینه:
- کل زمان پرتاب:
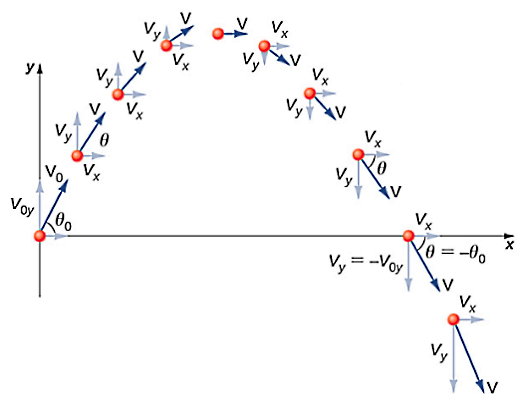
این حرکت یک نمودار سهمی شکل دارد و با معادلات حرکت در دو بعد قابلتحلیل است، کافی است حرکت جسم پرتاب شده در هر لحظه را توسط دو معادله زیر بررسی کنیم:
حرکت دایره ای یکنواخت
حرکت دایرهای یکنواخت یک حرکت دو بعدی دیگر است که در آن جسم با یک سرعت ثابت در مسیر دایرهای شکل حرکت میکند. اگر چه اندازه سرعت در این نوع حرکت ثابت میماند، اما جهت آن پیوسته تغییر میکند، بنابراین شتابی ایحاد میشود که به آن شتاب مرکزگرا گفته میشود. شتاب مرکزگرا که همواره به سمت مرکز مسیر دایرهای شکل است، باعث میشود جسم مسیر دایرهای خود را حفظ کند.
فرمول شتاب مرکزی در حرکت دایرهای جسمی با سرعت روی مسیر دایرهای شکلی با شعاع بهصورت زیر تعریف میشود:
این نوع حرکت در بسیاری از کاربردهای روزمره و مهندسی دیده میشود، مانند حرکت چرخهای خودرو، چرخش ماهوارهها به دور زمین و یا حرکت اجسام روی مسیرهای منحنی شکل.
حرکت نسبی
آخرین مبحثی که در بخش سینماتیک از فیزیک ۱ مطرح میشود، مفهوم حرکت نسبی است. این نوع حرکت بیان میکند که حرکت یک جسم همواره نسبت به چارچوب مرجع خاصی اندازهگیری میشود و هیچ حرکت مطلقی وجود ندارد. به عبارت دیگر، سرعت و موقعیت مکانی یک جسم کاملا بستگی به ناظر یا دستگاه مختصاتی دارد که حرکت از دید آن مشاهده میشود.
بنابراین اگر جسمی با دو چارچوب مرجع مختلف برای مثال چارچوب A (مانند زمین) و چارچوب B (مانند یک قطار یا رودخانه در حال حرکت) داشته باشیم، در این صورت سرعت جسم نسبت به چارچوب A برابر است با مجموع سرعت جسم نسبت به چارچوب B و سرعت چارچوب B نسبت به چارچوب A. یعنی داریم:
سرعت جسم نسبت به A = سرعت جسم نسبت به B + سرعت B نسبت به A
این مفهوم به ویژه در مسائل حرکت اجسام متحرک نسبت به یکدیگر، مانند قطارهایی که در مقابل هم حرکت میکنند یا هواپیماهایی که نسبت به هوا یا زمین سرعت دارند، کاربرد دارد. در انتهای این بخش اگر تمایل دارید سینماتیک را در قالب حل مثال و تمرین بهتر یاد بگیرید، پیشنهاد میکنیم مطلب «تمام فرمول های سینماتیک با مثال و تمرین» از مجله فرادرس را مطالعه کنید.
دینامیک
دینامیک شاخهای است که بررسی میکند چگونه نیروهای مختلف میتوانند باعث تغییر وضعیت حرکتی اجسام شوند. برخلاف سینماتیک که فقط اثر نیرو روی حرکت را توصیف میکند، در دینامیک بررسی میکنیم چه رابطهای بین نیرو و تغییر وضعیت حرکتی جسم وجود دارد. نیرو به معنای اعمال هر گونه فشار یا کشش و یک کمیت برداری است. در طبیعت انواع مختلفی از نیروها را داریم، نیروی گرانش، نیروهای الکترومغناطیسی، نیروی اصطکاک، نیروی مقاومت هوا (درگ) و ...
قوانین نیوتن و کاربردهای آن
برای اینکه بتوانیم آثار نیرویهای مختلف وارد بر یک جسم را مطالعه کنیم، لازم است قوانین نیوتن را به شکلی دقیق بررسی کنیم. اولین قانون بیان میکند اگر به جسمی هیچ نیروی خالصی وارد نشود، آن جسم یا در حالت سکون باقی میماند یا با سرعت ثابت در مسیر خطی مستقیم حرکت میکند. به بیان دیگر، تغییر در وضعیت حرکت یک جسم تنها زمانی رخ میدهد که یک نیروی برآیند و مخالف صفر به جسم اعمال شود. این شرایط موضوع قانون دوم نیوتن است که نشان میدهد چگونه نیرو باعث شتاب گرفتن یا تغییر سرعت یک جرم میشود:
طبق این قانون هر چه جرم یک جسم بیشتر باشد، شتاب آن کمتر است و برعکس. سومین قانون که عمل و عکسالعمل نیز نامیده میشود، بیان میکند که هرگاه جسم A به جسم B نیرویی اعمال کند، جسم B نیز بهصورت همزمان نیرویی برابر و در خلاف جهت به A وارد میکند. این اصل نشاندهنده تقارن در تعامل نیروها است. به کمک این قوانین ساده میتوانیم بسیاری از پدیدههای روزمره و علمی را تحلیل کنیم. اما پیش از آن لازم است فرمول برخی از این نیروها را بدانیم:
- نیروی اصطکاک: نیرویی که حرکت نسبی سطوح را محدود کرده و انرژی جنبشی را به گرما تبدیل میکند ().
- نیروی درگ: وقتی جسمی در هوا یا آب حرکت میکند، نیرویی در خلاف جهت حرکت آن وجود دارد که موجب کاهش سرعت جسم میشود. این نیرو به شکل و سرعت جسم بستگی دارد ().
- قانون هوک: هنگامی که نیرویی باعث فشردگی یا کشیدگی فنری شود ().
- نیروی مرکزی (مرکزگرا): نیرویی که جسم را به سمت مرکز یک مسیر دایرهای شکل میکشاند ().

به این ترتیب، تحلیل درست وضعیت تعادلی (استاتیکی) یا غیرتعادلی (دینامیکی) در حرکت اجسام پیچیده با ترسیم نمودار جسم آزاد و سپس استفاده از قوانین نیوتن همراه با این فرمولها امکانپذیر است.
کار و انرژی
مفاهیم کار، انرژی و توان از اصول بنیادی فیزیک ۱ هستند که درک آنها برای تحلیل دینامیک سیستمهای فیزیکی و تحولات انرژی ضروری است. کار در فیزیک همان انتقال انرژی است و توان نیز نرخ انجام کار یا انتقال انرژی را بیان میکند. این مفاهیم به هم وابستهاند، به این شکل که انرژی یک کمیت بنیادی است، کار ساز و کار انتقال آن را فراهم کرده و توان، سرعت این انتقال را اندازهگیری میکند.
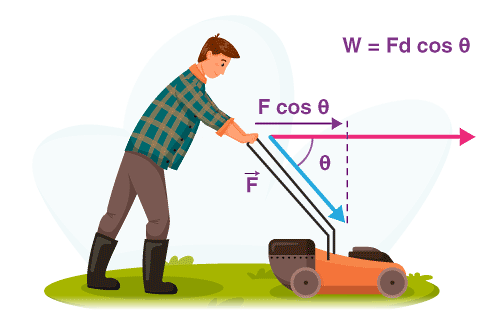
زمانی که یک نیروی ثابت مانند به جسمی وارد شده و موجب جابجایی آن به اندازه در یک خط مستقیم شود، فرمول کار انجام شده یا بهصورت حاصلضرب داخلی بردار نیرو و بردار جابجایی تعریف میشود:
کار یک کمیت نردهای و واحد آن ژول است. این تعریف نشان میدهد که تنها آن مولفهای از نیرو که در راستای جابجایی عمل میکند، در انجام کار موثر است.
کار نیروی متغیر
اگر نیروی اعمال شده ثابت نباشد و با مکان یا تغییر کند، کار انجام شده به روش انتگرالگیری محاسبه میشود. بنابراین فرمول کلی برای کار نیروی متغیر بهصورت زیر است:
مثبت بودن کار حاصل از این نیرو به معنای انجام کار توسط نیرو است، در حالی که کار منفی نشاندهنده انجام کار بر روی سیستم است.
قضیه کار و انرژی
میدانیم انرژی جنبشی انرژیای است که یک جسم به علت حرکت خود دارد و با فرمول محاسبه میشود. بر این اساس میتوانیم قضیه کار و انرژی را بررسی کنیم که بیان میکند کار خالص انجام شده روی یک جسم با تغییرات در انرژی جنبشی آن برابر است:
این قضیه مهم، کار را به عنوان نوعی انتقال انرژی که منجر به جابجایی میشود، در نظر میگیرد و بین نیروها، حرکت و انرژی ارتباط برقرار میکند.
توان
توان یا معادل است با نرخ انجام کار یا انتقال انرژی و میتوان آن را بهصورت کار در واحد زمان یا بهطور کلیتر، نرخ تغییرات انرژی مکانیکی کل بیان کرد. همچنین برای سیستمهای مکانیکی توان میتواند بهصورت حاصلضرب داخلی نیروی اعمال شده در سرعت جسم محاسبه شود:
واحد SI توان وات یا ژول بر ثانیه است. توان بیشتر به این معنا است که مقدار کار یکسان در زمان کوتاهتری انجام میشود. این مفهوم فراتر از محاسبه انرژی است و جنبه زمانی تبدیل یا تحویل انرژی را در نظر میگیرد.
نیروهای پایستار
نیروهای پایستار یا Conservative Forces در فیزیک ۱ به گروهی از نیروها گفته میشود که کار انجام شده توسط آنها تنها به موقعیت اولیه و نهایی جسم بستگی دارد، نه به مسیری که جسم طی کرده است. این استقلال از مسیر، امکان تعریف نوعی انرژی پتانسیل مرتبط با این نیروها را برای ما فراهم میکند، برای مثال نیروی گرانش یا نیروی کشسانی فنر.
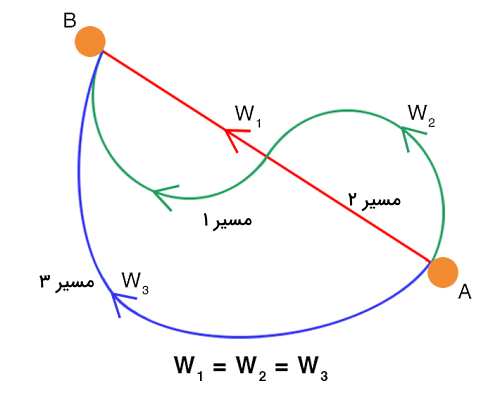
اما نیروهای ناپایستار مانند اصطکاک و مقاومت هوا انرژی را در قالب گرما یا صوت هدر داده و اجازه بازیابی کامل انرژی مکانیکی را نمیدهند. ویژگی استقلال از مسیر در نیروهای پایستار، موجب تعریف تابع انرژی پتانسیل برای آنها خواهد شد.
پایستگی انرژی
قانون پایستگی انرژی بیان میکند که در یک سیستم بسته که تنها نیروهای پایستار روی آن عمل میکنند، کل انرژی مکانیکی یا ثابت میماند. فرمول ریاضی این توضیح به شکل زیر است:
همچنین با توجه به اینکه میدانیم انرژی مکانیکی برابر است با مجموع انرژی جنبشی و انرژی پتانسیل، رابطه بالا به شکل زیر ساده میشود:
این اصل توضیح میدهد که چگونه انرژی بین اشکال مختلف خود یعنی جنبشی و پتانسیل (مانند یک جسم در حال سقوط یا یک فنر نوسان کننده) بدون اتلاف شدن در حال تبدیل است، البته با این شرط که نیروهای ناپایستار مانند اصطکاک ناچیز باشند.
تکانه و برخورد
در این بخش از فیزیک ۱ مفاهیمی مانند تکانه، ضربه، برخورد و چارچوب مرکز جرم معرفی میشوند. تکانه معیاری است از حرکت که تغییرات آن توسط ضربه (اثر تجمعی نیرو در طول زمان) تعیین میشود. همچنین قانون پایستگی تکانه را داریم که یک اصل بنیادی است و در تمامی برخوردها در یک سیستم ایزوله همواره برقرار میماند، صرفنظر از اینکه انرژی جنبشی پایسته باشد یا خیر.
مفهوم مرکز جرم نیز یک ابزار قدرتمند برای سادهسازی تحلیل حرکت سیستمهای پیچیده است که بهطور مستقیم به پایستگی تکانه مرتبط میشود، زیرا حرکت مرکز جرم یک سیستم ایزوله همیشه ثابت است. مشاهده فیلم آموزش فیزیک پایه ۱ – مرور و حل مساله فرادرس در این زمینه میتواند مفید باشد:
تکانه خطی و ضربه
اولین قدم برای آشنایی با این مفاهیم این است که ببینیم تکانه به چه معنا است. تکانه خطی که با نماد نمایش داده میشود، یک کمیت برداری در فیزیک است که به چارچوب مرجع انتخابی بستگی دارد، در حالی که اصل پایستگی تکانه در هر چارچوب مرجع اینرسی صادق است. این کمیت برای جسمی به جرم که با سرعت در حال حرکت است توسط فرمول زیر محاسبه میشود:
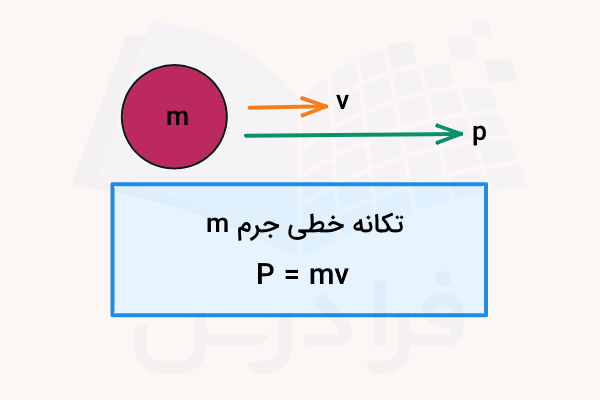
تکانه معیاری است از اندازه حرکت یک جسم و هم به جرم و هم به سرعت آن بستگی دارد، به این معنا که جسمی با جرم بیشتر یا سرعت بیشتر، تکانه بیشتری دارد و برعکس. جهت تکانه همیشه همان جهت سرعت جسم است و واحد آن در سیستم بینالمللی واحدها (SI) کیلوگرم متر بر ثانیه یا است. کمیت بعدی ضربه است که در فیزیک ۱ با نماد نشان داده میشود و معادل است با تغییرات تکانه خطی یک ذره یا جسم که در نتیجه برهمکنش آن با ذره، جسم یا سیستم دیگری طی مدت زمان کوتاهی رخ داده است. این تغییر به عنوان ضربه نیروها و به شکل زیر تعریف میشود:
ضربه نیز یک کمیت برداری است و دارای همان واحد تکانه یعنی نیوتن در ثانیه () یا است. همچنین ضربه را میتوان با انتگرالگیری از نیرو و در بازه زمانی مشخصی از لحظه اولیه تا لحظه نهایی و به شکل زیر نیز بهدست آورد:
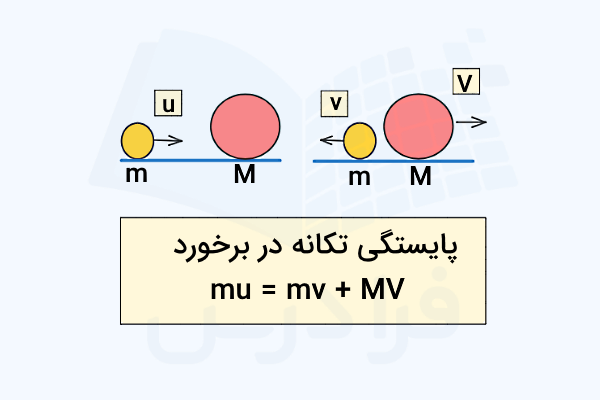
رابطه بین تغییرات تکانه و ضربه را میتوان در قالب قضیهای به نام قضیه تکانه - ضربه نیز بیان کرد که طبق آن که ضربه وارد شده به یک جسم دقیقا برابر با تغییرات تکانه آن است. این رابطه نشان میدهد که یک نیروی قویتر یا بازه زمانی طولانیتر اعمال نیرو، منجر به تغییر تکانه و در نتیجه ضربه بزرگتری میشود. برای مثال، در تصویر زیر ملاحظه میکنید که اگر زمان اعمال نیروی را دو برابر کنیم، تغییرات تکانه و در نتیجه ضربه حاصل نیز دو برابر خواهد شد.

به این ترتیب نیروی متوسط یا وارد شده بر یک ذره در بازه زمانی را میتوان بهصورت تعریف کرد:
به عنوان مثال، اگر یک توپ بسکتبال با زمین برخورد کند و ضربهای به اندازه در مدت زمان به آن وارد شود، بزرگی نیروی متوسط وارد شده به توپ از طرف زمین طبق رابطه بالا برابر است با . این قضیه یک ارتباط مستقیم بین نیرو، مدت زمان اعمال آن و تغییر در اندازه حرکت (تکانه) یک جسم برقرار میکند. همچنین قانون دوم نیوتن بهصورت نیز بیان میکند که نرخ تغییرات تکانه برابر است با نیروی خالص یا برآیندی که به جسم وارد شده است.
با انتگرالگیری از قانون دوم نیوتن نسبت به زمان، به قضیه تکانه - ضربه میرسیم. این معادله نشان میدهد که ضربه یا اثر تجمعی نیرو در طول زمان مستقیما مسئول تغییرات تکانه یک جسم است. بنابراین برای تغییر تکانه یک جسم میتوان نیروی بزرگی را طی مدت زمان کوتاهی اعمال کرد (مانند ضربه چکش) یا نیروی کوچکی را بکار برد اما برای مدت زمان طولانیتر (مانند هل دادن یک جسم سنگین). آگاهی از این ارتباط درک ما از چگونگی تاثیر نیروها بر حرکت اجسام را عمیقتر کرده و موجب میشود تا از این نکته در کاربردهای عملی فراوانی مانند ایمنی (طراحی کیسه هوا برای افزایش زمان برخورد و کاهش نیروی متوسط) و ورزش (دنبال کردن ضربه در گلف) استفاده کنیم.
انواع برخورد
در فیزیک ۱ زمانی که دو یا چند جسم یا ذره در مدت زمان نسبتا کوتاهی نیروهای قوی بر یکدیگر وارد کنند، میگوییم برخورد رخ داده است. برای اینکه بتوانیم برخورد را مطالعه کنیم، توجه به تکانه ذرات یا اجسامی که با هم برخورد دارند، قبل و بعد از برخورد ضروری است، اما پیش از آن ابتدا بهتر است با انواع برخورد آشنا شویم.
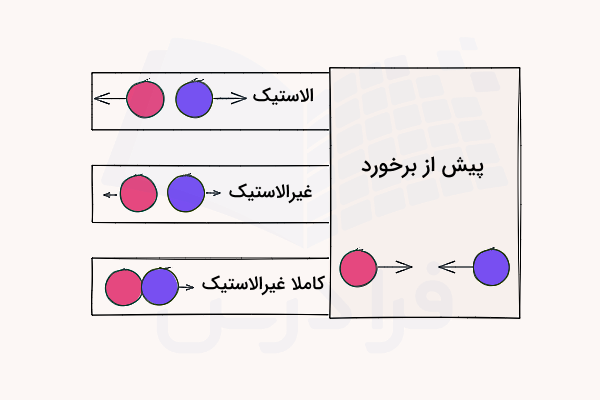
انواع برخورد را میتوان بر اساس تبدیل انرژی جنبشی به سایر فرمهای انرژی مانند گرما، تغییر شکل، صوت و ... و با در نظر گرفتن پایسته ماندن تکانه کل به سه گروه تقسیمبندی کرد. همانطور که در تصویر بالا ملاحظه میکنید، در برخورد الاستیک ذرات پس از برخورد با یکدیگر با سرعتهایی کاملا برابر با سرعتهای قبل از برخورد از هم جدا میشوند، در حالی که در برخورد غیرالاستیک سرعتها کاهش یافته و در برخورد کاملا غیرالاستیک دو ذره به هم میچسبند. ویژگیهای هر نوع برخورد در ادامه به شکل دقیقتری بیان شده است:
- برخورد الاستیک یا کشسان: در این نوع برخورد علاوهبر تکانه کل، انرژی جنبشی کل سیستم نیز قبل و بعد از برخورد پایسته میماند. بنابراین اجسام پس از برخورد از یکدیگر جدا شده و با همان سرعتی که به هم نزدیک شدهاند، از هم دور میشوند. مثالهای متداول آن شامل برخورد دو توپ بیلیارد یا برخورد کشسان دو دیسک در هاکی روی یخ است. در این نوع برخورد انرژی جنبشی بهطور کامل حفظ میشود که نشاندهنده عدم اتلاف انرژی قابلتوجه است.
- برخورد غیرالاستیک یا غیرکشسان: در این نوع برخورد تکانه کل سیستم پایسته میماند، اما انرژی جنبشی کل کاهش پیدا کرده و به اشکال دیگر انرژی (مانند گرما، صدا یا انرژی لازم برای تغییر شکل دائمی جسم) تبدیل میشود. مثال رایج برای برخورد غیرکشسان، برخورد یا تصادف اتومبیلها است که با تغییر شکل بدنه آنها همراه است.
- برخورد کاملا غیرالاستیک یا کاملا غیرکشسان: این مورد یک حالت خاص از برخورد غیرالاستیک است که در آن دو یا چند جسم پس از برخورد به یکدیگر میچسبند و به عنوان یک جرم واحد به حرکت خود ادامه میدهند. در این نوع برخورد حداکثر انرژی جنبشی ممکن از دست میرود. برای نمونه، برخورد چکش ثور با آیرونمن که پس از برخورد با هم حرکت میکنند یا برخورد یک گلوله که در یک بلوک چوبی فرو میرود، مثالهایی از این نوع برخورد بهشمار میرود.
پایستگی تکانه
قانون پایستگی تکانه یک اصل بنیادین در فیزیک ۱ است که بیان میکند برای یک سیستم ایزوله شده یا بسته که هیچ نیروی خارجی به آن وارد نمیشود، تکانه کل سیستم پایسته میماند. پایستگی تکانه یکی از تقارنهای بنیادی فضا - زمان و به نوعی یک تقارن انتقالی محسوب میشود و طبق آن، همیشه تکانه کل سیستم قبل از برخورد برابر است با تکانه کل سیستم پس از برخورد:
این قانون برای دو ذره مانند ذراتی که در بخش قبل برخورد آنها را توصیف کردیم، به شکل زیر درمیآید:
به همین شکل برای هر تعداد ذره در سیستم این قانون همواره در تمام برخوردها برقرار است. دقت کنید سیستم ایزوله سیستمی است که جرم آن ثابت و نیروی خارجی برآیند وارد بر آن نیز صفر باشد.در همین راستا بهتر است بدانیم که نیروهای داخلی (نیروهایی که اجزای سیستم بر یکدیگر وارد میکنند) میتوانند تکانه اجزای سیستم را تغییر دهند، اما تکانه کل سیستم را تغییر نمیدهند. این امر به این دلیل است که این نیروها طبق قانون سوم نیوتن به صورت جفت نیروهای کنش و واکنش هستند و یکدیگر را خنثی میکنند. برای مثال در برخورد دو اتومبیل، تکانه هر کدام بهصورت جداگانه تغییر میکند، اما تکانه کل سیستم (با فرض ناچیز بودن اصطکاک) قبل و بعد از برخورد یکسان است.
قانون پایستگی تکانه ابزار قدرتمندی برای تحلیل برخوردها یا انفجارها است، حتی زمانی که نیروهای درگیر بسیار پیچیده یا ناشناخته باشند. برای حل مسائل حوزه برخورد، کافی است ابتدا سیستم را به عنوان یک سیستم بسته تعریف کنیم. سپس معادله پایستگی تکانه را مینویسیم. اگر برخورد الاستیک باشد، معادله پایستگی انرژی جنبشی نیز اضافه میشود، در حالی که انرژی جنبشی در برخوردهای غیرالاستیک کاهش پیدا میکند. بنابراین پایستگی تکانه در انواع برخوردها (الاستیک، غیرالاستیک و کاملا غیرالاستیک) در یک سیستم ایزوله همواره برقرار میماند.
چارچوب مرکز جرم
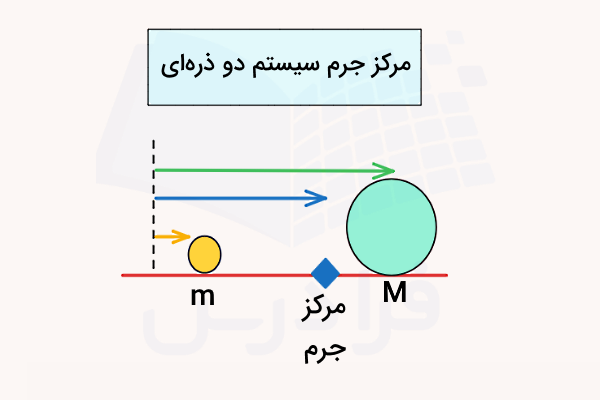
مرکز جرم یک نقطه خاص در فضا است و حرکت آن به گونهای است که گویی تمام جرم سیستم در آن نقطه متمرکز شده و تمام نیروهای خارجی نیز بر آن وارد میشوند. این مفهوم برای تحلیل حرکت سیستمهایی متشکل از ذرات متعدد یا اجسام گسترده بسیار مفید است. موقعیت مرکز جرم یا برای سیستمی از ذرات بهصورت میانگین وزنی موقعیت هر ذره و به شکل زیر تعریف میشود:
این مفهوم به ما اجازه میدهد تا یک سیستم پیچیده از ذرات را با ذرهای واقع شده در مرکز جرم آن معادل در نظر بگیریم و به کمک این سادهسازی بتوانیم تحلیل دینامیکی سیستمهای چند ذرهای را راحتتر انجام دهیم. همچنین سرعت مرکز جرم که با تکانه و جرم کل سیستم مرتبط است، توسط فرمول زیر محاسبه میشود:
گفتیم اگر برآیند نیروهای وارد بر یک سیستم صفر باشد (سیستم ایزوله)، تکانه کل آن پایسته میماند. در نتیجه، سرعت مرکز جرم نیز ثابت میماند و داریم . این نشان میدهد که حتی اگر اجزای سیستم در حال حرکت و برهمکنش با هم باشند، مرکز جرم سیستم با سرعت ثابتی حرکت میکند. دقت کنید حرکت مرکز جرم مسیر کلی حرکت سیستم را نشان میدهد، حتی اگر اجزای داخلی آن بهصورت پیچیدهای حرکت کنند.
مرکز جرم و سیستم ذرات
در بخش قبل یاد گرفتیم که مرکز جرم یک سیستم ذرات یا یک جسم پیوسته معادل با نقطهای است که فرض میشود تمام جرم جسم در آن متمرکز شده است تا بتوانیم حرکت را آسانتر تحلیل کنیم. در واقع با در نظر گرفتن یک سیستم بهعنوان یک جرم نقطهای واحد که در مرکز جرم آن قرار دارد، کاربرد قوانین نیوتن که برای جرمهای نقطهای فرمولبندی شدهاند، در مورد اجسام گسترده نیز امکانپذیر میشود. پس پیچیدگی ریاضیاتی کاهش یافته و مسائل دشوار راحتتر حل میشوند.
در مورد یک جسم صلب منفرد، همواره مکان مرکز جرم نسبت به خود جسم ثابت است، به این معنا که اگر جسم دارای چگالی یکنواخت باشد، مرکز جرم و مرکز هندسی آن بر هم منطبق خواهند بود. دقت کنید مرکز جرم گاهی میتواند خارج از مرزهای فیزیکی جسم قرار گیرد، مانند آنچه در مورد اجسام توخالی یا با شکل باز مانند نعل اسب مشاهده میشود. در سیستمهای شامل چند جسم مجزا مانند سیارات در منظومه شمسی نیز مرکز جرم ممکن است با موقعیت هیچ یک از اجزای سیستم منطبق نباشد.
سیستم های دو ذره ای و چند ذره ای
در این بخش به جزئیات روشهای تعیین مرکز جرم در مورد انواع سیستم ذرات گسسته مانند سیستمهای دو ذرهای و چند ذرهای (بس ذرهای) میپردازیم. اگر سیستمی متشکل از ذره گسسته با جرم باشد که هر کدام در مکان قرار دارند، در این صورت بردار مکان مرکز جرم یا از میانگین وزنی بردارهای مکان آنها به دست میآید. با فرض جرم کل سیستم به شکل ، مرکز جرم چنین سیستمی برابر است با:
با گسترش این فرمول به مختصات دکارتی سه بعدی خواهیم داشت:
یک حالت خاص از سیستمهای گسسته، سیستم دوه ذرهای است که شامل دو ذره با جرمهای و در بردارهای موقعیت و است. مرکز جرم این سیستم بهصورت زیر محاسبه میشود:
مرکز جرم یک سیستم دو ذرهای همیشه روی خط مستقیمی که دو جرم را به هم متصل میکند، قرار میگیرد. اگر توزیع نسبی جرم بین این دو ذره تغییر کند، مرکز جرم نیز در طول این خط حرکت خواهد کرد.
توزیع جرم های پیوسته
برای اجسامی با توزیع جرم پیوسته علامت سیگما یا مجموع در فرمول بخش قبل به انتگرال تبدیل میشود، به این صورت که اگر چگالی جرم را با و جرم کل را با نشان دهیم، در این صورت بردار موقعیت مرکز جرم یا بهصورت زیر تعریف میشود:
همچنین برای یک حجم سه بعدی خواهیم داشت:
یک تکنیک مهم برای سادهسازی محاسبات مرکز جرم در مورد اجسام پیوسته این است که از تقارن آنها استفاده کنیم. برای مثال، اگر جسمی دارای محور تقارن چرخشی باشد، مرکز جرم آن همواره بر روی آن محور قرار خواهد گرفت. پس در مورد یک میله یکنواخت، مرکز جرم آن دقیقا در مرکز هندسی آن قرار دارد و این موضوع بدون نیاز به محاسبات و تنها با تشخیص تقارن، قابل تعیین است.
تکانه خطی کل سیستم ذرات
در بخشهای قبل راجعبه مفهوم تکانه خطی یک ذره منفرد در فیزیک ۱ صحبت کردیم. در این بخش میخواهیم ببینیم تکانه کل سیستمی از ذرات چگونه بهدست میآید. برای سیستمی متشکل از ذره منفرد، تکانه خطی کل یا سیستم جمع برداری تکانههای خطی تمام ذرات تشکیلدهنده آن است. پس اگر ذره ام دارای جرم و سرعت باشد، داریم:
رابطه بین تکانه خطی و حرکت مرکز جرم با عنوان «قانون اول اویلر» شناخته میشود که یک رابطه بنیادی و سادهکننده در مکانیک است و بیان میکند که تکانه خطی کل یک سیستم از ذرات برابر با حاصلضرب جرم کل سیستم در سرعت مرکز جرم آن است:
این رابطه بسیار مهم است، چون امکان تحلیل حرکت انتقالی یک سیستم پیچیده را از حرکات داخلی آن (مانند چرخشها یا ارتعاشات داخلی) جدا میکند. بنابراین تکانه خطی کل یک سیستم را میتوان با ردیابی حرکت مرکز جرم آن تعیین کرد، بدون توجه به حرکات پیچیده ذرات منفرد داخل سیستم.
از طرفی به خاطر داریم که قانون پایستگی تکانه خطی بیان میکند برای یک سیستم بسته و منزوی تکانه خطی کل با گذشت زمان ثابت باقی میماند. بنابراین اگر تکانه کل ثابت باشد، میتوانیم نتیجهگیری کنیم که مرکز جرم چنین سیستمی با سرعت ثابت حرکت خواهد کرد. این اصل برای تمام سیستمهایی که نیروهای داخلی آن طبق قانون سوم نیوتن یکدیگر را خنثی میکنند، صادق است.
دینامیک سیستم های با جرم متغیر
تا اینجا آموختیم که در فیزیک ۱ یک چارچوب مرجع مفید برای تحلیل برخوردها و سیستمهای چند ذرهای، چارچوب مرکز جرم است که در آن تکانه کل سیستم صفر است. این انتخاب محاسبات را بهطور قابلتوجهی آسان میکند. در این بخش روشهای ریاضیاتی موردنیاز برای تحلیل سیستمهایی را توضیح میدهیم که جرم آنها با گذشت زمان تغییر میکند.
تغییرات جرم سیستم ممکن است به علت کاهش جرم سیستم (بر اثر فرسایش یا پرتاب) یا اضافه شدن جرم به آن رخ دهد. در نتیجه اعمال مستقیم قانون دوم نیوتن به شکل () در مورد چنین سیستمهایی میتواند گمراهکننده باشد زیرا جرم تابعی از زمان است، در حالی که میدانیم در شکل استاندارد قانون دوم نیوتن جرم ثابت فرض شده است.
مهمترین مثال عملی از یک سیستم با جرم متغیر، موشک است که مقادیر قابل توجهی از جرم خود را به شکل سوخت در حال سوختن در طول پرواز از دست میدهد. مثالهای دیگر عبارت اند از دانههای برف در حال سقوط که جرم جمع میکنند، تکهای یخ که روی آب ذوب میشود یا شهابسنگی که وارد جو زمین شده و دچار فرسایش میشود. معادله کلی حرکت برای سیستمی با جرم متغیر که از اصل پایستگی تکانه حاصل میشود، به شکل زیر است:
- : برآیند نیروی خارجی وارد بر سیستم (مانند نیروهای آیرودینامیکی و گرانش)
- : سرعت نسبی جرم در حال خروج یا ورود نسبت به مرکز جرم سیستم
- : نرخ تغییر جرم سیستم که برای افزایش جرم مثبت و برای فرسایش یا پرتاب جرم منفی است.
- : جرم لحظهای بدنه اصلی سیستم
- : شتاب بدنه اصلی یا شتاب مرکز جرم آن، اگر جسم بهعنوان یک ذره در نظر گرفته نشود.
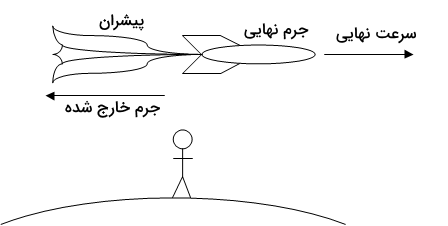
معادله ایدهآل حرکت یک موشک که به عنوان «معادله موشک سیولکوفسکی» نیز شناخته میشود، از معادله بالا استخراج میشود. کافی است شرایط را ایدهآل در نظر بگیریم، یعنی فرض کنیم هیچ نیروی خارجی بر موشک وارد نمیشود. در این حالت معادله بالا بهصورت زیر خواهد شد:
در نهایت با حذف از دو طرف، انتگرالگیری از طرفین معادله دیفرانسیل بهدست آمده و سپس جداسازی متغیرها و در نظر گرفتن جرم اولیه و سرعت اولیه و جرم نهایی و سرعت نهایی ، خواهیم داشت:
در معادله موشک سرعت خروجی موثر پیشران، جرم کل اولیه موشک شامل پیشران و جرم کل نهایی موشک بدون پیشران است.
حرکت دورانی
حرکت دورانی به معنای چرخش یک جسم یا ذره حول یک محور مشخص است. آشنایی با مفاهیم و فرمولهای این نوع حرکت برای تحلیل و طراحی سیستمهای مکانیکی چرخشی از چرخدندههای ساده گرفته تا سامانههای فضایی پیچیدهتر، ضروری است. برخلاف حرکت خطی که در آن تمام نقاط یک جسم صلب با سرعت و جهت یکسان حرکت میکنند، در حرکت دورانی سرعت خطی نقاط مختلف جسم متغیر است و به فاصله آن نقاط از محور چرخش بستگی دارد. همین تفاوت تحلیل سینماتیک دورانی را از نظر ریاضیاتی پیچیدهتر کرده است.
مفاهیم مهم در مطالعه حرکت دورانی عبارتاند از گشتاور، لختی دورانی، تکانه زاویهای، کار و انرژی و ترکیب حرکت انتقالی و دورانی. برای درک بهتر این موضوعات، ابتدا حرکت دورانی را معادل چرخشی حرکت خطی در نظر میگیریم، به این معنا که برای هر کمیت فیزیکی یا هر معادلهای که در حرکت خطی وجود دارد، یک همتای متناظر در حرکت دورانی تعریف میکنیم. این تطابق فقط یک سادهسازی نیست، بلکه بازتابی از تقارن قوانین فیزیک است.
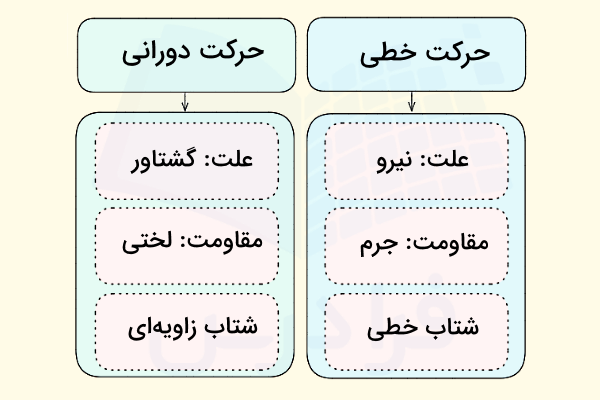
برای مثال در نظر گرفتن مشتق اول و دوم نسبت به زمان با عنوان سرعت و شتاب یا وابستگی درجه دو برای انرژی جنبشی در هر دو نوع حرکت خطی و دورانی نشان میدهد که دینامیک این دو نیز از اصول مکانیک نیوتنی یکسانی تبعیت میکند. تصویر بالا نشان میدهد که تفاوتهای اساسی این دو نوع حرکت چیست. مشابه و متناظر بودن روابط و فرمولها در این دو نوع حرکت ما را به این نتیجه میرساند که قوانین بنیادی فیزیک نسبت به جابجاییها و چرخشها پایسته یا ناوردا هستند (پایستگی تکانه خطی و پایستگی تکانه زاویهای).
کمیت ها در حرکت دورانی
به منظور توصیف کمی حرکت دورانی لازم است مجموعهای از متغیرها یا کمیتهای خاص تعریف شوند که در واقع معادلهای زاویهای متغیرها در سینماتیک خطیاند. مهمترین کمیتها در حرکت دورانی مشابه مهمترین کمیتهای حرکت خطی و شامل جابجایی زاویهای، سرعت زاویهای و شتاب زاویهای است.
جابجایی زاویهای یا معادل با زاویهای است که یک نقطه یا خط از یک جسم دوار حول یک محور مشخص به اندازه آن چرخیده است. این کمیت میتواند بر حسب رادیان، درجه یا دور بیان شود. در سیستم بینالمللی واحدها یا SI، واحد رادیان بهعنوان واحد استاندارد این کمیت در نظر گرفته میشود. میدانیم برای یک ذره که در یک مسیر دایرهای شکل با شعاع حرکت میکند، جابجایی زاویهای و طول کمان طی شده یا توسط رابطه زیر به هم مربوط میشوند:

کمیت بعدی سرعت زاویهای است که با نمایش داده میشود و معادل است با نرخی که موقعیت زاویهای یا جهتگیری یک جسم در طول زمان تغییر میکند. پس سرعت زاویهای نشان میدهد که جسم با چه سرعتی حول یک محور میچرخد. این کمیت برداری است و جهت آن معمولا با استفاده از قانون دست راست تعیین میشود، به این صورت که اگر انگشتان دست راست در جهت چرخش خم شوند، انگشت شست جهت بردار سرعت زاویهای را نشان میدهد.
اندازه سرعت زاویهای به شکل نرخ تغییرات زاویه در واحد زمان تعریف میشود:
که اگر آن را به شکل لحظهای و در قالب مشتقگیری ساده کنیم، به فرمول زیر میرسیم:
به همین شکل با مشتقگیری مجدد از این رابطه به شتاب زاویهای میرسیم:
بنابراین شتاب زاویهای همان نرخ تغییرات سرعت زاویهای با زمان است و مانند سرعت زاویهای، یک کمیت برداری محسوب میشود. همچنین شتاب مماسی یا یک نقطه روی یک جسم دوار توسط شتاب زاویهای و شعاع مسیر و از طریق رابطه زیر قابلتوصیف است:
این رابطه نشان میدهد که شتاب مماسی یک نقطه با فاصله گرفتن آن نقطه از محور چرخش افزایش مییابد، در حالی که شتاب زاویهای برای تمام نقاط یک جسم صلب در حال چرخش یکسان است. دقت کنید تفاوت شتاب زاویهای، شتاب مماسی و شتاب مرکزگرا اساس تحلیل مسیرهای منحنی شکل پیچیده را فراهم میکنند. شتاب زاویهای عامل تغییر در سرعت چرخشی کل جسم صلب است. این کمیت زاویهای بهطور یکنواخت برای کل جسم اعمال میشود. اما شتاب مماسی یک اثر خطی است که نرخ تغییر اندازه سرعت خطی یک نقطه خاص روی جسم دوار را توصیف میکند. این شتاب توسط شتاب زاویهای ایجاد میشود، مماس بر مسیر دایرهای است و مسئول افزایش یا کاهش سرعت حرکت خطی هر نقطه است.
همچنین شتاب مرکزگرا یا مرکزی () را داریم که یک اثر خطی است و نرخ تغییر جهت سرعت خطی یک نقطه خاص را توصیف میکند. این شتاب همواره به سمت مرکز دایره است و بدون وجود آن، امکان رخ دادن حرکت دایرهای وجود نداشت، یعنی جسم در یک خط مستقیم حرکت میکرد. دقت کنید شتاب مماسی و مرکزگرا همیشه بر یکدیگر عمود هستند و شتاب خطی کل یک نقطه در حرکت دایرهای، جمع برداری مولفههای مماسی و مرکزگرای آن است.
معادلات سینماتیک دورانی
معادلات سینماتیک دورانی در فیزیک ۱ کاملا مشابه با معادلات حرکت خطیاند. جدول زیر این فرمولها را نشان میدهد:
| نام کمیت | فرمول |
| سرعت زاویهای متوسط | |
| سرعت زاویهای نهایی | |
| شتاب زاویهای متوسط | |
| معادله سرعت زاویهای - زمان | |
| معادله مستقل از شتاب زاویهای | |
| معادله زاویه - زمان (درجه دو) | |
| معادله مستقل از زمان |
همچنین انرژی جنبشی دورانی را داریم که به دلیل چرخش جسم حول یک محور ایجاد میشود. این انرژی بخشی از انرژی جنبشی کل جسم است. فرمول انرژی جنبشی دورانی بر اساس کمیتی به نام لختی دورانی نوشته میشود که در بخش بعد آن را معرفی میکنیم.
لختی دورانی
لختی دورانی، جرم زاویهای یا لختی چرخشی یا ممان اینرسی کمیتی است که مقاومت یک جسم را در مقابل تغییر در حرکت دورانی یا گرفتن شتاب زاویهای توصیف میکند. این مفهوم با کمیت جرم در حرکت خطی متناظر است و همانطور که جرم مقاومت یک جسم را در برابر شتاب خطی نشان میدهد، لختی دورانی نیز مقاومت آن را در مقابل شتاب زاویهای نشان میدهد.
لختی دورانی همیشه نسبت به یک محور چرخش مشخص تعریف میشود و به توزیع جرم جسم حول آن محور بستگی دارد. بنابراین هر جسم بسته به اینکه حول کدام محور بچرخد، ممکن است لختی دورانی متفاوتی داشته باشد. واحد SI لختی دورانی کیلوگرم در متر مربع است. بنابراین برخلاف جرم، لختی دورانی یک خاصیت هندسی است که به توزیع جرم و محور چرخش انتخاب شده بستگی دارد، بر همین اساس روش محاسبه لختی دورانی یا برای یک جرم نقطهای مانند نسبت به یک محور مشخص برابر است با حاصلضرب آن جرم در مربع فاصله عمودی از محور چرخش یا :
اما در مورد توزیعهای پیوستهای از جرم مانند اجسام صلب، محاسبه لختی دورانی معمولا نیازمند انتگرالگیری است. لختی دورانی یک عنصر جرم بینهایت کوچک مانند از طریق انتگرالگیری این عنصر دیفرانسیلی روی کل جرم بهدست میآید:
این انتگرالها برای اشکال هندسی متداول مانند میله، دیسک یا کره انجام شده و در نتیجه، دارای فرمولهای استانداردی هستند. برای مثال، فرمول لختی دورانی برای میله نازکی با جرم و طول حول محور چرخش عبوری از مرکز و عمود بر طول آن برابر است با ، در حالی که همین فرمول اگر محور چرخش را از یک انتهای میله و عمود بر طول آن در نظر بگیریم، میشود .
قضیه محورهای موازی
این قضیه روش مناسبی است برای پیدا کردن لختی دورانی یک جسم حول هر محوری که موازی با محور عبوری از مرکز جرم آن جسم است:
در این فرمول لختی دورانی حول محوری است که از مرکز جرم میگذرد، جرم کل و فاصله عمودی بین دو محور موازی است.
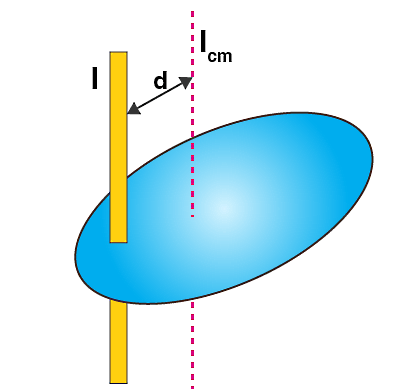
گشتاور نیرو
گشتاور نیرو مهمترین کمیت برداری در حرکت دورانی است که تمایل به ایجاد یا تغییر چرخش در یک جسم حول یک نقطه یا محور را توصیف میکند. فرمول گشتاور یا بهصورت حاصلضرب خارجی بردار نیرو در بردار فاصله عمودی یا از نقطه اثر نیرو تا محور چرخش تعریف میشود:
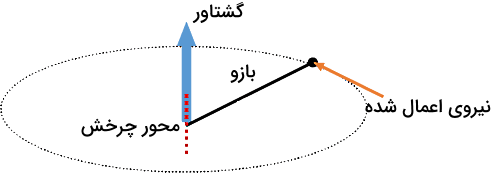
این فاصله عمودی را «بازوی گشتاور» مینامیم. واحد SI گشتاور نیوتن در متر است و جهت آن با استفاده از قانون دست راست تعیین میشود. همچنین میتوان گشتاور نیروی برآیند وارد بر یک سیستم را با نرخ تغییرات تکانه زاویهای آن سیستم برابر در نظر گرفت:
این رابطه، معادل چرخشی قانون دوم نیوتن برای حرکت خطی است، یعنی بهجای نیروی برآیند گشتاور و متناظر با تکانه خطی، تکانه زاویهای را داریم. همچنین رابطه گشتاور نیرو با شتاب زاویهای یا برای یک جسم صلب توسط لختی دورانی ثابت آن و بهصورت زیر بیان میشود:
پایستگی تکانه زاویه ای
اصل پایستگی تکانه زاویهای در فیزیک ۱ بیان میکند که در یک سیستم بسته که هیچ گشتاور خارجی برآیندی به آن وارد نمیشود، تکانه زاویهای کل سیستم ثابت میماند. این مسئله یک قانون بنیادی در فیزیک است، مشابه قانون پایستگی انرژی و تکانه خطی. گفتیم از نظر ریاضیاتی پایستگی تکانه زاویهای را میتوان از قانون دوم نیوتن استخراج کرد:
که طبق آن اگر گشتاور برآیند وارد بر جسمی صفر باشد، نرخ تغییرات تکانه زاویهای نیز برابر با صفر است و این به معنای ثابت بودن تکانه زاویهای است.
ترکیب دوران و انتقال
بسیاری از اجسام در دنیای واقعی بهطور همزمان حرکت انتقالی (جابجایی از یک مکان به مکان دیگر) و حرکت دورانی (چرخش حول یک محور) دارند. به همین علت در این بخش از فیزیک ۱ به این موضوع میپردازیم. برای مثال، غلتش بدون لغزش یک نمونه از این حرکت ترکیبی است که در آن یک جسم (مانند چرخ یا توپ) همزمان هم میچرخد و هم در امتداد یک سطح حرکت میکند، به گونهای که نقطه تماس آن با سطح در هر لحظه ساکن است.
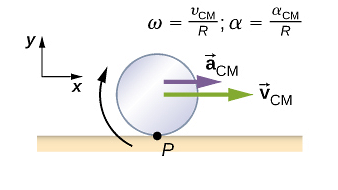
در این حالت سرعت مرکز جرم جسم با سرعت زاویهای و شعاع جسم از طریق رابطه بالا مرتبط است. پس در حرکت انتقالی تمام نقاط جسم با سرعت یکسان (سرعت مرکز جرم) حرکت میکنند، اما در حرکت دورانی حول مرکز جرم، نقاط مختلف جسم با سرعتهای مماسی متفاوتی حرکت میکنند که متناسب با فاصله آنها از محور چرخش است در حالی که نقاط روی محور ساکن هستند.
در غلتش بدون لغزش نیز نقطه تماس با سطح همان محور چرخش لحظهای است که سرعت آن صفر است. این در حالی است که نقطه مقابل یعنی دورترین فاصله از نقطه تماس، با دو برابر سرعت مرکز جرم حرکت میکند. همچنین یکی دیگر از مفاهیم مهم در ترکیب دوران و انتقال برای یک جسم، انرژی جنبشی کل آن است که از مجموع انرژی جنبشی انتقالی و انرژی جنبشی دورانی بهدست میآید. فرمول انرژی جنبشی کل برای یک جسم در وضعیت غلتش بدون لغزش بهصورت زیر است:
یادگیری مباحث مختلف فیزیک با فرادرس
در این مطلب از ملجه فرادرس آموختید که فیزیک ۱ چیست. در این قسمت قصد داریم مجموعهای از دروس انتخابی فیزیک را به شما معرفی کنیم که شامل برخی موضوعات کاربردیتر فیزیک است. با مشاهده این فیلمهای آموزشی از مجموعه فرادرس میتوانید یادگیری و تسلط خود را در برخی حوزههای تخصصیتر فیزیک تقویت کنید:
- فیلم آموزش رایگان تکنیک خلاء + گواهینامه
- فیلم آموزش فیزیک بدن انسان یا فیزیک پزشکی + گواهینامه
- فیلم آموزش مبانی طراحی اپتیکی + گواهینامه
- فیلم آموزش کار با میکروسکوپ الکترونی روبشی SEM
تعادل و استاتیک
تعادل در فیزیک ۱ شرایطی است که در آن برآیند تمام نیروها و گشتاورهای وارد بر جسم صفر میشود، به این معنا که یا جسم یا در حالت سکون قرار دارد و یا با سرعت ثابتی در حال حرکت است. بهعنوان مثال، کتابی که روی یک میز در حالت سکون قرار دارد، در تعادل استاتیکی است، زیرا نیروی عمودی سطح از میز به کتاب نیروی گرانش وارد بر کتاب را خنثی میکند و در نتیجه نیروی برآیند صفر میشود.

برای اینکه یک جسم در تعادل استاتیکی باشد، دو شرط لازم است:
- برقراری تعادل انتقالی: جمع برداری تمام نیروهای خارجی وارد بر جسم صفر است ().
- برقراری تعادل دورانی: جمع برداری تمام گشتاورهای خارجی حول هر نقطه دلخواه صفر است ().
پس با اینکه شرط صفر بودن نیروی برآیند برای داشتن تعادل انتقالی ضروری است، اما برای داشتن تعادل استاتیکی فقط برقرار بودن این شرط کافی نیست و باید تعادل دورانی نیز بررسی شود.
گرانیگاه چیست؟
گفتیم مرکز جرم یا Center of Mass نقطهای در یک جسم یا سیستم است که میتوان تمام جرم را در آن نقطه متمرکز در نظر گرفت. به این ترتیب اگر نیروی خارجی دقیقا روی مرکز جرم جسمی اعمال شود، فقط شتاب خطی داریم. بنابراین از نظر مفهومی این نقطه مکانی در فضا را نشان میدهد که میانگین توزیع جرم در آن قرار گرفته است. در این بخش از مطلب فیزیک ۱ مفهوم دیگری به نام «مرکز ثقل یا گرانیگاه» را معرفی میکنیم.
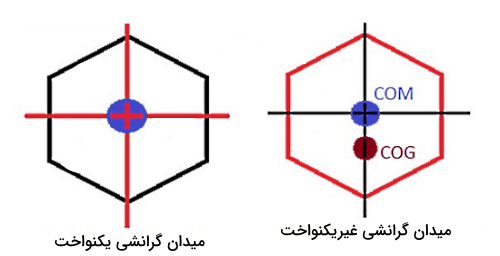
گرانیگاه یا Center of Gravity به نقطهای گفته میشود که گشتاور برآیند ناشی از نیروهای گرانشی حول آن صفر است. در یک میدان گرانشی یکنواخت مانند نزدیکی سطح زمین، مرکز جرم و مرکز ثقل بر هم منطبق هستند و اغلب بهجای یکدیگر استفاده میشوند. اما در یک میدان گرانشی غیر یکنواخت (مانند ماهوارههایی که به دور یک سیاره میچرخند)، این دو نقطه میتوانند کمی متفاوت باشند. برای مثال، در تصویر بالا ملاحظه میکنید که در یک میدان گرانشی غیریکنواخت مرکز جرم و مرکز ثقل منطبق بر هم نیستند (گرانیگاه در این شرایط معمولا به سمت منبع گرانش نزدیکتر است).
نوسان
نوسان در فیزیک ۱ نوعی حرکت تکراری یا رفت و برگشتی جسم یا سیستم حول یک نقطه تعادل پایدار است. ماهیت این حرکت چرخهای است، یعنی در بازههای زمانی منظم تکرار میشود. همچنین یک نیروی بازگرداننده که همواره سیستم را به سمت نقطه تعادل خود بازمیگرداند، برای رخ دادن چنین حرکتی لازم است.
نوسان با موج مرتبط است، به این معنا که یک موج را میتوان بهعنوان نوسانی در نظر گرفت که از طریق محیط یا فضا منتشر شده و انرژی و تکانه را با خود حمل میکند. نوسانات را میتوان با چندین ویژگی کلیدی توصیف کرد:
- دامنه یا : حداکثر جابجایی جسم نوسانکننده از نقطه تعادل آن است.
- دوره تناوب یا : مدت زمانی که برای کامل شدن یک چرخه کامل نوسان یا یک چرخه کامل موج لازم است.
- بسامد یا : تعداد چرخههای کامل نوسان یا امواج که در واحد زمان (معمولا در ثانیه) از یک نقطه خاص عبور میکنند ().
- بسامد زاویهای یا : نشاندهنده جابجایی زاویهای در واحد زمان است ().
- طول موج یا : فاصله بین بخشهای یکسان مجاور در موج است.
- سرعت موج یا : سرعتی که موج با آن منتشر میشود ().
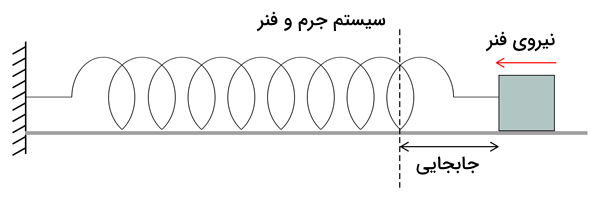
حرکت هماهنگ ساده یا به اختصار SHM نوع خاصی از نوسان است که در آن نیروی بازگرداننده وارد بر جسم با جابجایی آن از نقطه تعادل تناسب مستقیم دارد. قانون هوک نمونه کلاسیکی چنین نیروی بازگردانندهای است. این ویژگی منجر به وابستگی سینوسی حرکت به زمان شده و در نتیجه، روابط فازی خاصی بین جابجایی، سرعت و شتاب خواهیم داشت. در این نوع حرکت، انرژی پتانسیل و انرژی جنبشی مدام به یکدیگر تبدیل میشوند.
دو نمونه SHM عبارتاند از:
- سیستم جرم و فنر: دوره تناوب نوسان آن با داده میشود که در آن جرم و ثابت فنر است.
- آونگ ساده: در زاویههای کوچک، جابجایی یک آونگ ساده به SHM نزدیک میشود و دوره تناوب آن با داده میشود که در آن طول آونگ و شتاب گرانش است.
دقت کنید طبق روابط بالا، دوره تناوب آونگ از جرم آن و دوره تناوب سیستم جرم و فنر از طول فنر (در موارد ایدهآل) مستقل است.












