مفاهیم و کاربردهای ضرب داخلی — به زبان ساده
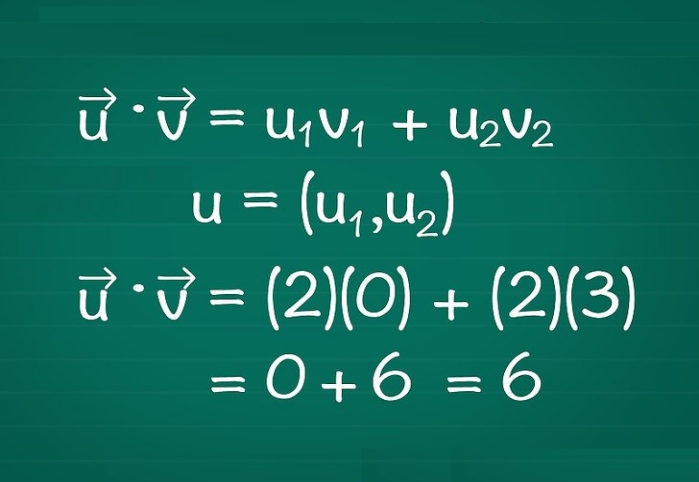
در مطالب گذشته وبلاگ فرادرس، مفاهیم مربوط به ضرب داخلی و ضرب خارجی را بیان کردیم. با این حال در مطالب مذکور، تنها مقدماتی از این مباحث مطرح شدند. از این رو در این مطلب قصد داریم تا مفاهیم و کاربردهایی بیشتر را در مورد ضرب داخلی توضیح دهیم.
تعریف ضرب داخلی
فرض کنید $$ \overrightarrow { v } $$ و $$ \overrightarrow { w } $$ دو بردار به صورت $$ \overrightarrow { v } = \left < v _ { 1 } , v _ { 2 } \right > $$ و $$ \overrightarrow { w } = \left < w _ { 1 } , w _ { 2 } \right > $$ باشند. در این صورت حاصل ضرب داخلی دو بردار $$ \overrightarrow { v } $$ و $$ \overrightarrow { w } $$ به صورت زیر تعریف میشود.
$$ \large \begin {align} \overrightarrow { v } \cdot \overrightarrow { w } &= \left < v _ { 1 } ,v _ { 2 } \right > \cdot \left < w _ { 1 } , w _ { 2 } \right > \\[5pt] &= v _ { 1 } w _ { 1 } + v_{ 2 } w _ { 2 } \end {align} $$
برای نمونه دو بردار $$ \overrightarrow { v } = \left < 3 , 4 \right > , \overrightarrow { w } = \left < 1 , - 2 \right > $$ را در نظر بگیرید. در این صورت حاصلضرب داخلی دو بردار برابر است با:
$$ \large \begin {align*} \overrightarrow { v } \cdot \overrightarrow { w } & = \left < 3 , 4 \right > \cdot \left < 1 ,- 2 \right > \\ & = ( 3 ) ( 1 ) + ( 4 ) ( - 2 ) = - 5 \end {align*} $$
همانطور که از مثال فوق نیز میتوان دید، ضرب داخلی، دو بردار را به عنوان ورودی دریافت کرده و خروجی آن عددی اسکالر است. در ادامه مهمترین ویژگیهای ضرب داخلی ذکر شدهاند.
- جابجایی: $$ \overrightarrow { v } \cdot \overrightarrow { w } = \overrightarrow { w } \cdot \overrightarrow { v } $$
- پخشپذیری: $$ \overrightarrow { u } \cdot \left ( \overrightarrow { v } + \overrightarrow { w } \right ) = \overrightarrow { u } \cdot \overrightarrow { v } + \overrightarrow { u } \cdot \overrightarrow { w } $$
- نردهای (اسکالر) بودن ضرب داخلی: $$ ( k \overrightarrow { v } ) \cdot \overrightarrow { w } = k ( \overrightarrow { v } \cdot \overrightarrow { w } ) = \overrightarrow { v } \cdot ( k \overrightarrow { w } ) $$
- توان دوم بودنِ اندازه بردار: $$ \overrightarrow { v } \cdot \overrightarrow { v } = \| \overrightarrow { v } \| ^ 2 $$
هریک از ویژگیهای فوق را میتوان با استفاده از قوانین ریاضیاتی اثبات کرد. به منظور اثبات ویژگی جابجایی، در ابتدا دو بردار $$ \overrightarrow { v } $$ و $$ \overrightarrow { w } $$ را در نظر بگیرید. در این صورت ویژگی جابجایی به صورت زیر اثبات میشود.
$$ \large {\begin {array} {rcll} \overrightarrow { v } \cdot \overrightarrow { w } & = & \left < v _ { 1 } , v _ { 2 } \right > \cdot \left < w _ { 1 } , w _ { 2 } \right > & \\ & = & v _ { 1 } w _ { 1 } + v _ { 2 }w _ { 2 } & \\ & = & w _ {1 }v _ { 1 } + w _ { 2 } v _ { 2 } & \\ & = & \left < w _ { 1} , w _ { 2 } \right > \cdot \left < v _ { 1 } , v _ { 2 } \right > & \\ & = & \overrightarrow {w} \cdot \overrightarrow { v } & \\ \end {array}} $$
توجه داشته باشید که ویژگی پخشپذیری نیز به طور مشابه قابل اثبات است. لذا اثبات این ویژگی به خواننده واگذار میشود.
مثال ۱
دو بردارِ $$ \overrightarrow { v } $$ و $$ \overrightarrow { w } $$ را در نظر بگیرید. با این فرض رابطه زیر را اثبات کنید.
$$ \large \| \overrightarrow { v } - \overrightarrow { w } \|^2 = \|\overrightarrow { v } \|^2 -2 ( \overrightarrow { v } \cdot \overrightarrow { w } ) + \|\overrightarrow { w } \| ^ 2 $$
توجه داشته باشید که در ویژگیهای بالا بیان شد که حاصلضرب داخلی یک بردار در خودش برابر با توان دوم اندازه بردار است. بنابراین این اثبات را میتوان به ترتیب انجام داد.
$$ \begin {array} {rcl} \| \overrightarrow { v } - \overrightarrow { w } \|^2 & = & (\overrightarrow{v} - \overrightarrow{w}) \cdot (\overrightarrow{v} - \overrightarrow { w } ) \\ & = & (\overrightarrow{v} + [-\overrightarrow{w}]) \cdot (\overrightarrow{v} + [-\overrightarrow{w}]) \\ & = & (\overrightarrow { v } + [-\overrightarrow { w } ]) \cdot \overrightarrow{v} +(\overrightarrow { v } + [-\overrightarrow{w}]) \cdot [-\overrightarrow{w}] \\ & = & \overrightarrow { v } \cdot (\overrightarrow{v} + [-\overrightarrow { w }]) + [-\overrightarrow{w}] \cdot (\overrightarrow{v} + [-\overrightarrow { w } ]) \\ & = & \overrightarrow{v} \cdot \overrightarrow{v} + \overrightarrow { v } \cdot [-\overrightarrow{w}] + [-\overrightarrow { w }]\cdot \overrightarrow{v} + [-\overrightarrow{w}]\cdot[-\overrightarrow{w}] \\ & = & \overrightarrow{v} \cdot \overrightarrow{v} + \overrightarrow { v } \cdot [(-1)\overrightarrow{w}] + [(-1)\overrightarrow { w } ]\cdot \overrightarrow{v} +[(-1)\overrightarrow{w}]\cdot[(-1)\overrightarrow{w}] \\ & = & \overrightarrow{v} \cdot \overrightarrow { v } + (-1)( \overrightarrow { v } \cdot \overrightarrow{w}) + (-1)(\overrightarrow { w } \cdot \overrightarrow{v}) + [(-1)(-1)] ( \overrightarrow { w } \cdot\overrightarrow { w } ) \\ & = & \overrightarrow { v } \cdot \overrightarrow { v } + ( - 1 ) ( \overrightarrow { v } \cdot \overrightarrow { w } ) + ( - 1 ) ( \overrightarrow { v } \cdot \overrightarrow { w } ) + \overrightarrow { w } \cdot\overrightarrow{w} \\ & = & \overrightarrow{v} \cdot \overrightarrow{v} -2(\overrightarrow{v} \cdot \overrightarrow { w } ) + \overrightarrow { w } \cdot\overrightarrow { w } \\ & = & \|\overrightarrow { v } \|^2-2(\overrightarrow{v} \cdot \overrightarrow{w}) + \|\overrightarrow { w }\|^2 \\ \end {array} $$
بیان هندسی ضرب داخلی
اگر $$ \overrightarrow { v } $$ و $$ \overrightarrow { w } $$ دو بردارِ فرضی باشند، در این صورت میتوان زاویه $$\theta$$ را نیز میان آنها در نظر گرفت. در نتیجه میتوان گفت رابطه هندسیِ ضرب داخلی به صورت زیر بیان میشود.
$$ \large \overrightarrow { v } \cdot \overrightarrow { w } = \|\overrightarrow { v } \| \|\overrightarrow { w } \| \cos ( \theta ) $$
اثبات رابطه فوق را در حالتی در نظر میگیریم که دو بردار موازی باشند. در حقیقت در این حالت زاویه $$ \theta = 0 $$ در نظر گرفته میشود. در این صورت میتوان این بردارها را با استفاده از بردارهای یکه $$ \widehat { v } , \widehat { w } $$ نشان داد. توجه داشته باشید که با توجه به موازی بودن دو بردار میتوان رابطه بین بردارهای یکه را به صورت $$ \widehat { v }=\widehat { w } $$ نشان داد. از طرفی بردار $$ \overrightarrow { w } $$ را میتوان به صورت زیر بیان کرد:
$$ \large { \overrightarrow { w } = \|\overrightarrow{w}\| \widehat { v } = \frac {\| \overrightarrow { w } \|} { \| \overrightarrow { v } \|} (\| \overrightarrow{v} \| \widehat { v } ) = \frac { \| \overrightarrow { w } \|}{\| \overrightarrow { v } \| } \overrightarrow { v } } $$
نسبت دو بردار، عددی مثبت است. در حقیقت میتوان این نسبت را به صورت زیر نشان داد.
$$ \large k = \frac {\| \overrightarrow { w } \|} { \| \overrightarrow { v } \| } > 0 $$
عدد فوق نشان میدهد که عددی مثبت تحت عنوان $$k$$ وجود دارد که میتوان آن را در رابطه زیر قرار داد.
$$ \large \overrightarrow { w } = k \overrightarrow { v } $$
بنابراین حاصلضرب داخلی دو بردار را میتوان به صورت زیر بیان کرد:
$$ \large \begin {align*} \overrightarrow { v } \cdot \overrightarrow { w } & = \overrightarrow { v } \cdot (k \overrightarrow { v } )
\\ & = k ( \overrightarrow { v } \cdot \overrightarrow { v } ) = k \|\overrightarrow { v } \|^2 \\ & = k \| \overrightarrow { v } \| \|\overrightarrow { v} \| \end {align*} $$
با توجه به مثبت بودن $$k$$، میتوان رابطه زیر را ارائه کرد.
$$\large k \|\overrightarrow { v } \| = | k | \|\overrightarrow { v } \| = \| k \overrightarrow { v } \| $$
بنابراین حاصلضرب داخلی نیز به صورت زیر قابل بازنویسی است.
$$ \large \begin {align*} k \| \overrightarrow { v } \| \|\overrightarrow { v } \| & = \| \overrightarrow { v } \| ( k \|\overrightarrow {v } \| ) = \|\overrightarrow { v } \| \|k \overrightarrow { v } \| \\ & = \|\overrightarrow { v } \| \|\overrightarrow { w } \| \end {align*} $$
با توجه به این که مقدار کسینوس برابر با $$ \cos(0) = 1 $$ است، بنابراین میتوان ضرب داخلی را به صورت زیر ارائه داد.
$$\large \begin {align*} \overrightarrow { v } \cdot \overrightarrow { w } & = k \| \overrightarrow { v } \| \| \overrightarrow { v } \| = \|\overrightarrow{v} \| \|\overrightarrow { w } \| \\ & = \|\overrightarrow { v } \| \|\overrightarrow { w } \| \cos(0) \end {align*} $$
در حالتی که زاویه بین دو بردار برابر $$\pi$$ باشد، مقدار $$k$$ نیز منفی است. در حقیقت اندازه بردار $$w$$ را میتوان به صورت زیر نشان داد.
$$\large k \|\overrightarrow { v } \| = -| k | \| \overrightarrow { v } \| = -\| k \overrightarrow { v } \| = -\| \overrightarrow { w } \| $$
در حقیقت رابطه فوق به صورت زیر قابل بیان است.
$$ \large \overrightarrow { v } \cdot \overrightarrow { w } = -\|\overrightarrow { v } \| \| \overrightarrow { w } \| = \| \overrightarrow { v } \| \|\overrightarrow { w } \| \cos( \pi ) $$
در حالتی عمومیتر اگر $$ 0 < \theta < \pi $$ در نظر گرفته شود، در این صورت سه بردارِ $$ \| \overrightarrow{v} \| , \| \overrightarrow{w} \| $$ و $$ \| \overrightarrow{v} - \overrightarrow{w} \| $$، مثلثی را تشکیل میدهند. بنابراین با استفاده از قانون کسینوسها رابطه زیر قابل بیان است.
$$ \| \overrightarrow { v } - \overrightarrow { w } \| ^ 2 = \|\overrightarrow { v } \| ^ 2 + \|\overrightarrow { w } \|^2 - 2 \|\overrightarrow { v } \| \|\overrightarrow { w } \| \cos ( \theta ) $$
در نتیجه اندازه بردار نیز به صورت زیر قابل بیان است:
$$ \large \|\overrightarrow { v } - \overrightarrow { w } \| ^ 2 = \|\overrightarrow { v } \|^2 -2 ( \overrightarrow { v } \cdot \overrightarrow { w } ) + \|\overrightarrow { w } \| ^ 2 $$
با برابر قرار دادن دو رابطه فوق، عبارت زیر بدست خواهد آمد.
$$\large \overrightarrow {v}.\overrightarrow {w} = |v||w|\cos \theta $$
بنابراین زاویه بین دو بردار برابر است با:
$$ \large \theta = \arccos \left( \dfrac { \overrightarrow{v} \cdot \overrightarrow { w } } { \| \overrightarrow { v } \| \|\overrightarrow{w} \| } \right ) = \arccos ( \widehat{v} \cdot \widehat { w } ) $$
مثال ۲
زاویه بین بردارهای $$\overrightarrow { v } \ , \ \overrightarrow{w} $$ که در ادامه ذکر شده را بدست آورید.
- $$ \overrightarrow{v} = \left < 3 , - 3 \sqrt { 3} \right > \ , \ \overrightarrow { w } = \left < - \sqrt { 3 } , 1 \right > $$
- $$ \overrightarrow{v} = \left < 2 , 2 \right > \ , \ \overrightarrow { w } = \left < { 5 } , -5 \right > $$
- $$ \overrightarrow{v} = \left < 3 , -4 \right > \ , \ \overrightarrow { w } = \left < { 2 } , 1 \right > $$
بدیهی است که به منظور پاسخ به سئوال، باید از رابطه $$ \theta =arc \cos ( \frac { \overrightarrow { v } . \overrightarrow { w } } { || \overrightarrow { v } || \ ||\overrightarrow { w } || } ) $$ استفاده کرد.
(۱): در اولین قدم حاصل ضرب داخلی را مطابق با رابطه زیر محاسبه میکنیم.
$$ \large \begin {align*} \overrightarrow { v } \cdot \overrightarrow { w } & = \left < 3, -3\sqrt{3} \right> \cdot \left < - \sqrt { 3 } , 1 \right > \\ & = - 3 \sqrt{3} - 3\sqrt{3} = -6 \sqrt { 3 } \end {align*} $$
در قدم دوم باید اندازه بردارها را محاسبه کرد.
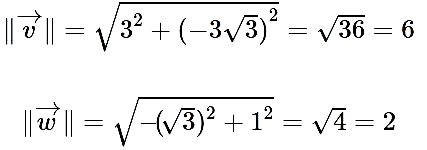
در نتیجه نهایتا میتوان زاویه بین دو بردار را به صورت زیر محاسبه کرد.
$$ \large { \theta = \arccos\left(\frac { - 6 \sqrt { 3 } }{ 1 2 } \right ) = \arccos \left (-\frac { \sqrt { 3 } } { 2 } \right ) = \frac { 5 \pi } { 6 } } $$
زاویه بین دیگر بردارهای ارائه شده در این مثال را نیز میتوان به همین صورت بدست آورد.
(۲): نکته جالب در این مثال این است که نیازی به محاسبه اندازه دو بردار وجود ندارد. دلیل این امر صفر بودن حاصلضرب داخلی است.
$$ \large \begin {gather*} \overrightarrow{v} \cdot \overrightarrow{w} = \left< 2, 2 \right> \cdot \left<5, -5\right> = 10-10 = 0 \\~\\ \| u \| = \sqrt { 2 ^2 + 2 ^ 2 } = 2 \sqrt { 2 } \ , \ \| v \| = \sqrt {5^2+5^2} = 5 \sqrt { 2 } \\~\\ \theta = \arccos\left( \frac { \overrightarrow { v } \cdot \overrightarrow { w } }{\| \overrightarrow { v } \| \|\overrightarrow { w } \|}\right ) = \arccos ( 0 ) = \frac { \pi } { 2 } \end {gather*} $$
(۳): در این حالت نیز زاویه بین دو بردار همانند حالات قبل بدست میآید.
$$ \large \begin {gather*} \overrightarrow { v } \cdot \overrightarrow { w } = \left < 3 , - 4 \right > \cdot \left < 2, 1\right > = 6 - 4 = 2 \\~\\ \| \overrightarrow{v} \| = \sqrt{3^2+(-4)^2} = \sqrt{25} = 5 \ , \ \overrightarrow { w } = \sqrt { 2 ^ 2 + 1 ^ 2 } = \sqrt { 5 } \\~\\ \theta = \arccos \left ( \frac { 2 } { 5 \sqrt { 5} } \right ) = \arccos \left ( \frac { 2 \sqrt { 5} } { 2 5 } \right ) \end {gather*} $$
در مثالی که در آخر ذکر شد، دو بردار به یکدیگر عمود بودند. توجه داشته باشید که همواره حاصل ضرب داخلی دو بردار عمود به هم برابر با صفر است. همچنین میتوان گفت که اگر ضرب داخلی دو بردار برابر با صفر باشد، در این صورت دو بردار بر هم عمود هستند.
$$ \large { \overrightarrow { v } \perp \overrightarrow { w } \Leftrightarrow \overrightarrow { v } \cdot \overrightarrow { w } = 0 } $$
گزاره فوق در مسائل هندسی کاربرد بسیاری خواهد داشت. در ادامه مثالی از این کاربرد ارائه شده است.
مثال ۳
$$L_1$$ را برابر با خطی با معادله $$ y = m _ { 1 } x + b _ { 1 } $$ در نظر بگیرید. همچنین خط دوم یا $$L_2$$ را برابر با معادله $$ y = m _ { 2 } x + b _ { 2 } $$ فرض کنید. با این فرضیات نشان دهید که دو خط $$L_1$$ و $$L_2$$ زمانی به یکدیگر عمود هستند که رابطه زیر بین شیبها برقرار باشد.
$$\large m _ { 1 } \cdot m _ { 2 } = - 1 $$
روش حل به این صورت است که باید بردار $$v_1$$ متناظر با $$L_1$$ و $$v_2$$ متناظر با $$L_2$$ را یافته و حاصل ضرب داخلی آنها را بر حسب شیبهای $$m_1$$ و $$m_2$$ بیان کرد. به منظور یافتن بردارهای مذکور کافی است دو نقطه را روی هرکدام از خطوط یافته و با وصل کردن آنها بردارها بدست میآیند. به منظور راحتی کار از دو نقطه $$x=0$$ و $$x=1$$ برای محاسبه بردارها استفاده میکنیم. در ابتدا این دو نقطه را روی $$L_1$$ محاسبه میکنیم.
$$ L _ 1 \ \ : \large \begin {cases} x=0 \Rightarrow y = b _ 1 \\ x = 1 \Rightarrow y = m _ 1 + b _ 1 \end {cases} $$
بنابراین بردار $$ v _ 1 $$ برابر است با:
$$\large \overrightarrow { v_ { 1 } } = \left < 1 - 0 , ( m _ { 1 } +b _ { 1 } ) - b _ {1 } \right > = \left <1 , m_ { 1 } \right > $$
دقیقا مشابه با همین حالت، دو نقطه $$x=0$$ و $$x=1$$ را در معادله $$ L _ 2 $$ قرار میدهیم.
$$ L _ 2 \ \ : \large \begin {cases} x=0 \Rightarrow y = b _ 2 \\ x = 1 \Rightarrow y = m _ 2 + b _ 2 \end {cases} $$
بنابراین بردار $$ v _ 2 $$ نیز برابر خواهد بود با:
$$ \large \overrightarrow{ v _ { 2 } } = \left < 1 , m _ { 2 } \right > $$
حال با بدست آمدن دو بردار، حاصل ضرب داخلی آنها را به صورت زیر بدست میآوریم:
$$ \large \begin {align*} \overrightarrow{ v _ { 1 } } . \overrightarrow { v _ { 2 } } & = 1 × 1 + m _ 1 × m _ 2 \end {align*} $$
در صورت سوال گفته شده که دو خط بر هم عمود هستند؛ بنابراین ضرب داخلی بردارهای مرتبطِ آنها باید صفر شود. در نتیجه با صفر قرار دادن رابطه فوق ارتباط بین $$ m _ 1 $$ و $$ m _ ۲ $$ برابر خواهد بود با:
$$ \large \begin {gather*} \overrightarrow{ v _ { 1 } } . \overrightarrow { v _ { 2 } } = 1 × 1 + m _ 1 × m _ 2 = 0 \\ \Rightarrow m _ 1 m _ 2 = - 1 \end {gather*} $$
تصویرِ بردار
تاکنون از ضرب داخلی به منظور شناسایی وضعیت دو خط استفاده کردیم. این در حالی است که یکی دیگر از کاربردهای ضرب داخلی در بدست آوردن تصویر یک بردار روی بردار دوم است. بدین منظور مطابق با شکل زیر دو بردار $$ \overrightarrow {v} $$ و $$ \overrightarrow {w} $$ را در نظر بگیرید.
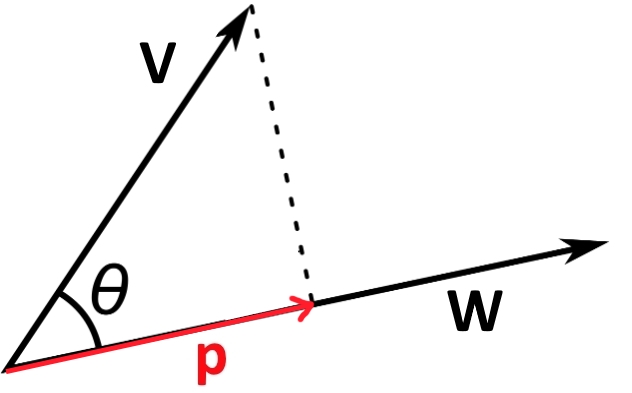
همانطور که از شکل فوق نیز میتوان دید، جهت بردار $$ \overrightarrow {p} $$ در راستای بردار $$ \overrightarrow {w} $$ است. بنابراین کافی است اندازه این بردار را بدست آورده و آن را در بردار یکه $$ \widehat {w} $$ ضرب کرد. اندازه بردار $$ \overrightarrow {p} $$ برابر است با:
$$ \large \begin {align*} \| \overrightarrow { p } \| & = \| \overrightarrow{v} \| \cos ( \theta ) \\\\ & = \frac { \| \overrightarrow { v } \| \| \overrightarrow { w } \| \cos ( \theta ) } { \| \overrightarrow { w } \|} \\\\ & = \frac { \overrightarrow { v } \cdot \overrightarrow { w } } { \|\overrightarrow { w } \| } \end {align*} $$
مقدار فوق عددی اسکالر است. از این رو باید آن را در بردار یکه $$ \widehat {w} $$ ضرب کرده و بردار $$ \overrightarrow {p} $$ بدست خواهد آمد.
$$ \large \begin {align*} \overrightarrow { p } = \| \overrightarrow { p } \| \widehat { p } = ( \overrightarrow { v } \cdot \widehat { w } ) \widehat { w } \end {align*} $$
از طرفی بردار یکه $$ \widehat {w} $$ برابر است با:
$$\large \begin {align*} \widehat { w } = \frac { \overrightarrow { w } } { | w | } \end {align*} $$
از طرفی پیشتر بیان کرده بودیم که توان دوم اندازه یک بردار را میتوان به صورت حاصلضرب داخلی بردار در خودش در نظر گرفت. در مورد $$w$$ نیز میتوان رابطه زیر را بیان کرد:
$$\large \begin {align*} { \overrightarrow { w } }.{ \overrightarrow { w } } = |w | ^ 2 \end {align*} $$
بنابراین نهایتا تصویر بردار $$\overrightarrow v$$ در راستای $$\overrightarrow w$$ را میتوان با ادغام روابط فوق و به صورت زیر بدست آورد.
$$ \large \begin {align*} \overrightarrow { p } & = ( \overrightarrow { v } \cdot \widehat { w } ) \widehat { w } \\\\ & = \left ( \dfrac { \overrightarrow { v } \cdot \overrightarrow { w } } { \| \overrightarrow { w } \|^2} \right ) \overrightarrow { w } = \left ( \dfrac { \overrightarrow { v } \cdot \overrightarrow { w } } { \overrightarrow { w } \cdot \overrightarrow { w } } \right ) \overrightarrow { w } \end {align*} $$
در ادامه با استفاده از مثالی مفهوم تصویر بردار را بیشتر توضیح خواهیم داد.
مثال ۴
دو بردار $$ \begin {align*} \overrightarrow { v } = \left < 1,8 \right > \end {align*} $$ و $$ \begin {align*} \overrightarrow { w } = \left < - 1,2 \right > \end {align*} $$ را در نظر بگیرید. با این فرض، تصویر بردار $$v$$ را در راستای بردار $$w$$ بیابید.
در اولین قدم حاصل ضرب داخلی دو بردار را به شکل زیر محاسبه میکنیم.
$$\large \overrightarrow{v} \cdot \overrightarrow{w} = \left<1,8\right> \cdot \left<-1,2\right> = (-1) + 16 = 15$$
در نتیجه تصویر بردار $$v$$ نیز برابر خواهد بود با:
$$\large \overrightarrow{p} = \frac{\overrightarrow{v} \cdot \overrightarrow{w}}{\overrightarrow{w} \cdot \overrightarrow{w}} \overrightarrow{w} = \frac{15}{5} \left<-1,2\right> = \left<-3,6\right>$$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضیات، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشی دروس دبیرستان
- مجموعه آموزشهای ریاضی و فیزیک
- بردار و اسکالر -- به زبان ساده
- بردار — به زبان ساده
- ضرب خارجی بردارها — به زبان ساده
^^











سلام ببخشید من در تمام منابع اینترنت در رابطه با اثبات ضرب داخلی تحقیق کردم و فقط به صورت سر بسته اشاره شده و از تفریق بردار ها استفاده شده دلیل این استفاده چیست خب چرا از مجموع بردار ها استفاده نشده میدونم شما اثبات کردید ولی کسی که این فرمول رو درست کرده چطوری و با چه منطقی این رابطه رو اثبات کرده