حرکت شناسی در فیزیک — به زبان ساده

در آموزشهای گذشته فیزیک در مورد حرکت پرتابی صحبت کردیم. اما همانطور که احتمالا میدانید این نوع حرکت، حالت خاصی از حرکت در صفحه دوبعدی محسوب میشود. از این رو در این مطلب قصد داریم تا معادلات مربوط به حرکت شناسی در صفحه دوبعدی را توضیح داده و مثالهایی نیز از آن ارائه دهیم.
حرکت شناسی
ذره به مفهومی اطلاق میشود که نشاندهنده یک موقعیت نقطهای در فضا باشد. به مجموعهای از ذرات نیز که در فضایی اندک جمع شده باشند، جسم گفته میشود. اما گاهی میتوان این مفاهیم را به جای یکدیگر نیز بهکار برد. برای نمونه زمین در مقیاس مدارش که به دور خورشید حرکت میکند، میتواند به عنوان یک ذره در نظر گرفته شود. این در حالی است که برای شخصِ قرار گرفته روی زمین، جسمی با ابعاد بینهایت به نظر میآید.
حال ذرهای را در نظر بگیرید که با سرعت $$ v $$ در حال حرکت باشد. برای این ذره جابجایی پس از گذشت مدت زمان $$ t $$ برابر است با:
$$ \large s = v t $$
همچنین اگر سرعت اولیه جسم برابر با $$ v _ 0 $$ بوده و شتاب ثابت $$ a $$ را داشته باشد، میتوان جابجایی $$ s $$ و سرعت لحظهای $$ v _ f $$ را به صورت زیر بیان کرد:
$$ \large \begin {align*} v _ f & = v _ i + a t \\ s & = v _ i t + \frac { 1 }{ 2 } a t ^ 2 \\ { v _ f } ^ 2 & = { v _ i } ^ 2 + 2 a s \end {align*} $$
حال فرض کنید که معادلات فوق برای جسمی نوشته میشود که از ارتفاع $$ h $$ سقوط میکند. با فرض اینکه زمان سقوط آن $$ t $$، ارتفاع سقوط برابر با $$ h $$ و سرعت برخورد جسم با زمین برابر با $$ v $$ باشد، معادلات فوق را میتوان برای این پارامترها بهصورت زیر بازنویسی کرد.
$$ \large \begin {align*} v & = g t \\ h & = \frac { 1 }{ 2 } g t ^ 2 \\ { v } ^ 2 & = 2 g h \end {align*} $$
اما کلیترین حالت حرکت زمانی است که خود شتاب نیز متغیر باشد. در این شرایط رابطه بین پارامترها را میتوان برحسب مشتق، به صورت زیر بیان کرد:
$$ \large \begin {align*} a & = \dfrac { d v } { d t } \\ v & = \dfrac { d s } { d t } \\ v d v & = a d s \end {align*} $$
در این حالت میتوان گزارههای زیر را بیان کرد:
- شتابِ $$ a $$ در صورت افزایشی بودنِ $$ v $$، مثبت است.
- شتابِ $$ a $$ در صورت کاهشی بودن $$ v $$، منفی است.
- در حالتی که جسم به سمت پایین حرکت کند، شتاب ذره یا همان $$ g $$، مثبت است.
به مثالهایی که در ادامه ارائه شده توجه فرمایید.
مثال ۱
مطابق با شکل زیر توپی از برجی به ارتفاع 24.38 متر رها میشود. در همان لحظه توپ دوم با سرعت ۱۲.۱۹ متر بر ثانیه به سمت بالا پرتاب میشود. در چه ارتفاع و در چه زمانی دو توپ از کنار هم عبور میکنند. همچنین سرعت نسبی این دو توپ در هنگام رد شدن از کنار یکدیگر چقدر است.
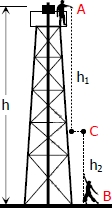
دادههای این مسئله بهصورت زیر هستند.
$$\begin {gather*} h = 24.38 \ m \\
v _ A = 0 \\
v _ B = 12.19 \ m / s \\
g = 9.81 \ m / s ^ 2 \end {gather*} $$
در ابتدا مسافت طی شده توسط جرم رها شده را برابر با $$ h _ 1 $$ و فاصله طی شده توسط جسم پرتاب شده را برابر با $$ h _ 2 $$ مینامیم. توجه داشته باشید که هر دوی این مسافتها مربوط به لحظه رسیدن این دو جسم به یکدیگر هستند. با استفاده از رابطه مربوط به جابجایی، ارتباط بین مسافت سقوط و زمان از نقطه $$ A $$ به $$ C $$ بهصورت زیر قابل بیان است:
$$ \large \begin {gather*} h _ 1 = 12 g t ^ 2 \\
h _ 1 = 12 ( 9.81 ) t ^ 2 \\
h _ 1 = 4.905 t ^ 2 \end {gather*} $$
از طرفی برای جسم پرتاب شده در مسیر $$ B $$ به $$ C $$ نیز رابطه زیر قابل بیان است.
$$ \large \begin {gather*} s = v_i t + \frac { 1 } { 2 } a t ^ 2 \\
h _ 2 = v _ B t−12 g t ^ 2 \\
h _ 2 = 12.19 t−12 ( 9.81 ) t ^ 2 \\
h _ 2 = 12.19 t − 4.905 t ^ 2 \end {gather*} $$
بدیهی است که حاصل جمع دو مسافت طی شده در بالا برابر با ارتفاع برج خواهد بود. در نتیجه با جمع کردن این دو مسافت و برابر قرار دادن آن با ارتفاع برج، زمان برخورد آنها و دیگر مجهولات همچون ارتفاع آنها در لحظه سقوط بدست خواهند آمد. در نتیجه لحظه رسیدن دو جسم بهصورت زیر بدست میآید.
$$ \large \begin {gather*} h _ 1 + h _ 2 = h \\
4.905 t ^ 2 + ( 12.19 t − 4.905 t ^ 2 ) = 24.38 \\
12.19 t = 24.38 \\
t = 2 \ sec \end {gather*} $$
همچنین در ارتفاع زیر، دو توپ به یکدیگر خواهند رسید.
$$ \large \begin {gather*} h _ 1 = 4 . 9 0 5(22) \\
h _ 1 = 19.62 m \end {gather*} $$
بنابراین تاکنون زمانی که دو توپ از کنار هم رد میشوند و ارتفاع سقوط آنها را بدست آوردیم. از طرفی سرعت جسم اول (جسم رها شده) در لحظه بدست آمده، برابر است با:
$$ \large \begin {gather*} v _ { C 1 } = g t = 9.81 ( 2 ) \\
v _ { C 2 } = 19 . 62 \ m / s \end {gather*} $$
به همین صورت سرعت جسم $$ B $$ نیز در لحظه رسیدن دو جسم، برابر با مقدار زیر بدست میآید.
$$ \large \begin {gather*} v _ { C 2 } = v _ B - g t = 12.19 - 9 . 8 1( 2 ) \\ v _ { C 2 } = -7.43 \, \text{ m/s}\end {gather*} $$
همانطور که مشاهده میکنید مقدار این سرعت، عددی منفی بدست آمده است. بنابراین میتوان گفت که اندازه سرعت در این لحظه به سمت پایین است. در نتیجه نهایتا سرعت نسبی دو جسم در لحظه رسیدن آنها به هم برابر است با:
$$ \large \begin {gather*} v _ r = v _ { C 1 } + v _ {C 2 } = 19.62 - 7.43 \end {gather*} $$
توجه داشته باشید که دو جسم در یک جهت حرکت میکنند به همین دلیل مقادیر مطلق سرعتهای بدست آمده از یکدیگر کم شدهاند.
مثال ۲
فرض کنید بالای چاه آبی ایستادهایم و سنگی را رها میکنیم. با فرض اینکه $$ 5 $$ ثانیه پس از پرتاب صدای برخود سنگ با آب را بشنویم، ارتفاع چاه آب چقدر است. سرعت صوت را برابر با $$ 341.376 $$ متر بر ثانیه در نظر بگیرید.
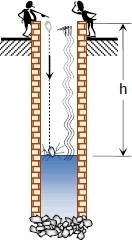
اجازه دهید با هم فیزیک این مسئله را مرور کنیم. در ابتدا سنگ به سطح آب میرسد با سطح آب برخورد میکند؛ سپس امواج صوتی از سطح آب منتشر شده و به گوش میرسد. بنابراین مجموع زمان سقوط جسم و زمان انتقال امواج به گوش ما برابر با کل مدت زمانی است که بین رها شدن جسم و رسیدن صدای آن طول میکشد. اگر زمان رسیدن سنگ به سطح آب را با $$ \begin {gather*} t _ { stone } \end {gather*} $$ و زمان بازگشت صوت از سطح را با $$ \begin {gather*} t _ { sou nd } \end {gather*} $$ نشان دهیم، در این صورت حاصل جمع آنها برابر است با:
$$ \large t _ { stone } + t _ { sound } = 5 $$
از طرفی مدت زمانی که طول میکشد که سنگ به سطح آب برسد، برابر است با:
$$ \large h = \frac { 1 } { 2 } g t _ { stone } ^ 2 $$
$$ \large t _ { stone } = \sqrt { \dfrac { 2 h } { g } } $$
به همین صورت اگر $$ v $$ را برابر با سرعت صوت در نظر بگیریم، در این صورت مدت زمان انتقال امواج صوتی از سطح آب به سطح زمین، نیز برابر است با:
$$ \large \begin {gather*} h = v t \ \\ t = \dfrac { h } { v } \end {gather*} $$
در نتیجه زمان بین رها شدن سنگ و شنیدن صدای برخورد برابر است با:
$$ \large \begin {gather*} \sqrt { \dfrac { 2 h } { g } } + \dfrac { h } { v } = 5 \end {gather*} $$
در معادله فوق تنها مجهول برابر با $$ h $$ است. از این رو با حل این معادله، مقدار $$ h $$ نیز برابر با مقدار زیر بدست میآید.
$$ \large \begin {gather*} \sqrt {{ \left( \dfrac { 2 h } { 9 .81 } \right) }} + \dfrac { h } { 341.376 } = 5 \\ \sqrt { \left( \dfrac { 2 h } { 9 .81 } \right) } = 5 - \dfrac { h } { 341.376 } \\ \sqrt { \left( \dfrac { 2 h } { 9 .81 } \right) } = 5 - \left( \dfrac { 2 h } { 9 .81 } \right) \\ \left( \dfrac { 2 h } { 9 .81 } \right) = \left ( 5 - \left( \dfrac { 2 h } { 9 .81 } \right) \right ) ^ 2 \\ \left( \dfrac { 2 h } { 9 .81 } \right) = 25 - \left( \dfrac { 2 h } { 9 .81 } \right) + \left( \dfrac { 2 h } { 9 .81 } \right) \\ \left( \dfrac { 2 h } { 9 .81 } \right) h ^ 2 - \left( \dfrac { 2 h } { 9 .81 } \right) h + 25 = 0 \\ \\ h = 27\,065.05 \, \text{ , } \, 107.64 \end {gather*} $$
بنابراین دو مقدار برای $$ h $$ بدست میآید. اما این سوال مطرح میشود که کدامیک از این پاسخها قابل قبول هستند؟ بدین منظور کافی است با استفاده از ارتفاع بدست آمده، زمان سقوط را دوباره بدست آورد. زمانی به عنوان پاسخ صحیح خواهد بود که مقدار آن مثبت و کمتر از $$ 5 $$ ثانیه باشد. ارتفاع اولیه، مقدار زیر را به ما میدهد.
$$ h = 27 065.05 \ m $$
$$ \large \begin {gather*} \Rightarrow t = \sqrt { \dfrac { 2 ( 27\,065.05 ) } { 9.81 } } \\ t = 74.2 ~ \text{sec} ~ \gt 5 ~ \text{sec} \\ \end {gather*} $$
همانطور که میبینید پاسخ بدست آمده بیشتر از $$ 5 $$ ثانیه است؛ بنابراین عدد $$ 27 065.05 $$ را نمیتوان به عنوان پاسخ در نظر گرفت. برای ارتفاع دوم نیز مدت زمان مرتبط با آن برابر است با:
$$ \large \begin {gather*} h = 107.64 \ m \\ t = \sqrt { \dfrac { 2 ( 107 . 64 ) } { 9.81 } } \\ t = 4.68 ~ \text {sec} \lt 5 ~ \text {sec} \end {gather*} $$
بنابراین ارتفاع این چاه برابر با $$ h = 107.64 m $$ است.
در صورت علاقهمندی به مباحث مرتبط در زمینه فیزیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:










