استاتیک – به زبان ساده

شاید مهم‌ترین کاربرد قوانین مکانیک، مطالعه ساختارهای ساکن باشد. به این بخشِ بنیادین از علم مکانیک «استاتیک» (Statics) گفته می‌شود. مهندسان از اصول استاتیک به‌منظور طراحی پل‌ها، خانه‌ها، تونل‌ها و دیگر ساختارهای ایستا به نحوی استفاده می‌کنند که از عدم فروپاشی آن‌ها اطمینان لازم، حاصل شود.

معادلات حاکم بر یک سیستم ایستا

جسمی شامل N ذره را تصور کنید که تعدادی نیروی خارجی به آن وارد می‌شود. در بخش اول مطلب تکانه بیان کردیم که برای چنین سیستمی، تغییرات تکانه خطی نسبت به زمان، نیروی خالص وارد شده به جسم را نشان می‌دهد. بنابراین برای این سیستم می‌توان گفت:

معادله ۱         $${dP \over dt}=F$$

در معادله بالا P تکانه خطیِ کلِ سیستم محسوب می‌شود و نیروی F نیز به صورت زیر بیان می‌شود.

$$F=\sum_{i=1}^{N} F_i$$

عبارت بالا تمامی نیروهای وارد شده به سیستم را نشان می‌دهد. بنابراین توجه داشته باشید که $$F_i$$ برابر با نیروی وارد شده به بخش iام سیستم است. در بخش‌های گذشته بیان کردیم که معادله ۱ نشان دهنده حرکت انتقالیِ مرکز جرم یک سیستم است. اما واقعیت این است که برای توصیف کامل یک سیستم، نیازمند تحلیل و بررسی حرکت دورانی آن نیز هستیم. در بخش سوم مبحث تکانه معادلات مربوط به حرکت دورانی سیستمِ متشکل از N ذره را مورد بررسی قرار دادیم. در بخش مذکور، معادله دوران یک سیستم را به صورت زیر توصیف کردیم:

$${dL \over dt}= τ$$

در معادله بالا، L بیان کننده تکانه زاویه‌ای کلی سیستم - حول مرکز دوران - است. هم‌چنین τ (گشتاور خالص خارجی به سیستم) را می‌توان به صورت زیر بیان کرد:

$$τ = \sum_{i=1}^{i=n} {r_i×F_i}$$

در معادله بالا r_i نشان دهنده بردار جابجایی ذره iامِ سیستم است. به نظر شما به‌منظور ایستا بودن یک سیستم، نیروها و گشتاورهای وارد شده به آن بایستی به چه شکل باشند. تغییر نکردن یک سیستم در زمان، به این معنی است که تکانه زاویه‌ای و خطی آن ثابت است. بنابراین دو عبارت $$dP \over dt$$و $$dL \over dt$$ بایستی برابر با صفر باشند. به یاد دارید که این عبارات برابر با نیرو و گشتاور وارد شده به سیستم هستند. بنابراین در حالت سکون می‌توان گفت:

$$F \enspace \enspace \enspace \enspace =0$$

$$\tau \enspace \enspace \enspace \enspace =0$$

به عبارت دیگر نیرو و گشتاور خالصِ وارد شده به یک سیستم ساکن، صفر است. واضح است که اصول بیان شده، شرایط لازم برای سیستمی محسوب می‌شوند که با گذشت زمان تغییری در آن اتفاق نمی‌افتد. اما آیا این اصول برای یک سیستم ساکن نیز کافی هستند؟ پاسخ این سوال منفی است. توجه داشته باشید که شرایط بالا تنها ساکن بودن یک سیستم صلب را تضمین می‌کنند. در حقیقت اگر یک سیستم از چندین بخش تشکیل شده باشد، یا به عبارت دیگر صلب نباشد، ساکن بودن آن، تنها با استفاده از قوانین بالا تضمین نخواهد شد.

قبل از اینکه به بررسی اصول مبحث استاتیک بپردازیم، نیاز داریم تا چندین نکته مهم را آشکار کنیم. اول آنکه آیا مهم است گشتاور وارد شده به سیستم حول چه نقطه‌ای محاسبه می‌شود؟ آیا اگر گشتاور حول یک نقطه صفر باشد، به این معنی است که این مقدار حول تمامی نقاط سیستم نیز صفر است؟ همان‌طور که می‌دانید گشتاور وارد شده به یک سیستم را می‌توان با ضرب خارجیِ بردار ذرات سیستم، در نیروی وارد شده به آن‌ها محاسبه کرد. بنابراین گشتاور خالص وارد شده به سیستم برابر است با:

$$\tau=\sum_{i=1}^{N} {r_i×F_i}$$

این مقدار گشتاور وارد شده به سیستم حول مرکز را نشان می‌دهد. به‌منظور محاسبه این مقدار حول نقطه دلخواه x₀ می‌توان از فرمول زیر استفاده کرد.

$$\tau'=\sum_{i=1}^{N} {(r_i-r_o)×F_i}$$

با باز کردن این معادله، ‌می‌توان آن را به صورت زیر بازنویسی کرد.

$$\tau'=\sum_{i=1}^{N} {r_i×F_i}-r_o×(\sum_{i=1}^{N} {F_i})=\tau +r_o×F$$

در حالتی که سیستم در حالت سکون باشد، نیروی F و گشتاور $$\tau$$ با یکدیگر برابر هستند. بنابراین داریم:

$$F=\tau=0 \enspace \enspace \rightarrow \enspace \enspace \tau'=0$$

معادله بالا می‌گوید برای سیستمی که در حالت سکون قرار گرفته، صفر بودن گشتاور حول یک نقطه، به این معنی است که گشتاور حول هر نقطه دلخواه نیز صفر است. بنابراین همواره به‌منظور بررسی استاتیکی یک سیستم، معادله گشتاور را حول نقطه‌ای می‌نویسند که محاسبات در آن نقطه راحت‌تر است.

سوال دیگر این است که نیروی وزن وارد شده به سیستم، بایستی در چه نقطه‌ای در نظر گرفته شود. نیروی ناشی از وزن بخش iامِ سیستم، برابر است با:

$$F_i=m_ig$$

در این معادله g شتاب گرانشی است. گشتاورِ ناشی از وزن را می‌توان به‌صورت زیر بیان کرد:

$$\tau=\sum_{i=1}^{N} {r_i×m_ig}=(\sum_{i=1}^{N}{m_ir_i})×g=r_{cm}×Mg$$

در معادله بالا M برابر با جرم کل سیستم و $$r_{cm}=\sum_{i=1}^{N}{m_ir_i \over M}$$، موقعیت بردار مرکز جرم آن است. معادله بالا نشان می‌دهد که به منظور محاسبه گشتاور وارد شده، می‌توان جرم کل سیستم را در مرکز جرمِ جسم فرض کرد. شکل زیر مرکز جرم یک چوب بیسبال را نشان می‌دهد.

برای آشنایی بهتر با مفهوم استاتیک و حل مسائل مرتبط با آن می‌توانید از مجموعه آموزش استاتیک درس، تمرین، حل مثال و تست فرادرس استفاده کنید. 

ساکن بودن یک جسم در میدان گرانشی

به منظور درک بهتر مفاهیم ارائه شده در بالا، مطابق شکل زیر جسمی را تصور کنید که حول نقطه مشخصی لولا شده است.

فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

با در نظر گرفتن وزن، حالت تعادل این جسم را توصیف کنید.

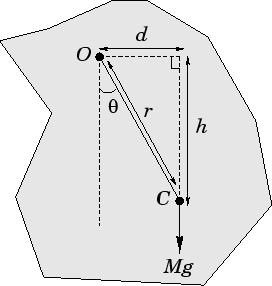
نقطه O و C را به ترتیب محل لولا و مرکزِ جرمِ این جسم تصور کنید. همچنین در این شکل r نشان‌دهنده فاصله بین نقاط O و C، $$\theta$$ نشان دهنده زاویه بین خط OC و محور عمودی است. در حالت کلی نیروهای وزن (Mg) و عکس العمل لولا (R) به این سیستم وارد می‌شوند. همان‌طور که در بالا نیز بیان شد، دو شرط اصلی برای ساکن ماندن یک سیستم این است که جمع تمامی نیروها و گشتاورهای وارد شده به آن صفر باشد.

معادله تعادل نیروها برای این سیستم به قرار زیر است.

$$R-Mg=0 \enspace \enspace \rightarrow \enspace \enspace \enspace R=Mg$$

بنابراین نیرویی که لولا به جسم وارد می‌کند برابر با نیروی وزن آن است. در قدم بعدی به‌منظور نوشتن معادله تعادل گشتاور، بایستی نقطه‌ای انتخاب شود که راحت‌ترین محاسبه انجام شود. به همین منظور در این مسئله لولا را انتخاب می‌کنیم چرا که نیروی R از معادله مربوط به گشتاور حذف خواهد شد.

با فرض این‌که جسم در زاویه $$\theta$$ قرار گرفته باشد، معادله تعادل گشتاور، حول لولا را می‌توان به شکل زیر بیان کرد:

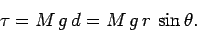
با برابر قرار دادن $$sin(\theta)$$ با صفر، زاویه ۰ درجه برای $$\theta$$ بدست می‌آید. به عبارت دیگر برای تعادل این جسم، مرکز جرم آن بایستی دقیقا زیر لولا قرار گیرد. در بخش آینده، مبحث استاتیک را به‌طور کامل‌تر تشریح خواهیم کرد و مثال‌های بیشتری را در مورد تعادل اجسام مختلف، ارائه خواهیم داد.

^^