حرکت خطی در فیزیک — به زبان ساده

حرکت خطی حرکت یک ذره یا یک جسم روی یک خط مستقیم است. در این آموزش، با حرکت خطی آشنا می‌شویم و چند مثال را درباره آن بیان می‌کنیم.

در مطالعه فیزیک، حرکت پایه‌ای‌ترین مبحث است. در بین مباحث حرکت نیز، حرکت خطی یا مستقیم‌الخط ساده‌ترین نوع حرکت محسوب می‌شود.

حرکت خطی

در حرکت خطی، تعاریف زیر را داریم:

• موقعیت یا مکان (Position)، مکانی است که یک جسم در آنجا قرار دارد و تابعی از زمان است:

$$\large x (t)$$ یا $$\large s ( t)$$

• سرعت (Velocity) برابر با مشتق موقعیت است:

$$\large { v = \frac { { d x } } { { d t } } . }$$

• شتاب (Acceleration) برابر با مشتق سرعت است:

$$\large {a = \frac { { d v } } { { d t } } . }$$

موقعیت و سرعت با قضیه اساسی حسابان با هم ارتباط دارند:

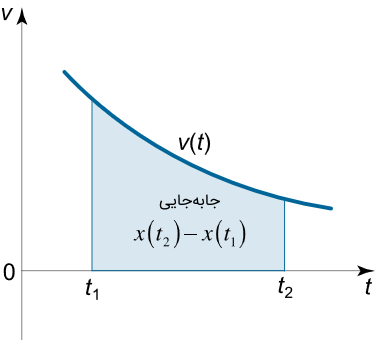
$$\large { { \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { v \left ( t \right ) d t } = \left . { x \left ( t \right ) } \right | _ { { t _ 1 } } ^ { { t _ 2 } } } = { x \left ( { { t _ 2 } } \right ) – x \left ( { { t _ 1 } } \right ) } }$$

که در آن، $${t_1} \le t \le {t_2}$$ است. کمیت $$x\left( {{t_2}} \right) – x\left( {{t_1}} \right)$$ جابه‌جایی (Displacement) نامیده می‌شود. جابه‌جایی برابر با مساحت زیر منحنی سرعت $$v ( t)$$ است.

به طور مشابه، از آنجایی که شتاب همان نرخ تغییرات سرعت است، داریم:

$$\large { { \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { a \left ( t \right ) d t } = \left . { v \left ( t \right ) } \right | _ { { t _ 1 } } ^ { { t _ 2 } } } = { v \left ( { { t _ 2 } } \right ) – v \left ( { { t _ 1 } } \right ) } }$$

که در آن، $$v\left( {{t_2}} \right) – v\left( {{t_1}} \right)$$ تغییرات خالص سرعت در بازه زمانی $${t_1} \le t \le {t_2}$$ است.

تندی (Speed)  $$\left| {v\left( t \right)} \right|$$ قدر مطلق سرعت است؛ یعنی تندی همیشه مثبت است.

تندی متوسط $${v_{av}}$$ به صورت زیر تعریف می‌شود:

جابه‌جایی کل $$s$$ یک ذره بین زمان‌های $$t_ 1$$ و $$t_ 2$$ به صورت زیر به دست می‌آید:

$$\large s = \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { \left | { v \left ( t \right ) } \right | d t } .$$

مثال‌های حرکت خطی

در این بخش چند مثال را حل می‌کنیم.

مثال ۱

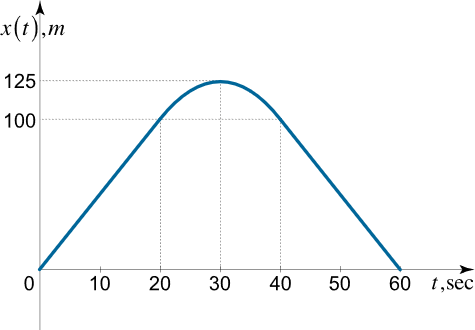
منحنی شکل ۲، سرعت ذره‌ای را نشان می‌دهد که در طول یک خط راست حرکت می‌کند. در $$t = 0$$، موقعیت ذره $$x = 0$$ است.

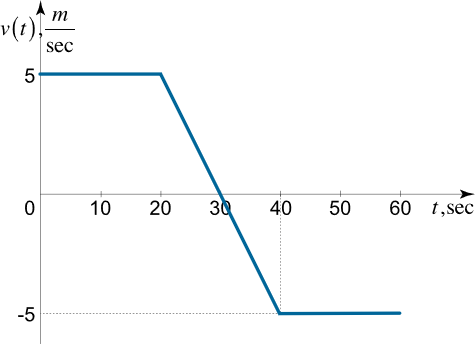
• (الف) منحنی شتاب $$a$$ را برحسب زمان رسم کنید.
• (ب) منحنی موقعیت $$x$$ برحسب زمان را رسم کنید.
• (ج) تندی متوسط ذره را بین $$t = 0$$ و $$t = 60\,\text{sec}$$ محاسبه کنید.

حل (الف): شتاب بین زمان‌های ۲۰ تا ۴۰ ثانیه به صورت زیر به دست می‌آید و غیر از آن صفر است:

$$\large { a = \frac { { { v _ 2 } – { v _ 1 } } } { { { t _ 2 } – { t _ 1 } } } } = { \frac { { \left ( { – 5 } \right ) – 5 } } { { 4 0 – 2 0 } } } = { \frac { { – 1 0 } } { { 2 0 } } = – 0 . 5 \frac { \text{m} } { { { \text{sec} ^ 2 } } } . }$$

بنابراین، نمودار شتاب به صورت زیر خواهد بود.

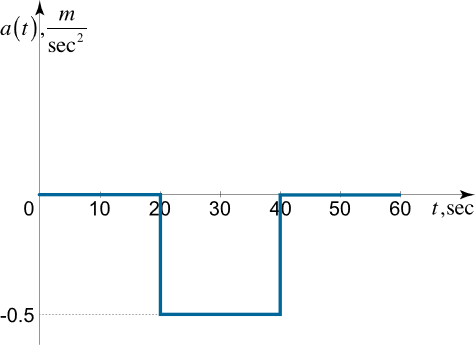
حل (ب): موقعیت ذره در لحظات ۲۰، ۳۰، ۴۰ و ۶۰ ثانیه به صورت زیر محاسبه می‌شود:

$$\large { t = 2 0 \, \text {s:} \; \; } \kern0pt { x = 2 0 \cdot 5 = 1 0 0 \, \text {m} ; }$$

$$\large { t = 3 0 \, \text {s:} \; \; } \kern0pt { x = 1 0 0 + 1 0 \cdot 5 \cdot \frac { 1 } { 2 } = 1 2 5 \, \text {m} ; }$$

$$\large { t = 4 0 \, \text {s:} \; \; } \kern0pt { x = 1 2 5 + 1 0 \cdot \left ( { - 5 } \right ) \cdot \frac { 1 } { 2 } = 1 0 0 \, \text {m} ; }$$

$$\large { t = 6 0 \, \text {s:} \; \; } \kern0pt { x = 1 0 0 + 2 0 \cdot \left ( { - 5 } \right ) = 0 \, \text {m} . }$$

بنابراین، نمودار موقعیت ذره به صورت زیر رسم می‌شود.

حل (ج): دو بازه زمانی زیر را در نظر بگیرید:

۱) $$0 \le t \le 30\,\text{sec}$$

۲) $$30\,\text{sec} < t \le 60\,\text{sec}$$

وقتی ذره در $$t = 60 \, \text{sec}$$ به موقعیت اولیه $$x = 0$$ برمی‌گردد، کل مسافت پیموده شده از $$t = 0$$ تا $$t = 60\,\text{sec}$$ برابر است با:

$$\large { s = \int \limits _ 0 ^ { 3 0 } { \left | { v \left ( t \right ) } \right | d t } + \int \limits _ { 3 0 } ^ { 6 0 } { { \left | { v \left ( t \right ) } \right | } d t } } = { 1 2 5 + 1 2 5 } ={ 2 5 0 \, \text {m} . }$$

تندی متوسط نیز به صورت زیر است:

$$\large { { { v _ { a v } } = \frac { s } { { \Delta t } } = \frac { { 2 5 0 } } { { 6 0 } } } = { 4 . 1 7 \, \frac { \text {m} } { \text {sec} } . } }$$

مثال ۲

ذره‌ای روی یک خط راست حرکت می‌کند و معادله موقعیت آن $$x\left( t \right) = {t^3} – 9{t^2} + 24t – 5$$ است ($$t$$ زمان و برحسب ثانیه است). در چه لحظه‌ای جهت حرکت این ذره تغییر می‌کند؟

حل: سرعت ذره با مشتق‌گیری از تابع مکان به دست می‌آید:‌

$$\large \begin {align*} v \left ( t \right ) = x ^ \prime \left ( t \right ) &= { \left ( { { t ^ 3 } – 9 { t ^ 2 } + 2 4 t – 5 } \right ) ^ \prime } \\ &= { 3 { t ^ 2 } – 1 8 t + 2 4 } = { 3 \left ( { { t ^ 2 } – 6 t + 8 } \right ) }\\ & = { 3 \left ( { t – 2 } \right ) \left ( { t – 4 } \right ) . } \end {align*}$$

همان‌طور که می‌بینیم، سرعت در لحظات $$t = 2\,\text{s}$$ و $$t = 4\,\text{s}$$ برابر با صفر است. بنابراین، جهت حرکت ذره در این زمان‌ها تغییر می‌کند.

مثال ۳

ذره‌ای با معادله $$x\left( t \right) = 2{t^3} + 6{t^2} – 6t + 1$$ روی محور $$x$$ در حال حرکت است که در آن، زمان $$t \ge 0$$ بوده و برحسب ثانیه است. زمانی را پیدا کنید که در آن، سرعت و شتاب ذره با هم برابرند.

حل: از تابع مکان دو بار مشتق می‌گیریم تا توابع سرعت و شتاب به دست آیند:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) } = { \left ( { 2 { t ^ 3 } + 6 { t ^ 2 } – 6 t + 1 } \right ) ^ \prime } ={ 6 { t ^ 2 } + 1 2 t – 6 }$$

$$\large { a \left ( t \right ) = v ^ \prime \left ( t \right ) } = { \left ( { 6 { t ^ 2 } + 1 2 t – 6 } \right ) ^ \prime } = { 1 2 t + 1 2 . }$$

با برابر قرار دادن $$v$$ و $$a$$، خواهیم داشت:

$$\large { 6 { t^ 2 } + 1 2 t – 6 } = { 1 2 t + 1 2 , }$$

$$\large 6{t^2} = 18,$$

یا

$$\large {t^2} = 3.$$

این معادله دارای ریشه مثبت $$t = \sqrt 3$$ است. در نتیجه، جواب مسئله $$t = \sqrt 3\,\text{s}$$ است.

مثال ۴

تابع مکان ذره‌ای که در طول محور $$x$$ حرکت می‌کند، $$x\left( t \right) = {t^3} – 4{t^2} + 5t – 2$$ است ($$t \ge 0$$). بازه‌ای را پیدا کنید که در آن، ذره به سمت چپ حرکت می‌کند.

حل: سرعت ذره با مشتق‌گیری از تابع مکان به دست می‌آید:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) } = { \left ( { { t ^ 3 } – 4 { t ^ 2 } + 5 t – 2 } \right ) ^ \prime } = { 3 { t ^ 2 } – 8 t + 5 . }$$

با حل این معادله درجه دوم، داریم:

$$\large \begin {align*} & 3 { t ^ 2 } – 8 t + 5 = 0 , \; \; \Rightarrow { D = { \left ( { – 8 } \right ) ^ 2 } – 4 \cdot 3 \cdot 5 = 4 , \; \; } \\ & \Rightarrow { { t _ { 1 , 2 } } = \frac { { – \left ( { – 8 } \right ) \pm \sqrt 4 } } { 6 } } = { \frac { { 8 \pm 2 } } { 6 } } = { 1 , \frac { 5 } { 3 } . } \end {align*}$$

تابع سرعت را به صورت زیر می‌نویسیم:

$$\large { 3 { t ^ 2 } – 8 t + 5 } = { 3 \left ( { t – 1 } \right ) \left ( { t – \frac { 5 } { 3 } } \right ) . }$$

می‌بینیم که سرعت در بازه $$1 \lt t \lt \frac{5}{3}$$ منفی است. بنابراین، در این بازه زمانی، ذره به سمت چپ حرکت می‌کند.

مثال ۵

ذره‌ای در طول محور $$x$$ حرکت کرده و از قانون $$x\left( t \right) = 2{t^2} + 4$$ تبعیت می‌کند که در آن، $$x$$ برحسب متر و $$t$$ برحسب ثانیه است.

• (الف) سرعت ذره را به دست آورید.
• (ب) شتاب ذره را محاسبه کنید.
• (ج) تندی میانگین ذره را از $$t = 2\,\text{s}$$ تا $$t = 4\,\text{s}$$ محاسبه کنید.

حل (الف): از $$x\left( t \right)$$ مشتق می‌گیریم:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) } = { \left ( { 2 { t ^ 2 } + 4 } \right ) ^ \prime } = { 4 t . }$$

بنابراین، سرعت ذره از معادله زیر تبعیت می‌کند:

$$\large v = 4 t \, \frac { \text {m} } { \text {s} } .$$

حل (ب): برای یافتن شتاب، از تابع سرعت مشتق می‌گیریم:

$$\large { a = v ^ \prime \left ( t \right ) } = { \left ( { 4 t } \right ) ^ \prime } = { 4 \, \frac { \text {m} } { { { \text {s} ^ 2 } } } } .$$

می‌بینیم که ذره با سرعت ثابت حرکت می‌کند.

حل (ج): برای به دست آوردن تندی متوسط، ابتدا مکان ذره را در $$t = 2\,\text{s}$$ و $$t = 4\,\text{s}$$ تعیین می‌کنیم:

$$\large { x \left ( { { t _ 1 } } \right ) = x \left ( 2 \right ) } = { 2 \cdot { 2 ^ 2 } + 4 } = { 1 2 \, \text {m} } \\ \large { x \left ( { { t _ 2 } } \right ) = x \left ( 4 \right ) } = { 2 \cdot { 4 ^ 2 } + 4 } = { 3 6 \, \text {m} }$$

در نهایت، تندی متوسط در این بازه زمانی به صورت زیر محاسبه می‌شود:

$$\large { { v _ { a v } } = \frac { { x \left ( { { t _ 2 } } \right ) – x \left ( { { t _ 1 } } \right ) } } { { { t _ 2 } – { t _ 1 } } } } = { \frac { { 3 6 – 1 2 } } { { 4 – 2 } } } = { 1 2 \, \frac { \text {m} } { \text {s} } . }$$

مثال ۶

جسمی با معادله مکان $$x\left( t \right) = – \large{\frac{{{t^3}}}{6}}\normalsize + 2{t^2} – 1$$ روی محور $$x$$ حرکت می‌کند. در چه زمانی شتاب صفر است؟ سرعت جسم را در این لحظه (شتاب صفر) به دست آورید.

حل: سرعت با مشتق‌گیری از تابع مکان به دست می‌آید:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) } = { \left ( { – \frac { { { t ^ 3 } } } { 6 } + 2 { t ^ 2 } – 1 } \right ) ^ \prime } = { – \frac { { { t ^ 2 } } } { 2 } + 4 t . }$$

به طور مشابه، برای به دست آوردن شتاب، از تابع سرعت نسبت به زمان مشتق می‌گیریم:

$$\large { a \left ( t \right ) = v ^ \prime \left ( t \right ) } = { \left ( { – \frac { { { t ^ 2 } } } { 2 } + 4 t } \right ) ^ \prime } = { – t + 4 . }$$

زمانی که در آن، شتاب برابر با صفر است،‌ به صورت زیر محاسبه می‌شود:

$$\large { a \left ( t \right ) = 0 , \; \; } \Rightarrow { - t + 4 = 0 , \; \; } \Rightarrow { t = 4 \, \text {s} . }$$

سرعت ذره در $$t = 4$$ نیز برابر است با:

$$\large { v ( 4 ) = – \frac { { { 4 ^ 2 } } } { 2 } + 4 \cdot 4 } = { 8 \, \frac { \text {m} } { \text {s} } . }$$

مثال ۷

انتگرالی را به دست آورید که مسافت کل پیموده شده ذره‌ای را با سرعت $$v\left( t \right) = {t^2} – 4$$ در بازه $$[0 , 3 ]$$ نتیجه دهد.

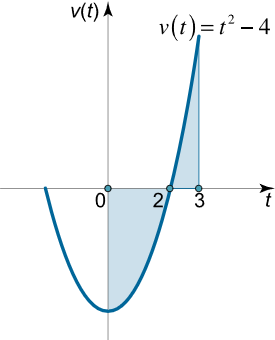
حل: برای یافتن کل مسافت پیموده شده، باید از تابع تندی انتگرال بگیریم. توجه کنید که علامت سرعت در لحظه $$t= 2$$ تغییر می‌کند. بنابراین، بازه $$[0 , 3 ]$$ را به دو زیربازه $$[ 0 , 2 ]$$ و $$[2 , 3 ]$$ تقسیم می‌کنیم. کل مسافت پیموده شده $$s$$ توسط ذره در بازه $$[0 , 3 ]$$ به فرم زیر خواهد بود:

$$\large { s = \int \limits _ 0 ^ 2 { \left | { { t ^ 2 } – 4 } \right | d t } } + { \int \limits _ 2 ^ 3 { \left | { { t ^ 2 } – 4 } \right | d t } . }$$

با توجه به اینکه سرعت در زیربازه اول منفی، و در زیربازه دوم مثبت است،‌ داریم:

$$\large { s = – \int \limits _ 0 ^ 2 { \left ( { { t ^ 2 } – 4 } \right ) d t } } + { \int \limits _ 2 ^ 3 { \left ( { { t ^ 2 } – 4 } \right ) d t } . }$$

با بازنویسی جملات، جواب نهایی به صورت زیر خواهد بود:

$$\large { s = \int \limits _ 2 ^ 3 { \left ( { { t ^ 2 } – 4 } \right ) d t } } - { \int \limits _ 0 ^ 2 { \left ( { { t ^ 2 } – 4 } \right ) d t } . }$$

مثال ۸

ذره‌ای روی محور $$x$$ به گونه‌ای حرکت می‌کند که در $$t \ge 0$$ معادله مکان به صورت $$x\left( t \right) = t\ln t$$ است. شتاب ذره را در لحظه‌ای که سرعت صفر است،‌ به دست آورید.

حل: سرعت ذره‌ با مشتق‌گیری از معادله مکان به دست می‌آید:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) } = { \left ( { t \ln t } \right ) ^ \prime } = { 1 \cdot \ln t + t \cdot \frac { 1 } { t } } = { \ln t + 1 . }$$

با یک‌ بار دیگر مشتق‌گیری از تابع مکان، می‌توان شتاب را نیز به دست آورد:

$$\large { a \left ( t \right ) = v ^ \prime \left ( t \right ) } = { \left ( { \ln t + 1 } \right ) ^ \prime } = { \frac { 1 } { t } . }$$

لحظه صفر بودن سرعت نیز به صورت زیر محاسبه می‌شود:

$$\large { v \left ( t \right ) = 0 , \; \; } \Rightarrow { \ln t + 1 = 0 , \; \; } \Rightarrow { \ln t = – 1 , \; \; } \Rightarrow { t = \frac { 1 } { e } . }$$

با جایگذاری این زمان، شتاب در لحظه سرعت صفر برابر است با:

$$\large a = \frac { 1 } { { \frac { 1 } { e } } } = e .$$

مثال ۹

وقتی دو ذره از مبدأ و با سرعت‌های $$v\left( t \right) = \cos t$$ و $$u\left( t \right) = \sin 2t$$ شروع به حرکت کنند، در چند لحظه روی بازه $$\left[ {0,2\pi } \right]$$ تندی آن‌ها با هم برابر است؟

حل: این مسئله را به صورت گرافیکی حل می‌کنیم. منحنی تندی دو ذره روی بازه $$[0, 2 \pi]$$ مطابق شکل زیر است.

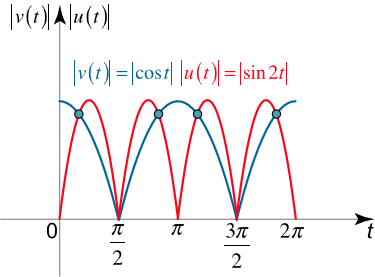
همان‌طور که در شکل بالا مشخص است، منحنی‌ها چهار بار با هم تقاطع دارند. بنابراین، در چهار لحظه، روی بازه $$[ 0 , 2 \pi ]$$ تندی دو ذره با هم برابر است.

مثال ۱۰

ذره‌ای در طول یک خط مستقیم و با معادله $$x\left( t \right) = {t^3} – 6{t^2} + 5$$ حرکت می‌کند، که در آن، $$x$$ بر حسب متر و $$t$$ برحسب ثانیه است. کل مسافت پیموده شده توسط این ذره در ۶ ثانیه چقدر است؟

حل: برای یافتن کل مسافت پیموده شده توسط یک ذره، باید از تندی $$\left| {v\left( t \right)} \right|$$ انتگرال‌ بگیریم:

$$\large s = \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { \left | { v \left ( t \right ) } \right | d t }$$

سرعت ذره به صورت زیر به دست می‌آید:

$$\large { v \left ( t \right ) = x ^ \prime \left ( t \right ) = \left ( { { t ^ 3 } – 6 { t ^ 2 } + 5 } \right ) ^ \prime } = { 3 { t ^ 2 } – 1 2 t } = { 3 t \left ( { t – 4 } \right ) . }$$

همان‌طور که از معادله بالا مشخص است، سرعت در بازه زمانی $$0 \lt t \lt 4$$ منفی و در $$t \gt 4$$ مثبت است. بنابراین، انتگرال را به صورت زیر به دو قسمت تقسیم می‌کنیم:

$$\large { s = \int \limits _ 0 ^ 6 { \left | { v \left ( t \right ) } \right | d t } } = { \int \limits _ 0 ^ 4 { \left | { v \left ( t \right ) } \right | d t } } + { \int \limits _ 4 ^ 6 { \left | { v \left ( t \right ) } \right | d t } . }$$

از آنجایی که سرعت در انتگرال اول منفی و در انتگرال دوم مثبت است، خواهیم داشت:

$$\large { s = – \int \limits _ 0 ^ 4 { v \left ( t \right ) d t } } + { \int \limits _ 4 ^ 6 { v \left ( t \right ) d t } . }$$

نتیجه این انتگرال برابر است با:

$$\large \begin {align*} s & = – \left . { \left ( { { t ^ 3 } – 6 { t ^ 2 } + 5 } \right ) } \right | _ 0 ^ 4 + { \left . { \left ( { { t ^ 3 } – 6 { t ^ 2 } + 5 } \right ) } \right | _ 4 ^ 6 } \\ &= { – \left [ { \left ( { 6 4 – 9 6 + 5 } \right ) – 5 } \right ] } + { \left [ { \left ( { 2 1 6 – 2 1 6 + 5 } \right ) – \left ( { 6 4 – 9 6 + 5 } \right ) } \right ] } \\ & = { 3 2 + 3 2 } = { 6 4 . } \end {align*}$$

بنابراین، کل مسافت پیموده شده ذره برابر با ۶۴ متر است.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس فیزیک
• آموزش فیزیک پایه ۱
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله
• حرکت غلتشی — به زبان ساده
• حرکت دایره ای — به زبان ساده
• حرکت پرتابی — به زبان ساده

^^