در آموزشهای پیشین مجله فرادرس با مفاهیم حرکتشناسی و حرکت خطی در یک بعد آشنا شدیم. همچنین مباحثی مانند حرکت غلتشی ، حرکت دایرهای ، حرکت روی سطح شیبدار ، حرکت سقوط آزاد ، حرکت پرتابی و حرکت هماهنگ ساده را بیان کردیم. در این آموزش، با حرکت دو بعدی روی سطح صاف آشنا میشویم.
موقعیت و مسیر در حرکت دو بعدی
فرض کنید جسمی در صفحه وجود دارد. موقعیت یا مکان این جسم را به صورت زیر نشان میدهیم:
r = x i + y j \large { \mathbf { r } = x \mathbf { i } + y \mathbf { j } } r = x i + y j
که در آن، x x x y y y مختصات کارتزین و i \mathbf {i} i j \mathbf { j } j بردارهای یکه در راستای محورهای x x x y y y x x x y y y
r = x ( t ) i + y ( t ) j . \large { \mathbf { r } = x \left ( t \right ) \mathbf { i } + y \left ( t \right ) \mathbf { j } } . r = x ( t ) i + y ( t ) j .
این معادله برداری، مسیر ذره را مشخص میکند.
سرعت و تندی در حرکت دو بعدی
سرعت v \mathbf{v} v مشتق زمانی بردار مکان ذره تعریف میشود:
v = d r d t . \large { \mathbf { v } = \frac { { d \mathbf { r } } } { { d t } } } . v = d t d r .
یا به فرم مختصاتی، داریم:
v = d x d t i + d y d t j , \large { \mathbf { v } = \frac { { d x } } { { d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } } , v = d t d x i + d t d y j ,
که v x = d x d t {v_x} = \large{\frac{{dx}}{{dt}}}\normalsize v x = d t d x v y = d y d t {v_y} = \large{\frac{{dy}}{{dt}}}\normalsize v y = d t d y
تندی v v v
v = v x 2 + v y 2 = ( d x d t ) 2 + ( d y d t ) 2 . \large { { v = \sqrt { v _ x ^ 2 + v _ y ^ 2 } } = { \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } . } } v = v x 2 + v y 2 = ( d t d x ) 2 + ( d t d y ) 2 .
شتاب a \mathbf{a} a
a = d v d t = d 2 r d t 2 . \large { \mathbf { a } = \frac { { d \mathbf { v } } } { { d t } } } = \frac { { { d ^ 2 } \mathbf { r } } } { { d { t ^ 2 } } } . a = d t d v = d t 2 d 2 r .
وقتی v \mathbf{v} v
a = d v x d t i + d v y d t j = d 2 x d t 2 i + d 2 y d t 2 j , \large { \mathbf { a } = \frac { { d { v _ x } } }{ { d t } } \mathbf { i } + \frac { { d { v _ y } } } { { d t } } \mathbf { j } } = { \frac { { { d ^ 2 } x } } { { d { t ^ 2 } } } \mathbf { i } + \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } \mathbf { j } , } a = d t d v x i + d t d v y j = d t 2 d 2 x i + d t 2 d 2 y j ,
که a x = d v x d t = d 2 x d t 2 { a _ x } = \large { \frac { {d { v _ x } } } { { d t } } } \normalsize = \large { \frac { { { d ^ 2 } x } } { { d { t ^ 2 } } } } \normalsize a x = d t d v x = d t 2 d 2 x a y = d v y d t = d 2 y d t 2 \large { a _ y } = \large { \frac { { d { v _ y } } } { { d t } } } \normalsize = \large { \frac { { { d ^ 2 } y } }{ { d { t ^ 2 } } } } \normalsize a y = d t d v y = d t 2 d 2 y
اندازه شتاب به صورت زیر محاسبه میشود:
a = a x 2 + a y 2 = ( d v x d t ) 2 + ( d v y d t ) 2 = ( d 2 x d t 2 ) 2 + ( d 2 y d t 2 ) 2 . \large { a = \sqrt { a _ x ^ 2 + a _ y ^ 2 } } = { \sqrt { { { \left ( { \frac { { d { v _ x } } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d { v _ y } } } { { d t } } } \right ) } ^ 2 } } } = { \sqrt { { { \left ( { \frac { { { d ^ 2 } x } } { { d { t ^ 2 } } } } \right ) } ^ 2 } + { { \left ( { \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } } \right ) } ^ 2 } } . } a = a x 2 + a y 2 = ( d t d v x ) 2 + ( d t d v y ) 2 = ( d t 2 d 2 x ) 2 + ( d t 2 d 2 y ) 2 .
حرکت با شتاب ثابت
فرض کنید ذره یا جسمی با شتاب ثابت a \mathbf { a } a
a = d v d t = const . \large { \mathbf { a } = \frac { { d \mathbf { v } } } { { d t } } = \text {const} . } a = d t d v = const .
سرعت در لحظه t t t
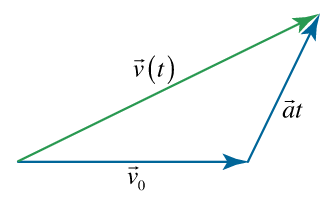
v ( t ) = v 0 + a t , \large { \mathbf { v } \left ( t \right ) = { \mathbf { v } _ 0 } + \mathbf { a } t , } v ( t ) = v 0 + a t ,
که v 0 {\mathbf{v}_0} v 0 t = 0 t = 0 t = 0
شکل ۱: بردار سرعت مکان در زمان t t t
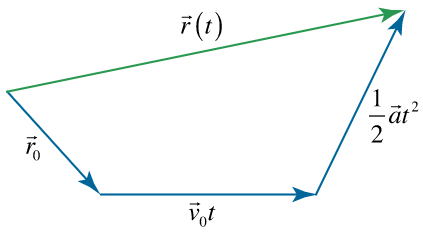
r ( t ) = r 0 + v 0 t + 1 2 a t 2 , \large { \mathbf { r } \left ( t \right ) = { \mathbf { r } _ 0 } + { \mathbf { v } _ 0 } t + \frac { 1 } { 2 } \mathbf { a } { t ^ 2 } } , r ( t ) = r 0 + v 0 t + 2 1 a t 2 ,
که در آن، r 0 {\mathbf{r}_0} r 0 t = 0 t = 0 t = 0
شکل ۲: بردار مکان حرکت سقوط آزاد
حرکت سقوط آزاد یک جسم با شتاب ثابت به دلیل جاذبه است. این جسم با سرعت زیر سقوط میکند:
a = – g j , \large {\mathbf{a} = – g\mathbf{j}}, a = – g j ,
که g = 9.8 m s 2 g = 9.8\,\large{\frac{\text{m}}{\text{s}^2}}\normalsize g = 9.8 s 2 m j \mathbf{j} j
تندی قائم v ( t ) v\left( t \right) v ( t ) y ( t ) y ( t) y ( t )
v ( t ) = v 0 – g t ( m s ) , \large { v \left ( t \right ) = { v _ 0 } – g t \; \; \left ( { \frac { \text {m} } { \text {s} } } \right ) } , v ( t ) = v 0 – g t ( s m ) ,
y ( t ) = y 0 + v 0 t – 1 2 g t 2 ( m ) , \large {y\left( t \right) = {y_0} + {v_0}t – \frac{1}{2}g{t^2}\;\;\left({\text{m}}\right)}, y ( t ) = y 0 + v 0 t – 2 1 g t 2 ( m ) ,
که v 0 v _ 0 v 0
مثالهای حرکت دو بعدی
در این بخش، چند مثال متنوع را بررسی میکنیم.
مثال ۱
ذرهای در صفحه x y x y x y x = t x = t x = t y = t 3 y = t ^ 3 y = t 3 x x x y y y متر هستند. سرعت و تندی ذره را در t = 1 s t = 1\,\text{s} t = 1 s
حل: طبق تعریف، سرعت برابر است با:
v = d x d t i + d y d t j , \large { \mathbf { v } = \frac { { d x } } { { d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } } , v = d t d x i + d t d y j ,
که در آن:
d x d t = d d t ( t ) = 1 , d y d t = d d t ( t 3 ) = 3 t 2 . \large { \frac { { d x } } { { d t } } = \frac { d } { { d t} } \left ( t \right ) = 1 , \; \; } \kern0pt { \frac { { d y } } { { d t } } = \frac { d } { { d t } } \left ( { { t ^ 3 } } \right ) = 3 { t ^ 2 } . } d t d x = d t d ( t ) = 1 , d t d y = d t d ( t 3 ) = 3 t 2 .
بنابراین، بردار سرعت در t = 1 t = 1 t = 1
v ( t = 1 ) = i + 3 j . \large { \mathbf { v } \left ( { t = 1 } \right ) = \mathbf { i } + 3 \mathbf { j } . } v ( t = 1 ) = i + 3 j .
و تندی در این زمان، برابر است با:
∣ v ∣ = ( d x d t ) 2 + ( d y d t ) 2 = 1 2 + 3 2 = 10 m s . \large { { \left | { \mathbf { v } } \right | = \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } } } = { \sqrt { { 1 ^ 2 } + { 3 ^ 2 } } } = { \sqrt { 1 0 } \, \frac { \text {m} } { \text {s} } . } ∣ v ∣ = ( d t d x ) 2 + ( d t d y ) 2 = 1 2 + 3 2 = 10 s m .
مثال ۲
جسمی روی یک مسیر با معادلات x ( t ) = t + cos t x\left( t \right) = t + \cos t x ( t ) = t + cos t y ( t ) = t – sin t y\left( t \right) = t – \sin t y ( t ) = t – sin t
حل: برای به دست آوردن شتاب، از x ( t ) x ( t ) x ( t ) y ( t ) y ( t) y ( t )
x ′ ( t ) = ( t + cos t ) ′ = 1 – sin t , x ′ ′ ( t ) = ( 1 – sin t ) ′ = – cos t , y ′ ( t ) = ( t – sin t ) ′ = 1 + cos t , y ′ ′ ( t ) = ( 1 + cos t ) ′ = – sin t . \large \begin {align*} x ^ \prime \left ( t \right ) & = \left ( { t + \cos t } \right ) ^ \prime = { 1 – \sin t , } \\ x ^ { \prime \prime } \left ( t \right ) & = \left ( { 1 – \sin t } \right ) ^ \prime = { – \cos t , } \\ y ^ \prime \left ( t \right ) & = \left ( { t – \sin t } \right ) ^ \prime = { 1 + \cos t , } \\ y ^ { \prime \prime } \left ( t \right ) & = \left ( { 1 + \cos t } \right ) ^ \prime = { – \sin t . } \end {align*} x ′ ( t ) x ′′ ( t ) y ′ ( t ) y ′′ ( t ) = ( t + cos t ) ′ = 1– sin t , = ( 1– sin t ) ′ = – cos t , = ( t – sin t ) ′ = 1 + cos t , = ( 1 + cos t ) ′ = – sin t .
اکنون میتوانیم اندازه بردار شتاب را محاسبه کنیم:
a = ∣ a ∣ = ( x ′ ′ ( t ) ) 2 + ( y ′ ′ ( t ) ) 2 = ( – cos t ) 2 + ( – sin t ) 2 = cos 2 t + sin 2 t = 1. \large \begin {align*} a = \left | \mathbf { a } \right | & = { \sqrt { { { \left ( { x ^ { \prime \prime } \left ( t \right ) } \right ) } ^ 2 } + { { \left ( { y ^ { \prime \prime } \left ( t \right ) } \right ) } ^ 2 } } } \\ & = { \sqrt { { { \left ( { – \cos t } \right ) } ^ 2 } + { { \left ( { – \sin t } \right ) } ^ 2 } } }\\ & = { \sqrt { { { \cos } ^ 2 } t + { { \sin } ^ 2 } t } } = { 1 . } \end {align*} a = ∣ a ∣ = ( x ′′ ( t ) ) 2 + ( y ′′ ( t ) ) 2 = ( – cos t ) 2 + ( – sin t ) 2 = cos 2 t + sin 2 t = 1.
مثال ۳
ذرهای روی هذلولی y = 12 x y = \large{\frac{{12}}{x}}\normalsize y = x 12 x x x متر بر ثانیه است. تندی ذره را در ( 3 , 4 ) ( 3 , 4 ) ( 3 , 4 )
حل: ابتدا بردار سرعت ذره را با استفاده از فرمول زیر به دست میآوریم:
v = d x d t i + d y d t j . \large \mathbf { v } = \frac { { d x } } {{ d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } . v = d t d x i + d t d y j .
مشتق d x d t \large{\frac{{dx}}{{dt}}}\normalsize d t d x
d x d t = 3 m s . \large \frac { { d x } } { { d t } } = 3 \, \frac { \text {m} } { \text {s} } . d t d x = 3 s m .
عبارت d y d t \large{\frac{{dy}}{{dt}}}\normalsize d t d y قاعده زنجیرهای حساب میکنیم:
d y d t = d d t ( 12 x ) = – 12 x 2 d x d t . \large { \frac { { d y } } { { d t } } = \frac { d } { {d t } } \left ( { \frac { { 1 2 } } { x } } \right ) } = { – \frac { { 1 2 } } { { { x ^ 2 } } } \frac { { d x } } { { d t } } . } d t d y = d t d ( x 12 ) = – x 2 12 d t d x .
در نقطه داده شده، داریم:
d y d t = – 12 3 2 ⋅ 3 = – 4 m s . \large \frac { { d y } } { { d t } } = – \frac { { 1 2 } }{ { { 3 ^ 2 } } } \cdot 3 = – 4 \, \frac { \text {m} } { \text {s} } . d t d y = – 3 2 12 ⋅ 3 = –4 s m .
و تندی ذره برابر است با:
v = ( d x d t ) 2 + ( d y d t ) 2 = 3 2 + ( – 4 ) 2 = 5 m s . \large { v = \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } } = { \sqrt { { 3 ^ 2 } + { { \left ( { – 4 } \right ) } ^ 2 } } } = { 5 \, \frac { \text {m} } { \text {s} } . } v = ( d t d x ) 2 + ( d t d y ) 2 = 3 2 + ( –4 ) 2 = 5 s m .
مثال ۴
ذرهای در راستای یک منحنی با معادلات x = 1 + t x = 1 + t x = 1 + t y = 1 – t y = 1 – t y = 1– t x y x y x y
حل: از معادله اول t t t
x = 1 + t , ⇒ t = x – 1 , ⇒ y = 1 – ( x – 1 ) , ⇒ y = 2 – x . \large { x = 1 + t , \; \; } \Rightarrow { t = x – 1 , \; \; } \Rightarrow { y = 1 – \left ( { x – 1 } \right ) , \; \; } \Rightarrow { y = 2 – x . } x = 1 + t , ⇒ t = x –1 , ⇒ y = 1– ( x –1 ) , ⇒ y = 2– x .
بنابراین، مسیر ذره خط راست y = 2 – x y = 2 – x y = 2– x
d x d t = d d t ( 1 + t ) = 1 , d y d t = d d t ( 1 – t ) = – 1. \large \begin{align*} \frac { { d x } } { { d t } } & = \frac { d } { { d t } } \left ( { 1 + t } \right ) = 1 , \\ \frac { { d y } } { { d t } } & = \frac { d } { { d t } } \left ( { 1 – t } \right ) = – 1 . \end {align*} d t d x d t d y = d t d ( 1 + t ) = 1 , = d t d ( 1– t ) = –1.
در نتیجه، داریم:
v = d x d t i + d y d t j = 1 ⋅ i + ( – 1 ) ⋅ j = i – j . \large { \mathbf { v } = \frac { { d x } } { { d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } } = { 1 \cdot \mathbf { i } + \left ( { – 1 } \right ) \cdot \mathbf { j } } = { \mathbf { i } – \mathbf { j } . } v = d t d x i + d t d y j = 1 ⋅ i + ( –1 ) ⋅ j = i – j .
تندی نیز به شکل زیر به دست میآید:
v = ( d x d t ) 2 + ( d y d t ) 2 = 1 2 + ( – 1 ) 2 = 2 . \large { v = \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } } = { \sqrt { { 1 ^ 2 } + { { \left ( { – 1 } \right ) } ^ 2 } } } = { \sqrt 2 . } v = ( d t d x ) 2 + ( d t d y ) 2 = 1 2 + ( –1 ) 2 = 2 .
و در نهایت، جواب برابر است با:
y = 2 – x , v = 2 . \large y = 2 – x,\;v = \sqrt 2 . y = 2– x , v = 2 .
مثال ۵
ذرهای روی یک مسیر با معادلات پارامتری x ( t ) = 2 t x\left( t \right) = {2^t} x ( t ) = 2 t y ( t ) = 8 t y\left( t \right) = {8^t} y ( t ) = 8 t t ≥ 0 t \ge 0 t ≥ 0
حل: از معادله اول، داریم:
x ( t ) = 2 t , ⇒ t = log 2 x . \large { x \left ( t \right ) = { 2 ^ t } , \; \; } \Rightarrow { t = { \log _ 2 } x . } x ( t ) = 2 t , ⇒ t = log 2 x .
این عبارت را در معادله دوم جایگذاری کرده و معادله x y x y x y
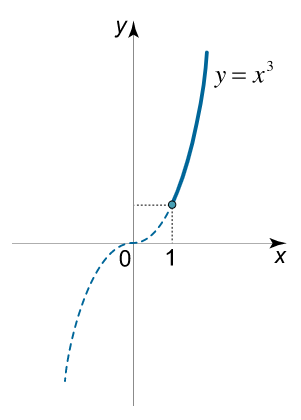
y = 8 t , ⇒ y = 8 log 2 x = ( 2 3 ) log 2 x = 2 log 2 x 3 = x 3 . \large { y = { 8 ^ t } , \; \; } \Rightarrow { y = { 8 ^ { { { \log } _ 2 } x } } } = { { \left ( { { 2 ^ 3 } } \right ) ^ { { { \log } _ 2 } x } } } = { { 2 ^ { { { \log } _ 2 } { x ^ 3 } } } } = { { x ^ 3 } . } y = 8 t , ⇒ y = 8 l o g 2 x = ( 2 3 ) l o g 2 x = 2 l o g 2 x 3 = x 3 .
از آنجا که t ≥ 0 t \ge 0 t ≥ 0 x ≥ 2 0 = 1 x \ge {2^0} = 1 x ≥ 2 0 = 1
در نتیجه، منحنی سهمی y = x 3 y = x ^ 3 y = x 3 x ≥ 1 x \ge 1 x ≥ 1
شکل ۳: منحنی مسیر حرکت مثال ۶
مکان یک ذره با معادلات x ( t ) = 1 2 – t 2 x \left ( t \right ) = \large { \frac { 1 } { 2 } } \normalsize – { t ^ 2 } x ( t ) = 2 1 – t 2 y ( t ) = 2 t \large y \left ( t \right ) = \sqrt 2 t y ( t ) = 2 t x x x y y y d d d تابعی از t t t
حل: فاصله از مبدأ به صورت زیر تعریف میشود:
d ( t ) = x 2 ( t ) + y 2 ( t ) . \large d \left ( t \right ) = \sqrt { { x ^ 2 } \left ( t \right ) + { y ^ 2 } \left ( t \right ) } . d ( t ) = x 2 ( t ) + y 2 ( t ) .
با جایگذاری x ( t ) x ( t) x ( t ) y ( t ) y ( t) y ( t )
d ( t ) = ( 1 2 – t 2 ) 2 + ( 2 t ) 2 = 1 4 – t 2 + t 4 + 2 t 2 = t 4 + t 2 + 1 4 = ( t 2 + 1 2 ) 2 = t 2 + 1 2 ( m ) . \large \begin {align*} d \left ( t \right ) & = \sqrt { { { \left ( { \frac { 1 } { 2 } – { t ^ 2 } } \right ) } ^ 2 } + { { \left ( { \sqrt 2 t } \right ) } ^ 2 } } = { \sqrt { \frac { 1 } { 4 } – { t ^ 2 } + { t ^ 4 } + 2 { t ^ 2 } } } \\ & = { \sqrt { { t ^ 4 } + { t ^ 2 } + \frac { 1 } { 4 } } } = { \sqrt { { { \left ( { { t ^ 2 } + \frac { 1 } { 2 } } \right ) } ^ 2 } } } = { { { t ^ 2 } + \frac { 1 } { 2 } } \, \left ( \text {m} \right ) . } \end {align*} d ( t ) = ( 2 1 – t 2 ) 2 + ( 2 t ) 2 = 4 1 – t 2 + t 4 + 2 t 2 = t 4 + t 2 + 4 1 = ( t 2 + 2 1 ) 2 = t 2 + 2 1 ( m ) .
مثال ۷
ذرهای روی یک منحنی با معادلات x = tan t x = \tan t x = tan t y = sec t y = \sec t y = sec t t = π 6 t = \large{\frac{\pi }{6}}\normalsize t = 6 π
حل: از x x x y y y t t t
d x d t = d d t ( tan t ) = 1 cos 2 t , d y d t = d d t ( sec t ) = d d t ( 1 cos t ) = – 1 cos 2 t ⋅ ( – sin t ) = sin t cos 2 t . \large \begin {align*} \frac { { d x } } { { d t } } & = \frac { d } { { d t } } \left ( { \tan t } \right ) = \frac { 1 } { { { { \cos } ^ 2 } t } } , \\ \frac { { d y } } { { d t } } & = \frac { d } { { d t } } \left ( { \sec t } \right ) = { \frac { d } { { d t } } \left ( { \frac { 1 } { { \cos t } } } \right ) } = { – \frac { 1 } { { { { \cos } ^ 2 } t } } \cdot \left ( { – \sin t } \right ) } = { \frac { { \sin t } } { { { { \cos } ^ 2 } t } } . } \end {align*} d t d x d t d y = d t d ( tan t ) = cos 2 t 1 , = d t d ( sec t ) = d t d ( cos t 1 ) = – cos 2 t 1 ⋅ ( – sin t ) = cos 2 t sin t .
برای محاسبه تندی، از فرمول زیر استفاده میکنیم:
v = ( d x d t ) 2 + ( d y d t ) 2 . \large v = \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } . v = ( d t d x ) 2 + ( d t d y ) 2 .
بنابراین، خواهیم داشت:
v = ( 1 cos 2 t ) 2 + ( sin t cos 2 t ) 2 = 1 + sin 2 t cos 2 t . \large { v = \sqrt { { { \left ( { \frac { 1 } { { { { \cos } ^ 2 } t } } } \right ) } ^ 2 } + { { \left ( { \frac { { \sin t } } { { { { \cos } ^ 2 } t } } } \right ) } ^ 2 } } } = { \frac { { \sqrt { 1 + { { \sin } ^ 2 } t } } } { { { { \cos } ^ 2 } t } } . } v = ( cos 2 t 1 ) 2 + ( cos 2 t sin t ) 2 = cos 2 t 1 + sin 2 t .
با جایگذاری t = π 6 t = \large{\frac{\pi }{6}}\normalsize t = 6 π
v = 1 + sin 2 π 6 cos 2 π 6 = 1 + ( 1 2 ) 2 ( 3 2 ) 2 = 1 + 1 4 3 4 = 5 2 3 4 = 2 5 3 . \large { v = \frac { { \sqrt { 1 + { { \sin } ^ 2 } \frac { \pi } { 6 } } } } { { { { \cos } ^ 2 } \frac { \pi } { 6 } } } } = { \frac { { \sqrt { 1 + { { \left ( { \frac { 1 } { 2 } } \right ) } ^ 2 } } } } { { { { \left ( { \frac { { \sqrt 3 } } { 2 } } \right ) } ^ 2 } } } } = { \frac { { \sqrt { 1 + \frac { 1 } { 4 } } } } { { \frac { 3 } { 4 } } } } = { \frac { { \frac { { \sqrt 5 } } { 2 } } } { { \frac { 3 } { 4 } } } } = { \frac { { 2 \sqrt 5 } } { 3 } . } v = cos 2 6 π 1 + sin 2 6 π = ( 2 3 ) 2 1 + ( 2 1 ) 2 = 4 3 1 + 4 1 = 4 3 2 5 = 3 2 5 .
مثال ۸
ذرهای در صفحه x y x y x y x ( t ) = 3 t 3 – 3 t 2 x\left( t \right) = 3{t^3} – 3{t^2} x ( t ) = 3 t 3 –3 t 2 y ( t ) = 20 t 2 + 2 t y\left( t \right) = 20{t^2} + 2t y ( t ) = 20 t 2 + 2 t t ≥ 0 t \ge 0 t ≥ 0 x x x y y y t t t t = 2 s t = 2\,\text{s} t = 2 s
حل: ابتدا سرعت ذره را به دست میآوریم:
d x d t = d d t ( 3 t 3 – 3 t 2 ) = 9 t 2 – 6 t , d y d t = d d t ( 20 t 2 + 2 t ) = 40 t + 2. \large \begin {align*} \frac { { d x } } { {d t } } & = \frac { d } { { d t } } \left ( { 3 { t ^ 3 } – 3 { t ^ 2 } } \right ) = { 9 { t ^ 2 } – 6 t , } \\ \frac { { d y } } { { d t } } & = \frac { d } { { d t } } \left ( { 2 0 { t ^ 2 } + 2 t } \right ) = { 4 0 t + 2 . } \end {align*} d t d x d t d y = d t d ( 3 t 3 –3 t 2 ) = 9 t 2 –6 t , = d t d ( 20 t 2 + 2 t ) = 40 t + 2.
بنابراین، بردار سرعت به صورت زیر است:
v = d x d t i + d y d t j = ( 9 t 2 – 6 t ) i + ( 40 t + 2 ) j . \large { \mathbf { v } = \frac { { d x } } { { d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } } = { \left ( { 9 { t ^ 2 } – 6 t } \right ) \mathbf { i } } + { \left ( { 4 0 t + 2 } \right ) \mathbf { j } . } v = d t d x i + d t d y j = ( 9 t 2 –6 t ) i + ( 40 t + 2 ) j .
یک بار دیگر مشتق میگیریم و شتاب را حساب میکنیم:
d 2 x d t 2 = d d t ( 9 t 2 – 6 t ) = 18 t – 6 , d 2 y d t 2 = d d t ( 40 t + 2 ) = 40. \large \begin {align*} \frac { { { d ^ 2 } x } } { { d { t ^ 2 } } } & = \frac { d } { { d t } } \left ( { 9 { t ^ 2 } – 6 t } \right ) = { 1 8 t – 6 , } \\ \frac { { { d ^ 2 } y } } { { d { t ^ 2 } } } & = \frac { d }{ { d t } } \left ( { 4 0 t + 2 } \right ) = { 4 0 . } \end {align*} d t 2 d 2 x d t 2 d 2 y = d t d ( 9 t 2 –6 t ) = 18 t –6 , = d t d ( 40 t + 2 ) = 40.
بنابراین:
a = d 2 x d t 2 i + d 2 y d t 2 j = ( 18 t – 6 ) i + 40 j . \large \mathbf { a } = \frac { { { d ^ 2 } x } }{ { d { t ^ 2 } } } \mathbf { i } + \frac { { { d ^ 2 } y } }{ { d { t ^ 2 } } } \mathbf { j } = \left ( { 1 8 t – 6 } \right ) \mathbf { i } + 4 0 \mathbf { j } . a = d t 2 d 2 x i + d t 2 d 2 y j = ( 18 t –6 ) i + 40 j .
زمان t = 2 s t = 2\,\text{s} t = 2 s
a = 30 i + 40 j . \large \mathbf { a } = 3 0 \mathbf { i } + 4 0 \mathbf { j } . a = 30 i + 40 j .
در نتیجه، اندازه بردار شتاب برابر است با:
a = ∣ a ∣ = 30 2 + 40 2 = 50 m s 2 . \large { a = \left | \mathbf { a } \right | = \sqrt { { { 3 0 } ^ 2 } + { { 4 0 } ^ 2 } } } = { 5 0 \, \frac { \text {m} } {{{\text{s}^2}}}.} a = ∣ a ∣ = 30 2 + 40 2 = 50 s 2 m .
مثال ۹
توپی با تندی v 0 = 19.6 m s {v_0} = 19.6\,\large{\frac{\text{m}}{\text{s}}}\normalsize v 0 = 19.6 s m
(الف) چه زمانی طول میکشد توپ به زمین برخورد کند؟ شتاب گرانشی را 9.8 m s 2 9.8\,\large{\frac{\text{m}}{\text{s}^2}}\normalsize 9.8 s 2 m
(ب) حداکثر ارتفاع توپ نسبت به زمین چقدر است؟
حل (الف): مختصات y y y
y ( t ) = v 0 t – g t 2 2 . \large y \left ( t \right ) = { v _ 0 } t – \frac { { g { t ^ 2 } } }{ 2 } . y ( t ) = v 0 t – 2 g t 2 .
وقتی توپ به زمین برخورد کند، y y y
y ( t ) = v 0 t – g t 2 2 = 0. \large { y \left ( t \right ) = { v _ 0 } t – \frac { { g { t ^ 2 } } } { 2 } } = { 0 . } y ( t ) = v 0 t – 2 g t 2 = 0.
معادله را برای t t t
t ( v 0 – g t 2 ) = 0 , ⇒ t 1 = 0 , t 2 = 2 v 0 g . \large { t \left ( { { v _ 0 } – \frac { { g t } } { 2 } } \right ) = 0 , \; \; } \Rightarrow { { t _ 1 } = 0 , \; } \kern0pt { { t _ 2 } = \frac { { 2 { v _ 0 } } } { g } . } t ( v 0 – 2 g t ) = 0 , ⇒ t 1 = 0 , t 2 = g 2 v 0 .
ریشه دوم، لحظهای را نشان میدهد که توپ به زمین برخورد میکند:
t 2 = 2 v 0 g = 2 ⋅ 19.6 9.8 = 4 s . \large { { t _ 2 } = \frac { { 2 { v _ 0 } } } { g } } = { \frac { { 2 \cdot 1 9 . 6 } } { { 9 . 8 } } } = { 4 \, \text {s} . } t 2 = g 2 v 0 = 9.8 2 ⋅ 19.6 = 4 s .
حل (ب): زمان رسیدن توپ به نقطه حداکثر ارتفاع، از معادله v ( t ) = 0 v\left( t \right) = 0 v ( t ) = 0
v ( t ) = v 0 – g t = 0 , ⇒ t = v 0 g . \large { v \left ( t \right ) = { v _ 0 } – g t = 0 , \; \; } \Rightarrow { t = \frac { { { v _ 0 } } } { g } . } v ( t ) = v 0 – g t = 0 , ⇒ t = g v 0 .
حداکثر ارتفاع برابر است با:
y max = v 0 t – g t 2 2 = v 0 ( v 0 g ) – g 2 ( v 0 g ) 2 = v 0 2 g – v 0 2 2 g = v 0 2 2 g = ( 19.6 ) 2 2 ⋅ 9.8 = 19.6 m \large \begin {align*} { y _ { \max } } & = { v _ 0 } t – \frac { { g { t ^ 2 } } } { 2 } = { { v _ 0 } \left ( { \frac { { { v _ 0 } } } { g } } \right ) – \frac { g } { 2 } { \left ( { \frac { { { v _ 0 } } } { g } } \right ) ^ 2 } } \\ & = { \frac { { v _ 0 ^ 2 } } { g } – \frac { { v _ 0 ^ 2 } } { { 2 g } } } = { \frac { { v _ 0 ^ 2 } } { { 2 g} } } = { \frac { { { { \left ( { 1 9 . 6 } \right ) } ^ 2 } } } { { 2 \cdot 9 . 8 } } } = { 1 9 . 6 \, \text {m} } \end {align*} y m a x = v 0 t – 2 g t 2 = v 0 ( g v 0 ) – 2 g ( g v 0 ) 2 = g v 0 2 – 2 g v 0 2 = 2 g v 0 2 = 2 ⋅ 9.8 ( 19.6 ) 2 = 19.6 m
مثال ۱۰
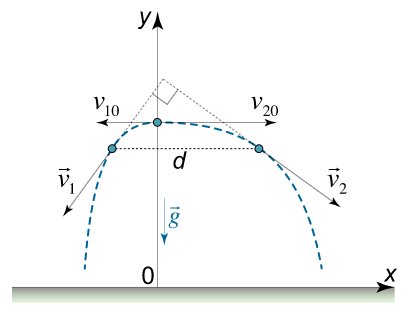
دو توپ در نقطه یکسانی قرار دارند و با سرعتهای اولیه v 10 = 4 m s {v_{10}} = 4\,\large{\frac{\text{m}}{\text{s}}}\normalsize v 10 = 4 s m v 20 = 9 m s {v_{20}} = 9\,\large{\frac{\text{m}}{\text{s}}}\normalsize v 20 = 9 s m d d d
شکل ۴: پرتاب دو توپ حل: ابتدا مؤلفههای سرعت توپها را مینویسیم:
v 1 x = – v 10 , v 1 y = – g t , v 2 x = v 20 , v 2 y = – g t . \large { { v _ { 1 x } } = – { v _ { 1 0 } } , \; } \kern0pt { { v _ { 1 y } } = – g t , } \\ \large { { v _ { 2 x } } = { v _ { 2 0 } } , \; } \kern0pt { { v _ { 2 y } } = – g t . } v 1 x = – v 10 , v 1 y = – g t , v 2 x = v 20 , v 2 y = – g t .
بنابراین، بردارهای سرعت به شکل زیر هستند:
v 1 = – v 10 i – g t j , v 2 = v 20 i – g t j . \large { \mathbf { v } _ 1 } = – { v _ { 1 0 } } \mathbf { i } – g t \mathbf { j } , \\ \large { \mathbf { v } _ 2 } = { v _ { 2 0 } } \mathbf { i } – g t \mathbf { j } . v 1 = – v 10 i – g t j , v 2 = v 20 i – g t j .
وقتی بردارهای سرعت عمود بر هم باشند، ضرب نقطهای آنها برابر با صفر است و بنابراین، داریم:
v 1 ⊥ v 2 , ⇒ v 1 ⋅ v 2 = 0 , ⇒ ( – v 10 ) v 20 + ( – g t ) ( – g t ) = 0 , ⇒ g 2 t 2 = v 10 v 20 , ⇒ t = v 10 v 20 g . \large \begin {align*} & { \mathbf { v } _ 1 } \bot { \mathbf { v } _ 2 } , \; \; \Rightarrow { { \mathbf { v } _ 1 } \cdot { \mathbf { v } _ 2 } = 0 , \; \; } \Rightarrow { \left ( { – { v _ { 1 0 } } } \right ){ v _ { 2 0 } } + \left ( { – g t } \right ) \left ( { – g t } \right ) = 0 , \; \; } \\ & \Rightarrow { { g ^ 2 } { t ^ 2 } = { v _ { 1 0 } } { v _ { 2 0 } } , \; \; } \Rightarrow { t = \frac { { \sqrt { { v _ { 1 0 } } { v _ { 2 0 } } } } } { g } . } \end {align*} v 1 ⊥ v 2 , ⇒ v 1 ⋅ v 2 = 0 , ⇒ ( – v 10 ) v 20 + ( – g t ) ( – g t ) = 0 , ⇒ g 2 t 2 = v 10 v 20 , ⇒ t = g v 10 v 20 .
از آنجا که مؤلفههای قائم سرعت دو توپ یکسان است، همواره در ارتفاع یکسانی قرار دارند. بنابراین، خط فاصله d d d t = v 10 v 20 g t = \large{\frac{{\sqrt {{v_{10}}{v_{20}}} }}{g}}\normalsize t = g v 10 v 20
d = v 10 t + v 20 t = ( v 10 + v 20 ) t = ( v 10 + v 20 ) v 10 v 20 g . \large { d = { v _ { 1 0 } } t + { v _ { 2 0 } } t } = { \left ( { { v _ { 1 0 } } + { v _ { 2 0 } } } \right ) t } = { \left ( { { v _ { 1 0 } } + { v _ { 2 0 } } } \right ) \frac { { \sqrt { { v _ { 1 0 } } { v _ {2 0 } }} } } { g } . } d = v 10 t + v 20 t = ( v 10 + v 20 ) t = ( v 10 + v 20 ) g v 10 v 20 .
و در نهایت، با قرار دادن مقادیر معلوم، خواهیم داشت:
d = ( 4 + 9 ) 4 ⋅ 9 9.8 = 7.96 m \large { d = \left ( { 4 + 9 } \right ) \frac { { \sqrt { 4 \cdot 9 } } } { { 9 . 8 } } } = { 7 . 9 6 \, \text {m} } d = ( 4 + 9 ) 9.8 4 ⋅ 9 = 7.96 m
مثال ۱۱
ذرهای در صفحه x y x y x y x = a t x = at x = a t y = b t 2 y = b t ^ 2 y = b t 2 a , b > 0 a , b > 0 a , b > 0
(لف) مسیر y ( x ) y ( x ) y ( x )
(ب) تندی ذره را به عنوان تابعی از زمان بیان کنید.
(ج) زاویه φ \varphi φ x x x
حل (الف): از معادله اول t t t
x = a t , ⇒ t = x a , ⇒ y = b ( x a ) 2 = b a 2 x 2 . \large { x = a t , \; \; } \Rightarrow { t = \frac { x } { a } , \; \; } \Rightarrow { y = b { \left ( { \frac { x } { a } } \right ) ^ 2 } } = { \frac { b } { { {a ^ 2 } } } { x ^ 2 } . } x = a t , ⇒ t = a x , ⇒ y = b ( a x ) 2 = a 2 b x 2 .
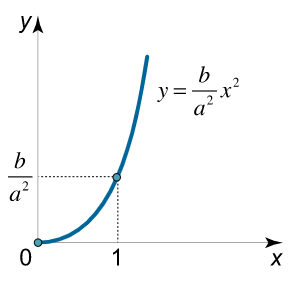
بنابراین، مسیر ذره شاخه سمت راست سهمی y = b a 2 x 2 y = \frac{b}{{{a^2}}}{x^2} y = a 2 b x 2
شکل ۵: منحنی مسیر حرکت حل (ب): برای تعیین تندی ذره، ابتدا از مختصات x x x y y y t t t
d x d t = d d t ( a t ) = a , d y d t = d d t ( b t 2 ) = 2 b t . \large \begin {align*} \frac { { d x } } { { d t } } & = \frac { d } { { d t } } \left ( { a t } \right ) = a , \\ \frac { { d y } } { { d t } } & = \frac { d } { { d t } } \left ( { b { t ^ 2 } } \right ) = 2 b t . \end {align*} d t d x d t d y = d t d ( a t ) = a , = d t d ( b t 2 ) = 2 b t .
بنابراین، بردار سرعت به صورت زیر است:
v = d x d t i + d y d t j = a i + 2 b t j . \large { \mathbf { v } = \frac { { d x } } { { d t } } \mathbf { i } + \frac { { d y } } { { d t } } \mathbf { j } } = { a \mathbf { i } + 2 b t \mathbf { j } . } v = d t d x i + d t d y j = a i + 2 b t j .
از آنجا که تندی قدر مطلق سرعت است، داریم:
v = ( d x d t ) 2 + ( d y d t ) 2 = a 2 + 4 b 2 t 2 . \large { v = \sqrt { { { \left ( { \frac { { d x } } { {d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } } = { \sqrt { { a ^ 2 } + 4 { b ^ 2 } { t ^ 2 } } . } v = ( d t d x ) 2 + ( d t d y ) 2 = a 2 + 4 b 2 t 2 .
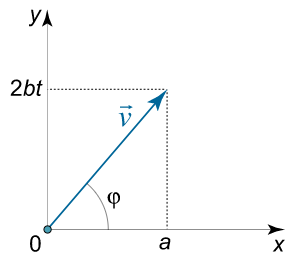
حل (ج): بردار سرعت به فرم زیر است:
v = a i + 2 b t j . \large \mathbf { v } = a \mathbf { i } + 2 b t \mathbf { j } . v = a i + 2 b t j .
بنابراین، شیب زاویه φ \varphi φ
tan φ = 2 b t a . \large \tan \varphi = \frac { { 2 b t } } { a } . tan φ = a 2 b t .
و خود زاویه به صورت زیر به دست خواهد آمد:
φ = arctan ( 2 b t a ) . \large \varphi = \arctan \left ( { \frac { { 2 b t } } { a } } \right ) . φ = arctan ( a 2 b t ) .
x x x شکل ۶: زاویه بین بردار سرعت و محور x x x اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:

 " width="295" height="263">
" width="295" height="263">












بسیار عالی به خاطر سایت خوبتون