حرکت سقوط آزاد — به زبان ساده

در مجموعه مقالات مجله فرادرس، با «سینماتیک» (Kinematics) (حرکتشناسی) حالتهای سادهای نظیر حرکت با سرعت ثابت و حرکت با شتاب ثابت آشنا شدید. در این مقاله از مجله فرادرس قصد داریم تا با زبانی ساده و ارائه چند مثال، به طور خاص مبحث حرکت سقوط آزاد در فیزیک را بررسی کنیم.
مبحث سقوط آزاد، به بررسی سقوط یک جسم در میدان گرانشی میپردازد. حرکت سقوط آزاد را حرکتی یک بعدی در نظر میگیریم. توجه شود که معادلات این حرکت تنها برای حالت سقوط، یعنی حرکتی از ارتفاع بیشتر به کمتر، صادق نبوده و برای حرکتی از ارتفاع کمتر به بیشتر نیز صادق است.
گرانش (جاذبه زمین)
یک جسم سنگین و یک پَر را در نظر بگیرید که از ارتفاعی مشخص به پایین سقوط میکنند. اگر از مقاومت هوا صرفنظر کنیم، کدام یک از آنها زودتر به سطح زمین میرسد؟
یکی از واقعیتهای غیرمنتظره در خصوص سقوط اجسام، این است که اگر از مقاومت هوا صرفنظر کنیم، در تمامی نقاط کُره زمین، سقوط همه اجسام به سمت مرکز زمین و با شتابی ثابت صورت میگیرد که این شتاب مستقل از جرم اجسام است. شاید پذیرفتن این مطلب که جسم سنگین و پر به صورت یکسان و همزمان به سطح زمین رسند، برایتان غیرقابل قبول باشد. اغلب مردم انتظار دارند که اجسام سنگینتر، به هنگام سقوط، شتاب بیشتری داشته و زودتر به سطح زمین برسند. این مطلب همیشه درست نبوده و در غیاب مقاومت هوا، هر دو جسم به صورت همزمان به سطح زمین میرسند.

در حالت عادی و دنیای روزمره ما، مقاومت هوا همیشه وجود دارد. در واقع همانند مقاومتی که آب برای یک سنگ که به درون آن انداخته میشود یا مقاومتی که سطح برای حرکت دادن یک جسم ایجاد میکند، هوا هم برای اجسامی که در آن حرکت میکنند، مقاومت ایجاد کرده و باعث میشود یک جسم سبکتر، آهستهتر از یک جسم سنگین (در زمان و ارتفاع یکسان) سقوط کند.
در این مقاله به بررسی سقوط مواردی میپردازیم که مقاومت (اصطکاک) هوا در آنها وجود ندارد. به این حالت (بدون مقاومت هوا)، حرکت سقوط آزاد گفته میشود. در این حالت نیرو گرانشی باعث میشود که اجسام به سمت مرکز زمین با شتاب ثابت گرانشی سقوط کنند. این شتاب ثابت باعث میشود که ما بتوانیم به راحتی از معادلات سینماتیکی (حرکتی) برای بررسی حرکت سقوط آزاد اجسام استفاده کنیم. سقوط آزاد را میتوان حرکتی یک بعدی در راستای قائم (عمودی) در نظر گرفت.
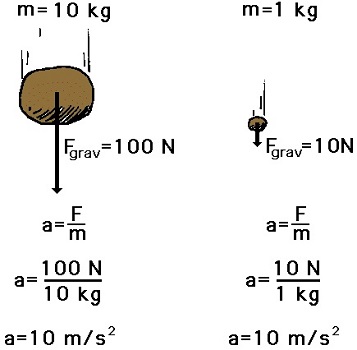
شتاب ناشی از گرانش، در همهجای کره زمین (البته نه در ارتفاعهای خیلی بالا) ثابت بوده و مقدار متوسط آن به صورت زیر است:
موقعیت جغرافیایی روی مقدار g موثر است. اما برای راحتی کار در مسائل ساده، همیشه مقدار آن را ثابت در نظر میگیریم. با صرف نظر از چرخش زمین، جهت شتاب گرانشی همیشه به سمت پایین (مرکز زمین) است. البته توجه داشته باشید که علامت شتاب در معادلات سینماتیکی به مختصاتی که ما آن را تعریف میکنیم بستگی دارد. اگر جهت بالا را مثبت در نظر بگیریم، شتاب g را به صورت منفی () در معادلات جایگذاری میکنیم؛ چرا که جهت به سمت زمین (پایین) است و اگر جهت پایین را مثبت تعریف کنیم، شتاب g را به صورت مثبت () در معادلات جایگذاری میکنیم. معمولاً در اکثر مراجع به هنگام بررسی مسائل حرکت سقوط آزاد در فیزیک پایه، جهت بالا را مثبت تعریف کرده و لذا علامت را به صورت منفی در نظر میگیرند.
حرکت سقوط آزاد (حرکت یک بعدی با شتاب ثابت)
همانطور که پیشتر بیان کردیم، برای بررسی حرکت سقوط آزاد اجسام، میتوانیم از معادلات سینماتیکی بهره ببریم. از آنجایی که سقوط آزاد، حرکتی یک بعدی در راستای قائم است، برای روشنی و نمایش بهتر مطلب نماد را به جای و شتاب ثابت گرانشی را به جای در معادلات قرار میدهیم. باز هم یادآور میشویم که اگر جهت بالا را مثبت در نظر گرفتید، را به صورت منفی در معادلات استفاده کنید. در مسائل این مقاله، ما جهت بالا را مثبت در نظر میگیریم.
پیرو مطالب گفته شده، معادلات سینماتیکی برای حرکت یک بعدی با شتاب ثابت در راستای قائم (مسائل حرکت سقوط آزاد) به شکل زیر هستند (جهت بالا مثبت فرض شده است):
(1)
(2)
(3)
در ادامه به بررسی چند مثال میپردازیم.
مثال ۱
فرض کنید که در بالای یک بلندی ایستاده و سنگی را رها میکنید. پس از گذشت ۱ ثانیه، سنگ چه مسافتی را طی میکند؟ پس از گذشت این زمان، سرعت سنگ چقدر است؟
برای حل این مسئله، جهت رو به بالا را مثبت در نظر میگیریم. در نتیجه شتاب ثابت گرانشی را با علامت منفی در معادلات جایگذاری میکنیم. همچنین مکانی که سنگ رها شده را ۰ در نظر میگیریم؛ یعنی مکان اولیه سنگ در نقطه ۰ محور مختصاتی است (). همچنین توجه داشته باشید که رها کردن یک جسم، به منزله سقوط آن بدون سرعت اولیه است. پس در اینجا بوده و در نتیجه از رابطه (۱) داریم:
در واقع جابهجایی طی شده توسط سنگ بوده و مسافت طی شده است. برای به دست آوردن سرعت پس از گذشت ۱ ثانیه نیز از رابطه (۲) استفاده میکنیم.
بیان کردیم که سقوط آزاد حرکتی یک بعدی با شتاب ثابت است. یعنی با توجه به مفهوم شتاب، با گذشت هر ثانیه، مقدار بر سرعت جسم افزوده میشود. در اینجا که سرعت اولیه صفر است، در پایان ثانیه اول، مقدار بر سرعت سنگ اضافه میشود.
حال فرض کنید ارتفاعی که در آن قرار دارید نسبت به سطح زمین 10 متر باشد. در این صورت سرعت سنگ به هنگام برخورد با زمین چقدر است؟ این سقوط (زمان رها شدن تا برخورد) چقدر طول میکشد؟
برای به دست آوردن سرعت سنگ هنگام برخورد با سطح زمین، از معادله (۳) استفاده میکنیم.
دقت شود از آنجایی که جهت بالا را مثبت و نقطه رها شدن سنگ را ۰ مختصات تعریف کردیم، ارتفاع بلندی را به صورت منفی در معادله قرار دادیم. دقت کنید که اگر ارتفاع را به صورت مثبت در معادله قرار میدادیم، حاصل یک عبارت توان دو حقیقی منفی میشد که غیر قابل قبول است. همچنین از آنجایی که جهت بالا را مثبت در نظر گرفتیم، برای سرعت جسم به هنگام برخورد علامت منفی () قابل قبول است.
برای به دست آوردن زمان کل، یعنی مدت زمانی که سنگ رها شده و به سطح زمین برخورد کرده، میتوانیم از هر دو رابطه (۱) و (۲) به صورت زیر استفاده کنیم:
مثال ۲
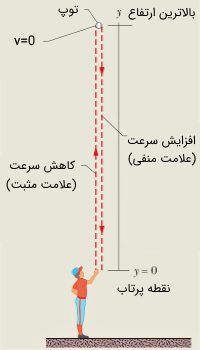
توپی را با سرعت اولیه به طرف بالا (مستقیم) پرتاب میکنیم. پس از گذشت چند ثانیه، توپ به بالاترین ارتفاع ممکن میرسد؟ این ارتفاع چقدر است؟ ()
برای پاسخ به این سوال، میتوانیم از رابطه (۱) و (۲) استفاده کنیم. در اینجا نیز حرکت به سمت بالا را مثبت و نقطه پرتاب را ۰ مختصات در نظر میگیریم. پس در لحظه پرتاب () و () بوده و در نتیجه از رابطه (۲) داریم:
دقت شود که در بالاترین ارتفاع ممکن، سرعت جسم صفر است. در واقع با پرتاب یک جسم به بالا، رفته رفته سرعت آن کم میشود و در بالاترین ارتفاع ممکن، به صفر میرسد، در این لحظه علامت سرعت عوض شده و به هنگام سقوط بر سرعتش افزوده میشود. برای به دست آوردن بالاترین ارتفاع ممکن، از رابطه (۱) داریم:
حال مدت زمانی که طول میکشد تا توپ به نقطه پرتاب خود رسد را محاسبه کنید. سرعت توپ به هنگام عبور از نقطه پرتاب چقدر است؟
برای پاسخ به این سوال میتوانیم باز هم از معادله (۱) استفاده کنیم. به هنگام رسیدن توپ به نقطه پرتاب، بوده و در نتیجه داریم:
زمان مربوط به زمان پرتاب و مدت زمانی است که طول میکشد توپ به نقطه پرتاب برگردد. سرعت توپ در این نقطه به هنگام برگشت از بالاترین نقطه از معادله (۲) به صورت زیر است:
مثال ۳
از بالای پلی به ارتفاع سنگی را با سرعت اولیه به طرف بالا پرتاب میکنیم. مدت زمانی که طول میکشد سنگ به زمین برخورد کند را محاسبه کنید.
برای حل این سوال، از رابطه (۱) استفاده میکنیم. در اینجا نیز حرکت به سمت بالا را مثبت و نقطه پرتاب را صفر مختصات در نظر میگیریم (). پس به هنگام برخورد سنگ با زمین، یعنی پایین پل، است. در نتیجه داریم:
پرتاب از زمان آغاز شده و در نتیجه پاسخ مورد قبول است.
برای حل مثال داده شده میتوان از راه حل دوم نیز استفاده کرد. در این حالت، مسیر سنگ پرتاب شده را مطابق تصویر به دو قسمت تقسیم میکنیم.
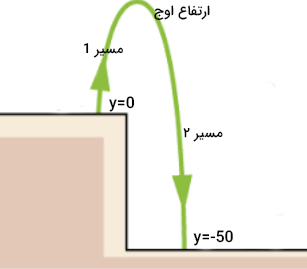
سنگ مسیر 1 را در مدت زمان و مسیر ۲ را در مدت زمان طی خواهد کرد. مدت زمانی است که سنگ از نقطه پرتاب تا رسیدن به ارتفاع اوج طی خواهد کرد در نتیجه داریم.
ارتفاع اوج از رابطه زیر به دست خواهد آمد.
اکنون زمان یعنی زمان رسیدن از نقطه اوج تا رسیدن به زمین را به دست میآوریم.
بنابراین مدت زمانی که طول میکشد تا سنگ به زمین برخورد کند برابر با جمع زمانهای و و مساوی با ۵ ثانیه خواهد بود.
مثال ۴
یک موشک کوچک به همراه «لانچر» (Booster) آن را در نظر بگیرید. قسمت لانچر در ارتفاع 5 کیلومتری از سطح زمین و در سرعت از موشک جدا میشود. بیشترین ارتفاعی که لانچر میتواند به آن برسد، چقدر است؟ (از مقاومت هوا صرفنظر کنید.)

برای پاسخ به این سوال، میتوانیم از رابطه (۳) استفاده کنیم. برای پاسخ به این سوال، میتوانیم اینگونه فرض کنیم که لانچر با سرعت اولیه به سمت بالا پرتاب شده است. نقطه پرتاب (در واقع نقطه جدا شدن از موشک) را نیز در ارتفاع در نظر میگیریم. همچنین به یاد دارید که سرعت در بالاترین ارتفاع مقدار صفر را دارد. در نتیجه:
رابطه فوق نشان میدهد که لانچر به اندازه از نقطه پرتاب (جدا شدن از موشک در ارتفاع 5 کیلومتری) بالاتر رفته و در نتیجه بیشترین ارتفاع ممکن آن از سطح زمین است.
مثال ۵
جسمی را از ارتفاع 2۰۰ متری به طرف پایین رها () میکنیم. پس از چند ثانیه جسم مذکور به زمین برخورد میکند؟ در حدفاصل زمانهای و جسم چه مقدار جابهجا شده است؟
از آنجایی که جسم رها شده است، سرعت اولیه ندارد. همچنین حرکت به سمت بالا را مثبت (یعنی با علامت منفی) و نقطه رها شدن را صفر مختصات در نظر میگیریم. در نتیجه از رابطه (۱) داریم:
برای پاسخ به قسمت دوم سوال نیز از رابطه (۱) استفاده میکنیم.
جابهجایی جسم مذکور در مدت زمان بین و به صورت محاسبه میشود. در نتیجه داریم:
مثال 6
توپی را از بالای یک ساختمانی به ارتفاع 98 متر با سرعت اولیه به پایین پرتاب میکنیم. پس از گذشت چند ثانیه و با چه سرعتی توپ به زمین برخورد میکند؟
همانند مثالهای پیشین، سمت بالا را مثبت و نقطه پرتاب را صفر مختصات در نظر میگیریم. همچنین علامت سرعت منفی است (رو به پایین). از رابطه (۱) نتیجه میشود:

واضح است که پاسخ مورد قبول است. برای محاسبه سرعت به هنگام برخورد از معادله (۲) داریم:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر از سایت و مجله فرادرس نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش فیزیک پایه ۱
- مجموعه آموزشهای مهندسی مکانیک
- حرکت با شتاب ثابت -- به زبان ساده
- حرکت پرتابی — به زبان ساده
- معادله دیفرانسیل حرکت — از صفر تا صد
- اصطکاک — به زبان ساده
^^













ممنون از شما اساتید محترم🙏🏻
مثالها عالی و مناسب و کاربردی بود
بسیار عالی
ممنون از لطف شما
مطالب بسیار عالی ارائه میشود.
با تشکر از آموزش عالی. مثال 5 دلتاy نباید 200- باشه؟
با سلام،
اصلاح مورد نظر در متن انجام شد،
با تشکر از همراهی شما با مجله فرادرس
سلام
وقتی در یک قرقره که به سقف وصل است یک بازوش یک جسم 3 کیلویی و در بازه ی دیگر اش یک جسم 6 کیلویی وصل باشد و این دو جسم حرک داشته باشند در این صورت شتاب رو به چه صور ت بدست می آوریم؟ کمی بیشتر توضیح بدید ممنون
باسلام اگر اسیاب عمودی به ارتفاع ۴۰ مترکه هر۲متر یک باکت ودر هرباکت ۲۰۰کیلو اب داشته باشیم وهر ۵ ثانیه یک باکت پر شود و سرعت۲۴ متر در دقیقه باشد وقرقره ما۳متر قطر داشته باشد قرقره ۲.۵۴ دور در دقیقه میزند . سوال محور قرقره چند اسب بخار خواهد داشت واگر به وسیله گییربکس دور را به ۱۵۰۰ دور تبدیل کنیم چند اسب بخار خواهیم داشت . باتشکر
اکه منظورتون از سوالات ماشین آتوود هست در این شرایط نیرو کشش طناب با هم هر دو مساوی هست و جهت حرکت هم برخلاف یک دیگر هستند و در شتاب هم یکسان هستند درصورتی که هر طناب و قرقره جسمش ناچیز باشه و اگر ناچیز باشه جسم طناب و قرقره
در جسم سنگین جهت حرکت رو به پایین هست mg-T=ma
در جسم سبک جهت حرکت روبه بالا هست T-mg=ma
a=(m2-m1)g/m1+m2 اینم از مساوی قرار دادن دو جسم به دست میاد
با سلام . ممنون بابت مطالب خوبتون .
من یک سنسور شتاب سنج دارم که شتاب رو در سه جهت نشان می دهد .
در حالت ساکن شتاب 1g به صورت عمود بر سطح زمین و در جهت بالا را نشان می دهد .
همچنین در حالت سقوط آزاد شتاب صفر را نشان می دهد .
مقادیری که این سنسور نشان می دهد دقیق می باشد منتهی در تناقض با مفهوم شتاب و گرانش در فیزیک کلاسیک هست .
ممنون میشم تعریف دقیق شتاب و گرانش و شتاب گرانشی را بذارید .
با سلام؛
سوال شما اشاره به تفاوت شتاب معمولی و شتاب مختصاتی دارد. شتاب مختصاتی نسبت به چارچوب مرجع ثابتی اندازهگیری میشود و در مورد 99 درصد مسايل فیزیک نیوتنی صدق میکند.
شتاب اندازهگیری شده توسط شتابسنج مربوط به مساله مطرح شده توسط انیشتن است. در این مساله، آسانسوری در فضای بدون جرم در نظر گرفته شده است. مقدار شتاب اندازهگیری توسط شتابسنج در این حالت برابر صفر است. اگر نیروی خارجی بر آسانسور وارد شود، مقدار شتاب نشان داده شده توسط شتابسنج مربوط به آن نیرو خواهد بود.
همچنین ذکر این نکته مهم است که باید به نحوه عملکرد شتابسنج دقت کنید.
در مثال ۳ سنگ ابتدا به طرف بالا پرتاب وتا اوج یک زمان مشخص tدارد و درنتیجه ارتفاع معلوم yراطی میکند سپس در بازگشت با سرعت اولیه ۰ مسیر ۵۰ متر بعلاوه y را باید طی کند تا به سطح زمین برسد کل زمان صرف شده از شروع پرتاب باجواب شما خیلی اختلاف دارد یک باربررسی کنید.
با سلام،
پاسخ به دست آمده صحیح است و برای درک بهتر راه حل دوم نیز اضافه شده است.
با تشکر از همراهی شما با مجله فرادرس
سلام خسته نباشید
در مثال ۲ چطور V0 رو ۲۰ متد بر ثانیه بدست اوردین ؟ داخل صورت مساله که چیزی نبود !
سلام و روز شما به خیر؛
مطلب مورد بازبینی و ویرایش قرار گرفت. از اینکه ما را با دقت مطالعه میکنید سپاسگزاریم.
سلام در مثال یک قسمت سوم تقریبا ک گفته ک
V^2 = – 2gy== – 2*9.8*-10
این 10 از کجا اومد مگ y تو مرحله قبلی 4/9 بدست نیورد چجوری اینجا شده 10
سلام و روز شما به خیر؛
اگر مثال را بار دیگر با دقت مطالعه کنید ملاحظه میکنید که در حالت دوم گفته شده که ارتفاع به 10 متر تغییر کرده است.
از اینکه با مجله فرادرس همراه هستید خرسندیم.
سلام این مسئله چجوری حل می شود
سوال 1 :اتومبيلی با سرعت
h
km
حرکت می کند. راننده متوجه می شود که 34m جلوتر از او مانعی وجود
56
دارد و ترمز می کند. چهار ثانية بعد, اتومبيل به مانع برخورد می کند. الف( شتاب ثابت اتومبيل، پيش از برخورد
چقدر بوده است؟ ب( در لحظة برخورد، سرعت اتومبيل چقدر بوده است؟
سلام یه سوال!
اگه یه جسمی که ۵۰ کیلوگرم وزن داره از ارتفاع ۱۵ متری رها بشه، لحظه برخورد به زمین چقدره وزنش؟ یا با چه نیرویی به زمین میخوره؟
سلام چرا جی را منفی در نظر می گیریم ؟در صورتی که با پایین رفتن جسم به شتابش افزوده می شود؟
سلام، وقت شما بخیر؛
در فیزیک به صورت قراردادی دستگاه مختصات راستگرد در نظر میگیریم. در این دستگاه سمت شمال را با علامت مثبت و سمت جنوب را با علامت منفی نمایش میدهیم. این موضوع در راستای x و z نیز صادق است و سمت راست در راستای x را مثبت و سمت چپ را با علامت منفی نشان میدهیم و یا در راستای z بردارهای به سمت داخل را منفی و بردارهای به سمت خارج را مثبت معرفی میکنیم.
بدین ترتیب علامت منفی یا مثبت در کمیتهای برداری نشاندهنده جهت بردار است و نه افزایش یا کاهش یک کمیت.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
شتاب گرانشی را میتوان با پرتاب یک جسم به طرف بالا و اندازه گیری لازم برای عبور از دو نقطه معین مسیر در هر دوجهت اندازه گرفت. اگر زمان لازم برای عبور جسم از یک خط افقی A در هر دو جهت برابر با Ta و برای خط دیگر Bبرابر با TB باشد با فرض ثابت بودن شتاب نشان دهید که اندازه این شتاب برابر است
جواب این سوال رو میخوام میشه حل کنید برام
سلام، وقت شما بخیر؛
در سوال شما اطلاعاتی در مورد سرعت اولیه جسم داده نشده است و صورت سوال کمی گنگ به نظر میرسد با اینحال با توجه به اطلاعاتی که شما ارائه دادهاید میتوان تا حدودی سوال را بررسی کرد. اگر زمان رفت و برگشت برای یک نقطه از مسیر یکسان باشد به این معنی است که آن نقطه در وسط مسیر حرکت شما قرار گرفته است که در نتیجه زمان رفت و برگشت یکسان است. در حقیقت TA و TB هر دو زمان لازم برای رسیدن جسم به نقطه میانی مسیر حرکت است. با استفاده از دستگاه معادله برای هر دو حالت A و B و دانستن سرعت اولیه برای هر دو حالت میتوان ثابت بودن شتاب را در هر دو مسیر نشان داد. همچنین این فرض را نیز باید مطرح کرد که نیروی مقاومت هوا در هر دو حالت مقادیر یکسانی دارند یا از آنها صرف نظر شده است.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.