تکانه زاویه‌ای سیستم — از صفر تا صد

پیش‌تر در وبلاگ فرادرس در مورد اصول تکانه و تکانه زاویه‌ای یک ذره بحث کردیم. اما در تجربه روزمره و در واقعیت معمولا با یک سیستم تشیکل شده از مجموعه‌ای از ذرات مواجه هستیم. برای نمونه موشکی را فرض کنید که از نقطه A به نقطه B حرکت می‌کند. به منظور بررسی تکانه زاویه‌ای چنین سیستمی، بایستی مجموع تکانه زاویه‌ای ذرات آن را مورد بررسی قرار داد.

تکانه زاویه‌ای یک جسم صُلب

جسم صلبی را به نحوی در نظر بگیرید که با سرعت زاویه‌ای ω حول محور مشخصی دوران می‌کند. تصور کنید که سیستم مفروض، از N ذره تشکیل شده است. از این رو مشخصات آن، به شکل زیر نمایش داده می‌شود.

فیلم آموزش مکانیک تحلیلی 1 مرور و حل مثال در فرادرس

کلیک کنید

m_i: جرم ذره iام

r_i: بردار مکان ذره iام

v_i: بردار سرعت ذره iام

توجه داشته باشید که در این مسئله فرض شده که محور دوران ذره، از مرکز مختصات عبور می‌کند. در این حالت تکانه زاویه‌ای جسم مفروض (L) برابر با حاصل جمع تکانه‌های ذرات سیستم، در نظر گرفته می‌شود. بنابراین می‌توان گفت:

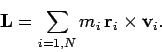
با فرضیات صورت گرفته، سرعت خطی هریک از ذرات جسم برابر است با:

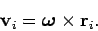
لازم به ذکر است که اجزا تشکیل دهنده معادلات بالا، همگی بردار هستند. برای نمونه، ω برداری است که در راستای محور دوران است. بنابراین رابطه بالا به شکل زیر در خواهد آمد.

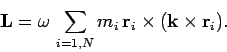
برای محاسبه مولفه تکانه زاویه‌ای در راستای محور دوران (L_k)، می‌توان معادله ۲ را به صورت زیر در بردار k، (بردار واحد در راستای محور Z) ضرب داخلی کرد.

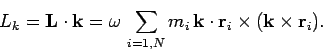
از ضرب خارجی بردارها می‌دانیم که رابطه a×b.c=a.b×c در بردارها برقرار است. بنابراین معادله بالا را می‌توان به شکل زیر بازنویسی کرد.

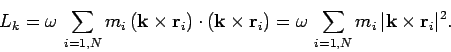
که برابر است با:

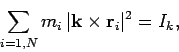
از معادلات ۳ و ۴ می‌توان مولفه لختی دورانی در راستای محور Z را به صورت زیر محاسبه کرد.

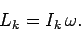
بنابراین می‌توان گفت که تکانه زاویه‌ای یک جسم حول محور دورانیش، برابر با حاصلضرب لختی دورانی - حول آن محور - در سرعت زاویه‌ای آن است. 

سوال : به نظر شما آیا رابطه زیر همواره صحیح است؟

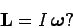
پاسخ سوال، منفی است. چرا که تکانه زاویه‌ای حول یک محور خاص برابر با حاصلضرب لختی دورانی، حول آن محور در سرعت زاویه‌ای جسم است. توجه داشته باشید که در حالت کلی ممکن است بردار گشتاور زاویه‌ای و سرعت زاویه‌ای با یکدیگر موازی نباشند.

جسم صلبی را تصور کنید که بردار سرعت زاویه‌ای آن به صورت (ω = (ω_x , ω_y , ω_z در نظر گرفته شده است. بنابراین، اگر تکانه زاویه‌ای به شکل (L=(L_x , L_y , L_z فرض شود، می‌توان اجزا آن را به ترتیبی که در زیر آمده، محاسبه کرد.

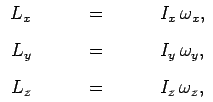
در این سه معادله، I_y،I_x و I_z به ترتیب لختی‌های دورانی جسم، حول محورهای y،x و z هستند. توجه داشته باشید که در این مثال مبدا دستگاه مختصات، روی محور دوران قرار گرفته است. توجه داشته باشید که در هر دستگاه مختصاتی که از سه محور عمود بر هم ساخته شده، می‌توان رابطه زیر را نوشت.

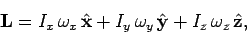
در معادله بالا  $$\hat{x}$$، $$\hat{y}$$ و $$\hat{z}$$  به ترتیب، بردارهای واحد در راستای محورهای y، x و z هستند. از رابطه بالا می‌توان برداشت کرد که الزاما بردارهای ω و L هم‌راستا نیستند. دلیل این نابرابری، متفاوت بودن لختی دورانی حول محورهای مختلف است.

توجه داشته باشید که همواره سه محور دورانی عمود بر هم وجود دارند که بردار تکانه زاویه‌ای و سرعت زاویه‌ای هم جهت هستند. به این محورها، محورهای اصلی می‌گویند.

چگونه می‌توان محورهای اصلی دوران را یافت؟

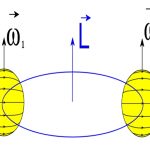
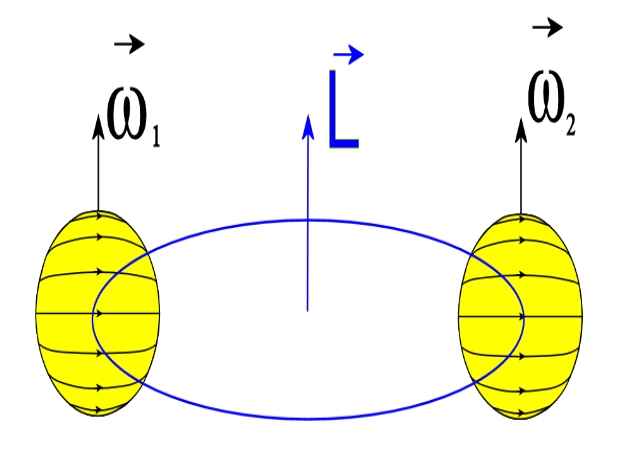
در ساده‌ترین حالت می‌توان گفت محوری که منطبق بر خط تقارن یک جسم باشد، محوری اصلی آن خواهد بود. شکل زیر محور دورانی را نشان می‌دهد که خط تقارن جسم نیز محسوب می‌شود. بنابراین این محور، اصلی در نظر گرفته می‌شود.

فیلم آموزش مکانیک تحلیلی 2 – جامع و کاربردی در فرادرس

کلیک کنید

همان‌طور که در این شکل می‌بینید، دو جرمِ m، در فاصله مشخصی از یکدیگر در حال دوران هستند.

این دو جرم، در موقعیتی با زاویه θ نسبت به محور دوران قرار گرفته‌اند. اگر توجه فرمایید، جهت بردار تکانه زاویه‌ای هر کدام از جر‌م‌ها، نشان داده شده است. از این رو با جمع زدن این دو بردار، جهت تکانه زاویه‌ای معادل نیز بدست بدست می‌آید. همانگونه که در شکل نیز نشان داده شده، جهت بردار تکانه زاویه‌ای معادل، هم راستا با بردار سرعت زاویه‌ای است.

تکانه زاویه‌ای یک سیستم چند بخشی

سیستمی با N ذره را به نحوی در نظر بگیرید که روی یکدیگر نیز تاثیرگذار هستند. فرض کنید r_i بردار مکان ذره iام و m_i جرم آن باشد. حال تصور کنید که این ذره نیرویی برابر با f_ji را به ذره jام وارد کند. بنابراین طبق قانون سوم نیوتن، این نیرو در خلاف جهت نیروی f_ij است. در نتیجه می‌توان نوشت:

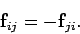
بنابراین تاکنون فرض شده که با سیستمی از چندین ذره روبرو هستیم که دو به دو به یکدیگر نیرو وارد می‌کنند. هم‌چنین تصور کنید، نیروهایی که ذرات به یکدیگر وارد می‌کنند، در راستای خطی است که آن‌ها را به یکدیگر متصل کرده. برای درک بهتر به شکل زیر توجه فرمایید.

همان‌طور که در بخش اول مبحث تکانه نیز بیان کردیم، مشتق زمانی تکانه خطی، معادل با برآیند نیروهای وارد شده به یک ذره است. بنابراین با توجه به فرضیات بیان شده، معادله حرکتِ ذره iام را می‌توان به صورت زیر نوشت.

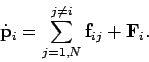
در این معادله $$\dot p$$ مشتق تکانه خطی است. حال بردار r را در $$\dot p$$، ضرب خارجی می‌کنیم.

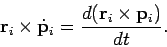
هم‌چنین می‌دانیم که تکانه زاویه‌ای ذرات حول مرکزِ دوران، برابر با حاصل ضرب خارجیِ بردار آن‌ها در بردار تکانه خطی است. بنابراین می‌توان بردار تکانه زاویه‌ای را به شکل زیر نوشت.

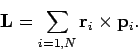
با جایگذاری معادلات ۶ و ۷ در معادله ۵، می‌توان تغییرات تکانه زاویه‌ای با زمان را بر حسب نیروهای وارد شده به ذرات، به صورتی که در ادامه آمده، بیان کرد:

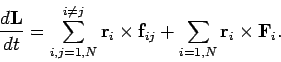
توجه داشته باشید که عبارت اولِ سمت راست معادله فوق را می‌توان به شکل زیر بیان کرد.

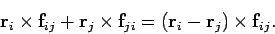
از آنجایی که دو بردار f_ij و (r_i-r_j) با یکدیگر موازی هستند، ضرب خارجی آن‌ها نیز صفر است. از این رو رابطه فوق نیز همواره برابر با صفر خواهد بود.

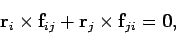
با فرض صفر بودن عبارت اول سمت راست معادله بالا، آنچه که در معادله مذکور باقی می‌ماند، همان مفهوم گشتاور را بیان می‌کند. نهایتا معادله ۸ به صورت زیر بازنویسی می‌شود.

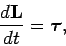
τ، گشتاور خالص وارد شده به کل سیستم، حول مرکز مختصات است. در حقیقت معادله بالا، رابطه حرکت دورانی برای یک سیستم کامل محسوب می‌شود. این معادله بیان می‌کند که اگر به سیستمی هیچ گشتاور خارجی وارد نشود، تکانه زاویه‌ای آن با زمان ثابت می‌ماند. پایستگی تکانه زاویه‌ای مفهومی بسیار مفید در تحلیل یک سیستمِ کامل است. برای درک بهتر، به دو مثالی که در ادامه آمده، توجه فرمایید.

مثال ۱

مطابق شکل زیر، دو جرمِ m را تصور کنید که توسط میله‌ای رابط، با سرعت زاویه‌ای ω در حال دوران هستند. فرض کنید که این جرم‌ها، به موتورهایی مجهز شده‌اند که آن‌ها را در فاصله d از مرکز، نگه می‌دارند. رابطه میان سرعتِ دوران و فاصله d به چه صورت است؟

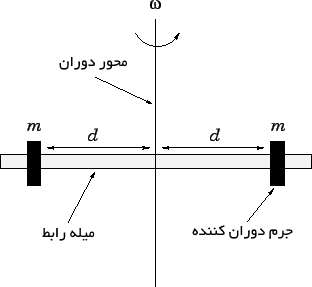
حتما می‌دانید که گشتاور خارجی به سیستم وارد نمی‌شود، بنابراین قانون پایستگی تکانه زاویه‌ای برای سیستم مفروض صادق است. همان‌طور که در بخش لختی دورانی نیز بیان شد، لختی چنین سیستمی برابر است با:

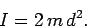
هم‌چنین از آنجایی که این سیستم، حول محور اصلی خود در حال دوران است، تکانه زاویه‌ای آن را می‌توان به شکل زیر محاسبه کرد.

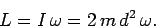
همان‌گونه که بیان شد، لختی دورانی این سیستم ثابت است؛ بنابراین برای این سیستم مقدار 2md²ω، بایستی ثابت باشد. در نتیجه رابطه بین ω و d بایستی به ترتیب زیر باشد.

در حقیقت معادله بالا بیان می‌کند که با نزدیک شدن جرم‌ها به مرکز، سرعت زاویه‌ای سیستم نیز افزایش و در صورت دور شدن آن‌ها، کاهش می‌یابد. در انیمیشن زیر می‌توان تغییر سرعت زاویه‌ای را بر حسب تغییرات فاصله مشاهده کرد.

مثال ۲

چوب ساکنی به جرم M و طول ۲b را مطابق شکل زیر تصور کنید. جسم مفروض، حول نقطه مشخصی لولا شده و گلوله‌ای به جرم m به سمت آن شلیک می‌شود. سرعت گلوله را در لحظه برخورد، برابر با v تصور کنید. بدیهی است که در نتیجه این برخورد، چوب مد نظر شروع به دوران می‌کند. سرعت دورانی (ω) چوب، پس از برخورد چقدر است؟

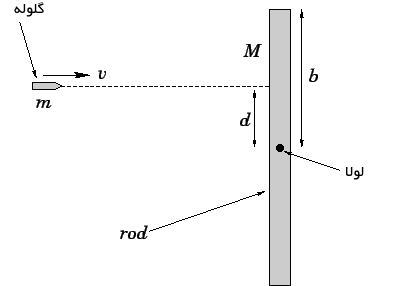
اگر مجموعه گلوله و چوب را به عنوان سیستم در نظر بگیریم، هیچ نیروی خالص خارجی به آن‌ها وارد نشده است. [نیرویی که گلوله به چوب وارد می‌کند، درون سیستم است و از بیرون نیرویی به مجموعه آن دو، وارد نمی‌شود.] در نتیجه تکانه زاویه‌ای کل سیستم، پایسته بوده و قبل و پس از برخورد، برابر هستند. بنابراین می‌توان گفت:

تکانه سیستم، پس از برخورد = تکانه سیستم، (گلوله + چوب) قبل از برخورد

گلوله به چوب برخورد کرده و هر دوی آن‌ها شروع به دوران می‌کنند. بنابراین پس از برخورد، مجموعه گلوله و چوب، دارای تکانه زاویه‌ای هستند. بنابراین می‌توان گفت:

تکانه سیستم قبل از برخورد = mdv

تکانه زاویه‌ای گلوله پس از برخورد = md²ω

تکانه زاویه‌ای چوب پس از برخورد = Iω = $${1 \over ۳}Mb^2$$ω

$$\rightarrow$$   تکانه زاویه‌ای سیستم پس از برخورد =md²ω + $${1 \over ۳}Mb^2$$ω

با برابر قرار دادن تکانه‌های قبل و پس از برخورد داریم:

mdv = $${1 \over ۳}Mb^2\omega+md^2\omega$$

$$\rightarrow \quad \quad ω = {mvd \over ({1 \over ۳}Mb^2)+md^2}$$

اگر امکان محاسبه لختی دورانیِ جسم‌های گوناگون وجود داشته باشد، می‌توان سرعت دورانی سیستم‌های مختلف را محاسبه کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مکانیک، احتمالا می‌توانید از آموزش‌های زیر نیز استفاده کنید.

• لختی دورانی چیست -- به زبان ساده
• تکانه از صفر تا صد -- بخش اول: اصول و مفاهیم
• تکانه از صفر تا صد -- بخش دوم: تکانه زاویه‌ای
• آموزش مروری دینامیک مهندسی و حل سؤالات

^^