حرکت با شتاب ثابت – به زبان ساده

با فکر کردن درباره حرکت یک جسم، چرا‌ و چگونه‌های زیادی در ذهن ما نقش می‌بندد. برای پاسخ به این سوالات باید به سراغ فیزیک مکانیک برویم. علم مکانیک از دو دیدگاه به هم مرتبط «سینماتیک» (Kinematic) و «دینامیک» (Dynamic) به این سوالات پاسخ می‌دهد. سینماتیک یا حرکت‌شناسی در خصوص چگونگی حرکت و دینامیک در خصوص رابطه حرکت و نیرو بحث می‌کنند. در این مقاله قصد داریم با زبانی ساده به طور خاص، سینماتیک حرکت با شتاب ثابت را به همراه چندین مثال بررسی کنیم. با ما در ادامه این مطلب همراه باشید.

حرکت با شتاب ثابت

فرض کنید که سرعت جسم در حال حرکتی به طور یکنواخت تغییر کند، به طوری که بتوان سرعت آن را در نمودار زیر بر حسب زمان رسم کرد. در اینجا سرعت به طور خطی با زمان تغییر کند. می‌دانیم که هرگاه سرعت یک جسم در طول حرکت تغییر کند، حرکت آن را شتابدار می‌نامیم.

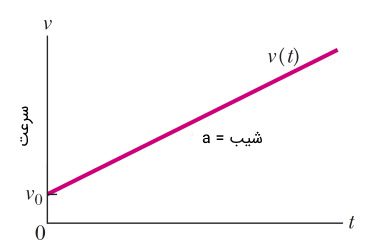
معادله‌ای که نمودار فوق را توصیف می‌کند، معادله یک خط به صورت زیر است:

$$v=at+v_{0}$$
(1)

ضریب زمان در معادله فوق، همان شیب خط نمودار شکل (1) بوده که شتاب نام دارد. معادله (۱) سرعت حرکت جسمی را توصیف می‌کند که با شتابی ثابت در حال حرکت است. از آنجایی که شتاب این نوع حرکت ثابت بوده و در طول مسیر تغییری نکرده است، نمودار آن به شکل زیر در می‌آید:

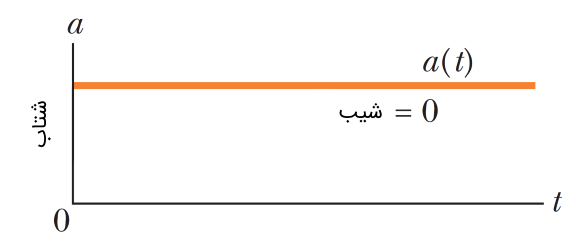
دقت داشته باشید که حرکت سرعت ثابت حالت خاصی از حرکت با شتاب ثابت است ($$a=0$$). واضح است که در حرکت با شتاب ثابت، شتاب متوسط و شتاب لحظه‌ای برابر هستند.

$$\overline{a}=\frac{\triangle v}{\triangle t}$$
(2)

$$a=\lim_{\triangle t \rightarrow 0}\frac{\triangle v}{\triangle t}=\frac{\text{d}v}{\text{d}t}$$
(3)

می‌دانیم که اگر جسمی به مقدار ($$\triangle x$$) در مدت زمان ($$\triangle t$$) جابه‌جا شود، سرعت متوسط آن به صورت زیر است:

$$\overline{v}=\frac{\triangle x}{\triangle t}$$
(4)

که از رابطه فوق نتیجه می‌شود ($$t_{1}=0$$):

$$x=\overline{v}t+x_{0}$$
(5)

در صورتی که شتاب یک جسم ثابت باشد، می‌توانیم سرعت متوسط آن را به صورت زیر تعریف کنیم:

$$\overline{v}=\frac{v+v_{0}}{2}$$
(6)

حال معادله (۱) را در نظر بگیرید. با اضافه کردن $$v_{0}$$ به طرفین این معادله و ضرب کردن آن در $$\frac{1}{2}$$، داریم:

$$\frac{v+v_{0}}{2}=v_{0}+\frac{1}{2}at$$
(7)

با قرار دادن رابطه فوق در معادله (5) می‌توانیم به معادله حرکت به فرم زیر برسیم:

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}$$
(8)

همان‌طور که مشاهده می‌کنید، معادله‌ای که مکان یک حرکت با شتاب ثابت را توصیف می‌کند، معادله‌ای درجه دوم است.

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

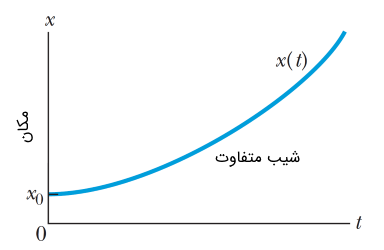
یک راه ساده برای به دست آوردن معادله‌های سینماتیکی از روی یکدیگر استفاده از تکنیک‌های ریاضی مشتق و انتگرال است. از آنجایی که شیب خط رابطه نزدیکی با مفهوم مشتق دارد، با مشتق گرفتن از معادله مکان (8) به راحتی به معادله سرعت می‌رسیم. همچنین با مشتق گرفتن از معادله سرعت به معادله شتاب رسیده که در اینجا عددی ثابت است. پس شتاب لحظه‌ای، مشتق سرعت نسبت به زمان و مشتق مرتبه دوم مکان نسبت به زمان است.

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}\Rightarrow \frac{dx}{dt}=v=at+v_{0}$$
(9)

$$v=at+v_{0}\Rightarrow \frac{d^{2}x}{dt^{2}}=\frac{dv}{dt}=a$$
(10)

از آنجایی که می‌توانیم عمل انتگرال را عکس مشتق در نظر بگیریم، با انتگرال از معادله شتاب، به معادله سرعت و از انتگرال گرفتن از معادله سرعت به معادله حرکت می‌رسیم. می‌دانیم که انتگرال با مساحت سطح زیر نمودار در ارتباط است. پس مساحت سطح زیر نمودار سرعت - زمان، مقدار جابه‌جایی ($$\triangle x$$) و سطح زیر نمودار شتاب - زمان، مقدار تغییرات سرعت ($$\triangle v$$) را نتیجه می‌دهد.

$$\int dv=\int adt \Rightarrow v=at+v_{0}$$
(11)

$$\int dx=\int vdt=\int (at+v_{0})dt \Rightarrow x=\frac{1}{2}at^{2}+v_{0}t+x_{0}$$
(12)

یکی از رابطه‌های که از معادلات فوق می‌توان نتیجه گرفت، رابطه مستقل از زمان برای حرکت با شتاب ثابت به صورت زیر است.

$$v^{2}-v_{0}^{2}=2a(x-x_{0})$$
(13)

رابطه فوق با تنها کردن $$t$$ از معادله (۱) و جایگذاری آن در معادله (5) و استفاده از معادله (6) به دست آمده است. حرکت با شتاب ثابت را می‌توان به دو حالت تندشونده و کندشونده تقسیم کرد. در واقع اگر سرعت متحرکی زیاد شود، حرکت را تندشونده ($$v_{x}a_{x}>0$$) و هنگامی که سرعت متحرکی کاهش پیدا کند (ترمز ماشین)، حرکت را کندشونده ($$v_{x}a_{x}<0$$) می‌نامیم. اندیس $$x$$ جهت نمایش حرکت یک بعدی آورده شده است.

به طور خلاصه، فرمول‌های اصلی زیر را برای حرکت با شتاب ثابت داریم:

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}$$

$$v=at+v_{0}$$

$$v^{2}-v_{0}^{2}=2a(x-x_{0})$$

$$x=\overline{v}t+x_{0}$$

$$\overline{v}=\frac{v+v_{0}}{2}$$

در برخی از مسائل ممکن است که سرعت جسمی بر حسب کیلومتر بر ساعت (واحد استاندارد سنجس خودروها) داده شود. از آنجایی که واحد استاندارد سرعت در سیستم SI، متر بر ثانیه است، به راحتی با ضرب سرعت داده شده بر حسب $$\frac{km}{hr}$$ در عدد $$\frac{5}{18}$$، آن را به $$\frac{m}{s}$$ تبدیل کنید.

$$1\frac{km}{hr}=\frac{1000m}{3600s}=\frac{5}{18}\frac{m}{s}$$

در مقاله «حرکت سقوط آزاد -- به زبان ساده» دیدیم که با صرف‌نظر از مقاومت ایجاد شده توسط مولکول‌های هوا برای اجسامی که در آن حرکت می‌کنند، حرکت سقوط آزاد را می‌توان یک حرکت با شتاب ثابت در نظر گرفت. در واقع تمامی روابطی که در بالا به آن‌ها پرداختیم، برای حرکت سقوط آزاد نیز استفاده می‌شوند. تنها تفاوت در آن‌ها، استفاده از نماد $$y$$ به جای $$x$$ (حرکت عمودی یک بعدی) و شتاب ثابت گرانشی $$g$$ به جای $$a$$ است.

مثال

در ادامه برای درک بهتر مبحث حرکت با شتاب ثابت و چگونگی استفاده از روابط، به بررسی چند مثال می‌پردازیم.

مثال ۱

هواپیمای کوچکی با سرعت اولیه $$70\frac{m}{s}$$ در حال پرواز است، سرعتش را با شتاب $$1.5\frac{m}{s^{2}}$$ کاهش می‌دهد. پس از گذشت ۴0 ثانیه، سرعت آن به چقدر می‌رسد؟

برای حل این سوال می‌توانیم از رابطه (۱) یعنی معادله سرعت حرکت با شتاب ثابت استفاده کنیم. توجه شود که در اینجا به دلیل اینکه جهت شتاب خلاف جهت سرعت (ترمز) است، آن را با علامت منفی در معادله جایگذاری می‌کنیم. یعنی حرکت هواپیما کندشونده است. با جایگذاری مقادیر معلوم از صورت مسئله، در معادله (۱) نتیجه می‌شود:

$$v=at+v_{0}=-1.5\times40+70=10\frac{m}{s}$$

از معادله فوق، نتیجه می‌گیریم که در پایان ثانیه ۴۰، سرعت هواپیما به $$10\frac{m}{s}$$ رسیده است.

مثال ۲

ماشین‌های مخصوص مسابقات درگ (Drag) می‌توانند به شتاب متوسط حدود $$26\frac{m}{s^{2}}$$ دست یابند. فرض کنید که یک ماشین از حالت سکون به مدت زمان $$5.56s$$ با این شتاب حرکت می‌کند. پس از گذشت این زمان ماشین چه مسافتی را طی کرده است؟ (مسیر درگ خط مستقیم است)

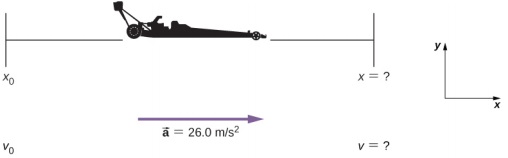
مسابقات درگ از حالت سکون ($$v_{0}=0$$) شروع شده و نقطه شروع حرکت را در $$x_{0}=0$$ فرض می‌کنیم. در نتیجه:

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}\rightarrow x=\frac{1}{2}at^{2}=\frac{1}{2}\times26\times5.56^{2}=402m$$

حال می‌خواهیم سرعت ماشین را در پایان در پایان زمان $$5.56s$$ به دست آوریم. از معادله (۱) نتیجه می‌شود:

$$v=at+v_{0}\rightarrow v=at=26\times5.56\cong145\frac{m}{s}$$

برای محاسبه سرعت فوق می‌توانیم از رابطه مستقل از زمان (13) نیز استفاده کنیم. پس سرعت ماشین در مکان ($$x=402m$$) به صورت زیر است:

$$v^{2}-v_{0}^{2}=2a(x-x_{0})\Rightarrow v^{2}=2ax\rightarrow v=\sqrt{2\times26\times402}\cong145\frac{m}{s}$$

مثال ۳

ماشینی در مسیر مستقیم با سرعت ثابت $$36\frac{m}{s}$$ در حال حرکت است. ناگهان ترمز گرفته و سرعت خود را با شتاب $$4\frac{m}{s^{2}}$$ کاهش می‌دهد. مدت زمانی که طول می‌کشد ماشین به طور کامل متوقف شود، چند ثانیه است؟ در این زمان، ماشین چه مسافتی را طی کرده است؟

برای پاسخ به قسمت اول این سوال، می‌توانیم از رابطه (۱) استفاده کنیم. واضح است هنگامی که ماشین متوقف می‌شود، سرعت آن صفر است. از آنجا که ماشین ترمز کرده است، پس علامت شتاب منفی بوده (جهت سرعت و شتاب خلاف جهت یکدیگر است) و در نتیجه حرکت کندشونده است.در نتیجه:

$$v=at+v_{0}\Rightarrow t=\frac{v_{0}}{a}=\frac{36}{4}=9s$$

برای به دست آوردن مسافتی که ماشین در طول ۹ ثانیه طی می‌کند (در واقع جابه‌جا می‌شود)، می‌توانیم از رابطه (8) استفاده کنیم.

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}\Rightarrow \triangle x=x-x_{0}=\frac{1}{2}\times-4\times9^{2}+36\times9=162m$$

از محاسبات فوق، پی میبریم که ماشین مذکور از زمانی که ترمز می‌کند، ۹ ثانیه طول می‌کشد که به طور کامل متوقف شود. همچنین از لحظه ترمز گرفتن تا توقف، مسیر 162 متر را نیز طی کرده است (162متر در 9 ثانیه).

مثال ۴

یک فضا‌پیما با شتاب ثابت $$20\frac{m}{s^{2}}$$ مدار زمین را به سمت ماه ترک می‌کند. فضاپیمای مذکور در مدت زمان ۲ دقیقه مسافت ۱۰۰۰ کیلومتر را طی می‌کند. این فضاپیما با چه سرعتی مدار زمین را ترک کرده است؟

برای پاسخ به این سوال می‌توانیم از معادله حرکت (۸) استفاده کنیم. مقدار جابه‌جایی جسم در مدت زمان 2 دقیقه برابر با 1000 کیلومتر است. پس داریم:

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}\Rightarrow \triangle x=x-x_{0}=\frac{1}{2}\times-20\times120^{2}+v_{0}\times120=1000\times10^{3}\rightarrow v_{0}=7133.3\frac{m}{s}$$

سرعت فضاپیما را در انتهای زمان ۲ دقیقه به دست آورید:

$$v=at+v_{0}=20\times120+7133.3=9533.3\frac{m}{s}$$

مثال ۵

خودرویی با سرعت $$10\frac{m}{s}$$ در حال حرکت است. چه مدت طول می‌کشد که مسافت ۲۰۰ متر را با شتاب $$2\frac{m}{s^{2}}$$ طی کند؟

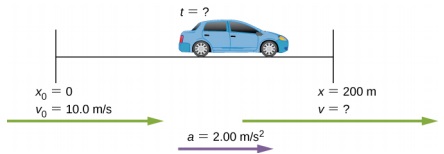
برای راحتی کار می‌توانیم  $$x_{0}=0$$ فرض کنیم. از معادله حرکت (۸) داریم:

$$x=\frac{1}{2}at^{2}+v_{0}t+x_{0}\Rightarrow 200=\frac{1}{2}\times2\times t^{2}+10\times t \rightarrow t=-20s \ , \ 10s$$

واضح است که زمان منفی غیر قابل قبول است. سرعت خودرو در پایان ثانیه 10 از معادله سرعت (۱) برابر است با:

$$v=at+v_{0}=2\times10+10=30\frac{m}{s}$$

نتیجه می‌گیریم که خودرو مذکور در مدت زمان 10 ثانیه به مقدار 200متر جا‌به‌جا شده و در نقطه $$x=200m$$ سرعتش به $$v=30\frac{m}{s}$$ رسیده است. از آنجایی که سرعت و شتاب در یک جهت هستند، حرکت شتاب ثابت این خودرو از نوع تندشونده است.

مثال ۶

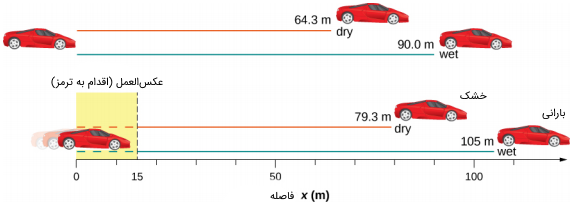
در زمینی خشک نرخ استاندارد ترمز گرفتن و کاهش سرعت $$7\frac{m}{s^{2}}$$ و در همان زمین به هنگام بارش باران نرخ کاهش سرعت $$5\frac{m}{s^{2}}$$ است. فرض کنید ماشینی با سرعت ثابت $$30\frac{m}{s}$$ در این زمین در حال حرکت است و ناگهان در مقابل خود مانعی را می‌بیند. در هر دو حالت زمین خشک و مرطوب، فاصله‌ای که خودرو تا توقف کامل طی می‌کند را به دست آورید.

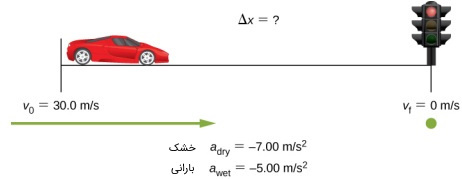
برای پاسخ به این سوال از معادله مستقل از زمان (۱۳) استفاده می‌کنیم. برای راحتی کار $$x_{0}$$ را فرض می‌کنیم. در نتیجه:

$$v^{2}-v_{0}^{2}=2a(x-x_{0})\Rightarrow x_{dry}=\frac{0-30^{2}}{2\times-7}=64.3m$$

$$v^{2}-v_{0}^{2}=2a(x-x_{0})\Rightarrow x_{wet}=\frac{0-30^{2}}{2\times-5}=90m$$

اگر زمان عکس‌العمل نشان دادن راننده (ترمز گرفتن) $$0.5s$$ باشد، مانع حداقل در چه فاصله‌ای از ماشین باید قرار گرفته باشد تا ماشین مذکور با آن برخورد نکند؟

مقدار مسافتی که ماشین در حدفاصل دیدن مانع و ترمز گرفتن، طی کرده است:

$$x=vt=30\times0.5=15m$$

پس برای اینکه ماشین با مانع برخورد نکند حداقل باید از فاصله‌های زیر (زمین خشک و بارانی) اقدام به ترمز کند:

$$x_{braking}+x_{reaction}=x_{T_{dry}}=64.3+15=79.3m$$

$$x_{braking}+x_{reaction}=x_{T_{wet}}=90+15=105m$$

مثال ۷

معادله حرکت جسمی در سیستم استاندارد SI به صورت $$x=t^{3}-6t^{2}+4t+1$$ است. معادله سرعت و شتاب این جسم به چه صورتی است؟ آیا این حرکت از نوع شتاب ثابت است؟

از دو رابطه (9) و (10)، مشتق معادله مکان نسبت به زمان، معادله سرعت و مشتق معادله سرعت نسبت به زمان، معادله شتاب را نتیجه می‌دهد. در نتیجه داریم:

$$\frac{\text{d}x}{\text{d}t}=v=3t^{2}-12t+4$$

$$\frac{d^{2}x}{dt^{2}}=\frac{\text{d}v}{\text{d}t}=a=6t-12$$

از آنجایی که در معادله فوق، شتاب جسم مذکور ثابت نبوده و با گذشت زمان تغییر می‌کند، حرکتش از نوع شتاب ثابت نیست. برای آشنایی با مسائل مختلف سقوط آزاد، که خود نوعی حرکت با شتاب ثابت به حساب می‌آید، به مقاله «حرکت سقوط آزاد -- به زبان ساده» رجوع کنید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۱
• مجموعه آموزش‌های مهندسی مکانیک
• حرکت پرتابی — به زبان ساده
• معادله دیفرانسیل حرکت — از صفر تا صد
• اصطکاک — به زبان ساده

^^