جرم چیست؟ – تعریف، نحوه و واحد اندازه گیری در فیزیک
تمام اجسامی که در اطراف خود میشناسیم از ماده تشکیل شدهاند. به مقدار ماده تشکیلدهنده هر جسم دلخواه، جرم آن جسم گفته میشود. هر جسمی مانند میز، صندلی، کتاب، و حتی موی سر، جرم دارد. در این مطلب، به پرسش جرم چیست به زبان ساده پاسخ میدهیم و در ادامه، در مورد مفهوم جرم در فیزیک و شیمی، تفاوت وزن و جرم، مرکز جرم در فیزیک و قانون پایستگی جرم صحبت خواهیم کرد.
- میآموزید جرم چیست و با چه واحدهایی اندازهگیری میشود.
- با اندازهگیری جرم با استفاده از ترازو آشنا میشوید.
- میتوانید تفاوت های جرم و وزن را تشخیص دهید.
- با مثلث wmg آشنا شده و میتوانید با استفاده از آن، جرم و وزن اجسام را محاسبه کنید.
- قانون پایستگی جرم در واکنشهای شیمیایی را میشناسید.
- با تفاوت جرم گرانشی، لختی، بحرانی و مولی آشنا میشوید.


جرم چیست ؟
در فیزیک، جرم یکی از پایهترین ویژگیهای ماده و یکی از بنیادیترین کمیتها است. به مقدار ماده موجود در هر جسم، جرم میگوییم. جرم نیز مانند هر کمیت فیزیکی با واحد مشخصی اندازه گرفته میشود. به طور حتم، گاهی میوه خریدهاید. سوال متداولی که میوهفروش از شما میپرسد؛ چند کیلو میوه میخواهید؟ برای پاسخ به این پرسش ساده، عددی را به او میگویید. به طور مثال، ۲ کیلو سیب میخواهم. کلمه کیلو خلاصه شده کلمه کیلوگرم است. بنابراین، یکی از واحدهای اندازهگیری جرم، کیلوگرم است.
در ادامه، در مورد واحد اندازهگیری جرم صحبت خواهیم کرد.

واحد اندازه گیری جرم در فیزیک چیست ؟
شاید از خود پرسیده باشید که واحد اندازهگیری جرم چیست و چگونه اندازهگیری میشود. گرم (g) و کیلوگرم (kg)، رایجترین واحدهای اندازهگیری جرم در سیستم متری هستند. جرم گیره کاغذ کوچک در حدود یک گرم و جرم چوب بیسبال در حدود یک کیلوگرم است. بنابراین، برای بیان جرم اجسام کوچک و سبک از واحد گرم و اجسام بزرگ و سنگین از واحد کیلوگرم استفاده میکنیم.
جرم و وزن با یکدیگر رابطه دارند، اما مفهوم آنها با یکدیگر متفاوت است. جرم برخی اجسام در جدول زیر آورده شدهاند.
| جسم | جرم جسم |
| گیره کاغذ | یک گرم |
| مداد | پنج گرم |
| موش کوچک | ۲۰ گرم |
| بچه گربه | بین ۲۰۰ تا ۳۰۰ گرم |
| کتاب متوسط | در حدود یک کیلوگرم |
| گربه | بین ۳ تا ۵ کیلوگرم |
| گاو | در حدود ۷۵۰ کیلوگرم |
جرم اجسام گفته شده در جدول را با یکدیگر مقایسه کنید. جرم مداد از گیره کاغذ بیشتر، بنابراین مداد از گیره کاغذ سنگینتر است. اما جرم مداد از بچه گربه، کمتر است از اینرو، مداد از بچه گربه سبکتر خواهد بود.
تخمین جرم
گفتیم برای تعیین جرم جسمی دلخواه از ترازو استفاده میکنیم، اما همیشه به این وسیله دسترسی نداریم. در نتیجه، گاهی لازم است که جرم اجسام را با توجه به ظاهر آنها تخمین بزنیم. به چند مثال در این مورد توجه کنید.
مثال اول تخمین جرم
کدامیک از گزینههای زیر به جرم گوسفند نزدیکتر است؟
- ۵۰ کیلوگرم
- ۵۰ گرم

پاسخ:
گفتیم جرم گیره کاغذ در حدود یک گرم و جرم چوب بیسبال در حدود یک کیلوگرم است. آیا جرم گوسفند به ۵۰ گیره کاغذ نزدیکتر است یا به ۵۰ چوب بیسبال؟ پاسخ منطقی به این پرسش، ۵۰ چوب بیسبال است.
مثال دوم تخمین جرم
منطقیترین و معقولترین واحد برای اندازهگیری جرم میز آشپزخانه کدام گزینه است؟
- گرم
- کیلوگرم
پاسخ:
جابجایی میز آشپزخانه به راحتی امکانپذیر نیست. بنابراین، بیان واحد جرم آن برحسب کیلوگرم منطقیتر خواهد بود.
مثال سوم تخمین جرم
کدام یک از گزینههای زیر به جرم گاو نزدیکتر است؟
- ۷ کیلوگرم
- ۷۰۰ کیلوگرم
پاسخ:
برای پاسخ به این مثال، کمی در مورد جرم ۷ کیلوگرم فکر کنید. به نظر شما جرم چه اجسام یا حیواناتی به این مقدار نزدیک است. جرم گربهای بزرگ یا نوزادی چندماهه در حدود ۷ کیلوگرم است. اندازه بیشتر گاوها، بزرگتر از گربهای بزرگ یا نوزاد است. از اینرو، ۷۰۰ کیلوگرم، پاسخ منطقیتری به نظر میرسد.
گفتیم جرم اجسام را با استفاده از ترازو بهدست میآوریم. در ادامه، در مورد چگونگی اندازهگیری جرم با استفاده از ترازو توضیح میدهیم.
اندازه گیری جرم جسم با استفاده از ترازو
گفتیم جرم اجسام مختلف را با استفاده از ترازو اندازه میگیریم. ترازوها انواع مختلفی دارند. سادهترین نوع آن که در منازل استفاده میشود، ترازوی آشپزخانه است. به تصویر زیر دقت کنید. اعداد نوشته شده در قسمت بالا بر حسب کیلوگرم و گرم بیان شدهاند. حداکثر جرمی که میتواند توسط این ترازو اندازه گرفته شود برابر ۲ کیلوگرم است.
یکی از سوالاتی که همیشه پرسیده میشود آن است که یک کیلوگرم، چند گرم است. این نکته را به یاد داشته باشید که کیلو معادل عدد ۱۰۰۰ است، بنابراین یک کیلوگرم برابر ۱۰۰۰ گرم است. در ترازوی نشان داده شده در تصویر، هر یک کیلوگرم به ۵ قسمت مساوی تقسیم شده و هر قسمت برابر ۲۰۰ گرم است.

بین هر قسمت ۲۰۰ تایی (به عنوان مثال، بین ۲۰۰ تا ۴۰۰ یا ۰ تا ۲۰۰) به هشت قسمت مساوی تقسیم شده است. خطهای پررنگ وسط (دایره قرمز)، برابر ۱۰۰، ۳۰۰، ۵۰۰، ۷۰۰ و ۹۰۰ گرم هستند. همچنین، هر قسمت کوچک، برابر ۲۵ گرم است.

برای اندازهگیری جرم جسمی دلخواه، ابتدا خط قرمزرنگ ترازو را روی عدد صفر قرار میدهیم.

سپس، جسم موردنظر را روی ترازو قرار میدهیم و عدد نشان داده شده توسط خط قرمزرنگ را یادداشت میکنیم. همانطور که در تصویر زیر نشان داده شده است، جرم جسم مورد نظر در حدود ۴۳۰ گرم است.

به هنگام اندازهگیری جرم جسم با استفاده از ترازو، به چند نکته باید توجه داشته باشم:
- به آخرین عدد ترازو باید توجه کنیم (در اینجا دو کیلوگرم). اگر جرم جسمی بیشتر از آخرین عدد نوشته شده باشد، باید از ترازوی دیگری برای بهدست آوردن جرم آن استفاده کنیم.
- اگر ترازو عقربهای باشد، آخرین عدد نوشته شده روی آن مشخص خواهد بود. در صورت استفاده از ترازوی دیجیتال، نهایت جرمی که اندازه میگیرد در کنار آن نوشته شده است.
- توجه به دقت ترازو برای بیان جرم اندازهگیری شده بسیار مهم خواهد بود. به عنوان مثال، در ترازوی نشان داده شده در تصویر، دقت برابر ۲۵ گرم است. برای بهدست آوردن جرمهای دقیقتر، باید از ترازویی با دقت بالاتر استفاده کنیم.
پیشنهاد میکنیم برای یادگیری بیشتر مفاهیم مربوط به جرم، فیلم آموزش جرم چیست فرادرس که لینک ان در ادامه آورده شده است را مشاهده کنید.
تبدیل واحدهای جرم در سیستم متری به یکدیگر
گفتیم گرم و کیلوگرم، واحدهای اصلی جرم در سیستم متری هستند. آیا میدانید یک گرم چند کیلوگرم یا یک گرم چند میلیگرم است؟ برای پاسخ به این سوال جرم داده شده بر حسب گرم را بر عدد ۱۰۰۰ تقسیم میکنیم. عدد بهدست آمده، جرم آن جسم را برحسب کیلوگرم میدهد.
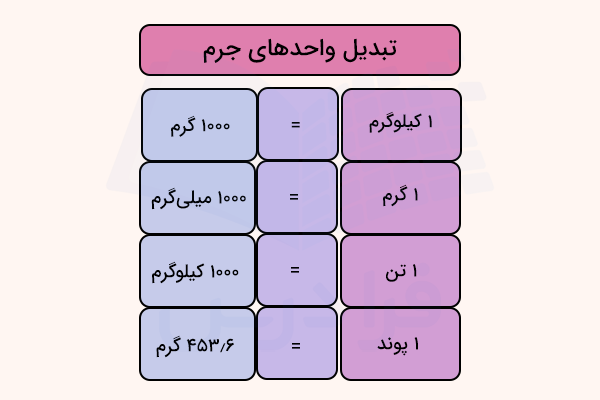
علاوه بر گرم و کیلوگرم، دیگر واحدهای متری برای اندازهگیری جرم، در جدول زیر نشان داده شدهاند.
| واحد اندازگیری جرم | مقدار عددی آن |
| میلیگرم (mg) | یا |
| سنتیگرم (cg) | یا |
| دسیگرم (dg) | یا |
| گرم (g) | ۱۰۰۰ میلیگرم |
| دکاگرم (dag) | ۱۰ گرم |
| هکتوگرم (hg) | ۱۰۰ گرم |
| کیلوگرم | ۱۰۰۰ گرم |
| تن (t) | ۱۰۰۰ کیلوگرم |
| اونس | ۲۸/۳۵ گرم |
| پوند | ۴۵۳/۶ گرم |
دانستن چگونگی تبدیل این واحدهای جرم به یکدیگر برای حل برخی مسائل فیزیک، لازم و ضروری است. از این رو، چند مثال در این مورد حل خواهیم کرد.
مثال ۱
جرم جسمی را با استفاده از ترازو اندازه گرفتهایم و مقدار آن برابر ۵ کیلوگرم و ۴۵ گرم است. جرم جسم را برحسب گرم بهدست آورید.
پاسخ:
در این مثال، میخواهیم ۵ کیلوگرم و ۴۵ گرم را به گرم تبدیل کنیم. در ابتدا، ۵ کیلوگرم را به گرم تبدیل میکنیم:
۱۰۰۰ گرم = یک کیلوگرم
۵۰۰۰ گرم = ۱۰۰۰ × 5 = ۵ کیلوگرم
در ادامه، ۴۵ گرم را به ۵۰۰۰ گرم اضافه میکنیم:
۵۰۴۵ گرم = ۵۰۰۰ گرم + ۴۵ گرم
بنابراین، ۵ کیلوگرم و ۴۵ گرم برابر ۵۰۴۵ گرم است.
مثال ۲
۷ کیلوگرم چند گرم است؟
پاسخ:
میدانیم هر یک کیلوگرم برابر ۱۰۰۰ گرم است. بنابراین، ۷ کیلوگرم برابر ۷۰۰۰ گرم خواهد بود.
مثال ۳
کیلوگرم، چند گرم است؟
پاسخ:
همانند دو مثال قبل، عدد داده شده برحسب کیلوگرم را در ۱۰۰۰ ضرب میکنیم:
مثال ۴
۳ کیلوگرم چند میلیگرم است؟
پاسخ:
همانطور که در جدول بالا دیده میشود، یک کیلوگرم معادل ۱۰۰۰ گرم و یکی میلیگرم برابر گرم است. برای حل این مثال، ابتدا ۳ کیلوگرم را به گرم تبدیل میکنیم.
در ادامه، ۳۰۰۰ گرم را برحسب میلیگرم مینویسیم. گفتیم یک میلیگرم برابر گرم یا یک گرم برابر ۱۰۰۰ میلیگرم است. در نتیجه، ۳۰۰۰ گرم برابر ۳۰۰۰۰۰۰ یا میلیگرم خواهد بود.
نکته: جرم یک میلیلیتر آب برابر یک گرم است.
برای آشنایی بیشتر با مفهوم جرم، آزمایش سادهای را با یکدیگر انجام میدهیم و جرم اجسام مختلف را در منزل اندازه میگیریم.
آزمایش اندازه گیری جرم
به طور حتم میدانید که جرم اجسام مختلف را با وسیلهای به نام ترازو اندازه میگیرند. در این آزمایش، با انجام آزمایشی ساده در خانه، جرم برخی اجسامی که میشناسیم را اندازه خواهیم گرفت.
وسایل مورد نیاز
وسایل موردنیاز برای انجام این آزمایش عبارت هستند از:
- خطکش یا تختهای نازک به طول ۵۰ سانتیمتر که به عنوان اهرم از آن استفاده میشود.
- دو عدد لیوان پلاستیکی یا کاغذی
- خودکار به عنوان تکیهگاه
- ماژیک برای علامتگذاری
- جسمی دلخواه با جرم نامشخص
- استوانه مدرج برای اندازهگیری حجم آب
- متر نواری

برای انجام آزمایش، مرحلههای زیر را به ترتیب انجام میدهیم.
مرحله ۱
لیوانهای پلاستیکی را در دو انتهای اهرم (خطکش یا تخته) قرار میدهیم و با استفاده از ماژیک محل قرار گرفتن آنها را علامت میزنیم. با انجام این کار، محل دقیق لیوانها برای ادامه کار، مشخص خواهند بود. یکی از لیوانها برای نگهداری جسم با جرم نامشخص استفاده میشود. در لیوان دیگر، مقداری آب با حجم مشخص میریزیم و از آن برای تعیین جرم جسم موردنظر استفاده میکنیم.

مرحله ۲
در صورت استفاده از خطکش به عنوان اهرم، وسط آن را با استفاده از ماژیک علامت بزنید. اگر از تخته استفاده میکنید، با استفاده از متر نواری، وسط آن را مشخص کنید.
مرحله ۳
خودکاری را که به عنوان تکیهگاه استفاده میشود، زیر تخته یا خطکش چوبی و درست در وسط آن قرار دهید. گاهی ممکن است با قرار دادن مرکز تخته روی خودکار، تخته در حالت تعادل قرار نگیرد و سمت چپ یا سمت راست آن کمی سنگینتر باشد. دلیل این موضوع آن است توزیع جرم در تخته یا خطکش چوبی یکنواخت نیست. اگر با این مورد مواجه شدید، کافی است خودکار را کمی جابجا کنید.

مرحله ۴
لیوانها را روی تخته یا خطکش چوبی قرار میدهیم. از آنجا که جرم آنها با یکدیگر برابر است، تخته یا خطکش در حالت تعادل قرار میگیرد.

مرحله ۵
جسم با جرم نامشخص را در یکی از لیوانها قرار میدهیم. تعادل به هم میخورد و لیوان حاوی جسم سنگینتر در ارتفاع پایینتری نسبت به لیوان خالی قرار میگیرد. برای برقراری تعادل، در لیوان خالی آب میریزیم. این کار را به آهستگی و با دقت زیاد و تا جایی انجام میدهیم که سمت سنگینتر به سمت بالا حرکت کند و تعادل برقرار شود.

مرحله ۶
مقدار حجم اولیه آب () در استوانه مدرج را میدانیم. پس از ریختن آب در لیوان، حجم آب باقیمانده () در استوانه را اندازه میگیریم. بنابراین، حجم آب ریخته شده در لیوان برابر است.
فرض کنید حجم آب ریخته شده در لیوان ۸۰ میلیلیتر باشد. میدانیم جرم یک میلیلیتر آب برابر یک گرم است، بنابراین جرم ۸۰ میلیلیتر آب برابر ۸۰ گرم خواهد بود. در نتیجه، جرم جسم نامشخص برابر ۸۰ گرم بهدست میآید. برای محاسبه میزان خطای محاسبه جرم، جرم جسم را با استفاده از ترازوی آشپزخانه اندازه بگیرید.
با استفاده از این روش میتوانیم جرم هر جسم کوچکی را اندازه بگیریم.
تفاوت وزن و جرم چیست ؟
اکنون میدانیم جرم چیست و با چه واحدهایی در سیستم متری اندازهگیری میشود، اما تفاوت آن با وزن، به عنوان یکی از مبحثهای مهم علم فیزیک مطرح میشود. استفاده از لغت وزن در زندگی روزمره بسیار رایجتر از جرم است. در بسیاری از مواقع، افراد این دو مفهوم فیزیکی را به اشتباه به جای یکدیگر استفاده میکنند. در این بخش، به زبان ساده توضیح میدهیم که تفاوت وزن و جرم چیست و ارتباط آنها با یکدیگر چگونه است.
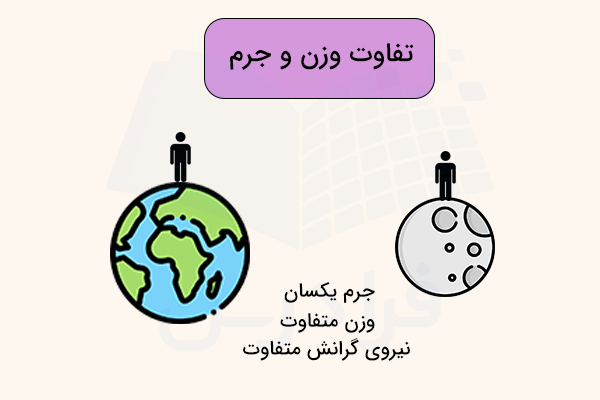
جرم را به صورت مقدار ماده موجود در جسم تعریف کردیم. اما وزن نیرویی است که به دلیل جاذبه گرانشی بر جسم وارد میشود و واحد اندازهگیری آن نیوتن است. فرض کنید جرم جعبهای را با استفاده از ترازو اندازه میگیریم و عدد ۵ کیلوگرم را بهدست میآوریم. سوالی که ممکن است مطرح شود آن است که جرم جسم و وزن آن چه مقدار است. جرم بر حسب کیلوگرم بیان میشود، بنابراین جرم جسم برابر ۵ کیلوگرم خواهد بود. اما وزن آن از حاصلضرب جرم جسم در شتاب جاذبه گرانشی، بهدست میآید. وزن جسمی به جرم ۵ کیلوگرم روی زمین به صورت زیر محاسبه میشود:
بنابراین، جرم و وزن، دو مفهوم کاملا متفاوت، اما با یکدیگر متناسب هستند. هرچه وزن جسمی بیشتر باشد، جرم آن نیز بیشتر خواهد بود.
پرسش:
اگر جرم جسمی روی زمین برابر ۵ کیلوگرم باشد، جرم آن روی ماه چه مقدار خواهد بود؟
پاسخ:
جرم جسم موردنظر روی ماه نیز برابر ۵ کیلوگرم خواهد بود. آیا وزن جسم نیز یکسان است؟ خیر، وزن جسم روی زمین با مقدار وزن آن روی ماه، متفاوت خواهد بود.
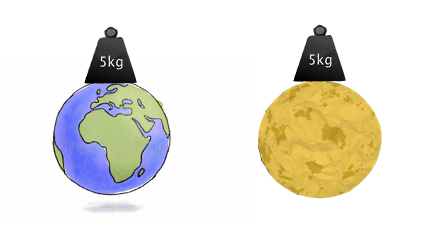
وزن جسم روی زمین برابر ۴۹ نیوتن و وزن آن روی ماه برابر است با:
بنابراین، وزن جسم روی ماه بسیار کمتر از وزن آن روی زمین است.
در نتیجه، وزن و جرم دو مفهوم متفاوت هستند ولی از طریق شتاب جاذبه گرانشی به یکدیگر مربوط میشوند. وزن ما روی خورشید در حدود ۲۰ تا ۳۰ برابر وزن ما روی زمین است. پیشنهاد می کنیم برای یادگیری تبدیل این واحدها، مطلب تبدیل واحد وزن و جرم مجله فرادرس را مطالعه کنید.
مثلث Wmg در تعیین جرم چیست و چگونه استفاده میشود ؟
رابطه بین وزن، جرم و شتاب جاذبه گرانشی در مثلثی به نام مثلث Wmg نشان داده میشود.
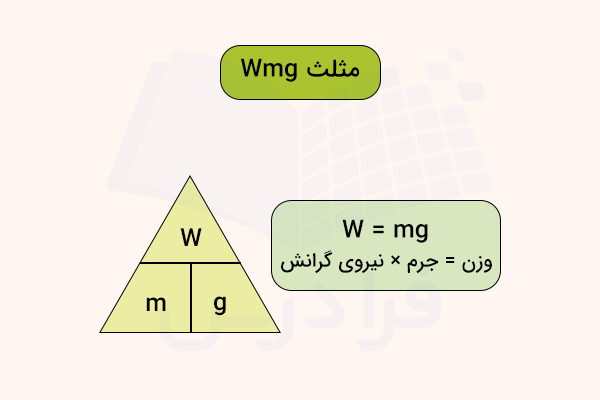
برای محاسبه هر یک از کمیتهای فوق میتوان از مثلث بالا یا جدول زیر استفاده کرد. برای استفاده از مثلث، به نکتههای زیر توجه کنید:
- خط افقی در مثلث، نشاندهنده تقسیم و خط عمودی بیانگر ضرب است.
- برای محاسبه جرم، به صورت زیر عمل میکنیم:
- جرم را با انگشت میپوشانیم.
- W را بر g تقسیم میکنیم.
- برای محاسبه شتاب جاذبه گرانشی نیز به صورت مشابه عمل خواهیم کرد.
مثال اول مثلث Wmg
جسمی به جرم ۱۲ کیلوگرم در سیاره X قرار دارد. نیروی وزن جسم در این سیاره برابر ۵۸۸ نیوتن است.
- مقدار شتاب جاذبه گرانشی در این سیاره چه مقدار است؟
- مقدار شتاب جاذبه این سیاره چند برابر آن در زمین است؟
پاسخ:
وزن جسم با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق:
- برابر وزن جسم است.
- برابر جرم جسم است.
- برابر شتاب جاذبه گرانشی است.
در قسمت اول این مثال، مقدار شتاب جاذبه گرانشی خواسته شده است. با قرار دادن جرم و وزن جسم در رابطه مربوط به وزن، شتاب جاذبه گرانشی سیاره X را بهدست میآوریم.
قسمت ۲: در این قسمت، نسبت بین شتاب جاذبه گرانشی سیاره X و زمین را بهدست میآوریم.
بنابراین، مقدار شتاب جاذبه گرانشی سیاره X، در حدود ۵ برابر مقدار آن روی زمین است.
مثال دوم مثلث Wmg
جعبهای به جرم ۲۴ کیلوگرم روی میزی در حالت سکون قرار دارد. مقدار نیروی جاذبه وارد شده بر جسم چه مقدار است؟
پاسخ:
برای پاسخ به این مثال باید بدانید که نیروی جاذبه گرانشی همان نیروی وزن است.
تفاوت وزن و جرم در جدول زیر به صورت خلاصه بیان شده است.
| جرم | وزن | |
| تعریف | به مقدار ماده هر جسم، جرم آن گفته میشود. | به مقدار نیروی وارد شده بر جسمی به جرم m به دلیل جاذبه گرانشی، وزن گفته میشود. |
| علامت | جرم (Mass) با حرف انگلیسی m نشان داده میشود. | وزن (Weight) با حرف انگلیسی W نشان داده میشود. |
| فرمول | جرم جسم، همواره کمیتی ثابت و یکی از راههای محاسبه وزن استفاده از فرمول جرم = حجم × چگالی، است. | وزن، برابر اندازه نیروی گرانش وارد بر جرم و فرمول محاسبه آن برابر است. |
| واحد اندازهگیری | واحد SI جرم، برابر کیلوگرم است. | واحد SI وزن، برابر نیوتن است. |
| نوع کمیت | جرم کمیتی نردهای است. | وزن، نیرو و کمیتی برداری است، بنابراین اندازه و جهت دارد. جهت آن به سمت مرکز گرانش است. |
| وسیله اندازهگیری | جرم با استفاده از ترازویی ساده اندازه گرفته میشود. | وزن با استفاده از ترازوی فنری یا رابطه داده شده در بالا بهدست میآید. |
پرسش: پر و توپی از ارتفاع مشخصی رها میشوند. کدامیک زودتر به زمین میرسند؟
با انجام آزمایشی ساده به این پرسش پاسخ میدهیم.
آزمایش توپ و پر
وسایل موردنیاز برای انجام این آزمایش عبارت هستند از:
- توپ کوچک
- پارچه یا پر
- دو ورقه کاغذ
انجام آزمایش
برای انجام این آزمایش ساده به ترتیب زیر عمل کنید:
- پارچه یا پر را در یک دست و توپ را در دست دیگر بگیرید.
- در حالی که ایستادهاید، دستان خود را به سمت جلو دراز و همزمان دو جسم را رها کنید. کدامیک از آنها زودتر به زمین میرسند؟

- اکنون، توپ و ورقهای کاغذ را از ارتفاع مشخصی، همزمان رها کنید. چه اتفاقی میافتد؟ کدامیک زودتر به زمین میرسند؟
- یکی از کاغذها را مچاله کنید. سپس، کاغد مچاله شده را به همراه کاغذ مچاله نشده، همزمان از ارتفاع مشخصی رها کنید، چه اتفاقی میافتد؟
- در پایان، کاغذ مچاله شده و توپ را همزمان رها کنید. چه اتفاقی رخ میدهد؟
قبل از خواندن پاسخ پرسشهای مطرح شده، کمی به جواب آنها فکر کنید.
توضیح آزمایش و پاسخ به پرسشهای مطرح شده
گرچه توپ و پر از ارتفاع مشخصی رها شدهاند، توپ بسیار سریعتر از پر یا پارچه به زمین میرسد. همچنین، توپ سریعتر از ورقه کاغذ به زمین خواهد رسید. کاغذ مچاله شده، چندین ثانیه زودتر از کاغذ مچاله نشده به زمین میرسد. جرم دو ورقه کاغذ یکسان است، چرا کاغذ مچاله شده زودتر به زمین میرسد؟
میتوانید کاغذ مچاله نشده و مچاله شده را بار دیگر پرتاب کنید و زمان رسیدن آنها به زمین را بار دیگر با یکدیگر مقایسه کنید. کاغذ مچاله شده باز هم زودتر از کاغذ صاف به زمین خواهد رسید. سقوط توپ و کاغذ مچاله شده، به طور قطع شما را شگفتزده خواهد کرد، زیرا توپ و کاغذ مچاله شده به طور همزمان به زمین خواهند رسید.
اینگونه به نظر میرسد که اجسام سنگینتر (اجسام با جرم بیشتر) زودتر به زمین میرسند، اما این موضوع همیشه صحیح نیست. در واقع، جرم و وزن، زمان رسیدن اجسام به زمین را مشخص نمیکنند.
شتاب چیست؟
برای درک بهتر این موضوع، باید بدانیم که چه چیزی سبب سقوط اجسام میشود. نیروی گرانش یا نیروی جاذبه عامل سقوط اجسام است. اگر توپی را به سمت بالا پرتاب کنید، پس از بالا رفتن تا ارتفاع مشخصی، به سمت زمین بازمیگردد، زیرا نیروی جاذبه به سمت مرکز زمین بر آن وارد میشود. تمام اجسام با سرعت یکسانی سقوط میکنند، زیرا مقدار نیروی جاذبه وارد شده بر آنها یکسان است. اجازه دهید برای توضیح این موضوع، کمی بیشتر وارد جزییات فیزیک حاکم بر سقوط اجسام شویم. همه اجسام در اطراف ما با سرعت مشخصی در حرکت هستند، حتی جسمی که به نظر ساکن میآید. سرعت نهتنها میگوید جسم چه قدر سریع حرکت میکند، بلکه اطلاعاتی در مورد جهت حرکت آن جسم نیز به ما میدهد. به مقدار تغییرات سرعت در راستا و زمانی مشخص، شتاب میگوییم. اگر جسمی با سرعت ثابتی حرکت کند، شتاب آن برابر صفر خواهد بود.
اما سوالی که ممکن است مطرح شود آن است که چگونه میتوان به جسمی شتاب داد؟ برای آنکه جسمی با شتاب حرکت کند باید نیرویی با اندازه مشخص بر آن وارد شود. اگر به توپی ضربهای با اندازه مشخص وارد کنید (نیرو)، سرعت توپ تغییر خواهد کرد، بنابراین با شتاب معینی شروع به حرکت میکند. بر طبق قانون دوم نیوتن، نیرو برابر حاصلضرب جرم در شتاب حرکت آن است. از آنجا که جرم جسم همواره ثابت است، شتاب و نیرو به طور مستقیم به یکدیگر مربوط میشوند.
گفتیم دلیل سقوط هر جسمی، نیروی گرانش یا نیروی جاذبه به سمت مرکز زمین است. هرچه جسم به سطح زمین نزدیکتر میشود، اندازه سرعت آن بیشتر خواهد شد. مقدار شتاب جاذبه وارد شده از طرف زمین بر هر جسمی یکسان است. از اینرو، انتظار میرود اگر دو جسم با جرمهای متفاوت از ارتفاع یکسانی از سطح زمین رها شوند، زمان یکسانی به سطح زمین برخورد کنند. نخستین بار که این موضوع مطرح شد، هیچکس آن را باور نکرد. زیرا تیله شیشهای و پر را ارتفاع یکسانی رها میکردند و زمان رسیدن آنها به زمین را اندازه میگرفتند و نتیجه یکسانی را بهدست نمیآوردند.
حرکت سقوط آزاد
دلیل این امر، متفاوت بودن شتاب جاذبه پر یا تیله نیست. در واقع، هوا نیرویی به نام نیروی مقاومت هوا، در خلاف جهت حرکت اجسام بر آنها وارد میکند. هرچه جرم جسمی کمتر باشد، اندازه نیروی مقاومت هوای وارد شده بر آن بیشتر خواهد بود. اگر دو جسم با جرمهای متفاوت از ارتفاع مشخصی از سطح ماه رها شوند، با سرعت و زمان یکسانی سقوط خواهند کرد. بررسی سرعت و شتاب این اجسام در قالب حرکت سقوط آزاد در فیزیک بررسی میشود. شکل جسم بر مقدار نیروی مقاومتی که از طرف هوا بر آن وارد میشود، تاثیر خواهد گذاشت. به عنوان مثال، اگر کاغذی را به صورت افقی یا عمودی رها کنیم، مقدار نیروی مقاومت هوا در هر حالت متفاوت خواهد بود.
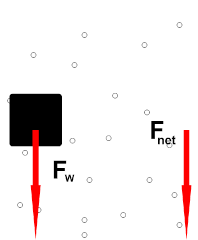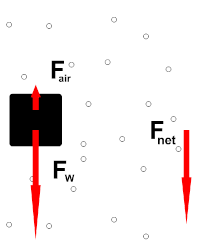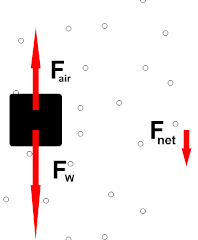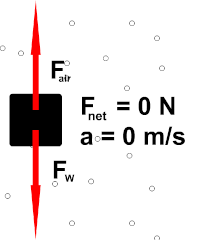
اجسام گفته شده در آزمایش (توپ، کاغذ معمولی، کاغذ مچاله شده و پارچه یا پر)، با سرعت یکسانی شروع به سقوط میکنند، اما پس از مدت بسیار کوتاهی، نیروی مقاومت هوا در خلاف جهت حرکت، بر آنها وارد میشود. بنابراین، دو نیروی وزن در جهت پایین و نیروی مقاومت هوا در جهت بالا، بر هر یک از این اجسام وارد خواهند شد.
از آنجا که توپ مسطح و کروی است، مقدار نیروی مقاومت هوای وارد شده بر آن بسیار کوچک است. اما مقدار این نیرو برای پارچه، پر و کاغذ مچاله نشده، بزرگ است، بنابراین سرعت سقوط آنها کاهش مییابد.
وزن در سیارات دیگر
در پاسخ به پرسش جرم چیست، توضیح دادیم که مقدار جرم در همه جا ثابت است، اما مقدار وزن تغییر میکند. فردی به جرم ۴۷ کیلوگرم را در نظر بگیرید. جرم این فرد در همه جای کیهان یکسان است، اما وزن او متفاوت خواهد بود. جدول زیر وزن این فرد را در سیارههای مختلف نشان میدهد.
| سیاره | مقدار شتاب جاذبه سیاره () | مقدار وزن فرد در سطح سیاره (نیوتن) |
| عطارد | ۳/۷ | ۱۹۳/۹ |
| زهره | ۸/۸۵ | ۴۱۶ |
| زمین | ۹/۸ | ۴۶۰/۶ |
| مریخ | ۳/۸۲ | ۱۷۹/۴ |
| مشتری | ۲۵/۹ | ۱۲۱۶ |
| زحل | ۱۱/۱۷ | ۵۲۵/۱ |
| اورانوس | 8/99 | 422/4 |
| نپتون | ۱۱/۲۷ | ۵۲۹/۷ |
اکنون میدانیم تفاوت وزن و جرم چیست و چگونه به یکدیگر مربوط میشوند. در ادامه، در مورد قانون پایستگی جرم صحبت خواهیم کرد.
قانون پایستگی جرم چیست ؟
پایستگی جرم یکی از بنیادیترین مفاهیم در شیمی است. پایستگی جرم بدان معنا است که مقدار جرم در واکنش شیمیایی همواره پایسته و ثابت است. به بیان دیگر، هیچ اتمی به وجود نمیآید یا از بین نمیرود، تنها پیوندهای بین آنها تغییر میکند. واکنش معروف تشکیل نمکطعام را در نظر بگیرید:
ابتدا واکنش بالا را موازنه میکنیم. تعداد اتمهای کلر در سمت راست و چپ واکنش به ترتیب یک و دو است. بنابراین، واکنش بالا به صورت زیر موازنه میشود:
پس از موازنه کردن واکنش، جرمهای نسبی دو طرف واکنش را با یکدیگر مقایسه میکنیم:
علاوه بر پایستگی جرم نسبی دو سمت واکنش، میتوان جرم واقعی هر سمت واکنش را نیز بررسی کرد. فرض کنید ۲/۳ گرم سدیم با ۳/۵ گرم گاز کلر واکنش دهد. اگر واکنش به طور کامل انجام شود، ۵/۸ گرم سدیمکلرید تولید خواهد شد. توجه به این نکته مهم است که استثنای مهمی برای قانون پایستگی جرم در واکنشهای شیمیایی وجود دارد. اگر یکی از واکنشدهندهها گاز باشد، جرم تغییر خواهد کرد، زیرا گاز ممکن است از هوا وارد واکنش شیمیایی شود، بنابراین به هنگام محاسبه جرم، در نظر گرفته نخواهد شد.
اگر فلزی مانند منیزیم را گرم کنیم، با اکسیژن واکنش میدهد و اکسید منیزیم تشکیل میشود. از آنجا که جرم نسبی اکسیدمنیزیم (۸۰) بیشتر از منیزیم (۴۸) است، وزن اکسیدمنیزیم بیشتر خواهد بود. به عنوان مثال، یک گرم منیزیم، ۱/۶ گرم اکسیدمنیزیم تشکیل میدهد. بنابراین، اکسیژنی که از هوای اطراف میآید با منیزیم واکنش میدهد و اکسیدمنیزیم با جرم بیشتر از منیزیم تشکیل میشود.
حال فرض کنید واکنش موردنظر داخل محفظهای بسته رخ میدهد. در این حالت، گاز، داخل محفظه محبوس شده است. بنابراین، به هنگام محاسبه جرم واکنشدهندهها، جرم منیزیم جامد و اکسیژن گازی در نظر گرفته میشود. در نتیجه، جرم واکنشدهندهها با جرم محصول نهایی برابر خواهد بود. واکنش زیر را در نظر بگیرید:
در واکنش فوق، کلسیمکربنات به اکسیدکلسیم و دیاکسیدکربن تجزیه شده است. دیاکسیدکربن گازی وارد هوا میشود. بنابراین، اینگونه به نظر میرسد که جرم محصول کاهش یافته است. مشابه حالت قبل، اگر واکنش در محفظهای بسته انجام شود، گاز داخل محفظه باقی میماند. از اینرو، جرم دو طرف واکنش یکسان خواهد بود.
مرکز جرم چیست ؟
مرکز جرم، موقعیتی است که نسبت به جسم یا سیستمی از اجسام تعریف شده یا به بیان بسیار ساده، مرکز جرم، یک نقطه است. به عنوان مثال، خطکشی ساده را در نظر بگیرید. مرکز جرم خطکش نقطهای است که گویا تمام جرم خطکش در آن نقطه جمع شده است. مرکز جرم اجسام سخت با چگالی یکنواخت، در نقطه مرکزی قرار گرفته است. به عنوان مثال، مرکز جرم دیسکی یکنواخت در مرکز آن قرار دارد. گاهی مرکز جرم درون جرم قرار نمیگیرد. به عنوان مثال، مرکزجرم حلقه در مرکز و خارج از آن قرار گرفته است.
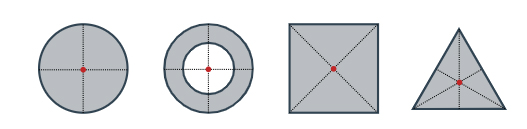
بهدست آوردن مرکز جرمِ شکلهای هندسی ساده، بسیار آسان است. هرچه شکل پیچیدهتر شود، انجام این کار نیز سختتر خواهد بود. بنابراین، باید از تعریف ریاضی کلی مرکز جرم استفاده شود. سیستمی متشکل از n جسم به جرمهای در نظر بگیرید. اگر فاصله مبدأ تا هر یک از این جرمها برابر باشد، رابطه زیر برای مرکز جرم برقرار خواهد بود.
سوالی که ممکن است مطرح شود آن است که چرا سعی در تعیین مرکز جرم اجسام مختلف داریم. نکته جالب در مورد مرکز جرم جسم یا سیستم آن است که هر نیروی یکنواختِ وارد شده بر جسم، در این نقطه اعمال میشود. از اینرو، با دانستن مکان مرکزجرم، حل مسائل مکانیک برای توصیف حرکت سیستمهای پیچیده، بسیار راحتتر خواهد بود. مرکز جرم به گونهای است که گویا تمام جرم جسم در این نقطه جمع شده است.
مرکز جرم را چگونه به دست می آوریم ؟
اکنون میدانیم مرکز جرم چیست، مرحله بعد چگونگی یافتن مرکز جرم اجسام مختلف است. تصویر زیر را در نظر بگیرید. پنج جسم با جرمهای مختلف در فاصلههای مختلفی نسبت به مبدأ قرار گرفتهاند.
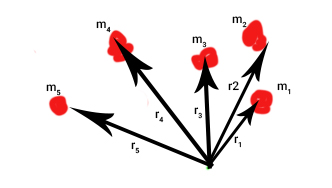
بردار که جرم را به مبدأ متصل کرده از دو مولفه x و y تشکیل شده است. بنابراین، مولفههای x و y مرکز جرم به صورت زیر به دست میآیند:
در نتیجه، مختصات مرکز جرم برابر است. رابطههای بالا برای سیستمهای متشکل از جرمهای گسسته و جدا از هم استفاده میشوند.
مثال محاسبه مرکز جرم
سیستمی از سه جسم مسطح با چگالی یکنواخت، تشکیل شده است. مرکز جرم آن را بهدست آورید.
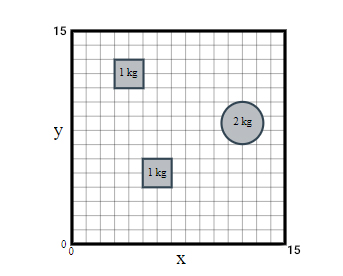
پاسخ: مکان مرکز جرم در راستای محور x برابر است با:
مکان مرکز جرم در راستای محور y برابر است با:
گاهی میتوان اجسام پیچیده را مجموعهای از شکلهای ساده با جرم یکنواخت در نظر و هر کدام از این شکلها را به صورت جرمی نقطهای در نقطه مرکزی، در نظر گرفت. اگر حفره یا حفرههایی درون جسمی قرار داشته باشند، به صورت جسمی با جرم منفی در نظر گرفته خواهند شد.
مثال دوم محاسبه مرکز جرم
جسم نشان داده شده در تصویر زیر را در نظر بگیرید.
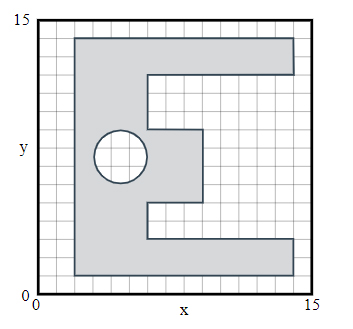
بهدست آوردن مرکز جرم این جسم در حالت عادی کار آسانی نیست. شکل فوق را میتوان به چهار مستطیل و یک دایره تقسیم کرد. مساحت هر یک از اجزای تشکیل دهنده در تصویر زیر نشان داده شده است.
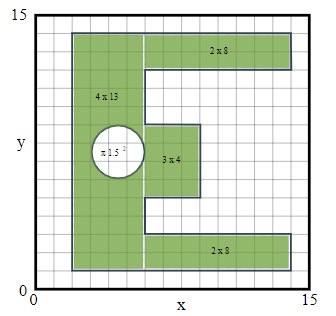
از آنجا که چگالی جسم یکنواخت است، جرم هر شکل به مساحت آن وابسته خواهد بود. مساحت هر قسمت در تصویر فوق نشان داده شده است. مولفه x مرکز جرم، به صورت زیر بهدست میآید:
به این نکته توجه داشته باشید که جرم حفره، منفی در نظر گرفته شده است. مولفه y مرکز جرم برابر است با:
علاوه بر حل مسائل فیزیک مکانیک، مرکز جرم کاربردهای زیادی در زندگی روزمره دارد. یکی از کاربردهای آن، پرش از ارتفاع است.
مثال سوم محاسبه مرکز جرم
جسمی به جرم ۵ کیلوگرم در مبدأ قرار دارد و جسمی به جرم ۹ کیلوگرم در نقطه قرار گرفته است. مکان مرکز جرم این سیستم را بهدست آورید.

پاسخ: قبل از حل این مثال به این پرسش فکر کنید، مرکز جرم کجا قرار گرفته است. مرکز جرم در فاصله دو جرم قرار دارد. مرکز جرم به جرم ۵ کیلوگرمی نزدیکتر است یا به جرم ۹ کیلوگرمی؟ مرکز جرم به جسم با جرم بیشتر نزدیکتر است. بنابراین، مرکز جرم جایی بین و قرار دارد.
شاید نام مرکز ثقل را شنیده باشد، آیا می دانید تفاوت آن با مرکز جرم چیست؟
مرکز ثقل چیست؟
مرکز ثقل نقطهای است که نیروی گرانشی در آن نقطه بر سیستم یا جسم وارد میشود. میدان گرانشی در بیشتر مسائل مکانیک، یکنواخت در نظر گرفته میشوند. در این صورت، مکان مرکز ثقل به طور دقیق منطبق بر محل مرکز جرم است. بنابراین، در بیشتر مواقع، مرکز ثقل و مرکز جرم یکسان در نظر گرفته میشوند.
مرکز جرم جسم واقعی
با استفاده از تعدادی آزمایشهای تجربی میتوان مرکز جرم اجسام فیزیکی را تعیین کرد. یکی از این روشها، روش لبه میز است.
روش لبه میز
از این روش برای پیدا کردن مرکز جرم اجسام کوچک و سخت با حداقل یک سطح تخت و مسطح، استفاده میشود. جسم به آرامی و بدون چرخش، در امتداد سطح میز به سمت لبه، کشیده میشود. در نقطهای که جسم در آستانه افتادن قرار میگیرد، خطی موازی لبه میز و گذرنده از این نقطه رسم میشود. سپس جسم به اندازه ۹۰ درجه چرخانده و فرایند را بار دیگر تکرار میکنیم. نقطه تقاطع دو خط برابر مرکز جرم جسم است.
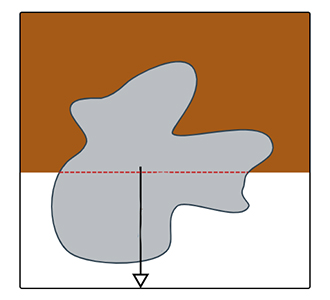
تا اینجا میدانیم جرم چیست و مرکز جرم چگونه تعیین میشود. در ادامه، در مورد جرم گرانشی و جرم لختی صحبت خواهیم کرد.
جرم گرانشی و جرم لختی چیست ؟
با دانستن مقدار جرم جسمی دلخواه، به دو نکته مستقل در مورد آن جسم پی میبریم. به عنوان مثال، اگر جرم کامیونی بسیار زیاد باشد، مقدار اینرسی یا لختی آن نیز بسیار زیاد خواهد بود. در واقع، کامیون تمایل بسیار کمی برای شتاب گرفتن یا افزایش سرعت دارد. در مقابل، اگر کامیون موردنظر با سرعت زیادی حرکت کند، توقف آن بسیار سخت خواهد بود. به بیان دیگر، توقف یا شتابدار کردن کامیون با جرم زیاد به نیروی بسیار زیادی نیاز دارد. بنابراین به مقدار نیروی موردنیاز برای شتاب دادن به جسمی دلخواه، جرم لختی گفته میشود. هرچه جرم جسمی بزرگتر باشد مقدار این نیرو بیشتر، و هرچه جرم جسم کوچکتر باشد، مقدار این نیرو کمتر خواهد بود.
جرم لختی به بهترین شکل توسط قانون دوم نیوتن بیان میشود:
در رابطه فوق:
- جمع تمام نیروهای وارد شده بر جسم است.
- شتاب حرکت جسم است.
- جرم لختی است.
همانطور که در رابطه فوق دیده میشود، جرم لختی در مخرج کسر قرار گرفته و با شتاب حرکت به صورت معکوس متناسب است. هرچه مقدار این جرم بیشتر باشد، جسم با شتاب کمتری حرکت خواهد کرد.
جرم، نکته دیگری را نیز در مورد برهمکنش جسم با گرانش به ما میگوید. به هنگام برخورد با نیروی گرانشی، اولین نامی که به یاد میآوریم، ایزاک نیوتن است. اگر جرم جسم بسیار زیاد باشد، مقدار نیروی جاذبه گرانشی وارد شده بر آن بسیار بزرگ خواهد بود.
در رابطه فوق:
- نیروی جاذبه گرانشی وارد شده بر جسم است.
- مقدار شتاب جاذبه گرانشی است.
- جرم گرانشی است.
در کیهان، جرمهای لختی و گرانشی با یکدیگر برابر هستند، اما مفهوم آنها به طور کامل با یکدیگر متفاوت است. فرض کنید هیچ نیروی گرانشی در جهان وجود نداشت، چه اتفاقی رخ میداد؟ در این حالت، باز هم اجسام تمایلی به حرکت شتابدار توسط نیروهای وارد شده بر آنها نداشتند. دانشمندان آزمایشهای زیادی برای تعیین تفاوت در مقدارهای دو جرم لختی و گرانشی انجام دادهاند، اما تاکنون موفق به یافتن تفاوت در مقدار این دو جرم نشدهاند.
گفتیم جرم لختی از نظر اندازه برابر جرم گرانشی است، اما سوالی که ممکن است مطرح شود آن است که این دو جرم چگونه اندازه گرفته میشوند. جرم گرانشی در بیشتر موارد با استفاده از ترازو و جرم لختی با اتصال جسم به فنر اندازه گرفته میشوند.
اندازه گیری جرم لختی
جرم لختی توسط فنری با ثابت فنر مشخص اندازه گرفته میشود. جرم به انتهای فنر متصل و فنر پس از اتصال جرم به آن، کشیده میشود. در ادامه، جسم به همراه فنر آزادانه شروع به نوسان میکنند. جرم لختی از رابطه زیر بهدست میآید:
در رابطه فوق:
- جرم لختی است.
- ثابت فنر است.
- مقدار فرکانس زاویهای است.
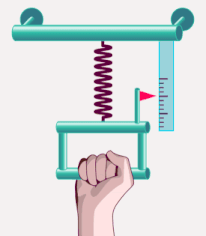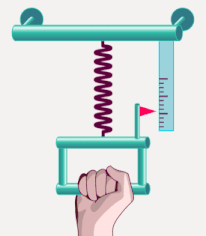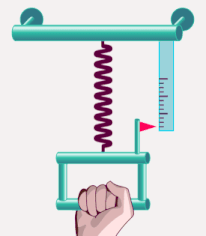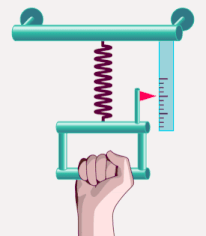
مثال جرم لختی
نیوتن سالها قبل به این نتیجه رسید که شتاب جسم به جرم جسم و مقدار نیروی وارد شده بر آن بستگی دارد. به عنوان مثال، جسمی با جرم نامشخص را در نظر بگیرید. نیرویی برابر ۲ نیوتن بر آن اعمال میشود و جسم با شتاب ۳ متر بر مجذور ثانیه شروع به حرکت میکند. با قرار دادن جرم و شتاب در رابطه معروف قانون دوم نیوتن، مقدار جرم برابر ۰/۴ کیلوگرم بهدست میآید. اکنون، فرض کنید همان نیرو بر جرم متفاوتی اعمال میشود و به جرم شتابی برابر یک متر بر مجذور ثانیه میدهد. باز، این مقدارها را در رابطه دوم نیوتن قرار میدهیم و مقدار جرم ۲ کیلوگرم بهدست میآید. با مقایسه این دو مثال، به رابطه بین جرم و اینرسی پی میبریم. اجسام با جرم بیشتر، اینرسی بزرگتر و اجسام با جرم کمتر، اینرسی کوچکتری دارند.
اندازه گیری جرم گرانشی
برای اندازهگیری این جرم میتوان از میدان گرانشی زمین همراه با ترازو استفاده کرد.
مثال جرم گرانشی
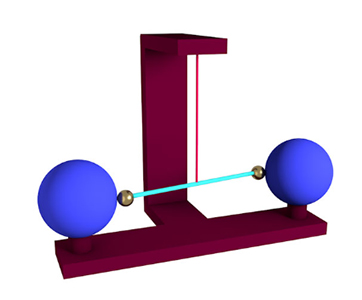
بر طبق محاسبات انجام شده توسط نیوتن، هرگاه دو جسم با جرمهای متفاوت در فاصله معینی از یکدیگر قرار بگیرند، توسط نیرویی به نام نیروی گرانشی یا نیروی جاذبه گرانشی به سمت یکدیگر کشیده خواهند شد. اندازه این نیرو به دو عامل بستگی دارد:
- متناسب با جرم دو جسم است.
- با فاصله دو جسم از یکدیگر به طور معکوس متناسب است.
جرم جسمی روی ترازو با استفاده از فرمول نیروی گرانشی بهدست میآید. هنگامی که ترازو در حالت تعادل قرار گرفت، نیروی وارد شده بر دو طرف ترازو از طرف میدان گرانشی زمین، با یکدیگر برابر خواهند بود. جرم مجهول را با ، جرم معلوم را با و جرم زمین را با نشان میدهیم. همچنین، نیروهای و به ترتیب نیروهای وارد شده بر جرمهای مجهول و معلوم هستند.
تنها مقدار مجهول در تساوی بالا است و به راحتی محاسبه میشود.
اکنون میدانیم مفهوم جرم چیست و به چند نوع تقسیم میشود. در ادامه، در مورد جرم مولی و جرم بحرانی در فیزیک صحبت میکنیم.
جرم بحرانی در فیزیک چیست ؟
دو تا سه نوترون در هر شکافت هستهای تولید میشوند، اما همه آنها برای ادامه واکنش شکافت، در دسترس نیستند. اگر شرایط به گونهای باشد که از بین رفتن نوترونها سریعتر از نرخ تولید آنها باشد، واکنش زنجیرهای ادامه نخواهد یافت. به نقطهای که واکنش زنجیرهای در آستانه پایداری قرار میگیرد، جرم بحرانی گفته میشود.
در بمب اتم، مقداری ماده شکافتپذیر بیشتر از جرم بحرانی باید جمع و در حدود یک میلیونیم ثانیه برای رخ دادن واکنش زنجیرهای قبل از انفجار بمب، در کنار یکدیگر قرار بگیرند. مقدار جرم بحرانی ماده شکافتپذیر به چندین عامل بستگی دارد:
- شکل ماده
- ترکیب و چگالی آن
- سطح خلوص
کره، حداقل سطح ممکن برای جرم داده شده را دارد، بنابراین نشت نوترونها را به حداقل میرساند. اگر ماده شکافتپذیر توسط بازتابنده نوترونی مناسبی احاطه شود، از دست دادن نوترونها و در نتیجه، جرم بحرانی کاهش مییابد.
جرم مولی چیست ؟
تاکنون میدانیم مفهوم جرم چیست و با چه واحدهایی اندازهگیری میشود. برای اندازهگیری جرم ترکیبهای شیمیایی در شیمی، از مفهومی به نام جرم مولی استفاده میکنیم. جرم مولی به صورت جرم بر مول تعریف میشود. به بیان دیگر، جرم مولی برابر جمع جرم تمام اتمهای موجود در یک مول از ماده است و با واحد گرم بر مول بیان میشود. جرم مولی برای عناصر و مولکولها حساب میشود. در حالتی که تنها یک عنصر یا اتمهای تکی داریم، جرم مولی برابر جرم اتمیِ اتم تکی خواهد بود. هنگامی که اتمهای تکی از طریق پیوند شیمیایی به یکدیگر متصل و مولکولها را تشکیل میدهند، جرم مولی برابر جرم تمام اتمهای شرکتکننده در پیوند است.
توجه به این نکته مهم است که تعریف جرم مولی با جرم مولکولی متفاوت است، زیرا جرم مولکولی، جرم مولکول داده شده و جرم مولی، جرم یک مول از مولکول داده شده است.
جرم مولی از جمع جرمهای اتمیِ ترکیب داده شده، محاسبه میشود. جرم عنصرهای مختلف در جدول تناوبی نوشته شده است. به عنوان مثال، آب با ترکیب شیمیایی را در نظر بگیرید. جرم آب به صورت زیر بهدست میآید:
آزمون جرم
در این قسمت به منظور درک بهتر مفهوم جرم، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
تمرین و آزمون
جسمی به جرم ۱۲ کیلوگرم روی سطح زمین قرار دارد. وزن جسم چه مقدار است؟
۱۱۷/۶ نیوتن
۱۰۷/۰ نیوتن
۱۲۰/۰ نیوتن
۱۱۴/۷ نیوتن
جرم را به صورت مقدار ماده موجود در جسم تعریف کردیم. اما وزن نیرویی است که به دلیل جاذبه گرانشی بر جسم وارد میشود و واحد اندازهگیری آن نیوتن است. وزن جسم از حاصلضرب جرم جسم در شتاب جاذبه گرانشی، بهدست میآید. در این مسئله، جرم جسم برابر ۱۲ کیلوگرم است. وزن روی زمین به صورت زیر محاسبه میشود:
توجه به این نکته مهم است که مقدار شتاب جاذبه زمین، g، برابر ۹/۸ متر بر مجذور ثانیه است.
وزن جسمی به جرم ۱۱۰ کیلوگرم روی ماه، برابر ۱۷۶ نیوتن است. مقدار شتاب جاذبه ماه برابر است با:
۱/۸ متر بر مجذور ثانیه
۲/۶ متر بر مجذور ثانیه
۱/۶ متر بر مجذور ثانیه
۱/۰۸ متر بر مجذور ثانیه
همانطور که در مطالب بالا فهمیدیم، رابطه بین وزن، جرم و شتاب جاذبه گرانشی در مثلثی به نام مثلث Wmg نشان داده میشود.
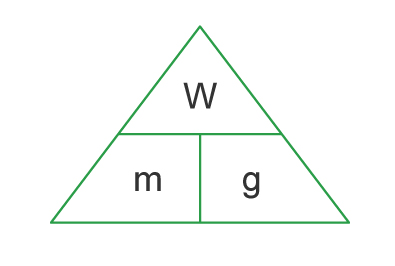
برای محاسبه هر یک از کمیتهای فوق میتوان از مثلث بالا استفاده کرد. برای استفاده از این مثلث، به نکتههای زیر توجه کنید:
- خط افقی در مثلث، نشاندهنده تقسیم و خط عمودی بیانگر ضرب است.
- برای محاسبه جرم، به صورت زیر عمل میکنیم:
- جرم را با انگشت میپوشانیم.
- W را بر g تقسیم میکنیم.
- برای محاسبه شتاب جاذبه گرانشی نیز به صورت مشابه عمل خواهیم کرد.
وزن جسم با استفاده از رابطه زیر بهدست میآید:
در این مسئله، مقدار شتاب جاذبه گرانشی روی سطح ماه خواسته شده است. با قرار دادن جرم و وزن جسم در رابطه مربوط به وزن، شتاب جاذبه گرانشی ماه را بهدست میآوریم.
جسمی به جرم ۵ کیلوگرم در مرکز و جرم دیگری به جرم ۹ کیلوگرم، روی محور افقی و در فاصله ۲ متری از مبدا قرار گرفته است. مرکز جرم این دو جسم در چه مکانی قرار دارد؟
مرکز جرم دو جسم روی محور افقی و در فاصله ۱/۲۹ متری از مبدا قرار گرفته است.
مرکز جرم دو جسم روی محور عمودی و در فاصله ۱/۲۹ متری از مبدا قرار گرفته است.
مرکز جرم دو جسم روی محور افقی و در فاصله ۲/۲۹ متری از مبدا قرار گرفته است.
مرکز جرم دو جسم روی محور عمودی و در فاصله ۲/۲۹ متری از مبدا قرار گرفته است.
بردار که جرم را به مبدأ متصل کرده از دو مولفه x و y تشکیل شده است. بنابراین، مولفههای x و y مرکز جرم به صورت زیر به دست میآیند:
در نتیجه، مختصات مرکز جرم برابر است. در این مسئله، دو جسم به جرمهای ۵ و ۹ کیلوگرم داریم که به ترتیب در مکانهای و قرار گرفتهاند. برای دو جسم با استفاده از رابطه زیر بهدست میآید:
از آنجا که هیچ کدام از دو جسم روی محور عمودی قرار نگرفتهاند و مولفه y آنها برابر صفر است، نیز برابر صفر خواهد بود.
جسمی به جرم ۸ کیلوگرم در مکان قرار گرفته است. جسم ۱۰ کیلوگرمی در چه مکانی روی محور عموی y باید قرار بگیرد تا مرکز جرم دو جسم در مکان قرار داشته باشد؟
جسم ۱۰ کیلوگرمی در فاصله ۶/۵ متری از مبدا و روی محور قرار دارد.
جسم ۱۰ کیلوگرمی در فاصله ۶/۵ متری از مبدا و روی محور قرار دارد.
جسم ۱۰ کیلوگرمی در فاصله ۵/۷ متری از مبدا و روی محور قرار دارد.
جسم ۱۰ کیلوگرمی در فاصله ۵/۷ متری از مبدا و روی محور قرار دارد.
مولفههای x و y مرکز جرم به صورت زیر به دست میآیند:
از آنجا که دو جسم روی محور افقی قرار گرفتهاند، برابر صفر است. همچنین، برابر ۴/۵ متر است. برای یافتن مکان جرم ۱۰ کیلوگرمی از رابطه استفاده میکنیم و مقدار را بهدست میآوریم. همچنین، مقدار برابر ۳ متر است.
سه آجر به طول L و جرم M به صورت نشان داده شده در تصویر زیر روی هم قرار گرفتهاند. مولفه مرکز جرم سه آجر برابر است با:
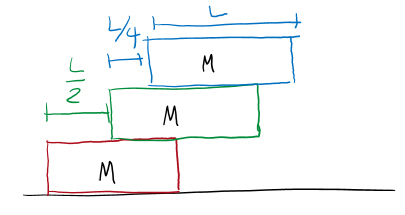
جرم زمین برابر ، جرم ماه برابر و فاصله متوسط بین ماه تا مرکز زمین برابر است. بزرگی نیروی گرانشی وارد شده از طرف زمین بر ماه چه مقدار است؟
سیارهای بزرگتر از زمین نیروی گرانشی برابر ۶۵/۰ نیوتن بر جسمی وارد میکند. اگر قدرت میدان گرانشی برابر ۱۱/۶ نیوتن بر کیلوگرم باشد، جرم گرانشی جسم برابر است با:
۵/۰۰ کیلوگرم
۶/۶۰ کیلوگرم
۴/۶۰ کیلوگرم
۵/۶۰ کیلوگرم
میدان گرانشی و جرم سیاهره بتا دوبرابر میدان گرانشی و جرم زمین است. کدامیک از گزینههای زیر رابطه بین شعاع سیاره بتا و شعاع زمین را به درستی نشان میدهد؟
r_ { Beta } = \sqrt { 2 } \ r _ { Earth }
شعاع و جرم سیاره آلفا به ترتیب نصف و دو برابر شعاع و جرم زمین است. بهترین تخمین برای بزرگی میدان گرانشی در سطح سیاره آلفا چه مقدار است؟
۸۰ متر بر مجذور ثانیه
۲/۰ متر بر مجذور ثانیه
۱۶۰ متر بر مجذور ثانیه
۴۰ متر بر مجذور ثانیه
جمعبندی
در این مطلب، به پرسش جرم چیست به زبان ساده پاسخ دادیم. سپس، در مورد تفاوت جرم با وزن صحبت و سقوط آزاد اجسام مختلف را با یکدیگر مقایسه کردیم. با خواندن این مطلب میدانیم:
- جرم چیست و چگونه اندازهگیری میشود.
- تفاوت وزن و جرم چیست.
- جرم لختی و گرانشی و تفاوتهای آنها چیست.
- قانون پایستگی جرم چیست و چه استثنایی در این قانون وجود دارد.
- جرم با چه واحدهایی اندازه گرفته میشود.













سلام ، اگر جمعیت زمین(نوع بشر) ۴ برابر شود؛ جرم زمین چه تغییری میکند ؟ و اگر چند نوع موجود منقرض شوند چه؟ منظورم اینه که زمین یک سیستم است و پایستگی جرم دارد یا نه ، منظومه شمسی پایستگی جرم دارد یا کهکشان راه شیری یا کل کیهان؟
با سلام و احترام
مقاله ی به شدت جذابی است از این بابت خیلی برای بنده جالب بود زمانی که شروع به مطالعه آن نمودم کلیات آن مورد بررسی قرار گرفت و بعد از ادامه دادن مقاله جزئیات آن به طور کامل و با ذکر نمونه مورد بررسی قرار گرفت به شخصه تبریک میگویم به نگرش و طرز فکر گسترده شخص سرکار عالی
دست مریضاد و تشکر ویژه بابت مطالب مفید و ارزشمندتان
با آرزوی موفقیت روزافزون