رسم نمودار سه بعدی در متلب – از صفر تا صد
نرمافزار متلب یکی از قدرتمندترین نرمافزارهای مهندسی و علوم پایه برای رسم نمودار و شبیهسازیهای مختلف است. رسم نمودارهای دو و سهبعدی نقش بسیار مهمی در بررسی دادهها در علومپایه و مهندسی دارند. در مطالب قبلی مجله فرادرس رسم نمودار دوبعدی در متلب به زبان ساده، توضیح داده شده است. در این مطلب، رسم نمودار سه بعدی در متلب را توضیح خواهیم داد.
رسم نمودار سه بعدی در متلب
رسم نمودارهای سهبعدی یکی مهمترین بخشهای رسم نمودار در نرمافزار متلب است. رسم نمودار سهبعدی در متلب به دو بخش کلی زیر تقسیم میشود:
- رسم نمودارهای سهبعدی با استفاده از خطوط و نقاط: برای رسم این نمودارهای سهبعدی در متلب از دستورهای plot3 و scatter3 استفاده میشود.
- رسم سطح سهبعدی: قبل از توضیح در مورد چگونگی رسم سطوح سه بعدی در متلب، ابتدا در مورد مفهوم کلی ایجاد سطح سهبعدی در کامپیوتر صحبت خواهیم کرد.
پس از صحبت در مورد دو دستور بالا، به دستورهای مختلف متلب برای رسم نمودارهای سهبعدی مختلف نگاهی میاندازیم و به اختصار در مورد هر یک از آنها توضیح میدهیم.
- patch
- meshgrid
- surf
- contour
- surfc
در پایان، سطوح سهبعدی و خطوط را بهمنظور تولید نمودارهای سهبعدی بسیار جالب، با یکدیگر ترکیب خواهیم کرد.
قبل از آنکه در مورد مطالب تقسیمبندی شده در بالا برای رسم نمودار سهبعدی در متلب توضیح دهیم، خالی از لطف نیست مروری کلی بر رسم نمودار دوبعدی داشته باشیم.
مروری بر رسم نمودار دوبعدی در متلب
برای رسم نمودار دوبعدی در متلب:
- نقاط موردنظر را تعریف میکنیم.
- متلب نقاط تعریف شده را با استفاده از خط مستقیم به یکدیگر متصل میکند.
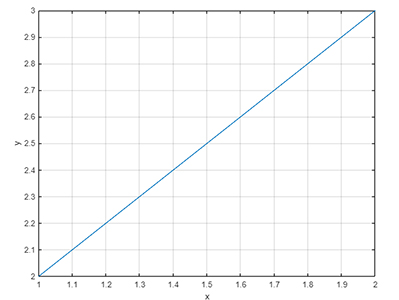
به عنوان مثال، اگر بخواهیم خطی را از نقطه $$(1 \, 2 )$$ به نقطه $$(2 \, 3 )$$ بکشیم، ابتدا دو نقطه داده شده را در متلب به صورت زیر تعریف میکنیم:
1x = [1 2];
2y = [2 3]; سپس، برای رسم این خط از دستور figure و plot به صورت زیر استفاده میکنیم:
1figure
2plot (x,y)
3xlabel ('x')
4ylabel ('y')
5grid onکد بالا، خطی مستقیم از نقطه $$(1 \, 2 )$$ به نقطه $$(2 \, 3 )$$ به صورت نشان داده شده در تصویر زیر، رسم میکند.
رسم نمودار سه بعدی با استفاده از دستور plot3
تبدیل نمودار دوبعدی رسم شده در بالا به نموداری سهبعدی بسیار راحت است. در این حالت، نقطه دیگری به نام z تعریف میکنیم.
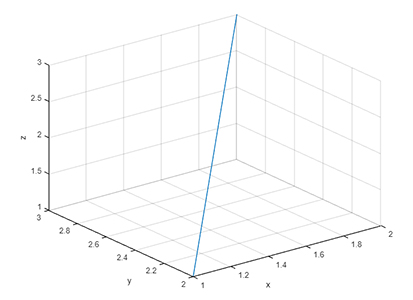
1x = [1 2]; y = [2 3]; z = [1 3];میخواهیم خطی سه بعدی از نقطه $$(1 2 1)$$ به نقطه $$(2 2 3)$$، رسم کنیم. دستور figure بدون تغییر باقی میماند، اما به جای دستور plot از plot3 استفاده و برای نامگذاری محور سوم، یعنی z، از دستور zlabel استفاده میکنیم. بنابراین، کد نوشته شده برای رسم خط در سهبعد به صورت زیر خواهد بود:
1 figure
2 plot3 (x, y , z)
3 xlabel ('x')
4 ylabel ('y')
5 zlabel ('z')
6 grid onکد بالا، خطی مستقیم از نقطه $$(1 2 1)$$ به نقطه $$(2 2 3)$$، به صورت نشان داده شده در تصویر زیر، رسم میکند.
ویژگی بسیار مهمی که به هنگام رسم نمودار سه بعدی در متلب مشاهده میکنیم، دکمه چرخش است.

با کمک این گزینه میتوان نمودار سه بعدی در متلب را در راستای دلخواه چرخاند و آن را از زاویههای مختلف بررسی کرد.
سوالی که ممکن است مطرح شود آن است که آیا میتوان برای رسم نمودارهای سهبعدی، نقاطی با سه مقدار x y z تعریف کرد. بله، این کار به سادگی و به صورت زیر امکانپذیر است.
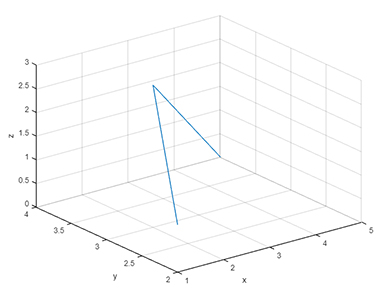
1 x = [1 2 5];
2 y = [2 3 4];
3 z = [1 3 0]; اکنون با استفاده از کد گفته شده در بالا، نمودار نقاط داده شده را رسم میکنیم. خط رسم شده از دو قسمت تشکیل شده است.
در ادامه، x y z را به شکل پیچیدهتر و و به صورت پارامتری، تعریف میکنیم. t را به شکل برداری و سپس x y z را برحسب t، به صورت زیر تعریف میکنیم:
1t = linspace(0, 6*pi, 30);
2x = 3*cos(t);
3y = 1*sin(t);
4z = 0.01*t.^2;کد تغییری نکرده است، تنها مقدارهای x y z، تغییر کردهاند. کد را بار دیگر اجرا میکنیم. نمودار سهبعدی رسم شده به شکل مارپیچی به سمت بالا خواهد بود.
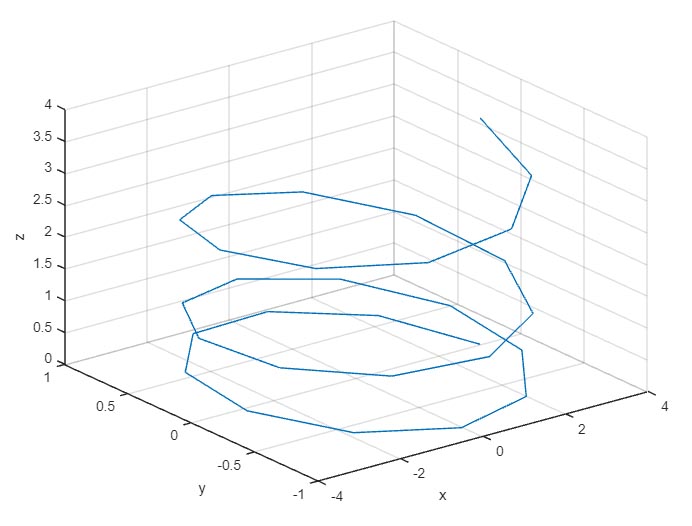
انتظار داریم تصویر دوبعدی مارپیچ به شکل بیضی باشد، اما همانطور که در تصویر زیر دیده میشود، تصویر دوبعدی در صفحه xy بیشتر به دایره شبیه است.
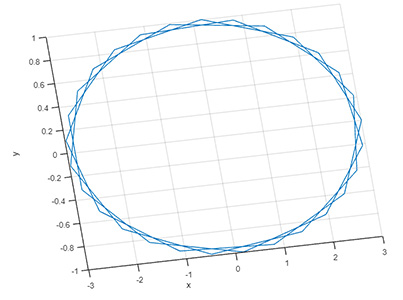
دلیل این موضوع آن است که محورها از نظر مقیاس یکسان نیستند. برای یکسانسازی محورهای xyz، از دستور $$axis ('equal')$$ استفاده میکنیم. توجه به این نکته مهم است که تنها تفاوت دستورهای plot و plot3 در رسم نمودارها، در دو و سهبعد است.
تاکنون با دستور plot3 برای رسم نمودار سه بعدی در متلب آشنا شدیم. در ادامه، در مورد تابع scatter صحبت میکنیم.
رسم نمودار سه بعدی با استفاده از دستورscatter3
مقدارهای x y z را تغییر نمیدهیم. کد نیز شبیه کد قبل است، با این تفاوت که plot3 با scatter3 جایگزین میشود.
1figure
2scatter3 (x, y , z)
3xlabel ('x')
4ylabel ('y')
5zlabel ('z')
6grid onقبل از رسم نمودار، کمی مکث و به تفاوت این دو دستور فکر کنید. تابع scatter3 همانطور که از نامش مشخص است، نقطهها را به صورت پراکنده در سهبعد رسم خواهد کرد.
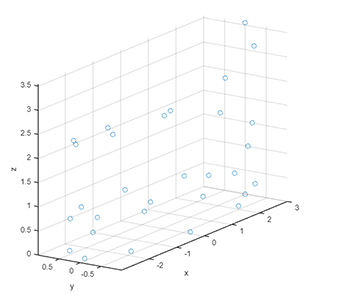
توجه به این نکته مهم است که با استفاده از دستور plot3 نیز میتوان نقطهها را به شکل پراکنده رسم کرد. برای این کار کافی است که به دستور plot3 عبارت 'mo' را نیز اضافه کنید.
1plot3 (x, y, z, 'mo')با اجرای این دستور، نمودار همانند scatter3 به صورت پراکنده و به شکل دایرههای ارغوانی، رسم میشود.
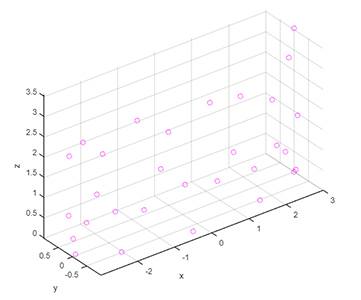
بنابراین، به راحتی میتوان از دستور plot3 به جای scatter3 استفاده کرد.
پرسش ۱: نقطههای پراکنده و خطوط مختلف در یک نمودار، چگونه همزمان رسم میشوند؟
پاسخ
برای انجام این کار از دستور hold on به صورت زیر استفاده میکنیم:
1figure
2hold on
3plot3 (x, y, z)
4plot3 (x, y, z, 'mo')
5xlabel ('x')
6ylabel ('y')
7zlabel ('z')
8grid on
9axis ('equal')همانطور که در تصویر زیر دیده میشود، نقاط به صورت دایره نشان داده و توسط خط آبیرنگ به یکدیگر وصل شدهاند.
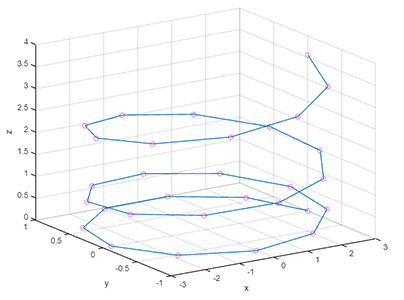
تاکنون با رسم خط و نقطه در سهبعد در نرمافزار متلب آشنا شدیم. در ادامه، در مورد رسم سطح سهبعدی در متلب صحبت خواهیم کرد. اما قبل از توضیح در مورد این موضوع، خالی از لطف نیست که کمی در مورد چگونگی رسم سطح سهبعدی در کامپیوتر توضیح دهیم.
رسم سطوح سه بعدی در کامپیوتر
ابتدا در مورد رسم نمودارهای دوبعدی صحبت میکنیم. نمودارهای دوبعدی در حالت کلی به صورت زیر تعریف میشوند:
$$y=f(x)$$
تابع f، مقدار x را به عنوان ورودی دریافت میکند و خروجی y را تحویل میدهد. نمودار دوبعدی دلخواه $$f(x)$$، دو مقدار x و y دارد و به صورت زیر رسم میشود:
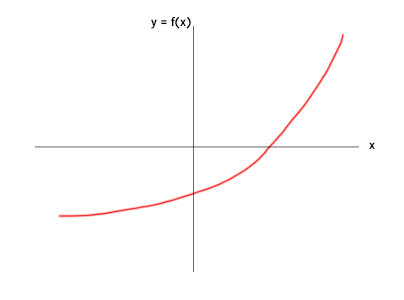
اما رسم نمودار در کامپیوتر به صورت تصویر نشان داده شده، پیوسته نخواهد بود. نمودار دوبعدی در کامپیوتر را به صورت زیر رسم میکنیم:
- محور x را به قسمتهای دلخواه تقسیم میکنیم.
- مقدار تابع $$f(x)$$ را در نقطههای تقسیم شده روی محور x، بهدست میآوریم.
- این نقطهها را توسط خط به یکدیگر وصل میکنیم.
اما سوال اصلی آن است که سه مرحله بالا، چگونه برای رسم نمودار سهبعدی استفاده میشوند. در حالت سه بعدی نیز تابع f را داریم، اما به جای یک ورودی، دو ورودی خواهیم داشت.
$$y = f(x_1 \, x_2)$$
مقدارهای $$x_1$$ و $$x_2$$ را به تابع f میدهیم و خروجی y را دریافت میکنیم. برای رسم این نمودار، به محورهای مختصات x و y، محور سومی به نام z نیز اضافه خواهد شد. به بیان دیگر، محور سوم، حاصل تابع $$y = f(x_1 \, x_2)$$ است. نمودار سهبعدی رسم شده به جای خط یا نقاط متصل به یکدیگر، سطح است. در ادامه، در مورد چگونگی رسم این سطح در کامپیوتر صحبت خواهیم کرد.
در مورد رسم نمودار دوبعدی گفتیم که محور x را به نقطههای گسستهای تقسیم میکنیم. برای حالت سه بعدی نیز مورد مشابهی انجام میشود.
- ابتدا دو نقطه با مقدارهای ۱+ و ۱-، روی محور $$x_1$$ انتخاب و علامتگذاری میکنیم.
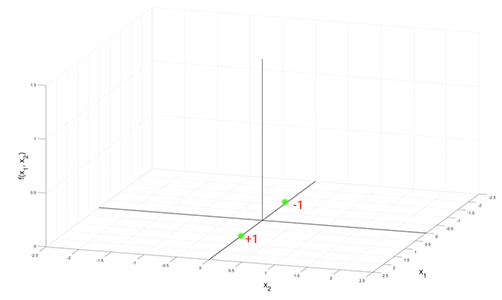
- سپس، سه نقطه با مقدارهای ۲-، ۰٫۱- و ۱٫۷+ روی محور $$x_2$$ انتخاب میکنیم.
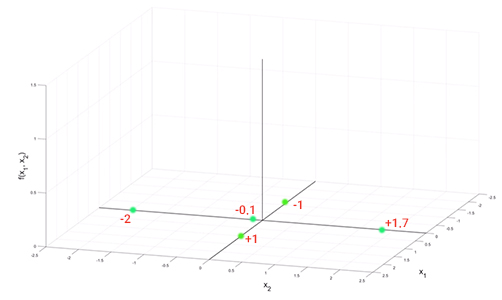
- از هر یک از نقاط سبزرنگ نشان داده شده روی محور $$x_1$$ خطی موازی محور $$x_2$$ و از هر یک از نقاط سبزرنگ نشان داده شده روی محور $$x_2$$ خطی موازی محور $$x_1$$، رسم میکنیم. محل تقاطع خطوط رسم شده را با نقطههای قرمزرنگ نشان میدهیم.
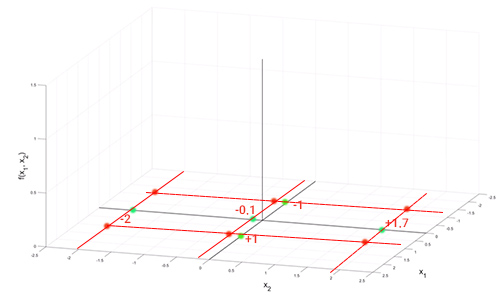
- مختصات هر یک از نقطههای نشان داده شده در تصویر بالا را در کنار آنها مینویسیم.
مرحلههای گفته شده در بالا برای رسم سطح یا رویه سه بعدی بسیار مهم هستند. نرمافزار متلب با استفاده از تابعی به نام meshgrid ، مرحلههای بالا را انجام میدهد. در ادامه، با دادن هر یک از نقطههای بهدست آمده به تابع $$y = f(x_1 \, x_2)$$، مقدار آن را در این نقطهها محاسبه میکنیم. اکنون تعدادی نقطه در فضا داریم، اما سوال اصلی آن است که چگونه سطح سهبعدی را به صورت سطحی پیوسته در فضا رسم کنیم. صفحه در فضای سهبعدی توسط سه نقطه تعریف میشود. از اینرو، سه نقطه دلخواه را انتخاب و صفحهای از آنها عبور میدهیم. در حقیقت، این کار را میتوانیم برای هر سه نقطه دلخواه، انجام دهیم و سطح سهبعدی را رسم کنیم.
در این بخش، با رسم سطح یا رویه سهبعدی در کامپیوتر آشنا شدیم. در بخش بعد، چگونگی رسم آن را در متلب توضیح میدهیم.
رسم سطوح سه بعدی در متلب
روشهای مختلفی برای رسم سطوح سهبعدی در متلب وجود دارند. در ادامه، هر روش را به اختصار توضیح میدهیم.
استفاده از دستور patch برای رسم نمودار سه بعدی در متلب
یکی از سادهترین روشها برای رسم سطح سهبعدی در متلب، استفاده از دستور patch است. دستور patch ، مثلث رسم میکند. تنها کاری که باید انجام دهیم تعریف سه نقطه در فضا و اتصال آنها به صورت مثلث به یکدیگر است.
برای انجام این کار، از همان سه نقطه تعریف شده در مطالب بالا، استفاده خواهیم کرد.
1x = [1 2 5];
2y = [2 3 4];
3z = [1 3 0];به طور مشابه، دستور figure را خط اول مینویسیم، اما به جای دستور plot3، از دستور patch استفاده میکنیم.
1figure
2patch (x, y, z, 'm')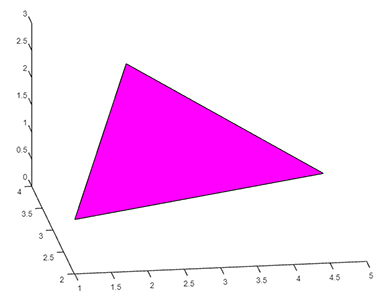
یکی از راههای رسم سطح سهبعدی در متلب، استفاده پیوسته از دستور patch و اتصال مثلثهای رسم شده به یکدیگر است. گرچه اینروش از نظر مفهومی صحیح است، اما فرایند بسیار خستهکنندهای است. در نتیجه، از تابع mesh استفاده میکنیم.
استفاده از دستور mesh برای رسم نمودار سه بعدی در متلب
برای استفاده از دستور mesh ، مراحل گفته شده برای رسم نمودار سهبعدی در کامپیوتر را انجام میدهیم. ابتدا دامنه موردنظر برای رسم سطح سهبعدی را تعریف میکنیم. به بیان دیگر، بردار یکبعدی $$x_1$$ و بردار یکبعدی $$x_2$$ را به عنوان ورودی به نرمافزار میدهیم.
1x1 = [-1 1];
2x2 = [-2 -0.1 1.7];پس از تعریف $$x_1$$ و $$x_2$$، با استفاده از تابع meshgrid ، شبکهای گذرنده از آنها رسم میکنیم. در مطالب بالا و پس از تعریف بردارهای یکبعدی $$x_1$$ و $$x_2$$ و نشان دادن نقطههای آنها با دایرههای کوچک سبز، خطوطی گذرنده و موازی محورهای $$x_1$$ و $$x_2$$ رسم و محل تقاطع خطوط را مشخص کردیم. با تابع meshgrid نیز کار مشابهی انجام میدهیم.
1[X1, X2] = meshgrid (x1, x2); برای آشنایی بیشتر با تابع meshgrid ، متغیرهای $$X_1$$ و $$X_2$$ را فراخوانی و مقدارهای نسبت داده شده به آنها را مشاهده میکنیم.
1>> X1
2
3X1 =
4
5 -1 1
6 -1 1
7 -1 1
8>> X2 =
9
10 -2.0000 -2.0000
11 0.1000 0.1000
12 1.7000 1.7000از مقدارهای $$X_1$$ و $$X_2$$ برای بهدست آوردن مقدار تابع f، استفاده میشود. تابعی دلخواه به صورت زیر تعریف میکنیم:
1z = X1.*X2تمام مقدمات لازم برای رسم سطح دلخواه سهبعدی را در متلب انجام دادهایم. برای رسم تابع سهبعدی z از دستور mesh به شکل زیر استفاده میکنیم:
1figure
2mesh (X1, X2, z)با اجرای دستور بالا، سطح سهبعدی نشان داده شده در تصویر زیر رسم میشود.
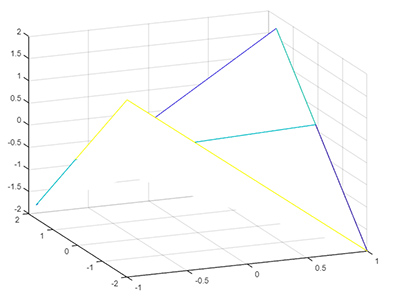
نمودار رسم شده از تعدادی مثلث متصل به یکدیگر تشکیل شده است. ما به دنبال نمودار سهبعدی زیباتر و مفهومیتری هستیم. برای رسم نموداری زیباتر و مفهومیتر، ابتدا $$x_1$$ و $$x_2$$ را به صورت زیر تعریف میکنیم.
1x1 = linspace (-pi, pi, 20);
2x2 = linspace (-10, 16, 30);همچنین، تابع z را به شکل زیر مینویسیم.
1z = cos (X1).*X2;مشابه حالت قبل، با استفاده از دستور mesh ، بار دیگر نمودار سه بعدی z را رسم میکنیم. این نمودار، در مقایسه با نمودار قبل، مفهوم دستور mesh را واضحتر نشان میدهد.
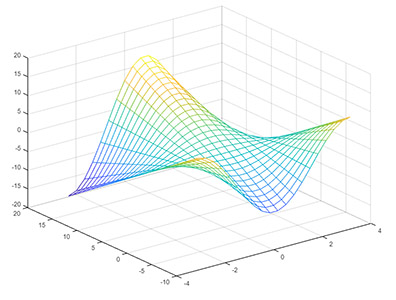
نمودار فوق را حتی میتوان با نامگذاری محورها، زیباتر و مفهومیتر رسم کرد.
1xlabel ('x_1');
2ylabel ('x_2');
3zlabel ('z = f(x_1, x_2)');
4grid on
5title ('Using the ''mesh'' function')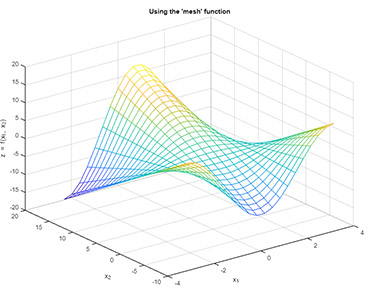
علاوه بر دستورهای plot3 و mesh ، دستورهای دیگری نیز برای رسم نمودار سه بعدی در متلب وجود دارند که در ادامه، در مورد آنها صحبت خواهیم کرد.
رسم نمودار سه بعدی در متلب با استفاده از دستور surf
دستور surf شباهت بسیاری به دستور mesh دارد.
1figure
2surf (X1, X2, z)
3xlabel ('x_1');
4ylabel ('x_2');
5zlabel ('z = f(x_1, x_2)');
6grid on
7title ('Using the ''surf'' function')
همانطور که مشاهده میکنید، دستورهای mesh و surf شباهت بسیار زیادی با یکدیگر دارند، با این تفاوت که دستور surf برای هر قسمت از نمودار تقسیمبندی شده، رنگ مناسبی انتخاب کرده است.
به نمودار سهبعدی رسم شده با دستور surf دقت کنید. نمودار توسط خطوط مشکی تقسیمبندی شده است. اگر چگالی نقطههای نمودار یا تعداد تقسیمبندی آن بسیار زیاد باشد، تمام نمودار با رنگ مشکی نشان داده خواهد شد. برای درک بهتر این موضوع، $$x_1$$ و $$x_2$$ را به صورت زیر تعریف کنید:
1x1 = linspace (-pi, pi, 200);
2x2 = linspace (-10, 16, 300);نمودار پس از اجرای دستور surf به شکل زیر نشان داده میشود. همانطور که مشاهده میکنید، قسمت بیشتر این نمودار مشکی است و تشخیص شکل دقیق آن مشکل خواهد بود.
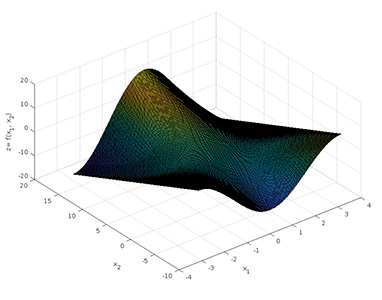
برای رهایی از خطوط مشکی، از دستور shading interp استفاده میشود.
گاهی دانستن معنای رنگهای نشان داده شده در نمودار سهبعدی برحسب ارتفاع، کمک بزرگی برای درک بهتر آن است. برای انجام این کار از دستوری به نام colorbar استفاده میشود. پس از رسم نمودار، ستونی عمودی شامل طیف رنگی استفاده شده در نمودار، کنار آن نمایش داده میشود و محدوده هر رنگ را برحسب ارتفاع نشان میدهد.
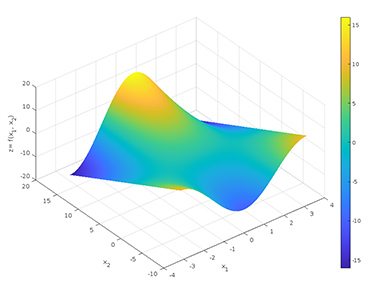
اگر علاقهای به طیف رنگی استفاده شده در نمودار نداشته باشید، به راحتی میتوانید آن را تغییر دهید. عبارت 'help colormap' را در متلب بنویسید و به صفحه Documentation بروید. در پایان صفحه Documentation، جدولی با عنوان نام نقشه رنگی و مقیاس رنگی استفاده شده برای هر نقشه را مشاهده خواهید کرد. با استفاده از این جدول، به راحتی میتوانید مقیاس رنگی مورد علاقه خود را انتخاب کنید.

رسم نمودار سه بعدی با استفاده از دستور contour
ابتدا نمودار سهبعدی را با استفاده از دستور contour رسم میکنیم.
1figure
2contour (X1, X2, z)
3xlabel ('x_1');
4ylabel ('x_2');
5zlabel ('f(x_1,x_2) = z');دستور contour، سطوح همتراز یا سطوح با مقدار ثابت نمودار سهبعدی فوق را در صفحه $$x_1 x_2 $$ نمایش میدهد.
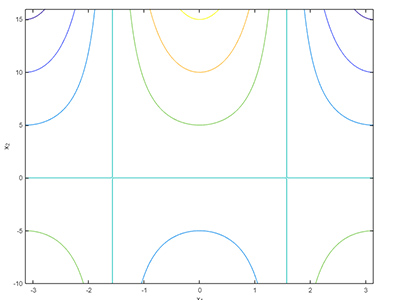
ترکیب دو دستور surf و contour در دستوری به نام surfc
دستور surfc، دو دستور surf و contour را با یکدیگر ترکیب و نمودار سهبعدی را به همراه تصویر سطوح همتراز آن در صفحه $$x_1 x_2 $$، رسم میکند.
تاکنون در مورد رسم خط و سطوح سهبعدی در متلب صحبت کردیم. در ادامه، خط و سطح سهبعدی را با یکدیگر ترکیب و رسم میکنیم. ابتدا، مقدارهای $$x_1$$ و $$x_2$$ و z را به صورت زیر تعریف میکنیم:
1x1_line = linspace (-1, 1, 20);
2x2_line = linspace (0, 10, 20);
3z_line = cos(x1_line).*x2_line; اکنون میخواهیم خط تعریف شده را با سطح موردنظر، در کنار یکدیگر رسم کنیم.
1figure
2hold on
3surfc (X1, X2, z)
4plot3 (x1_line, x2_line, z_line, 'm')
5xlabel ('x_1')
6ylabel ('x_2')
7zlabel ('z = f(x_1, x_2)')
8grid on
9title (' A Composite Plot')
10view ([35 30])
11shading interp
12colormap (jet(50))
13colorbarترکیب نمودار و خط سهبعدی در تصویر زیر نشان داده شده است.

مثال رسم نمودار سه بعدی در متلب
برای آشنایی بیشتر با رسم نمودار سه بعدی در متلب، چند مثال در این مورد حل خواهیم کرد.
مثال اول
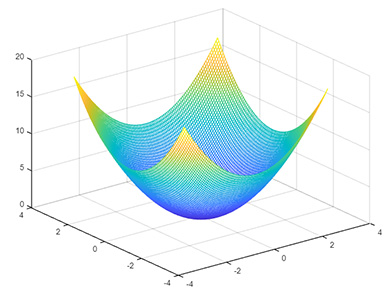
نمودار $$z = x^2 + y^2$$ را با استفاده از نرمافزار متلب رسم کنید. $$x$$ را در بازه ۳- تا ۳ تعریف کنید و $$y$$ را برابر با آن قرار دهید.
پاسخ: برای رسم این نمودار، ابتدا $$x$$ و $$y$$ را به صورت برداری تعریف و سپس شبکهای از نقاط با استفاده از دستور meshgrid میسازیم.
1x1 = linspace(-3, 3);
2x2 = x1;
3[X1, X2] = meshgrid(x1, x2);
4z= X1.^2+X2.^2;
5mesh(X1, X2, z)نمودار رسم شده به شکل زیر خواهد بود:
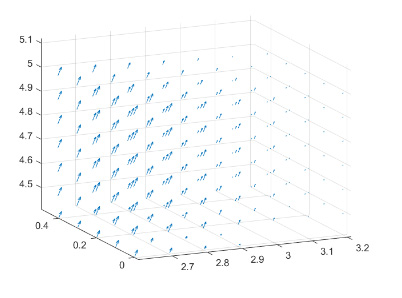
مثال دوم
نمودار برداری، نوعی نمودار است که مؤلفههای جهتدار uvw را با استفاده از مؤلفههای دکارتی xyz میدهد. برای رسم نمودار برداری از دستور quiver3 استفاده میکنیم.
1[x, y, z] = meshgrid(0:0.1:5);
2u= sin(x).*cos(y);
3v= sin(x).*cos(y);
4w= sin(x).*cos(y);
5quiver3(x, y, z, u, v, w);پس از اجرای کد بالا، نمودار رسم شده به شکل زیر خواهد بود:
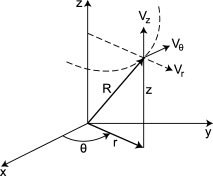
رسم نمودار سه بعدی در مختصات استوانه ای در متلب
در این قسمت در مورد رسم نمودار سهبعدی در مختصات استوانهای صحبت میکنیم. مختصات استوانهای راه دیگری برای بیان موقعیت نقطهای دلخواه در فضای سهبعدی است. در حالت کلی، برای بیان موقعیت نقطه یا بردار در فضای سهبعدی از مختصات دکارتی و مؤلفههای xyz، استفاده میکنیم. برای بیان موقعیت نقطه در مختصات استوانهای از سه مؤلفه استفاده میشود:
- $$r$$: فاصله نقطه تا مبدا مختصات
- $$\theta$$: زاویه خط متصلکننده نقطه و مبدا مختصات با صفحه xy
- $$z$$: ارتفاع نقطه انتخابی
در متلب، برای تبدیل مختصات استوانهای یا قطبی به مختصات دکارتی، از دستور pol2cart استفاده میشود. توجه به این نکته مهم است که مؤلفه z در مختصات دکارتی و استوانهای یکسان است و تغییری نخواهد کرد.
1[x,y,z] = pol2cart(theta,rho,z)دستور فوق، مؤلفههای مختصات استوانهای را به مؤلفههای مختصات دکارتی در سهبعد تبدیل میکند. برای درک بهتر این دستور، آن را به صورت زیر در متلب اجرا کنید.
1[x, y, z] = pol2cart (pi/2, 3, 5)پس از run، خروجی به صورت زیر خواهد بود:
1x =
2
3 1.8370e-16
4
5
6y =
7
8 3
9
10
11z =
12
13 5مقدار بهدست آمده برای x به قدری کوچک است که آن را صفر در نظر میگیریم. سوالی که ممکن است مطرح شود چگونگی تبدیل مختصات دکارتی به مختصات استوانهای است. برای انجام این کار از دستور cart2pol استفاده میکنیم.
1[theta, r, z] = cart2pol(2, -1, 3)
2
3theta =
4
5 -0.4636
6
7
8r =
9
10 2.2361
11
12
13z =
14
15 3در مطالب بالا در مورد چگونگی رسم نمودار سه بعدی در متلب در مختصات دکارتی توضیح دادیم. برای رسم نمودارهای سهبعدی از دستورات surf و mesh استفاده میکنیم. برای رسم نمودار سهبعدی در مختصات استوانهای نیز از این دستورات میتوان استفاده کرد، اما قبل از آن باید مختصات استوانهای را به دکارتی تبدیل کنیم.
برای رسم نمودار سهبعدی در مختصات استوانهای مراحل زیر را طی میکنیم:
- تابعی که باید رسم شود برابر $$z = f (r\, \theta)$$ است.
- $$\theta$$ را به صورت برداری تعریف میکنیم:
1theta = linspace (0, 2*pi)- $$r$$ را به صورت برداری تعریف میکنیم:
1r = linspace (-5, 5)- با استفاده از دستور meshgrid شبکهای برای ورودیهای تعریف شده، ایجاد میکنیم:
1[theta, r] = meshgrid(theta, r)- از تابع استوانهای داده شده، برای ایجاد ماتریسی متشکل از مقدارهای مختلف z استفاده میکنیم.
- تمام مقدارهای بهدست آمده در مختصات استوانهای را با استفاده از دستور pol2cart به مختصات دکارتی تبدیل میکنیم.
- در پایان، نمودار خواسته شده را با استفاده از دستورهای mesh یا surf رسم میکنیم.
پس از آشنایی با گامهای لازم برای رسم نمودار سهبعدی در مختصات استوانهای، مثال سادهای را با یکدیگر حل خواهیم کرد.
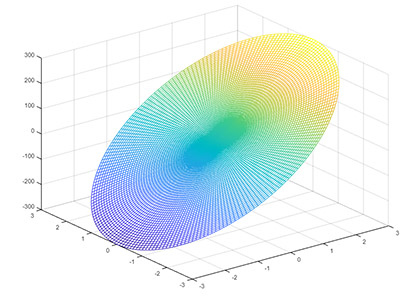
مثال اول رسم نمودار سه بعدی در مختصات استوانه ای
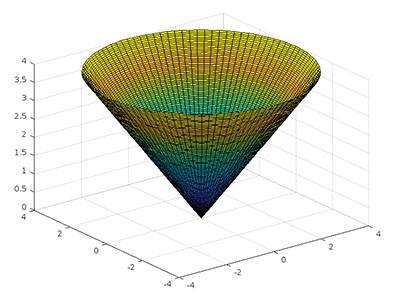
تابع $$z = r \cos \theta$$ را با استفاده از نرمافزار متلب رسم کنید.
پاسخ: برای رسم تابع داده شده، کدی کوتاه به صورت زیر مینویسیم:
1theta = linspace(0, pi);
2r = linspace (-3, 3);
3[theta, r] = meshgrid(theta, r);
4z = r*cos(theta);
5[x, y, z] = pol2cart(theta, r, z);
6mesh(x, y, z)شکل رسم شده به صورت زیر خواهد بود:
مثال دوم رسم نمودار سه بعدی در مختصات استوانه ای
تابع $$z = r$$ را با استفاده از نرمافزار متلب رسم کنید.
پاسخ: گرچه تابع داده شده، تنها به فاصله بستگی دارد، اما برای رسم آن زاویه را نیز تعریف میکنیم. برای رسم آن، کدی مشابه کد نوشته شده برای مثال قبل مینویسیم:
1theta = linspace (0, 2*pi);
2r = linspace(0, 4);
3[theta, r] = meshgrid(theta, r);
4z=r;
5[x,y,z] = pol2cart(theta, r, z);
6surf (x, y, z)شکل رسم شده به صورت زیر خواهد بود:
برای آنکه هر بار برای رسم نمودار سهبعدی در مختصات استوانهای، دستورات بالا را ننویسید، کد لازم را به صورت mfile ذخیره کنید.
1 % script for plotting a cylindrical function.
2 %Theta: change t1 and t2 to set the starting and ending values for theta.
3 t1 = 0;
4 t2 = pi/2;
5 theta = linspace(t1, t2);
6 % r: change r1 and r2 to set the starting and ending values for theta.
7 r1 = -5;
8 r2 = 5;
9 r = linspace(r1, r2);
10 % Create meshgrid for inputs:
11 [theta, r] = meshgrid(theta, r);
12 %Apply the function to create a matrix of z-values. Change the function to match what you want to plot,
13 z = r*cos(theta);
14 % Convert to cartesian and plot using mesh:
15 [x, y, z] = pol2cart(theta, r, z);
16 mesh(x, y, z)رسم نمودار سه بعدی در مختصات کروی در متلب
تاکنون با رسم نمودار سه بعدی در متلب در مختصات دکارتی و استوانهای آشنا شدیم. در ادامه، در مورد رسم نمودار سهبعدی در مختصات کروی صحبت خواهیم کرد. برای توصیف موقعیت نقطهای دلخواه در مختصات کروی، از دو زاویه و شعاع استفاده میشود.
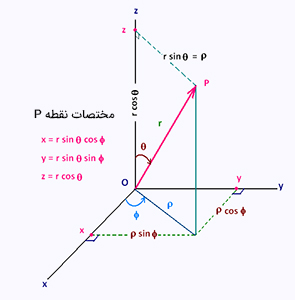
دو زاویه $$\theta$$ و $$\phi$$ در فاصله $$0<\; \theta<\; 2pi$$ و $$0<\; \phi<\; \pi$$ قرار میگیرند. در حالت کلی، اگر نقطه موردنظر در صفحه xy قرار داشته باشد، مقدار $$\phi$$ برابر $$\frac {\pi} {2}$$ و اگر روی محور z و در جهت مثبت آن باشد، مقدار $$\phi$$ برابر صفر است. اما تعریف $$\phi$$ در متلب، متفاوت است.
در این نرمافزار، اگر نقطه در صفحه xy باشد، مقدار $$\phi$$ برابر صفر و اگر روی محور z و در جهت مثبت آن باشد، مقدار $$\phi$$ برابر $$\frac {\pi} {2}$$ خواهد بود. در نتیجه، زاویه $$\phi$$ بین $$\frac {\pi} {2} - $$ و $$\frac {\pi} {2}$$ قرار میگیرد. به این نکته نیز توجه داشته باشید که $$\sin \phi$$ به $$\cos \phi$$ تبدیل میشود، اما نگران فرمولهای تبدیل بین دو مختصات نباشید، زیرا متلب تمام آنها را برای شما انجام خواهد داد.
برای تبدیل مختصات دکارتی به کروی و برعکس در متلب، از دو دستور زیر استفاده میشود:
1[theta, phi. rho] = cart2sph(x, y, z);
2[x, y, z] = sph2cart(theta, phi, rho); برای رسم نمودار سهبعدی در مختصات کروی مراحل زیر را طی میکنیم:
- تابعی که باید رسم شود برابر $$\rho = f( \theta' \phi)$$ است.
- $$\theta$$ را به صورت برداری تعریف میکنیم:
1theta = linspace(0, 2*pi)- زاویه $$\phi$$ را به صورت برداری تعریف میکنیم:
1phi = linspace(-pi/2, pi/2)- با استفاده از دستور meshgrid شبکهای برای ورودیهای تعریف شده، ایجاد میکنیم:
1[theta, phi] = meshgrid(theta, phi)- از تابع کروی داده شده، برای ایجاد ماتریسی متشکل از مقدارهای مختلف $$\rho$$ استفاده میکنیم.
- تمام مقدارهای بهدست آمده در مختصات کروی را با استفاده از دستور sph2cart به مختصات دکارتی تبدیل میکنیم.
مثال اول رسم نمودار سه بعدی در مختصات کروی
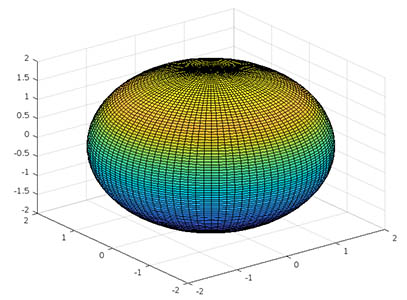
تابع $$\rho = 2$$ را با استفاده از نرمافزار متلب رسم کنید.
پاسخ: برای رسم این نمودار در مختصات کروی، کدی به شکل زیر مینویسیم:
1theta = linspace(0, 2*pi);
2phi = linspace(-pi/2, pi/2);
3[theta, phi] = meshgrid(theta, phi);
4rho = 2;
5[x, y, z] = sph2cart(theta, phi, rho);
6surf(x, y, z)پس از اجرای کد، شکل رسم شده به صورت زیر خواهد بود.
مثال دوم رسم نمودار سه بعدی در مختصات کروی
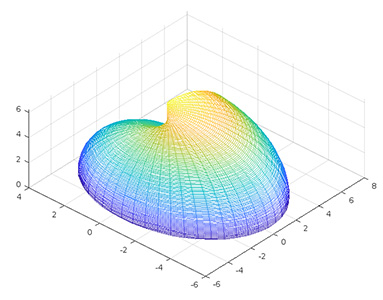
تابع $$\rho = \frac {\theta} {2}$$ را با استفاده از نرمافزار متلب رسم کنید.
پاسخ: برای رسم این نمودار در متلب، کدی مشابه مثال قبل مینویسیم، با این تفاوت که دو زاویه $$\theta$$ و $$\phi$$ را در بازههای متفاوتی نسبت به بازههای استاندارد تعریف شده برای آنها، تعریف میکنیم.
1theta = linspace(0, 4*pi);
2phi = linspace(0, pi/2);
3[theta, phi] = meshgrid(theta, phi);
4rho = theta/2;
5[x, y, z] = sph2cart(theta, phi, rho);
6mesh(x, y, z)نمودار رسم شده به صورت زیر خواهد بود:
رسم نمودارهای میلهای سهبعدی در متلب نیز یکی از بخشهای مهم رسم نمودار سه بعدی در متلب است. در ادامه، رسم این نمودارها را توضیح میدهیم.
رسم نمودار میله ای سه بعدی در متلب
با استفاده از دستورهای زیر میتوان نمودارهای میلهای سهبعدی در متلب رسم کرد:
- bar3(z)
- bar3(y, z)
- bar3(__, width)
- bar3(__, style)
- bar3(__, color)
- bar3(ax, __)
دستور bar3(z)
دستور bar3(z)، نمودار میلهای سهبعدی برای مقدارهای مختلف z رسم میکند. هر میله متناظر با یک مقدار z است.
- برای رسم یک سری نمودار میلهای، z را به عنوان بردار مشخص کنید. برای برداری به طول m، تابع، میلههایی روی محور y از مقدار یک تا m رسم خواهد کرد.
- برای رسم چند سری میلهای، z را به صورت ماتریسی مشخص کنید. هر ستون ماتریس، متعلق به یک سری میله است. برای ماتریس $$m \times n$$، تابع موردنظر، میلههایی روی محور x از مقدار یک تا n و میلههایی روی محور y از مقدار یک تا m، رسم خواهد کرد.
مثال اول دستور bar3(z)
بردار z را با ۵ مقدار تعریف و این مقدارها را به صورت یک سری نمودار میلهای سهبعدی رسم میکنیم. ارتفاع هر میله و مقدار y آن به ترتیب متناظر با مقدار z و اندیس مربوط به آن است.
1z = [50 40 30 20 10];
2figure
3bar3(z)به نمودار میلهای سهبعدی رسم شده در ادامه دقت کنید. همانطور که مشاهده میکنید ارتفاع هر میله برابر مقدار متناظر آن در بردار z است. به عنوان مثال، ارتفاع میله سوم برابر ۳۰ یا همان سومین مؤلفه بردار z است.
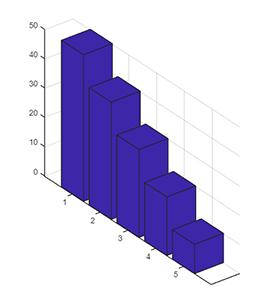
مثال دوم دستور bar3(z)
در مثال اول، با استفاده از دادههای برداری، نمودار میلهای سهبعدی رسم کردیم. در این مثال، z را به صورت ماتریس تعریف و نمودار میلهای متناظر با آن را رسم میکنیم. به عنوان مثال، اگر z را به صورت ماتریسی با ۳ سطر و ۴ ستون به صورت زیر تعریف کنیم:
1z = [1 4 7; 2 5 8; 3 6 9; 4 7 10]
2
3z =
4
5 1 4 7
6 2 5 8
7 3 6 9
8 4 7 10نمودار میلهای متناظر با این ماتریس از ۳ سری برابر تعداد ستونهای آن و هر سری از ۴ میله برابر تعداد سطرهای ماتریس، تشکیل شده است. همچنین، ارتفاع هر میله، برابر مقدار عددی z در ماتریس خواهد بود. نمودار میلهای z به شکل زیر است.
1figure
2bar3(z)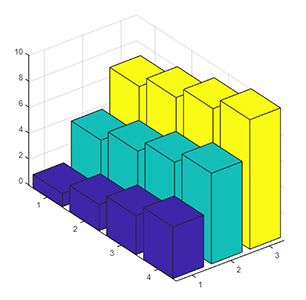
دستور bar3(y, z)
با استفاده از این دستور میتوان نمودارهای میلهای سهبعدی در مکان مشخص شده y و با ارتفاع مشخص z، رسم کرد. اگر z به صورت ماتریسی تعریف شود، مؤلفههای ماتریس در هر سطر، در مکان یکسانی در امتداد محور z قرار میگیرند. برای درک بهتر این مطلب، به دو مثال زیر توجه کنید.
مثال اول bar3(y, z)
y و z را به صورت برداری تعریف میکنیم:
1y = [1950 1960 1970 1980 1990]
2
3y =
4
5 1950 1960 1970 1980 1990
6
7z = [16 8 4 2 1]
8
9z =
10
11 16 8 4 2 1
12قبل از رسم نمودار میلهای، کمی به چگونگی ترسیم آن در متلب فکر و سعی کنید به پرسشهای زیر پاسخ دهید:
- نمودار از چند نمودار میلهای تشکیل شده است؟ تعداد مؤلفههای بردار z تعیینکننده تعداد میلههای رسم شده خواهد بود، بنابراین تعداد میلهها برابر ۵ است.
- هر مؤلفه z نشاندهنده چه چیزی در نمودار است؟ هر مؤلفه، ارتفاع میله را تعیین میکند.
- هر مؤلفه y نشاندهنده چه چیزی در نمودار است؟ هر مؤلفه y، محل قرار گرفتن میله در راستای محور y را مشخص خواهد کرد.
در ادامه، نمودار میلهای را رسم میکنیم.
1figure
2bar3(y, z)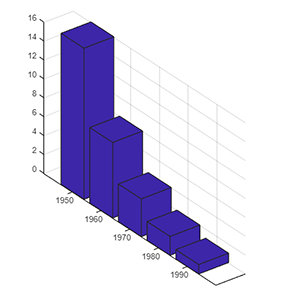
مثال دوم bar3(y, z)
z را به صورت ماتریسی با سه سری مشخص کنید.
1z = [70 50 33 10; 75 55 35 15; 80 60 40 20]
2
3
4z =
5
6 70 50 33 10
7 75 55 35 15
8 80 60 40 20y را نیز به صورت برداری تعریف میکنیم.
1y = [ 2 5 8]
2
3y =
4
5 2 5 8همانند مثال قبل، قبل از رسم این نمودار کمی در مورد آن فکر و سعی کنید به پرسشهای زیر پاسخ دهید:
- این نمودار از چند سری میله تشکیل شده است؟
- هر سری چند میله دارد؟
- ارتفاع هر میله چه مقدار است؟
به نمودار زیر دقت کنید.
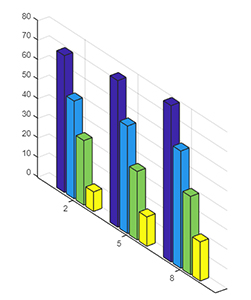
این نمودار از سه سری برابر تعداد سطرهای ماتریس z و هر سری از ۴ میله برابر تعداد ستونهای ماتریس z تشکیل شده است. همچنین، ارتفاع هر میله متناظر با هر یک از مؤلفههای ماتریس z است.
تاکنون با دستورهای bar3(z) و bar3(y, z) آشنا شدهایم. در ادامه، در مورد چگونگی استفاده از رنگ و ضخامت در این دستورها صحبت خواهیم کرد.
استفاده از رنگ و ضخامت در دستور bar3
مجموعهای از مختصات y بین صفر تا $$\pi$$ ایجاد و تابعهای سینوس y را به صورت نمودار میلهای سهبعدی رسم کنید. همچنین، برای نمودارهای میلهای رسم شده رنگ مناسبی انتخاب نمایید.
1y = 0: pi/16: pi;
2z = [sin(y')/4 sin(y')/2 sin(y')];
3figure
4bar3(y, z, 1, 'r')توجه به این نکته مهم است که 'y ترانهاده ماتریس y است. در صورتی که در کد بالا به جای 'y از y استفاده کنیم، کد اجرا نمیشود و با خطای زیر روبرو خواهیم شد.
1Error using bar3
2Y must be the same length as Z.نمودار میلهای سهبعدی کد بالا به شکل زیر خواهد بود:
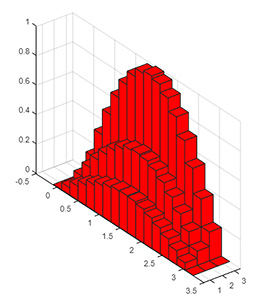
شخصی سازی رنگ ها
ماتریس داده z را به سبک 'stacked' و با ضخامت ۰٫۵، رسم و سطوح رسم شده در b ذخیره میکنیم. در این حالت، b آرایهای متشکل از ۴ مؤلفه است. در ادامه، رنگ هر مؤلفه b را با استفاده از دستور FaceColor ، به دلخواه تغییر میدهیم.
1z = [19 30 21 30; 40 16 32 12]; figure
2b = bar3(z,0.5,'stacked')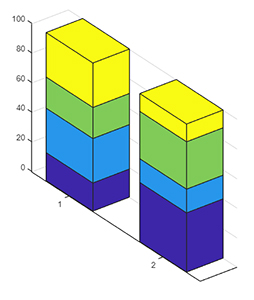
رنگ هر سری نمودار میلهای را با استفاده از دستور FaceColor برای سطح متناظر با b به صورت زیر تغییر میدهیم.
1b(1).FaceColor = 'k';
2b(2).FaceColor = 'white';
3b(3).FaceColor = [.5 .7 .8];
4b(4).FaceColor = [.9 .7 .8];جمعبندی
در این مطلب، با رسم نمودار سهبعدی با استفاده از دستورهای مختلف در متلب آشنا شدیم. در حالت کلی، برای رسم نمودار سه بعدی در متلب، گامهای زیر را طی میکنیم:
- دو بردار $$x_1$$ و $$x_2$$ را با استفاده از دستور linspace تعریف میکنیم.
- با استفاده از دستور meshgrid شبکهای برای ورودیهای تعریف شده، ایجاد میکنیم.
- تابع سهبعدی موردنظر را تعریف میکنیم.
- با استفاده از دستورهای گفته شده برای رسم نمودار سهبعدی، نمودار موردنظر خود را رسم میکنیم.
در ادامه، در مورد رسم نمودارهای میلهای سهبعدی در متلب توضیح دادیم و نمودارهایی را به عنوان نمونه و آشنایی بیشتر، رسم کردیم.










