ضریب شکست و روش عملی محاسبه آن — به زبان ساده

در مقاله «آینه تخت -- به زبان ساده» و مباحث فیزیک پایه دیدیم که نور هنگام ورود به محیطی دیگر، خم شده و یا تغییر مسیر میدهد. در واقع نور در جسم، مسیری متفاوت با مسیر اولیه خود را طی میکند. همچنین به هنگام خارج شدن از جسم دوباره تغییر مسیر داده و در مسیری متفاوت به راه خود ادامه میدهد. این تغییر مسیر که در مرز مشترک دو محیط (مثلا هوا و شیشه) رخ میدهد، شکست نام دارد. پدیده شکست به دلیل تفاوت سرعت نور در دو محیط مختلف رخ میدهد. همانطور که میدانید، سرعت نور در خلأ ثابت بوده و برابر با مقدار است؛ اما نور (فوتونها) در محیطهای مختلف با سرعتهای کمتری نسبت به خلأ حرکت میکند. این امر را میتوان در پارامتری به اسم ضریب شکست توضیح داد.

میزان خم شدن یا انحراف نور از مسیر اولیهاش را که ناشی از این کاهش سرعت است، میتوان بر اساس پارامتری به اسم ضریب شکست محاسبه کرد. ضریب شکست یک جسم، از طریق نسبت سرعت نور در خلأ به سرعت نور در آن محیط محاسبه میشود (). در ادامه این مقاله در نظر داریم تا با زبانی ساده نحوه محاسبه ضریب شکست اجسام شفاف را در قالب آزمایشی ۷ مرحلهای و جالب شرح دهیم.
محاسبه ضریب شکست اجسام شفاف
همانطور که اشاره کردیم، در ادامه میخواهیم ضریب شکست اجسام شفاف تا نیمه شفاف را در طیف مرئی به دست آوریم. توجه داشته باشید که پارامتر ضریب شکست تنها برای سنجش سرعت نور در محیطهای مختلف کاربرد نداشته و پارامتری جامعتر برای تعیین سرعت امواج الکترومغناطیسی در محیطهای مختلف است. همچنین ضریب شکست یک جسم برای طیفهای مختلفی از امواج الکترومغناطیسی متفاوت است و در واقع تابعی از طول موج یا فرکانس موج الکترومغناطیسی است. در مقالات آینده مجله فرادرس، در مطلبی تخصصیتر، بیشتر به بررسی ضریب شکست و عوامل موثر بر آن خواهیم پرداخت.
در صورتی که قصد انجام مراحل زیر را دارید، دقت تمام به نکات ایمنی، به خصوص هنگام استفاده از نور لیزر را داشته باشید. پیشنهاد میکنیم این عمل را در محیط آزمایشگاه و با رعایت استانداردهای مربوطه انجام دهید.
۱. محاسبه پهنا یا عرض جسم
جسمی که میخواهیم ضریب شکست آن را در این آموزش به دست آوریم، شیشه است. قدم اول، محاسبه پهنا یا عرض جسم شفاف است. ممکن است که سازنده جسم به ابعاد آن در کاتالوگ محصول اشاره کرده باشد، اما برای محاسبات دقیقتر و کاهش خطا، بهتر است که یکبار دیگر خود عمل اندازهگیری را انجام دهید.
2. ارسال نور از منبع نقطهای با زاویه 90 درجه
قدم دوم در این آزمایش، ارسال نور تکرنگ (تک فرکانس) از یک منبع نقطهای نور به صورت عمودی و از فاصلهای مشخص، به جسم مد نظر است. میتوانید برای این کار از نشانگرهای (Pointer) لیزری استفاده کنید. متناسب با توان منبع لیزری، نکات ایمنی را رعایت و حتما از عینکهای مخصوص استفاده کنید.
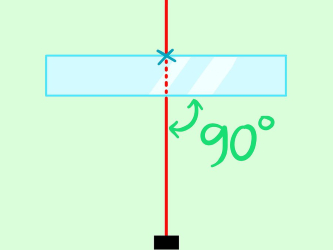
پس از ارسال نور با زاویه ۹۰ درجه (عمودی) به جسم، آن سمت دیگر جسم را که نور در آن ظاهر میشود، علامتگذاری کنید.
3. ارسال نور از منبع نقطهای با زاویهای مشخص
حال منبع نقطهای نور را به سمت راست یا چپ همانند شکل زیر، طوری حرکت دهید که زاویه برخورد نور با جسم، زاویهای حاده () باشد (به شکل دقت کنید). توجه داشته باشید که نقطه برخورد نور در همان نقطهای باشد که در مرحله دوم نور به آن وارد شد.
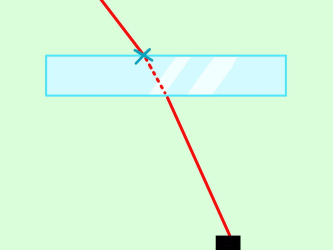
پس از این کار، آن سمت جسم که نور ظاهر میشود را علامت گذاری کنید. همچنین فاصله منبع تا جسم را اندازهگیری کنید. برای راحتی کار میتوانید از دو منبع نوری یکسان (طول موج یکسان) استفاده کنید تا منبع نوری اول که به صورت عمود بر جسم تابیده شده است، سرجای خود ثابت باقی بماند.
4. تعیین مثلث تشکیل شده در هوا
با انجام مرحله دوم و سوم، مطابق با شکل زیر، میتوان فرض کرد که یک مثلث در هوا تشکیل شده است. از آنجایی که فاصله منبع نوری اول که به طور عمودی بر جسم میتابد و فاصله منبع نوری دوم از منبع نوری اول مشخص است، میتوانیم از قانون فیثاغورس ضلع سوم را حساب کنیم.
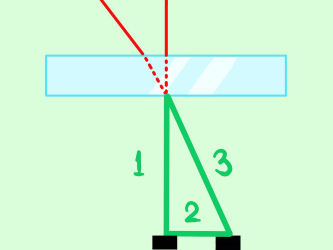
جهت یادآوری، قانون فیثاغورس بیان میکند که مربع وتر (ضلع بزرگتر) با مجموع مربعهای دو ضلع دیگر برابر است. به طور مثال در شکل فوق داریم:
5. تعیین مثلث تشکیل شده در جسم
همانند شکل زیر، میتوان یک مثلث در جسم مذکور در نظر گرفت.
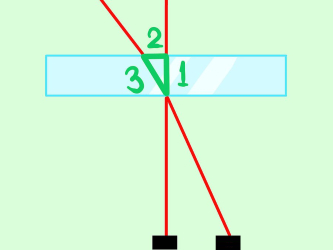
ضلع اول این مثلث، همان پهنای جسم بوده که در مرحله اول آن را اندازه گرفتیم. ضلع دوم نیز از علامتهایی که در مرحله دوم و سوم بر جسم زدیم، قابل محاسبه است. ضلع سوم نیز از قانون فیثاغورس محاسبه میشود.
6. تعیین زاویهها
از آنجایی که طول اضلاع هر دو مثلث قائمالزاویه به صورت کامل مشخص است، میتوانیم با استفاده از قوانین مثلثاثی در مثلث قائمالزاویه به محاسبه زاویههایی که در شکل زیر مشخص شده است، بپردازیم.
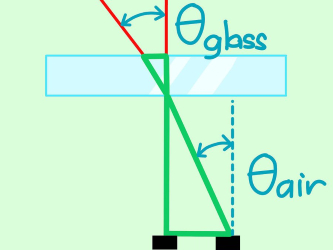
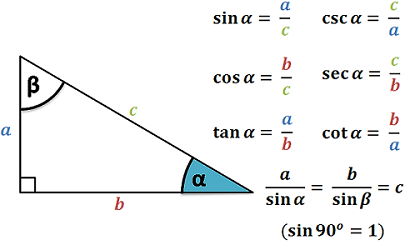
دو زاویهای که در شکل فوق مشخص شدهاند، زوایای تابش () و شکست () نام دارند. جهت یادآوری روابط زیر در یک مثلث قائمالزاویه برقرار هستند:
7. استفاده از قانون اسنل
حال با استفاده از «قانون اسنل» (Snell's law) میتوانیم ضریب شکست جسم مد نظر را به دست آوریم. با یاد داریم که قانون اسنل به صورت زیر است که در آن زاویه تابش و زاویه شکست است.
جهت اینکه درک شهودی بهتری نسبت به قانون اسنل و شکلی که در فوق آورده شده است، داشته باشید، به شکل زیر دقت کنید.
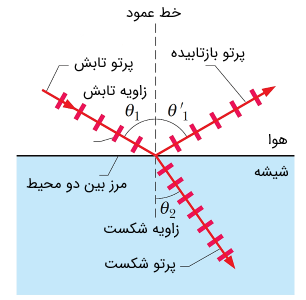
در مقدمه متن بیان کردیم که ضریب شکست، از نسبت سرعت نور در خلأ (که بر طبق نظریه نسبیت خاص اینشتین جزو ثابتهای فیزیکی است)، به سرعت نور در آن محیط نتیجه میشود (). پس مطابق با این گفته ضریب شکست خلأ را برابر با یک در نظر میگیریم. ضریب شکست هوا را نیز با تقریب خیلی خوبی میتوان یک فرض کرد. در نتیجه از قانون اسنل میتوانیم ضریب شکست جسم مذکور را به صورت زیر به دست آوریم:
توجه داشته باشید که شکلهای کارتونی فوق، ممکن است باعث خطا در فهم مسئله شود. به طور مثال، شکل مرحله پنج به گونهای است که به نظر میآید زاویه تابش و شکست یکسان هستند. در واقع نور به هنگام ورود به محیط دوم که ضریب شکستی متفاوت دارم از مسیر ابتدایی خود منحرف میشود. در ادامه ضریب شکست برخی مواد در طول موج 589 نانومتر (نور زرد سدیم) در غالب جدول زیر آورده شده است. به یاد داشته باشید که طول موج خلأ برای تمام طیف الکترومغناطیسی برابر با ۱ است.
| ضریب شکست برخی از مواد مختلف در طول موج | |||
| خلأ | 1 | هوا (دما و فشار ) | 1.00029 |
| آب ۲۰ درجه سانتیگراد | 1.33 | استون | 1.36 |
| اتیل الکل | 1.36 | شیشه (سنگ) کوارتز | 1.46 |
| شیشه معمولی | 1.52 | نمک سدیم کلرید | 1.54 |
| پلیاستر | 1.55 | کربن دیسولفید | 1.63 |
| شیشه flint | 1.65 ~ 1.89 | یاقوت (Sapphire) | 1.77 |
| الماس | 2.42 | روغن سیلیکون | 1.52 |
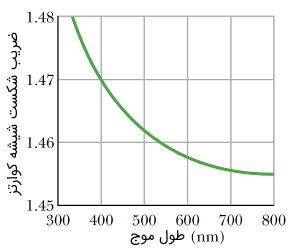
همانطور که پیشتر اشاره کردیم، ضریب شکست مواد تابعی از طول موج (فرکانس) امواج الکترومغناطیسی است. به طور مثال تغییرات ضریب شکست شیشه کوارتز با تغییر طول موج به صورت زیر است:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش فیزیک پایه ۳
- آموزش الکترومغناطیس مهندسی
- مجموعه آموزش مهندسی الکترونیک
- آموزش نرم افزار لومریکال (Lumerical) برای شبیه سازی ادوات نوری – مقدماتی
- فیبر نوری -- به زبان ساده
- آینه مقعر -- به زبان ساده
^^













سلام
ممنون که مطالب علمی رو به زبان ساده بیان می کنید
یه سوال داشتم…
ایا شکست نور در کیفیت یک تصویر موثر است؟
در اثر شکست نور بین عدسی دوربین و هوا
و در تصاویر زیرآب چطور؟
در تصاویر زی اب دو بار شکست نور داریم؟
با سلام؛
خیر
نور به هنگام عبور از لنز دوربین خم میشود و مسیر خود را تغییر میدهد. به همین دلیل تصویری بزرگتر یا کوچکتر ایجاد خواهد شد. نور پس از برخورد به آینه کوچک داخل دوربین نیز منعکس خواهد شد.
با تشکر از همراهی شما با مجله فرادرس
درود بر شما استاد بزرگوار
من میخام شکست نور در سنگ خام الماس سیاه که بلور دارداز طریق بلورها محاسبه کنم آیا امکانش هست ممنون
ممنون خیلی خوب وعالی توضیح داده شده بود
بسیار مفید است وخیلی ممنون بابت زحماتتون