خط تقارن چیست؟ – تعریف محور تقارن به زبان ساده + مثال های تصویری


خط تقارن، مانند آینهای است که بازتاب شکلها را نمایش میدهد. شکلهای دو طرف خط تقارن، هماندازه و قرینه یکدیگر هستند. به عبارت دیگر، خط تقارن، شکل را به دو قسمت مساوی تقسیم میکند. علاوه بر این، با تا زدن شکل از روی این خط، دو قسمت مساوی آن کاملا بر روی یکدیگر منطبق میشوند. بسیاری از شکلهای موجود در طبیعت (صورت موجودات، دانه برف و غیره)، دارای تقارن محوری و خط تقارن فرضی هستند. در این آموزش، به سوال «خط تقارن چیست ؟» پاسخ میدهیم و با حل چندین مثال تصویری، وجود خط تقارن در اشکال هندسی و نحوه رسم این خط را مورد بررسی قرار میدهیم.
تقارن چیست؟
تقارن، یکی از مفاهیم نامآشنا ریاضیات، فیزیک، ادبیات، فلسفه و بسیاری از حوزههای دیگر است. در ریاضیات، تقارن، معمولا به عنوان یکی از ویژگیهای هندسی شکلها معرفی میشود.
به عنوان مثال، تصویر زیر را در نظر بگیرید. در شکل سمت راست، خطی وجود دارد که شکل را به دو قسمت مساوی تقسیم میکند. به این شکل، یک شکل دارای تقارن یا اصطلاحا متقارن میگوییم.

در شکل سمت چپ، هیچ خطی را نمیتوانیم پیدا کنیم که شکل را به دو قسمت مساوی تقسیم کند. بنابراین، این شکل، با عنوان شکل بدون تقارن یا اصطلاحا نامتقارن شناخته میشود. مثال بالا، یکی از انواع تقارن با عنوان تقارن محوری بود. در ادامه، به معرفی بیشتر این نوع تقارن خواهیم پرداخت.
انواع تقارن چیست ؟
تقارن در هندسه به انواع محوری (بازتابی)، چرخشی (مرکزی) و انتقالی تقسیم میشود:
- تقارن چرخشی
- با چرخاندن شکل حول یک نقطه ثابت و به اندازه مشخص، شکل دوباره بر روی خودش منطبق میشود. در تقارن مرکزی (تقارن چرخشی مرتبه دوم)، با چرخاندن شکل به اندازه ۱۸۰ درجه، هیچ تغییری در آن رخ نمیدهد.
- تقارن انتقالی
- با حرکت دادن شکل در یک راستای مشخص، تغییری در شکل به وجود نمیآید.
- تقارن محوری
البته تقارن دیگری با عنوان تقارن لغزشی نیز وجود دارد که ترکیبی از تقارن انتقالی و محوری است. به دلیل، اهمیت تقارن محوری در مبحث خط تقارن، این نوع تقارن را به صورت جداگانه تعریف میکنیم.

تقارن محوری چیست؟
تقارن محوری، یکی از شناخته شدهترین و متداولترین انواع تقارن است. در این نوع تقارن، شکل به دو قسمت مساوی تقسیم میشود و هر قسمت، بازتاب قسمت دیگر را نمایش میدهد. به همین دلیل، به تقارن محوری، تقارن بازتابی نیز میگویند. برای درک تقارن محوری، میتوان از یک آینه استفاده کرد. آینه، وسیلهای است که تصویر اجسام را بازتاب میدهد. تصویر زیر را در نظر بگیرید.

اگر چند قطعه را مانند تصویر بالا در مقابل آینه قرار دهیم، درون آینه، بازتاب آن قطعات به نمایش درمیآید. به این ترتیب، یک شکل با تقارن محوری تشکیل میشود. تقارن محوری و خط تقارن، دو مفهوم جداییناپذیر هستند. هر جایی که تقارن محوری وجود داشته باشد، قطعا یک خط تقارن نیز وجود خواهد داشت. با این تعاریف و توضیحات ارائه در بخشهای قبلی، اکنون میتوانیم به سراغ تعریف خط تقارن یا همان محور تقارن برویم.
خط تقارن یا محور تقارن چیست؟
«خط تقارن» (Line of Symmetry) یا «محور تقارن» (Axis of Symmetry)، خطی است که با تا زدن شکل از روی آن، شکل به دو نیمه مساوی تقسیم میشود؛ به طوری که این دو نیمه، همدیگر را کاملا میپوشانند. به عنوان مثال، پروانه نمایش داده شده در تصویر زیر را در نظر بگیرید.

پروانه، حشرهای با شکل متقارن (تقارن محوری) است. بر روی تصویر بالا، خطی را در فاصله بین دو شاخک پروانه و همراستا با بدن آن رسم میکنیم.
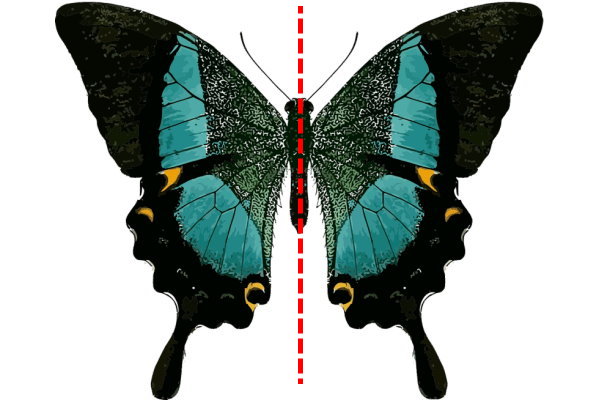
خط بالا، پروانه را به دو قسمت مساوی تقسیم میکند. اکنون، سمت راست تصویر را از روی خط تا میزنیم.

به این ترتیب، هر دو طرف تصویر پروانه، کاملا بر روی هم منطبق میشوند. به خط رسم شده، خط یا محور تقارن شکل پروانه میگویند. اغلب شکلهای موجود در طبیعت، دارای تقارن محوری و خط تقارن فرضی هستند. تصویر زیر، نمونه دیگری از تقارن محوری و خط تقارن در طبیعت را نمایش میدهد. در برگ درختان و گیاهان، محور تقارن به خوبی قابل مشاهده است.

بسیاری از سازههای مصنوعی نیز به تقلید از طبیعت، با تقارن محوری و خط تقارن ساخته میشوند؛ چراکه تقارن، به شکلها زیبایی میبخشد. تصویر زیر، تاج محل، یکی از جاذبههای گردشگری کشور هند را نمایش میدهد.

در این تصویر، خط تقارن فرضی این سازه رسم شده است. هر شکلی که در یک سمت محور تقارن تاج محل مشاهده میکنید، در سمت دیگر آن نیز با همان ابعاد وجود دارد.
انواع خط تقارن چه هستند ؟
خطوط تقارن، معمولا بر اساس جهتگیری آنها تقسیمبندی میشوند. بر این اساس، انواع خطوط تقارن عبارت هستند از:
- خط تقارن افقی
- خطی که شکل را به صورت افقی به دو قسمت مساوی و قرینه تقسیم میکند. حرف «C» در زبان انگلیسی، دارای خط تقارن افقی است.
- خط تقارن عمودی
- خطی که شکل را به صورت عمودی به دو قسمت مساوی و قرینه تقسیم میکند. اعداد «۷» و «۸» در زبان فارسی، دارای خط تقارن عمودی هستند.
- خط تقارن مورب
- خطی که شکل را به صورت مایل به دو قسمت مساوی و قرینه تقسیم میکند. شکل ستاره «*»، دارای خط تقارن مورب است. البته این شکل میتواند خط تقارن افقی و عمودی نیز داشته باشد.
مثال ۱: تشخیص وجود خط تقارن در شکل ها
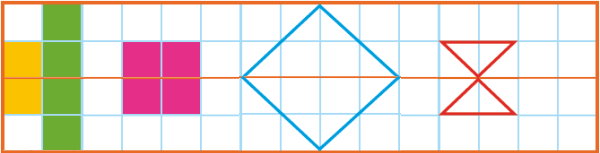
کدامیک از شکل های زیر خط تقارن دارند؟

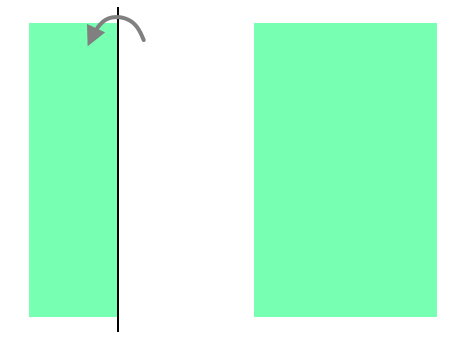
خط تقارن، شکل را به دو قسمت مساوی تقسیم میکند. علاوه بر این، اگر شکل را از روی خط تقارن تا بزنیم، این دو قسمت مساوی بر روی یکدیگر قرار میگیرند. برای شروع حل مسئله، شکل سبز را در نظر بگیرید. با بررسی این شکل، حداقل یک خط را میتوانیم پیدا کنیم که ویژگی خط تقارن را داشته باشد. به عنوان مثال، خط زیر، یکی از خطوط تقارن شکل سبز را نمایش میدهد.

اگر شکل سبز را از روی خط تقارنش تا بزنیم، هر دو قسمت، دقیقا بر روی یکدیگر قرار میگیرند. بنابراین، این شکل، خط تقارن دارد.
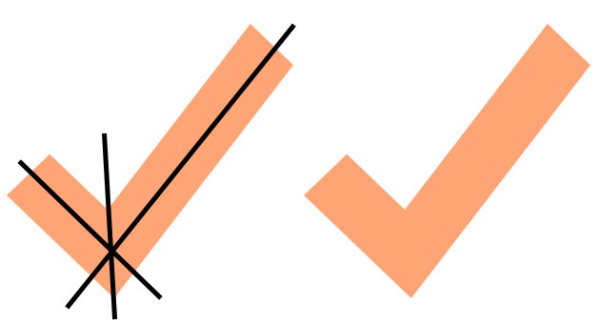
شکل نارنجی، خط تقارن ندارد. در این شکل، هیچ خطی را نمیتوانیم پیدا کنیم که آن را به دو قسمت مساوی تقسیم کند. به عنوان مثال، اگر شکل نارنجی را از روی خطوط نمایش داده شده در تصویر زیر یا هر خط دیگری تا بزنیم، بخشهای دو طرف خط بر روی یکدیگر منطبق نمیشوند.
مثال ۲: بررسی صحت خط تقارن شکل ها
تمام خطهای زیر، شکل را به دو قسمت مساوی تقسیم میکنند. با توجه به این نکته، کدامیک از آنها خط تقارن نیست؟
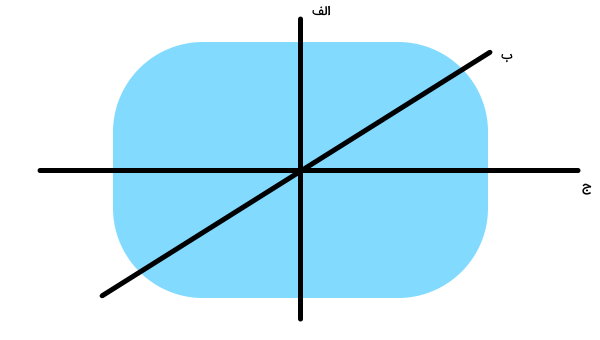
بر اساس تعریف خط تقارن، اگر شکلی را از روی خط تقارنش تا کنیم، بخشهای دو طرف خط، یکدیگر را به طور کامل میپوشانند. به این ترتیب، برای تشخیص خط تقارن، شکل را از روی خط رسم شده تا میزنیم. این کار را از خط (لف) شروع میکنیم.

خط (الف)، شکل را به دو قسمت مساوی تقسیم میکند. اکنون، شکل را از روی این خط تا میزنیم.

همانطور که مشاهده میکنید، هر دو طرف خط به طور کامل یکدیگر را میپوشانند. بنابراین، خط (الف)، خط تقارن است. اکنون به سراغ خط (ب) میرویم.
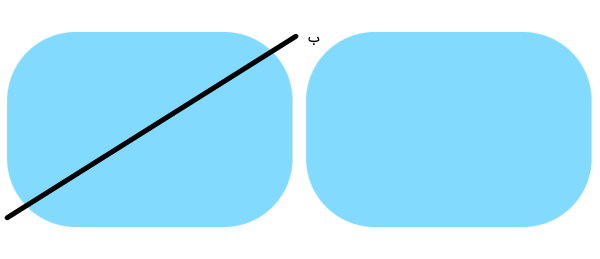
خط (ب) نیز شکل را به دو قسمت مساوی تقسیم میکند. شکل را از روی این خط تا میزنیم.
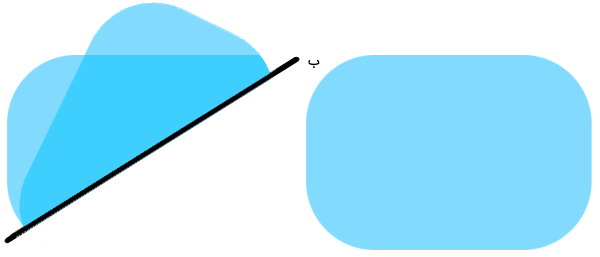
همانطور که مشاهده میکنید؛ با تا زدن شکل از روی خط (ب)، دو طرف خط به طور کامل همدیگر را نمیپوشانند. بنابراین، خط (ب)، خط تقارن نیست. در نهایت، نوبت به بررسی خط (ج) میرسد. خط (ج) نیز مانند خطوط (الف) و (ب)، شکل را به دو قسمت مساوی تقسیم میکند.
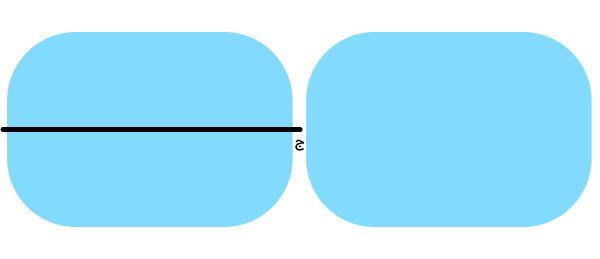
شکل را از روی خط (ج) تا میزنیم. به این ترتیب، هر دو طرف خط، به طور کامل بر روی یکدیگر منطبق میشوند. در نتیجه، خط (ج)، خط تقارن است.
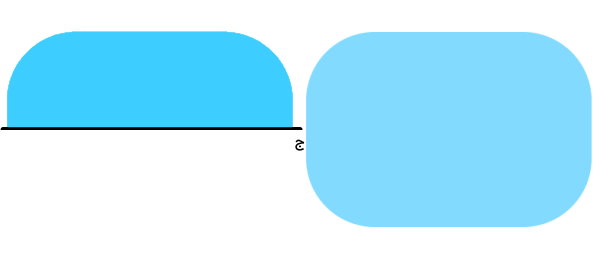
در این مثال، چندین بار اشاره کردیم که تمام خطوط (الف)، (ب) و (ج)، شکل را به دو قسمت مساوی تقسیم میکنند. هدف از اشاره به این موضوع، درک کامل تعریف خط تقارن بود. خط تقارن، نهتنها شکل را به دو قسمت مساوی تقسیم میکند؛ بلکه در صورت تا زدن شکل از روی آن، هر دو قسمت شکل کاملا بر روی هم قرار میگیرند. در بخش «تفاوت محور تقارن و مرکز تقارن»، به توضیح بیشتر این موضوع میپردازیم.
مثال ۳: رسم نیمه دیگر شکل های متقارن
در تصویر زیر، نیمی از چند شکل و محور تقارن آنها رسم شده است. با توجه به خط تقارن، نیمهی دیگر شکلها را رسم کنید.
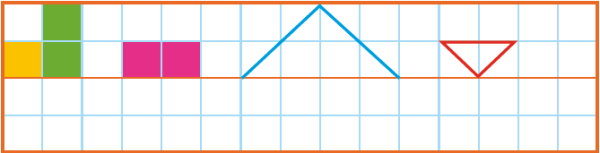
هنگام رسم نیمه دیگر شکلهای دارای تقارن محوری، محور تقارن را مانند یک آینه در نظر بگیرید. هر چیزی که در یک طرف آینه وجود داشته باشد، در طرف دیگر آن نیز با همان اندازه وجود خواهد داشت. شکل اول از سمت چپ را در نظر بگیرید. این شکل، از سه مربع (دو مربع سبز و یک ربع زرد) تشکیل میشود.

برای توضیح روند رسم نیمه دیگر شکلها با توجه به محور تقارن، هر یک از مربعها را با یک عدد مشخص میکنیم.
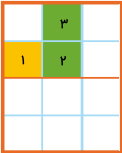
مربع شماره ۱ (مربع زرد)، به محور تقارن چسبیده است. در طرف دیگر محور تقارن و روبهروی این مربع، خانه چسبیده به محور تقارن را زرد میکنیم.

در قدم بعدی، به سراغ مربع شماره ۲ (مربع سبز) میرویم. این مربع نیز به محور تقارن چسبیده است. بنابراین، در طرف دیگر محور تقارن و روبهروی این مربع، خانه چسبیده به محور تقارن را سبز میکنیم.
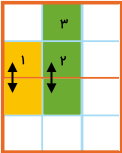
در نهایت، نوبت به مربع شماره ۳ (دیگر مربع سبز) میرسد. این مربع، به اندازه یک خانه از محور تقارن فاصله دارد. در طرف دیگر محور تقارن و روبهروی این مربع، به اندازه یک خانه از محور تقارن فاصله میگیریم و شکل را سبز میکنیم.
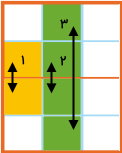
به این ترتیب، نیمه دیگر شکل با توجه به خط تقارن رسم میشود.

همین کار را برای شکلهای دیگر تکرار میکنیم. تصویر زیر، نیمه دیگر تمام شکلهای مورد سوال را نمایش میدهد.
مثال ۴: تعیین محل خط تقارن
تصویر زیر، یک شکل با تقارن محوری را نمایش میدهد. خط تقارن شکل را با استفاده از خطکش رسم کنید.

به منظور توضیح نحوه رسم محور تقارن شکل بالا، گوشههای آن را با حروف مشخص میکنیم.
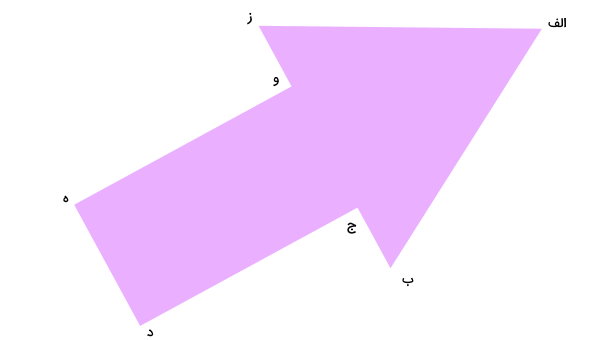
با دقت به شکلهای متقارن، میتوان اجزای شبیه به هم را پیدا کرد. در شکل بالا، گوشههای زیر، شبیه به یکدیگر هستند:
- گوشه (ب) و گوشه (ز)
- گوشه (ج) و گوشه (و)
- گوشه (د) و گوشه (ه)
برای رسم محور تقارن، نقطه میانی فاصله بین گوشههای مشابه را پیدا میکنیم. به عنوان مثال، با استفاده از خطکش، فاصله بین گوشههای (ج) و (و) را به دست میآوریم.
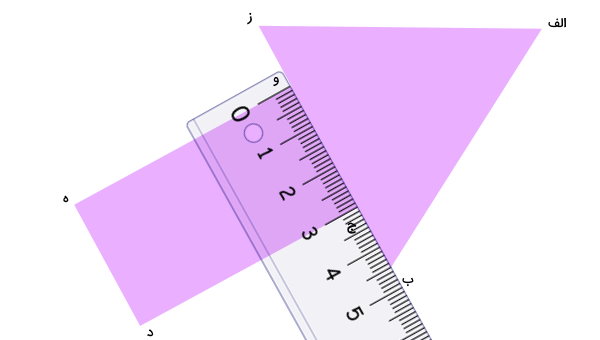
سپس، وسط این فاصله را توسط یک نقطه علامت میزنیم.
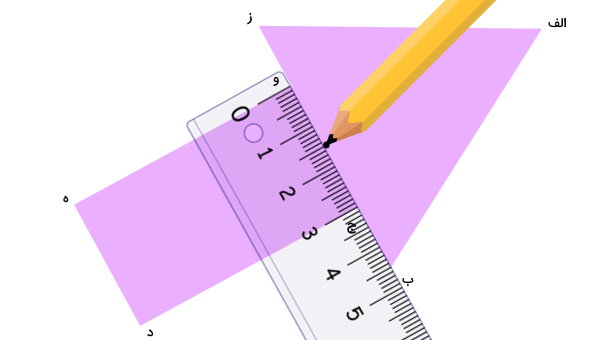
این کار را برای گوشههای (د) و (ه) نیز تکرار میکنیم.
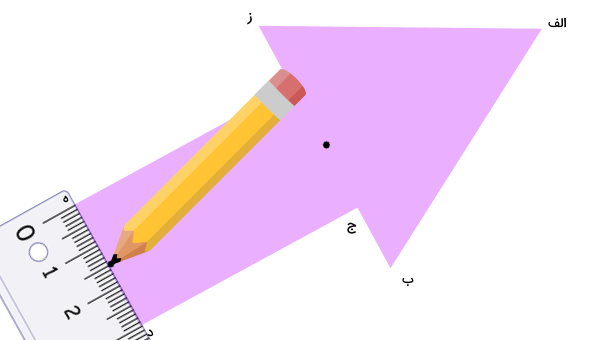
نقاط رسم شده طی مراحل بالا، دو نقطه از خط تقارن هستند.
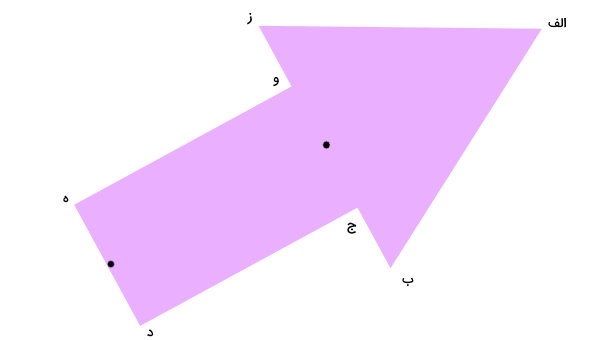
این دو نقطه را به یکدیگر وصل میکنیم.

خط رسم شده، محور تقارن شکل است.

مثال ۵: تعیین نوع خط تقارن شکل ها
در هر یک از شکلهای زیر، نوع خط تقارن را مشخص کنید.
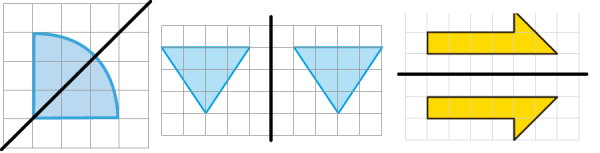
نوع خط تقارن، به راستای آن بستگی دارد. راستای خط تقارن در شکلهای بالا به ترتیب از راست به چپ، افقی، عمودی و مورب است. بنابراین:
- شکل سمت راست، خط تقارن افقی دارد.
- شکل وسط، خط تقارن عمودی دارد.
- شکل سمت چپ، خط تقارن مورب دارد. در برخی از موارد، خط تقارن محوری، با عنوان خط تقارن قطری شناخته میشود.
مثال ۶: رسم خط تقارن در اعداد
کدامیک از اعداد زیر دارای خط تقارن هستند؟
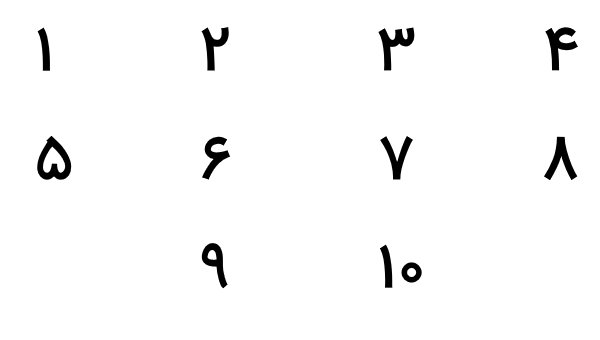
تصویر بالا، شکل اعداد فارسی (۱ تا ۱۰) را نمایش میدهد. با دقت به این شکلها میتوان مشاهده کرد که اعداد ۱، ۵، ۷ و ۸ دارای تقارن محوری هستند. بنابراین، این اعداد، خط تقارن دارند. به عنوان نمونه، عدد ۷ را در نظر بگیرید. خط تقارن این عدد از نوع عمودی بوده و به صورت زیر رسم میشود.

مثال ۷: رسم خط تقارن در حروف انگلیسی
تصویر زیر، حروف انگلیسی را نمایش میدهد. از میان این حروف، کدامیک خط تقارن عمودی، افقی و یا مورب دارد؟

از میان حروف انگلیسی، حرفهای X ،W ،V ،U ،T ،O ،M ،I ،H ،A و Y، دارای خط تقارن عمودی هستند. تصویر زیر، محور تقارن عمودی حرف A را نمایش میدهد.

حرفهای O ،I ،H ،E ،D ،C ،B و X، خط تقارن افقی دارند. در تصویر زیر، خط تقارن حرف B را به عنوان نمونه رسم کردهایم.

از میان حرفهای انگلیسی، فقط حرف O دارای محور تقارن مورب است؛ آن هم در صورتیکه این حرف به شکل یک دایره نوشته شود. برخی از حرفهای دیگر نظیر X ،S ،O ،N ،I ،H و Z نیز دارای تقارن مرکز هستند. اگر این حروف را به اندازه ۱۸۰ درجه دوران دهیم، دوباره به شکل اول خود درمیآیند.
قرینه شکل و خط تقارن چه رابطه ای با یکدیگر دارند ؟
یکی از مفاهیم هندسی که ارتباط بسیار نزدیکی با مفهوم خط تقارن دارد، قرینه شکل است. قرینه یک شکل، بازتاب نقاط آن شکل نسبت به یک خط یا نقطه است.
شکلهای دارای تقارن محوری، از دو بخش قرینه تشکیل میشوند. به عنوان مثال، تصویر زیر را در نظر بگیرید.

تصویر بالا، بازتاب کوه بر روی سطح آب را نمایش میدهد. بازتاب کوه، همان قرینه شکل کوه است. این دو (کوه و قرینه آن) در کنار یکدیگر، شکلی با تقارن محوری را به وجود میآورند. در نتیجه، قرینه شکل، بازتاب شکل نسبت به خط تقارن است. برای مطالعه بیشتر در مورد مبحث قرینه شکل و نحوه رسم قرینه، مطالعه مطلب «قرینه شکل چیست؟ — به زبان ساده + مثال و حل تمرین» را به شما پیشنهاد میکنیم.
خط تقارن در اشکال هندسی
بسیاری از اشکال هندسی شناخته شده، دارای خط یا محور تقارن هستند. در این بخش، به معرفی خط تقارن در انواع شکلهای هندسی میپردازیم.
خط تقارن دایره چیست ؟
قطر دایره، این شکل را به دو قسمت مساوی و قرینه تقسیم میکند.
از اینرو، قطر دایره به عنوان محورهای تقارن آن در نظر گرفته میشود.

دایره، بینهایت قطر دارد. بنابراین، تعداد محورهای تقارن دایره نیز برابر با بینهایت خواهد بود.
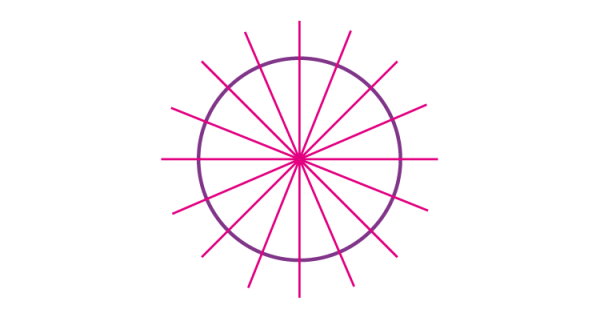
همانطور که از تصویر بالا میتوان مشاهده کرد، خطوط تقارن دایره از نوع عمودی، افقی و مورب هستند.
خط تقارن قطاع دایره چیست ؟
قطاع دایره، شکلی متشکل از دو شعاع و یک کمان دایره است. از شناخته شدهترین قطاعهای دایره میتوان به نیمدایره اشاره کرد. این شکل، با رسم قطر (محور تقارن) و تقسیم دایره به دو قسمت مساوی به وجود میآید.
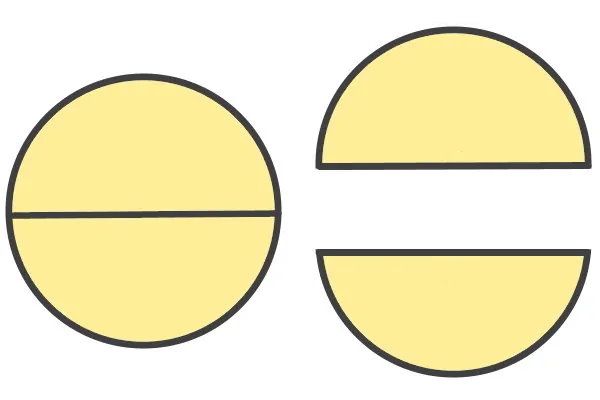
شعاعهای مقابل به کمان نیمدایره، با یکدیگر یک زاویه نیمصفحه را تشکیل میدهند. با رسم نیمساز این زاویه، محور تقارن نیمدایره رسم میشود. نیمدایره، یک محور تقارن دارد.
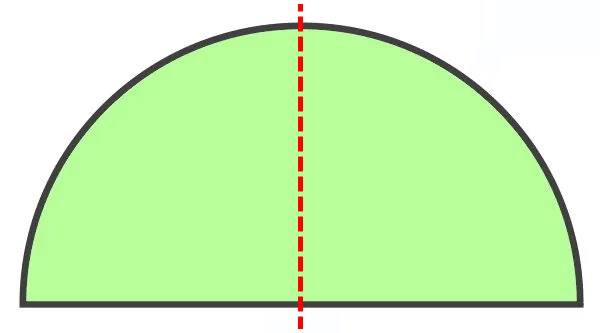
یک ربعدایره (یکچهارم دایره) را در نظر بگیرید. این شکل، یک محور تقارن دارد. در واقع، تعداد خطوط تقارن در تمام قطاعهای دایره برابر با یک است. دقیقا مانند نیمدایره، این خطوط، نیمساز زاویه بین شعاعهای قطاع هستند.
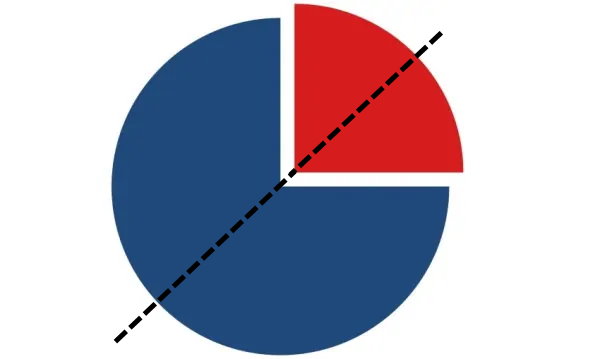
خط تقارن در مثلث چیست ؟
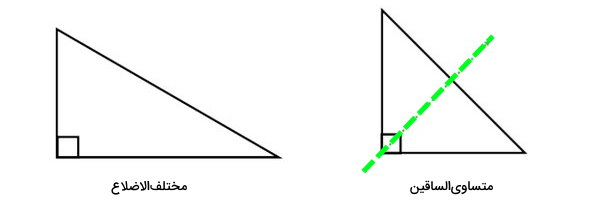
مثلث، یک شکل سهضلعی است. محور تقارن در این شکل، به نوع آن بستگی دارد. مثلثها بر اساس اندازه ضلعهایشان به سه نوع مختلفالاضلاع (ضلعهای نامساوی)، متساویالساقین (دو ضلع مساوی) و متوازیالاضلاع (سه ضلع مساوی) تقسیم میشوند.

مثلثهای مختلفالاضلاع، هیچ خط تقارنی ندارند. برای مثلثهای متساویالساقین میتوان یک خط تقارن رسم کرد. مثلثهای متساویالاضلاع نیز دارای سه خط تقارن هستند. خطوط تقارن مثلثها، نیمساز زوایای داخلی، عمود منصف و ارتفاع ضلعها (قاعدهها) هستند.
خط تقارن مثلث قائم الزاویه چیست ؟
یکی دیگر از انواع شناخته شده مثلثها، مثلث قائمالزاویه است. این مثلث، میتواند مختلفالاضلاع یا متساویالساقین باشد. بنابراین، تعداد محور تقارن مثلث قائم الزاویه برابر با صفر یا یک خواهد بود.
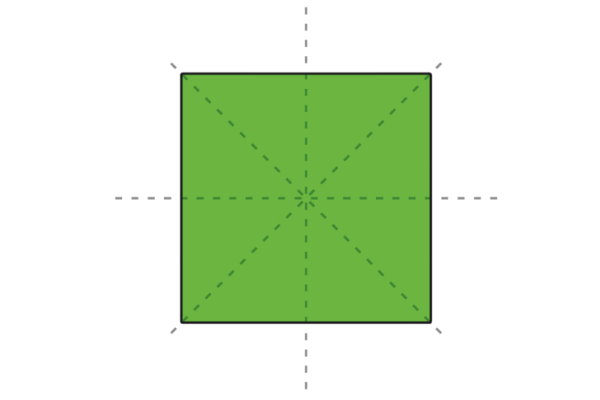
خط تقارن مربع چیست ؟
مربع، شکلی با چهار ضلع مساوی و چهار زاویه ۹۰ درجه است. برای این شکل میتوان چهار خط تقارن رسم کرد. از میان چهار محور تقارن مربع، دو محور تقارن، عمود منصف ضلعها بوده و دو محور تقارن دیگر، بر روی قطرها منطبق هستند.
مربع، یکی از انواع چندضلعیهای منتظم و از انواع خاص متوازیالاضلاع در نظر گرفته میشود. محورهای تقارن این شکلها را نیز در بخشهای بررسی خواهیم کرد.
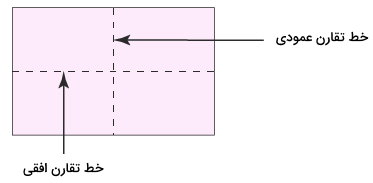
خط تقارن مستطیل چیست ؟
مستطیل، چهار زاویه ۹۰ درجه و چهار ضلع دارد. ضلعهای روبهرویی در این شکل با هم مساوی و موازی هستند. مستطیل، دو محور تقارن دارد. هر دو محور تقارن این شکل، عمود منصفهای طول و عرض آن محسوب میشوند. برخلاف مربع، قطرهای مستطیل، خطوط تقارن این شکل نیستند.
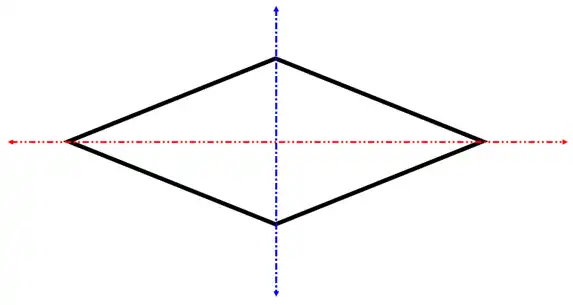
خط تقارن لوزی چیست ؟
لوزی، از چهار ضلع با اندازههای برابر تشکیل میشود. مربع، یکی از حالتهای خاص لوزی با زوایای داخلی قائمه است. قطرهای لوزی، محورهای تقارن این شکل هستند. بنابراین، هر لوزی، دو محور یا خط تقارن دارد.
خط تقارن متوازی الاضلاع چیست ؟
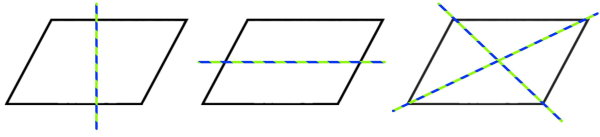
متوازیالاضلاع، یکی از انواع چهارضلعیها است که ضلعهای روبهرویی آن، موازی یکدیگرند. مربع، مستطیل و لوزی، از انواع خاص متوازیالاضلاع در نظر گرفته میشوند. متوازیالاضلاع، محور تقارن ندارد. به عبارت دیگر، هیچ خط عمودی، افقی یا مورب را نمیتوان یافت که این شکل را به دو قسمت مساوی و قرینه تقسیم کند.
خط تقارن ذوزنقه چیست ؟
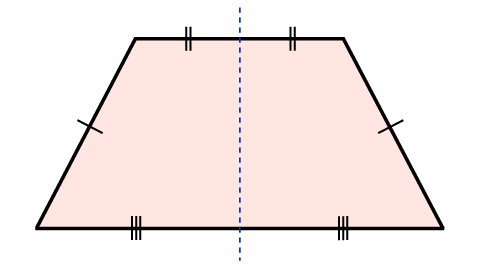
ذوزنقه، یکی دیگر از انواع چهارضلعیها است. این شکل، از دو ضلع موازی و از دو ضلع غیر موازی تشکیل میشود. از انواع ذوزنقهها میتوان به ذوزنقه مختلفالاضلاع و ذوزنقه متساویالساقین اشاره کرد. ذوزنقههای مختلفالاضلاع (حاده، منفرجه و قائمالزاویه)، خط تقارن ندارند؛ اما ذوزنقههای متساویالساقین، دارای یک خط تقارن هستند.
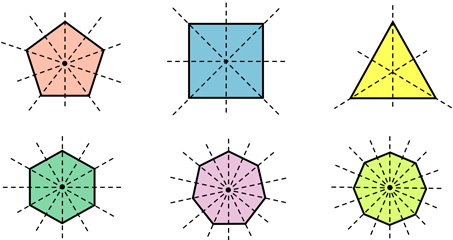
خط تقارن چند ضلعی منتظم چیست ؟
چندضلعیهای منتظم، خطوط شکسته بستهای هستند که از ضلعها و زاویههای داخلی برابر تشکیل میشوند. محور تقارن چند ضلعی منتظم برابر با تعداد ضلعهای آن است. در فردضلعیهای منتظم (مثلث متساویالاضلاع، پنجضلعی منتظم، هفتضلعی منتظم و غیره)، میانه ضلعها، به عنوان محور تقارن در نظر گرفته میشود.
در زوجضلعیهای منتظم (مربع، ششضلعی منتظم، هشتضلعی منتظم و غیره)، قطرها و میانهها، محورهای تقارن هستند.
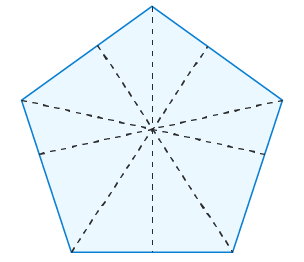
خط تقارن پنج ضلعی منتظم چیست ؟
پنجضلعی منتظم، پنج ضلع با اندازههای برابر دارد. برای رسم محورهای تقارن این چندضلعی منتظم، هر یک از راسها را به مرکز ضلعهای روبهرویی آنها وصل میکنیم. پنجضلعی منتظم، پنج خط تقارن دارد.
خط تقارن شش ضلعی منتظم چیست ؟
ششضلعی منتظم، یکی از شناخته شدهترین انواع چندضلعیهای منتظم است. خطوط تقارن این شکل، از اتصال راسهای روبهرویی به وجود میآید. ششضلعی منتظم، شش خط تقارن دارد.
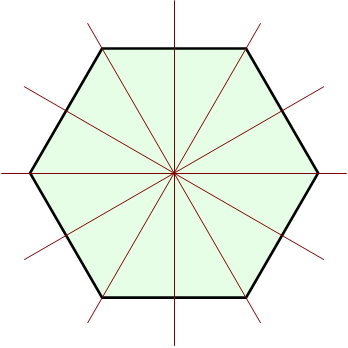
دقیقا مشابه با پنجضلعی و ششضلعی منتظم، هفت ضلعی منتظم دارای هفت خط تقارن و هشت ضلعی منتظم دارای هشت خط تقارن است. به عبارت دیگر، n چندضلعی منتظم، n خط تقارن دارد.
خط تقارن چند ضلعی غیر منتظم چیست ؟
در چندضلعیهای غیرمنتظم، اندازه تمام ضلعها و زاویهها با یکدیگر برابر نیست. به عنوان مثال، مستطیل، با وجود چهار زاویه قائمه، یک چندضلعی غیرمنتظم محسوب میشود؛ چراکه تمام ضلعهای آن، اندازههای برابر ندارند. لوزی نیز با وجود چهار ضلع هماندازه، به دلیل برابر نبودن تمام زاویههای داخلی، یک چندضلعی غیرمنتظم در نظر گرفته میشود. در بخشهای قبلی، با خط تقارن این نوع چندضلعیها آشنا شدیم.
اغلب چندضلعیهای غیر منتظم، خط تقارن ندارند. به عنوان مثال، ششضلعی نمایش داده شده در تصویر زیر، متقارن نیست. بنابراین، هیچ خط تقارنی را نمیتوان برای آن رسم کرد.
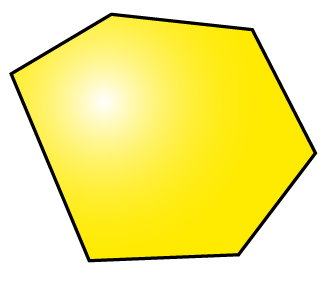
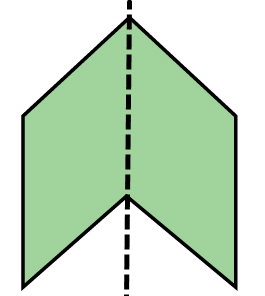
برخلاف شکل بالا، ششضلعی نمایش داده شده در تصویر زیر، با وجود غیرمنتظم بودن، متقارن است.

برای ششضلعی غیرمنتظم بالا میتوانیم یک خط تقارن رسم کنیم.
خط تقارن ستاره چیست ؟
ستاره، یکی از انواع چندضلعیهای مقعر با ضلعهای هماندازه است. خط تقارن این شکلها، از روی دو راس مقابل به هم میگذرد. تعداد خطوط تقارن ستاره، با تعداد پرهای آن برابری میکند. به عنوان مثال، یک ستاره ششپر، شش خط تقارن دارد.
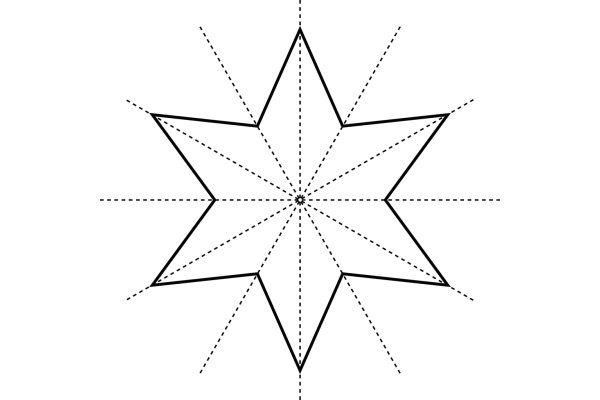
خط تقارن زاویه چیست ؟
زاویه، شکلی متشکل از دو ضلع و یک راس است. تصویر زیر، اجزای یک زاویه را نمایش میدهد.
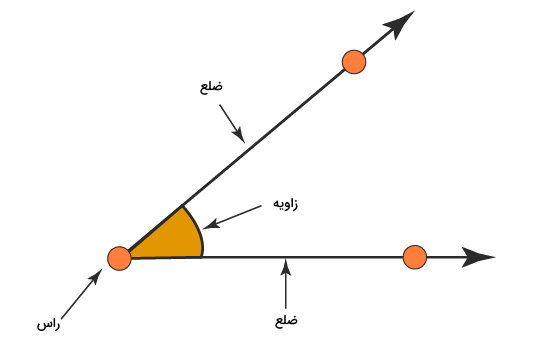
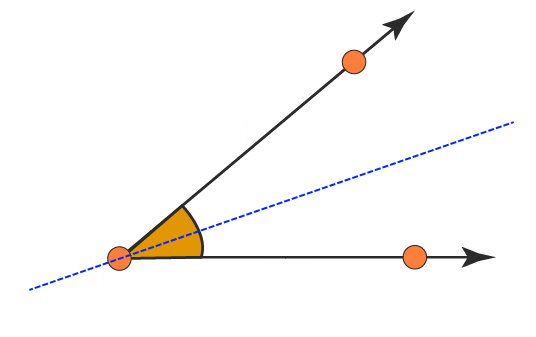
در هر زاویه، امکان رسم محور تقارن وجود دارد. با رسم این محور، زاویه، به دو زاویه مساوی تقسیم میشود. به عبارت دیگر، خط تقارن زاویه، نیمساز آن است.
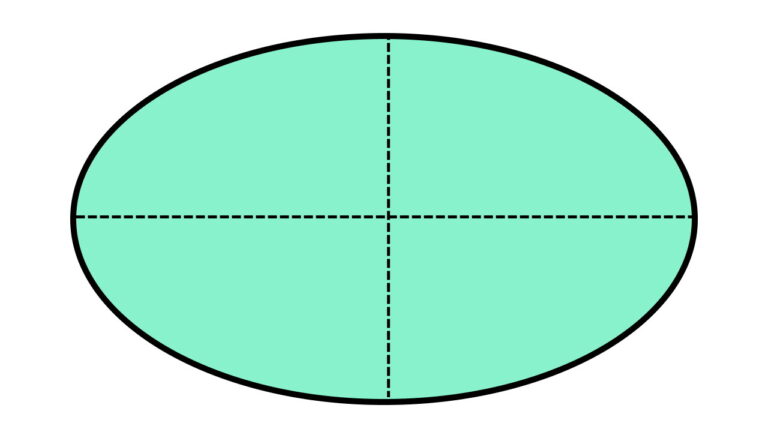
خط تقارن بیضی چیست ؟
بیضی، منحنی بستهای به شکل یک دایره کشیده شده یا فشرده شده است. تصویر زیر، اجزای مختلف یک بیضی افقی را نمایش میدهد. محورهای اصلی و فرعی بیضی، پارهخطهایی هستند که از مرکز این شکل عبور میکنند. این محورها، به عنوان بزرگترین و کوچکترین قطر بیضی شناخته میشوند.
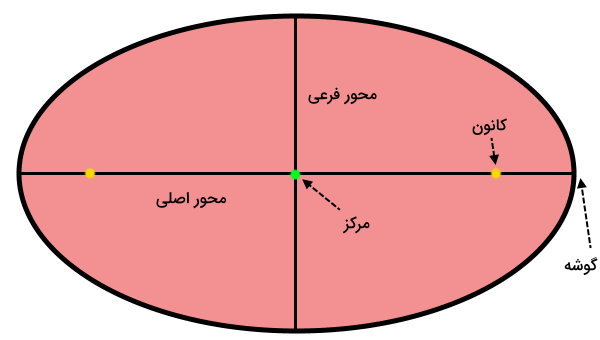
قطرهای اصلی و فرعی، بیضی را به دو قسمت مساوی و قرینه تقسم میکنند. از اینرو، قطرهای بیضی، خط تقارن این شکل هستند. در نتیجه، هر بیضی از دو خط یا محور تقارن تشکیل میشود.
خط تقارن سهی چیست ؟
سهمی، نمایش تصویری معادله درجه دو در دستگاه مختصات است. سهمیها از اجزایی نظیر منحنی، خط هادی، کانون، راس و محور تقارن تشکیل میشوند.
محور یا خط تقارن سهمی، خط مستقیمی است که منحنی آن را به دو قسمت مساوی و متقارن تقسیم میکند. هر سهی، یک محور تقارن دارد.
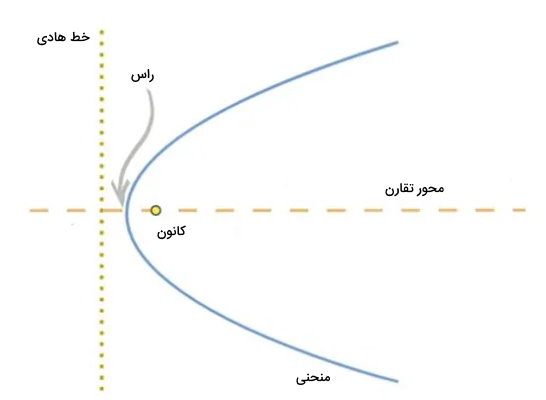
سهمیها به چهار نوع افقی، عمودی، چپگرد و راستگرد تقسیم میشوند. محور تقارن سهمی، نوع آن را تعیین میکند. به عنوان مثال، تصویر بالا، یک سهمی افقی را نمایش میدهد. شیب محور تقارن این سهمی برابر با صفر است. تصویر زیر، یک سهمی عمودی را نشان میدهد. شیب محور تقارن این سهمی، تعریف نشده است.
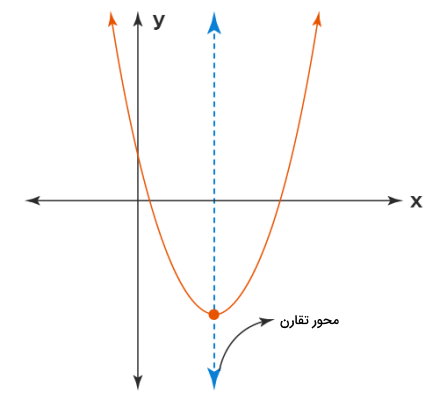
معادله خط تقارن سهمی
به محل برخورد محور تقارن با منحنی، راس سهمی میگویند. مختصات راس سهمی، یکی از پارامترهای مهم در تعیین معادله خط تقارن است. اگر مانند تصویر بالا، جهتگیری سهمی به سمت پایین یا بالا باشد، محور تقارن، یک خط عمودی خواهد بود. در این حالت، معادله خط تقارن، معادله یک خط عمودی است که از راس سهمی میگذرد.
در صورت جهتگیری رو به راست یا چپ سهمی، محور تقارن، یک خط افقی خواهد بود. در این حالت، معادله خط تقارن، معادله یک خط افقی است که از راس سمی عبور میکند. در دستگاه مختصات x-y، داریم:
- معادله خط تقارن سهمی عمودی به راس برابر با است.
- معادله خط تقارن سهمی افقی به راس برابر با است.
معادله سهمی معمولا به فرم استاندارد یا بر حسب راس نوشته میشود. در ادامه، به معرفی فرمول خط تقارن سهمی بر اساس این معادلات میپردازیم.
فرم استاندارد معادله سهمی و خط تقارن
فرم استاندارد معادله سهمی عبارت است از:
ضرایب معادله بالا، اعداد حقیقی هستند. بر اساس این معادله، فرمول محور تقارن سهمی به صورت زیر نوشته میشود:
معادله سهمی و خط تقارن بر حسب راس
معادله سهمی بر حسب راس عبارت است از:
، مختصات راس سهمی را نمایش میدهد. بر این اساس، فرمول محور تقارن سهمی به صورت زیر نوشته میشود:
مثال ۸: پیدا کردن معادله خط تقارن سهمی
معادله خط تقارن سهمی زیر را پیدا کنید:
معادله سهمی بالا به فرم استاندارد نوشته شده است. بنابراین داریم:
معادله محور تقارن با توجه به فرم استاندارد معادله سهمی، از فرمول زیر به دست میآید:
ضرایب معلوم را درون فرمول بالا قرار میدهیم:
جدول خط تقارن شکل های هندسی
جدول زیر، تعداد خطهای تقارن برخی از شکلهای هندسی را نمایش میدهد.
| عنوان شکل | تعداد محور تقارن | |
| سهضلعی | مثث مختلف الاضلاع | ۰ |
| مثلث قائم الزاویه |
۰ (مختلفالاضلاع) ۱ (متساویالساقین) | |
| مثلث متساوی الساقین | ۱ | |
| مثلث متساوی الاضلاع | ۳ | |
| چهارضلعی | متوازی الاضلاع | ۰ |
| مستطیل | ۲ | |
| لوزی | ۲ | |
| ذوزنقه مختلف الاضلاع | ۰ | |
| ذوزنقه قائم الزاویه | ۰ | |
| ذوزنقه متساوی الساقین | ۱ | |
| مربع | ۴ | |
| چندضلعی منتظم | سه ضلعی منتظم | ۳ |
| چها ضلعی منتظم | ۴ | |
| پنج ضلعی منتظم | ۵ | |
| شش ضلعی | ۶ | |
| هفت ضلعی منتظم | ۷ | |
| هشت ضلعی منتظم | ۸ | |
| قطاع دایره | ربع دایره | ۱ |
| نیمدایره | ۱ | |
| دایره کامل | بینهایت | |
| بیضی | ۲ | |
تفاوت محور تقارن و مرکز تقارن
در تقارن مرکزی، نقطهای وجود دارد که با دوران شکل به اندازه ۱۸۰ درجه حول آن نقطه، شکل دوباره بر روی خودش منطبق میشود. به عبارت دیگر، با چرخش ۱۸۰ درجهای شکل حول یک نقطه خاص، تغییری در آن رخ نمیدهد. به این نقطه خاص، «مرکز تقارن» (Center of Symmetry) میگویند. تصویر زیر را در نظر بگیرید. این تصویر، شکلی مشابه با حرف S در زبان انگلیسی را نمایش میدهد.
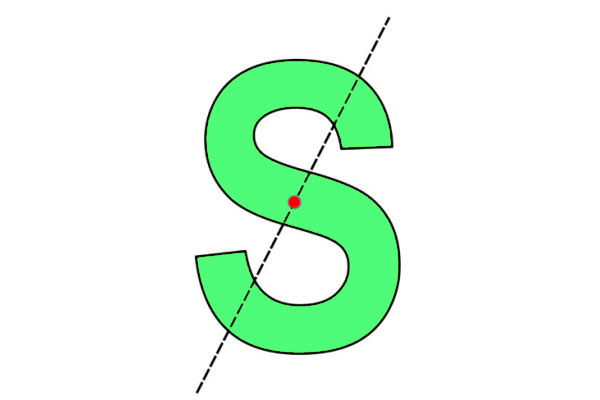
نقطه قرمز در تصویر بالا، مرکز تقارن شکل است. اگر شکل را به اندازه ۱۸۰ درجه حول نقطه قرمز دوران دهیم، دقیقا همین شکل به وجود میآید. خط گذرنده از مرکز تقارن، شکل را به دو قسمت مساوی تقسیم میکند. تا به اینجا، این ویژگی، تفاوتی با ویژگی خط تقارن ندارد. با این وجود، اگر شکل را از روی خط نمایش داده شده در تصویر بالا تا بزنیم، نتیجه زیر حاصل میشود.
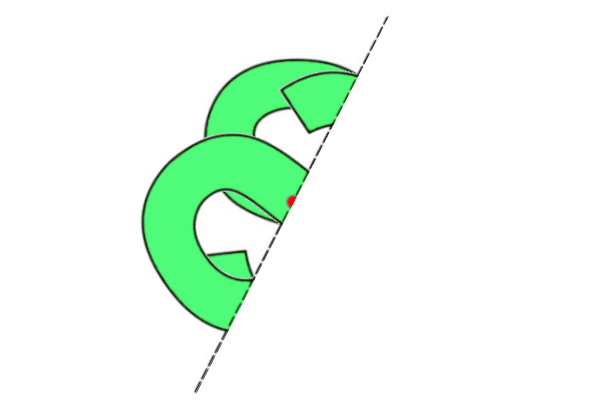
همانطور که مشاهده میکنید، با تا زدن شکل از روی خط گذرنده از مرکز تقارن، دو طرف آن بر روی هم منطبق نشدند. تفاوت خط تقارن و نقطه تقارن نیز در همین ویژگی است.
سوالات متداول در رابطه با خط تقارن در هندسه
در این بخش، به برخی از سوالات پرتکرار در رابطه با خط یا محور تقارن به طور مختصر پاسخ میدهیم.
خط تقارن یعنی چه؟
خطی که یک شکل را به دو قسمت مساوی تقسیم کند و با تا زدن شکل از روی آن، هر دو قسمت مساوی کاملا بر هم قرار گیرند، خط یا محور تقارن است.
مربع چند خط تقارن دارد ؟
تعداد محورهای تقارن مربع برابر با چهار است.
مستطیل چند خط تقارن دارد ؟
مستطیل، دو محور تقارن دارد.
دایره چند خط تقارن دارد ؟
تعداد محورهای تقارن دایره برابر با بینهایت است.
مثلث چند خط تقارن دارد ؟
سه محور تقارن در مثلث متساویالاضلاع، یک محور تقارن در مثلث متساویالساقین و صفر محور تقارن در باقی مثلثها وجود دارد.
متوازی الاضلاع چند خط تقارن دارد ؟
متوازیالاضلاع، هیچ خط تقارنی ندارد.
کدام شکل خط تقارن ندارد ؟
از میان شکلهای معروف هندسی، متوازیالاضلاع، مثلث مختلفالاضلاع، ذوزنقه مختلفالاضلاع و ذوزنقه قائم الزاویه، محور تقارن ندارند.
هر n ضلعی منتظم چند محور تقارن دارد ؟
هر n ضلعی منتظم، n خط تقارن دارد. به عنوان مثال، یک هفت ضلعی منتظم، ۷ خط تقارن دارد.
در کدام شکل قطر خط تقارن نیست ؟
از میان شکلهای معروف هندسی، در متوازیالاضلاع، ذوزنقه، مستطیل و فردضلعیهای منتظم، قطر خط تقارن نیست.
کدام چهار ضلعی خط تقارن ندارد ؟
متوازیالاضلاع، خط تقارن ندارد.
کدام مثلث سه خط تقارن دارد ؟
مثلث متساوی الاضلاع سه خط تقارن دارد.
پنج ضلعی چند خط تقارن دارد ؟
پنجضلعی منتظم، 5 محور تقارن دارد.
شش ضلعی چند خط تقارن دارد ؟
ششضلعی منتظم، ۶ محور تقارن دارد.
بیضی چند خط تقارن دارد ؟
بیضی، ۲ خط تقارن دارد.
فرق خط تقارن با محور تقارن چیست ؟
خط تقارن، همان محور تقارن است. این خط با عنوان خط بازتاب نیز شناخته میشود.
فرق خط تقارن و قطر در چیست ؟
قطر، پارهخطی است که دو گوشه غیر مجاور در یک چندضلعی را به یکدیگر وصل میکند. برخی از قطرها، خط تقارن چندضلعی نیز هستند. با این وجود، هر قطری، خط تقارن نیست.
فرق خط تقارن با قرینه چیست ؟
قرینه، شکلی است که در طرفین خط تقارن قرار دارد. خط تقارن یک شکل، آن شکل را به دو قسمت مساوی و قرینه تقسیم میکند.
هر شکل چند محور تقارن دارد ؟
شکلهای نامتقارن، محور تقارن ندارند. دایره، بیشمار محور تقارن دارد. شکلهای متقارن، بین ۰ تا بینهایت محور تقارن دارند.
به خط تقارن زاویه چه میگویند ؟
به محور تقارن هر زاویه، نیمساز آن زاویه میگویند.









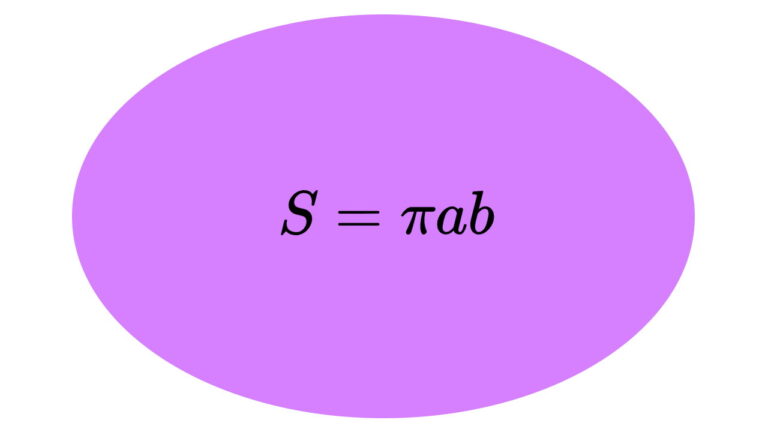

عالی بود 👌🏻