فاصله نقطه از خط – به زبان ساده

در آموزش‌های قبلی از مجموعه مطالب ریاضی مجله فرادرس، با روش محاسبه فاصله دو نقطه از یکدیگر آشنا شدیم. در این آموزش، روش محاسبه فاصله نقطه از خط را بیان می‌کنیم.

منظور از فاصله نقطه $$P$$ از خط $$L$$ کوتاه‌ترین فاصله بین $$P$$ و $$L$$ است؛ این فاصله حداقل طول لازم برای حرکت از نقطه $$P$$ به یک نقطه روی خط $$L$$ است. در واقع، این مسیر با طول حداقل را می‌توان به عنوان پاره‌خط عمود بر $$L$$ نشان داد.

تعریف فاصله نقطه از خط

در مطالب پیشین مجله فرادرس با مفاهیمی مانند نقطه، خط و صفحه آشنا شدیم. برای یک نقطه و یک خط (یا یک صفحه در فضای سه‌بعدی)، از نظر فنی می‌توان تعداد نامحدودی خط بین یک نقطه و خط یا یک نقطه و صفحه رسم کرد. اکنون سؤال این است که کدام‌یک فاصله «صحیح» بین نقطه و خط یا نقطه و صفحه را به ما می‌دهد؟ وقتی می‌گوییم فاصله، منظورمان کوتاه‌ترین فاصله نقطه از خط یا صفحه است. این اتفاق وقتی می‌افتد که خطِ بین نقطه و خط یا صفحه، بر آن‌ها عمود باشد.

اما چرا کوتاه‌ترین پاره‌خط بین نقطه و خط، خط عمود است؟ این امر به این دلیل است که وتر طولانی‌ترین ضلع در مثلث قائم‌الزاویه است. اگر خط عمود را از نقطه به خط رسم کنیم، هر پاره‌خط دیگری که از نقطه به خط وصل می‌شود وتر مثلث خواهد بود و واضح است که بزرگ‌تر از خط عمود است. این گفته همیشه درباره مثلث قائم‌الزاویه صحیح است.

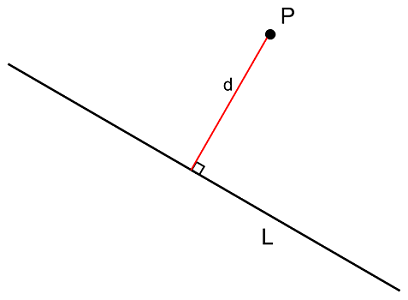
مثال: فاصله نقطه $$P$$ از خط $$P$$ در شکل زیر چقدر است؟

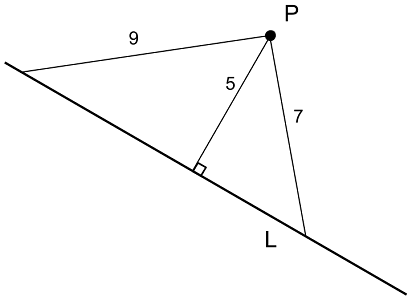
پاسخ: طول هر پاره‌خط بین نقطه و خط متفاوت است، اما طبق تعریف فاصله نقطه از خط به دنبال طول پاره‌خطی هستیم که بر $$L$$ عمود است. به عبارت دیگر، کوتاه‌ترین فاصله بین آن‌ها است و در نتیجه، جواب $$5$$ خواهد بود.

فرمول فاصله نقطه از خط

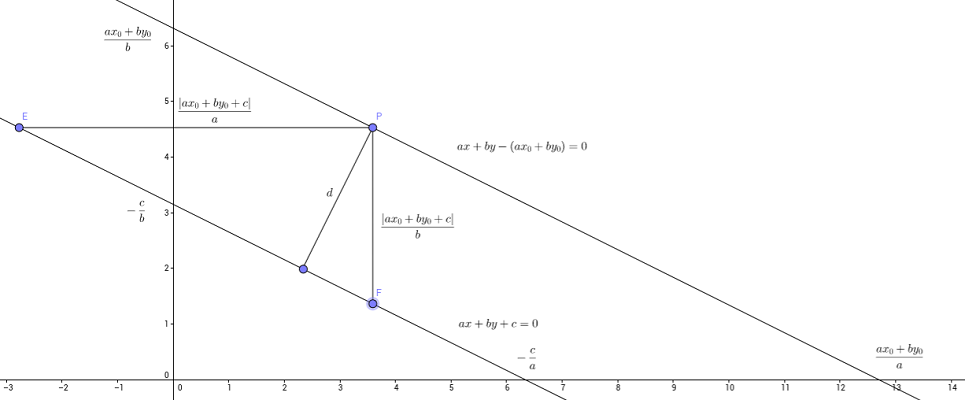
فاصله نقطه $$P = ( x _ 0 , y _ 0 )$$ از خط $$L :a x + b y + c = 0$$ برابر است با:

$$\large d = \frac { | a x _ 0 + b y _ 0 + c | }{ \sqrt { a ^ 2 + b ^ 2 } } .$$

فیلم آموزش ریاضی – پایه نهم + گواهینامه در فرادرس

کلیک کنید

اثبات: خط $$L$$ با معادله عمومی $$a x + b y + c = 0$$ را در نظر بگیرید. شیب این خط $$- \frac { a } { b }$$ است. همچنین، نقطه $$P = ( x _ 0 , y _ 0 )$$ را در نظر بگیرید. فاصله بین خط $$L$$ و نقطه $$P$$ را می‌توان با یک خط عمود بر $$L$$ نشان داد که آن را $$T$$ می‌نامیم. شیب خط $$T$$ باید $$\frac b a$$ باشد، زیرا بر $$L$$ عمود است. اکنون، برای یافتن فاصله نقطه $$P$$ از خط $$L$$، می‌توانیم از تکنیک‌های هندسه استفاده کنیم. بدین منظور، خطی موازی $$L$$ رسم می‌کنیم که از $$P$$ عبور می‌کند. این خط را $$S$$ می‌نامیم. به طور مشابه، خط دیگری را موازی با $$T$$ در نظر می‌گیریم که از مبدأ $$( 0 , 0 )$$ می‌گذرد. این خط را $$R$$ می‌نامیم.

از آنجا که $$S$$ از $$P$$ عبور می‌کند و شیب آن مشابه $$L$$ است، معادله آن را می‌توان به شکل زیر نوشت:

$$\large y - y _ 0 = - \dfrac { a } { b } ( x - x _ 0 ) \implies y = \dfrac { - a x + a x _ 0 + b y _ 0 } { b } .$$

معادله خط $$R$$ نیز به صورت زیر است:

$$\large y = \dfrac { b } { a } x .$$

بنابراین، خط $$S$$ در نقطه زیر با خط $$R$$ متقاطع است:

$$\large \frac { b } { a } x = \dfrac { - a x + a x _ 0 + b y _ 0 } { b } \\ \frac{b ^ 2}{a} x = - a x +a x_0 + by_0 \\ b^ 2 x = -a ^ 2 x + a ^ 2 x_ 0 + ab y _0 \\ ( b ^ 2 + a ^ 2) x = a (a x_ 0 + b y _0 ) \\ \implies x = \dfrac { a ( a x _ 0 + b y _ 0 ) } { a ^ 2 + b ^ 2 }$$

این نقطه را در معادله خط $$R$$ قرار می‌دهیم تا نقطه تقاطع خط‌های $$S$$ و $$R$$ را به دست آوریم:

$$\large P _ 1 \left ( \dfrac { a ( a x _ 0 + b y _ 0 ) } { a ^ 2 + b ^ 2 } , \dfrac { b ( a x _ 0 + b y _ 0 ) } { a ^ 2 + b ^ 2 } \right ) .$$

اکنون محل برخورد خطوط $$L$$ و $$R$$ را بررسی می‌کنیم. این برخورد زمانی رخ می‌دهد که هر دو $$y = \frac {b} { a} x$$ و $$a x + b y + c = 0 \implies y = - \frac { a x + c } { b }$$ برابر باشند. با برابر قرار دادن این دو معادله، $$x$$ به دست می‌آید:

$$\large - \dfrac { a x + c } { b } = \dfrac { b } { a } x \implies x = - \dfrac { a c } { a ^ 2 + b ^ 2 } .$$

با قرار دادن $$x$$ در یکی از معادلات، مقدار $$y$$ به دست می‌آید:

$$\large y = \dfrac { b } { a } \left ( - \dfrac { a c } { a ^ 2 + b ^ 2 } \right ) = - \dfrac { b c } { a ^ 2 + b ^ 2 } .$$

بنابراین، نقطه تقاطع خطوط $$L$$ و $$R$$ برابر است با:

$$\large P _ 2 \left ( - \dfrac { a c } { a ^ 2 + b ^ 2 } , - \dfrac { b c } { a ^ 2 + b ^ 2 } \right ) .$$

اکنون، با استفاده از فرمول فاصله $$d = \sqrt { ( x _ 2 - x _ 1 ) ^ 2 + ( y _ 2 - y _ 1 ) ^ 2 }$$، فاصله بین $$P _ 1$$ و $$P _ 2$$ به صورت زیر خواهد بود:

$$\large \begin {aligned} d & = \sqrt { \left ( - \ \dfrac { a c }{ a ^ 2 + b ^ 2 } - \dfrac { a ( a x _ 0 + b y _ 0 ) } { a ^ 2 + b ^ 2 } \right ) ^ 2 + \left ( - \ \dfrac { b c } { a ^ 2 + b ^ 2 } - \dfrac { b ( a x _ 0 + b y _ 0 ) } { a ^ 2 + b ^ 2 } \right ) ^ 2 } \\\\ & = \sqrt { \dfrac { \big [ - a ( a x _ 0 + b y _ 0 + c ) \big ] ^ 2 + \big [ - b ( a x _ 0 + b y _ 0 + c ) v \big ] ^ 2 } { \big ( a ^ 2 + b ^ 2 \big ) ^ 2 } } \\\\ & = \sqrt { \dfrac { \big ( a ^ 2 + b ^ 2 \big ) ( a x _ 0 + b y _ 0 + c ) ^ 2 } { \big ( a ^ 2 + b ^ 2 \big ) ^ 2 } } \\\\ & = \sqrt { \dfrac { ( a x _ 0 + b y _ 0 + c ) ^ 2 } { a ^ 2 + b ^ 2 } } \\\\ & = \dfrac { | a x _ 0 + b y _ 0 + c | } { \sqrt { a ^ 2 + b ^ 2 } } . \end {aligned}$$

دقت کنید که در فرمول بالا استفاده از قدر مطلق ضروری است، زیرا فاصله باید یک عدد مثبت باشد.

در ادامه، اثبات هندسی فرمول فاصله نقطه از خط را بیان می‌کنیم.

اثبات: ابتدا خطی موازی $$L$$ رسم می‌کنیم که از $$P$$ عبور می‌کند و معادله آن $$a x + b y - ( a x _ 0 + b y _ 0 ) = 0$$ است. در ادامه، یک مثلث قائم‌الزاویه را تشکیل می‌دهیم که ارتفاع آن $$d$$ است. هردو ضلع قائم مثلث را می‌توان با اختلاف بین محل‌های برخورد نسبت به محورهای $$x$$ و $$y$$ به دست آورد. وتر طبق قضیه فیثاغورس به دست می‌آید:

$$\large | a x _ 0 + b y _ 0 + c | \frac { \sqrt { a ^ 2 + b ^ 2 } } { a b } .$$

در نهایت، با توجه به مساحت مثلث، می‌توان تساوی زیر را نوشت و از آن $$d$$ را به دست آورد:

$$\large \begin {aligned} \frac { 1 } { 2 } | a x _ 0 + b y _ 0 + c | \frac { \sqrt { a ^ 2 + b ^ 2 } } { a b } \times d & = \frac { 1 } { 2 } | a x _ 0 + b y _ 0 + c | ^ 2 \frac { 1 } { a b } \\ \\ \Rightarrow d & = \dfrac { | a x _ 0 + b y _ 0 + c | } { \sqrt { a ^ 2 + b ^ 2 } } . \ _ \square \end {aligned}$$

روش برداری محاسبه فاصله نقطه از خط

فاصله نقطه از خط را می‌توان در قالب بردارها نیز بیان کرد. قضیه زیر این موضوع را به خوبی نشان می‌دهد.

قضیه: خطی با معادله برداری $$\overrightarrow { r } = \overrightarrow { a } + \lambda \overrightarrow { b }$$ و نقطه $$\overrightarrow { x }$$ را در نظر بگیرید. فاصله نقطه از خط برابر است با:

$$\large \left \| { \overrightarrow { x } - \big ( \overrightarrow { a } + \lambda' \overrightarrow { b } \big ) } \right \|$$

که در آن:

$$\large \lambda' = \frac { \overrightarrow { x } \cdot \overrightarrow { b } - \overrightarrow { a } \cdot \overrightarrow { b } } { \left \| \overrightarrow { b } \right \| ^ 2 } .$$

اثبات: پایه خط عمود روی خط را از $$\overrightarrow { x }$$ در نظر بگیرید. آن را $$\overrightarrow { r }$$ می‌نامیم. می‌خواهیم مقدار $$\left \| \overrightarrow { x } - \overrightarrow { r } \right \|$$ را به دست آوریم. طبق تعریف، این مقدار، فاصله نقطه از خط است.

از آنجا که $$\overrightarrow { r }$$ در خط صدق می‌کند، برای $$\lambda ^ \prime$$ در $$\overrightarrow { r } = \overrightarrow { a } + \lambda' \overrightarrow { b }$$ صدق می‌کند. از آنجا که عمود بر خط است، داریم:

$$\large \begin {aligned} ( \overrightarrow { x } - \overrightarrow { r } ) \cdot \overrightarrow { b } & = 0 \\ \big ( \overrightarrow { x } - \overrightarrow { a } - \lambda' \vec { b } \big ) \cdot \overrightarrow { b } & = 0 \\ \overrightarrow { x } \cdot \overrightarrow { b } - \overrightarrow { a } \cdot \overrightarrow { b } - \lambda' \left \| \overrightarrow { b } \right \| ^ 2 & = 0 \\ \lambda' & = \frac { \overrightarrow { x } \cdot \overrightarrow { b } - \overrightarrow { a } \cdot \overrightarrow { b } } { \left \| \overrightarrow { b } \right \| ^ 2 } . \ _ \square \end {aligned}$$

نکته جالب این رویکرد این است که برای هر ابعادی می‌توان از آن استفاده کرد.

محاسبه فاصله نقطه از خط با ضرب داخلی

همان‌طور که گفتیم، فاصله نقطه $$P = ( x _ 0 , y _ 0 )$$ از خط $$L :a x + b y + c = 0$$ برابر است با:

$$\large d = \frac { | a x _ 0 + b y _ 0 + c | }{ \sqrt { a ^ 2 + b ^ 2 } } .$$

در این بخش می‌خواهیم با استفاده از ضرب داخلی این فرمول را اثبات کنیم.

اثبات: شکل زیر را در نظر بگیرید.

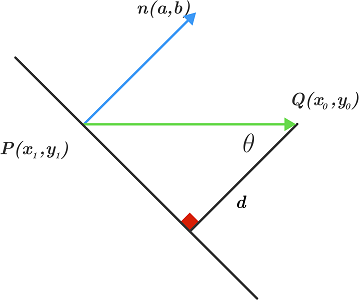
در این شکل، $$d$$ فاصله عمودی نقطه $$Q ( x _ 0 , y _ 0 )$$ از خط $$a x + b y + c = 0$$ است. همچنین $$\overrightarrow { n }$$ را به عنوان بردار نرمال (عمود) خط در نظر بگیرید که از نقطه $$P ( x _ 1 , y_ 1 )$$ شروع می‌شود.

با توجه به شکل بالا می‌توان گفت که فاصله $$d$$ تصویر متعامد بردار $$\overrightarrow { PQ}$$ است. همچنین، از مثلثات می‌توانیم رابطه زیر را بنویسیم:

$$\large d = \left \| \overrightarrow { P Q } \right \| \cos \theta .$$

اکنون می‌توان هم صورت و هم مخرج دو سمت معادله را بر اندازه بردار نرمال $$\overrightarrow { n }$$ تقسیم کرد:

$$\large d = \frac { \left \| \overrightarrow { P Q } \right \| \left \| \overrightarrow { n } \right \| \cos \theta } { \left \| \overrightarrow { n } \right \| } .$$

می‌دانیم که طبق تعریف ضرب داخلی $$\left \| \overrightarrow { P Q } \right \| \left \| \overrightarrow { n } \right \| \cos \theta$$ به معنی ضرب داخلی بردار $$\overrightarrow { PQ}$$ و بردار نرمال $$\overrightarrow { n }$$ است:

$$\large \begin {aligned} d & = \frac { \overrightarrow { P Q } \cdot \overrightarrow { n } } { \left \| \overrightarrow { n } \right \| }\\ \overrightarrow { P Q } & = ( { x } _ { 0 } - { x } _ { 1 } , { y } _ { 0 } - { y } _ { 1 } ) . \end {aligned}$$.

بنابراین، خواهیم داشت:

$$\large \begin {aligned} \overrightarrow { P Q } \cdot \overrightarrow { n } & = ( { x } _ { 0 } - { x } _ { 1 } , { y } _ { 0 } - { y } _ { 1 } ) \cdot ( a , b ) \\ & = a ( { x } _ { 0 } - { x } _ { 1 } ) + b ( { y } _ { 0 } - { y } _ { 1 } ) . \end {aligned}$$

همچنین، $$\left \| \overrightarrow { n } \right \| =\sqrt { { a }^{ 2 } + { b } ^ { 2 } }$$ را داریم. در نتیجه، فاصله برابر است با:

$$\large d = \frac { \left | a ( { x } _ { 0 } - { x } _ { 1 } ) + b ( { y } _ { 0 } - { y } _ { 1 } ) \right | } { \sqrt { { a } ^ { 2 } { + b } ^ { 2 } } } = \frac { \left | a ( { x } _ { 0 } ) - a ( { x } _ { 1 } ) + b ( { y } _ { 0 } ) - { b ( y } _ { 1 } ) \right | } { \sqrt { { a } ^ { 2 } { + b } ^ { 2 } } } .$$

با توجه به معادله $$c = - a ( x _ 1 ) - b ( y _ 1 )$$، رابطه زیر را داریم:

$$\large d = \frac { \left \lvert a ( { x } _ { 0 } ) + b ( { y } _ { 0 } ) + c \right \rvert } { \sqrt { { a } ^ { 2 } { + b } ^ { 2 } } } .$$

بنابراین، برای خط $$a x + b y + c$$ و نقطه $$( x _ 0 , y _ 0 )$$، فاصله عمودی را می‌توان از فرمول بالا به دست آورد.

مثال‌های محاسبه فاصله نقطه از خط

در این بخش چند مثال از محاسبه فاصله نقطه از خط را حل می‌کنیم.

مثال ۱: فاصله نقطه $$( 5 , 1 )$$ را از خط $$y = 3 x + 1$$ به دست آورید.

حل: فرمول فاصله نقطه از خط به صورت زیر است:

$$\large d = \dfrac { \big | a x _0 + b y _ 0 + c \big | }{ \sqrt { a ^ 2 + b ^ 2 } } .$$

با در نظر گرفتن $$(x_0, y_0) = (5, 1)$$ و $$0 = 3 x - y + 1$$، خواهیم داشت:

$$\large d = \dfrac { \big | 3 \cdot 5 - 1 \cdot 1 + 1 \big | }{ \sqrt { 3 ^ 2 + ( - 1 ) ^ 2 } } = \dfrac { 1 5 } { \sqrt { 1 0 } } .$$

مثال ۲: فاصله بین دو خط $$y = 2x + 5$$ و $$y = 2 x + 2 0 1 6$$ را پیدا کنید.

حل: توجه کنید که این دو خط موازی هستند (شیب یکسانی دارند)، بنابراین می‌توانیم نقطه‌ای را روی یکی از خطوط انتخاب کرده و سپس از فرمول استفاده کنیم. اما، آیا انتخاب نقاط متفاوت نتایج تفاوت خواهد داشت؟ خیر. برای اطمینان از این موضوع، دو نقطه متفاوت را روی خط $$y = 2 x + 5$$ در نظر می‌گیریم.

اگر $$( x _ 0 , y _ 0 ) = ( 1 , 7 )$$ و $$2 x - y + 2016 = 0$$ را داشته باشیم، آنگاه با اعمال فرمول فاصله نقطه از خط داریم:

$$\large d = \dfrac { \left | 2 \cdot 1 - 1 \cdot 7 + 2 0 1 6 \right | } { \sqrt { 2 ^ 2 + ( - 1 ) ^ 2 } } = \dfrac { 2 0 1 1 } { \sqrt { 5 } } .$$

اگر $$( x _ 0 , y _ 0 ) = (2 , 9 )$$ و $$2 x - y + 2016 = 0$$ باشند، آنگاه با استفاده از فرمول فاصله نقطه از خط مقدار زیر به دست می‌آید:

$$\large d = \dfrac { \left | 2 \cdot 2 - 1 \cdot 9 + 2016 \right | } { \sqrt { 2 ^ 2 + ( - 1 ) ^ 2 } } = \dfrac { 2 0 1 1} { \sqrt { 5 } } .$$

می‌بینیم که نتیج یکسان هستند.

مثال ۳: فاصله بین نقطه $$( 1 , 2 , 3 )$$ و صفحه $$x + 2 y - 3 z = 44$$ را به دست آورید.

حل: برای محاسبه فاصله نقطه از صفحه، فرمول زیر را داریم:

$$\large d = \dfrac { \left | a x _ 0 + b y _ 0 + c z _ 0 + d \right | } { \sqrt { a ^ 2 + b ^ 2 + c ^ 2 } } .$$

بنابراین، با استفاده از اطلاعات مسئله و این فرمول، فاصله به سادگی به دست می‌آید:

$$\large d = \dfrac { \left | 1 \cdot 1 + 2 \cdot 2 - 3 \cdot 3 + 4 4 \right | } { 1 ^ 2 + 2 ^ 2 + ( - 3 ) ^ 2 } = \dfrac { 4 0 }{ \sqrt { 1 4 } } .$$

مثال ۴: معادله خط نیمساز زاویه بین دو خط زیر را به دست آورید:

$$\large \begin {aligned} a _ 1 x + b _ 1 y + c _ 1 & = 0 \\ a _ 2 x + b _ 2 y + c _ 2 & = 0 . \end {aligned}$$

حل: توجه کنید که بین دو خط دو نیمساز زاویه وجود دارد: یکی زاویه حاده را نصف می‌کند و دیگری زاویه منفرجه را (اگر خطوط عمود باشند، دو زاویه قائمه تشکیل می‌شود). یکی از ویژگی‌های نیمساز زاویه بین دو خط این است که فاصله هر نقطه روی آن از هر دو خط برابر است. این گفته را می‌توان با رسم خطوط عمود بر دو خط از نقطه روی نیمساز و مثلث‌های حاصل ثابت کرد.

اگر $$( x _ 0 , y _ 0 )$$ نقطه‌ای روی خط نیمساز زاویه باشد، می‌توان فاصله آن از خطوط را برابر قرار داد:

$$\large \left | \frac { a _ 1 x _ 0 + b _ 1 y _ 0 + c _ 1 }{ \sqrt { a _ 1 ^ 2 + b _ 1 ^ 2 } } \right | = \left | \frac { a _ 2 x _ 0 + b _ 2 y _ 0 + c _ 2 } { \sqrt { a _ 2 ^ 2 + b _ 2 ^ 2 } } \right | .$$

با حذف علامت قدر مطلق از دو طرف تساوی، داریم:

$$\large \frac { a _ 1 x _ 0 + b _ 1 y _ 0 + c _ 1 } { \sqrt { a _ 1 ^ 2 + b _ 1 ^ 2 } } = \pm \frac { a _ 2 x _ 0 + b _ 2 y _ 0 + c _ 2 } { \sqrt { a _ 2 ^ 2 + b _ 2 ^ 2 } } .$$

اکنون جمله‌های مشابه را به یک سمت تساوی جابه‌جا می‌کنیم که منجر به معادله‌ای به فرم زیر می‌شود:

$$\large a _ 3 x _ 0 + b _ 3 y _ 0 + c _ 3 = 0 .$$

که در آن:

$$\large \begin {aligned} a _ 3 & = \frac { a _ 1 } { \sqrt { a _ 1 ^ 2 + b _ 1 ^ 2 } } \pm \frac { a _ 2 } { \sqrt { a _ 2 ^ 2 + b _ 2 ^ 2 } } \\ b _ 3 & = \frac { b _ 1 } { \sqrt { a _ 1 ^ 2 + b _ 1 ^ 2 } } \pm \frac { b _ 2 } { \sqrt { a _ 2 ^ 2 + b _ 2 ^ 2 } } \\ c _ 3 & = \frac { c _ 1 } { \sqrt { a _ 1 ^ 2 + b _ 1 ^ 2 } } \pm \frac { c _ 2 } { \sqrt { a _ 2 ^ 2 + b _ 2 ^ 2 } } . \end {aligned}$$

بنابراین، معادله نیمسازها به شکل زیر است:

$$\large a _ 3 x + b _ 3 y + c _ 3 = 0 .$$

علامت $$\pm$$ به این معناست که دو مقدار ممکن برای $$a _ 3$$، $$b _ 3$$ و $$c _ 3$$ وجود دارد و به همان ترتیبی که در بالا گفتیم، دو نیمساز زاویه داریم.

جمع‌بندی

در این مطلب از مجله فرادرس فاصله نقطه از خط را توضیح دادیم. سپس، با بیان فرمول فاصله نقطه از خط، مثال‌هایی را برای درک بهتر این موضوع حل کردیم.