توابع محدب و مقعر — از صفر تا صد

در این آموزش از مجموعه آموزش‌های ریاضیات مجله فرادرس، تقعر و تحدب توابع را معرفی می‌کنیم که برای تعیین آن‌ها از مشتق دوم استفاده می‌شود.

تعریف تابع محدب و مقعر

تابع $$y = f\left( x \right),$$ را در نظر بگیرید که فرض شده در بازه $$\left[ {a,b} \right]$$ پیوسته است. این تابع را «محدب رو به پایین» (Convex Downward) یا «محدب» (Convex)‌ می‌نامیم، اگر برای هر دو نقطه $$x_1$$ و $$x_2$$ در بازه $$\left[ {a,b} \right]$$، نامعادله زیر برقرار باشد:

$$f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \le \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2}.$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

اگر نامعادله فوق، اکید باشد، آن‌گاه تابع $$f(x)$$ را در بازه $$\left[ {a,b} \right]$$ «اکیداً محدب» می‌نامیم.

به‌طور مشابه، می‌توانیم یک تابع مقعر را تعریف کنیم. تابع $$f(x)$$ را «محدب رو به بالا» (Convex Upward) یا «مقعر» (Concave) می‌نامیم، اگر برای هر دو نقطه $$x_1$$ و $$x_2$$ در بازه $$\left[ {a,b} \right]$$، نامساوی زیر برقرار باشد:

$$f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \ge \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2}.$$

اگر نامساوی بالا برای هر $${x_1},{x_2} \in \left[ {a,b} \right]$$ به‌طوری که $${x_1} \ne {x_2}$$، به‌صورت اکید برقرار باشد، تابع $$f(x)$$‌ را در بازه $$\left[ {a,b} \right]$$ اکیداً مقعر می‌نامیم. لازم به یادآوری است که تحدب به‌معنای برآمدگی است و وقتی می‌گوییم تحدب رو به بالا است، یعنی جهت برآمدگی به بالا است. منظور از تقعر نیز فرورفتگی است.

تفسیر هندسی تحدب و تقعر

شکل زیر تفسیر هندسی تابع محدب را نشان می‌دهد:

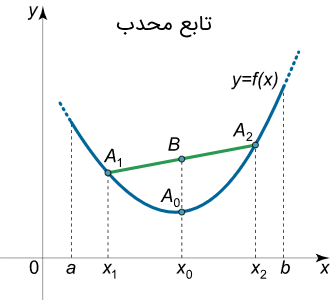
همان‌طور که از شکل بالا مشخص است، در تابع محدب یا تابعی که تحدب آن به پایین است، نقطه میانی $$B$$ در وتر $$A_1A_2$$ بالای نقطه $$A_0$$ از نمودار تابع قرار دارد یا منطبق بر آن است.

تابع مقعر نیز به‌صورت زیر است:

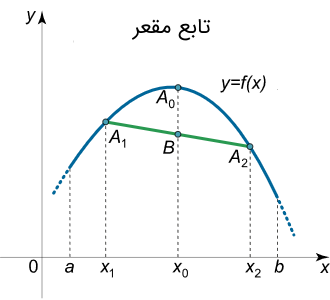
به طریق مشابه، در تابع مقعر یا تابعی که تحدب آن به بالا است، نقطه میانی $$B$$ در وتر $$A_1A_2$$ پایین‌تر از نقطه $$A_0$$ از نمودار تابع قرار دارد یا منطبق بر آن است.

توابع محدب یک ویژگی واضح دیگر نیز دارند که به نقطه مماس بر منحنی آن‌ها مربوط می‌شود. تابع $$f(x)$$ در بازه $$\left[ {a,b} \right]$$ محدب است، اگر و تنها اگر منحنی آن، بالای خط مماس بر منحنی در نقطه $$x_0$$ از بازه $$\left[ {a,b} \right]$$ قرار گیرد. شکل زیر این موضوع را به‌خوبی نشان می‌دهد:

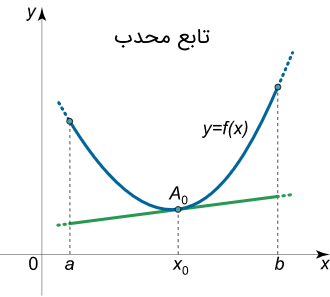
به‌طور مشابه، تابع $$f(x)$$ را در بازه $$\left[ {a,b} \right]$$ مقعر می‌گوییم، اگر و تنها اگر، منحنی آن، پایین‌تر از خط مماس بر منحنی در نقطه $$x_0$$ از بازه $$\left[ {a,b} \right]$$ نباشد. شکل زیر این گفته را نشان می‌دهد.

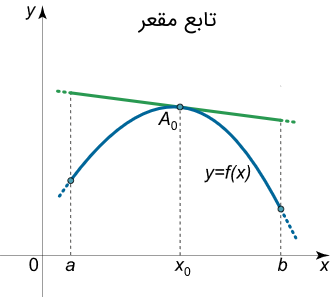
شرایط کافی تحدب

فرض کنید مشتق اول $$f’\left( x \right)$$ از تابع $$f\left( x \right)$$ در بازه بسته $$\left[ {a,b} \right]$$، و مشتق دوم $$f^{\prime\prime}\left( x \right)$$ در بازه باز $$\left( {a,b} \right)$$ وجود داشته باشند. در این صورت، می‌توانیم شرایط کافی زیر را برای تحدب بیان کنیم:

• اگر برای همه $$x \in \left( {a,b} \right)$$، نامساوی $$f^{\prime\prime}\left( x \right) \ge 0$$ برقرار باشد، آن‌گاه تابع $$f(x)$$ در بازه $$\left[ {a,b} \right]$$ محدب است.
• اگر برای همه $$x \in \left( {a,b} \right)$$، نامساوی $$f^{\prime\prime}\left( x \right) \le 0$$ برقرار باشد، آن‌گاه تابع $$f(x)$$ در بازه $$\left[ {a,b} \right]$$ مقعر است.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

برای فهم بهتر، اثبات مورد اول را بیان می‌کنیم. فرض کنید مشتق دوم تابع $$f(x)$$ در بازه $$\left( {a,b} \right)$$، غیرصفر باشد ($$f^{\prime\prime}\left( x \right) \ge 0$$). نقطه $$x_0$$ را در بازه $$\left[ {{x_1},{x_2}} \right]$$ در نظر بگیرید. فرض کنید طول این بازه برابر با $$2h$$ باشد. دو نقطه $$x_1$$ و $$x_2$$ را به‌صورت زیر می‌نویسیم:

$${{x_1} = {x_0} – h,\;\;\;}\kern-0.3pt{{x_2} = {x_0} + h.}$$

در ادامه، از بسط سری تیلور (به فرم لاگرانژ) تابع $$f\left( x \right)$$ در نقطه $$x_0$$ استفاده می‌کنیم:

$${f\left( {{x_1}} \right) = f\left( {{x_0} – h} \right) }
= {f\left( {{x_0}} \right) – f’\left( {{x_0}} \right)h + \frac{{f^{\prime\prime}\left( {{\xi _1}} \right){h^2}}}{{2!}},}$$

$${f\left( {{x_2}} \right) = f\left( {{x_0} + h} \right) }
= {f\left( {{x_0}} \right) + f’\left( {{x_0}} \right)h + \frac{{f^{\prime\prime}\left( {{\xi _2}} \right){h^2}}}{{2!}},}$$

که در آن، $${x_0} – h \lt {\xi _1} \lt {x_0}$$ و $${x_0} \lt {\xi _2} \lt {x_0} + h$$.

اگر دو معادله را با هم جمع کنیم، داریم:

$${f\left( {{x_1}} \right) + f\left( {{x_2}} \right) }
= {2f\left( {{x_0}} \right) + \frac{{{h^2}}}{2}\left[ {f^{\prime\prime}\left( {{\xi _1}} \right) + f^{\prime\prime}\left( {{\xi _2}} \right)} \right].}$$

از آن‌جایی که $${\xi _1},{\xi _2} \in \left( {a,b} \right)$$، مشتق‌های دوم سمت راست معادله،‌ غیرمنفی هستند. در نتیجه:

$$f\left( {{x_1}} \right) + f\left( {{x_2}} \right) \ge 2f\left( {{x_0}} \right)$$

یا

$$f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) \le \frac{{f\left( {{x_1}} \right) + f\left( {{x_2}} \right)}}{2}$$

به عبارت دیگر، بنا بر تعریف، تابع $$f(x)$$ محدب است.

ویژگی توابع محدب و مقعر

در این‌جا، چند ویژگی توابع محدب را با فرض اینکه همه توابع روی بازه $$\left[ {a,b} \right]$$ پیوسته باشند، بیان مي‌کنیم.

1. اگر توابع $$f$$ و $$g$$ محدب (مقعر) باشند، آن‌گاه ترکیب خطی $$af + bg$$ که در آن، $$a$$ و $$b$$ اعداد حقیقی مثبت هستند، محدب (مقعر) خواهد بود.
2. اگر تابع $$u=g(x)$$ محدب، و تابع $$y = f\left( u \right)$$ محدب و غیرکاهشی باشد،‌ آن‌گاه تابع ترکیبی $$y = f\left( {g\left( x \right)} \right)$$ محدب خواهد بود.
3. اگر تابع $$u = g\left( x \right)$$ مقعر، و تابع $$y = f\left( u \right)$$ محدب و غیرکاهشی باشد، آن‌گاه $$y = f\left( {g\left( x \right)} \right)$$ محدب است.
4. هر ماکزیمم محلی تابع مقعر که در بازه $$\left[ {a,b} \right]$$ تعریف می‌شود، ماکزیمم سراسری است.
5. هر مینیمم محلی تابع محدب که در بازه $$\left[ {a,b} \right]$$ تعریف می‌شود، مینیمم سراسری است.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

مثال ۱

نمودار مربوط به یک تابع دلخواه را به‌ازای ترکیبات مختلف $$y$$، $$y'$$ و $$y''$$ رسم کنید.

حل: برای نمونه، ترکیب زیر را در نظر بگیرید:

$${y \gt 0,\;\;y’ \lt 0,\;\;\;}\kern-0.3pt{y^{\prime\prime} \gt 0}$$

نمودار مربوط به ترکیب بالا، در نیمه بالایی صفحه مختصات قرار دارد و اکیداً کاهشی است (زیرا $$y’ \lt 0$$). از آن‌جایی که $$y^{\prime\prime} \gt 0$$ است، تابع محدب است. نمودار مربوط به این تابع و سایر حالت‌های ممکن، در شکل زیر نشان داده شده است.

مثال ۲

مقادیری از $$x$$‌ را به‌دست آورید که به‌ازای آن، تابع $$f\left( x \right) = {x^3} + a{x^2} + bx + c$$ مقعر باشد.

حل: ابتدا مشتق دوم تابع را محاسبه می‌کنیم:

$${f’\left( x \right) = {\left( {{x^3} + a{x^2} + bx + c} \right)^\prime } }
= {3{x^2} + 2ax + b;}$$

$${f^{\prime\prime}\left( x \right) = {\left( {3{x^2} + 2ax + b} \right)^\prime } }
= {6x + 2a.}$$

تابع، مقعر است اگر $$f^{\prime\prime}\left( x \right) \le 0$$. بنابراین:

$${f^{\prime\prime}\left( x \right) \le 0,\;\;}\Rightarrow
{6x + 2a \le 0,\;\;}\Rightarrow
{6x \le – 2a,\;\;}\Rightarrow
{x \le – \frac{a}{3}.}$$

مثال ۳

بازه‌های تحدب و تقعر تابع $$f\left( x \right) = \sqrt {2 + {x^2}}$$‌ را به‌دست آورید.

حل: این تابع برای همه $$x \in \mathbb{R}$$ تعریف شده و مشتق‌پذیر است. ابتدا مشتق دوم تابع را به‌دست می‌آوریم:

$$\require{cancel}
{f’\left( x \right) = {\left( {\sqrt {2 + {x^2}} } \right)^\prime } }
= {\frac{1}{{2\sqrt {2 + {x^2}} }} \cdot {\left( {2 + {x^2}} \right)^\prime } }
= {\frac{{\cancel{2}x}}{{\cancel{2}\sqrt {2 + {x^2}} }} }
= {\frac{x}{{\sqrt {2 + {x^2}} }};}$$

$${f^{\prime\prime}\left( x \right) = {\left( {\frac{x}{{\sqrt {2 + {x^2}} }}} \right)^\prime } }
= {\frac{{x’\sqrt {2 + {x^2}} – x{{\left( {\sqrt {2 + {x^2}} } \right)}^\prime }}}{{{{\left( {\sqrt {2 + {x^2}} } \right)}^2}}} }
= {\frac{{\sqrt {2 + {x^2}} – x \cdot \frac{x}{{\sqrt {2 + {x^2}} }}}}{{2 + {x^2}}} }\\
= {\frac{{{{\left( {\sqrt {2 + {x^2}} } \right)}^2} – {x^2}}}{{\left( {2 + {x^2}} \right)\sqrt {2 + {x^2}} }} }
= {\frac{{2 + \cancel{x^2} – \cancel{x^2}}}{{\sqrt {{{\left( {2 + {x^2}} \right)}^3}} }} }
= {\frac{2}{{\sqrt {{{\left( {2 + {x^2}} \right)}^3}} }}.}$$

همان‌طور که می‌بینیم، مشتق دوم همواره مثبت است. بنابراین، برای همه مقادیر $$x$$ محدب است.

مثال 4

وضعیت تحدب تابع $$f\left( x \right) = \arctan x$$‌ را در نقطه $$x=1$$ تعیین کنید.

حل: مانند مثال‌های قبلی، مشتق دوم تابع را محاسبه می‌کنیم:

$${f’\left( x \right) = {\left( {\arctan x} \right)^\prime } }
= {\frac{1}{{1 + {x^2}}};}$$

$${f^{\prime\prime}\left( x \right) = {\left( {\frac{1}{{1 + {x^2}}}} \right)^\prime } }
= {{\left[ {{{\left( {1 + {x^2}} \right)}^{ – 1}}} \right]^\prime } }
= { – {\left( {1 + {x^2}} \right)^{ – 2}} \cdot 2x }
= { – \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}}.}$$

مقدار مشتق دوم در نقطه $$x=1$$ برابر است با:

$${f^{\prime\prime}\left( 1 \right) = – \frac{{2 \cdot 1}}{{{{\left( {1 + {1^2}} \right)}^2}}} }
= { – \frac{1}{2} \lt 0.}$$

از آن‌جایی که مشتق دوم منفی است، تابع در نقطه $$x=1$$ محدب رو به بالا یا همان مقعر است.

مثال ۵

بازه تقعر یا تحدب تابع زیر را محاسبه کنید.

$$f\left( x \right) = \frac{1}{{1 + {x^2}}}$$

حل: تابع برای همه $$x \in \mathbb{R}$$ تعریف شده و مشتق‌پذیر است. ابتدا مشتق دوم تابع را به‌دست می‌آوریم:

$${f’\left( x \right) = {\left( {\frac{1}{{1 + {x^2}}}} \right)^\prime } }
= {{\left[ {{{\left( {1 + {x^2}} \right)}^{ – 1}}} \right]^\prime } }
= { – \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}};}$$

$${f^{\prime\prime}\left( x \right) = {\left( { – \frac{{2x}}{{{{\left( {1 + {x^2}} \right)}^2}}}} \right)^\prime } }
= {\frac{{{6{x^2}} – {2}}}{{{{\left( {1 + {x^2}} \right)}^3}}}.}$$

حال از بازه‌های متناظر با مثبت و منفی بودن مشتق دوم را محاسبه می‌کنیم:

حالت اول:

$${f^{\prime\prime}\left( x \right) \gt 0,\;\;} \Rightarrow {{\large\frac{{6{x^2} – 2}}{{{{\left( {1 + {x^2}} \right)}^3}}}\normalsize} \gt 0,\;\;}$$

$$\Rightarrow
{x \in \left( { – \infty , – {\large\frac{1}{{\sqrt 3 }}\normalsize}} \right) \cup \left( {{\large\frac{1}{{\sqrt 3 }}\normalsize},\infty } \right);}$$

حالت دوم:

$${f^{\prime\prime}\left( x \right) \lt 0,\;\;} \Rightarrow
{{\large\frac{{6{x^2} – 2}}{{{{\left( {1 + {x^2}} \right)}^3}}}\normalsize} \lt 0,\;\;}\Rightarrow {6{x^2} – 2 \lt 0,\;\;}\Rightarrow {{x^2} \lt {\large\frac{1}{3}\normalsize},\;\;}\Rightarrow {x \in \left( { – {\large\frac{1}{{\sqrt 3 }}\normalsize}, {\large\frac{1}{{\sqrt 3 }}\normalsize}} \right).}$$

در حل نامعادلات فوق از این واقعیت استفاده کرده‌ایم که مخرج مشتق دوم به‌ازای همه مقادیر $$x$$ بزرگ‌تر از صفر است: $${\left( {1 + {x^2}} \right)^3} \gt 0$$.

در نهایت، با توجه به علامت مشتق دوم می‌توان گفت:

• تابع در بازه $$\left( { – {\large\frac{1}{{\sqrt 3 }}\normalsize}, {\large\frac{1}{{\sqrt 3 }}\normalsize}} \right)$$ مقعر؛
• و در بازه‌های $$\left( { – \infty , – {\large\frac{1}{{\sqrt 3 }}\normalsize}} \right)$$ و $$\left( {{\large\frac{1}{{\sqrt 3 }}\normalsize}, \infty} \right)$$ محدب است.

مثال ۶

بازه یا بازه‌های تحدب یا تقعر تابع زیر را محاسبه کنید:

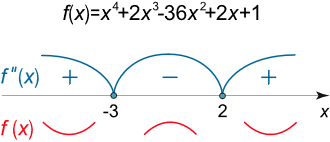
$${f\left( x \right) }={ {x^4} + 2{x^3} – 36{x^2} + 2x + 1.}$$

حل: ابتدا مشتق دوم تابع را محاسبه می‌کنیم:

$${f’\left( x \right) = {\left( {{x^4} + 2{x^3} – 36{x^2} + 2x + 1} \right)^\prime } }
= {4{x^3} + 6{x^2} – 72x + 2;}$$

$${f^{\prime\prime}\left( x \right) = {\left( {4{x^3} + 6{x^2} – 72x + 2} \right)^\prime } }
= {12{x^2} + 12x – 72 }
= {12\left( {{x^2} + x – 6} \right).}$$

اکنون معادله $$f^{\prime\prime}\left( x \right) = 0$$ را حل و آن را تعیین علامت می‌کنیم:

$${f^{\prime\prime}\left( x \right) = 0,\;\;}\Rightarrow
{12\left( {{x^2} + x – 6} \right) = 0,\;\;}\Rightarrow
{D = 1 + 4 \cdot \left( { – 6} \right) = 25,\;\;}\Rightarrow
{{x_{1,2}} = \frac{{ – 1 \pm 5}}{2} = – 3;2.}$$

همان‌طور که در شکل زیر نیز نشان داده شده است، تابع در بازه‌های $$\left( { – \infty , – 3} \right)$$ و $$\left( {2, + \infty } \right)$$ اکیداً محدب و در بازه $$\left( {-3, 2} \right)$$ اکیداً مقعر است.

اگر این مطلب برای شما مفید بوده است و به یادگیری بیشتر در این زمینه علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• روش‌های مشتق‌گیری — به همراه مثال
• مشتق زنجیره ای — به زبان ساده
• ماکزیمم و مینیمم تابع — به زبان ساده

^^