انتگرال سطحی در فیزیک — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، درباره انتگرال و روش‌های محاسبه آن بحث کردیم. در این آموزش‌ها، مباحثی مانند انتگرال توابع مثلثاتی، انتگرال‌گیری جزء به جزء، انتگرال دوگانه و انتگرال سه‌گانه را معرفی کردیم. همچنین با انتگرال سطحی آشنا شدیم. انتگرال سطحی در مباحث مختلف فیزیک کاربرد فراوانی دارد. در این آموزش، چند مورد از مهم‌ترین کاربردهای انتگرال سطحی در فیزیک را بررسی می‌کنیم.

در فیزیک، از انتگرال­‌های سطحی به ویژه برای محاسبه موارد زیر استفاده می‌شود:

• جرم یک پوسته
• مرکز جرم و گشتاورهای لختی یک پوسته
• نیروی گرانشی و نیروی فشار
• جریان سیال و شارش جرمی عبوری از یک سطح
• بار الکتریکی توزیع شده روی یک سطح
• میدان‌های الکتریکی (قانون گاوس در الکتروستاتیک)

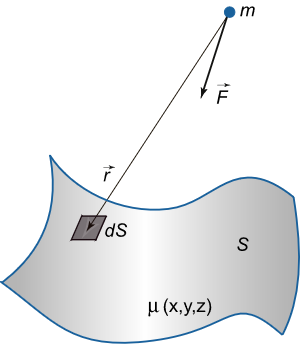
جرم یک سطح

فرض کنید $$S$$ یک پوسته نازک صاف باشد و جرم بر واحد سطح آن با تابع پیوسته $$\mu \left( {x,y,z} \right)$$ تعریف شود. آن‌گاه جرم کل پوسته با استفاده از انتگرال سطحی تابع اسکالر به دست می‌آید:

$$\large m = \iint \limits _ S { \mu \left ( { x , y , z } \right ) d S } .$$

مرکز جرم و گشتاورهای لختی یک سطح

اگر جرم $$m$$ روی پوسته نازک $$S$$ با تابع چگالی پیوسته $$\mu \left( {x,y,z} \right)$$ توزیع شود، مختصات مرکز جرم این پوسته با روابط زیر محاسبه خواهد شد:

$$\large { { x _ C } = \frac { { { M _ { y z } } } }{ m } , \; \; \; } \kern-0.3pt { { y _ C } = \frac { { { M _ { x z } } } } { m } , \; \; \; } \kern-0.3pt { { z _ C } = \frac { { { M _ { x y } } } }{ m } }$$

که در آن،

$$\large \begin {align*} { M _ { y z } } & = \iint \limits _ S { x \mu \left ( { x , y , z } \right ) d S } , \; \; \; \kern-0.3pt \\ { M _ { x z } } & = \iint\limits_S {y\mu \left( {x,y,z} \right)dS} ,\;\;\; \kern-0.3pt \\{ M _ { x y } } & = \iint\limits_S {z\mu \left( {x,y,z} \right)dS} \end {align*}$$

به ترتیب، گشتاورهای اول حول صفحات $$x=0$$، $$y=0$$ و $$z=0$$ نامیده می‌­شوند.

گشتاورهای لختی حول محورهای $$x$$، $$y$$ و $$z$$ را می‌توان با روابط زیر تعیین کرد:

$$\large \begin{align*} { I _ x } & = \iint \limits _ S { \left ( { { y ^ 2 } + { z ^ 2 } } \right ) \mu \left ( { x , y , z } \right ) d S } , \; \; \; \kern-0.3pt \\ { I _ y } & = \iint \limits _ S { \left ( { { x ^ 2 } + { z ^ 2 } } \right ) \mu \left ( { x , y ,z } \right ) d S } , \; \; \; \kern-0.3pt \\ { I _ z } & = \iint \limits _ S { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) \mu \left ( { x , y , z } \right ) d S } \end {align*}$$

گشتاورهای لختی پوسته حول صفحات $$xy$$، $$yz$$ و $$xz$$ به صورت زیر تعریف می‌شوند:

$$\large \begin{align*} { I _ { x y } } & = \iint \limits _ S { { z ^ 2 } \mu \left ( { x ,y , z } \right ) d S } , \; \; \; \kern-0.3pt \\ { I _ { y z } } & = \iint \limits _ S { { x ^ 2 } \mu \left ( { x , y , z } \right ) d S } , \; \; \; \kern-0.3pt \\ { I _ { x z } } & = \iint \limits _ S { { y ^ 2 } \mu \left ( { x , y , z } \right ) d S } . \end {align*}$$

نیروی گرانشی

اگر $$m$$ جرمی در نقطه $$\left( {{x_0},{y_0},{z_0}} \right)$$ باشد که خارج از سطح $$S$$ قرار دارد (شکل 1)، آن‌گاه نیروی جاذبه بین سطح $$S$$ و جرم $$m$$ به صورت زیر خواهد بود:

$$\large { \mathbf { F } } = { G m \iint \limits _ S { \mu \left ( { x , y , z } \right ) \frac { \mathbf { r } } { { { r ^ 3 } } } d S } }$$

که در آن، $$\mathbf { r } = \left ( { x – { x _ 0 } , y – { y _ 0 } , z – { z _ 0 } } \right )$$، $$G$$ ثابت گرانشی و $${\mu \left( {x,y,z} \right)}$$ تابع چگالی است.

نیروی فشار

فرض کنید سطح $$S$$ که با بردار مکان $$\mathbf{r}$$ نشان داده می‌شود، توسط نیروی وارد بر آن تحت فشار قرار گیرد (مانند سدها، بال‌های هواپیما و مخازن گازی فشرده و غیره). نیروی کل ایجادشده $$\mathbf{F}$$ توسط فشار $$p\left( \mathbf{r} \right)$$ با انتگرال سطحی زیر محاسبه می‌شود:

$$\large \mathbf { F } = \iint \limits _ S { p \left ( \mathbf { r } \right ) d \mathbf { S } } .$$

طبق تعریف، فشار در هر نقطه در راستای عمود بر سطح $$S$$ است. از این رو، می‌توان نوشت:

$$\large { \mathbf { F } = \iint \limits _ S { p \left ( \mathbf { r } \right ) d \mathbf { S } } } = { \iint \limits _ S { p \mathbf { n } d S } }$$

که در آن، $$\mathbf{n}$$ بردار نرمال یکه عمود بر سطح $$s$$ است.

شار سیال و شار جرمی

اگر میدان برداری، سرعت سیال $$\mathbf{v}\left( \mathbf{r} \right)$$ باشد، شار عبوری از سطح $$s$$، شار سیال نامیده می‌شود که با حجم سیال گذرنده از سطح $$s$$ بر واحد زمان برابر است و با رابطه زیر تعریف می‌شود:

$$\large \Phi = \iint \limits _ S { \mathbf { v } \left ( \mathbf { r } \right ) \cdot d \mathbf { S } } .$$

به طور مشابه، شار میدان برداری $$\mathbf{F} = \rho \mathbf{v}$$ ($$\rho$$ چگالی سیال است)، شار جرمی نامیده می‌شود که برابر است با جرم عبوری از سطح $$s$$ بر واحد زمان و از رابطه زیر به دست می‌آید:

$$\large \Phi = \iint \limits _ S { \rho \mathbf { v } \left ( \mathbf { r } \right ) \cdot d \mathbf { S } } .$$

بار سطحی

فرض کنید $$\sigma \left( {x,y} \right)$$ چگالی بار سطحی باشد. آن‌گاه مقدار کل بار توزیع‌شده روی سطح رسانای $$s$$ با انتگرال سطحی زیر تعیین می‌شود:

$$\large Q = \iint \limits _ S { \sigma \left ( { x , y } \right ) d S } .$$

قانون گاوس

شار الکتریکی $$\mathbf{D}$$ از هر سطح بسته $$s$$ با بار محصور شده $$Q$$ توسط سطح متناسب است:

$$\large { \Phi = \iint \limits _ S { \mathbf { D } \cdot d \mathbf { S } } } = { \sum \limits _ i { { Q _ i } } }$$

که در آن، $$\mathbf{D} = \varepsilon {\varepsilon _0}\mathbf{E}$$، $$\mathbf{E}$$ مقدار شدت میدان الکتریکی، $$\varepsilon$$ ثابت گذردهی ماده و $${\varepsilon _0} = 8,85\; \times{10^{ – 12}}\,\text{F/m}$$ ثابت گذردهی خلأ است.

برای حالت گسسته، بار کل $$Q$$، از جمع روی تمام بارهای محصور شده به دست می‌آید.

قانون گاوس، یک قانون کلی کاربردی برای هر سطح بسته است. اگر سطح بسته تقارن کافی داشته باشد، محاسبه میدان الکتریکی آسان‌تر خواهد بود. در واقع، قانون گاوس همان معادله اول ماکسول است.

مثال‌ها

در ادامه، چند مثال را از کاربردهای انتگرال سطحی در فیزیک بررسی می‌کنیم.

مثال ۱

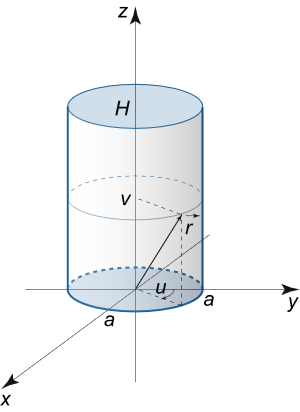
جرم سطح استوانه‌ای پارامتربندی‌ شده به صورت $$\mathbf { r } \left ( { u , v } \right ) = a \cos u \cdot \mathbf { i } + \; a \sin u \cdot \mathbf { j } + \; v \cdot \mathbf { k }$$ را بیابید که در آن، $$0 \le u \le 2\pi$$ و $$0 \le v \le H$$ است (شکل 2). چگالی سطحی تابعی به صورت $$\mu \left ( { x , y , z } \right ) = { z ^ 2 } \left ( { { x ^ 2 } + { y ^ 2 } } \right )$$ است.

حل: جرم سطح با رابطه زیر به دست می‌آید:

$$\large m = \iint \limits _ S { \mu \left ( { x , y , z } \right ) d S } .$$

ابتدا المان سطحی $$dS$$ را محاسبه می­‌کنیم:

$$\large d S = \left | { \frac { { \partial \mathbf { r } } } { { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } } } \right | d u d v .$$

در ادامه، مشتقات جزئی و ضرب خارجی آن‌ها را به دست می‌آوریم:

$$\large \begin{align*} \frac { { \partial \mathbf { r } } } { { \partial u } } & = – a \sin u \cdot \mathbf { i } + { a \cos u \cdot \mathbf { j } } + { 0 \cdot \mathbf { k } , } \\ \frac { { \partial \mathbf { r } } } { { \partial v } } & = 0 \cdot \mathbf { i } + { 0 \cdot \mathbf { j } } + { 1 \cdot \mathbf { k } } \end {align*}$$

$$ \large \begin{align*}<br /> & \Rightarrow \frac { { \partial \mathbf { r } } } { { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } }<br /> = { \left | { \begin {array} { * { 2 0 } { c } }<br /> \mathbf { i } & \mathbf { j } & \mathbf { k } \\<br /> { – a \sin u } & { a \cos u } & 0 \\<br /> 0 & 0 & 1<br /> \end {array} } \right | }<br /> = { a \cos u \cdot \mathbf { i } } + { a \sin u \cdot \mathbf { j } , } \\<br /> & \Rightarrow \left | { \frac { { \partial \mathbf { r } } }{ { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } } } \right | = { \sqrt { { a ^ 2 } { { \cos } ^ 2 } u + { a ^ 2 } { { \sin } ^ 2 } u } } = { a . }<br /> \end {align*} $$

بنابراین، $$dS = adudv$$ است. اکنون می‌توانیم جرم سطح را محاسبه کنیم:

$$\large \begin{align*} m & = \iint \limits _ S { \mu \left ( { x , y , z } \right ) d S } = { \iint \limits _ S { { z ^ 2 } \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d S } } \\ & = { \iint \limits _ { D \left ( { u , v } \right ) } { { v ^ 2 } \left ( { { a ^ 2 } { { \cos } ^ 2 } u + { a ^ 2 } { { \sin } ^ 2 } u } \right ) a d u d v } } = { { a ^ 3 } \int \limits _ 0 ^ { 2 \pi } { d u } \int \limits _ 0 ^ H { { v ^ 2 } d v } } \\ & = { 2 \pi { a ^ 3 } \int \limits _ 0 ^ H { {v ^ 2 } d v } } = { 2 \pi { a ^ 3 } \left [ { \left . { \left ( { \frac { { { v ^ 3 } } } { 3 } } \right ) } \right | _ 0 ^ H } \right ] } = { \frac { { 2 \pi { a ^ 3 } { H ^ 3 } } } { 3 } . } \end {align*}$$

مثال 2

جرم سطحی سهمی $$z ={x^2} + {y^2}, 0 \le z \le 1$$ با چگالی $${\mu \left( {x,y,z} \right)} = z$$ را به دست آورید.

حل:‌ از فرمول زیر برای محاسبه جرم استفاده می‌کنیم:

$$\large m = \iint \limits _ S { \mu \left ( { x , y , z } \right ) d S } .$$

تصویر $$D\left( {x,y} \right)$$ سطح سهمی $$S$$ روی صفحه $$xy$$ دایره‌ای به شعاع $$1$$ است که مرکز آن در مبدأ قرار گرفته است. از این رو، می‌توان نوشت:

$$\large \begin{align*} m & = \iint \limits _ S { \mu \left ( { x , y , z } \right ) d S } = { \iint \limits _ S { z d S } } \\ & = { \iint \limits _ { D \left ( { x , y } \right ) } { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) \cdot } \kern0pt { \sqrt { 1 + 4 { x ^ 2 } + 4 { y ^ 2 } } d x d y } } \end {align*}$$

با استفاده از تبدیل مختصات دکارتی به مختصات قطبی داریم:

$$\large \begin{align*} { m } & = { \iint \limits _ { D \left ( { r , \varphi } \right ) } { { r ^ 2 } \sqrt { 1 + 4 { r ^ 2 } } r d r d \varphi } } = { \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ 1 { { r ^ 3 } \sqrt { 1 + 4 { r ^ 2 } } d r} } \\ & = { 2 \pi \int \limits _ 0 ^ 1 { { r ^ 3 } \sqrt { 1 + 4 { r ^ 2 } } d r } . } \end {align*}$$

با قرار دادن $$1 + 4{r^2} = {u^2}$$ و در نتیجه $$8rdr = 2udu$$ یا $$rdr = {\large\frac{{udu}}{4}\normalsize}$$ انتگرال را حل می‌کنیم. هنگامی که $$r = 0$$ است، $$u = 1$$ و هنگامی که $$r = 1$$ است، $$u = \sqrt 5$$ خواهد بود. از این رو، خواهیم داشت:

$$\large \begin{align*} { m } & = { 2 \pi \int \limits _ 1 ^ { \sqrt 5 } { \frac { { { u ^ 2 } – 1 } } { 4 } \sqrt { { u ^ 2 } } \frac { { u d u } } { 4 } } } = { \frac { \pi } { 8 } \int \limits _1 ^ { \sqrt 5 } { \left ( { { u ^ 2 } – 1 } \right ) { u ^ 2 } d u } } \\ & = { \frac { \pi }{ 8 } \int \limits _ 1 ^ { \sqrt 5 } { \left ( { { u ^ 4 } – { u ^ 2 } } \right ) d u } } = { \frac { \pi } { 8 } \left [ { \left . { \left ( { \frac { { { u ^ 5 } } } { 5 } – \frac { { { u ^ 3 } } } { 3 } } \right ) } \right | _ 1 ^ { \sqrt 5 } } \right ] } \\ & = { \frac { \pi } { 8 } \left [ { \left ( { \frac { { { { \left ( { \sqrt 5 } \right ) } ^ 5 } } } { 5 } – \frac { { { { \left ( { \sqrt 5 } \right ) } ^ 3 } } } { 3 } } \right ) } \right . } - { \left . { \left ( { \frac {1 } { 5 } – \frac { 1 } { 3 } } \right ) } \right ] } \\ & = { \frac { \pi } { 8 } \left ( { \frac { { 1 0 \sqrt 5 } } { 3 } + \frac { 2 } {{ 1 5 } } } \right ) } = { \frac { { \pi \left ( { 2 5 \sqrt 5 + 1 } \right ) } } { { 6 0 } } .} \end {align*}$$

مثال ۳

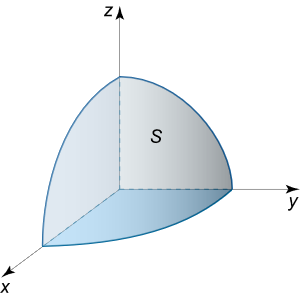
مرکز جرم یک‌هشتم اول کره‌ای با معادله $${ x ^ 2 } + { y ^ 2 } + { z ^ 2 } = { a ^ 2 }$$ و چگالی ثابت $${\mu_0}$$ را محاسبه کنید.

حل: واضح است که جرم یک‌هشتم اول کره (شکل 3) از رابطه زیر به دست می‌آید:

$$\large { m = \frac { 1 } { 8 } \iint \limits _ S { { \mu _ 0 } d S } } = { \frac { { { \mu _ 0 } } } { 8 } \iint \limits _ S { d S } } = { \frac { { { \mu _ 0 } } } { 8 } \cdot 4 \pi { a ^ 2 } } = { \frac { { { \mu _ 0 } \pi { a ^ 2 } } } { 2 } . }$$

گشتاور اول $${M_{yz}}$$ را محاسبه می‌کنیم:

$$\large \begin{align*} { { M _ { y z } } } & = { \iint \limits _ S { x \mu \left ( { x , y , z } \right ) d S } } = { { \mu _ 0 } \iint \limits _ S { x d S } } \\ & = { { \mu _ 0 } \iint \limits _ { D \left ( { x , y } \right ) } { x \cdot } } \kern0pt { { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } d x d y } } \end {align*}$$

که در آن، تصویر $${D\left( {x,y} \right)}$$ سطح روی صفحه $$xy$$ قسمتی از دایره است که در ربع اول قرار می‌گیرد (شکل 4).

از آن‌جایی که:

$$\large \begin{align*} { \frac { { \partial z } } { { \partial x } } } & = { \frac { \partial } { { \partial x } } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } = { \frac { { – x } } { { \sqrt { { a ^ 2 } – { x ^ 2 } – { y^ 2 } } } } , } \\ { \frac { { \partial z } } { { \partial y } } } & = { \frac { \partial } { { \partial y } } \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } = { \frac { { – y } } { { \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } } } \end {align*}$$

آن‌گاه:

$$\large { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } } = { \frac { a } { { \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } } . }$$

بنابراین، گشتاور اول $${M_{yz}}$$ برابر است با:

$$\large { { M _ { y z } } \text { = } } \kern0pt { { \mu _ 0 } a \int \limits _ { D \left ( { x , y } \right ) } { \frac { { x d x d y } } { { \sqrt { { a ^ 2 } – { x ^ 2 } – { y ^ 2 } } } } } . }$$

استفاده از مختصات قطبی برای حل این انتگرال مناسب است:

$$\large \begin{align*} { { M _ { y z } } } & = { { \mu _ 0 } a \iint \limits _ { D \left ( { r , \varphi } \right ) } { \frac { { r \cos \varphi \cdot r d r d \varphi } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } } } \\ & = { { \mu _ 0 } a \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \cos \varphi d \varphi } \int \limits _ 0 ^ a { \frac { { { r ^ 2 } d r } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } } } \\ & = { { \mu _ 0 } a \cdot \left [ { \left . { \left ( { – \sin \varphi } \right ) } \right | _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } } \right ] \cdot } \kern0pt { \int \limits _ a ^ 0 { \frac { { { a ^ 2 } – { r ^ 2 } – { a ^ 2 } } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } d r } } \\ & = { { \mu _ 0 } a \left [ { \int \limits _ a ^ 0 { \sqrt { { a ^ 2 } – { r ^ 2 } } d r } } \right . } - { \left . { {a ^ 2 } \int \limits _ a ^ 0 { \frac { { d r } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } } } \right ] . } \end {align*}$$

انتگرال اول $${ \int \limits _ a ^ 0 { \sqrt { { a ^ 2 } – { r ^ 2 } } d r } }$$ را با استفاده از تغییر پارامتر $$r = a \sin t , d r = a \cos t d t$$ حل می‌کنیم. در نتیجه، بازه پارامتر  $$t$$، از $${\large\frac{\pi }{2}\normalsize}$$ تا $$0$$ خواهد بود. بنابراین، خواهیم داشت:

$$\large \begin{align*} { \int \limits _ a ^ 0 { \sqrt { { a ^ 2} – { r ^ 2 } } d r } } & = { \int \limits _ { \large \frac { \pi } { 2 } \normalsize } ^ 0 { \sqrt { { a ^ 2 } – { a ^ 2 } { { \sin } ^ 2 } t } \cdot } \kern0pt { a \cos t d t } } = { { a ^ 2 } \int \limits _ { \large \frac { \pi } { 2 } \normalsize } ^ 0 { { { \cos } ^ 2 } t d t } } \\ & = { { a ^ 2 } \int \limits _ { \large \frac { \pi }{ 2 } \normalsize } ^ 0 { \frac { { 1 + \cos 2 t } } { 2 } d t } } = { \frac { { { a ^ 2 } } } { 2 } \left [ { \left . { \left ( { t + \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ { \large \frac { \pi }{ 2 } \normalsize } ^ 0 } \right ] } \\ & = { \frac { { { a ^ 2 } } } { 2 } \cdot \left ( { – \frac { \pi } { 2 } } \right ) } = { – \frac { { \pi { a ^ 2 } } } { 4 } . } \end {align*}$$

اکنون انتگرال دوم را حل می‌کنیم:

$$\large { \int \limits _ a ^ 0 { \frac { { d r } } { { \sqrt { { a ^ 2 } – { r ^ 2 } } } } } } = { \left . { \left ( { \arcsin \frac { r } { a } } \right ) } \right | _ a ^ 0 } = { \arcsin 0 – \arcsin 1 } = { – \frac { \pi } { 2 } . }$$

با جای‌گذاری جواب‌های به دست آمده خواهیم داشت:

$$\large { { M _ { y z } } } = { { \mu _ 0 } a \left [ { – \frac { { \pi { a ^ 2 } } } { 4 } – { a ^ 2 } \left ( { – \frac { \pi } { 2 } } \right ) } \right ] } = { { \mu _ 0 } a \cdot \frac { { \pi { a ^ 2 } } } { 4 } } = { \frac { { { \mu _ 0 } \pi { a ^ 3 } } } { 4 } . }$$

در نتیجه مختصه $$x_C$$ مرکز جرم برابر است با:

$$\large { { x _ C } = \frac { { { M _ { y z } } } } { m } = \frac { { \frac { { { \mu _ 0 } \pi { a ^ 3 } } } { 4 } } } { { \frac { { { \mu _ 0 } \pi { a ^ 2 } } } { 2 } } } } = { \frac { a }{ 2 } . }$$

با استفاده از تقارن، می‌توان نتیجه گرفت که دو مختصه دیگر مقدار یکسانی دارند. بنابراین، مختصات مرکز جرم پوسته برابر است با:

$$\large { \left ( { { x _ C } , { y _ C } , { z _ C } } \right ) } = { \left ( { \frac { a } { 2 } , \frac { a } { 2 } , \frac { a } { 2 } } \right ) . }$$

مثال ۴

گشتاور لختی پوسته کروی یکنواخت $${ x ^ 2 } + { y ^ 2 } + { z ^ 2 } = 1 \left ( { z \ge 0 } \right )$$ با چگالی $${\mu_0}$$ را حول محور $$z$$ به دست آورید.

حل: گشتاور لختی $${I_z}$$ این پوسته کروی به صورت زیر است:

$$\large { { I _ z } } = { \iint \limits _ S { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) \mu \left ( { x , y , z } \right ) d S } } = { { \mu _ 0 } \iint \limits _ S { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d S } }$$

که در آن سطح $$S$$ نیم‌کره‌ای با معادله $${ x ^ 2 } + { y ^ 2 } + { z ^ 2 } = 1 \left ( { z \ge 0 } \right )$$ است.

از آن‌جایی که معادله نیم‌کره بالایی $$z = \sqrt { 1 – { x ^ 2 } – { y ^ 2 } }$$ است، المان سطحی برابر است با:

$$\large { d S \text { = } } \kern0pt { \sqrt { 1 + { { \left ( { \frac { { \partial z } } { { \partial x } } } \right ) } ^ 2 } + { { \left ( { \frac { { \partial z } } { { \partial y } } } \right ) } ^ 2 } } d x d y } = { \frac { { d x d y } } { { \sqrt { 1 – { x ^ 2 } – { y ^ 2 } } } } . }$$

بنابراین، می‌توان انتگرال سطحی را به صورت انتگرال دوگانه نوشت:

$$\large { { I _ z } } = { { \mu _ 0 } \iint \limits _ S { \left ( { { x ^ 2 } + { y ^ 2 } } \right ) d S } } = { { \mu _ 0 } \iint \limits _ { D \left ( { x , y } \right ) } { \frac { { { x ^ 2 } + { y ^ 2 } } } { { \sqrt { 1 – { x ^ 2 } – { y ^ 2 } } } } d x d y } }$$

که در آن، ناحیه انتگرال‌گیری $${D\left( {x,y} \right)}$$، دایره‌ای به صورت $${x^2} + {y^2} \le 1$$ است. با استفاده از تبدیل مختصات دکارتی به قطبی داریم:

$$\large \begin{align*} { { I _ z } } & = { { \mu _ 0 } \iint \limits _ { D \left ( { x , y } \right ) } { \frac { { { x ^ 2 } + { y ^2 } } } { { \sqrt { 1 – { x ^ 2 } – { y ^ 2 } } } } d x d y } } \\ & = { { \mu _ 0 } \iint \limits _ { D \left ( { r , \varphi } \right ) } { \frac { { { r ^ 2 } } } { { \sqrt { 1 – { r ^ 2 } } } } r d r d \varphi } } \\ & = { { \mu _ 0 } \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ 1 { \frac { { { r ^ 3 } d r } } { { \sqrt { 1 – { r ^2 } } } } } . } \end {align*}$$

برای حل انتگرال دوم، از تغییر متغیر $$1 – {r^2} = t,\Rightarrow – 2rdr = dt$$ یا $$rdr = – {\large\frac{{dt}}{2}\normalsize}$$ استفاده می‌کنیم. بازه $$t$$ نیز از $$1$$ تا $$0$$ خواهد بود. در نتیجه خواهیم داشت:

$$\large \begin{align*} { { I _ z } } & = { 2 \pi { \mu _ 0 } \int \limits _ 0 ^ 1 { \frac { { { r ^ 3 } d r } } { { \sqrt { 1 – { r ^ 2 } } } } } } = { 2 \pi { \mu _ 0 } \int \limits _ 0 ^ 1 { \frac { { { r ^ 2 } \cdot r d r } } { { \sqrt { 1 – { r ^ 2 } } } } } } \\ & = { 2 \pi { \mu _ 0 } \int \limits _ 1 ^ 0 { \frac { { \left ( { 1 – t } \right ) \left ( { – \frac { { d t } } { 2 } } \right ) } } { { \sqrt t } } } } = { \pi { \mu _ 0 } \int \limits _ 1 ^ 0 { \frac { { t – 1 } } { { \sqrt t } } d t } } \\ & = { \pi { \mu _ 0 } \left [ { \int \limits _ 1 ^ 0 { \sqrt t d t } – \int \limits _ 1 ^ 0 { \frac { { d t } } { { \sqrt t } } } } \right ] } = { \pi { \mu _ 0 } \left [ { \left . { \left ( { \frac { { { t ^ { \frac { 3 } { 2 } } } } } { { \frac { 3 } { 2 } } } – \frac { { { t ^ { \frac { 1 } { 2 } } } } } { { \frac { 1 } { 2 } } } } \right ) } \right | _ 1 ^ 0 } \right ] } \\ & = { \pi { \mu _ 0 } \left [ { \left . { \left ( { \frac { 2 } { 3 } \sqrt { { t ^ 3 } } – 2 \sqrt t } \right ) } \right | _ 1 ^ 0 } \right ] } = { \frac { 4 } { 3 } \pi { \mu _ 0 } . } \end {align*}$$

مثال ۵

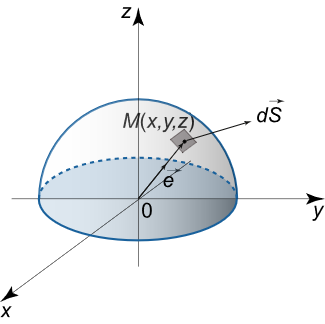
نیروی جاذبه بین نیم‌کره‌ای به شعاع $$r$$ و با چگالی ثابت $$\mu _0$$ که در مبدأ متمرکز شده است و جرم نقطه‌ای $$m$$ واقع در مبدأ را محاسبه کنید.

حل: نقطه $$M\left( {x,y,z} \right)$$ روی نیم‌کره را که متعلق به المان سطحی $$dS$$ است، در نظر بگیرید (شکل 5).

نیروی جاذبه $$d\mathbf{F}\left( M \right)$$ بین المان سطحی $$dS$$ و جرم نقطه‌ای $$M$$ را می‌توان به شکل زیر نوشت:

$$\large { d \mathbf { F } \left ( M \right ) } = { \frac { { G { \mu _ 0 } m d S } } { { { r ^ 2 } } } \mathbf { e } \left ( { O , M } \right ) }$$

که در آن، $$G$$ ثابت گرانشی و $$\mathbf{e}\left( {O,M} \right)$$ بردار یکه جهت‌­دار از نقطه $$O$$ تا نقطه $$M$$ است.

از آن‌جایی که $${ \mathbf { e } \left ( { O , M } \right ) } = { \left ( { { \large \frac { x } {r } \normalsize } , { \large \frac { y } { r } \normalsize } , { \large \frac { z } { r } \normalsize } } \right ) }$$ است، می‌توان نوشت:

$$\large { d \mathbf { F } \left ( M \right ) } = { \frac { { G { \mu _ 0 } m d S } } { { { r ^ 3 } } } \left ( { x , y , z } \right ) . }$$

پس از انتگرال‌گیری روی نیم‌کره مفروض، داریم:

$$\large { { F _ x } = \frac {{ G { \mu _ 0 } m } }{ { { r ^ 3 } } } \iint \limits _ S { x d S } , \; \; \; } \kern-0.3pt { { F _ y } = \frac { { G { \mu _ 0 } m } } { { { r ^ 3 } } } \iint \limits _ S { y d S } , \; \; \; } \kern-0.3pt { { F _ z } = \frac { { G { \mu _ 0 } m } } { { { r ^ 3 } } } \iint \limits _ S { z d S } . }$$

در مختصات کروی، بردار مکان را به صورت زیر نشان می‌دهیم:

$$\large { \mathbf { r } \left ( { \psi , \theta } \right ) } = { r \cos \psi \sin \theta \cdot \mathbf { i } } + { r \sin \psi \sin \theta \cdot \mathbf { j } } + { r \cos \theta \cdot \mathbf { k } }$$

که در آن، $$0 \le \psi \le 2 \pi , 0 \le \theta \le { \large \frac { \pi }{ 2 } \normalsize }$$.

المان سطحی کره در مختصات کروی، $$d S = { r ^ 2 } \sin \theta d \psi d \theta$$ است. از این رو، مؤلفه‌های نیرو به این صورت خواهند بود:

$$\large \begin{align*} { F _ x } & = \frac { { G { \mu _ 0 } m } }{ { { r ^ 3 } } } \iint \limits _ S { x d S } = { \frac { { G { \mu _ 0 } m } } { { { r ^ 3 } } } \iint \limits _ { D \left ( {\psi , \theta } \right ) } { r \cos \psi \sin \theta \cdot } \kern0pt { { r ^ 2 } \sin \theta d \psi d \theta } } \\ & = { G { \mu _ 0 } m \int \limits _ 0 ^ { 2 \pi } { \cos \psi d \psi } \cdot } \kern0pt { \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } \\ & = { G { \mu _ 0 } m \cdot \left [ { \left . { \left ( { \sin \psi } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] \cdot } \kern0pt { \int \limits _0 ^ { \large \frac { \pi } { 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } \\ & = { G { \mu _ 0 } m \cdot 0 \cdot \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } = { 0  }; \end {align*}$$

$$\large \begin{align*} { F _ y } & = \frac { { G { \mu _ 0 } m } } { { { r ^ 3 } } } \iint \limits _ S { y d S } = { \frac { { G { \mu _ 0 } m } } { {{ r ^ 3 } } } \iint \limits _ { D \left ( { \psi , \theta } \right ) } { r \sin \psi \sin \theta \cdot } \kern0pt { { r ^ 2 } \sin \theta d \psi d \theta } } \\ & = { G { \mu _ 0 } m \int \limits _ 0 ^ { 2 \pi } { \sin \psi d \psi } \cdot } \kern0pt { \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } \\ & = { G { \mu _ 0 } m \cdot \left [ { \left . { \left ( { - \cos \psi } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] \cdot } \kern0pt { \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } \\ & = { G { \mu _ 0 } m \cdot 0 \cdot \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { \sin ^ 2 } \theta d \theta } } = { 0 ; } \end {align*}$$

$$\large \begin{align*} { F _ z } & = \frac { { G { \mu _ 0 } m } }{ { { r ^ 3 } } } \iint \limits _ S { z d S } = { \frac { { G { \mu _ 0 } m } } { {{ r ^ 3 } } } \iint \limits _ { D \left ( { \psi , \theta } \right ) } { r \cos \theta \cdot } \kern0pt { { r ^ 2 } \sin \theta d \psi d \theta } } \\ & = { G { \mu _ 0 } m \int \limits _ 0 ^ { 2 \pi } { d \psi } \cdot } \kern0pt { \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \sin \theta \cos \theta d \theta } } \\ & = { 2 \pi G { \mu _ 0 } m \cdot \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \sin \theta d \left ( { \sin \theta } \right ) } } \\ & = { 2 \pi G { \mu _ 0 } m \cdot \left [ { \left . { \left ( { \frac { { { { \sin } ^ 2 } \theta } } { 2 } } \right ) } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } \right ] } \\ & = { 2 \pi G { \mu _ 0 } m \cdot \frac { 1 } { 2 } } = { \pi G { \mu _ 0 } m . } \end {align*}$$

همان‌گونه که می‌بینیم، $${F_x}= {F_y} = 0$$ است. واضح است که این نتیجه به علت تقارن سطح یکنواخت حاصل شده است. بنابراین، نیروی برایند برابر با $$F = {F_z}= \pi G{\mu _0}m$$ و در راستای محور $$z$$ خواهد بود.

مثال ۶

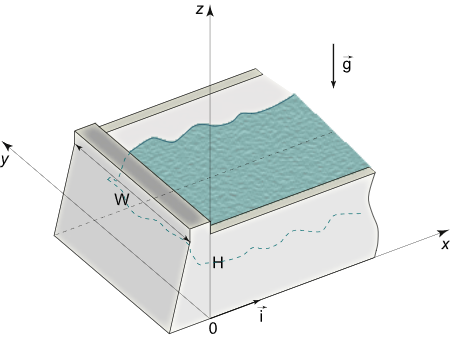
نیروی فشار وارد بر یک سد مخزنی آب به عرض $$W$$ و ارتفاع $$H$$ را تعیین کنید (شکل ۶).

حل: طبق شرط تعادل هیدرواستاتیکی، فشار نسبی روی سطح وابسته به $$z$$ سد با رابطه زیر نشان داده می‌شود:

$$\large p \left ( z \right ) = \rho g \left ( { H – z } \right )$$

که در آن، $$rho$$ چگالی آب و $$g$$ شتاب گرانشی است.

نیروی فشار کل وارد بر سطح سد به صورت زیر به دست می‌آید:

$$\large \begin{align*} \mathbf { F } & = \iint \limits _ S { p \mathbf { n } d S } = { \int \limits _ 0 ^ W { \int \limits _ 0 ^ H { \rho g \left ( { H – z } \right ) \cdot \left ( { – \mathbf { i } } \right ) d y d z } } } \\ & = { \rho g W \left ( { – \mathbf { i } } \right ) \left [ { \left . { \left ( { H z – \frac { { { z ^ 2 } } } { 2 } } \right ) } \right | _ 0 ^ H } \right ] } = { \frac { { \rho g W { H ^ 2 } } } { 2 } \left ( { – \mathbf { i } } \right ) . } \end {align*}$$

بردار $$\left( { – \mathbf{i}} \right)$$، جهت نیروی $$\mathbf{F}$$ را نشان می‌دهد. قدر مطلق نیرو برابر است با:

$$\large \left | \mathbf { F } \right | = \frac { { \rho g W { H ^ 2 } } } { 2 } .$$

مثال ۷

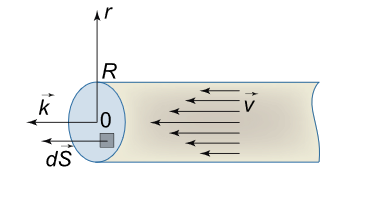
یک سیال چسبناک در طول یک لوله استوانه‌ای به شعاع $$R$$ با میدان سرعت $$\mathbf{v}=C{e^{ – r}}\mathbf{k}\left( {\text{m} \cdot {{\text{s}}^{ – 1}}} \right)$$ جریان می‌یابد، که در آن، $$\mathbf{k}$$ بردار یکه در راستای محور لوله و در جهت جریان، $$r$$ فاصله از محور و $$C$$ یک ثابت است (شکل 7). شار سیال گذرنده از سطح مقطع لوله را محاسبه کنید.

حل: برای تعیین شار سیال، باید انتگرال سطحی زیر را محاسبه کنیم:

$$\large \Phi = \iint \limits _ S { \mathbf { v } \cdot d \mathbf { S } } .$$

از آن‌جایی که بردارهای $$d\mathbf{S}$$ و $$\mathbf{v}$$ جهت‌های یکسانی دارند، می‌توان نوشت:

$$\large \Phi = \iint \limits _ S { C { e ^ { – r } } d S } .$$

با استفاده از تبدیل مختصات داریم:

$$\large { \Phi = C \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ R { { e ^ { – r } } r d r } } = { 2 \pi C \int \limits _ 0 ^ R { { e ^ { – r } } r d r } . }$$

این انتگرال را می‌توان با استفاده از روش جزء به جزء حل کرد:

$$\large { u = r , \; \; { e ^ { – r } } d r = d v , \; \; } \Rightarrow { d u = d r , \; \; } \kern-0.3pt { v = \int { { e ^ { – r } } d r } } = { – { e ^ { – r } } }$$

در نتیجه، داریم:

$$\large \begin{align*} \int \limits _ 0 ^ R { { e ^ { – r } } r d r } & = { \left . { \left ( { – r { e ^ { – r } } } \right ) } \right | _ 0 ^ R – \int \limits _ 0 ^ R { \left ( { – { e ^ { – r } } } \right ) d r } } = { \left . { \left ( { – r { e ^ { – r } } } \right ) } \right | _ 0 ^ R + \int \limits _ 0 ^ R { { e ^ { – r } } d r } } \\ & = { \left . { \left ( { – r { e ^ { – r } } } \right ) } \right |_ 0 ^ R – \left . { \left ( { – { e ^ { – r } } } \right ) } \right | _ 0 ^ R } = {\left. {\left[ { – {e^{ – r}}\left( {r + 1} \right)} \right]} \right|_0^R } \\ & = { – { e ^ { – R } } \left ( { R + 1 } \right ) + { e ^ 0 } } = { 1 – \left ( { R + 1 } \right ) { e ^ { – R } } . } \end {align*}$$

بنابراین، شار سیال برابر است با:

$$\large { \Phi } = { 2 \pi C \left [ { 1 – \left ( { R + 1 } \right ) { e ^ { – R } } } \right ] \; } \kern-0.3pt { \left ( { { \text {m} ^ 3 } \cdot { \text { s } ^ { – 1 } } } \right ) . }$$

مثال ۸

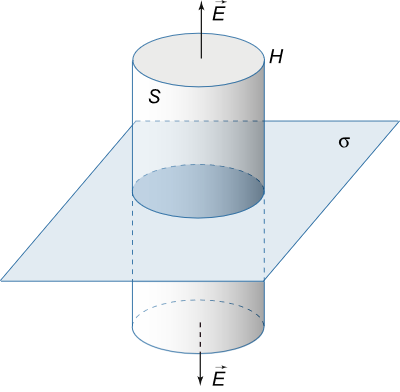
میدان الکتریکی یک صفحه بی‌نهایت با چگالی بار یکنواخت $$\sigma$$ را به دست آورید.

حل: با توجه به تقارن، راستای میدان الکتریکی برایند باید عمود بر صفحه باشد و در تمام نقاطی که فاصله یکسانی از صفحه دارند، مقدار یکسانی داشته باشد.

سطح گاوسی را استوانه‌ای با سطح مقطع $$S$$ و ارتفاع $$2H$$ در نظر می‌گیریم (شکل 8).

شار الکتریکی فقط در دو انتهای استوانه غیرصفر است؛ بنابراین، شار کل برابر است با $$\Phi = 2{\varepsilon _0}ES$$ که در آن، $$E$$ میدان الکتریکی در دو انتهای استوانه است. بار کل محصور شده توسط استوانه $$Q = \sigma S$$ است. در نتیجه با استفاده از قانون گاوس داریم:

$$\large { \Phi = { \varepsilon _ 0 } \iint \limits _ S { E \cdot d S } = Q , \; \; } \Rightarrow { 2 { \varepsilon _ 0 } E S = \sigma S \; \; \Rightarrow \; \; } \kern-0.3pt { E = \frac { \sigma }{ { 2 { \varepsilon _ 0 } } } . }$$

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری مباحث مشابه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضیات عمومی 2
• مجموعه آموزش‌های دروس فیزیک
• آموزش ریاضی فیزیک 1
• انتگرال توابع هیپربولیک — از صفر تا صد
• تقلب نامه (Cheat Sheet) مفاهیم و روابط انتگرال

^^