معادلات ماکسول (Maxwell’s Equations) – به زبان ساده

در مطالب گذشته فرادرس مفاهیم میدان الکتریکی و مغناطیسی بیان شدند. در ادامه گفتیم که چطور شار مغناطیسی متغیر با زمان می‌تواند میدان الکتریکی تولید کند. این ارتباط را با استفاده از قانون القای فارادی توصیف کردیم. با مطالعه مقالات مذکور احتمالا متوجه شده‌اید که میدان‌های الکتریکی،‌ مغناطیسی، بار الکتریکی و جریان الکتریکی به یکدیگر مرتبط هستند؛ در حقیقت هرکدام از این کمیت‌ها می‌تواند روی دیگری تاثیر‌گذار باشد. این ارتباط توسط «جیمز کلرک ماکسول» (James Clerk Maxwell)، دانشمند اسکاتلندی توضیح داده شد. او با استفاده از ۴ معادله، تحت عنوان «معادلات ماکسول» (Maxwell's equations) این ارتباط را توصیف کرد.

پس از مطالعه این مقاله، پیشنهاد می‌کنیم تا نگاهی بر مقاله «فرم دیفرانسیلی معادلات ماکسول — به زبان ساده [لینک مقاله]» داشته باشید تا پس از مرور مبانی الکترومغناطیس، با روند به دست آوردن فرم دیفرانسیلی معادلات ماکسول نیز آشنا شوید.

قانون گاوس و آمپر

در مطلب میدان مغناطیسی، ارتباط میان میدان مغناطیسی اطرافِ جریان الکتریکی، در قالب قانون آمپر، به‌صورت زیر بیان شد:

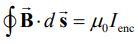
در شکل زیر شماتیک این قانون نشان داده شده است.

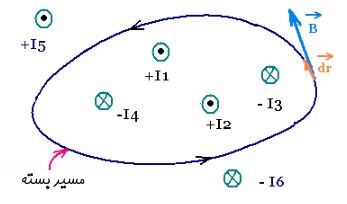
علاوه بر قانون آمپر، در مطلب القای فارادی نیز آموختیم که چگونه تغییرات میدان مغناطیسی می‌تواند، میدان الکتریکی تولید کند. میدان الکتریکی ناشی از تغییرات میدان مغناطیسی در زمان، مطابق با رابطه زیر بدست می‌آید.

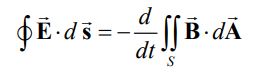
از نظر فیزیکی سمت راست رابطه بالا تابعی از زمان است؛ از این رو بدیهی است که سمت چپ رابطه نیز بایستی وابسته به زمان باشد. بنابراین به نظر می‌رسد که می‌توان میدان مغناطیسی را بر حسب تغییرات میدان الکتریکی در زمان بیان کرد. جهت بدست آوردن میدان مغناطیسی ناشی از میدان الکتریکی متغیر، مطابق با شکل زیر خازنی را تصور کنید که به اندازه Q باردار شده است.

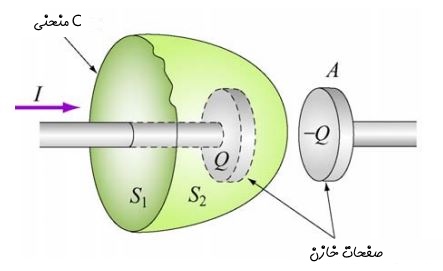
در مدت زمانی که خازن در حال شارژ شدن است، با اضافه شدن بار‌های الکتریکی بیشتر، میدان الکتریکی بین صفحات آن نیز افزایش می‌یابد. جهت استفاده از قانون آمپر در این حالت، مطابق شکل ۱ حلقه بسته C را در نظر بگیرید. حلقه C سطح دیسکی شکل و صاف S₁ را بوجود می‌آورد. هم‌چنین جریان الکتریکی I_enc=I از آن عبور می‌کند. این در حالی است که اگر سطح S₂ را به‌عنوان سطح آمپری در نظر بگیریم، جریان خالصی از آن عبور نخواهد کرد (I_enc=0). بنابراین سطح S₁ و S₂ به ترتیب میدان غیرصفر و صفر را روی منحنی C به ما می‌دهند که یک تناقض است.

ماکسول این تناقض را با اضافه کردن یک ترم به سمت راست قانون آمپر، حل کرد. این عبارت اضافه شده به صورت زیر است:

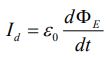
این ترم تحت عنوان «جریان جابجایی» (Displacement Current) شناخته می‌شود. ترم اضافه شده، تغییرات میدان الکتریکی با زمان را در خود دارد. نهایتا قانون ماکسول-آمپر به‌صورت زیر بیان می‌شود:

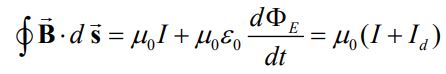
جهت درک مفهوم ترم اضافه شده،‌ شکل زیر را در نظر بگیرید.

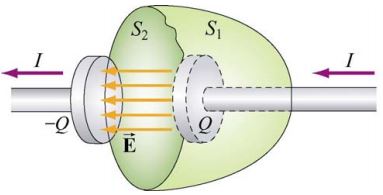
در شکل بالا شار الکتریکی عبوری از سطح S₂ برابر است با:

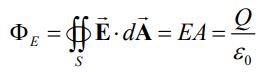
در رابطه بالا A مساحت سطح صفحات خازن است. از طرفی اگر نرخ ازدیاد بار‌های الکتریکی روی صفحات را برابر با I_d تصور کنیم، می‌توان جریان جابجایی I_d را به صورت زیر نوشت:

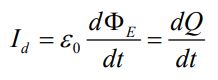
بدیهی است که سمت راست رابطه بالا جریان عبوری از سطح S₁ و S₂ را نشان می‌دهد. با مشتق‌گیری از رابطه ۱ و قرار دادن آن در رابطه ۲ داریم:

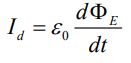
جریان بالا معادل با تغییرات شار الکتریکی نسبت به زمان است. در حقیقت این تغییرات، معادل با جریانی الکتریکی فرض شده که مطابق با رابطه بالا بدست می‌آید.

قانون گاوس در مغناطیس

قانون گاوس بیان می‌کند که شار الکتریکی عبوری از یک سطح بسته متناسب با میزان بار الکتریکی قرار گرفته در سطح مذکور است. به نظر شما چطور می‌توان این قانون را در حالت مغناطیسی نوشت. قانون گاوس در حالت مغناطیسی برابر است با:

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

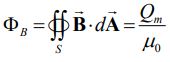
در رابطه بالا Q_m تک‌قطبی‌های مغناطیسی هستند که در سطح گاوسی قرار گرفته‌اند. در مطالب گذشته بلاگ فرادرس بیان شد که تاکنون تک‌قطبی مغناطیسی در طبیعت دیده نشده است. در حقیقت هر آهنربایی که در طبیعت وجود دارد، از قطب N و S تشکیل شده است. در نتیجه با صفر بودن Q_m، رابطه بالا به صورت زیر در می‌آید.

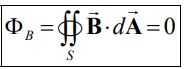
شکل زیر سطح گاوسی و خطوط میدان را در حالت الکتریکی و مغناطیسی نشان می‌دهد.

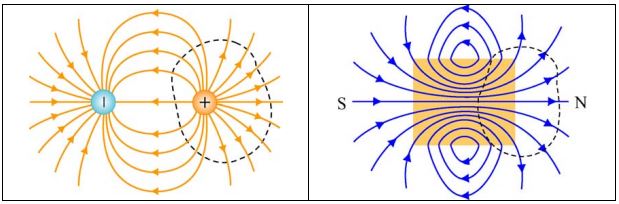
همان‌گونه که در شکل بالا نیز دیده می‌شود، در حالت الکتریکی خطوط میدان از سطح گاوسی خارج می‌شوند؛ این در حالی است که در حالت مغناطیسی اندازه خطوط وارد شده و خارج شده از سطح با هم برابر هستند؛ به همین دلیل انتگرال میدان مغناطیسی روی سطح مذکور صفر است.

معادلات ماکسول

تاکنون به ۴ معادله دست یافته‌ایم که روابط میان الکتریسیته ساکن، میدان الکتریکی و مغناطیسی را توصیف می‌کنند. جدول زیر این معادلات را به‌طور خلاصه نشان می‌دهد.

فیلم آموزش الکترومغناطیس مهندسی – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

مفهوم فیزیکی	معادله	قانون
شار الکتریکی عبوری از یک سطح بسته متناسب با میزان بار الکتریکی قرار گرفته درون آن است.		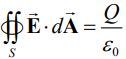قانون گاوس برای میدان $$\overrightarrow{E}$$
تغییر شار میدان مغناطیسی منجر به ایجاد میدان الکتریکی می‌شود.		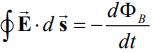قانون القای فارادی
شار مغناطیسی عبوری از یک سطح بسته برابر با صفر است.		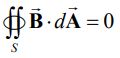قانون گاوس برای میدان $$\overrightarrow{B}$$
تغییرات شار الکتریکی در زمان منجر به تولید میدان مغناطیسی خواهد شد.		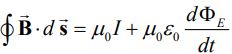قانون آمپر-ماکسول

به مجموعه معادلات بالا، معادلات ماکسول گفته می‌شود. روابط بالا را می‌توان به‌صورت دیفرانسیلی که در زیر آمده نیز نوشت:

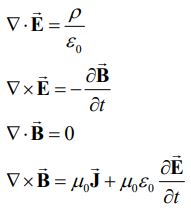
در روابط بالا ρ و $$\overrightarrow{J}$$ به‌ترتیب نشان دهنده چگالی بار و چگالی جریان الکتریکی هستند. در حالتی که بار الکتریکی وجود نداشته باشد، در روابط بالا Q و I برابر با صفر هستند. در نتیجه می‌توان روابط ارائه شده در جدول را به‌صورت زیر بازنویسی کرد:

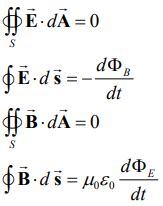
نتیجه مهم معادلات ماکسول، پیش‌بینی وجود امواج الکترومغناطیسی است که با سرعت نور منتقل می‌شوند. در حقیقت موج الکترومغناطیسی، دو میدان عمود بر هم الکتریکی و مغناطیسی است که اندازه آن‌ها با زمان و به صورت تابعی از یکدیگر تغییر می‌کنند. شناسایی این امواج در سال ۱۸۸۷ توسط دانشمند آلمانی، «هانریش هرتز» صورت گرفت. انیمیشن زیر نمونه‌ای از موجی الکترومغناطیسی را نشان می‌دهد که در آن میدان‌های الکتریکی و مغناطیسی به‌صورت تابعی از یکدیگر و با زمان تغییر می‌کنند.

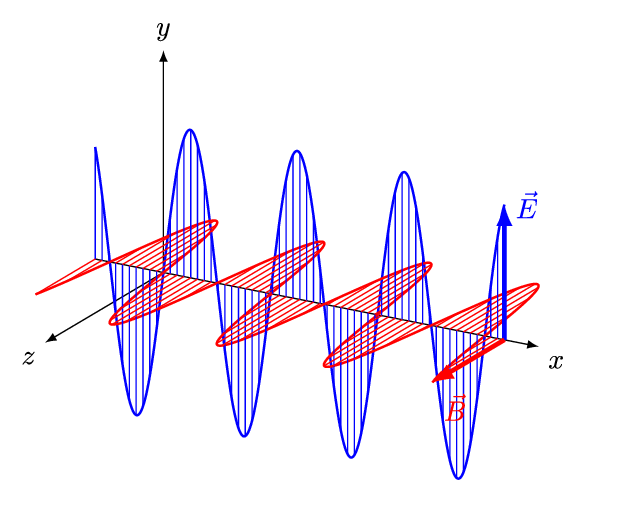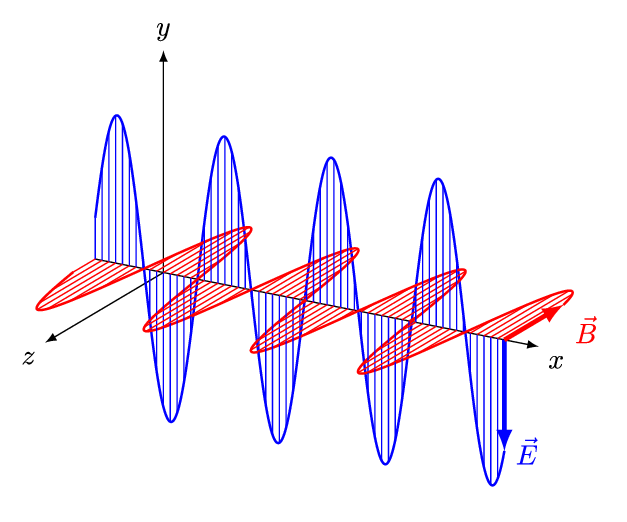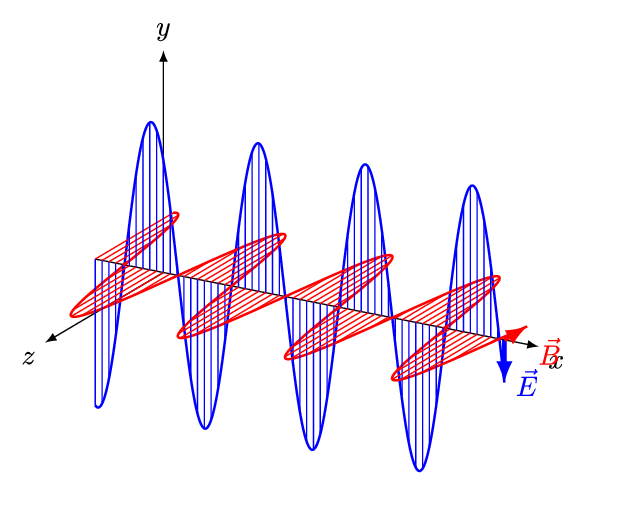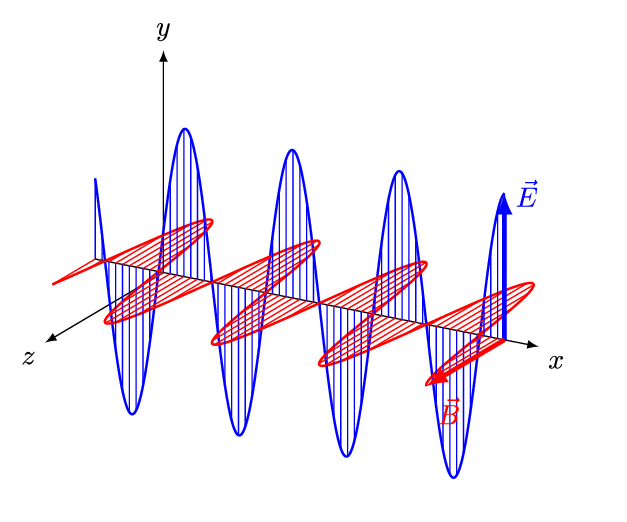
مطلب ارائه شده پیش‌نیازی جهت فراگیری امواج الکترومغناطیسی محسوب می‌شود. از این رو مطالعه آن موکدا توصیه می‌شود. در مطالب آینده بلاگ فرادرس، معادلات مربوط به امواج الکترومغناطیسی را تشریح خواهیم کرد.

^^