قانون گاوس (Gauss Law) و شار الکتریکی — به زبان ساده

پیش‌تر در وبلاگ فرادرس در مورد مفاهیم میدان الکتریکی و روش‌های محاسبه آن صحبت شد. در بخش مذکور در مورد این‌که چطور می‌توان میدان الکتریکی ناشی از یک بار نقطه‌ای و یا بار پیوسته را محاسبه کرد، بحث شد. همان‌طور که احتمالا از مثال‌های ارائه شده در آن مطلب دیدید، در اکثر مواقع میدان الکتریکی ناشی از توده‌ای بار پیوسته به سختی بدست می‌آید. در این قسمت روشی قدرتمند را معرفی خواهیم کرد که با استفاده از آن می‌توان میدان الکتریکی و در نتیجه پتانسیل الکتریکی ناشی از باری ذره‌‌ای و یا توده‌ای را بدست آورد.

در ادامه قصد داریم تا «قانون گاوس» (Gauss's law) در محاسبه میدان الکتریکی را تشریح کنیم. بدین منظور قبل از یاد‌گیری این روش لازم است تا با مفهومی در فیزیک، تحت عنوان «شار الکتریکی» (Electric Flux) آشنا باشید. از این رو ابتدا به ساکن به تشریح این مفهوم می‌پردازیم.

شار الکتریکی

به میزان خطوطی از میدان الکتریکی که از یک منبع و به صورت عمود بر یک صفحه می‌گذرند، شار الکتریکی گذرنده از آن سطح گفته می‌شود.

فیلم آموزش فیزیک ۲ دانشگاه در فرادرس

کلیک کنید

شکل زیر شار الکتریکی میدان E را نشان می‌دهد که از بخشی از سطح A عبور می‌کند.

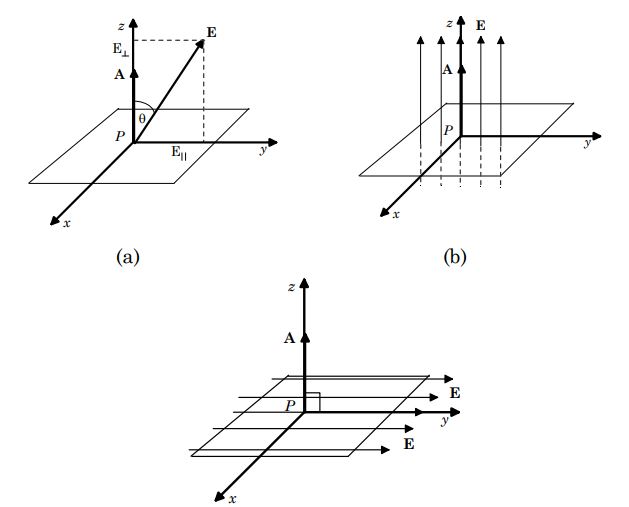
در شکل‌های بالا سه حالت متفاوت عبور میدان از سطح A نشان داده شده. در این اشکال $$\overrightarrow {A}$$ بردار سطح را نشان می‌دهد که در آن A اندازه این بردار است. جهت $$\overrightarrow {A}$$ نیز عمود بر سطوح در نظر گرفته می‌شود. در حقیقت مولفه‌ موازی میدان الکتریکی با بردار A در اندازه شار الکتریکی نقش دارد و مولفه عمود به بردار A در اندازه شار الکتریکی تاثیرگذار نیست. با توجه به مفاهیم بیان شده،‌ احتمالا حدس زده‌اید که شار الکتریکی به نحوی با ضرب داخلی بردارها در ارتباط است. بنابراین می‌توان شار الکتریکی Φ_E ناشی از میدان E که از سطح A می‌گذرد را با استفاده از رابطه زیر توصیف کرد.

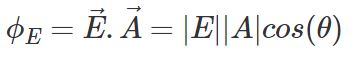
عبارت بالا تعداد خطوطی از میدان را نشان می‌دهد که از سطح A عبور می‌کند. در حقیقت این تعداد، بیان کننده قدرت میدان در سطح A است.

با توجه به شکل ۱ می‌توان میدان E در سطح A را به دو بخش موازی و عمود بر سطح تقسیم‌بندی کرد. میدان موازی و عمود را به ترتیب به صورت _||E و $$E_ \perp $$ نمایش می‌دهند. با استفاده از این نماد‌گذاری‌ها و همچنین با توجه به شکل ۱ میدان عمود به سطح A را می‌توان به صورت زیر بدست آورد.

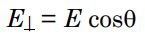
بر همین مبنا خطوطی که موازی با صفحه A هستند، برابر هستند با:

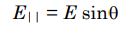
با توجه به این‌که تنها میدان‌های عمود به صفحه به عنوان شار حساب می‌شوند، در نتیجه شار میدان الکتریکی E در سطح A برابر با رابطه ۲ خواهد بود. در حقیقت مسیر رسیدن به ضرب داخلی به ترتیب زیر است:

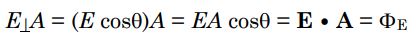
واضح است که $$\theta=0$$ حالتی را نشان می‌دهد که میدان E به طور کامل به سطح A عمود است. در قسمت b، شکل ۱ این حالت نشان داده شده. برای درک بهتر توجه شما را به مثالی که در ادامه آمده، جلب می‌کنیم.

مثال ۱

فرض کنید میدانی به اندازه $$500 \enspace V/m$$ با بردار عمود بر سطحی زاویه ۳۰ درجه ساخته. با فرض این‌که مساحت سطح برابر با $$0.5 \enspace m^2$$ باشد، شار الکتریکی عبوری از آن را بیابید.

همان‌گونه که بیان کردیم با ضرب داخلی دو بردار میدان و سطح، می‌توان شار الکتریکی را به صورت زیر بدست آورد.

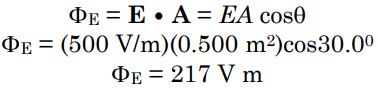
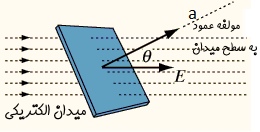
می‌توان از معادله بالا فهمید که واحد شار الکتریکی به صورت ولت.متر است. حال با درک مفهوم شار الکتریکی، زمان تشریح قانون گاوس فرا رسیده. در شکل زیر مولفه‌ای از میدان که در شار الکتریکی موثر است با بردار a نشان داده شده.

قانون گاوس

در بالا عنوان کردیم که به میزان خطوطی از میدان الکتریکی که از سطح A عبور می‌کند، شار الکتریکی گفته می‌شود. با توجه به این‌که میدان الکتریکی همواره ناشی از بار‌های الکتریکی است، از این رو این سوال مطرح می‌شود که آیا می‌توان ارتباطی میان شار الکتریکی و منبع تولید کننده میدان ایجاد کرد؟ پاسخ این سوال مثبت است.

فیلم آموزش الکترومغناطیس مهندسی در فرادرس

کلیک کنید

برای پاسخ به سوال مطرح شده در بالا، باری الکتریکی را فرض کنید که مطابق شکل زیر در نقطه‌ای به صورت ساکن قرار گرفته است. از مبحث میدان الکتریکی می‌دانیم که این بار منجر به ایجاد میدان الکتریکی اطراف خود می‌شود.

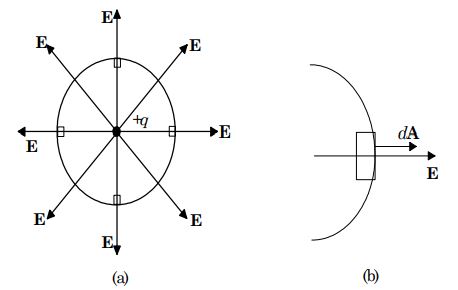
حال سطحی فرضی را اطراف این بار تصور کنید. در حالت سه‌بعدی این سطح بسته یک کره است. به سطح فرضی در نظر گرفته شده، «سطح گاوسی» (Gaussian Surface) گفته می‌شود. تصور کنید هدف ما محاسبه شار عبوری از این سطح بسته است. جهت میدان الکتریکی E در نقاط مختلف سطح فرض شده متفاوت است از این رو نمی‌توان از فرمول عمومی محاسبه شار استفاده کرد [منظور از فرمول عمومی رابطه $$\phi_E=EAcos(\theta)$$ است].

از این رو به‌منظور محاسبه شار روی سطح فرض شده می‌توان آن را به بینهایت بخش با مساحت dA تقسیم کرد. با استفاده از رابطه عمومی، شار عبوری از سطح دیفرانسیلی dA برابر است با:

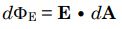
بدیهی است که با انتگرال‌گیری از رابطه بالا روی کل سطح بسته، کل شار عبوری از سطح کروی بسته، مطابق با رابطه زیر قابل محاسبه است.

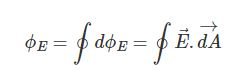
علامت $$\oint$$ به کار رفته شده در بالا به معنای انتگرال‌گیری رو کل سطح بسته‌ای است که می‌خواهیم شار الکتریکی عبوری از آن را محاسبه کنیم. با توجه به سطح در نظر گرفته شده در شکل ۲، بردار‌های $$\overrightarrow {E}$$ و $$\overrightarrow {A}$$ در تمامی سطح با یکدیگر هم‌جهت هستند.

از طرفی با توجه به مفاهیم عنوان شده در مطلب میدان الکتریکی می‌دانیم که یک ذره باردار، میدانی به اندازه E=kq/r² را در فاصله r از خود ایجاد می‌کند. با قرار دادن E در رابطه ۳، اندازه شار الکتریکی ناشی از این ذره مطابق با رابطه زیر بدست خواهد آمد.

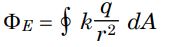
در رابطه بالا r شعاع کره گاوسیِ فرض شده، است که مقداری ثابت محسوب می‌شود. با توجه به ثابت بودن مقادیر k و q می‌توان آن‌ها را از انتگرال بیرون کشیده و رابطه بالا را به صورت زیر بازنویسی کرد.

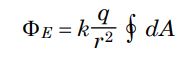
از مفاهیم انتگرال می‌دانید که انتگرال دیفرانسیل dA روی یک سطح بسته برابر با A است [در حقیقت انتگرال روی سطح بسته به این معنی است که تمامی دیفرانسیل‌های dA با هم جمع زده شوند که برابر با سطح کل می‌شود].  در نتیجه می‌توان نوشت:

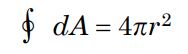
در نتیجه با جایگذاری عبارت بالا در رابطه ۴، شار الکتریکی برابر با مقدار زیر بدست می‌آید.

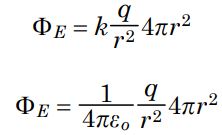
با ساده کردن رابطه بالا نهایتا مقدار شار الکتریکی برابر با عبارت زیر بدست می‌آید.

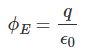
رابطه بالا قانون گاوس در الکتریسیته را نشان می‌دهد و می‌گوید: مقدار شار الکتریکی ناشی از بار q که در سطح بسته A قرار گرفته برابر با $$q \over {\epsilon_0}$$ است. بنابراین در حالت کلی می‌توان رابطه زیر را به‌منظور محاسبه شار خروجی از سطح بسته نوشت:

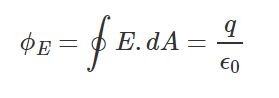
در رابطه بالا q بار خالص موجود در سطح بسته است. هم‌چنین در حالتی که توزیع بار در جسم به صورت توده‌ای باشد، می‌توان رابطه بالا را به شکل زیر بازنویسی کرد.

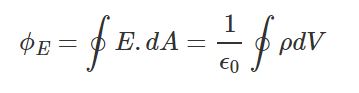
در حالت عمومی می‌توان از رابطه بالا به‌منظور محاسبه میدان الکتریکی استفاده کرد. از این رو در ادامه همین مطلب چندین مثال را به تفصیل مورد بررسی قرار خواهیم داد. برای نمونه در شکل زیر شار خالص عبوری از سطح بسته A برابر با صفر است چراکه بار خالص غیر صفری در آن وجود ندارد.

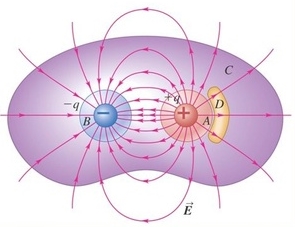
همان‌گونه که در شکل بالا می‌بینید، مجموع بار موجود در سطح بسته بنفش ‌رنگ برابر با صفر است. بنابراین مقدار شار خالص خروجی نیز از سطح مفروض صفر خواهد بود. توجه داشته باشید در حالتی که $$\phi _E$$ مثبت باشد، خطوط شار الکتریکی به سمت بیرون و در حالت منفی بودن آن خطوط شار نیز به سمت داخل است.

معمولا از این قانون به‌منظور محاسبه میدان الکتریکی اطراف توزیع‌ بار‌های مختلف استفاده می‌شود. در ادامه چند کاربرد را مورد بررسی قرار خواهیم داد. هم‌چنین به‌منظور درک بهتر این قانون و نحوه استفاده از آن دو مثال ذکر شده است.

مثال ۱: میدان الکتریکی ناشی از کره‌ای باردار

شکل زیر کره‌ای را نشان می‌دهد که باری به اندازه q در آن توزیع شده است. با فرض این‌که توزیع بار به صورت یکنواخت و چگالی بار برابر با ρ باشد، می‌خواهیم تغییرات میدان الکتریکی را بر حسب فاصله از کره بدست آوریم. برای استفاده از قانون گاوس در بدست آوردن میدان الکتریکی اولین و مهم‌ترین قدم انتخاب سطح بسته مناسب است.

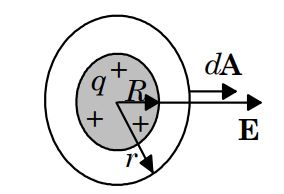
فرضیات مسئله به‌ ترتیب زیر هستند.

• q: بار توزیع شده درون کره
• R: شعاع کره
• ρ: چگالی بار توزیع شده روی کره

برای حل این مسئله دو حالت در نظر گرفته می‌شود. حالت اول زمانی است که بخواهیم میدان الکتریکی را درون کره بیابیم و در حالت دوم هدف ما محاسبه میدان الکتریکی بیرون از کره است.

۱. محاسبه میدان بیرون از کره

همان‌طور که بیان شد، به‌منظور تعیین میدان الکتریکی با استفاده از روش گاوسی، انتخاب سطح مناسب ضروری است. از این رو یکی از راه‌های مرسوم این است که نگاه کنیم و ببینیم که جسم یا ذره اصلی ما نسبت به کدام محور و یا مختصات زاویه‌ای تقارن دارد. مثلا برای این مسئله با توجه به کره‌ای شکل بودن جسم اصلی، ما نیز سطح گاوسی را به شکل یک کره در نظر می‌گیریم. سطح مذکور در شکل زیر نشان داده شده است.

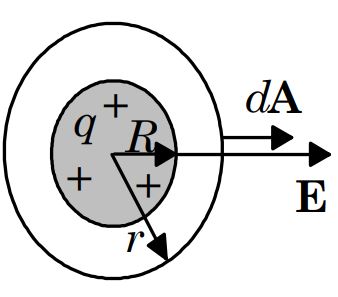
با توجه به این‌که توزیع بار به صورت کره‌ای، متقارن و یکنواخت است، بنابراین میدان الکتریکی E در تمامی نقاط سطح گاوسی، به صورت شعاعی، رو به بیرون از پوسته در نظر گرفته می‌شود. در حقیقت در این بخش از حل بایستی با استفاده از حس فیزیکی فرض درستی انجام دهیم و با توجه به آن ادامه مسئله را حل کنیم. هم‌چنین واضح است که بردار $$d {\overrightarrow {A}}$$ در تمامی نقاط سطح گاوسی در نظر گرفته شده، عمود بر سطح کره است. با توجه به این‌که بردار میدان $$ {\overrightarrow {E}}$$ نیز رو به بیرون در نظر گرفته شده، بنابراین جهت آن موازی با جهت $$d {\overrightarrow {A}}$$ است. با توجه به این فرضیات، قانون گاوس را می‌توان به شکل زیر نوشت:

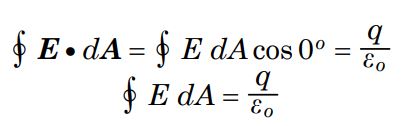
دوباره و با استفاده از استدلال متقارن بودن کره می‌توان به این نتیجه رسید که میدان الکتریکی در نقاطی که به فاصله شعاعی یکسان از کره قرار گرفته‌اند، یکسان خواهند بود. [ این جمله به این معنی است که اندازه میدان الکتریکی E، در چند نقطه که در فاصله برابرِ r از مرکز کره قرار گرفته‌اند، با یکدیگر برابر هستند]. در نتیجه می‌توان E را از انتگرال رابطه بالا بیرون کشید. نهایتا رابطه بالا به شکل در خواهد آمد.

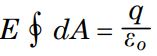
از طرفی انتگرال بسته مساحت نیز برابر با مساحت سطح گاوسی در نظر گرفته شده است. بنابراین داریم:

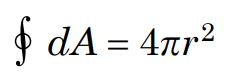
نهایتا میدان را می‌توان با استفاده از رابطه ۶، به شکل زیر بدست آورد.

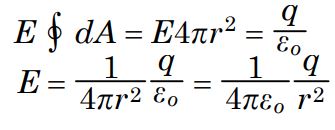
جالب این است که این نتیجه با استفاده از قانون کولن نیز بدست می‌آید. در حقیقت می‌توان کل بار موجود کره را در مرکز آن در نظر گرفت و سپس با استفاده قانون کولن و با ذره فرض کردن بار q،‌ میدان الکتریکی را بدست آورد.

۲. محاسبه میدان درون کره

در این حالت نیز سطح گاوسی را به شکل کره‌ای در نظر می‌گیریم که درون کره اصلی قرار گرفته. در حقیقت شعاع کره‌ فرض شده، از R کوچک‌تر است [r<R]. در شکل زیر کره باردار به همراه سطح گاوسی در نظر گرفته شده، نشان داده شده‌اند.

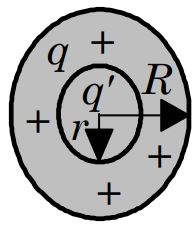
شعاع کره‌ گوسی در نظر گرفته شده را با r نشان می‌دهیم. هم‌چنین باری که این سطح را دربر گرفته برابر با 'q و حجم محدود به سطح در نظر گرفته شده برابر با 'v است. با توجه به این‌که توزیع بار در کره‌ به صورت یکنواخت در نظر گرفته شده بنابراین چگالی بار در تمامی فاصله‌ها برابر با ρ است. در حقیقت می‌توان گفت:

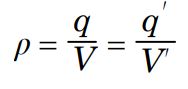
از این رو رابطه بالا را می‌توان بر حسب بار موجود در سطح گاوسی، به شکل زیر بازنویسی کرد.

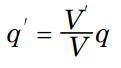
از طرفی حجم کل کره اصلی برابر است با:

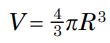
بدیهی است که حجم کره‌ گاوسی در نظر گرفته شده نیز برابر است با:

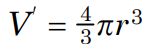
با جایگذاری دو رابطه بالا در رابطه ۷ داریم:

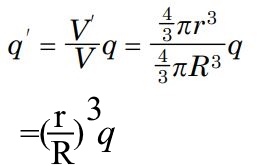
حال می‌توان قانون گاوس را برای سطح گاوسی در نظر گرفته شده به شکل زیر نوشت:

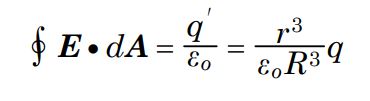
با توجه به این‌که مقادیر R، k و q ثابت هستند، در نتیجه با استفاده از رابطه بالا می‌توان تغییرات خطی میدان درون کره را درک کرد. شکل زیر تغییرات میدان الکتریکی را بر حسب شعاع r نشان می‌دهد. همان‌طور که می‌بینید در r=R روابط مربوط به میدان درون و بیرون از کره عددی یکسان را گزارش می‌دهند.

مثال ۲: میدان ناشی از میله‌ای باردار به طول بینهایت

میله‌ای به‌طول بینهایت را تصور کنید که باری با چگالی λ روی آن قرار گرفته است. شکل زیر بخشی از این میله را نشان داده است.

با توجه به رابطه مربوط به چگالی خطی بار‌های الکتریکی می‌توان گفت:

λ=q/L

هدف ما در این مسئله محاسبه میدان الکتریکی در فاصله r از میله است. هما‌نگونه که بیان شد، در اولین قدم بایستی سطح گاوسی مناسب را تشخیص دهیم. در مسئله قبل سطحی کروی شکل را در نظر گرفتیم و دلیل آن متقارن بودن مسئله بود. اما توجه داشته باشید که در این مسئله نمی‌توان از سطح کروی استفاده کرد، چرا که میدان ناشی از میله در همه جاها الزاما عمود بر سطح نیستند. قبل از مطالعه ادامه مطلب به نظر شما چه سطحی می‌تواند مناسب این مسئله باشد؟

با توجه به این‌که طول میله بینهایت است، بنابراین میدان‌های ناشی از بار‌های روی میله در تمامی نقاط، عمود بر خود میله خواهند بود. از این رو سطح گاوسی را به شکل استوانه‌ای در نظر می‌گیریم که میله مفروض محور آن است. در شکل زیر می‌بینید که چطور میدان ناشی از این میله به استوانه گاوسی فرض شده عمود است.

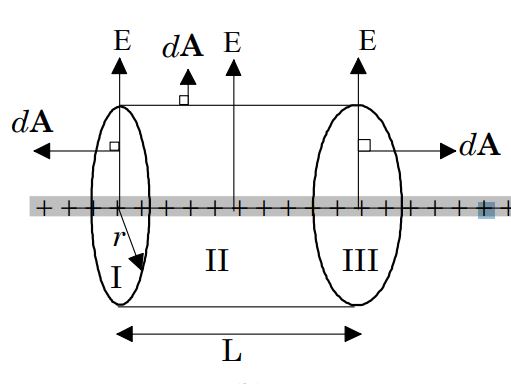
قانون گاوس برای استوانه مفروض را می‌توان به شکل زیر بیان کرد:

این انتگرال نشان دهنده شار عبوری از استوانه است. به‌منظور راحتی کار می‌توان سطح استوانه مفروض را به سه بخش تقسیم‌بندی کرد. در شکل ۳ سطوح در نظر گرفته شده، قابل مشاهده هستند.

1.  قاعده سمت چپ استوانه
2. بدنه استوانه
3.  قاعده سمت راست استوانه

شار کلی گذرنده از کل استوانه برابر با حاصل جمع شار تک‌تک سطوح است. بنابراین می‌توان گفت:

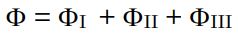
هر کدام از عبارات رابطه بالا شار گذرنده از همان سطح را نمایندگی می‌کنند. برای نمونه $$\phi_I$$ نشان دهنده شاری است که از سطح I عبوری می‌کند. معادل انتگرالی رابطه بالا را می‌توان به صورت زیر بیان کرد:

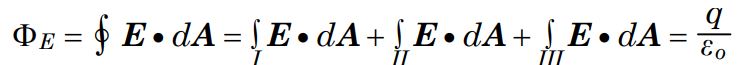
اگر توجه داشته باشید در سمت راست معادله بالا از علامت $$\int$$ به جای $$\oint$$ استفاده شده است. دلیل این امر این است که سطوح انتگرال‌گیری شده به صورت بسته نیستند. هما‌نگونه که توضیح دادیم، میدان اطراف میله، عمود بر راستای میله هستند. با توجه به این‌که بردار عمود بر دو قاعده در راستای میله هستند، از این رو میدان الکتریکی ناشی از میله نیز بر بردار سطوح قاعده عمود خواهند بود. برای درک بهتر به شکل ۳ توجه فرمایید.

برای نمونه فرض کنید می‌خواهیم انتگرال میدان را روی سطح شماره ۱ بیابیم. برای این کار، مهم‌ترین موضوع این است که بدانیم زاویه بین بردار عمود بر سطح ۱ و میدان الکتریکی در این سطح چقدر است. در بالا توضیح دادیم که این دو بردار، عمود بر هم هستند. در حقیقت زاویه بین آن‌ها ۹۰ درجه است. بنابراین شار الکتریکی گذرنده از سطح شماره ۱ برابر است با:

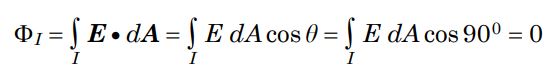
حال همین محاسبه را برای سطح شماره ۲ (این سطح بدنه استوانه است) انجام می‌دهیم. با توجه به این‌که میدان الکتریکی به صورت عمود به میله است، بنابراین زاویه آن با بردار عمود به بدنه نیز صفر درجه است. در نتیجه شار عبوری از سطح ۲ به صورت زیر بدست می‌آید.

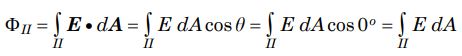
احتمالا می‌دانید که همچون سطح ۱ شار عبوری از سطح ۳ نیز برابر با صفر است. نهایتا با جمع زدن این سه شار به صورت زیر داریم:

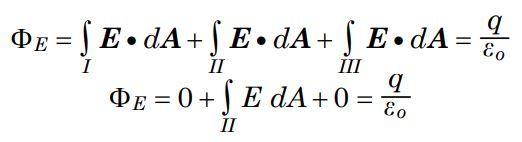
با توجه به متقارن بودن مسئله می‌توان درک کرد که اندازه میدان الکتریکی در فاصله‌ یکسانی از میله ثابت است. بنابراین با حرکت روی بدنه سطح گاوسی، اندازه میدان الکتریکی تغییر نخواهد کرد. با توجه به ثابت بودن میدان می‌توان آن را در هر جایی از معادلات، از زیر انتگرال بیرون کشید. بنابراین رابطه بالا را می‌توان به شکل زیر بازنویسی کرد.

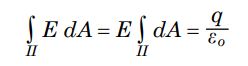
واضح است که در رابطه بالا $$\int_{II}dA$$ برابر با سطح بدنه استوانه است. از ریاضیات پایه می‌دانیم که مساحت بدنه استوانه برابر با حاصلضرب محیط قاعده در طول آن است. بنابراین مساحت استوانه برابر است با:

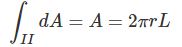
در رابطه بالا L برابر با طول استوانه و r شعاع آن است.

مثال 3: میدان الکتریکی درون یک رسانا

در این مثال می‌خواهیم میدان الکتریکی درون یک رسانا را بدست آوریم. بدین منظور مطابق شکل زیر کره‌ای رسانا را تصور کنید که بار الکتریکی q، توسط میله‌ای رسانا به آن منتقل شده است.

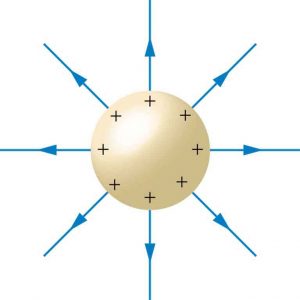
پس از منتقل شدن بارها به کره، به دلیل رسانا بودن کره مفروض، بارها یکدیگر را دفع کرده و تمایل دارند تا در دورترین فاصله ممکن از هم قرار گیرند؛ در نتیجه تمامی بار‌های منتقل شده به کره، به بیرونی‌ترین سطح کره منتقل خواهند شد. توجه داشته باشید که تنها در صورتی که بستر رسانا باشد این اتفاق خواهد افتاد و در حالتی که با کره‌ای مثلا پلاستیکی سر و کار داشته باشیم،‌ داستان به شکل دیگری خواهد بود.

بنابراین درون کره باری وجود نخواهد داشت. از طرفی به‌منظور تعیین میدان داخلی، می‌توان از سطح گاوسی کروی شکل درون جسم اصلی استفاده کرد. در نتیجه مطابق با شکل زیر، سطحی کروی شکل را درون سطح اصلی فرض می‌کنیم.

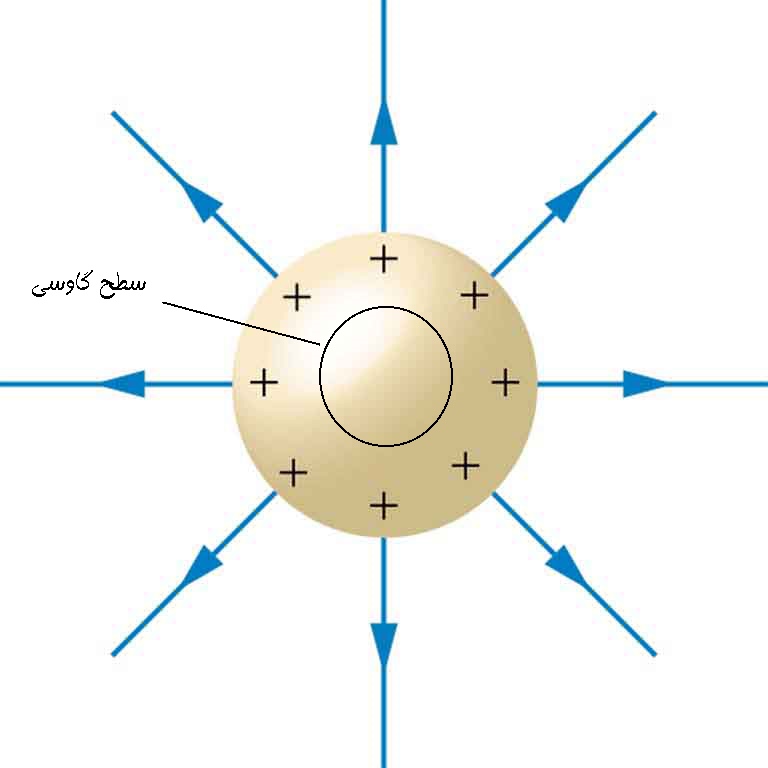
برای این سطح، قانون گاوس را می‌توان به شکل زیر بیان کرد:

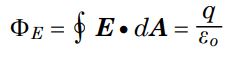
اما با توجه به اینکه باری درون سطح مفروض وجود ندارد، داریم:

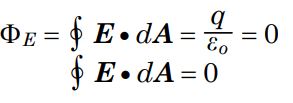
تنها زمانی رابطه بالا برقرار است که میدان  E در کره برابر با صفر باشد. بنابراین می‌توان گفت که همواره میدان درون یک رسانا صفر است.

قانون گاوس روشی بسیار مناسب به‌منظور محاسبه انواع میدان‌های الکتریکی و در نتیجه محاسبه پتانسیل الکتریکی محسوب می‌شود. از این رو توصیه می‌شود به‌منظور تسلط بیشتر به موضوع به این لینک مراجعه فرمایید. هم‌چنین در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی برق و فیزیک پایه، احتمالا آموزش‌های زیر برایتان کاربردی خواهند بود:

• میدان الکتریکی (Electric Field) چیست؟ -- از صفر تا صد
• قانون کولن چیست؟ -- به زبان ساده
• پتانسیل الکتریکی (Electric Potential) — از صفر تا صد

^^