انتگرال سه‌ گانه – از صفر تا صد

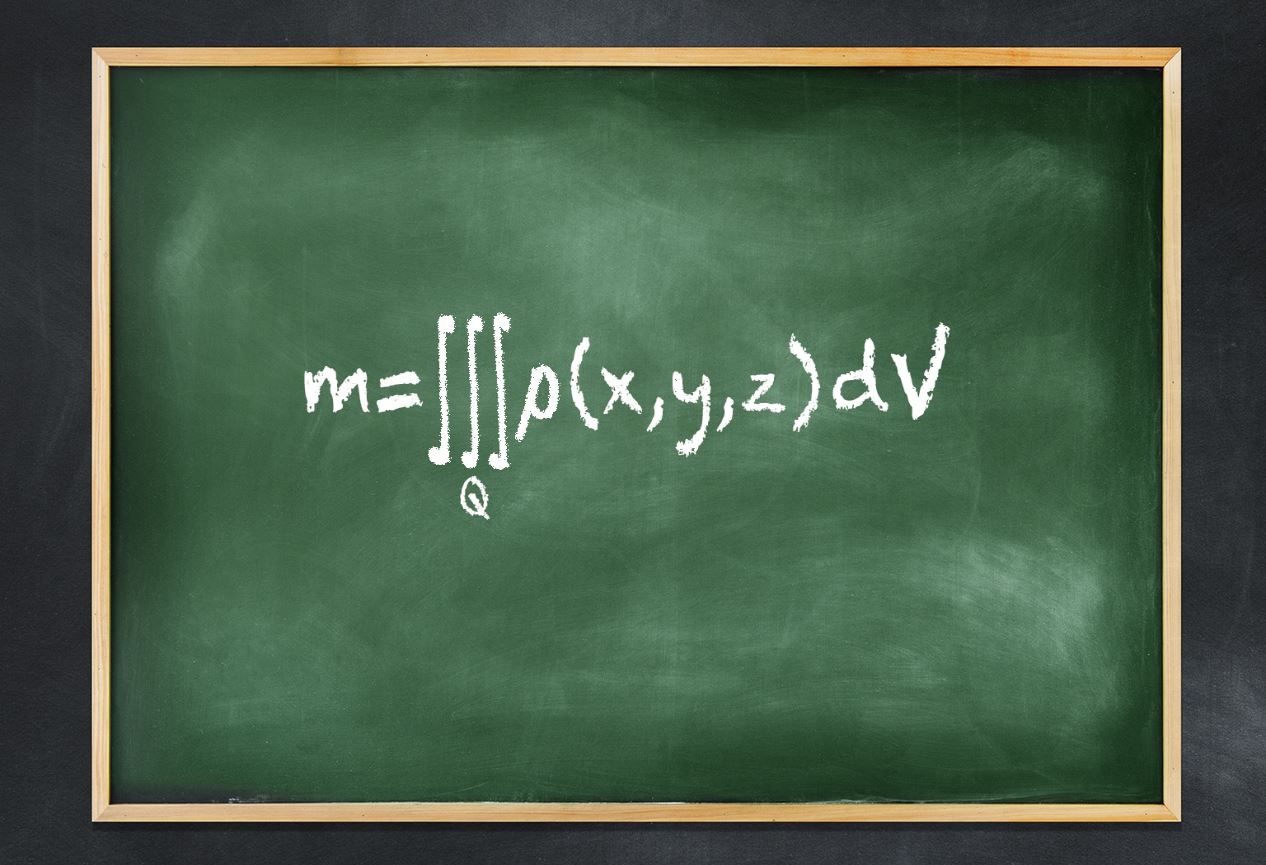
پیش‌تر با مفاهیم انتگرال و کاربرد‌های آن آشنا شدید. در این مطلب قصد داریم تا مفهوم انتگرال سه‌گانه را معرفی کنیم.

مفهوم انتگرال سه‌گانه

در انتگرال یگانه، انتگرال‌گیری روی یک تابعِ تک متغیره انجام می‌شد. از طرفی در انتگرال دوگانه بیان شد که ناحیه‌ انتگرال‌گیری در دو بعد است. به همین صورت در انتگرال سه‌گانه نیز ناحیه‌ انتگرال‌گیری به شکلی سه بعدی در نظر گرفته می‌شود.

فرض کنید می‌خواهیم از تابع $$f \left ( { x , y , z } \right ) \, d V$$ روی ناحیه E انتگرال بگیریم. چنین انتگرالی به صورت زیر نمایش داده می‌شود.

$$\large \iiint \limits _ { E } { { f \left ( { x , y , z } \right ) \, d V } }$$

برای نمونه ناحیه‌ای مکعبی شکل را به صورت زیر در نظر بگیرید.

$$\large B = \left[ { a , b } \right ] \times \left [ { c , d } \right ] \times \left [ { r , s } \right ]$$

توجه داشته باشید که بازه‌های انتگرال‌گیری بایستی متناسب با ترتیب dx،dy و dz باشند. برای نمونه اگر بازه $$[ r , s ]$$ بیرون باشد، dz نیز بایستی در آخر قرار گیرد. یکی از حالات انتگرال‌گیری در زیر نمایش داده شده است.

$$\large \iiint \limits _ { B } { { f \left ( { x , y , z } \right ) \, d V } } = \int _ { { \, r } } ^ { { \, s } } { { \int _ { { \, c } } ^ { { \, d } } { { \int _ { { \, a } } ^ { { \, b } } { { f \left ( { x , y , z } \right ) d x } } \, d y } } \, d z } }$$

همان‌طور که می‌بینید در انتگرال‌گیری بالا ترتیب دیفرانسیل‌ها به صورت dx,dy,dz بوده که متناسب با باز‌ه‌های $$[ r , s ]$$، $$[ c , d ]$$ و $$[ a , b ]$$ هستند. البته همین انتگرال را می‌توان به ترتیب دیگری نیز محاسبه کرد. در حالت کلی انتگرال فوق به ۶ طریق قابل بیان است. البته با مطالعه مثال‌های زیر می‌توانید به موضوع مسلط شوید.

مثال ۱

حاصل انتگرال سه‌گانه زیر را بیابید.

$$\large \iiint \limits _ { B } { { 8 x y z \, d V } } \hspace {0.5in} B = \left [ { 2 , 3 } \right ] \times \left [ { 1 , 2 } \right ] \times \left [ { 0 , 1 } \right ]$$

همان‌طور که در بالا نیز بیان شد، در حالاتی که ناحیه‌ انتگرال‌گیری به صورت مکعب باشد، ترتیب بازه‌های انتگرال‌گیری در پاسخ نهایی تاثیر‌گذار نیست.

$$\large \begin {align*} \iiint \limits _ { B } { { 8 x y z \, d V } } & = \int _ { { \, 1 } } ^ { { \, 2 } } { { \int _ { { \, 2 } } ^ { { \, 3 } } { { \int _ { { \, 0 } } ^ { 1 } { { 8 x y z \, d z } } \, d x } } \, d y } } \\ & = \int _ { { \, 1 } } ^ { { \, 2 } }{ { \int _ { { \, 2 } } ^ { { \, 3 } } { { \left. { 4 x y { z ^ 2 } } \right| _ 0 ^ 1 \, d x } } \, d y } } \\ & = \int _ { { \, 1 } } ^{{\, 2 } } { { \int _ { { \, 2 } } ^ { { \, 3 } } { { 4 x y \, d x } } \, d y } } \\ & = \int _ { { \, 1 } } ^ { { \, 2 } } { { \left. { 2 { x ^ 2 } y } \right|_2^3\,dy}}\\ & = \int_{{\,1}}^{{ \, 2 } } { { 1 0 y \, d y } } = 1 5 \end {align*}$$

توجه داشته باشید که ناحیه انتگرال‌گیری در مثال فوق یک مکعب است؛ لذا ناحیه‌های انتگرال‌گیری به هم وابسته نیستند. در ادامه مثال‌هایی را بیان خواهیم کرد که در آن‌ها نواحی انتگرال‌گیری به هم وابسته است.

نکته، حجم ناحیه سه‌بعدی E برابر است با:

$$\large \bf { V = \iiint \limits _ { E } { { \, d V } } }$$

در شرایطی کلی، سه حالت می‌تواند برای ناحیه انتگرال‌گیری وجود داشته باشد. در هریک از این حالات، تصویر ناحیه انتگرال‌گیری روی یکی از صفحات x-y ,x-z یا y-z در نظر گرفته می‌شود. به منظور توضیح حالت اول، فرض کنید ناحیه انتگرال‌گیری به صورت زیر باشد. همان‌طور که از شکل نیز بر می‌آید در این حالت تصویر ناحیه انتگرال‌گیری (D) روی صفحه x-y قرار گرفته است.

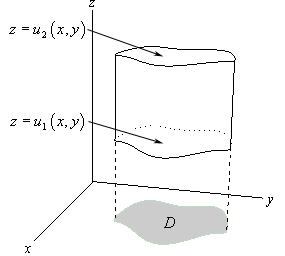
ناحیه انتگرال‌گیری بالا را می‌توان با استفاده از گزاره زیر بیان کرد:

$$\large E = \left \{ { \left ( { x , y , z } \right )| \left ( { x , y } \right ) \in D ,\, \, \, { u _ 1 } \left ( { x , y } \right ) \le z \le { u _ 2 } \left ( { x , y } \right ) } \right \}$$

در گذاره فوق $$\left ( { x , y } \right ) \in D$$ نمادی است که نشان می‌دهد نقطه (x,y) در ناحیه دوبعدی D قرار گرفته است. در این حالت در ابتدا انتگرال‌گیری روی z انجام شده و حاصل انتگرال تابع f به صورت زیر قابل بیان است.

$$\large \iiint \limits _ { E } { { f \left ( { x , y , z } \right ) \, d V } } = \iint \limits _ { D } { { \left [ { \int _ { { \, { u _ 1 } \left ( { x , y } \right ) } } ^ { { \, { u _ 2 } \left ( { x , y } \right ) } }{ { f \left ( { x , y , z } \right ) \, d z } } } \right ]\, d A } }$$

در مرحله بعدی می‌توان دیفرانسیل وسط را به دلخواه هریک از متغیر‌های x یا y انتخاب کرد. اما توجه داشته باشید که در هریک از حالات مذکور، بازه‌ها نیز بایستی متناسب با آن‌ها در نظر گرفته شوند.

مثال ۲

حاصل انتگرال $$\large \displaystyle \iiint \limits _ { E } { { 2 x \, d V } }$$ را روی ناحیه E محاسبه کنید. فرض کنید ناحیه E برابر با صفحه $$\large 2 x + 3 y + z = 6$$ باشد.

فیلم آموزش ریاضی عمومی ۲ – جامع و کاربردی در فرادرس

کلیک کنید

برای حل انتگرال سه‌گانه در ابتدا بایستی ناحیه‌ای که روی آن انتگرال گرفته می‌شود، ترسیم شود. در ادامه صفحه E ترسیم شده است.

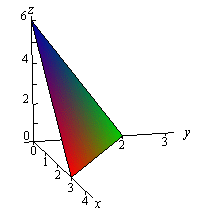
از طرفی با قرار دادن z=0 در معادله صفحه، تصویر E در صفحه x-y به‌ صورت زیر بدست می‌آید.

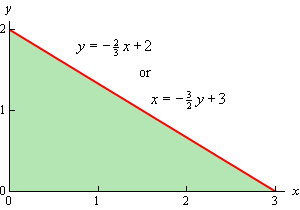
حال فرض کنید می‌خواهیم دیفرانسیل dV را به صورت dzdydx در نظر بگیریم. در این صورت z در بازه زیر قرار می‌گیرد.

$$\large 0 \le z \le 6 - 2 x - 3 y$$

برای تعیین بازه‌های x و y می‌توان از هریک از دو حالت زیر استفاده کرد.

$$\large 0 \leq x \leq 3$$
$$\large 0 \leq y \leq -\frac { 2 } { 3 } + 2$$
رابطه ۱

یا

$$\large 0 \leq x \leq -\frac { 2 } { 3 } y + 3$$
$$\large 0 \leq y \leq 2$$
رابطه ۲

با توجه به این‌که دیفرانسیلِ dy وسط قرار گرفته بنابراین بایستی از رابطه ۱ استفاده کرد. نهایتا حاصل انتگرال برابر است با:

$$\large{ \begin {align*} \iiint \limits _ { E } { { 2 x \, d V } } &= \iint \limits _ { D } { { \left [ { \int _ { { \, 0 } } ^ { { 6 - 2 x - 3 y } } { {2 x \, d z } } } \right ] \, d A } }\\ & = \iint \limits _ { D } { { \left. { 2 x z } \right|_ 0 ^ { 6 - 2 x - 3 y } \, d A } } \\ & = \int _{ { \, 0 } } ^ { { \, 3 } } { { \int _ { 0 } ^ { { - \frac { 2 } { 3 } x + 2 } } { { 2 x \left ( { 6 - 2 x - 3 y} \right ) \, d y } } \, d x } } \\ & = \int _ { 0 } ^ { 3 } { { \left. { \left ( { 1 2 x y - 4 { x ^ 2 } y - 3 x { y ^ 2 } } \right ) } \right|_ 0 ^ { - \frac { 2 } { 3 } x + 2 } \, d x } }\\ & = \int_{0}^{3}{ { \frac { 4 } { 3 } { x ^ 3 } - 8{x^2} + 12x\,dx}}\\ & = \left. {\left( { \frac { 1 } { 3 } { x ^ 4 } - \frac { 8 } { 3 } { x ^ 3 } + 6 { x ^ 2 } } \right ) } \right|_ 0 ^ 3 \\ & = 9 \end {align*}}$$

حالت دوم زمانی است که تصویر ناحیه انتگرال‌گیری روی صفحه y-z بیافتد. شکل زیر این ناحیه را نشان می‌دهد.

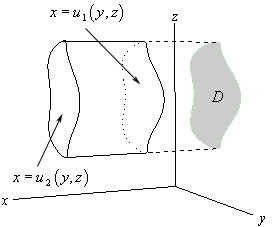
در این حالت می‌توان با استفاده از گذاره زیر ناحیه انتگرال‌گیری رو توصیف کرد.

$$\large E = \left \{ { \left ( { x , y , z } \right )|\left( { y ,z} \right ) \in D,\, \, \, { u _ 1 } \left ( { y , z } \right ) \le x \le { u _ 2 } \left( { y , z } \right ) } \right \}$$

در ابتدا انتگرال‌گیری روی x انجام شده و حاصل انتگرال را می‌توان به صورت زیر بدست آورد.

$$\large \iiint \limits _ { E } { { f \left ( { x , y , z } \right ) \, d V } } = \iint \limits _ { D } { { \left [ { \int _ { { \, { u _ 1 } \left ( { y , z } \right ) } } ^ { { \, { u _ 2 } \left ( { y , z } \right ) } }{ { f \left ( { x , y , z } \right ) \, d x } } } \right ] \, d A } }$$

همانند حالتِ اول، در این حالت نیز می‌توان حاصل انتگرال روی dA را به صورت dydz یا dzdy در نظر گرفت.

مثال ۳

حجم محصور بین صفحه $$x + y + z = 8$$ و صفحه y-z را در فاصله $$\displaystyle z = \frac{ 3 } { 2 } \, \, \sqrt y$$ و $$\displaystyle z = \frac { 3 } { 4 } y$$ بیابید. از صورت این مسئله کاملا مشخص است که در ابتدا بایستی نمودار‌های بیان شده، را رسم کنید.

در شکل زیر ناحیه بین دو تابع $$\displaystyle z = \frac{ 3 } { 2 } \, \, \sqrt y$$ و $$\displaystyle z = \frac { 3 } { 4 } y$$ نشان داده شده است. سوال، حجم محصور بین این ناحیه تا صفحه $$x + y + z = 8$$ را می‌خواهد.

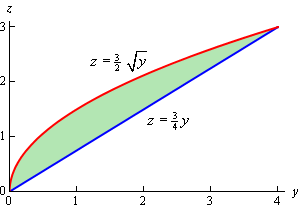
در شکل زیر صفحه $$x + y + z = 8$$ با ناحیه فوق برخورد داده شده است.

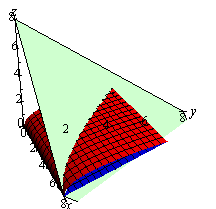
نهایتا حجم مدنظر به صورت زیر خواهد بود.

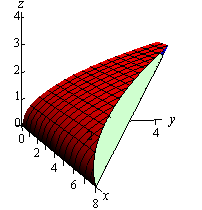
با توجه به اشکال ۲ و ۳ بازه‌های انتگرال‌گیری را می‌توان به صورت زیر در نظر گرفت:

$$\large \begin {array} { c } 0 \le y \le 4\\ \displaystyle \frac { 3 } { 4 } y \le z \le \frac { 3 } { 2 } \sqrt y \\ 0 \le x \le 8 - y - z \end {array}$$

در نتیجه حجمِ ناحیه مفروص برابر است با:

$$\large \begin {align*} V &= \iiint \limits _ { E } { { \, d V } } = \iint \limits _ { D } { { \left [ { \int _ { 0 } ^ { { 8 - y - z } } { { \, d x } } } \right ] \, d A } } \\ & = \int _ { 0 } ^ { 4 }{ { \int _ { { { { 3 y } } / { 4 } \; } } ^ { { { { 3 \sqrt y } } / { 2 } \; } } { { 8 - y - z \, d z } } \, d y } } \\ & = \int _ { 0 } ^ { 4 } { { \left. { \left ( { 8 z - y z - \frac { 1 } { 2 } { z ^ 2 } } \right ) } \right|_{ \frac { { 3 y } } { 4 } } ^ { \frac { { 3 \sqrt y } } { 2 } } \, d y } } \\ & = \int _ { 0 } ^ { 4 }{ { 1 2 { y ^ { \frac { 1 } { 2 } } } - \frac { { 5 7 } } { 8 } y - \frac{ 3 } { 2 }{ y ^ { \frac { 3 } { 2 } } } + \frac { { 3 3 } } { { 3 2 } }{ y ^ 2 } \, d y } } \\ & = \left. { \left ( { 8 { y ^ { \frac { 3 } { 2 } } } - \frac { { 5 7 } } { { 1 6 } } { y ^ 2 } - \frac { 3 } { 5 } { y ^ { \frac { 5 } { 2 } } } + \frac { { 1 1 } } { { 3 2 } } { y ^ 3 } } \right ) } \right |_0 ^ 4 = \frac { { 4 9 } } { 5 } \end{align*}$$

حالت سوم نیز زمانی است که تصویرِ ناحیه انتگرال‌گیری روی صفحه z-x باشد. تصویر ناحیه انتگرال‌گیری در ادامه نشان داده شده است.

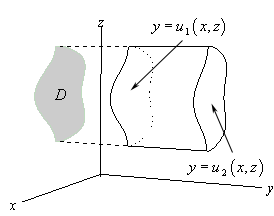
در این حالت، ناحیه E را می‌توان به صورت زیر توصیف کرد.

$$\large E = \left \{ { \left ( { x , y , z } \right )| \left ( { x , z } \right ) \in D, \, \, \, { u _ 1 } \left ( { x , z } \right ) \le y \le { u _ 2 } \left ( { x , z } \right ) } \right \}$$

با توجه به شکل بالا، حاصل انتگرال با استفاده از رابطه زیر قابل محاسبه است.

$$\large \iiint \limits _ { E } { { f \left ( { x , y , z } \right ) \, d V } } = \iint \limits _ { D } { { \left [ { \int _ { { \, { u _ 1 } \left ( { x , z } \right ) } } ^ { { \, { u _ 2 } \left ( { x , z } \right ) } }{ { f \left ( { x , y , z } \right ) \, d y } } } \right ] \, d A } }$$

فیلم آموزش محاسبه حجم با انتگرال معین + ۲ روش کاربردی (رایگان) در فرادرس

کلیک کنید

مثال ۴

حاصل انتگرال $$\displaystyle \iiint \limits _ { E } { { \sqrt { 3 { x ^ 2 } + 3 { z ^ 2 } } \, d V } }$$ را روی ناحیه E بدست آورید. فرض کنید E حجم محدود شده بین دو سطح $$y = 2 { x ^ 2 } + 2 { z ^ 2 }$$ و y=8 است.

همان‌طور که پیش‌تر نیز بیان شد، برای محاسبه انتگرال سه‌گانه در ابتدا بایستی سطوحی که هدف محاسبه انتگرال‌ روی آن‌ها است، به درستی ترسیم شوند. ناحیه انتگرال‌گیری در این مثال، در ادامه نشان داده شده است.

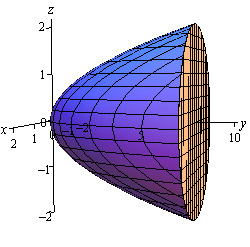
همان‌طور که در شکل فوق نیز می‌بینید، تصویر ناحیه انتگرال‌گیری روی صفحه x-z می‌افتد. بنابراین در ابتدا انتگرال‌ روی y گرفته می‌شود. معادله سطح آبی رنگ را می‌توان به صورت زیر بیان کرد:

$$\large 2 { x ^ 2 } + 2 { z ^ 2 } = 8 \hspace {0.25in} \Rightarrow \hspace {0.25in} { x ^ 2 } + { z ^ 2 } = 4$$

با در نظر گرفتن x و z به صورت زیر، معادله صفحه مذکور به شکل قطبی قابل بیان خواهد بود.

$$\large x = r \cos \theta \hspace {0.25in} \hspace {0.25in} z = r \sin \theta$$

با توجه به قطبی بیان شدن صفحه، y در معادله صفحه را برابر با z در مختصات قطبی در نظر می‌گیریم. بنابراین بازه‌های انتگرال‌گیری به‌صورت زیر بدست می‌آیند.

$$\large \begin {array} { c } 2 { x ^ 2 } + 2 { z ^ 2 } \le y \le 8\\ 0 \le r \le 2\\ 0 \le \theta \le 2 \pi \end {array}$$

بنابراین حاصل انتگرال برابر است با:

$$\large \begin {align*} \iiint \limits _ { E } { { \sqrt { 3 { x ^ 2 } + 3 { z ^ 2 } } \, d V } } & = \iint \limits _ { D } { { \left [ { \int _ { { 2 { x ^ 2 } + 2 { z ^ 2 } } } ^ { { \, 8 } } { { \sqrt { 3 { x ^ 2 } + 3 { z ^ 2 } } \, d y } } } \right ] \, d A } } \\ & = \iint \limits _ { D } { { \left. { \left ( { y \sqrt { 3 { x ^ 2 } + 3 { z ^ 2 } } } \right ) } \right|_{ 2 { x ^ 2 } + 2 { z ^ 2 } } ^ 8 \, d A } } \\ & = \iint \limits _ { D } { { \sqrt { 3 \left ( { { x ^ 2 } + { z ^ 2 } } \right ) } \left ( { 8 - \left ( { 2 { x ^ 2 } + 2 { z ^ 2 } } \right ) } \right ) \, d A } } \end {align*}$$

همان‌طور که مشاهده می‌فرمایید، عبارت تحت انتگرال به نسبت پیچیده است. لذا آن را به صورت زیر به شکل قطبی بیان می‌کنیم.

$$\large \begin {align*} \sqrt { 3 \left ( { { x ^ 2 } + { z ^ 2 } } \right ) } \left ( { 8 - \left ( { 2 { x ^ 2 } + 2 { z ^ 2 } } \right ) } \right ) &= \sqrt { 3 { r ^ 2 } } \left ( { 8 - 2 { r ^ 2 } } \right ) \\ & = \sqrt 3 \, \, r \left ( { 8 - 2 { r ^ 2 } } \right ) \\ & = \sqrt 3 \left( { 8 r - 2 { r ^ 3 } } \right ) \end {align*}$$

توجه داشته باشید که اندازه دیفرانسیل dA در مختصات قطبی برابر با dA=rdrdθ است. بنابراین حاصل انتگرال برابر می‌شود با:

$$\large \begin {align*} \iiint \limits _ { E } { { \sqrt { 3 { x ^ 2 } + 3 { z ^ 2 } } \, d V } } & = \iint \limits _ { D } { { \sqrt 3 \, \, \left ( { 8 r - 2 { r ^ 3 } } \right ) d A } } \\ & = \sqrt 3 \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \int _ { { \, 0 } } ^ { { \, 2 } } { { \left ( { 8 r - 2 { r ^ 3 } } \right ) r \, d r } } \, d \theta } } \\ & = \sqrt 3 \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \left. { \left ( { \frac { 8 } { 3 } { r ^ 3 } - \frac { 2 } { 5 }{ r ^ 5 } } \right ) } \right|_0 ^ 2 \, d \theta } } \\ & = \sqrt 3 \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \frac { { 1 2 8 } } { { 1 5 } } \, d \theta } }\\ & = \frac { { 2 5 6 \sqrt 3 \, \pi } } { { 1 5 } } \end {align*}$$

در این مطلب مفاهیم انتگرال سه گانه و کاربرد‌هایی از آن ارائه شد. در مطالب آینده بیشتر در مورد انتگرال‌های سه‌گانه در مختصات کروی و استوانه‌‌ای بحث خواهیم کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضی
• مجموعه آموزش‌های ریاضی و فیزیک
• انتگرال دوگانه - به زبان ساده
• قضیه گرین (Green Theorem) - به زبان ساده
• قضیه استوکس - به زبان ساده

^^