اثر مویینگی چیست؟ — به زبان ساده

به هنگام بارش باران، آب در سراشیبی خیابان به سمت پایین حرکت میکند. به طور کلی انتظار داریم که آب، مانند آبشار، به سمت پایین حرکت کند. اما نکته جالب توجه آن است که آب میتواند به سمت بالا و در خلاف جاذبه زمین نیز جریان داشته باشد. قسمت کوچکی از دستمال کاغذی را داخل لیوان آب قرار دهید. پس از گذشت مدت زمان مشخصی، تمام دستمال کاغذی خیس خواهد شد. در این حالت، آب به سمت بالا و در خلاف جهت نیروی جاذبه زمین حرکت کرده است. توضیح این پدیده جالب با استفاده از مفهومی به نام اثر مویینگی انجام میشود. مویینگی نقش مهمی در حرکت سیال در بدن ما دارد. همچنین، حرکت آب از ریشه گیاهان به سمت برگها با استفاده از اثر مویینگی انجام میشود. در این مطلب، در مورد این اثر صحبت میکنیم و نقش آن را در طبیعت و گیاهان، توضیح میدهیم.
اثر مویینگی چیست ؟
در تعریف بسیار بسیار ساده، به بالا رفتن مایع در فضایی باریک و در خلاف جهت جاذبه زمین، اثر مویینگی گفته میشود. برای درک بهتر این اثر به مثالهای زیر توجه کنید. با مطالعه این مطلب، تعریفهای پیچیدهتر این اثر را نیز یاد میگیرد.
مثال ۱
در این قسمت نشان خواهیم داد که جوهر مشکی واقعا مشکی نیست. ابتدا با استفاده از ماژیک، خطی روی دستمال کاغذی و در قسمت پایین آن رسم و قسمت بالای دستمال را با استفاده از چسب کاغذی به نی وصل میکنیم. سپس، دستمال را از قسمت خطدار، داخل ظرف آب به گونهای قرار میدهیم که خط داخل آب قرار نگیرد.

پس از آنکه دستمال کاغذی خیس شد، آب شروع به بالا رفتن از آن خواهد کرد. آب از دستمال کاغذی بالا میرود و جوهر را خیس میکند. در اینجا، نکته جالبی را خواهید دید. جوهر پس از خیس شدن، همانند آب به سمت بالا حرکت میکند. پس از ۴۰ دقیقه با صحنه بسیار جالبی روبرو خواهیم شد. اثری از جوهر سیاهرنگ رو دستمال کاغذی باقی نمیماند. به جای آن، با رنگینکمانی از رنگهای صورتی، آبی و زرد مواجه میشویم. در واقع، آب با حرکت به سمت بالا، چیزهای دیگری مانند رنگهای تشکیلدهنده جوهر را با خود همراه میکند.

برخی رنگها کوچکتر هستند، بنابراین سریعتر حرکت میکنند. در مقابل، رنگهای بزرگتر با سرعت کمتری حرکت میکنند. در نتیجه، جداسازی رنگهای جوهر سیاه به وضوح انجام میشود.
آزمایش را بار دیگر تکرار میکنیم، اما در این حالت به جای رسم خط روی دستمال، کلمهای را با ماژیکهای مختلف روی آن مینویسیم.

پس از گذشت ۶۰ دقیقه و خیس شدن دستمال کاغذی تا انتها، تصویر زیر بهدست میآید. کلمه science بدون تغییر مانده، زیرا با ماژیک ضدآب نوشته شده است.
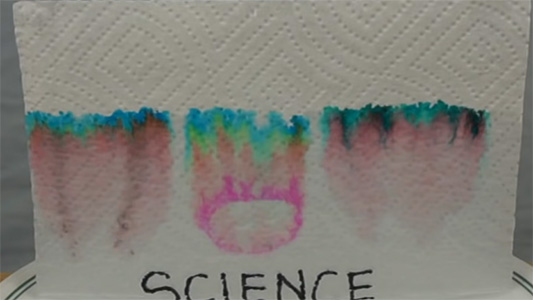
این آزمایش را میتوانید با ماژیکهای مختلف و رنگهای متنوع تکرار کنید.
مثال دوم
در این آزمایش، از وسیلههای زیر استفاده میکنیم.
- هفت لیوان آب
- رنگهای مختلف
- دستمال کاغذی به تعداد مناسب
دوسوم لیوانها را از آب پر میکنیم. سه لیوان آب ساده را روی میز قرار میدهیم و در مابقی لیوانها، قلمموی آغشته به رنگهای مختلف مانند قرمز، زرد و آبی قرار میدهیم و قلمموها را تا پخش شدن رنگ به طور یکنواخت در آب، داخل آن هم میزنیم. سپس لیوانها را کنار یکدیگر روی میز قرار میدهیم.

در این آزمایش ساده، آب را بین لیوانها با استفاده از دستمال کاغذی حرکت میدهیم. مدت زمان این آزمایش به اندازه لیوانها، دمای آب و مقدار دستمال کاغذی مورد استفاده، بستگی دارد. در ادامه، دستمال کاغذیها را به صورت زیر، داخل لیوانها قرار میدهیم.

مدت زمان انجام این آزمایش ممکن است طولانی باشد، بنابراین صبور باشید. با بررسی لیوانها در مدت زمانهای مختلف خواهید دید که مقدار آب درون آنها تغییر میکند. در پایان، آب داخل تمام لیوانها رنگی شده و مقدار آب داخل آنها یکسان است. به این نتیجه میرسیم که آب به دلیل اثر مویینگی از دستمال کاغذی بالا رفته و بین لیوانها حرکت کرده است.
در این آزمایش میتوان از لیوانهایی با اندازههای مختلف یا به جای دستمال کاغذی، از پارچه استفاده کرد. به این نکته توجه داشته باشید که به هنگام انجام آزمایش، گاهی رنگ آب داخل لیوان مخلوطی از چند رنگ و گاهی لایهای است.

برای توضیح این آزمایش باید بدانیم که عملکرد فضاهای کوچک با فضاهای بزرگ یکسان نیست. هنگامی که میشنویم مورچهها دانههایی در حدود ۱۰۰ برابر وزن خود را حمل میکنند، شگفتزده نخواهیم شد. اما اگر فردی اتومبیلی با وزنی چند برابر خود را حمل کند، به طور قطع شگفتزده خواهیم شد. این دو شرایط چه تفاوتی با یکدیگر دارند؟ آیا مورچه از انسان قویتر است؟ خیر، مورچه تنها از انسان کوچکتر است.
اگر انسانی را به اندازه مورچه کوچک کنیم، او اتومبیلی با وزنی بسیار بیشتر را بدون هیچ مشکلی بلند خواهد کرد. اندازه بسیار مهم است و قوانین حاکم بر حرکت و رفتار اجسام با اندازه آنها، تغییر میکنند. فیزیک کوانتوم، بهترین مثال در این مورد است. رفتار اجسام در مقیاس کوانتومی بسیار عجیب میشود. در این مقیاس، ذراتی وجود دارند که ناگهان به وجود میآیند و ناگهان از بین میروند. اجسام میتوانند در زمان یکسان در دو مکان متفاوت وجود داشته باشند. همچنین، ذراتی وجود دارند که رفتار آنها به این بستگی دارد که آنها را تماشا کنیم یا خیر. اما برای درک اثر مویینگی نیاز به دانستن فیزیک کوانتوم نداریم.
اثر مویینگی در مقیاس مولکولی قابل توضیح است. آب در این مقیاس بدون توجه به نیروی جاذبه و جهت آن، میتواند در هر جهتی حرکت کند. توجه به این نکته مهم است که اثر مویینگی در صورت وجود چسبندگی، رخ میدهد. اگر سطحی روغنی و آبگریز داشته باشیم، آب از این سطح بالا نخواهد رفت. در نتیجه، اثر مویینگی وجود ندارد. از این رو، اثر مویینگی به میزان ترشوندگی سطح بستگی خواهد داشت.
بیشتر اجسام در طبیعت آبدوست هستند. آب چسبندگی خوبی با سنگها، شیشه، پلاستیک و دستمال کاغذی دارد. دستمال کاغذی از فضاهای بسیار کوچکی به شکل لایه، تشکیل شده است. بین لایهها الیاف و بین آنها سلولهای سلولز سازنده دستمال کاغذی قرار گرفتهاند. بنابرای، آب توسط دستمال جذب میشود.
مثال سوم
انسان هزاران سال است که برای حرکت آب از سیفون استفاده میکند. در این آزمایش نحوه انتقال آب از مخزنی بسیار بزرگ به مخزنی کوچکتر را بدون تکان دادن مخزن بزرگتر، بررسی خواهیم کرد. یک راه ساده برای انجام این کار قرار دادن شلنگی در مخزن بزرگتر و مکیدن انتهای آزاد شلنگ است. اما این کار تنها برای چند دقیقه مفید و در ادامه خستهکننده و با بههمریختگی بسیار همراه است. در این قسمت، با استفاده از نی، سیفونی ساده میسازیم.
دو لیوان با اندازههای مختلف را روی میز قرار میدهیم. لیوان بزرگتر را پر از آب میکنیم. اگر نی را داخل آن قرار دهیم، اتفاق خاصی نمیافتد. اگر انتهای آزاد نی را که خارج از آب قرار دارد با انگشت اشاره بپوشانیم، اتفاق جالبی رخ خواهد داد. پس از مدت کوتاهی، انگشت خود را برمیداریم. آب از نی بالا میآید یا به بیان بهتر به سمت بالا میپرد.
اکنون انتهای آزاد نی را با انگشت میپوشانیم و آن را کامل داخل آب قرار میدهیم، سپس، انگشت خود را برمیداریم. آب از نی بالا میآید و داخل ظرف کوچکتر میریزد. به راحتی با نی سیفون ساختهایم و آب را بین دو لیوان انتقال دادهایم. شاید از خود بپرسید آیا با این روش میتوان تمام آب داخل ظرف بزرگتر را به ظرف کوچکتر انتقال داد یا انتقال آب در جایی متوقف خواهد شد.
با انجام این آزمایش خواهیم دید که تمام آب داخل ظرف بزرگتر به ظرف کوچکتر منتقل نخواهد شد و انتقال آب پس از گذشت مدت زمان مشخصی متوقف میشود. انتقال آب چه زمانی متوقف خواهد شد؟ برای پاسخ به این پرسش، به تصویر زیر دقت کنید.
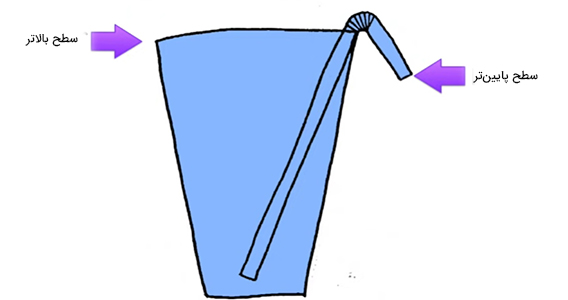
تا زمانی که آب به کمک نی از ارتفاع بیشتر به ارتفاع کمتر حرکت میکند، جریان آن ادامه خواهد داشت. زمانی که ارتفاع برابر شود، آب هیچ دلیلی برای بالا رفتن از نی ندارد. در ادامه، حالت دیگری از این آزمایش را بیان میکنیم.
در دو لیوان، آب به اندازه یکسان میریزیم و داخل هر کدام نی به صورت نشان داده شده در تصویر قرار میدهیم، آب بین دو لیوان حرکت نخواهد کرد. زیرا ارتفاع آنها یکسان و مقدار آب داخل نی یکسان است.
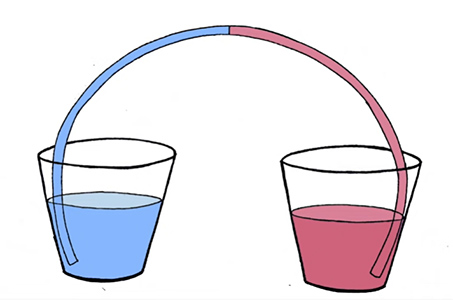
اکنون یکی از لیوانها را در ارتفاع بالاتری نسبت به لیوان دیگر قرار میدهیم. با انجام این کار، تعادل سیستم را به هم میزنیم. آب داخل لوله در قسمتی از آن بیشتر از قسمت دیگر است. بنابراین، داخل لوله اختلاف وزن داریم و آب در اثر اختلاف وزن، بین دو لیوان حرکت خواهد کرد.
مثال چهارم
در آزمایش آخر میخواهیم با استفاده از وسایلی ساده، آبشار درست کنیم:
- لیوان
- آبِ رنگی برای دنبال کردن مسیر آن
- لوله پلاستیکی شفاف دو عدد
- بطری بزرگ به همراه درپوش
- ظرف کوچک برای جمعآوری آب
- چسب نواری
مراحل ساخت آبشار عبارت هستند از:
- دو حفره کوچک به اندازه عبور لولههای پلاستیکی، داخل سرپوش بطری درست کنید. سپس، لولهها را از داخل هر حفره عبور دهید تا جایی که انتهای آنها تا میانه بطری برسد.
- لیوان را با آب پر کنید و چند قطره آبرنگ یا رنگ خوراکی مجاز داخل آن بریزید و تا پخش کامل رنگ داخل آب، آن را به هم بزنید.
- چند کتاب روی میز قرار دهید و لیوان آب را روی آن بگذارید.
- انتهای یکی از لولههای پلاستیکی شفاف را داخل لیوان آب قرار دهید.
- بطری را از قسمت سرپوش روی میز قرار دهید.
با قرار دادن سرپوش بطری روی میز، آبِ درون لیوان از طریق لوله پلاستیکی شفاف به داخل بطری میرود و از انتهای دیگر لوله، به شکل آبشاری خارج میشود.

جریان آب تا جایی ادامه مییابد که:
- آب داخل لیوان باشد.
- بطری از قسمت سرپوش، روی میز قرار داشته باشد.
اساس چهار آزمایش توضیح داده شده در بالا، اثر مویینگی است. تاکنون به صورت شهودی اثر مویینگی را فهمیدهایم. در ادامه، رابطه ریاضی حاکم بر آن را بهدست میآوریم.
اثر مویینگی آب
لوله آزمایشگاه کوچکی بردارید و آن را با آب پر کنید. در حالت کلی انتظار دارید که سطح آب صاف و بدون انحنا باشد. اما اگر به سطح آب داخل لوله دقت کنید، انحنایی به سمت داخل خواهد داشت. در واقع سطح آبِ نزدیک شیشه بالاتر و با حرکت به سمت مرکز، سطح آن پایینتر میآید. بنابراین، سطح آب به شکل مقعر است. به این پدیده، اثر مینیسک گفته میشود.
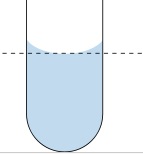
سوالی که ممکن است برای شما مطرح شود آن است که آیا سطح تمام مایعات، مقعر است. پاسخ به این پرسش، خیر است. به عنوان مثال، داخل لوله آزمایشگاه به جای آب، جیوه بریزید و به سطح آن دقت کنید. برخلاف آب، سطح جیوه در نزدیکی شیشه پایینتر و با حرکت به سمت مرکز، سطح آن بالاتر میرود. بنابراین، سطح جیوه به شکل محدب است.
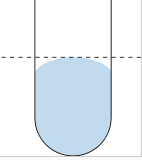
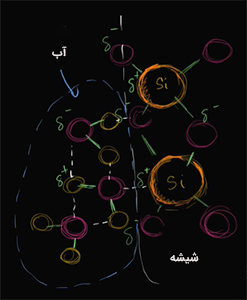
برای توضیح شکل مقعر سطح آب در مقابل شکل محدب سطح جیوه باید به نیروهای بینمولکولی توجه کنیم. گفتیم سطح آب در نزدیکی شیشه بالاتر از سطح آن در مرکز است. به زبان ساده میتوان گفت که نیروی جاذبه بین شیشه و آب بیشتر از نیروی جاذبه داخلی آب است. مولکولهای آب از طریق پیوند هیدروژنی، کنار یکدیگر قرار گرفتهاند. آیا این بدان معنا است که نیروی بین مولکولهای آب و شیشه از پیوند هیدروژنی بین آنها قویتر است؟
مولکولهای تشکیلدهنده شیشه به طور کامل قطبی هستند. شیشه از شبکه اکسید سیلیکون ساخته شده است. به ازای هر یک اتم سیلیکون، دو اتم اکسیژن وجود دارند. تفاوت الکترونگاتیوی بین اتمهای سیلیکون و اکسیژن در شیشه، بیشتر از تفاوت آن بین اتمهای هیدروژن و اکسیژن در آب است. حتی میتوان گفت مقدار الکترونگاتیوی سیلیکون از هیدروژن کمتر است. بنابراین، الکترونهای سیلیکون، به خصوص الکترونهای شرکتکننده در پیوند، توسط اکسیژنهای داخل شیشه گرفته میشوند. در نتیجه، سیلیکون، بار جزیی مثبت و اکسیژن، بار جزیی منفی بهدست میآورند.
اکنون میتوانید حدس بزنید که چه اتفاقی در محل تماس آب با شیشه رخ میدهد. مولکولهای آب با استفاده از پیوند هیدروژنی در کنار یکدیگر قرار گرفتهاند. اما نباید فراموش کنیم که انرژی جنبشی مولکولهای آب مخالف صفر است و آنها تا فاصله اندکی میتوانند حرکت داشته باشند. اتمهای هیدروژن در آب، بار جزیی مثبت دارند، بنابراین توسط اتمهای اکسیژن در شیشه با بار جزیی منفی، جذب میشوند. این نیروی جاذبه بیشتر از نیروی جاذبه بین اتمهای اکسیژن و هیدروژن در آب است، زیرا:
- تفاوت الکترونگاتیوی بین اکسیژن و سیلیکون در شیشه بیشتر از تفاوت آن بین اکسیژن و هیدروژن در آب است.
- بار جزیی اتمهای اکسیژن در شیشه بیشتر از بار جزیی اتمهای اکسیژن در آب است.
به نیروی بین مولکولهای آب و شیشه، نیروی چسبندگی گفته میشود. همچنین، به نیروی بین مولکولهای آب، نیروی پیوستگی میگوییم. توجه به این نکته مهم است که اگر آب را در ظرف پلاستیکی بریزیم، اثر مینیسک را مشاهده نمیکنیم، زیرا پلاستیک قطبی نیست.
نیروی چسبندگی ویژگیهای جالبی دارد. ظرف بزرگی را از آب پر کنید و روی میز قرار دهید. لوله آزمایشگاهی نازکی را بردارید و آن را به صورت وارونه داخل آب فرو ببرید. اتفاق بسیار جالبی رخ میدهد و آب برخلاف نیروی جاذبه زمین، از لوله بالا میرود. همانطور که میدانیم به این پدیده، اثر مویینگی گفته میشود.
هر چه لوله باریکتر باشد، مقدار نیروی چسبندگی بین مولکولهای آب و شیشه بیشتر خواهد بود. زیرا مولکولهای بیشتری از آب در تماس با شیشه قطبی لوله قرار میگیرند.
اثر مویینگی به زبان ریاضی
در مطالب بالا گفتیم که اگر ظرفی بزرگی را با آب پر کنیم و لوله شیشهای باریکی را به صورت وارونه در آن قرار دهیم، آب با استفاده از نیروی چسبندگی از لوله بالا میرود و بر نیروی جاذبه غلبه خواهد کرد. این اثر، مویینگی نامیده میشود. در این بخش، عاملهای موثر بر اثر مویینگی را بیان میکنیم و رابطه ریاضی حاکم بر آن را مینویسیم.
قبل از بهدست آوردن رابطه حاکم بر مویینگی، آزمایش سادهای را با یکدیگر انجام میدهیم. ظرف پر شده با آب را روی میز قرار میدهیم و لولههای شیشهای با اندازههای مختلف را به ترتیب و به صورت وارونه درون ظرف فرو میبریم. هر چه اندازه لوله مویین بزرگتر باشد، ارتفاع آب درون آن کمتر خواهد بود. اگر اندازه لوله بزرگ باشد، ارتفاع آب بسیار کم و قابل چشمپوشی است.
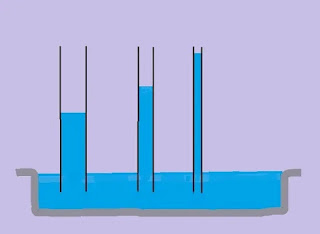
میدانیم نیروی چسبندگی بین مولکولهای آب و مولکولهای شیشه، دلیل اصلی بالا رفتن آب از لوله است. علاوه بر نیروی چسبندگی، نیروی جاذبه زمین نیز به سمت پایین بر آب وارد میشود. مقدار این نیرو برابر حاصلضرب جرم آب بالا رفته در لوله و شتاب جاذبه (g) است. برای بهدست آوردن جرم آب از رابطه زیر استفاده میکنیم:
$$\rho = \frac {m} {V} \ m = \rho \times V$$
در رابطه فوق:
حجم آب داخل لوله برابر است با:
$$V = \pi r^2 h$$
که $$h$$ ارتفاع آب داخل لوله است. بنابراین، مقدار نیروی جاذبه وارد شده بر آب برابر است با:
$$W = \pi r^2 h \rho g$$
مقدار نیرویی که به سمت بالا بر آب وارد میشود با محیط دایره شکلگرفته در سطح آب و ثابتی به نام ثابت نیروی چسبندگی متناسب است:
$$F_{up} = 2 \pi r A$$
$$A$$ ثابت نیروی چسبندگی نام دارد و نشاندهنده جاذبه بین مولکولهای مایع (در اینجا آب) و ماده تشکیلدهنده لوله (در اینجا شیشه) است. این دو نیرو در شرایط تعادلی با یکدیگر برابر هستند:
$$\pi r^2 h \rho g = 2 \pi r A$$
به رابطه دو نیروی وارد شده بر آب دقت کنید. هر دو نیرو با شعاع لوله متناسب هستند و مقدار آنها با افزایش $$r$$، افزایش خواهد یافت. اما سرعت افزایش نیروی وارد شده به سمت پایین یا نیروی جاذبه با افزایش شعاع لوله، بیشتر از مقدار افزایش نیروی وارد شده به سمت بالا (نیروی چسبندگی) خواهد بود. بنابراین، با بزرگتر شدن لوله، اندازه نیروی وزن از اندازه نیروی چسبندگی بزرگتر میشود. معادله فوق را برای $$h$$، حل میکنیم:
$$h = \frac {2 A} {\rho g r} $$
معادله جورین
رابطه فوق در کتابهای درسی نوشته نشده است، ولی با سادهسازی، به معادلهای شبیه به معادله جورین رسیدیم. فیزیکدانی انگلیسی به نام «جیمز جورین» (James Jurin) از نخستین فیزیکدانانی بود که روی اثر مویینگی کار کرد و رابطه معروف جورین را بهدست آورد:
$$h = \frac {2 \gamma \cos \theta} {\rho g r}$$

همانطور که در معادله فوق دیده میشود، ارتفاع مایع در لوله مویین به طور معکوس با شعاع لوله، متناسب است. همچنین، ثابت چسبندگی، $$A$$، بر حسب کمیتهای قابل اندازهگیری نوشته شده است:
- $$\gamma$$، ثابت کشش سطحی مایع و با دما متناسب است. این ثابت در مورد نیروهای پیوستگی بین مولکولهای آب صحبت میکند.
- $$\cos \theta$$، زاویه بین شکل مینیسک (مقعر یا محدب) و امتداد لوله است. این زاویه به ماده تشکیلدهنده مایع و لوله بستگی دارد (آب و شیشه). با افزایش چسبندگی بین مایع و لوله، زاویه $$\theta$$ کوچکتر و $$\cos \theta$$ به یک نزدیک میشود. اگر چسبندگی مایع بسیار کوچک باشد، مقدار زاویه $$\theta$$ به ۹۰ درجه نزدیک و $$\cos \theta$$ به سمت یک خواهد رفت.
قانون جورین نهتنها برای آب، بلکه در مایعات دیگری مانند جیوه نیز مشاهده میشود.
آزمایش بالا را به جای آب، با جیوه تکرار میکنیم. ظرفی را با جیوه پر میکنیم و لوله باریکی را به صورت وارونه در آن قرار میدهیم. جیوه به جای بالا رفتن از لوله، از آن پایین میرود و مینیسک زیر سطح جیوه تشکیل میشود. دلیل این اتفاق آن است که جیوه به شیشه نمیچسبد و نیروی چسبندگی بین مولکولهای جیوه و آب بسیار کوچک و نزدیک به صفر است. همچنین، سطح جیوه شکل محدب به خود میگیرد.
برهمکنش بین اتمهای جیوه با یکدیگر بسیار زیاد است، بنابراین نیروی پیوستگی بین آنها بسیار بزرگ خواهد بود. در این حالت، زاویه $$\theta$$ از ۹۰ درجه بزرگتر، $$\cos \theta$$ منفی، و ارتفاع جیوه کوچکتر از صفر است.
اثبات معادله جورین
در این قسمت معادله جورین را اثبات میکنیم. برای اثبات این معادله باید معادله با صورت معادله یانگ-لاپلاس در مرزهای کروی آشنا باشیم.
معادله یانگ لاپلاس
مرز جداکننده دو سیال امتزاجناپذیر یک و دو را در نظر بگیرید. قسمتی از فصل مشترک این دو سیال به نام S توسط منحنی بستهای به نام C، محصور شده است. بردارهای t و n به ترتیب بردار واحد مماس و عمود بر فصل مشترک دو سیال هستند و جهت n از سیال ۱ به سیال ۲ است.

$$p_1$$ و $$p_2$$ به ترتیب فشار سیال یک و دو و $$\gamma$$ کشش سطحی در مرز جداکننده دو سیال است. نیروی کل وارد بر S برابر است با:
$$f = int_{S} (p_1 - p_2) \overrightarrow{n} dS + \gamma oint_C \overrightarrow{t}\times \overrightarrow{n} dr$$
در رابطه فوق، $$doverrightarrow{S} = \overrightarrow{n} dS$$ مولفه $$S$$ و $$doverrightarrow{r} = \overrightarrow{t} dr$$ مولفه $$C$$ است. جمله اول رابطه بالا، نیروی عمودی کل به دلیل تفاوت فشار بین دو محیط و جمله دوم، نیروی مماسی کل است. توجه به این نکته مهم است که از نیروهای ویسکوز چشمپوشی شده است، زیرا هر دو سیال ساکن هستند. مقدار نیروی کل وارد بر $$S$$ در شرایط تعادلی برابر صفر است، بنابراین داریم:
$$int_{S} (p_1 - p_2) \overrightarrow{n} dS = - \gamma oint_C \overrightarrow{t}\times \overrightarrow{n} dr$$
مقدار نیروی کل در حالت کلی و در شرایط غیرتعادلی نیز باید برابر صفر باشد، زیرا جرم فصل مشترک بسیار کم و برابر صفر است.
با اعمال قضیه کرل بر منحنی بسته $$C$$ داریم:
$$oint_C \overrightarrow{F}. doverrightarrow{r} = int_{S}\overrightarrow{\triangledown} \times \overrightarrow{F}. d \overrightarrow{S}$$
در رابطه فوق، $$\overrightarrow{F}$$ میدان برداری کلی است.
قضیه کرل به صورت زیر نیز نوشته میشود:
$$oint_C \overrightarrow{F}. \overrightarrow{t}dr = int_{S}\overrightarrow{\triangledown} \times \overrightarrow{F}. \overrightarrow{n} dS$$
فرض کنید $$\overrightarrow{F} = \overrightarrow{g}\times \overrightarrow{b}$$، که در آن $$\overrightarrow{b}$$ برداری دلخواه است. بنابراین، معادله فوق به صورت زیر نوشته میشود:
$$oint_C ({\overrightarrow{g} \times \overrightarrow{b}}). \overrightarrow{t}dr = int_{S}\overrightarrow{\triangledown} \times (\overrightarrow{g}\times \overrightarrow{b}). \overrightarrow{n} dS$$
با استفاده از رابطه برداری $$\overrightarrow{\triangledown}\times (\overrightarrow{A}\times \overrightarrow{B}) = (\overrightarrow{\triangledown}. \overrightarrow{B}) \overrightarrow{A}- (\overrightarrow{\triangledown}. \overrightarrow{A}) \overrightarrow{B}- (\overrightarrow{B}. \overrightarrow{\triangledown}) \overrightarrow{A}- (\overrightarrow{A}. \overrightarrow{\triangledown}) \overrightarrow{B}$$ و ثابت بودن $$\overrightarrow{b}$$ داریم:
$$\overrightarrow{\triangledown}\times (\overrightarrow{g}\times \overrightarrow{b}) = - (\overrightarrow{\triangledown}. \overrightarrow{g}) \overrightarrow{b}+ (\overrightarrow{b}. \overrightarrow{\triangledown}) \overrightarrow{g}$$
با قرار دادن رابطه فوق در انتگرال، داریم:
$$\overrightarrow{b}. oint_C \overrightarrow{t}\times \overrightarrow{g} dr = \overrightarrow{b}. int_S [ (\overrightarrow{\triangledown}\overrightarrow{g}). \overrightarrow{n }- (\overrightarrow{\triangledown}.overrightarrow{g}) \overrightarrow{n} ) d S$$
از آنجا که $$\overrightarrow{b}$$ برداری دلخواه و ثابتی است، از طرفین معادله بالا حذف میشود:
$$ oint_C \overrightarrow{t}\times \overrightarrow{g} dr = int_S [ (\overrightarrow{\triangledown}\overrightarrow{g}). \overrightarrow{n }- (\overrightarrow{\triangledown}.overrightarrow{g}) \overrightarrow{n} ) d S$$
با تعریف $$\overrightarrow{g}= \gamma \overrightarrow {n}$$ و قرار دادن آن در معادله داریم:
$$ \gamma oint_C \overrightarrow{t}\times \overrightarrow{n} dr = \gamma int_S [ (\overrightarrow{\triangledown}\overrightarrow{n}). \overrightarrow{n }- (\overrightarrow{\triangledown}.overrightarrow{n}) \overrightarrow{n} ) d S \ $$
گفتیم $$\overrightarrow{n}$$ برداری واحد و عمود بر فصل مشترک جداکننده دو سیال است، بنابراین مقدار $$(\overrightarrow{\triangledown}\overrightarrow{n}). \overrightarrow{n }$$ برابر صفر است:
$$ \gamma oint_C \overrightarrow{t}\times \overrightarrow{n} dr = - \gamma int_S (\overrightarrow{\triangledown}.overrightarrow{n} ) \overrightarrow{n} d S \ $$
با ترکیب معادله مربوط به اختلاف فشار بین دو سیال و معادله فوق با یکدیگر داریم:
$$int_{S}[ (p_1 - p_2) - \gamma (\overrightarrow{\triangledown}. \overrightarrow{n})] \overrightarrow{n} dS = 0$$
در پایان، رابطه فوق را با توجه به دلخواه بودن $$S$$ به صورت زیر مینویسیم:
$$\triangle p = \gamma \overrightarrow{\triangledown}. \overrightarrow{n}$$
به رابطه فوق، معادله یانگ-لاپلاس گفته میشود.
فصل مشترک کروی
در حالت کلی، شکل تعادلی مرز مشترک دو سیال غیر قابلامتزاج، توسط حل معادله تعادلی نیرو در هر سیال و استفاده از معادله یانگ-لاپلاس، تعیین میشود. در حالتهایی که جرمی از سیال یک به طور کامل در سیال ۲، غوطهور میشود، مانند قطره مه در هوا یا حباب بخار در آب، شکل فصل مشترک تقریبا واضح است. در دو حالت میتوانیم از نیروی جاذبه صرفنظر کنیم:
- اندازه قطره یا حباب به اندازه کافی کوچک باشد.
- تفاوت چگالی دو سیال بسیار کوچک باشد.
در این صورت، فشارِ هر سیال، یکنواخت و اختلاف فشار بین دو سیال، ثابت است. همچنین، با توجه به معادله $$\triangle p = \gamma \overrightarrow{\triangledown}. \overrightarrow{n}$$، مقدار $$\overrightarrow{\triangledown}. \overrightarrow{n}$$ نیز ثابت خواهد بود. از آنجا که کره تنها سطح بستهای است که میانگین انحنای آن ثابت میماند، بنابراین مرز مشترک دو سیال به شکل کره خواهد بود.
اگر شعاع کرهای $$R$$ باشد، بردار عمود بر آن به صورت زیر نوشته خواهد شد:
$$\overrightarrow{n}= \overrightarrow{e}_r |_ {r = R}$$
از این رو، دیورژانس $$\overrightarrow{n}$$ در مختصات کروی برابر است با:
$$\overrightarrow{\triangledown}. \overrightarrow{n} = \frac{1}{r^2}\frac{\partial r^2}{\partial r}|_{r=R} = \frac{2}{R}$$
توجه به این نکته مهم است که جهت بردار $$\overrightarrow{n} $$ به سمت خارج کره است. با جایگزینی رابطه فوق در معادله یانگ-لاپلاس داریم:
$$\triangle p = \frac{2 \gamma}{R}$$
بنابراین، اختلاف فشار بین دو سیال متناسب با کشش سطحی و با شعاع حباب یا قطره به صورت معکوس، متناسب است. همچنین، با توجه به رابطه بهدست آمده به این نتیجه میرسیم که فشار داخل حباب یا قطره بیشتر از فشار خارج است.
پس از بهدست آوردن معادله لاپلاس و اختلاف فشار بین دو سیال با سطح مشترک کروی، در ادامه معادله جورین را اثبات میکنیم.
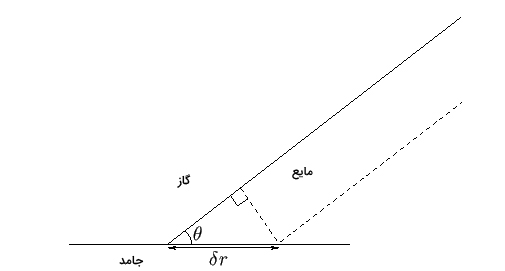
لولهای نازک به شکل استوانه و به شعاع $$a$$ (لوله مویین) را به صورت عمودی داخل مایعی با چگالی $$\rho$$ قرار میدهیم. میدانیم مایع به دلیل اثر مویینگی تا ارتفاع $$h$$ در لوله بالا میآید. فرض کنید شعاع لوله کوچکتر از طول مویینگی است. با توجه به مطالب گفته شده در بالا، نیروی جاذبه تاثیر قابلتوجهی بر شکل فصل مشترک هوا٫مایع در لوله مویین نخواهد گذاشت. بنابراین، مرز هوا٫مایع، کرهای به شعاع $$R$$ است. اگر $$\theta$$ زاویه تماس فصل مشترک با شیشه باشد:
$$R = \frac{a}{\cos \theta}$$
رابطه بهدست آمده برای شعاع کره را در میانگین انحنای فصل مشترک قرار میدهیم:
$$\overrightarrow{\triangledown}.overrightarrow{n} = - \frac{2}{R} = - \frac{2 \cos \theta}{a}$$
رابطه فوق را در معادله یانگ-لاپلاس قرار میدهیم:
$$\rho g h = \frac{2 \gamma \cos \theta}{a}$$
بنابراین، ارتفاع مایع در لوله مویین برابر است با:
$$h \simeq \frac{2 \gamma \cos \theta}{\rho g a}$$
به رابطه فوق، معادله جورین گفته میشود.
در مطالب بالا در مورد طول مویینگی صحبت کردیم و برای بهدست آوردن معادله جورین فرض کردیم که شعاع لوله مویین، کوچکتر از این طول است. در ادامه، خالی از لطف نیست کمی در مورد طول مویینگی و رابطه آن صحبت کنیم.
طول مویینگی چیست ؟
مرز جداکننده اتمسفر (جو) از مایعی با چگالی $$\rho$$ روی زمین در نظر بگیرید. اگر از چگالی هوا در برابر چگالی مایع چشمپوشی کنیم، فشار جو را میتوان ثابت در نظر گرفت. به بیان دیگر، فشار داخل مایع به صورت $$p = p_0 - \rho g z$$ با ارتفاع تغییر میکند. در این رابطه، $$z$$ برابر ارتفاع عمودی نسبت به سطح مایع است.
توجه داشته باشید که $$z$$ به سمت بالا افزایش مییابد. در این صورت، معادله لاپلاس به صورت زیر نوشته خواهد شد:
$$\rho g z = - \gamma \overrightarrow{\triangledown}. \overrightarrow{n}$$
جهت بردار عمود بر فصل مشترکِ $$\overrightarrow{n}$$ از مایع به سمت هوا است. طول مویینگی با استفاده از رابطه زیر بهدست میآید:
$$l = (\frac{\gamma }{\rho g})^2$$
مقدار $$l$$ برای آب خالص در دمای ۲۰ درجه سلسیوس برابر $$2.7 \times 10^{-3} m$$ است.
کاربردهای اثر مویینگی در زندگی روزمره چیست ؟
با کمی دقت به اطراف خود، کاربردهای زیادی از اثر مویینگی را مشاهده خواهیم کرد. اگر قسمتی از دستمال کاغذی را داخل آب قرار دهیم، در کمال شگفتی خواهیم دید که آب برخلاف جاذبه زمین از دستمال بالا میرود و تمام آن را خیس میکند. دلیل این حرکت، اثر مویینگی است. مولکولهای آب از دستمال بالا میروند و مولکولهای دیگر را با خود به سمت بالا میکشانند. همچنین، عملکرد بدن بدون اثر مویینگی دچار اختلال میشد.
- اگر مویینگی وجود نداشت، هیچ درخت و گیاهی را در اطراف خود مشاهده نمیکردیم. ریشه گیاهان و درختان قادر به انتقال آب از خاک به گیاه است. آب به درون ریشه گیاهان نفوذ میکند و از بافت گیاه بالا میرود. اثر مویینگی به آب کمک میکند تا به ریشهها برسد، اما قادر به انتقال آن به شاخهها و برگها نیست. برای انجام این کار به نیروهای چسبندگی و پیوستگی نیاز است.
- نفت در چراغ نفتی با استفاده از اثر مویینگی نخهای فتیله، از آن بالا میرود.
- با استفاده از حوله، دستان خود را خشک میکنید. این کار بدون اثر مویینگی امکانپذیر نبود.
- اسفنج، آب را در خود به دلیل اثر مویینگی، حفظ میکند.

اثر مویینگی در ساختمان چگونه است ؟
اثر مویینگی را به صورت بالا رفتن آب یا مایعی دیگر در فضای بسیار باریک و در خلاف جاذبه زمین، تعریف کردیم. یکی از اثرات مویینگی، در ساختمانها و به صورت افزایش رطوبت در بتن یا دیوار ساختمانها دیده میشود. هنگامی که مصالح ساختمانی مانند انواع آجرها، برخی سنگها، بلوکهای سیمانی و گچ در تماس با رطوبت قرار میگیرند، آب توسط منافذ قرار گرفته در آنها جذب میشود. اگر نیروی چسبندگی بین مولکولهای هر یک از مصالح بنایی بزرگتر از نیروی پیوستگی بین مولکولهای آب باشد، آب به دلیل اثر مویینگی به سمت بالا حرکت خواهد کرد.
به طور معمول، رطوبت میتواند تا یک متر بالاتر از منبع خود، حرکت کند. بنابراین، برای حفاظت از ساختمان و جلوگیری از پیشروی آب، ماده لاستیکی پلیمریزه شدهای مانند پلیمر قیر، نصب میکنند.

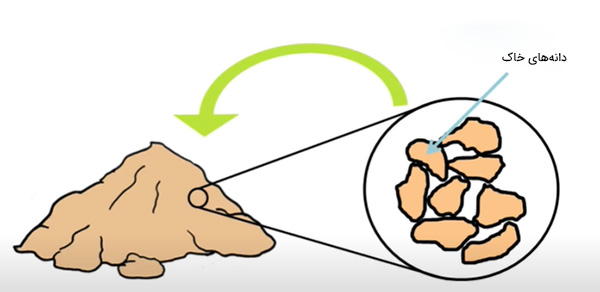
اثر مویینگی در خاک
خاک از ذرات جامد کوچکی به نام دانههای خاک تشکیل شده است. هنگامی که این ذرات کوچک برای تشکیل ذرات بزرگتر در کنار یکدیگر قرار میگیرند، فضای خالی بین آنها تشکیل میشود.
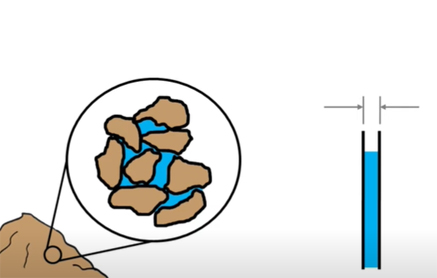
به هنگام بارش باران، آب از طریق فضاهای خالی قرار گرفته در بین دانههای خاک به داخل آن نفوذ میکند و در اثر نیروی جاذبه به سمت پایین جاری میشود. آب زیرزمینی به دو بخش تقسیم میشود:
- آبِ آزاد
- آبِ محبوس
آبِ آزاد تحت تاثیر نیروی جاذبه، در خاک جریان دارد. از این رو، به آن آبِ گرانشی نیز گفته میشود. آبِ آزاد به طور کامل، حفرهها را پر و اشباع میکند. برای اندازهگیری سطح آبِ آزاد، از چاه استفاده میشود. به ارتفاعی که آب در چاه بالا میآید، سطح آب آزاد میگوییم. فشار سطح آبِ آزاد برابر فشار جو است و فشار زیر سطح آن با افزایش عمق افزایش مییابد و بیشتر از فشار جو خواهد بود.
برخلاف آبِ آزاد، آبِ محبوس در حفرههای داخل خاک محبوس شده است و تحت تاثیر نیروی جاذبه حرکت نمیکند. اگر خاک تمیز باشد، آب محبوس همان آب جذب شده توسط خاک خواهد بود. اگر اندازه دانههای خاک بزرگ باشند، مقدار آب محبوس در حفرههای تشکیل شده بین آنها، ناچیز است.
گاهی مولکولهای آب بر نیروی جاذبه غلبه میکنند و در خاک به سمت بالا حرکت میکنند. همانطور که میدانیم به این پدیده اثر مویینگی گفته میشود. آب بدون اعمال نیروی خارجی از مسیرهای باریک بالا میرود. برای درک بهتر اثر مویینگی در خاک، حفرههای تشکیل شده بین دانههای خاک را با لولههای مویین مقایسه میکنیم. زیرا این حفرات به یکدیگر متصل شدهاند و کانالهای کوچکی شبیه لولههای مویین تشکیل دادهاند. گرچه سطح مقطع این کانالها با سطح مقطع لولههای مویین متفاوت است و دایرهای نیست، اما برای درک مویینگی در خاک، مقایسه مناسبی به نظر میرسد.
در مطالب بالا، در مورد ارتفاع آب در لوله مویین و رابطه آن با نیروی کشش، چگالی آب، و قطر لوله مویین صحبت کردیم. همچنین، در مورد اختلاف فشار داخل لوله مویین و سطح آب نیز توضیح دادیم. میدانیم ارتفاع آب در لوله مویین به طور معکوس با قطر لوله مویین، تغییر میکند. هر چه قطر لوله بیشتر باشد، ارتفاع آب کمتر خواهد بود و هرچه قطر لوله کمتر باشد، ارتفاع آب بیشتر است.
حفرات متصل به یکدیگر داخل خاک، تشکیل کانالهایی قابل مقایسه با لولههای مویین با قطرهای مختلف را میدهند. بنابراین، آب داخل خاک به دلیل اثر مویینگی تا ارتفاع معینی بالا میرود و بالاتر از سطح آب آزاد قرار میگیرد. آب، داخل حفراتِ خاک و زیر سطح آبِ آزاد، متراکم است.
هرچه اندازه دانههای تشکیلدهنده خاک کوچکتر باشد، اندازه حفرات تشکیل شده بین آنها نیز کوچکتر است. این حفرات کوچک به یکدیگر متصل میشوند و کانالهایی با اندازه بسیار کوچک تشکیل میدهند. این کانالهای کوچک شبیه لولههای مویین بسیار نازک هستند و آب تا ارتفاع مشخصی از آنها بالا میرود. در مقابل، حفرات بین دانههای بزرگتر، کانالهای بزرگتری تشکیل میدهند. بنابراین، ارتفاع آب در آنها کمتر از ارتفاع آب در کانالهای کوچکتر است.
توجه به این نکته مهم است که اثر مویینگی در خاک به اندازه حفرات بستگی دارد. همچنین، به یاد داشته باشید که توزیع اندازه حفرات حتی در خاکی با اندازه دانههای یکسان، متفاوت است. کانالهای تشکیل شده در خاک به طور کامل همانند لولههای مویین نیستند، زیرا شکل و اندازه آنها نامنظم است و لزوما پیوسته و عمودی نیستند.
هنگامی که آب به دلیل مویینگی از سطح آب آزاد بالاتر میرود، قسمت پایینتر خاک و نزدیک به سطح آبِ آزاد ممکن است به طور کامل اشباع شود. اما آب در ارتفاع بالاتر، تنها حفرات باریکتر را پر کرده است و حفرات بزرگتر توسط هوا اشغال شدهاند.
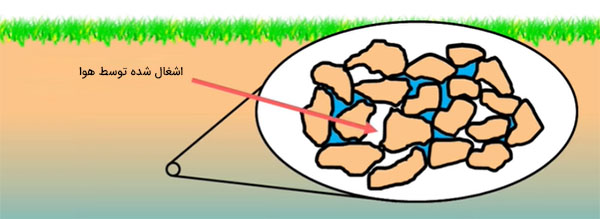
با توجه به مشاهده اثر مویینگی در آب و بالا رفتن آب در خاک، آب زیرزمینی به ناحیههای مختلفی تقسیم میشود:
- پایینترین قسمت خاک که به طور کامل اشباع شده است.
- فرض کنید بیشینه ارتفاعی که آب بالاتر از سطح آب آزاد قرار دارد برابر $$h_c$$ باشد. ناحیه دوم، بالای سطح آب آزاد و تا جایی ادامه مییابد که آب بالا رفته به طور کامل خاک را اشباع کند.
- در ناحیه سوم، آب تنها از حفرات باریک و کوچک عبور میکند. حفرات بزرگتر اجازه عبور آب از خود را نمیدهند. بنابراین، آب تا ارتفاع بیشینه یعنی $$h_c$$ بالا میرود. این ناحیه به طور نسبی اشباع شده است.
آزمایش اثر مویینگی
هدف از انجام این آزمایش نشان دادن وابستگی ارتفاع آب در لوله مویین به قطر لوله و دمای آب است.
در مطالب بالا با اثر مویینگی و فرمول ریاضی ارتفاع آب در لوله مویین آشنا شدیم:
$$h = \frac{2 \gamma}{r \rho g}$$
بر طبق رابطه فوق:
- با افزایش شعاع لوله مویین، ارتفاع آب در لوله کاهش مییابد.
- کشش سطحی و چگالی آب با تغییر دما، تغییر میکنند. بنابراین، ارتفاع آب در لوله به دما وابسته است. کشش سطحی و چگالی آب با افزایش دما، کاهش مییابند. به این نکته توجه داشته باشید، که این تغییر برای چگالی از محدوده دمایی ۴ درجه سلسیوس به بالا، رخ میدهد.
وسایل مورد نیاز این آزمایش عبارت هستند از:
- دو یا بیشتر از دو لوله مویین با شعاعهای متفاوت
- نگهدارنده لوله مویین
- ظرف آب
- کتری
- آب
- دو رنگ خوراکی متفاوت برای تغییر رنگ آب

مراحل انجام آزمایش به صورت زیر است:
- آب را با استفاده از رنگ خوراکی، رنگ کنید.
- لوله مویین را داخل ظرف آب قرار دهید.
- به بالا رفتن آب از لوله مویین دقت کنید.
- محل ارتفاع آب در هر لوله را با استفاده از ماژیک، مشخص کنید.
- مراحل فوق را با آب داغ، تکرار کنید.
نتیجه آزمایش اثر مویینگی
این آزمایش با آب سرد به رنگ آبی با دمایی در حدود ۱۰ درجه سلسیوس و آب داغ به رنگ قرمز در دمای حدود ۷۰ درجه سلسیوس انجام شد. تصویر زیر ارتفاع آب سرد (تصویر چپ) و آب گرم (تصویر راست) را در لولههای مویین مختلف نشان میدهد.

ارتفاع آب در لولههای مویین و دو دمای متفاوت، در تصویر زیر با رسم خط افقی نقطهچین، با یکدیگر مقایسه شدهاند. همانطور که مشاهده میشود، در دو لوله مویین یکسان، ارتفاع آب سرد بیشتر از ارتفاع آب گرم است.

اثر مویینگی در روغن
اگر در ظرفی روغن و در ظرف دیگر آب بریزیم و دو لوله مویین با اندازههای یکسان را در به صورت عمودی در آنها قرار دهیم، آب و روغن به دلیل اثر مویینگی از لولهها بالا میآیند. با مقایسه ارتفاع آنها، خواهیم دید که ارتفاع روغن نسبت به آب بیشتر است. شاید از خود بپرسید چرا با اینکه کشش سطحی روغن از آب کمتر است، روغن در لوله تا ارتفاع بیشتری نسبت به آب بالا میآید.
برای پاسخ به این سوال به رابطه ارتفاع آب در لوله مویین یا معادله جورین توجه میکنیم:
$$h = \frac{2 \gamma \cos \theta}{\rho g r}$$
همانطور که در رابطه فوق دیده میشود، ارتفاع مویینگی متناسب با کشش سطحی است. مقدار کشش سطحی آب در مقایسه با روغن، بزرگتر است، بنابراین انتظار میرود که ارتفاع آب در لوله مویین نسبت به روغن بیشتر باشد. اما کشش سطحی تنها عامل موثر بر ارتفاع نیست. دو عامل دیگر باید در نظر گرفته شوند:
- چگالی
- زاویه تماس
زاویه تماس و چگالی روغن، نسبت به آب کمتر است. از این رو، اثر کشش سطحی خنثی میشود و روغن تا ارتفاع بیشتری نسبت به آب، در لوله مویین بالا میرود.
اثر مویینگی در فناوری نانو
اثر مویینگی در مقیاس نانو، رابطه تنگاتنگی با ترشوندگی و زیرلایههای آبدوست دارد. همچنین، یکی از کاربردهای این اثر در دستگاه نانولیتوگرافی برای ساخت وسایل نانو یا حکاکی در ابعاد نانو روی زیرلایههای مناسب است. در این دستگاه، مینیسک توسط مویینگی، به دور نقطه تماس سوزن با زیرلایه شکل میگیرد.
نمونه سوالات اثر مویینگی
تاکنون با اثر مویینگی، فرمول ریاضی و کاربردهای آن در زندگی روزمره آشنا شدیم. در ادامه، برای درک بهتر این اثر و آشنایی با چگونگی استفاده از معادله آن، مثالهایی را حل خواهیم کرد.
پرسش اول
دمای آب برابر ۴۰ درجه سانتیگراد است و سطح شیشه را به طور کامل خیس میکند. بنابراین، سطح شیشه به طور کامل آبدوست و زاویه قطره آب با سطح آن در حدود صفر درجه است. اگر لوله شیشهای به قطر ۰٫۵ میلیمتر را در ظرف آب قرار دهیم، ارتفاعی که آب در لوله بالا میرود را بهدست آورید.
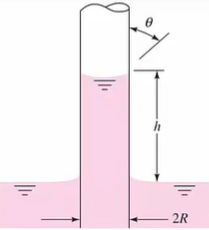
پاسخ: ارتفاع آب در لوله مویین با استفاده از رابطه زیر بهدست میآید:
$$h = \frac{4 Y \cos \theta}{\rho D g}$$
در رابطه فوق:
- $$Y$$ مقدار کشش سطحی است.
- $$D$$ قطر لوله شیشهای یا مویین است.
- $$\rho$$ چگالی آب است.
دمای آب برابر ۴۰ درجه سانتیگراد است. مقدارهای کشش سطحی و چگالی آب در این دما برابر هستند با:
$$Y = 0.0696 \frac{N}{m} \ \rho = 992 \frac{kg }{m^3}$$
با قرار دادن مقدارهای داده شده در رابطه ارتفاع، مقدار آن را بهدست میآوریم:
$$h = \frac{4 ( 0.0696) \cos (o^o)}{992 (0.0005 m) } = 0.0572 m = 5.72 cm$$
مساله فوق را به صورت دیگری بیان میکنیم. فرض کنید به جای لوله مویین، از دو صفحه موازی با طول $$L$$ استفاده شده است.
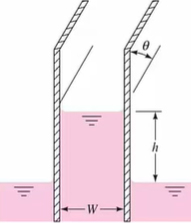
اگر $$L$$ در مقایسه با $$W$$ بسیار بزرگتر باشد، آب به راحتی از بین دو صفحه بالا خواهد رفت.
پرسش دوم
شعاع داخلی لوله مویینی برابر ۰٫۱۰ میلیمتر است.
- اگر لوله را به صورت عمود داخل آب قرار دهیم، ارتفاعی که آب از لوله بالا میرود را بهدست آورید.
- فشار هیدرواستاتیکی ایجاد شده توسط آب داخل لوله چه مقدار است؟
- اگر شعاع لوله مویین دو برابر شود، نتیجه بهدست آمده چه تغییری خواهد کرد؟
- اگر آزمایش را در سطح ماه انجام دهیم، نتیجه بهدست آمده چه تغییری میکند؟
- اگر آزمایش را در ماهوارهای در حالت بیوزنی انجام دهیم، نتیجه آزمایش چه تغییری خواهد کرد؟
پاسخ: میدانیم ارتفاع آب در لوله مویین با استفاده از تعادل نیروهای وارد شده بر آب، به دست میآید. نیروی جاذبه زمین به سمت پایین و نیروی کشش سطحی به سمت بالا بر آن وارد میشوند. برای سادگی فرض میکنیم که جهت نیروی کشش سطحی به سمت بالا و بزرگی آن متناسب با محیط داخلی لوله (محیط سطح آب) است.
قسمت ۱: به هنگام حل این پرسش باید فرض کنیم که آب به خوبی به دیوارههای لوله چسبیده است. این بدان معنا است که سطح آب به شکل نیمکره و نیروی کشش سطحی به سمت پایین است. بر طبق قانون سوم نیوتن، شیشه نیرویی برابر و در خلاف جهت بر آب (رو به بالا) وارد میکند. همچنین، نیروی جاذبه به سمت پایین بر آب وارد میشود. با فرض آنکه سطح آب ساکن است، این دو نیرو با یکدیگر برابر خواهند بود. مقدار نیروی جاذبه برابر است با:
$$F_G = mg = V \rho g = mr^2 h \rho g$$
نیروی کشش سطحی متناسب با محیط داخلی آب است و به صورت زیر نوشته میشود:
$$F = \gamma (2 \pi r)$$
در شرایط تعادلی، دو نیرو با یکدیگر برابر هستند:
$$F_G = F \ \pi r^2 h \rho g = \gamma (2 \pi r) \ h = \frac{2 \gamma}{r \rho g} = \frac{2times 0.073 }{1 \times 10^{-4} \times 1000 \times 9.81 \ } \ h = 0.149 m $$
قسمت ۲: فشار هیدرواستاتیکی آب در لوله مویین با استفاده از رابطه زیر بهدست میآید:
$$p = h \rho g = \frac{2 \gamma}{r \rho g} \rho g = \frac{2 \gamma}{r} \ p = 1.5 kPa$$
به این فشار، فشار مویینگی گفته میشود و در اثر کشش سطحی، ایجاد شده است.
قسمت ۳: ارتفاع آب در لوله مویین متناسب با عکس شعاع لوله است. بنابراین، اگر شعاع لوله دو برابر شود، ارتفاعی که آب در لوله بالا میرود، نصف خواهد شد.
قسمت ۴: شتاب جاذبه در سطح ماه یکششم مقدار آن در سطح زمین است. ارتفاع آب در لوله مویین با معکوس شتاب جاذبه متناسب است، بنابراین در سطح ماه ارتفاع آب، شش برابر آن در سطح زمین خواهد بود.
قسمت ۵: در حالت بیوزنی، نیروی وزن برابر صفر است. بنابراین، آب به دلیل ترشوندگی به بالای لوله مویین میرسد.
پرسش سوم
دو لوله مویین با قطرهای ۰٫۱ و ۰٫۳ میلیمتر را از یک انتها داخل ظرف آبی با دمای ۲۰ درجه سلسیوس، قرار میدهیم. اگر آب را گرم کنیم و دمای آن را تا ۷۰ درجه سلسیوس افزایش دهیم، اختلاف ارتفاع آب در هر لوله مویین، چه تغییری خواهد کرد؟
پاسخ: دادههای این پرسش عبارت هستند از:
$$r_1 = 0.05 mm \ r_2 = 0.15 mm \ gamma_ {20} = 73 \times 10^{-3} \frac{N}{m }\gamma_ {70} = 64 \times 10^{-3} \frac{N}{m \ } \ rho_{20} = 998.2 \frac{kg}{m^3} \ rho_{70} = 977.8 \frac{kg}{m^3}$$
برای حل این پرسش، ابتدا آن را به صورت کمی بررسی میکنیم. ارتفاع آب در لوله مویین به صورت معکوس با شعاع لوله، متناسب است. هر چه لوله باریک باشد، ارتفاع آب در آن بیشتر خواهد بود. همچنین، ارتفاع آب به کشش سطحی و کشش سطحی به دما وابسته است. با افزایش دما، مقدار کشش سطحی کاهش مییابد. چگالی آب نیز به دما وابسته است و در دماهای بالاتر از ۴ درجه سانتیگراد، مقدار آن با افزایش دما، کاهش خواهد یافت. در نتیجه، ارتفاع آب در لوله مویین با تغییر دمای آب، تغییر میکند. در این پرسش، از تغییر قطر لوله مویین به هنگام افزایش دمای آب، صرفنظر شده است.
برای حل این پرسش، گامهای زیر را برمیداریم:
- ارتفاع آب در هر دو لوله را در دمای ۲۰ درجه سلسیوس تعیین میکنیم.
- اختلاف ارتفاع آب را بهدست میآوریم.
- ارتفاع آب در هر دو لوله را در دمای ۷۰ درجه سلسیوس تعیین میکنیم.
- اختلاف ارتفاع آب را بهدست میآوریم و مقدار آن را با حالت اول مقایسه میکنیم.
در ابتدا، تفاوت ارتفاع آب در دو لوله در دمای ۲۰ درجه سلسیوس را بهدست میآوریم. ارتفاع آب در لوله یک و دو در دمای ۲۰ درجه سلسیوس برابر است با:
$$h_{20}^{(1)} = \frac{2 \gamma _{20} }{r_1 rho_{20} g} \ h_{20}^{(2)} = \frac{2 \gamma _{20} }{r_2 rho_{20} g}$$
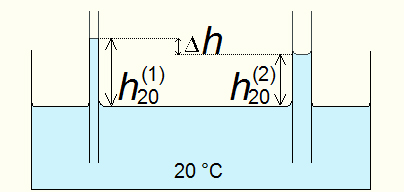
اختلاف ارتفاع آب در دو لوله در دمای ۲۰ درجه سلسیوس برابر است با:
$$\triangle h_{20}= h_{20} ^ {(1)} - h_{20} ^ {(2)} = \frac{2 \gamma _{20} }{g rho_{20} } (\frac{1}{r_1} - \frac{1}{r_2})$$
معادله مشابهی برای اختلاف ارتفاع آب در دو لوله در دمای ۷۰ درجه سلسیوس وجود دارد:
$$\triangle h_{70}= h_{70} ^ {(1)} - h_{70} ^ {(2)} = \frac{2 \gamma _{70} }{g rho_{70} } (\frac{1}{r_1} - \frac{1}{r_2})$$
با کم کردن دو رابطه بالا از یکدیگر، اختلاف ارتفاع آب در لولههای مویین پس از افزایش دما از ۲۰ به ۷۰ درجه سلسیوس، بهدست میآید:
$$\triangle h= \triangle h_{20} - \triangle h_{70} = \frac{2 }{g } (\frac{gamma_{20}}{rho_{20}} - \frac{gamma_{70}}{rho_{70}}) (\frac{1}{r_1} - \frac{1}{r_2})$$
با جایگزینی مقدارهای داده شده در معادله بالا، اختلاف ارتفاع در اثر افزایش دما برابر $$2.1 \times 10^{-2} m$$ بهدست میآید.
پرسش چهارم
اگر انتهای لوله مویین بسته باشد، ارتفاع آب چگونه تغییر خواهد کرد؟
پاسخ: اگر انتهای لوله مویین بسته باشد، آب تا ارتفاع کمی بالا خواهد آمد.
پرسش پنجم
با بررسی دقیق سؤال، جواب صحیح را از میان گزینههای موجود انتخاب کنید.
پرسش ششم
با بررسی دقیق سؤال، جواب صحیح را از میان گزینههای موجود انتخاب کنید.
نکات مهم در مورد اثر مویینگی
نکات مهمی در مورد اثر مویینگی وجود دارند که در ادامه، در مورد آنها صحبت میکنیم:
- ارتفاع مویینگی یا ارتفاع عمودی (Vertical elevation | ve) به ماهیت مایع و سطح جامد یعنی به کشش سطحی، چگالی مایع، شعاع مویینگی یا شعاع لوله مویین و زاویه تماس، بستگی دارد. سه حالت برای زاویه تماس وجود دارد:
- اگر زاویه تماس بزرگتر از ۹۰ درجه باشد، مینیسک یا سطح مایع محدب و ارتفاع منفی (زیر سطح مایع) است. این بدان معنا است که مایع در لوله مویین به سمت پایین حرکت میکند. جیوه مهمترین مثال برای این حالت است.
- اگر زاویه تماس برابر ۹۰ درجه باشد، مینیسک مسطح است. در این حالت، اثر مویینگی رخ نمیدهد.
- اگر زاویه تماس کمتر از ۹۰ درجه باشد، مینیسک مقعری و ارتفاع مثبت خواهد بود.
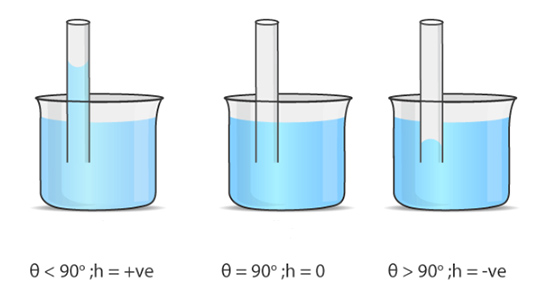
- مویینگی مستقل از شکل لوله مویین است. در حالت تعادل، ارتفاع آب در لوله مویین به شکل لوله بستگی ندارد (در صورت ثابت بودن شعاع لوله مویین).
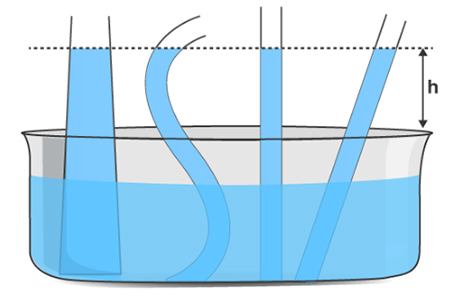
- نیروهای چسبندگی، پیوستگی و کشش سطحی دلیل اثر مویینگی هستند.
جمعبندی
در این مطلب، در مورد اثر مویینگی و عاملهای موثر بر آن صحبت کردیم. به تمایل مایع به بالا رفتن از لولهها یا منافذ باریک و در خلاف جهت نیروی جاذبه، مویینگی گفته میشود. ارتفاعی که آب یا مایعی دلخواه در لوله بالا میرود به زاویه تماس مایع با سطح، چگالی مایع، و کشش سطحی بستگی دارد. همچنین، نیروهای چسبندگی بین مولکولهای مایع و سطح جامد، نیروی پیوستگی بین مولکولهای مایع و کشش سطحی، بر مویینگی تاثیر میگذارند. در پایان، اثر مویینگی در خاک و ساختمان را به صورت خلاصه توضیح دادیم.










