کرل (Curl) در ریاضی – به زبان ساده

در آموزش‌های قبلی مجله فرادرس به بررسی دیورژانس پرداختیم. در این مطلب کرل (Curl) را معرفی خواهیم کرد. کرل و دیورژانس از مفاهیم پایه‌ای ریاضیات هستند. در آنالیز برداری، کرل یک بردار، برابر با حاصل ضرب خارجیِ عملگر دِل در آن بردار است. با توجه به اینکه حاصل ضرب خارجی دو بردار، به صورت یک تابع برداری است، می‌توان نتیجه گرفت که کرل نیز در نهایت به فرم یک تابع برداری در می‌آید.

در ادامه، رابطه عملگر کرل، تعبیر هندسی و کاربرد آن را بررسی می‌کنیم. در پایان، شیوه استفاده از این عملگر در قالب چند مثال نشان داده می‌شود.

کرل (Curl) چیست؟

تابع برداری $$F$$ را در فضای سه بعدی در نظر می‌گیریم:

$$\hat F= P \hat i + Q \hat j + R \hat k$$

در رابطه بالا $$P$$، $$Q$$ و $$R$$ مولفه‌های بردار $$F$$ به ترتیب در راستای $$x$$، $$y$$ و $$z$$ هستند. برای تعریف «کرل» (Curl) ابتدا باید «عملگر دِل» (Del Operator) را معرفی کنیم. این عملگر با نماد $$\nabla$$ نشان داده می‌شود. رابطه این عملگر در دستگاه مختصات کارتزین به صورت زیر است:

$$\nabla=\frac{\partial}{\partial x} \hat i+\frac{\partial}{\partial y} \hat j+\frac{\partial}{\partial z} \hat k$$

همانطور که در رابطه بالا مشخص است، عملگر دِل به صورت یک بردار بیان می‌شود که مولفه‌های آن به ترتیب، مشتق جزئی در راستای $$x$$، $$y$$ و $$z$$ هستند.

توجه کنید که این عملگر به تنهایی مفهومی را منتقل نمی‌کند و شیوه اعمال آن بر توابع مختلف، باعث ایجاد مفاهیم مختلف می‌شود. برای مثال، ضرب خارجی این عملگر در بردار $$F$$ منجر به مفهوم کرل می‌شود که رابطه آن برای بردار $$F$$ به صورت زیر نمایش داده می‌شود:

$$curl \, \hat F = \nabla \times \hat F$$

$$curl \, \hat F = \big( R_y-Q_z \big) \hat i + \big( P_z-R_x \big) \hat j + \big( Q_x-P_y \big) \hat k$$

که $$R_y$$ مشتق جزئی $$R$$ نسبت به $$y$$ است.

کرل یک تابع برداری را می‌توان به صورت ساده‌تر نیز نوشت. می‌دانیم گرادیان یک تابع به صورت زیر نوشته می‌شود:

$$\nabla f = \frac{\partial f}{\partial x} \hat i + \frac{\partial f}{\partial y} \hat j + \frac{\partial f}{\partial z} \hat k$$

بنابراین هر تابعی که بعد از عملگر «نابلا» ($$\nabla$$) یا دِل بیاید، مولفه‌هایی از ترکیب مشتقات جزئی تابع دارد. کرل یک تابع، حاصلِ ضرب خارجی $$\nabla$$ و تابع ‌$$F$$ است. پس:

$$curl \, \hat F=\nabla \times \hat F = \Large \begin{vmatrix} \hat i & \hat j & \hat k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P&Q&R \end{vmatrix}$$

نکته مهم و قابل توجه در این روابط، این است که کرل یک بردار، درنهایت به صورت یک «تابع برداری» (Vector Function) خواهد بود.

تعبیر هندسی کرل

فرض کنید تابع $$F$$ به صورت یک میدان برداری باشد. میدان برداری به حوزه‌ای از بردار گفته می‌شود. به عنوان یک مثال کاربردی می‌توان فرض کرد که بردار $$F$$، جریان یک سیال مانند مایع یا گاز باشد. می‌خواهیم مفهوم کرل را با استفاده از جریان سیال بررسی کنیم.

کرل یک میدان برداری به این مسئله می‌پردازد که آیا جریان در سیال می‌تواند گردش داشته باشد یا خیر. فرض کنیم در شکل زیر، میدان برداری $$F$$، بیانگر جریان سیال باشد. این میدان برداری نشان می‌دهد که سیال حول یک محور مرکزی در حال گردش است. سرعت سیال به وسیله میدان برداری مشخص می‌شود.

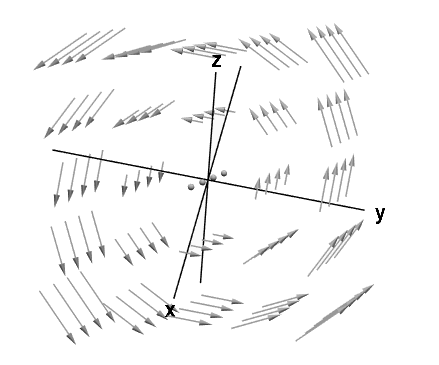
این چرخش‌های دایره‌ای در سیال با چشم قابل مشاهده است که به آن «چرخش ماکروسکوپی» (Macroscopic Circulation) می‌گویند. اگر جریان در سیال را به صورت میدان برداری در نظر بگیریم، مشاهده می‌شود که سیال به صورت دایره‌ای در خلاف جهت عقربه‌های ساعت، حول یک محور مشخص، در حال چرخش است. روی این محور، اندازه بردار صفر است. بنابراین سرعت سیال روی این محور صفر خواهد بود.

البته این بردار، مقدار کرل نیست. بلکه مشخص شده است که این بردار نیز کرل دارد. کرل این بردار را می‌توان به صورت «چرخش‌های میکروسکوپی» (Microscopic Circulation) در نظر گرفت.

فرض کنید یک کره خیلی کوچک را داخل سیالِ در حال چرخش قرار دهیم. این کره را به صورت ثابت در یک نقطه مشخص (معمولا مبدأ مختصات) قرار می‌دهیم تا کره نتواند مثل سیال گردش داشته باشد. اما کره می‌تواند حول مرکز خود روی یک نقطه ثابت، بچرخد. چرخش کره در شکل زیر نشان داده شده است.

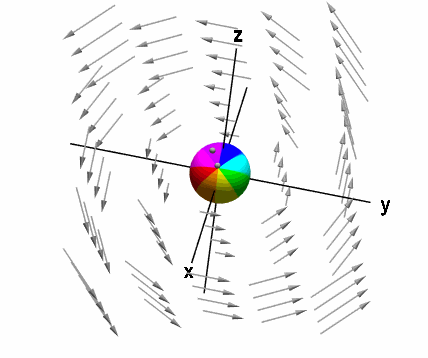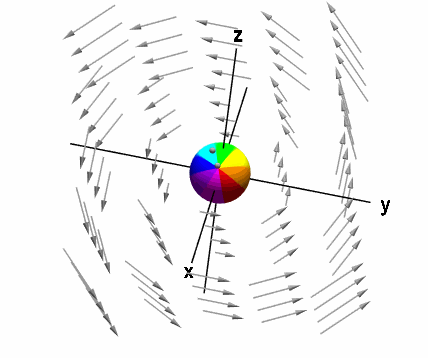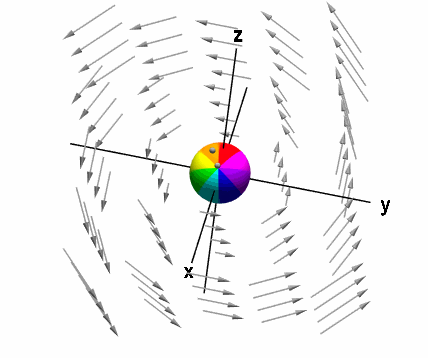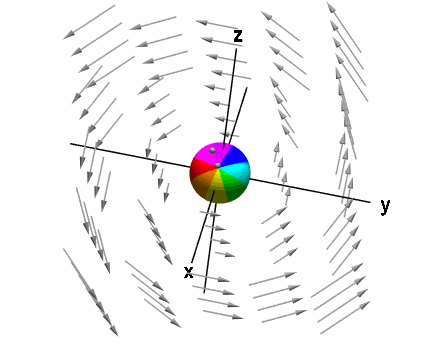
کرل میدان برداری $$F$$، به وسیله چرخش کره در نقطه مرکز آن مشخص می‌شود. (البته این کره بسیار کوچک است. زیرا همانطور که گفتیم کرل، چرخش میکروسکوپی است).

میدان برداری $$F$$، جهت چرخش این کره و سرعت چرخش آن را مشخص می‌کند. کرل میدان $$F$$ را به صورت $$curl \, \hat F$$ می‌نویسیم. می‌دانیم کرل یک تابع برداری، بردار است (بنابراین مفهوم آن به طور کلی با دیورژانس متفاوت است). جهت این بردار، جهت محور چرخش کره را مشخص می‌کند. همچنین اندازه این بردار، برابر سرعت چرخش کره است.

جهت بردار کرل، طبق قانون دست راست محاسبه می‌شود. به این صورت که اگر انگشتان دست راست را در جهت چرخش کره یا چرخش سیال قرار دهیم، شست دست راست، جهت کرلِ بردار را نشان می‌دهد.

برای مثالی که بیان شد، جهت این بردار با رنگ سبز نشان داده شده است. بردار سبز رنگ روی محور چرخش کره، کرل میدان برداری را نشان می‌دهد. اندازه این بردار، سرعت چرخش کره است. جهت این بردار نیز طبق قانون دست راست به دست می‌آید.

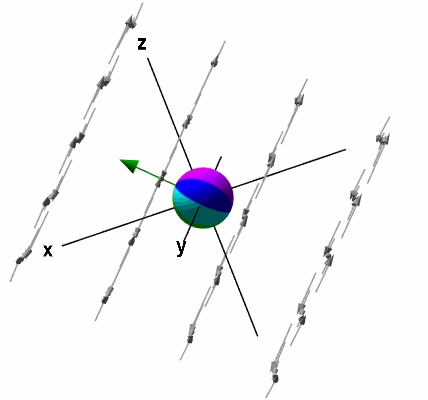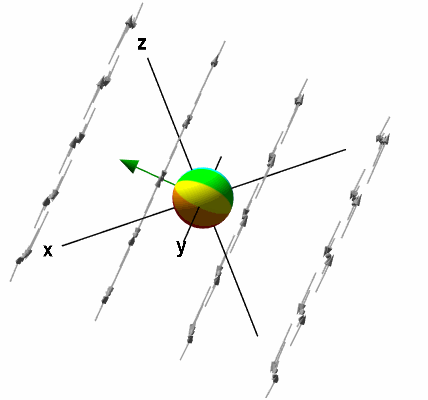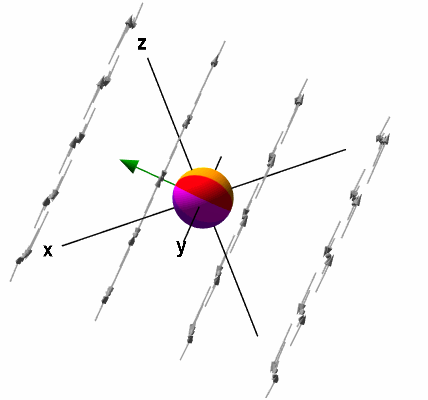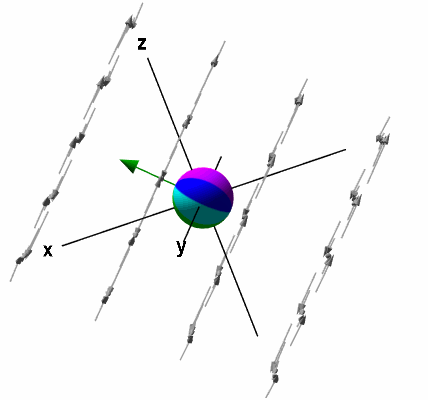
در این مثال، کرل این میدان برداری تابع مکان نیست. البته در حالت کلی ممکن است کرل، تابع مکان باشد.

میدان برداری $$F$$ را به شکل زیر می‌نویسیم:

$$\hat F= F_1 \hat i + F_2 \hat j + F_3 \hat k$$

کرل میدان برداری $$F$$، سه بعدی است. همانطور که گفتیم، کرل در جهات $$x$$ و $$y$$ و $$z$$ مولفه دارد. اگر بردار $$v$$ را کرل $$F$$ بنامیم، داریم:

$$\hat v =curl \, F= v_1 \hat i + v_2 \hat j + v_3 \hat k$$

مولفه $$\LARGE z$$ کرل

برای نمایش $$v_3$$، می‌توان مانند قبل کره را داخل سیال قرار داد. اما یک تفاوت مهم وجود دارد. به جای آنکه اجازه دهیم کره در هر جهتی چرخش کند،‌ آن را روی یک میله به موازات محور $$z$$ قرار می‌دهیم که تنها روی محور آن اجازه چرخش دارد.

با استفاده از قانون دست راست، می‌توان مشاهده کرد که جهت این بردار به موازات محور $$z$$ است.

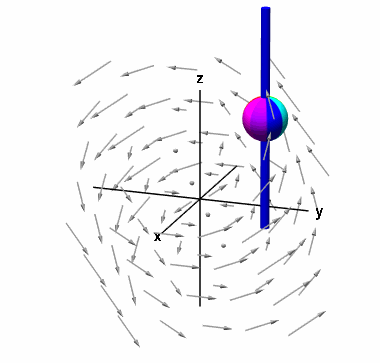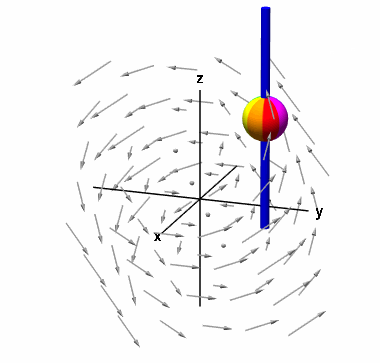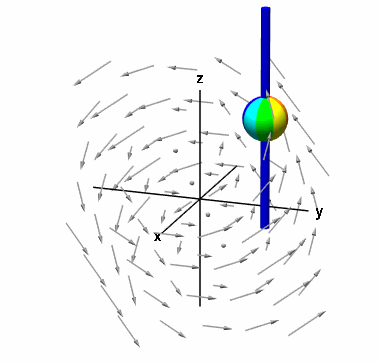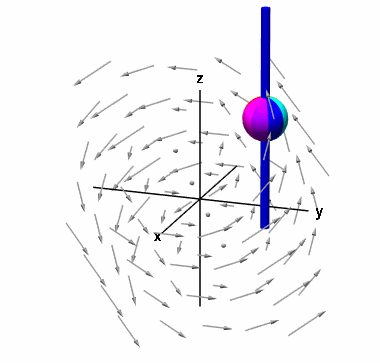
در واقع، این چرخش مربوط به مولفه $$v_3 \hat k$$ است. سرعت چرخش، به مقدار $$|v_3|$$ وابسته است. جهت چرخش کره روی محور نیز به علامت $$v_3$$ بستگی دارد. از شکل بالا، می‌توان مشاهده کرد که اگر از جهت مثبت محور $$z$$ به کره نگاه کنیم، کره در جهت خلاف عقربه‌های ساعت می‌چرخد. این یعنی مولفه $$z$$ کرل، مثبت است. اگر با نگاه از جهت مثبت $$z$$، کره در جهت عقربه‌های ساعت در حال چرخش باشد، مولفه $$z$$ کرل، منفی است.

از آنجایی که $$curl \, \hat F$$ با محور $$z$$ موازی نیست، مقدار مولفه در جهت $$z$$، یعنی $$v_3$$ کوچکتر از مقدار $$curl \, \hat F$$ است. به همین دلیل، کره نسبت به حالت قبل، سرعت چرخش کمتری دارد.

توجه به این نکته ضروری است که در این حالت، اگر سیال را به سمت بالا یا پایین جابجا کنیم، تغییری در حرکت کره ایجاد نمی‌شود. بنابراین می‌توان گفت مولفه $$z$$ کرل، به مولفه $$z$$ تابع برداری $$F$$ وابسته نیست. می‌توانیم از $$F_3$$ صرفنظر کنیم. پس چرخش کره تنها به مولفه $$x$$ تابع ($$F_1$$) و مولفه $$y$$ آن ($$F_2$$) وابسته است.

شکل زیر، یک قطاع از کره را نشان می‌دهد که در صفحه $$xy$$ قرار گرفته است. برای آنکه مفهوم بهتر منتقل شود، قطاع کره (دایره داخل شکل) را در جهت مثبت محورهای $$x$$ و $$y$$ جابجا کرده‌ایم. طبق این نمایش، محور $$z$$ به سمت بیرون صفحه ($$\bigodot$$) است.

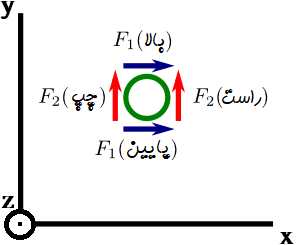
همانطور که بیان شد، اگر بخواهیم مولفه در جهت $$z$$ کرل، مثبت باشد، کره باید خلاف جهت عقربه‌های ساعت بچرخد.

اکنون مولفه $$y$$ کرل را در نظر می‌گیریم. برای آنکه کره یا قطاع آن خلاف جهت عقربه‌های ساعت بچرخد، مولفه $$F_2$$ در سمت راست باید بزرگتر از مولفه $$F_2$$ سمت چپ باشد. پس همچنان که در جهت مثبت محور $$x$$ جلو می‌رویم، $$F_2$$ باید بزرگتر شود. پس می‌توان گفت مشتق جزئی $$F_2$$ نسبت به $$x$$ ($$\frac{\partial F_2}{\partial x}$$) باید مثبت باشد.

حال مولفه $$x$$ کرل برداری را در نظر بگیرید. برای آنکه قطاع دایره‌ای در خلاف جهت عقربه‌های ساعت گردش کند، مولفه $$F_1$$ بالایی باید کوچکتر از مولفه $$F_1$$ پایینی باشد. پس می‌توان گفت مشتق جزئی $$F_1$$ نسبت به $$y$$ ($$\frac{\partial F_1}{\partial y}$$) باید علامت منفی داشته باشد. زیرا هرچه در جهت محور $$y$$ بالاتر می‌رویم، نیروی افقی در جهت محور $$x$$ کمتر می‌شود.

برای درک این مفهوم فرض کنید توپی داریم که می‌خواهیم آن را بچرخانیم. به این توپ از چهار طرف نیرو وارد می‌شود. اما فقط دو نیروی عمودی و افقی داریم و شدت این دو نیرو در جهات عمودی و افقی متفاوت است. مشخص است که برای چرخیدن توپ در جهت خلاف عقربه‌های ساعت، نیروی عمودی وارد به سمت راست آن باید قوی‌تر از نیروی وارد به سمت چپ توپ باشد.به همین ترتیب، نیروی افقی وارد شده به پایین توپ باید بزرگتر از نیروی افقی وارد شده به بالای توپ است. زیرا ما جهت‌های قراردادی برای نیروهای افقی و عمودی وارد شده در نظر گرفته‌ایم.

بنابراین می‌توان نتیجه گرفت مشتقات جزئی $$F_1$$ و $$F_2$$ باعث چرخش کره روی محور $$z$$ می‌شوند. اثرات این مشتقات جزئی در مولفه $$v_3$$ را با هم جمع می‌کنیم. پس می‌توان نوشت:

$$v_3=curl \hat F . \hat k = \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}$$

همانطور که گفتیم این مولفه از کرل، به مولفه $$z$$ تابع برداری وابسته نیست. اگر تابع برداری، تنها مولفه‌های $$x$$ و $$y$$ داشته باشد، $$v_3$$ تغییر نمی‌کند. بنابراین، رابطه بالا، به چرخش میکروسکوپی روی صفحه $$xy$$ اشاره دارد.

مولفه $$\LARGE y$$ کرل

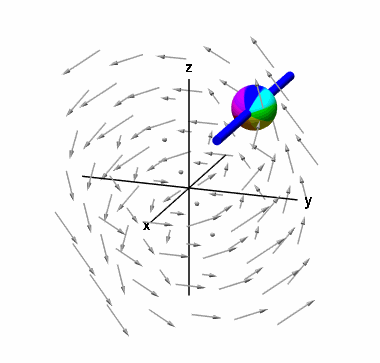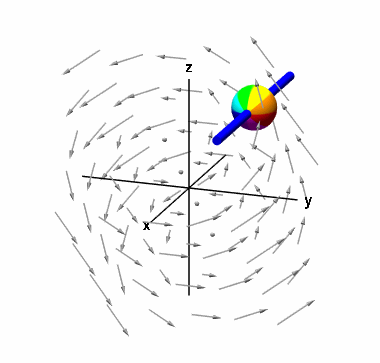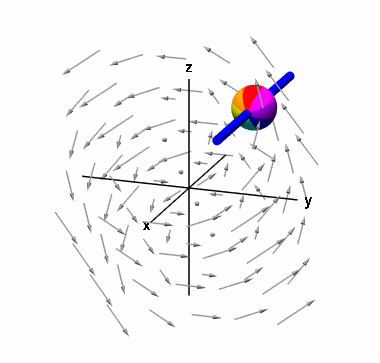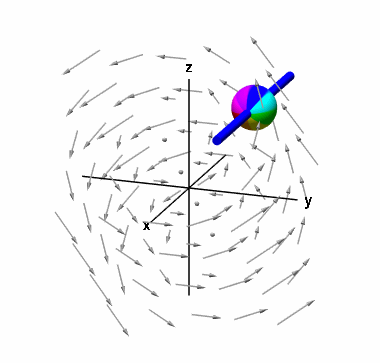
یک بار دیگر حالتی را در نظر می‌گیریم که کره در هر جهتی در حال حرکت است. می‌توان مشاهده کرد که جهت پیکان سبز رنگ بر محور $$y$$ عمود است. بنابراین در این مثال، کرل تابع برداری $$F$$ در جهت $$y$$، صفر خواهد بود. اگر کره را روی یک میله در جهت $$y$$ قرار دهیم، چرخش سیال باعث حرکت کره نمی‌شود. البته این موضوع، آزمایش دقیقی از کرل نیست. چون باید چرخش‌های میکروسکوپی را در نظر بگیریم.

مانند حالت قبل‌، برای مولفه $$y$$ کرل داریم:

$$v_2=curl \, \hat F . \hat j = \frac{\partial F_1}{\partial z} - \frac{\partial F_3}{\partial x}$$

در این مثال، $$v_2$$ برابر صفر است.

مولفه $$\LARGE x$$ کرل

در انتها، به محاسبه مولفه $$x$$ کرل می‌پردازیم. در این حالت، کره را روی یک میله در جهت $$x$$ قرار می‌دهیم.

مانند حالت اول، می‌توان این مولفه را محاسبه کرد:

$$v_1=curl \, \hat F . \hat i = \frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}$$

بنابراین، بردار کرل تابع $$F$$ که چرخش میکروسکوپی را در جهت های $$x$$ و $$y$$ و $$z$$ نشان می‌دهد، به صورت زیر است:

$$curl \hat F = \Bigg ( \frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z},\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x},\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y} \Bigg )$$

پس کرل یک تابع برداری، ترکیبی از مشتقات جزئی در جهت‌های مختلف است.

مثال ۱

کرل بردار زیر را محاسبه کنید.

$$\hat F =\large {x^2}y \hat i + xyz\,\hat j - {x^2}{y^2}\,\hat k$$

حل:

$$\begin{align*}{\mathop{\rm curl \,}\nolimits} \hat F & =\Large \left| {\begin{array}{*{20}{c}}{\hat i}&{\hat j}&{\hat k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\{{x^2}y}&{xyz}&{ - {x^2}{y^2}}\end{array}} \right|\\ & = \large \, - 2{x^2}y\,\hat i + yz\,\hat k - \left( { - 2x{y^2}\,\hat j} \right) - xy\,\hat i - {x^2}\hat k\\ & =\large \, - \left( {2{x^2}y + xy} \right)\hat i + 2x{y^2}\,\hat j + \left( {yz - {x^2}} \right)\hat k\\ \end{align*}<br /> $$

مثال ۲

کرل را برای تابع برداری زیر محاسبه کنید.

$$\large \hat F = \large y{z^2}\,\hat i + xy\,\hat j + yz\,\hat k$$

حل:

$$\begin{align*}{\mathop{\rm curl \,}\nolimits} \hat F & = \Large \left| {\begin{array}{*{20}{c}}{\hat i}&{\hat j}&{\hat k}\\{\displaystyle \frac{\partial }{{\partial x}}}&{\displaystyle \frac{\partial }{{\partial y}}}&{\displaystyle \frac{\partial }{{\partial z}}}\\{y{z^2}}&{xy}&{yz}\end{array}} \right|\\ & = \large z\,\hat i + 2yz\,\hat j + y\,\hat k - {z^2}\hat k\\ & = \large z\hat i + 2yz\,\hat j + \left( {y - {z^2}} \right)\hat k\end{align*}$$

در آموزش‌های بعدی به بررسی کرل و دیورژانس در دیگر دستگاه‌های مختصاتی می‌پردازیم.

در صورتی که این مطلب برای شما مفید بوده، آموزش‌های زیر را به شما پیشنهاد می‌شود:

• مفاهیم مشتق — به زبان ساده
• توابع چند متغیره — به زبان ساده
• گرادیان (Gradient) در ریاضیات — به زبان ساده

^^