رسم نمودار سینوس و کسینوس – به زبان ساده با مثال و تمرین

توابع سینوس و کسینوس در حل مسائل مثلثات، حسابان و حساب دیفرانسیل و انتگرال کاربرد دارند. بنابراین درک اینکه این توابع چگونه ایجاد می‌شوند و چطور می‌توان آن‌ها را رسم کرد، از اهمیت بالایی برخوردار است. در این مطلب از مجله فرادرس توضیح می‌دهیم چگونه می‌توان انواع نمودار سینوس و کسینوس را رسم کرد و چطور هر متغیر در معادله استاندارد این توابع، می‌تواند شکل و اندازه این نمودارها را تغییر دهد یا باعث شود روی محور افقی یا قائم جابجا شوند.

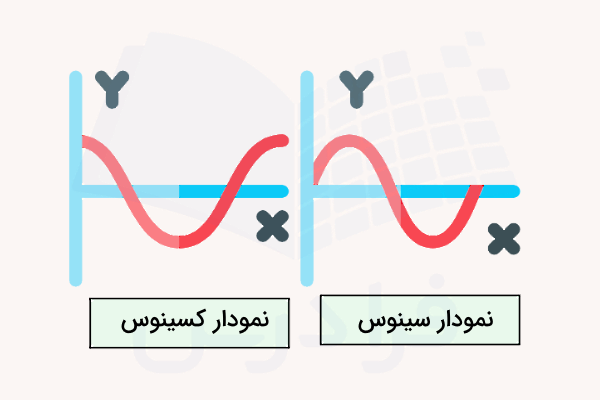
نمودار سینوس و کسینوس

اولین قدم برای رسم هر نموداری این است که ببینم تابع موردنظر ما چه معادله‌ای دارد و بر حسب چه متغیرهایی است. $$y=\sin(x)$$ و $$y=\cos(x)$$ از جمله توابع مثلثاتی هستند که می‌خواهیم در این نوشته به چگونگی رسم نمودار آن‌ها بپردازیم. همان‌طور که مشاهده می‌کنید، هر دوی این توابع برحسب متغیر x نوشته شده‌اند که البته ممکن است به‌صورت $$y=\sin\theta$$ یا $$y=\cos\theta$$ نیز نوشته شوند. در هر دو حالت، برای رسم نمودار سینوس و کسینوس، کافی است $$y$$ را بر حسب $$x$$ یا $$\theta$$ و طبق مراحل زیر رسم کنیم:

1. مرتب کردن معادله داده شده
2. تشخیص مقادیر دامنه، دوره تناوب و تغییر فاز
3. تعیین جابجایی نمودار روی محور عمودی
4. تعیین نقاط بحرانی و رسم نمودار

در بخش‌های بعد تمام این مراحل را توضیح خواهیم داد. نکته مهم در رسم نمودار سینوس و کسینوس این است که $$x$$ برای رسم چنین تابعی چه مقادیری می‌پذیرد. در حقیقت $$x$$ همان زاویه یا $$\theta$$ است. این زاویه ممکن است در متون مختلف با $$\phi$$ هم نشان داده شود. نمودار سینوس و کسینوس با در نظر گرفتن مقادیر مختلفی از زاویه بر حسب درجه یا رادیان و در قالب تابعی به نام $$y$$ رسم می‌شود.

معرفی توابع مثلثاتی سینوس و کسینوس

برای اینکه بتوانیم نمودار سینوس و کسینوس را به‌درستی رسم کنیم، نیاز است ابتدا این دو نسبت‌ مثلثاتی را بشناسیم و ببینیم چگونه تعریف می‌شوند، چه فرمولی دارند و در زاویه‌های مختلف چه مقداری می‌پذیرند. شناخت برخی از خصوصیات این دو تابع مانند دامنه و برد نیز مهم است.

تابع سینوس که با $$\sin(\theta)$$ نشان داده می‌شود، یکی از اصلی‌ترین نسبت‌های مثلثاتی است که زاویه $$\theta$$ در یک مثلث قائم‌الزاویه را به اندازه اضلاع آن مربوط می‌کند. برای درک این ارتباط بهتر است یک مثلث قائم‌الزاویه با زاویه $$\theta$$ را به شکل زیر در نظر بگیرید:

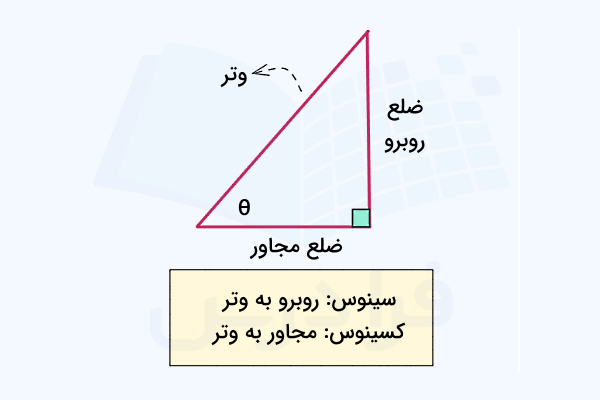
در این صورت سینوس زاویه $$\theta$$ یا $$\sin(\theta)$$ برابر است با نسبت اندازه ضلع مقابل به این زاویه به وتر مثلث قائم‌الزاویه. از طرفی تابع کسینوس یا $$\cos(\theta)$$ طبق مثلث بالا، برابر می‌شود با نسبت اندازه ضلع مجاور به زاویه $$\theta$$ به وتر مثلث قائم‌الزاویه. پس این دو تابع عموما برای یک زاویه تعریف می‌شوند که می‌تواند با واحدی مانند رادیان یا درجه اندازه‌گیری شود.

یادگیری مثلثات در مقطع متوسطه با فرادرس

اگر مشغول به تحصیل در مقطع متوسطه هستید، در این بخش می‌خواهیم چند دوره آموزشی فرادرس را به شما معرفی کنیم که در هر کدام بخشی از مبحث مثلثات بیان شده است. مشاهده این فیلم‌ها که بر اساس سرفصل‌های کتاب‌های درسی تهیه شده‌اند، به شما کمک می‌کند تا به این موضوع کاملا مسلط شوید:

1. فیلم آموزش رایگان سینوس، کسینوس و تانژانت + محاسبه نسبت‌ های مثلثاتی فرادرس
2. فیلم آموزش ریاضی دهم فرادرس
3. فیلم آموزش ریاضی یازدهم علوم تجربی فرادرس
4. فیلم آموزش ریاضی دوازدهم علوم تجربی فرادرس
5. فیلم آموزش حسابان یازدهم فرادرس
6. فیلم آموزش حسابان یازدهم – حل تمرین فرادرس
7. فیلم آموزش رایگان مثلثات– تناوب و تانژانت در حسابان دوازدهم فرادرس
8. فیلم آموزش حسابان دوازدهم فرادرس

رسم نمودار Y= Sin(x)

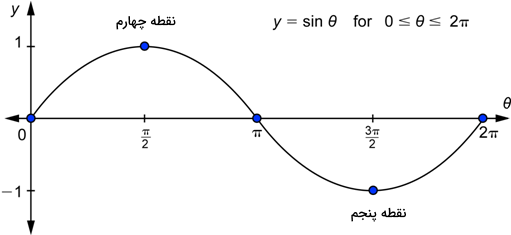
به‌ عنوان اولین مثال، می‌خواهیم ساده‌ترین نمودار سینوسی یعنی $$y=\sin(x)$$ را رسم کنیم. با در نظر گرفتن جدول زیر، مشاهده می‌کنید که به ازای هر $$x$$ یک $$\sin(x)$$ خواهیم داشت. مقادیر $$x$$ همان زاویه‌های موردنظر ما برای رسم نمودار سینوسی بر حسب درجه هستند و $$\sin(x)$$ اثر تابع سینوس روی هر زاویه است:

پیشنهاد می‌کنیم جدول بالا را در مورد تابع سینوس به همراه جدول دیگری که برای تابع کسینوس نشان خواهیم داد، به خاطر بسپارید. همچنین اگر علاقه‌مند هستند بدانید نحوه محاسبه $$\sin(x)$$ یا $$\cos(x)$$ بر اساس مقادیر مختلف $$x$$ به چه صورت است، می‌توانید مطلب «دایره مثلثاتی — به زبان ساده» از مجله فرادرس را مطالعه کنید. البته در این جدول فقط بازه $$0$$ تا $$\pi$$ برای مقادیر $$x$$ در نظر گرفته شده است. در ادامه می‌توانید جدول مربوط به بازه $$\pi$$ تا $$2\pi$$ را نیز به همین ترتیب رسم کنید.

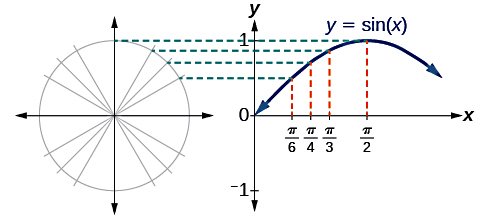
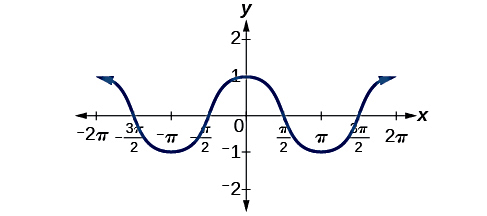
حالا برای رسم نمودار $$y=\sin(x)$$، کافی است در صفحه مختصات موردنظر خود مقادیر $$y$$ را روی محور عمودی یا قائم و مقادیر $$x$$ را که معادل با زاویه‌های بالا هستند، روی محور افقی در نظر بگیریم. سپس طبق شکل زیر، مکان هر کدام از نقاط بالا را با یک نقطه مشخص می‌کنیم. با اتصال این نقاط در قالب خطوط منحنی شکل، نمودار موردنظر ما رسم شده است:

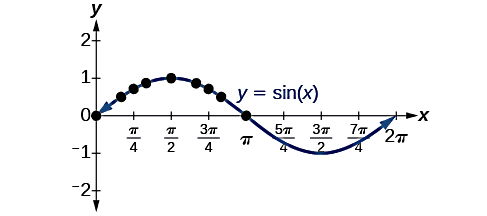
نکته مهم در مورد نمودار سینوس و کسینوس این است که متوجه تفاوت‌‌های این دو نمودار از نظر شکل باشید. برای مثال، در مورد نمودار سینوسی بالا مقدار تابع سینوسی در بازه $$0$$ تا $$\pi$$ مثبت است. این بازه با مقادیر تابع سینوس در ربع اول و دوم دایره مثلثاتی متناظر است. طبق شکل زیر، در ربع سوم و چهارم دایره مثلثاتی مقادیر تابع سینوسی منفی هستند که متناظر است با بازه $$\pi$$ تا $$2\pi$$ برای $$x$$:

رسم نمودار Y= Cos(x)

در ادامه قصد داریم روند بالا را برای رسم نمودار $$y=\cos(x)$$ طی کنیم ولی پیش از آن، مشاهده فیلم آموزشی حسابان پایه یازدهم همراه با حل تمرین فرادرس را به شما پیشنهاد می‌کنیم تا با حل تمرین‌های متنوع مربوط به بخش مثلثات آن، یادگیری عمیق‌تری داشته باشید. در ادامه لینک این آموزش را برای شما قرار داده‌ایم:

مجددا زاویه‌هایی به شکل زیر و مشابه با نمودار سینوس در نظر می‌گیریم. جدولی رسم می‌کنیم و مقدار تابع کسینوس را به ازای هر مقدار $$x$$ تعیین می‌کنیم:

با توجه به یکسان بودن مقادیر $$x$$ برای هر دو نمودار سینوس و کسینوس، تقاوت اثر این دو تابع مثلثاتی روی مقادیر $$x$$ کاملا مشخص است. برای مثال در اولین نقطه یعنی $$x=0$$، تابع سینوس برابر با $$0$$ است، در حالی که کسینوس این مقدار $$1$$ می‌شود. همچنین دیدیم که در بازه $$0$$ تا $$\pi$$، تمام مقادیر ستون دوم جدول سینوس مثبت شدند، اما برای کسینوس در بازه $$\frac{\pi}{2}$$ تا $$\pi$$ مقادیر منفی هستند.

مشابه نمودار سینوس، می‌توانید برای بازه $$\pi$$ تا $$2\pi$$ نیز جدول بالا را ادامه دهید. در نهایت با اتصال نقاط به‌دست آمده نموداری به شکل زیر خواهیم داشت:

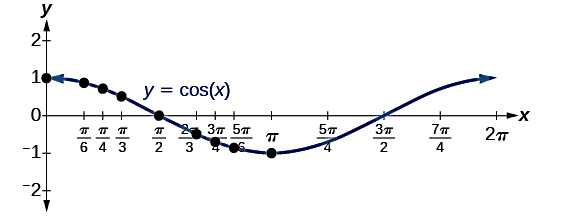
از آنجا که با کمک گرفتن از دایره مثلثاتی می‌توانیم مقادیر سینوس و کسینوس را به ازای هر عدد حقیقی محاسبه کنیم، پس هر دوی این توابع برای تمام اعداد حقیقی تعریف می‌شوند، یعنی دامنه توابع سینوس و کسینوس برابر است با تمام اعداد حقیقی یا $$R$$.

از طرفی مقادیر سینوس و کسینوس به عنوان مختصات تمام نقاط قرار گرفته روی محیط دایره‌ای با شعاع واحد، به نام دایره مثلثاتی در نظر گرفته می‌شوند. بنابراین انتظار داریم برد هر دو تابع در محدوده $$[-1, +1]$$ قرار داشته باشد، یعنی بیشترین و کمترین مقادیر ممکن برای $$y$$ همواره برابر با $$+1$$ و $$-1$$ است. با توجه به چنین بردی، انتظار داریم نمودار تابع سینوس  یا کسینوس شبیه موجی شوند که در حال نوسان بین دو مقدار $$+1$$ و $$-1$$ است.

مراحل رسم نمودار سینوس و کسینوس

در این بخش قصد داریم مراحل رسم نمودار سینوس و کسینوس را قدم به قدم توضیح دهیم. با رعایت دقیق این مراحل، قادر خواهید بود نمودار انواع معادلات سینوسی یا کسینوسی را رسم کنید. معادله سینوسی یا کسینوسی به‌صورت عبارت یا تابعی برابر با مقدار $$y$$ به شما داده می‌شود که معمولا این عبارت بر حسب $$\theta$$ و چند مقدار ثابت عددی نوشته شده است.

بنابراین هدف رسم نمودار $$y$$ برحسب $$\theta$$ است که در آن مقادیر $$y$$ روی محور عمودی یا قائم و مقادیر $$\theta$$ روی محور افقی در صفحه مختصات رسم شده قرار می‌گیرند. با این پیش‌فرض‌ها، مراحل رسم نمودار سینوس و کسینوس عبارت‌اند از:

1. مرتب کردن معادله داده شده
2. تشخیص مقادیر دامنه، دوره تناوب و تغییر فاز
3. تعیین جابجایی نمودار روی محور عمودی
4. تعیین نقاط بحرانی و رسم نمودار

در ادامه هر کدام از این مراحل را با جزئيات توضیح خواهیم داد. به خاطر داشته باشید اگر چه مراحل تعیین مولفه افقی نقاط بحرانی برای نمودار سینوس و کسینوس تقریبا یکسان است، اما تعیین مولفه عمودی برای این دو نمودار متفاوت است که در بخش‌‌های مربوط به آن توضیح لازم داده خواهد شد.

دوره تناوب تابع سینوس و کسینوس

یکی از مهم‌ترین خصوصیات توابع مثلثاتی مانند تابع سینوسی و کسینوسی داشتن دوره تناوب است، به این معنا که در رسم نموار سینوس و کسینوس، شکل تابع پس از $$2\pi$$ مجددا تکرار می‌شود. به همین علت به این توابع، توابع دوره‌ای هم گفته می‌شود. بنابراین دوره تناوب تابع سینوسی ساده به شکل $$\sin(x)$$ یا تابع کسینوسی ساده به فرم $$\cos(x)$$ برابر است با $$2\pi$$.

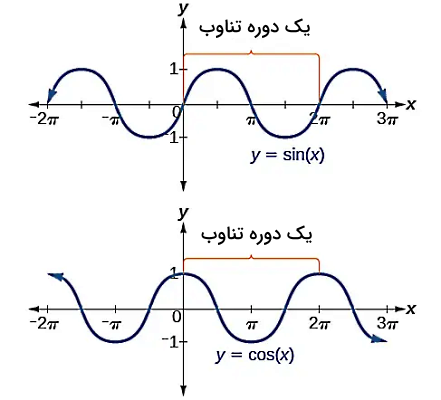
تابع دوره‌ای یا تابع تناوبی، تابعی است که به ازای یک جابجایی افقی و مشخصی معادل با $$P$$، مقدار آن تغییری نکند و برای آن رابطه $$f(x+P)=f(x)$$ به ازای تمام مقادیر $$x$$ تعریف شده برای $$f$$، همواره برقرار باشد. در این صورت هر مقدار حتی کوچک اما مخالف صفر $$P$$ را دوره تناوب تابع $$f$$ می‌نامیم. به تفاوت شکل دو نمودار سینوس و کسینوس در یک دوره تناوب دقت کنید. در ادامه این مطلب، پس از حل مثال‌های مختلف متوجه خواهید شد که اگر برای توابع سینوسی یا کسینوسی پیچیده‌تر، ممکن است دوره تناوب برابر با $$2\pi$$ نشود.

فرد یا زوج بودن توابع سینوس و کسینوس

یکی دیگر از خواص جالب توجه تابع سینوس و کسینوس، فرد یا زوج بودن این دو تابع است. تابع فرد به تابعی گفته می‌شود که با تغییر $$x$$ به $$-x$$ مقدار آن نیز منفی شود، یعنی برای یک تابع فرد رابطه زیر همیشه برقرار است:

$$f(-x)=-f(x)$$

در مورد تابع سینوس خواهیم داشت:

$$\sin(-x)=-\sin(x)$$

بنابراین می‌توانیم تابع سینوس را یک تابع فرد در نظر بگیریم. همچنین اگر به نمودار تابع سینوس توجه کنید، این نمودار نسبت به مبدا یا مرکز صفحه مختصات دارای تقارن است.

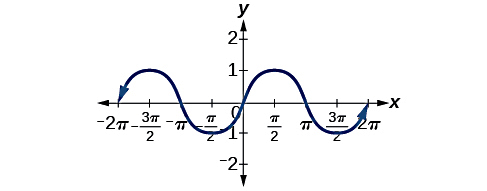
ولی در مورد نمودار کسینوس، با دقت به شکل زیر متوجه خواهید شد که این نمودار نسبت به محور قائم دارای تقارن است نه مبدا. در واقع این مشخصه بیانگر این است که تابع کسینوس یک تابع زوج محسوب می‌شود. طبق تعریف، تابع زوج با تغییر علامت $$x$$ تغییری نمی‌کند، یعنی داریم:

$$f(-x)=f(x)$$

بنابراین برای تابع زوج کسینوس رابطه بالا به شکل زیر درست است:

$$\cos(-x)=\cos(x)$$

مرحله اول مرتب کردن معادله داده شده

اولین مرحله برای رسم نمودار سینوس و کسینوس این است که معادله داده شده در صورت سوال را به یکی از دو شکل کلی زیر مرتب کنیم:

$$y=a\sin(b\theta-c)+d$$

یا

$$y=a\sin b(\theta-\frac{c}{b})+d$$

یا

$$y=a\cos(b\theta-c)+d$$

یا

$$y=a\cos b(\theta-\frac{c}{b})+d$$

هدف از انجام این کار این است که بتوانیم با مقایسه معادله خود و یکی از دو رابطه بالا، مقادیر عددی $$a, b, c, d$$ را تشخیص دهیم تا در قدم بعدی با استفاده از این مقادیر بتوانیم دامنه، دوره تناوب و شیفت فاز نمودار خود را به‌دست آوریم. به رعایت علامت منفی برای $$c$$ در معادله دقت کنید. اگر ضریب $$c$$ در معادله داده شده مثبت بود، حتما آن را به شکل $$-(-c)$$ بازنویسی کنید تا محاسبات شما درست انجام شود. همچنین ممکن است به‌جای $$\theta$$، تابع سینوس یا کسینوس ما بر حسب $$x$$ داده شود که در مراحل ما تفاوتی ایجاد نمی‌کند.

مرحله دوم تشخیص مقادیر دامنه، دوره تناوب و تغییر فاز

در مرحله بعدی، لازم است چند مشخصه مهم رسم نمودار سینوس و کسینوس مانند دامنه، دوره تناوب و تغییر فاز را محاسبه کنیم. در ادامه روش محاسبه هر کدام از این مقادیر را توضیح داده‌ایم:

تعیین دامنه

تعیین قدر مطلق مقدار $$a$$ در معادله‌ای که به فرم کلی $$y=a\sin(b\theta-c)+d$$ یا $$y=a\sin b(\theta-\frac{c}{b})+d$$ نوشته شده است، به ما دامنه را می‌دهد:

دامنه = $$|a|$$

دامنه در نمودار سینوس و کسینوس به معنای بیشترین فاصله نمودار از محور افقی یا معادل با میزان کشیدگی نمودار در راستای عمودی است. البته در صورتی که در معادله اصلی $$d$$ مخالف صفر باشد، دامنه نسبت به این خط افقی سنجیده خواهد شد. با توجه به مقدار $$a$$، می‌توانیم دو نتیجه‌گیری زیر را ارائه دهیم:

• اگر $$|a|$$ در معادله اصلی ما بزرگتر از یک باشد، در این حالت نمودار ما در راستای عمودی کشیده می‌شود.
• اگر $$|a|$$ در معادله اصلی ما کوچکتر از یک باشد، در این حالت نمودار ما در راستای عمودی فشرده می‌شود.

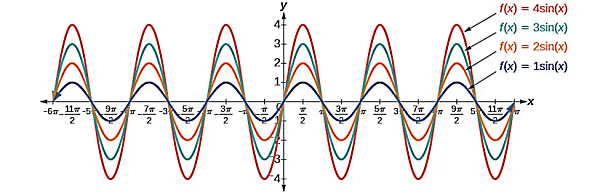
برای مثال طبق شکل بالا ابتدا تابع $$\sin(x)$$ را با رنگ آبی در نظر بگیرید که در آن $$|a|=1$$ است. مشاهده می‌کنید که همزمان با افزایش دامنه، نمودارهای سینوس در راستای محور قائم بیشتر کشیده می‌شوند.

تعیین دوره تناوب

یکی دیگر از مهم‌ترین پارامترهای رسم نمودار سینوس و کسینوس، دوره تناوب است. دوره تناوب با فرمول زیر تعیین می‌شود:

دوره تناوب = $$\frac{2\pi}{b}$$

با توجه به مقدار $$b$$، ممکن است یکی از دو حالت زیر را داشته باشیم:

• اگر $$|b|$$ در معادله اصلی ما بزرگتر از یک باشد، دوره تناوبی کوچکتر از $$2\pi$$ داریم. در این حالت نمودار ما در راستای افق فشرده می‌شود.
• اگر $$|b|$$ در معادله اصلی ما کوچکتر از یک باشد، دوره تناوبی بزرگتر از $$2\pi$$ داریم. در این حالت نمودار ما در راستای افق کشیده می‌شود.

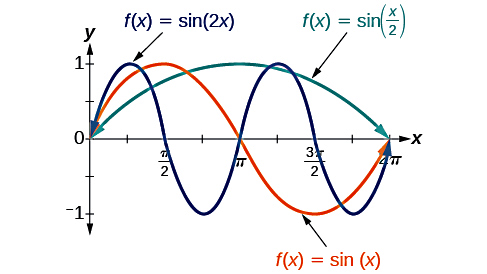
برای مثال وقتی که تابع سینوسی به شکل $$\sin(x)$$ داریم، $$|b|=1$$ است. در نتیجه دوره تناوب برابر است با:

$$\frac{2\pi}{1}=2\pi$$

این نمودار را در تصویر بالا با رنگ قرمز مشاهده می‌کنید. حالا اگر تابعی به فرم $$\sin(2x)$$ داشته باشیم، پس $$|b|=2$$ است و دوره تناوب می‌شود:

$$\frac{2\pi}{2}=\pi$$

که به معنای فشرده شدن این نمودار نسبت به حالت اول است (نمودار آبی). همچنین با داشتن تابعی به فرم $$\sin(\frac{x}{2})$$، مشخص است که $$|b|=\frac{1}{2}$$. پس دوره تناوب به‌صورت زیر بیشتر می‌شود که به معنای کشیدگی نمودار نسبت به حالت اول است (نمودار سبز):

$$\frac{2\pi}{\frac{1}{2}}=4\pi$$

دقت کنید در رسم نمودار سینوس و کسینوس معمولا رسم یک دوره تناوب کافی است. اما می‌توان با تکرار این دوره و رعایت مکان نقاط بحرانی با توجه به اینکه در حال رسم دومین، سومین یا ... دوره تناوب هستید، نمودار خود را کامل‌تر کنید.

تعیین تغییر فاز

آخرین بخش از این مرحله از رسم نمودار سینوس و کسینوس مشخص کردن مقدار جابجایی یا شیفت فاز در نمودار داده شده است. منظور از این بخش، جابجایی نمودار سینوس و کسینوس روی محور افقی است که با رابطه زیر می‌توانیم آن را مشخص کنیم:

تغییر فاز = $$\frac{c}{b}$$

در مورد شیفت فاز و بسته به علامت $$c$$، می‌توانیم دو حالت ممکن را داشته باشیم:

• اگر $$c$$ در معادله اصلی ما بزرگتر از صفر باشد، در این حالت نمودار ما در راستای افق به سمت راست جابجا می‌شود.
• اگر $$c$$ در معادله اصلی ما کوچکتر از صفر باشد، در این حالت نمودار ما در راستای افق به سمت چپ جابجا می‌شود.

واضح است که هر چه مقدار $$c$$ بیشتر باشد، میزان جابجایی نمودار هم بیشتر است. برای نمونه، شکل زیر را در نظر بگیرید که در آن نمودارهای سینوسی با رنگ سبز و قرمز نسبت به نمودار سینوسی ساده با رنگ آبی جابجایی داشته‌اند. دقت کنید با توجه به علامت منفی $$c$$ در معادله کلی طبق قراردادی که داشتیم، برای نمودار سینوسی قرمز رنگ $$c=+\frac{1}{4}$$. پس انتظار داریم این نمودار به سمت راست جابجا شود که در تصویر نیز به همین شکل است. نمودار سبز رنگ نیز دارای $$c=+1$$ است و شیفت به راست خیلی بیشتری نسبت به نمودار قرمز خواهد داشت.

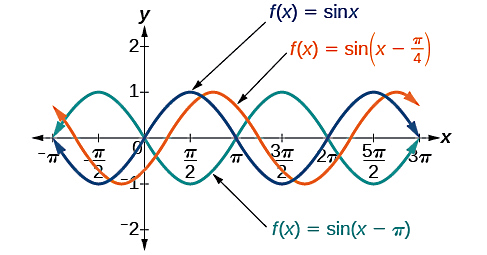
مرحله سوم تعیین جابجایی نمودار روی محور عمودی

پس از محاسبه مقادیر بالا، حالا باید ببینیم آیا نمودار داده شده روی محور قائم جابجا شده است یا خیر. مقدار جابجایی نمودار روی محور عمودی، همان شیفت یا تغییرات نمودار روی محور قائم است. این شیفت در صورتی رخ می‌دهد که در معادله داده شده با فرم کلی ابتدای این بخش، $$d$$ مخالف صفر داشته باشیم:

جابجایی عمودی = $$d$$

برای تعیین جابجایی عمودی، کافی است خطی با معادله $$y=d$$ را رسم کنیم. با توجه به این خط و مقدار دامنه، می‌توانیم مولفه عمودی یا مقادیر $$y$$ را برای نقاط بحرانی در مراحل بعد تعیین کنیم. برای مثال، در شکل زیر تفاوت دو نمودار سینوسی را مشاهده می‌کنید که در یکی جابجایی به اندازه دو واحد روی محور قائم داشته‌ایم:

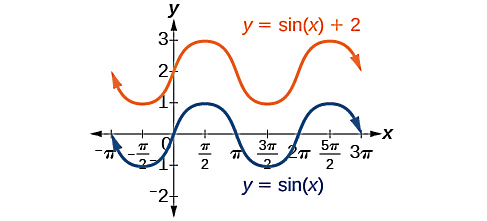
مرحله چهارم تعیین نقاط بحرانی و رسم نمودار

مهم‌ترین مرحله رسم نمودار سینوس و کسینوس، تعیین پنج نقطه بحرانی است که شامل نقاط ابتدا و انتهای دوره تناوب، نقطه میانی دوره و دو نقطه بین نقاط ابتدا/انتهای دوره و نقطه میانی هستند. هر کدام از نقاط دارای یک مقدار $$y$$ و یک مقدار $$\theta$$ است که در مجموع مختصات آن نقطه نامیده می‌شود:

1. اولین نقطه بحرانی یا $$(\theta _1, y_1)$$: نقطه شروع اولین دوره تناوب
2. دومین نقطه بحرانی یا $$(\theta _2, y_2)$$: نقطه پایانی اولین دوره تناوب
3. سومین نقطه بحرانی یا $$(\theta _3, y_3)$$: نقطه مرکزی اولین دوره تناوب
4. چهارمین نقطه بحرانی یا $$(\theta _4, y_4)$$: نقطه میانی بین اولین نقطه و نقطه مرکزی اولین دوره تناوب
5. پنجمین نقطه بحرانی یا $$(\theta _5, y_5)$$: نقطه میانی بین آخرین نقطه و نقطه مرکزی اولین دوره تناوب

در برخی از موارد، مقدار مولفه عمودی یا $$y$$ متناظر با این $$\theta$$ها برای نمودار سینوس و کسینوس متفاوت است. علت این تفاوت به شکل متفاوت این دو نمودار برمی‌گردد. در ادامه به این جزئیات بیشتر می‌پردازیم.

تعیین نقطه شروع دوره تناوب

برای اینکه بتوانیم این پنج نقطه را به‌راحتی مشخص کنیم، اولین مرحله تعیین اولین نقطه یا نقطه شروع دوره تناوب اول است که مکان آن روی محور افق یا $$\theta$$ آن برابر است با میزان شیفت فاز محاسبه شده در مرحله دوم:

$$\theta _1= \frac{c}{b}$$

همچنین لازم است به نکات زیر در مورد چگونگی تعیین مولفه قائم نقطه اول توجه کنید:

• در نمودار سینسوسی مثبت ($$0 < a$$)، پس از نقطه شروع بیشترین مقدار یا ماکزیمم $$y$$ را خواهیم داشت.
• در نمودار سینسوسی منفی ($$0 > a$$)، پس از نقطه شروع کمترین مقدار یا مینیمم $$y$$ را خواهیم داشت.
• نمودار کسینوسی مثبت ($$0 < a$$)، نقطه شروع بیشترین مقدار یا ماکزیمم $$y$$ را دارد.
• نمودار کسینوسی منفی ($$0 > a$$)، نقطه شروع کمترین مقدار یا مینیمم $$y$$ را دارد.

بنابراین در مورد نمودار کسینوس اولین نقطه دوره تناوب اول، دارای مولفه عمودی برابر با رابطه زیر است:

$$y_1=a+d$$

در حالی که برای نمودار سینوسی مکان این نقطه روی محور قائم می‌شود:

$$y_1=d$$

تعیین نقطه پایان دوره تناوب

برای یافتن نقطه انتهای دوره تناوب در رسم نمودار سینوس و کسینوس، کافی است $$\theta$$ به‌دست آمده از مرحله قبل را با دوره تناوب محاسبه شده در دومین مرحله جمع کنیم:

$$\theta _2= \frac{c}{b}+\frac{2\pi}{b}$$

مولفه قائم نقطه انتهایی دوره تناوب برای هر دو نمودار سینوس و کسینوس دقیقا با $$y$$ نقطه اول برابر است:

$$y_1=y_2$$

تعیین نقطه میانی دوره تناوب

سومین نقطه بحرانی باید دقیقا در مرکز دوره تناوب نمودار سینوس و کسینوس قرار بگیرد. بنابراین برای تعیین مکان آن روی محور افق، کافی است از نقطه اول به اندازه نصف دوره تناوب جلو برویم:

$$\theta _3= \theta _1+\frac{2\pi}{2b}= \theta _1+\frac{\pi}{b}$$

در مورد جایگاه مولفه قائم این نقطه و دو نقطه بعدی، باید به این نکته دقت کنید:

با توجه به شکل دو نمودار سینوس و کسینوس، موقعیت مولفه عمودی دو نقطه ابتدا و انتهای دوره برای هر دو نمودار یکسان است، اما تفاوت اساسی در نقاط بحرانی سه، چهار و پنج است. مقدار $$y$$ نقطه مرکزی دوره برای نمودار سینوسی همیشه مانند مقدار $$y$$ نقاط ابتدا و انتهای دوره است، در حالی که مقدار $$y$$ نقطه میانی دوره برای نمودار کسینوسی در بیشترین یا کمترین مقدار ممکن خود قرار می‌گیرد.

پس با توجه به این مسئله، مقدار $$y$$ نقطه سوم برای نمودار کسینوسی با رابطه زیر تعیین می‌شود:

$$y_3=y_1\pm |2a|$$

انتخاب علامت مثبت یا منفی برای $$a$$ کاملا بستگی به موقعیت نمودار دارد. این در حالی است که برای نمودار سینوسی مولفه قائم نقطه سوم مشابه با مولفه قائم دو نقطه ابتدا و انتهای دوره است.

تعیین نقاط چهارم و پنجم دوره تناوب

برای تعیین مکان چهارمین نقطه روی محور $$\theta$$، کافی است مکان متناظر با نقطه اول را با $$\frac{2\pi}{4b}$$ جمع کنیم، در حقیقت به اندازه یک چهارم دوره تناوب از اولین نقطه روی محور افقی جلو می‌رویم تا به نقطه چهارم برسیم:

$$\theta _4= \theta _1+\frac{2\pi}{4b}$$

همچنین مکان پنجمین نقطه بحرانی روی محور $$\theta$$ معادل است با اینکه به اندازه یک چهارم دوره تناوب از نقطه میانی در جهت مثبت محور افقی جلو برویم:

$$\theta _5= \theta _3+\frac{2\pi}{4b}$$

مکان چهارمین نقطه روی محور قائم برای نمودار سینوسی بسته به علامت $$a$$، معادل با بیشترین یا کمترین مقدار خواهد بود. اگر مولفه عمودی چهارمین نقطه بحرانی نمودار سینوسی دارای بیشترین مقدار باشد، مولفه متناظر پنجمین نقطه در کمترین ممکن برای $$y$$ قرار دارد و بالعکس. بنابراین به‌صورت کلی می‌توانیم برای مولفه عمودی این دو نقطه در نمودار سینوسی فرمول زیر را در نظر بگیریم:

$$y_{4,5}=y_1\pm |a|$$

در مورد نمودار کسینوسی هم، این دو نقطه دارای مولفه قائمی به شکل زیر خواهند بود:

$$y_{4,5}=y_1\pm |a|$$

دقت کنید در مورد نمودار کسینوس، اگر مولفه قائم نقطه چهارم مثبت باشد، همتای نقطه پنجم نیز حتما مثبت است و بالعکس. انتخاب علامت مثبت یا منفی در هر مسئله باید با توجه به نوع نمودار بررسی شود. آخرین مرحله اتصال پنج نقطه مرحله قبل به شکل یک منحنی است تا نمودار سینوس و کسینوس مورد نظر ما با یک دوره تناوب رسم شود. برای یادگیری و تسلط بیشتر حتما مثال‌‌های بخش بعد را بررسی کنید.

حل مثال و تمرین رسم نمودار سینوس و کسینوس

در بخش قبل آموختیم که مراحل رسم نمودار سینوس و کسینوس به چه صورت است. در این بخش با حل مثال‌‌های متنوع به شما کمک می‌کنیم تا مراحل گفته شده را قدم به قدم اجرا کنید و در نهایت بتوانید انواع نمودار‌های به‌ ظاهر پیچیده سینوس و کسینوس را به‌راحتی رسم کنید. در انتهای این بخش چند تمرین در قالب سوالات چهار گزینه‌ای برای شما در نظر گرفته‌ایم که می‌توانید میزان یادگیری خود را با حل آن‌ها بیازمایید.

مثال ۱

نمودار تابعی به شکل $$f(x)=-4\sin(x)$$ را رسم کنید:

پاسخ

طبق معادله کلی که برای توابع سینوس به شکل $$y=a\cos(b\theta-c)+d$$ در نظر گرفتیم، ثوابت مهم ما در این تابع عبارت‌اند از:

$$a=-4$$

$$b=1$$

$$c=0$$

$$d=0$$

بنابراین دامنه، دوره تناوب، تغییر فاز و شیفت روی محور عمودی به‌صورت زیر تعیین می‌شود:

$$\Rightarrow |a|=|-4|=4$$

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{b}=\frac{2\pi}{1}=2\pi$$

تغییر فاز = $$\frac{c}{b}$$

$$\Rightarrow \frac{c}{b}=0$$

جابجایی عمودی = $$d$$

$$\Rightarrow d= 0$$

نقطه شروع اولین دوره تناوب نمودار سینوسی از تغییر فاز یا $$-\frac{c}{b}$$ حاصل می‌شود که با صفر برابر شد:

$$\Rightarrow \theta _1= \frac{c}{b}= 0$$

اما مکان این نقطه روی محور قائم برای نمودار سینوسی برابر است با:

$$y_1=d=0$$

پس مختصات نقطه شروع دوره تناوب اول این نمودار برابر می‌شود با:

$$(\theta _1=0, y_1=0)$$

برای تعیین مکان نقطه نهایی اولین دوره تناوب نمودار روی محور افقی، باید نقطه اولیه را با دوره تناوب جمع کنیم:

$$\Rightarrow \theta _2= \frac{c}{b}+\frac{2\pi}{b}= 0+2\pi=2\pi$$

مولفه قائم این نقطه دقیقا مانند نقطه شروع دوره خواهد بود. پس مختصات نقطه نهایی اولین دوره تناوب این نمودار به‌صورت زیر است:

$$(\theta _2=2\pi, y_2=0)$$

سومین نقطه معادل است با نقطه مرکزی در دوره تناوب این نمودار، که برای مولفه افقی آن از رابطه زیر می‌توانیم استفاده کنیم:

$$\theta _3= \theta _1+\frac{2\pi}{2b}=0+\frac{\pi}{1}=\pi$$

چون نمودار سینوسی است، مکان نقطه سوم روی محور عمودی با مکان دو نقطه اول روی محور عمودی کاملا مشابه است. پس مختصات نقطه مرکزی خواهد شد:

$$(\theta _3=\pi, y_3=0)$$

نقطه چهارم با روابط زیر مشخص می‌شود:

$$\theta _4= \theta _1+\frac{2\pi}{4b}=0+\frac{\pi}{2}=\frac{\pi}{2}$$

$$y_{4}=y_1\pm |a|=0\pm |-4| =-4$$

در اینجا باید علامت منفی را برای دامنه انتخاب کنیم. علت آن این است که در نمودار سینوسی با علامت منفی برای دامنه، پس از نقطه شروع، نقطه حداقل یا مینیمم نمودار را روی محور عمودی خواهیم داشت. بنابراین با انتخاب علامت منفی این جمله درست خواهد بود، در غیر این صورت چهارمین نقطه ما بالای محور افق قرار می‌گیرد که با قاعده بیان شده در مورد نمودار سینوسی منفی مطابقت ندارد. پس مختصات نقطه چهارم برابر خواهد شد با:

$$(\theta _4=\frac{\pi}{2}, y_4=-4)$$

و در نهایت پنجمین نقطه به شکل زیر مشخص می‌شود:

$$\theta _5= \theta _3+\frac{2\pi}{4b}=\pi+\frac{\pi}{2}=\frac{3\pi}{2}$$

$$y_{5}=y_1\pm |a|=0\pm |-4| =+4$$

$$(\theta _5=\frac{3\pi}{2}, y_5=4)$$

مولفه عمودی پنجمین نقطه دقیقا هم‌اندازه با مولفه متناظر خود در چهارمین نقطه است، اما باید علامت مخالف آن داشته باشد. به همین جهت برای این نقطه علامت مثبت انتخاب شد. پس از اتصال نقاط به‌دست آمده، نمودار به‌صورت زیر خواهد شد. اعدادی که ما به‌دست آوردیم، دوره تناوب اول این نمودار در جهت مثبت محور افقی را رسم می‌کند. اما می‌توانیم با استفاده از خاصیت فرد بودن این تابع، ادامه آن را در سمت منفی محور افقی نیز به شکل زیر داشته باشیم:

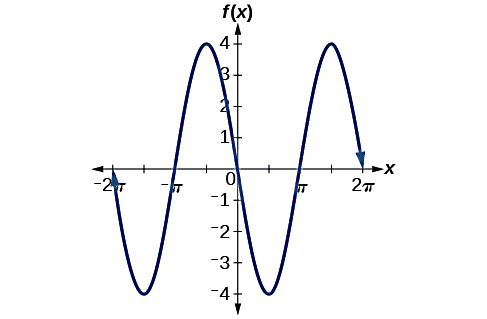
مثال ۲

نمودار تابع زیر را رسم کنید:

$$y=3\sin(2x)+1$$

پاسخ

ابتدا معادله داده شده را با فرم کلی تابع سینوسی مقایسه می‌کنیم تا ثوابت موردنظر تعیین شوند:

$$y=a\cos(b\theta-c)+d$$

$$a=3$$

$$b=2$$

$$c=0$$

$$d=1$$

حالا می‌رویم سراغ محاسبه دامنه، دوره تناوب، تغییر فاز و شیفت روی محور عمودی:

$$\Rightarrow |a|=|3|=3$$

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{b}=\frac{2\pi}{2}=\pi$$

تغییر فاز = $$\frac{c}{b}$$

$$\Rightarrow \frac{c}{b}=0$$

جابجایی عمودی = $$d$$

$$\Rightarrow d= 1$$

مکان اولین نقطه بحرانی روی محور افقی توسط رابطه تغییر فاز به‌دست می‌آید:

$$\Rightarrow \theta _1= \frac{c}{b}= 0$$

برای مکان همین نقطه در راستای قائم نیز داریم:

$$y_1=d=1$$

پس مختصات اولین نقطه از دوره تناوب اول برای این نمودار می‌شود:

$$(\theta _1=0, y_1=1)$$

مرحله بعد تعیین مکان نقطه نهایی اولین دوره تناوب روی محور افقی است:

$$\Rightarrow \theta _2= \frac{c}{b}+\frac{2\pi}{b}= 0+\pi=\pi$$

چون نمودار موردنظر ما سینوسی است، پس مولفه قائم این نقطه دقیقا مانند مولفه عمودی نقطه شروع دوره خواهد بود:

$$(\theta _2=\pi, y_2=1)$$

حالا باید نقطه مرکزی دوره تناوب را تعیین کنیم که برای مولفه افقی آن از رابطه زیر استفاده می‌کنیم:

$$\theta _3= \theta _1+\frac{2\pi}{2b}=0+\frac{\pi}{2}=\frac{\pi}{2}$$

باز هم چون نمودار سینوسی است، مکان نقطه سوم روی محور عمودی با مکان دو نقطه اول روی محور عمودی کاملا یکسان است. پس مختصات نقطه مرکزی خواهد شد:

$$(\theta _3=\frac{\pi}{2}, y_3=1)$$

چهارمین نقطه بحرانی دارای مختصاتی به‌صورت زیر خواهد بود:

$$\theta _4= \theta _1+\frac{2\pi}{4b}=0+\frac{\pi}{4}=\frac{\pi}{4}$$

$$y_{4}=y_1\pm |a|=1\pm |+3| =+4$$

چون نمودار سینوسی ما در این سوال دارای دامنه‌ای با علامت مثبت است یعنی $$0 < a$$، پس نقطه بعد از شروع دوره، نقطه‌ای است که بیشترین مقدار $$y$$ را دارد و باید در محاسبه بالا علامت مثبت را انتخاب کنیم. بنابراین مختصات نقطه چهارم برابر خواهد شد با:

$$(\theta _4=\frac{\pi}{4}, y_4=4)$$

و در نهایت پنجمین نقطه به شکل زیر مشخص می‌شود:

$$\theta _5= \theta _3+\frac{2\pi}{4b}=\frac{\pi}{2}+\frac{\pi}{4}=\frac{3\pi}{4}$$

$$y_{5}=y_1\pm |a|=1\pm |+3| =-2$$

$$(\theta _5=\frac{3\pi}{4}, y_5=-2)$$

مولفه عمودی پنجمین نقطه باید دارای بیشترین مقدار با علامت منفی باشد. به همین جهت برای این نقطه علامت منفی انتخاب شد. در انتها پنج نقطه بحرانی را به هم وصل می‌کنیم تا شکل زیر را داشته باشیم:

مثال ۳

نمودار $$y-3=-4\cos(\frac{\theta}{2}+\frac{\pi}{4})$$ را رسم کنید:

پاسخ

برای رسم نمودار کسینوس با معادله $$y-3=-4\cos(\frac{\theta}{2}+\frac{\pi}{4})$$، طبق بخش قبل قدم به قدم پیش می‌رویم. اولین مرحله این است که معادله را به شکل کلی که گفتیم درآوریم، یعنی یکی از دو شکل زیر:

$$y=a\cos(b\theta-c)+d$$

یا

$$y=a\cos b(\theta-\frac{c}{b})+d$$

معادله $$y-3=-4\cos(\frac{\theta}{2}+\frac{\pi}{4})$$ به اولین معادله بالا شبیه است، چون در این معادله متغیر $$\theta$$ دارای ضریبی به اندازه $$\frac{1}{2}$$ است. برای اینکه این معادله دقیقا فرم اولین معادله کلی را داشته باشد، کافی است عدد $$3$$ را به سمت دیگر تساوی ببریم:

$$y=-4\cos(\frac{\theta}{2}-(-\frac{\pi}{4}))+3$$

$$y=a\cos(b\theta-c)+d$$

حالا می‌توانیم با مقایسه دو رابطه بالا به‌راحتی مقادیر $$a, b, c, d$$ را تشخیص دهیم:

$$a=-4$$

$$b=\frac{1}{2}$$

$$c=-\frac{\pi}{4}$$

$$d=3$$

با داشتن مقادیر $$a, b, c, d$$، محاسبه مشخصه‌های اساسی نمودار مانند دامنه، دوره تناوب، تغییر فاز و شیفت روی محور عمودی با روابط زیر انجام می‌شود:

دامنه = $$|a|$$

$$\Rightarrow |a|=|-4|=4$$

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{b}=\frac{2\pi}{\frac{1}{2}}=4\pi$$

تغییر فاز = $$\frac{c}{b}$$

$$\Rightarrow \frac{c}{b}=\frac{-\frac{\pi}{4}}{\frac{1}{2}}=-\frac{\pi}{2}$$

جابجایی عمودی = $$d$$

$$\Rightarrow d= 3$$

پس از تعیین مشخصه‌های اساسی نمودار، نوبت به رسم خط $$y=d$$ می‌رسد که در اینجا معادل $$y=3$$ است:

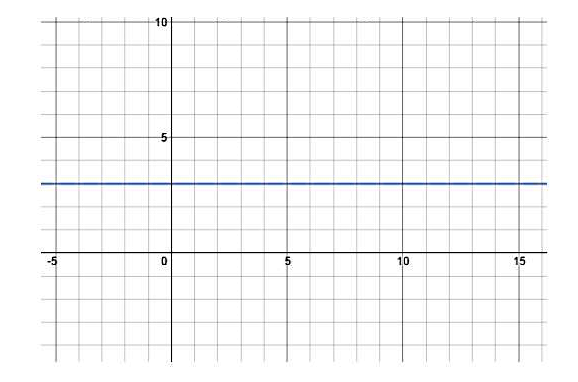
همان‌طور که در تصویر بالا مشاهده می‌کنید، روی محور قائم فواصلی برابر با $$5$$ واحد جدا شده‌اند و خط $$y=3$$ با بالا رفتن روی محور قائم به اندازه سه واحد و موازی با محور افقی به شکل بالا رسم می‌شود. حالا باید برویم سراغ تعیین نقطه شروع اولین دوره تناوب نمودار کسینوسی موردنظرمان، که برابر است با تغییر فاز یا $$-\frac{c}{b}$$:

$$\Rightarrow \theta _1= \frac{c}{b}= -\frac{\frac{\pi}{4}}{\frac{1}{2}}=-\frac{\pi}{2}$$

دقت کنید رابطه بالا مقدار نقطه اولیه را روی محور افقی یا مولفه $$\theta$$ این نقطه را تعیین می‌کند. برای اینکه محل دقیق نقطه مشخص شود، باید مقدار $$y$$ یا مولفه قائم آن روی محور عمودی نیز تعیین شود. در اینجا باید به مقدار دامنه و خط $$y=3$$ توجه کنیم. دامنه برابر با چهار واحد است، پس باید چهار واحد از خط $$y=3$$ به سمت پایین بیاییم:

$$\Rightarrow y_1= a + d =-4+3=-1$$

بنابراین مختصات نقطه شروع دوره تناوب اول این نمودار برابر است با:

$$(\theta _1=-\frac{\pi}{2}, y_1=-1)$$

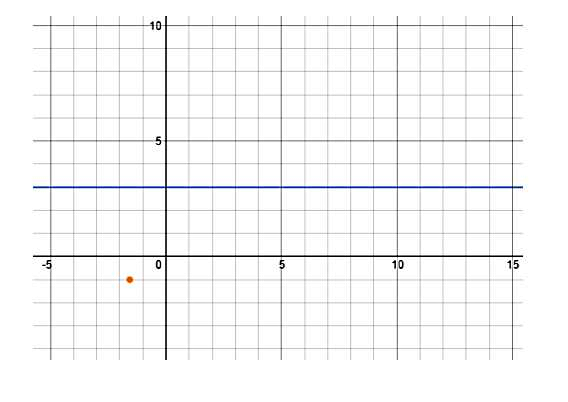
همچنین باید دقت کنیم که در مورد نمودار کسینوس با علامت منفی برای دامنه، این نقطه شروع نقطه حداقل یا مینیمم نمودار محسوب می‌شود. برای تعیین مکان نقطه نهایی اولین دوره تناوب نمودار روی محور افقی، باید نقطه اولیه را با دوره تناوب جمع کنیم:

$$\Rightarrow \theta _2= \frac{c}{b}+\frac{2\pi}{b}= -\frac{\pi}{2}+4\pi=\frac{7\pi}{2}$$

مولفه قائم این نقطه دقیقا مانند نقطه شروع دوره خواهد بود. پس مختصات نقطه نهایی اولین دوره تناوب این نمودار به‌صورت زیر است:

$$(\theta _2=\frac{7\pi}{2}, y_2=-1)$$

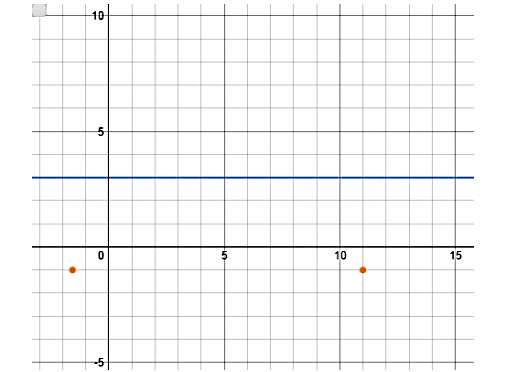
قدم بعدی مشخص کردن مختصات نقطه‌ای است که دقیقا در وسط دوره تناوب اول این نمودار قرار می‌گیرد:

$$\theta _3= \theta _1+\frac{\pi}{b}$$

$$\Rightarrow \theta _3=\theta _1+\frac{\pi}{b}= -\frac{\pi}{2}+2\pi= \frac{3\pi}{2}$$

اندازه مولفه قائم این نقطه برای نمودار کسینوس برابر است با مجموع دو برابر دامنه یا $$|2a|$$ و مقدار $$y$$ برای نقطه اول یا نقطه پایانی:

$$y_3=y_1\pm |2a|$$

$$y_3=y_1+|2a|=-1+|-8|=-1+8=7$$

$$(\theta _3=\frac{3\pi}{2}, y_3=7)$$

در این محاسبات حتما به قدر مطلق‌ها توجه کنید. از طرفی چون این معادله یک نمودار کسینوسی منفی ($$0 > a$$) خواهد داشت، پس در حالی که نقطه شروع و نقطه پایانی کمترین مقدار یا مینیمم $$y$$ را دارند، نقطه میانی باید بیشترین $$y$$ را با مقدار مثبت داشته باشد.

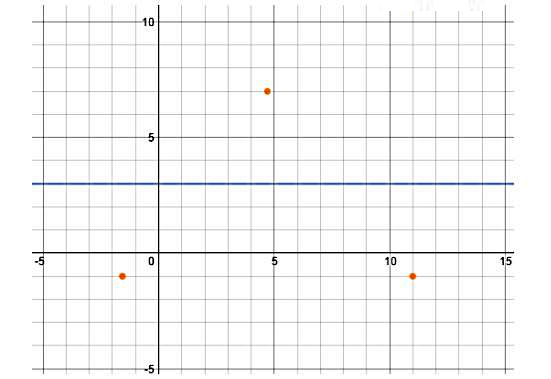
در نهایت مکان دو نقطه آخر از نقاط بحرانی این نمودار را باید پیدا کنیم. با توجه به اینکه دوره تناوب نمودار $$4\pi$$ به‌دست آمد، بنابراین فاصله نقطه شروع و نقطه میانی و همین‌طور فاصله نقطه میانی و نقطه انتهایی دوره باید برابر با $$2\pi$$ شود. از طرفی نقطه اولیه ما در مکان $$-\frac{\pi}{2}$$ قرار دارد، در حالی که نقطه میانی در مکان $$\frac{3\pi}{2}$$ است. بنابراین اگر از نقطه اولیه به اندازه $$\pi$$ جلو برویم، باید به نقطه چهارم برسیم و با حرکت از نقطه چهارم به اندازه $$\pi$$، باید به نقطه میانی یا نقطه سوم برسیم. پس مکان نقطه چهارم روی محور افقی برابر است با:

$$\Rightarrow \theta _4=\frac{-\pi}{2}+\pi= \frac{\pi}{2}$$

مکان نقطه چهارم روی محور عمودی برابر است با:

$$y_{4,5}=y_1\pm |a|$$

چون انتظار داریم نقطه چهار و پنج هر دو دارای مقادیر مثبتی از $$y$$ باشند، بنابراین در عبارت بالا باید مقدار دامنه را مثبت در نظر بگیریم:

$$y_{4,5}=y_1\pm a =-1+4=3$$

$$(\theta _4=\frac{\pi}{2}, y_4=3)$$

همان‌طور که می‌بینید با رفتن از نقطه چهارم به اندازه $$\pi$$، به مکان نقطه میانی روی محور افقی می‌رسیم:

$$\Rightarrow \theta _3=\frac{\pi}{2}+\pi= \frac{3\pi}{2}$$

و در نهایت یافتن مختصات افقی نقطه پنجم نیز با رفتن از نقطه میانی به اندازه $$\pi$$ حاصل خواهد شد:

$$\Rightarrow \theta _5= \frac{3\pi}{2}+\pi= \frac{5\pi}{2}$$

$$(\theta _5=\frac{5\pi}{2}, y_5=3)$$

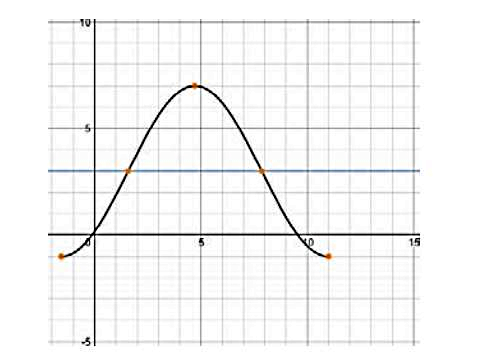
در انتها کافی است پنج نقطه به‌دست آمده را به شکل یک منحنی به هم متصل کنیم تا نمودار ما رسم شود:

مثال ۴

نمودار تابع سینوسی زیر را رسم کنید:

$$y=3\sin(2x-\frac{2\pi}{4})$$

پاسخ

دقت کنید منظور از $$x$$ در رابطه بالا همان $$\theta$$ است و می‌توانیم این دو را جایگزین کنیم. ابتدا باید رابطه بالا را با فرم کلی معادله سینوس و کسینوس مقایسه کنیم تا بتوانیم مقادیر ثابت موردنظر را به‌راحتی تعیین کنیم:

$$y=a\sin(b\theta-c)+d$$

$$y=3\sin(2\theta-\frac{2\pi}{4})$$

از معادله بالا مقادیر $$a, b, c, d$$ به شکل زیر استخراج می‌شوند:

$$a=3$$

$$b=2$$

$$c=\frac{2\pi}{4}$$

$$d=0$$

همان‌طور که می‌بینید در این معادله $$d$$ نداریم. پس شیفت یا جابجایی روی محور عمودی صفر است. با داشتن مقادیر $$a, b, c$$، محاسبه مشخصه‌های اساسی نمودار مانند دامنه، دوره تناوب، تغییر فاز با روابط زیر انجام می‌شود:

دامنه = $$|a|$$

$$\Rightarrow |a|=|3|=3$$

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{2}=\pi$$

تغییر فاز = $$\frac{c}{b}$$

$$\Rightarrow \frac{c}{b}= \frac{\frac{2\pi}{4}}{2}=\frac{\pi}{4}$$

جابجایی عمودی = $$d$$

$$\Rightarrow d= 0$$

پس خط $$y=d$$ در اینجا معادل $$y=0$$ است. حالا باید نقاط بحرانی مشخص شوند. نقطه شروع اولین دوره تناوب این نمودار سینوسی برابر است با:

$$\Rightarrow \theta _1= \frac{c}{b}= \frac{\frac{2\pi}{4}}{2}=\frac{\pi}{4}$$

برای اینکه محل دقیق این نقطه مشخص شود، باید مقدار $$y$$ یا مولفه قائم آن روی محور عمودی نیز تعیین شود:

$$y_1=d=‌‌0$$

بنابراین مختصات نقطه شروع دوره تناوب اول این نمودار برابر است با:

$$(\theta _1=\frac{\pi}{4}, y_1=0)$$

طبق نکاتی که گفتیم، در نمودار سینوسی مثبت یعنی وقتی که $$0 < a$$ است، پس از نقطه شروع بیشترین مقدار یا ماکزیمم $$y$$ را خواهیم داشت. با توجه به اینکه نمودار جابجایی قائم ندارد، پس $$y_1$$ باید دقیقا روی محور افقی قرار بگیرد، یعنی مقدار $$y_1$$ برابر با صفر است. برای تعیین مکان نقطه نهایی اولین دوره تناوب نمودار روی محور افقی، باید نقطه اولیه را با دوره تناوب جمع کنیم:

$$\Rightarrow \theta _2= \frac{c}{b}+\frac{2\pi}{b}=\frac{\pi}{4}+\pi=\frac{5\pi}{4}$$

مولفه قائم این نقطه دقیقا مانند مولفه قائم نقطه شروع دوره خواهد بود. پس مختصات نقطه نهایی اولین دوره تناوب این نمودار به‌صورت زیر است:

$$(\theta _2=\frac{5\pi}{4}, y_2=0)$$

حالا سومین نقطه یعنی نقطه مرکزی دوره تناوب را مشخص می‌کنیم که با کاربرد روابط زیر مشخص می‌شود:

$$\theta _3= \theta _1+\frac{\pi}{b}$$

$$\Rightarrow \theta _3=\theta _1+\frac{\pi}{b}= \frac{\pi}{4}+\frac{\pi}{2}= \frac{3\pi}{4}$$

از طرفی چون در این معادله یک نمودار سینوسی مثبت داریم که دارای $$0 < a$$ است، پس با توجه به اینکه نقطه چهارم ماکزیمم و نقطه پنجم مینیمم مقادیر $$y$$ را خواهند داشت، نقطه میانی یا سوم باید مانند دو نقطه اول دارای مولفه عمودی برابر با صفر باشد:

$$(\theta _3=\frac{3\pi}{4}, y_3=0)$$

حالا می‌رویم سراغ تعیین مختصات نقاط چهار و پنج. در مورد چهارمین نقطه کافی است از نقطه شروع، به اندازه یک چهارم دوره تناوب به سمت مثبت محور افقی جلو برویم:

$$\theta _4= \theta _1+\frac{2\pi}{4b}=\frac{\pi}{4}+\frac{\pi}{4}=\frac{\pi}{2}$$

تعیین مولفه عمودی این نقطه نیز با رابطه زیر طبق توضیحات داده شده امکان‌پذیر است:

$$y_4=y_1\pm |a| \Rightarrow y_4=0+3=3$$

$$(\theta _4=\frac{\pi}{2}, y_4=3)$$

در نهایت آخرین نقطه بحرانی دارای مکان‌های زیر روی دو محور در صفحه است:

$$\theta _5= \theta _3+\frac{2\pi}{4b}=\frac{3\pi}{4}+\frac{\pi}{4}=\pi$$

$$y_5=y_1\pm |a| \Rightarrow y_5=0-3=-3$$

$$(\theta _5=\pi, y_5=-3)$$

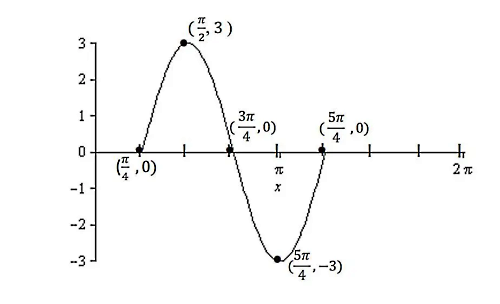
در مورد مکان دو نقطه آخر روی محور قائم باید در انتخاب علامت مثبت یا منفی دقت کنید. چون در اینجا نمودار سینوسی مثبت داشتیم، پس انتظار داریم مکان نقطه چهارم در بیشترین مقدار خود باشد. لذا علامت مثبت $$a$$ را در محاسبه مکان $$y_4$$ انتخاب می‌کنیم. اما پنجمین نقطه دارای $$y$$ برابر با نقطه چهارم اما با علامت منفی است. پس باید در محاسبه مکان آن علامت منفی انتخاب شود. در انتها با وصل کردن نقاط به‌دست آمده نمودار به شکل زیر رسم می‌شود:

مثال ۵

نمودار کسینوسی با معادله زیر را رسم کنید:

$$y=5\cos(3x+\frac{3\pi}{2})+1$$

پاسخ

در این سوال هم منظور از $$x$$ همان $$\theta$$ است و می‌توانیم این دو را جایگزین کنیم. ابتدا باید رابطه بالا را با فرم کلی معادله سینوس و کسینوس مقایسه کنیم تا بتوانیم مقادیر ثابت موردنظر را به‌راحتی تعیین کنیم:

$$y=a\cos(b\theta-c)+d$$

از معادله بالا مقادیر $$a, b, c, d$$ به شکل زیر استخراج می‌شوند:

$$a=5$$

$$b=3$$

$$c=-\frac{3\pi}{2}$$

$$d=1$$

همان‌طور که می‌بینید شیفت یا جابجایی نمودار روی محور عمودی به اندازه یک واحد مثبت است. با داشتن مقادیر $$a, b, c$$، محاسبه مشخصه‌های اساسی نمودار مانند دامنه، دوره تناوب، تغییر فاز با روابط زیر انجام می‌شود:

دامنه = $$|a|$$

$$\Rightarrow |a|=|5|=5$$

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{3}$$

تغییر فاز = $$\frac{c}{b}$$

$$\Rightarrow \frac{c}{b}= \frac{-\frac{3\pi}{2}}{3}=-\frac{\pi}{2}$$

جابجایی عمودی = $$d$$

$$\Rightarrow d= 1$$

نقطه شروع اولین دوره تناوب این نمودار کسینوسی برابر است با:

$$\Rightarrow \theta _1= \frac{c}{b}=-\frac{\pi}{2}$$

طبق توضیحی که برای نمودار کسینوسی دادیم، چون در اینجا با یک نمودار کسینوسی مثبت مواجه هستیم، یعنی داریم $$0 < a$$، بنابراین نقطه شروع دوره تناوب ما دارای بیشترین مقدار $$y$$ خواهد بود:

$$\Rightarrow y_1= 5 + 1 =6$$

بنابراین مختصات نقطه شروع دوره تناوب اول این نمودار برابر است با:

$$(\theta _1=-\frac{\pi}{2}, y_1=6)$$

در ادامه برای یک نمودار کسینوسی، انتظار داریم پس از نقطه شروع، کاهش مقدار $$y$$ را داشته باشیم تا مینیمم مقدار $$y$$ در نقطه میانی و سپس افزایش $$y$$ تا نقطه پایانی دوره. برای تعیین مکان نقطه نهایی اولین دوره تناوب نمودار روی محور افقی، باید نقطه اولیه را با دوره تناوب جمع کنیم:

$$\Rightarrow \theta _2= \frac{c}{b}+\frac{2\pi}{b}=-\frac{\pi}{2}+\frac{2\pi}{3}=\frac{\pi}{6}$$

مولفه قائم این نقطه دقیقا مانند مولفه قائم نقطه شروع دوره خواهد بود. پس مختصات نقطه نهایی اولین دوره تناوب این نمودار به‌صورت زیر است:

$$(\theta _2=\frac{\pi}{6}, y_2=6)$$

همچنین نقطه مرکزی دوره تناوب با کاربرد روابط زیر مشخص می‌شود:

$$\theta _3= \theta _1+\frac{\pi}{b}$$

$$\Rightarrow \theta _3=\theta _1+\frac{\pi}{b}= -\frac{\pi}{2}+\frac{\pi}{3}= -\frac{\pi}{6}$$

از طرفی همان‌طور که گفتیم مولفه عمودی برای این نقطه باید در بیشترین مقدار خود اما با علامت منفی قرار داشته باشد. پس خواهیم داشت:

$$y_3=y_1\pm |2a|$$

$$y_3=y_1\pm|2a|=6-|10|=-4$$

چون نمودار کسینوسی مثبتی داریم، نقطه میانی دوره تناوب اول آن باید دارای کمترین $$y$$ باشد. اگر علامت مثبت را در رابطه بالا انتخاب کنیم، مقدار $$y$$ برای این نقطه برابر با $$16$$ می‌شود! چنین مقداری با نمودار ما همخوانی ندارد. اما با انتخاب علامت منفی، $$y$$ مناسب با نوع نمودار را خواهیم داشت. پس مختصات نقطه مرکزی دوره برای این نمودار خواهد شد:

$$(\theta _3=-\frac{\pi}{6}, y_3=-4)$$

حالا می‌رویم سراغ تعیین مختصات نقاط چهار و پنج. در مورد چهارمین نقطه کافی است از نقطه شروع، به اندازه یک چهارم دوره تناوب به سمت مثبت محور افقی جلو برویم:

$$\theta _4= \theta _1+\frac{2\pi}{4b}=-\frac{\pi}{2}+\frac{\pi}{6}=-\frac{\pi}{3}$$

مولفه عمودی این نقطه با رابطه زیر تعیین می‌شود، فقط باید دقت کنید در انتخاب علامت اشتباه نکنید. با انتخاب علامت مثبت مقدار $$y$$ برای این نقطه برابر با عدد بزرگ $$11$$ می‌شود که با بقیه نقاط و شکل نمودار کسینوس همخوانی ندارد:

$$y_4=y_1\pm |a| \Rightarrow y_4=6-5=1$$

$$(\theta _4=-\frac{\pi}{3}, y_4=1)$$

پنجمین نقطه بحرانی که در مورد نمودار کسینوس دقیقا دارای $$y$$ برابر با نقطه چهارم است، دارای مکان‌ زیر روی محور افقی است:

$$\theta _5= \theta _3+\frac{2\pi}{4b}=-\frac{\pi}{6}+\frac{\pi}{6}=0$$

$$(\theta _5=0, y_5=1)$$

در نهایت با اتصال پنج نقطه به‌دست آمده، نمودار ما به شکل زیر خواهد شد:

مثال ۶

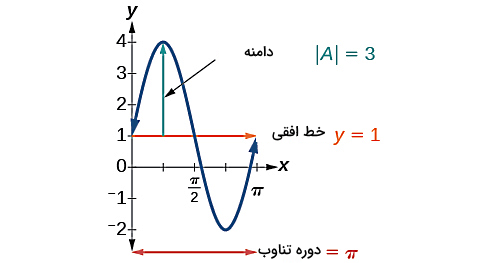
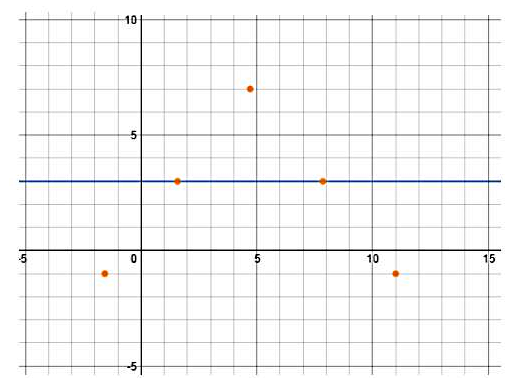
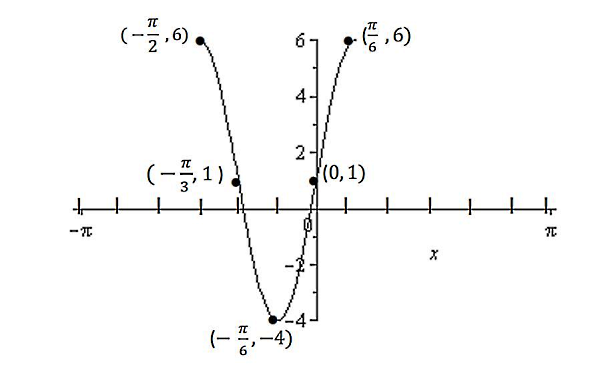
فرمول تابع زیر را با توجه به شکل داده شده تعیین کنید:

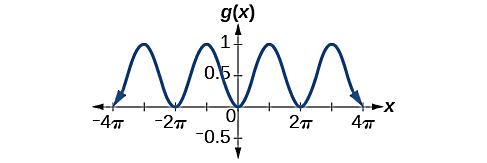
پاسخ

اولین قدم برای تشخیص معادله این نمودار، نوشتن فرم کلی معادله برای نمودار سینوس و کسینوس است که توضیح داده بودیم:

$$y=a\cos(b\theta-c)+d$$

با توجه به اینکه نمودار داده شده نسبت به محور عمودی متقارن است، بنابراین نمودار کسینوس را داریم. در اولین نگاه می‌توانیم تشخیص دهیم که دوره تناوب این نمودار برابر است با $$2\pi$$، چون در هر بازه برابر با $$2\pi$$ شکل نمودار تکرار شده است. پس با توجه به رابطه‌ای که برای دوره تناوب داشتیم، می‌توانیم بنویسیم:

دوره تناوب = $$\frac{2\pi}{b}$$

$$\Rightarrow \frac{2\pi}{b} =2\pi \Rightarrow b=1$$

از طرفی چون نقطه شروع اولین دوره تناوب دقیقا در $$(0, 0)$$ قرار دارد، بنابراین می‌توانیم نتیجه‌گیری کنیم که شیفت فاز نداریم. یعنی:

تغییر فاز = $$\frac{c}{b}=0$$

$$\Rightarrow c=0$$

پس تا اینجا دو ثابت $$b$$ و $$c$$ در معادله کلی تعیین شد. در مورد دامنه این نمودار، با توجه به اینکه بلافاصله پس از شروع اولین نقطه دوره تناوب، نقطه‌ای با بیشترین مقدار $$y$$ را داریم، پس باید یک نمودار کسینوسی منفی با $$0 > a$$ داشته باشیم. تشخیص مقدار $$a$$ از رابطه‌ای که برای مقدار $$y$$ در سومین نقطه بحرانی برای نمودار کسینوس گفتیم، انجام می‌شود:

$$y_3=y_1\pm |2a|$$

اولین دوره را در شکل در نظر می‌گیریم. سومین نقطه بحرانی در این شکل معادل است با نقطه‌ای با مختصات $$(\pi, 1)$$. بنابراین رابطه بالا به شکل زیر درمی‌آید:

$$\Rightarrow 1=0\pm |2a|$$

$$\Rightarrow a=\pm 0.5$$

و همان‌طور که گفتیم، انتخاب ما علامت منفی است. همچنین گفتیم مولفه قائم نقطه شروع دوره برای نمودار کسینوسی، دارای فرمولی به شکل زیر است:

$$y_1=a+d$$

با معلوم شدن $$a$$ و $$y_1$$، میزان جابجایی روی محور عمودی یا $$d$$ به‌دست می‌آید:

$$\Rightarrow 0=-0.5+d \Rightarrow d=0.5$$

بنابراین با ثوابت محاسبه شده، معادله این نمودار به شکل زیر می‌شود:

$$y=-0.5\cos x+0.5$$

دقت کنید چون در شکل محور افقی بر حسب $$x$$ است، ما هم معادله را بر حسب $$x$$ می‌نویسیم.

تمرین ۱

تمرین ۲

تمرین ۳