دایره مثلثاتی — به زبان ساده

دایره مثلثاتی، به دایره‌ای به شعاع واحد گفته می‌شود. با استفاده از این دایره‌ی ساده می‌توان نسبت‌های مثلثاتی (سینوس، کسینوس و تانژانت) را به سادگی بدست آورد. هم‌چنین با استفاده از مفهوم دایره‌ی مثلثاتی می‌توان طول‌ها و زوایا را در اشکال هندسی بدست آورد.

محاسبه سینوس، کسینوس و تانژانت

در ابتدا مطابق با شکل زیر دایره‌ای به قطر واحد را در نظر بگیرید.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

با توجه به این که شعاع دایره برابر با ۱ است، می‌توان نسبت‌های مثلثاتی را به صورت مستقیم بدست آورد. فرض کنید می‌خواهیم نسبت‌های مثلثاتی را در زاویه‌ای خاص بدست آوریم. در این صورت نقطه‌ی روی دایره را در زاویه مذکور قرار داده و از آن به مرکزِ دایره خطی رسم می‌کنیم. بدیهی است که طول این خط برابر با ۱ است. در نتیجه ارتفاع نقطه تا محور افقی برابر با سینوس و طول افقی نقطه تا مرکزِ دایره، اندازه کسینوس زاویه‌ی مذکور را نشان می‌دهد. اگر در زاویه مذکور خطی به دایره مماس شود، طول آن نشان دهنده اندازه تانژانت زاویه است.

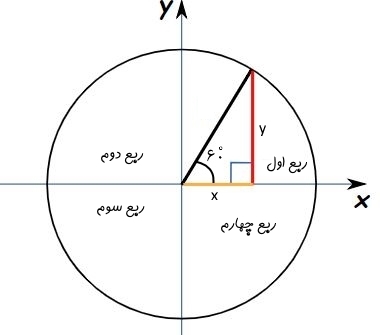
در شکل زیر دایره مثلثاتی، اندازه سینوس، کسینوس و تانژانت زاویه θ نشان داده شده‌اند.

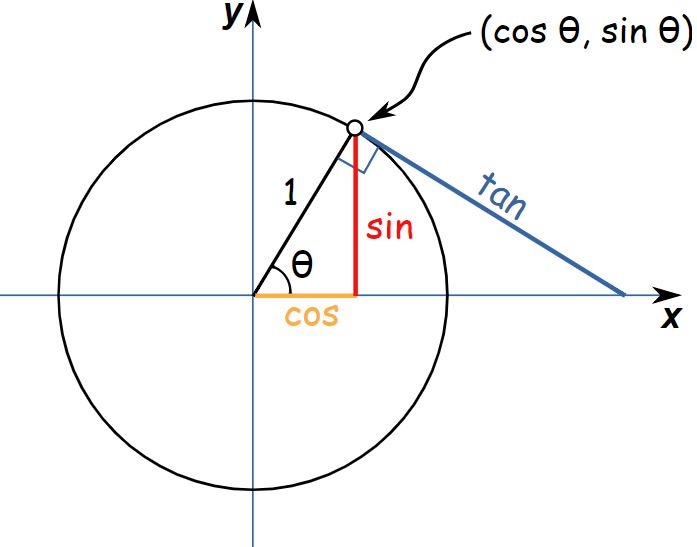
در شکل فوق طولِ خط قرمز رنگ، نشان دهنده سینوس، طول خط زرد رنگ، نشان دهنده کسینوس و خط آبی رنگ،‌ برابر با اندازه تانژانت است. برای نمونه احتمالا می‌دانید که سینوس زاویه‌ی صفر درجه برابر با صفر است (sin 0=0). حال می‌خواهیم با استفاده از دایره‌ی مثلثاتی، همین عدد را بدست آوریم. زاویه صفر درجه به این معنی است که نقطه دقیقا روی محور افقی قرار داشته باشد.

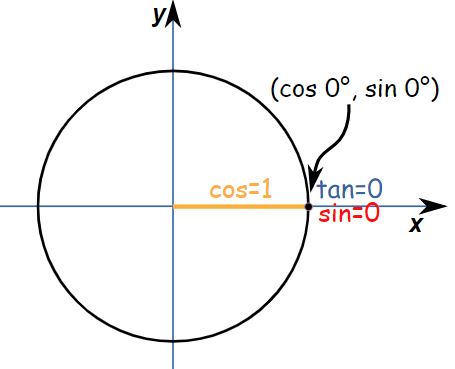
همان‌گونه که در شکل فوق می‌بینید فاصله عمودی نقطه تا محور افقی (یا همان ارتفاع نقطه) برابر با صفر است. بنابراین sin 0=0 نتیجه می‌شود. از طرفی فاصله نقطه تا محور عمودی برابر با شعاع دایره است. بنابراین از شکل فوق نتیجه می‌شود:

$$\large sin (0) =0$$
$$\large cos (0) =1$$

مطابق با شکل زیر فرض کنید نقطه‌‌ای در زاویه ۶۰ درجه نسبت به محور افق قرار گرفته است. با توجه به طول‌های بدست آمده، اندازه سینوس و کسینوس زاویه ۶۰ درجه چند است؟

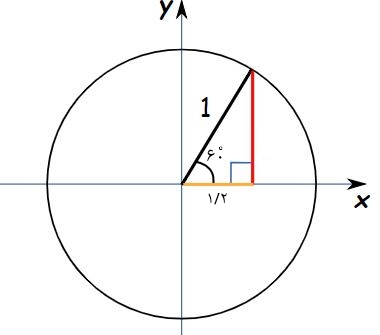
با توجه به تصویر فوق اندازه طول زرد رنگ برابر با $$1 \over 2$$ و اندازه طول قرمز رنگ برابر با ۰.۸۶۶ است (اگر اندازه‌گیری شود این عدد بدست خواهد آمد). بنابراین می‌توان گفت:

$$\large sin \enspace (60)=0.866$$
$$\large cos \enspace (60) =\frac{1}{2}$$

توجه داشته باشید که علامت مقادیر مثلثاتی با استفاده از قوانین کارتزینی قابل تعیین است. برای نمونه اگر نقطه‌‌ای در ربع سوم (پایین سمتِ چپ دایره) دایره قرار گیرد،‌ هر دو مقدار سینوس و کسینوس آن منفی خواهند بود (در ادامه تقسیم‌بندی ربع‌های دایره نشان داده شده).

فیثاغورس

همان‌گونه که قبلا نیز بیان شده، قانون فیثاغورس می‌گوید در یک مثلث قائم الزاویه، حاصل جمع مربع اضلاع برابر با مربع وتر خواهد بود.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

بنابراین در دایره مثلثاتی زیر نیز رابطه فیثاغورس به‌صورت ارائه شده، برقرار است.

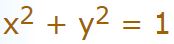
اگر در رابطه فوق، مقادیر متناظرشان را قرار دهیم، خواهیم داشت:

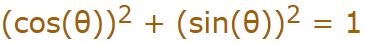
زوایای مهم

در محاسبات مربوط به مثلثات، زوایای پرکاربردی وجود دارند که در مسائل بسیار تکرار می‌شوند.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

در جدول زیر این زوایا به همراه مقادیر مثلثاتی آن‌ها ارائه شده است.

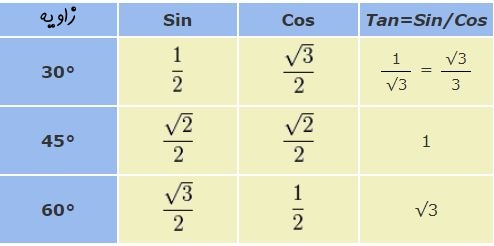
به‌منظور به خاطر سپردن مقادیر بالا به ترتیب از ۱ تا ۳ شمرده و آن‌ها را زیر رادیکال قرار داده و به ۲ تقسیم کنید.

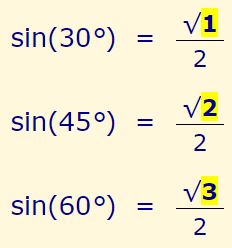
برای مقدار کسینوس به صورت عکس و از ۳ تا ۱ را بشمرید.

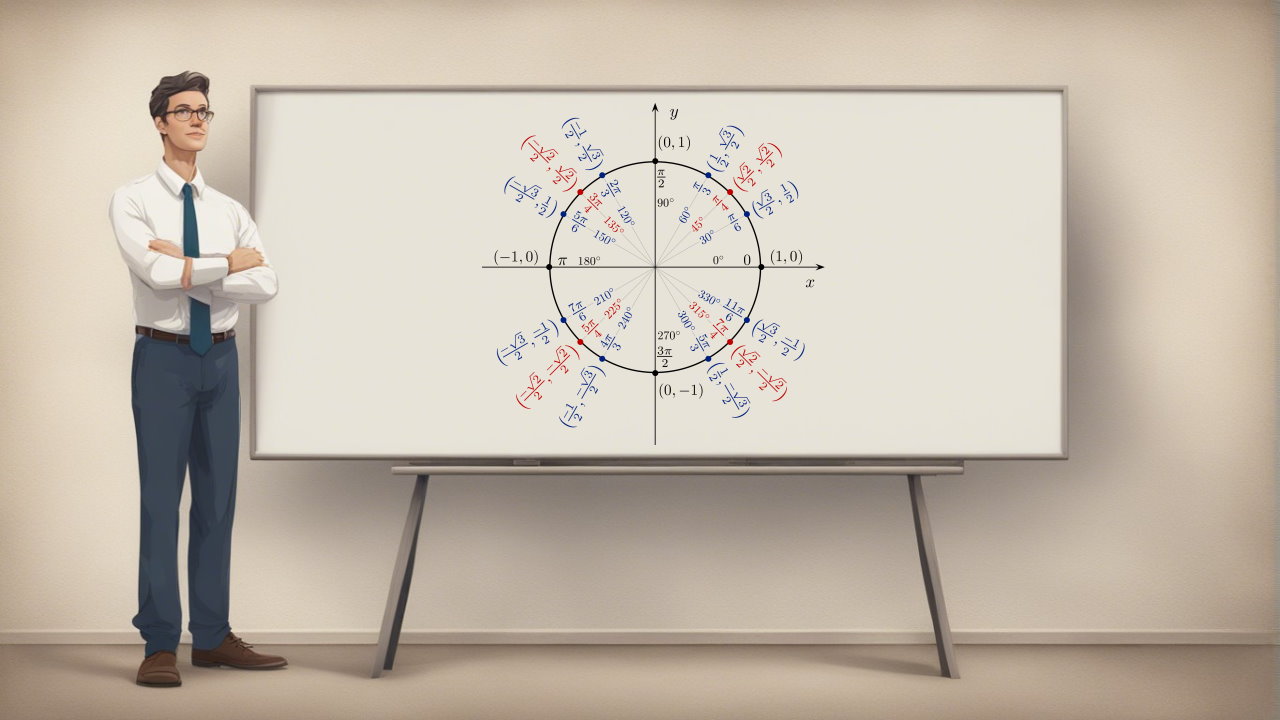
بنابراین تنها با دانستن سه عددِ $${1\over 2}, {\sqrt{2} \over 2},{\sqrt{3}\over 2}$$ مقدار مثلثاتی زوایا نیز معلوم می‌شوند. در شکل زیر مقادیر سینوس و کسینوس در زوایای مختلف روی دایره نشان داده شده است. البته در این مطلب روشی بسیار آسان جهت به‌خاطر سپردن مقادیر مثلثاتی ارائه شده که در صورت علاقه‌مندی می‌توانید به آن مراجعه کنید.

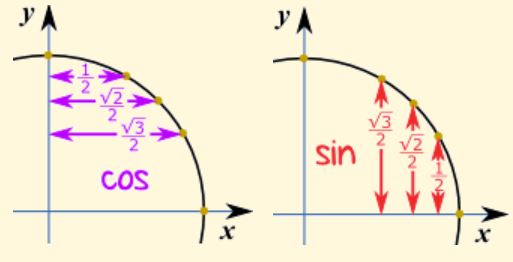
تانژانت

با توجه به مفاهیم پایه‌ای مثلثات، مقدار تانژانت برابر با حاصل تقسیم سینوس به کسینوس یک زاویه است. برای نمونه با استفاده از جدول فوق مقادیر سینوس و کسینوس در زاویه‌ی ۳۰ درجه معلوم هستند. بنابراین مقدار تانژانتِ ۳۰ درجه برابر است با:

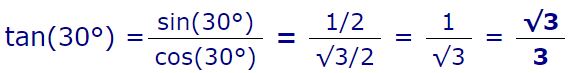
تمامی دایره

همان‌طور که می‌دانید علامت مقادیر سینوس و کسینوس بعد از ۹۰ درجه متفاوت می‌شوند.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در حقیقت در هرکدام از ربع‌های دایره علامت سینوس و کسینوس تغییر می‌کنند. در شکل زیر علامت سینوس در سمت راست و علامت کسینوس در سمت چپ نشان داده شده است.

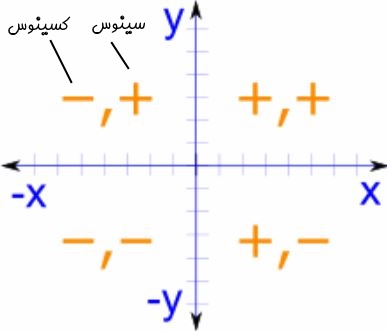
همان‌طور که می‌بینید در نیمه راست دایره مقادیر کسینوس مثبت هستند. هم‌چنین در نیمه‌ بالایی دایره مقادیر سینوس مثبت‌اند. عکس همین علامت‌ها نیز در نیمه دیگر رخ می‌دهد. در شکل زیر مقادیر سینوس و کسینوس در زوایای مختلف، روی شکل نشان داده شده است. پیشنهاد می‌کنیم به نحوه تکرار شدن اعداد و تغییر علامت آن‌ها در شکل ۱ دقت کنید.

مثال

مقدار $$\sin \frac{7\pi}{6}$$ را بیابید.

می‌توان زاویه $$\frac{7\pi}{6}$$ (یا همان ۲۱۰ درجه) را به‌صورت $$\pi +\frac{\pi}{6}$$ تصور کرد. بنابراین اگر از $$\frac{\pi}{6}$$ به اندازه‌ی π عبور کنیم به زاویه‌ی زیر خواهیم رسید.

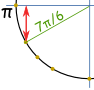
در حقیقت در ربع سوم قرار گرفته‌ایم. بنابراین حاصل سینوس بایستی منفی باشد. همان‌طور که در شکل ۱ نیز مشاهده می‌شود،‌ مقدار سینوس در زاویه مذکور برابر است با:

$$\large \sin \frac{7\pi}{6}=\frac{-1}{2}$$