قوانین مثلثات به زبان ساده + مثال و تمرین

مثلث قائم‌الز اویه زیر را در نظر بگیرید. رابطه بین زاویه‌های حاده و ضلع‌ها در مثلث‌های قائم‌الزاویه، توسط نسبت‌های مثلثاتی بیان می‌شود. در مثلث زیر، زاویه‌های α و β، حاده هستند. بنابراین، امکان به دست آوردن رابطه بین این زاویه‌ها بر حسب اندازه ضلع‌های دیگر (BC ،AB و BC) وجود دارد.

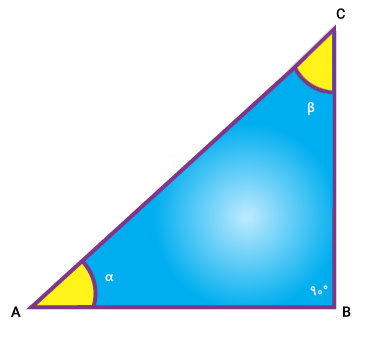
به عنوان مثال، در مثلث بالا، اگر زاویه راس A را داشته باشیم، می‌توانیم نسبت ضلع مقابل این زاویه به ضلع مجاور این زاویه را به دست بیاوریم. به این نسبت، تانژانت می‌گوییم. از دیگر نسبت‌های مثلثاتی اصلی می‌توانیم به سینوس، کسینوس، تانژانت، کتانژانت، کسکانت و سکانت اشاره کنیم. این نسبت‌ها به صورت زیر تعریف می‌شوند:

$$ \sin ( A ) = \frac { B C } { A C } $$

$$ \cos ( A ) = \frac { A B } { A C } $$

$$ \tan ( A ) = \frac { B C } { A B } $$

$$ \cot ( A ) = \frac { A B } { B C } $$

$$ \sec ( A ) = \frac { A C } { A B } $$

$$ \csc ( A ) = \frac { A C } { B C } $$

عبارت‌های مورد استفاده در روابط بالا عبارت هستند از:

A: زاویه راس A (یکی از زاویه‌های حاده مثلث قائم‌الزاویه)
$$ \sin ( A ) $$: سینوس زاویه راس A
$$ \cos ( A ) $$: کسینوس زاویه راس A
$$ \tan ( A ) $$: تانژانت زاویه راس A
$$ \cot ( A ) $$: کتانژانت زاویه راس A
$$ \sec ( A ) $$: سکانت زاویه راس A
$$ \csc ( A ) $$: کسکانت زاویه راس A
BC: ضلع مقابل به زاویه راس A
AB: ضلع مجاور به زاویه راس A
AC: وتر مثلث قائم‌الزاویه

تا به اینجا، با اصلی‌ترین قوانین مثلثات آشنا شدیم. در بخش‌های بعدی، قوانین بیشتری را مورد بررسی قرار خواهیم داد.

نسبت های مثلثاتی به زبان ساده + مثال و تمرین

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی

مثال ۱: محاسبه نسبت های مثلثاتی از روی اندازه ضلع‌ها

مثلث قائم‌الزاویه زیر را در نظر بگیرید. نسبت‌های مثلثاتی زوایای غیرقائمه آن را به دست بیاورید. سپس به سوالات زیر پاسخ دهید:

در چه صورتی می‌توانیم اندازه زاویه‌های غیرقائمه را تعیین کنیم؟
اگر سینوس زاویه ۳۶/۸۷ درجه برابر با ۰/۶ و تانژانت زاویه ۵۳/۱۳ درجه برابر با ۰/۷۵ باشد، اندازه زاویه راس‌های غیرقائمه چگونه است؟

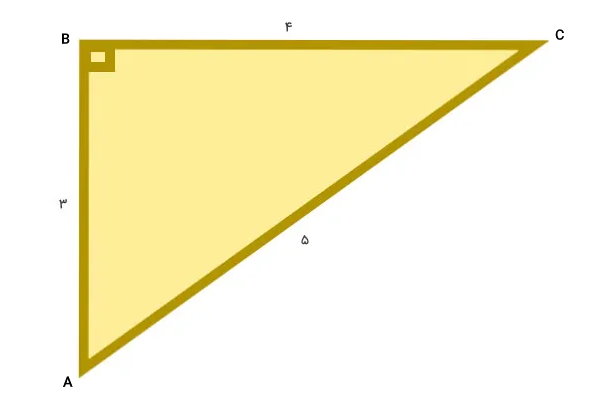
زاویه‌های رئوس A و C، غیرقائمه هستند. بنابراین، برای زاویه راس A، داریم:

$$ \sin ( A ) = \frac { B C } { A C } = \frac { ۴ } { ۵ } = ۰/۸ $$

$$ \cos ( A ) = \frac { A B } { A C } = \frac { ۳ } { ۵ } = ۰/۶ $$

$$ \tan ( A ) = \frac { B C } { A B } = \frac { ۴ } { ۳ } = ۱/۳۳ $$

$$ \cot ( A ) = \frac { A B } { B C } = \frac { ۳ } { ۴ } = ۰/۷۵ $$

$$ \sec ( A ) = \frac { A C } { A B } = \frac { ۵ } { ۳ } = ۱/۶۷ $$

$$ \csc ( A ) = \frac { A C } { B C } = \frac { ۵ } { ۴ } = ۱/۲۵ $$

برای زاویه راس C نیز داریم:

$$ \sin ( C ) = \frac { A B } { A C } = \frac { ۳ } { ۵ } = ۰/۶ $$

$$ \cos ( C ) = \frac { B C } { A C } = \frac { ۴ } { ۵ } = ۰/۸ $$

$$ \tan ( C ) = \frac { A B } { B C } = \frac { ۳ } { ۴ } = ۰/۷۵ $$

$$ \cot ( C ) = \frac { B C } { A B } = \frac { ۴ } { ۳ } = ۱/۳۳ $$

$$ \sec ( C ) = \frac { A C } { B C } = \frac { ۵ } { ۴ } = ۱/۲۵ $$

$$ \csc ( C ) = \frac { A C } { A B } = \frac { ۵ } { ۳ } = ۱/۶۷ $$

به این ترتیب، نسبت‌های مثلثاتی زوایای غیرقائمه مثلث ABC را به دست آوردیم. نسبت‌های مثلثاتی برای یک زاویه خاص، همواره مقدار مشخصی دارد. از این‌رو، اگر بدانیم کدام زاویه‌ها، دارای نسبت‌های مثلثاتی بالا هستند، می‌توانیم در مورد اندازه زاویه راس‌های مثلث اظهار نظر کنیم.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی

سینوس زاویه ۳۶/۸۷ درجه برابر با ۰/۶ است. با توجه به محاسبات بالا، این مقدار با سینوس زاویه راس C برابری می‌کند. بنابراین، می‌توانیم بگوئیم زاویه راس C برابر با ۳۶/۸۷ درجه است. تانژانت زاویه ۵۳/۱۳ درجه برابر با ۰/۷۵ است. این مقدار، با تانژانت زاویه راس A برابری می‌کند. در نتیجه، زاویه راس A برابر با ۵۳/۱۳ است. به این ترتیب، داریم:

زاویه راس A برابر با ۵۳/۱۳ درجه
زاویه راس B برابر با ۹۰ درجه
زاویه راس C برابر با ۳۶/۸۷ درجه

قانون فیثاغورس در مثلثات

یکی از مهم‌ترین و شناخته شده‌ترین قوانین مثلثات، امکان بیان قضیه فیثاغورس بر حسب توابع مثلثاتی است.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد

این قانون به صورت زیر نوشته می‌شود:

$$ \sin ^ ۲ ( \theta ) + \cos ^ ۲ ( \theta ) = ۱ $$

از روابط مشابه با این قانون می‌توان به اتحادهای زیر اشاره کرد:

$$ ۱ + \tan ^ ۲ ( \theta ) = \sec ^ ۲ ( \theta ) $$

$$ ۱ + \cot ^ ۲ ( \theta ) = \csc ^ ۲ ( \theta ) $$

روابط ارائه شده در این بخش، به منظور اثبات بسیاری از نسبت‌های مثلثاتی مورد استفاده قرار می‌گیرند.

فرم اویلری قانون فیثاغورس در مثلثات

فرم اویلری قانون فیثاغورس در مثلثات عبارت است از:

$$ e ^ { i \theta } = \cos ( \theta ) + i \sin ( \theta ) $$

مثال ۲: محاسبه سینوس از روی کسینوس

کسینوس یک زاویه برابر با ۰/۶ است. سینوس همان زاویه را پیدا کنید.

برای به دست آوردن مقدار سینوس یک زاویه از روی کسینوس همان زاویه، قانون فیثاغورس در مثلثات را می‌نویسیم:

$$ \sin ^ ۲ ( \theta ) + \cos ^ ۲ ( \theta ) = ۱ $$

مقدار کسینوس را درون رابطه بالا قرار می‌دهیم:

$$
\sin ^ ۲ ( \theta ) + ( ۰/۶ ) ^ ۲ = ۱
$$

$$
\sin ^ ۲ ( \theta ) + ۰/۳۶ = ۱
$$

$$
\sin ^ ۲ ( \theta ) = ۱ - ۰/۳۶
$$

$$
\sin ^ ۲ ( \theta ) = ۰/۶۴
$$

$$
\sin ( \theta ) = \sqrt { ۰/۶۴ }
$$

$$
\sin ( \theta ) = ۰/۸
$$

بنابراین، اگر کسینوس زاویه‌ای برابر با ۰/۶ باشد، سینوس آن برابر با ۰/۸ خواهد بود. در مثال ۱ دیدیم که این زاویه برابر با ۵۳/۱۳ درجه است.

قوانین مثلثات در دایره واحد

«دایره واحد» (Unit Circle)، دایره‌ای به شعاع ۱ است. رسم این دایره در دستگاه مختصات دوبعدی، امکان یادگیری قوانین مثلثات را ساده‌تر می‌کند.

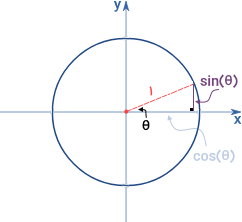
برای درک کاربرد دایره واحد در مثلثات، شکل زیر را در نظر بگیرید.

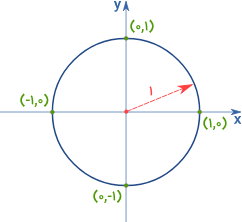
شکل بالا، یک دایره واحد را در دستگاه مختصات x-y نمایش می‌دهد. مرکز دایره بر روی مرکز مختصات قرار دارد. دایره واحد، محورهای x و y را در نقاط (۱,۰)، (۰,۱)، (۱,۰-) و (۱-,۰) قطع می‌کند. اگر یک نقطه از دایره را به محور x عمود کرده و سپس آن را به مرکز مختصات وصل کنیم، یک مثلث قائم‌الزاویه تشکیل می‌شود. اندازه وتر مثلث برابر با ۱ (شعاع دایره واحد) است. این وتر با محور x، زاویه θ می‌سازد.

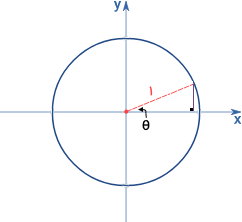
بر اساس قوانین مثلثات، می‌دانیم که در یک مثلث قائم‌الزاویه، سینوس یک زاویه غیرقائمه، از تقسیم ضلع مقابل به آن زاویه بر وتر به دست می‌آید. کسینوس یک زاویه نیز با تقسیم ضلع مجاور آن زاویه بر وتر برابری می‌کند. بنابراین، به دلیل واحد بودن اندازه وتر در مثلث بالا، ساق منطبق بر روی محور x، برابر با $$ \cos ( \theta ) $$ و ساق موازی با محور y برابر با $$ \sin ( \theta ) $$ خواهد بود.

مختصات هر نقطه از دایره واحد، سینوس و کسینوس زاویه‌ای است که خط واصل آن به مرکز مختصات با محور x‌ می‌سازد. به عبارت دیگر، عرض هر نقطه از دایره (مختصات نقطه بر روی محور x)، سینوس زاویه و ارتفاع هر نقطه از دایره (مختصات نقطه بر روی محور y)، کسینوس زاویه را نمایش می‌دهد. بنابراین می‌توانیم نقاط دایره را به صورت زیر نمایش دهیم:

$$ ( \sin \theta , \cos \theta ) $$

تصویر زیر، مختصات برخی از نقاط معروف دایره واحد (سینوس و کسینوس زوایای معروف) را نمایش می‌‌دهد.

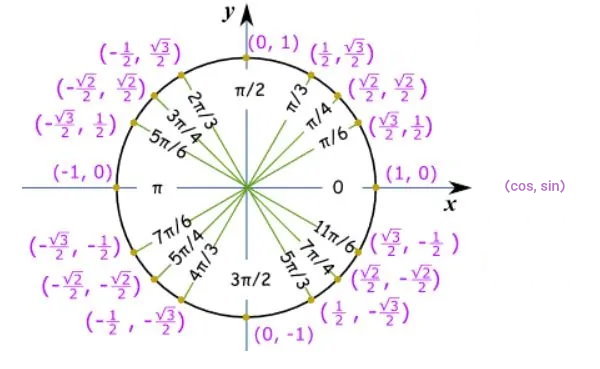
یکی از مهم‌ترین و پرکاربردترین قوانین مثلثات، علامت سینوس و کسینوس در ربع‌های مختلف دایره واحد است. علامت نسبت های مثلثاتی در چهار ربع دایره واحد به صورت زیر تعیین می‌شود:

ربع اول: در بازه ۰ تا ۹۰ درجه یا ۰ تا π/۲، همه نسبت‌های مثلثاتی مثبت هستند.
ربع دوم: در بازه ۹۰ تا ۱۸۰ درجه یا ۰ تا π، سینوس مثبت و بقیه نسبت‌های مثلثاتی منفی هستند.
ربع سوم: در بازه ۱۸۰ تا ۲۷۰ درجه یا π- تا π/۲-، تانژانت و کتانژانت مثبت، علامت سینوس و کسینوس منفی هستند.
ربع چهارم: در بازه ۲۷۰ تا ۳۶۰ درجه یا π/۲- تا ۰، کسینوس مثبت و بقیه نسبت‌های مثلثاتی منفی هستند.

برای تعیین علامت نسبت‌های مثلثاتی، می‌توانید عبارت اختصاری «هستک» (همه، سینوس، تانژانت و کتانژانت، کسینوس) را به خاطر داشته باشید. حروف این عبارت، نسبت‌های مثبت را به ترتیب در ربع‌های اول تا چهارم نمایش می‌دهند. روابط بسیار متعددی بین نسبت‌های مثلثاتی وجود دارند. در بخش‌های بعدی، به معرفی این روابط خواهیم پرداخت.

دایره مثلثاتی — به زبان ساده

فیلم آموزش ریاضی پایه دانشگاهی

مثال ۳: اثبات قضیه فیثاغورس در مثلثات توسط دایره واحد

قضیه فیثاغورس در مثلثات را اثبات کنید.

یکی از روش‌های اثبات قضیه فیثاغورس در مثلثات، استفاده از دایره واحد است. این دایره و یکی از نقاط روی آن را در نظر بگیرید. از روی نقطه انتخابی، خطی را بر محور x عمود کرده و نقطه را به مرکز مختصات وصل می‌کنیم.

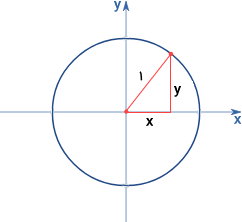
اثبات قضیه فیثاغورس در مثلثات توسط دایره واحد

بر اساس قضیه فیثاغورس در مثلث قائم‌الزاویه، می‌دانیم:

$$ x ^ ۲ + y ^ ۲ = ۱ $$

می‌دانیم که مختصات x هر نقطه از دایره واحد برابر با سینوس زاویه آن نقطه بر روی کمان دایره است. از طرفی، مختصات y هر نقطه از دایره واحد، با کسینوس زاویه آن نقطه بر روی کمان دایره برابری می‌کند. به این ترتیب داریم:

$$ x = \cos ( \theta ) $$

$$ y = \sin ( \theta ) $$

به جای x و y، معادل مثلثاتی آن‌ها را در قضیه فیثاغورس قرار می‌دهیم:

$$ \sin ^ ۲ ( \theta ) + \cos ^ ۲ ( \theta ) = ۱ $$

در نتیجه، رابطه فیثاغورس در مثلثات به کمک دایره واحد اثبات می‌شود.

بیان قوانین مثلثات به صورت نسبت های معکوس

اغلب نسبت‌های مثلثاتی اصلی را می‌توان به صورت عکس نسبت‌های دیگر بیان کرد. به عنوان مثال، تانژانت یک زاویه، با عکس کتانژانت آن برابری می‌کند.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

مهم‌ترین روابط عکس در قوانین مثلثات عبارت هستند از:

$$ \csc ( \theta ) = \frac { ۱ } { \sin ( \theta ) } $$

$$ \sec ( \theta ) = \frac { ۱ } { \cos ( \theta ) } $$

$$ \cot ( \theta ) = \frac { ۱ } { \tan ( \theta ) } $$

$$ \tan ( \theta ) = \frac { ۱ } { \cot ( \theta ) } $$

$$ \sin ( \theta ) = \frac { ۱ } { \csc ( \theta ) } $$

$$ \cos ( \theta ) = \frac { ۱ } { \sec ( \theta ) } $$

تمام روابط بالا، به راحتی و با مقایسه تعاریف قوانین اصلی مثلثات اثبات می‌شوند. به عنوان مثال، در مثلث قائم‌الزاویه، سینوس یک زاویه برابر با نسبت ضلع مقابل آن زاویه به وتر است:

$$ \sin \theta = \frac { O } { H } $$

O: ضلع مقابل به زاویه
H: وتر مثلث قائم‌الزاویه

نسبت بالا را عکس می‌کنیم:

$$
\frac { ۱ } { \sin \theta } = \frac { H } { O }
$$

بر اساس رابطه بالا، عکس سینوس یک زاویه، با نسبت وتر به ضلع مقابل آن زاویه برابری می‌کند. کسکانت یک زاویه نیز به صورت نسبت وتر به ضلع مقابل آن زاویه تعریف می‌شود:

$$
\csc \theta = \frac { H } { O }
$$

در نتیجه، کسکانت یک زاویه با سینوس آن زاویه برابر است:

$$
\csc \theta = \frac { ۱ } { \sin \theta }
$$

علاوه بر روابط معرفی شده، روابط دیگری نیز بین توابع مثلثاتی وجود دارد. به عنوان مثال، تانژانت یک زاویه، با تقسیم سینوس بر کسینوس آن زاویه برابری می‌کند:

$$ \tan ( \theta ) = \frac { \sin ( \theta ) } { \cos ( \theta ) } $$

برای تانژانت یک زاویه نیز داریم:

$$ \cot ( \theta ) = \frac { \cos ( \theta ) } { \sin ( \theta ) } $$

مثال ۴: محاسبه کتانژانت یک زاویه از روی تانژانت

تانژانت زاویه ۲۶/۵۷ درجه، تقریبا برابر با ۰/۵ است. کتانژانت این زاویه چند درجه است؟

برای به دست آوردن کتانژانت یک زاویه از روی تانژانت آن، از قوانین نسبت های معکوس در مثلثات استفاده می‌کنیم. بر اساس این قوانین، کتانژانت هر زاویه برابر با نسبت معکوس تانژانت همان زاویه است. بنابراین، داریم:

$$ \cot ۲۶/۵۷ ^ { \circ } = \frac { ۱ } { \tan ۲۶/۵۷ ^ { \circ } } $$

$$ \cot ۲۶/۵۷ ^ { \circ } = \frac { ۱ } { ۰/۵ } $$

$$ \cot ۲۶/۵۷ ^ { \circ } = \frac { ۱ } { \frac { ۱ } { ۲ } } $$

$$ \cot ۲۶/۵۷ ^ { \circ } = ۲ $$

در نتیجه، کتانژانت زاویه ۲۶/۵۷ درجه، تقریبا برابر با ۲ است.

مثال ۵: اثبات روابط مثلثاتی با استفاده از قوانین مثلثات

رابطه مثلثاتی زیر را اثبات کنید:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \csc \; ( \theta ) ~ \cot \; ( \theta )
$$

در رابطه بالا، عبارت سمت چپ، پیچیده‌تر از عبارت سمت راست است. بنابراین، اثبات رابطه مثلثاتی را با ساده‌سازی عبارت سمت چپ شروع می‌کنیم. می‌دانیم که:

$$ ۱ + \cot ^ 2 ( \theta ) = \csc ^ ۲ ( \theta ) $$

بنابراین، داریم:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \frac{ \csc ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~
$$

$$ \csc ^ ۲ \; ( \theta ) $$ را به صورت حاصل‌ضرب دو کسکانت می‌نویسیم:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \frac{ \csc \; ( \theta ) \cdot \csc \; ( \theta ) } { \sec \; ( \theta ) } ~
$$

بر اساس قوانین نسبت‌های معکوس در مثلثات، کسکانت یک زاویه، با نسبت معکوس سینوس همان زاویه برابر است. از این‌رو، یکی از کسکانت‌های صورت را به نسبت معکوس سینوس تبدیل می‌کنیم:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \frac{ \csc \; ( \theta ) \cdot \frac{ ۱ } { \sin \; ( \theta ) } } { \sec \; ( \theta ) } ~
$$

سکانت یک زاویه نیز با عکس کسینوس برابر است:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \frac{ \csc \; ( \theta ) \cdot \frac{ ۱ } { \sin \; ( \theta ) } } { \frac{ ۱ } { \cos \; ( \theta ) } } ~
$$

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \csc \; ( \theta ) \cdot \frac{ { \cos \; ( \theta ) } } { \sin \; ( \theta ) }
$$

نسبت کسینوس به سینوس یک زاویه، با کتانژانت آن زاویه برابری می‌کند:

$$
\frac{۱ ~ + ~ \cot ^ ۲ \; ( \theta ) } { \sec \; ( \theta ) } ~ = ~ \csc \; ( \theta ) \cot \; ( \theta )
$$

به این ترتیب، رابطه مثلثاتی خواسته شده اثبات می‌شود.

جدول نسبت های مثلثاتی زوایای معروف

هنگام حل مسائل مثلثاتی، به احتمال زیاد به زوایایی نظیر ۰، ۳۰، ۴۵، ۶۰ و ۹۰ درجه، برخورد خواهید کرد. این زوایا به همراه زوایای متمم و مکمل آن‌ها، کاربرد زیادی در مثلثات دارند. به همین دلیل، به عنوان زوایای معروف مثلثاتی شناخته می‌‌شوند.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی

جدول زیر، مقدار عددی نسبت‌های مثلثاتی زوایای معروف در ربع اول دایره واحد را نمایش می‌دهد.

-	۰ درجه	۳۰ درجه یا $$ \frac { \pi }{ ۶ } $$	۴۵ درجه یا $$ \frac { \pi }{ ۴ } $$	۶۰ درجه یا $$ \frac { \pi }{ ۳ } $$	۹۰ درجه یا $$ \frac { \pi }{ ۲ } $$
$$ \sin \theta $$	$$ ۰ $$	$$ \frac { ۱ }{ ۲ } $$	$$ \frac { ۱ }{ \sqrt { ۲ } } $$	$$ \frac { \sqrt { ۳ } }{ ۲ } $$	۱
$$ \cos \theta $$	۱	$$ \frac { \sqrt { ۳ } }{ ۲ } $$	$$ \frac { ۱ }{ \sqrt { ۲ } } $$	$$ \frac { ۱ }{ ۲ } $$	۰
$$ \tan \theta $$	۰	$$ \frac { ۱ }{ \sqrt { ۳ } } $$	۱	$$ \sqrt { ۳ } $$	تعریف نشده
$$ \cot \theta $$	تعریف نشده	$$ \sqrt { ۳ } $$	۱	$$ \frac { ۱ }{ \sqrt { ۳ } } $$	۰
$$ \csc \theta $$	تعریف نشده	۲	$$ \sqrt { ۲ } $$	$$ \frac { ۲ }{ \sqrt { ۳ } } $$	۱
$$ \sec \theta $$	۱	$$ \frac { ۲ }{ \sqrt { ۳ } } $$	$$ \sqrt { ۲ } $$	۲	تعریف نشده

مقادیر عددی نسبت‌های مثلثاتی زوایای معروف در ربع دوم دایره واحد در جدول زیر آورده شده‌اند.

-	۱۲۰ درجه یا $$ \frac { ۲ \pi }{ ۳ } $$	۱۳۵ درجه یا $$ \frac { ۳ \pi }{ ۴ } $$	۱۵۰ درجه یا $$ \frac { ۵ \pi }{ ۶ } $$	۱۸۰ درجه یا $$ \pi $$
$$ \sin \theta $$	$$ \frac { \sqrt { ۳ } }{ ۲ } $$	$$ \frac { \sqrt { ۲ } }{ ۲ } $$	$$ \frac { ۱ }{ ۲ } $$	۰
$$ \cos \theta $$	$$ - \frac { ۱ }{ ۲ } $$	$$ - \frac { \sqrt { ۲ } }{ ۲ } $$	$$ - \frac { \sqrt { ۳ } }{ ۲ } $$	۱-
$$ \tan \theta $$	$$ - \sqrt { ۳ } $$	۱-	$$ - \frac { ۱ }{ \sqrt { ۳ } } $$	۰
$$ \cot \theta $$	$$ - \frac { ۱ }{ \sqrt { ۳ } } $$	۱-	$$ - \sqrt { ۳ } $$	تعریف نشده
$$ \csc \theta $$	$$ \frac { ۲ }{ \sqrt { ۳ } } $$	$$ \frac { ۲ }{ \sqrt { ۲ } } $$	۲	تعریف نشده
$$ \sec \theta $$	۲-	$$ - \frac { ۲ }{ \sqrt { ۲ } } $$	$$ - \frac { ۲ }{ \sqrt { ۳ } } $$	۱-

نسبت‌های مثلثاتی زوایای معروف در ربع سوم دایره واحد برابر با مقادیر آورده شده در جدول زیر هستند.

-	۲۱۰ درجه یا $$ \frac { ۷ \pi }{ ۶ } $$	۲۲۵ درجه یا $$ \frac { ۵ \pi }{ ۴ } $$	۲۴۰ درجه یا $$ \frac { ۴ \pi }{ ۳ } $$	۲۷۰ درجه یا $$ \frac { ۳ \pi }{ ۲ } $$
$$ \sin \theta $$	$$ - \frac { ۱ }{ ۲ } $$	$$ - \frac { \sqrt { ۲ } }{ ۲ } $$	$$ - \frac { \sqrt { ۳ } }{ ۲ } $$	۱-
$$ \cos \theta $$	$$ - \frac { \sqrt { ۳ } }{ ۲ } $$	$$ - \frac { \sqrt { ۲ } }{ ۲ } $$	$$ - \frac { ۱ }{ ۲ } $$	۰
$$ \tan \theta $$	$$ \frac { ۱ }{ \sqrt { ۳ } } $$	۱	$$ \frac { ۱ }{ \sqrt { ۳ } } $$	تعریف نشده
$$ \cot \theta $$	$$ \sqrt { ۳ } $$	۱	$$ \frac { ۱ }{ \sqrt { ۳ } } $$	۰
$$ \csc \theta $$	۲-	$$ - \frac { ۲ }{ \sqrt { ۲ } } $$	$$ - \frac { ۲ }{ \sqrt { ۳ } } $$	۱-
$$ \sec \theta $$	$$ \frac { ۲ }{ \sqrt { ۳ } } $$	$$ - \frac { ۲ }{ \sqrt { ۲ } } $$	۲	تعریف نشده

مقادیر نسبت‌های مثلثاتی زوایای معروف در ربع چهارم دایره واحد نیز در جدول زیر نشان داده شده‌اند.

-	۳۰۰ درجه یا $$ \frac { ۵ \pi }{ ۳ } $$	۳۱۵ درجه یا $$ \frac { ۷ \pi }{ ۴ } $$	۳۳۰ درجه یا $$ \frac { ۱۱ \pi }{ ۶ } $$	۳۶۰ درجه یا $$ ۲ \pi $$
$$ \sin \theta $$	$$ - \frac { \sqrt { ۳ } }{ ۲ } $$	$$ - \frac { \sqrt { ۲ } }{ ۲ } $$	$$ - \frac { ۱ }{ ۲ } $$	۰
$$ \cos \theta $$	$$ \frac { ۱ }{ ۲ } $$	$$ \frac { \sqrt { ۲ } }{ ۲ } $$	$$ \frac { \sqrt { ۳ } }{ ۲ } $$	۱
$$ \tan \theta $$	$$ - \sqrt { ۳ } $$	۱-	$$ - \frac { ۱ }{ \sqrt { ۳ } } $$	۰
$$ \cot \theta $$	$$ - \frac { ۱ }{ \sqrt { ۳ } } $$	۱-	$$ - \sqrt { ۳ } $$	تعریف نشده
$$ \csc \theta $$	$$ - \frac { ۲ }{ \sqrt { ۳ } } $$	$$ - \frac { ۲ }{ \sqrt { ۲ } } $$	۲-	تعریف نشده
$$ \sec \theta $$	۲	$$ \frac { ۲ }{ \sqrt { ۲ } } $$	$$ \frac { ۲ }{ \sqrt { ۳ } } $$	۱

به خاطر سپردن زوایا و مقادیر نسبت‌های مثلثاتی آورده شده در جداول بالا، کار دشواری نیست. علاوه بر این موارد، زوایای دیگری وجود دارند که معمولا به طور مستقیم یا غیرمستقیم در مسائل مختلف ظاهر می‌شوند. زوایای ۹، ۱۵، ۲۲/۵، ۱۸، ۳۶ و ۳۷ درجه، از زوایای پرکاربرد در مسائل ریاضی به شمار می‌روند. سینوس این زوایا برابر است با:

$$ \sin ۹ ^ { \circ } = \displaystyle \frac { \sqrt { ۳ + \sqrt ۵ } - \sqrt { ۵ - \sqrt ۵ } } { ۴ } $$

$$ \sin ۱۵ ^ { \circ } = \displaystyle \frac { \sqrt ۳ - ۱ } { ۲ \sqrt ۲ } $$

$$ \sin ۱۸ ^ { \circ } = \displaystyle \frac { \sqrt ۵ - ۱ } { ۴ } $$

$$ \sin ۲۲/۵ ^ { \circ } = \displaystyle \frac { ۱ } { ۲ } ( \sqrt { ۲ - \sqrt ۲ } ) $$

$$ \sin ۳۶ ^ { \circ } = \displaystyle \frac { \sqrt { ۱۰ + ۲ \sqrt ۵ } } { ۴ } $$

$$ \sin ۳۷ ^ { \circ } \approx \displaystyle \frac { ۳ } { ۵ } $$

قوانین مثلثات برای زاویه منفی

نسبت‌های مثلثاتی یک زاویه با نسبت‌های مثلثاتی مقدار منفی همان زاویه، رابطه دارند.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی

قوانین مثلثات برای قرینه یک زاویه (مقدار منفی زاویه) به صورت زیر تعریف می‌شوند:

$$
\sin ( { - \theta } ) = - \sin { \theta }
$$

$$
\cos ( { - \theta } ) = \cos { \theta }
$$

$$
\tan ( { - \theta } ) = - \tan { \theta }
$$

$$
\cot ( { - \theta } ) = - \cot { \theta }
$$

$$
\sec ( { - \theta } ) = \sec { \theta }
$$

$$
\csc ( { - \theta } ) = - \csc { \theta }
$$

جهت اندازه‌گیری زاویه در دایره مثلثاتی، پادساعتگرد (خلاف جهت حرکت عقربه‌های ساعت) است. بنابراین اگر بخواهیم زاویه منفی را در دایره واحد نمایش دهیم، به اندازه مقدار مثبت آن در جهت ساعتگرد حرکت می‌کنیم. به عنوان مثال، زاویه منفی ۳۰ درجه را در نظر بگیرید.

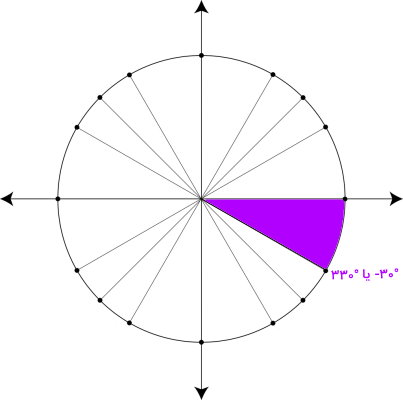
اگر زاویه دایره را در جهت پادساعتگرد اندازه بگیریم، زاویه منفی ۳۰ درجه بر روی زاویه ۳۳۰ درجه در ربع چهارم منطبق می‌شود. این زاویه، قرینه زاویه ۳۰ درجه در ربع اول است. با نگاه کردن به مقادیر این زوایا (۳۰ درجه و منفی ۳۰ درجه) در جدول مقادیر نسبت‌های مثلثاتی زوایای معروف می‌توانید روابط ارائه شده در این بخش را اعتبارسنجی کنید. به عنوان مثال، سینوس زاویه ۳۰ درجه برابر با $$ \frac { ۱ } { ۲ } $$ و سینوس زاویه ۳۳۰ درجه برابر با $$ - \frac { ۱ } { ۲ } $$ است. بنابراین:

$$
\sin ( { - ۳۰ ^ { \circ } } ) = - \sin { ۳۰ ^ { \circ } }
$$

قوانین مثلثات برای زوایای تناوبی

یکی از قوانین جالب در مثلثات این است که با تغییر زاویه‌های یک تابع به اندازه مشخص، به تابع دیگر می‌رسیم. این زاویه‌ها، معمولا مضربی از $$ \pi $$ یا $$ \frac { \pi } { ۲ } $$ هستند.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد

به عنوان مثال، برای سینوس و کسینوس زاویه‌ای که به اندازه $$ \frac { \pi } { ۲ } $$ با یک زاویه مشخص اختلاف دارد، روابط زیر تعریف می‌شوند:

$$ \sin ( \frac { \pi } { ۲ } - \theta ) = + \cos ( \theta ) $$

$$ \cos ( \frac { \pi } { ۲ } - \theta ) = + \sin ( \theta ) $$

$$ \sin ( \frac { \pi } { ۲ } + \theta ) = + \cos ( \theta ) $$

$$ \cos ( \frac { \pi } { ۲ } + \theta ) = - \sin ( \theta ) $$

به زاویه $$ \frac { \pi } { ۲ } $$ در روابط بالا، دوره تناوب می‌گویند. به همین دلیل، این روابط با عنوان «اتحادهای تناوبی » (Periodicity Identities) نیز شناخته می‌شوند. یکای زاویه در اتحادهای تناوبی، رادیان است. تمام قوانین مثلثات، ماهیت چرخه‌ای یا تناوبی دارند. این قوانین بعد از یک تناوب مشخص، خود را تکرار می‌کنند. اگر دوره تناوب نسبت‌های مثلثاتی را برابر با $$ \pi $$ یا ۱۸۰ درجه در نظر بگیریم، به روابط زیر می‌رسیم:

$$
\sin ( \pi - \theta ) = + \sin ( \theta )
$$

$$
\cos ( \pi - \theta ) = - \cos ( \theta )
$$

$$
\sin ( \pi + \theta ) = - \sin ( \theta )
$$

$$
\cos ( \pi + \theta ) = - \cos ( \theta )
$$

اتحادهای تناوبی برای دوره تناوب $$ \frac { ۳ \pi } { ۲ } $$ یا ۲۷۰ درجه عبارت هستند از:

$$ \sin ( \frac { ۳ \pi } { ۲ } - \theta ) = - \cos ( \theta ) $$

$$ \cos ( \frac { ۳ \pi } { ۲ } - \theta ) = - \sin ( \theta ) $$

$$ \sin ( \frac { ۳ \pi } { ۲ } + \theta ) = - \cos ( \theta ) $$

$$ \cos ( \frac { ۳ \pi } { ۲ } + \theta ) = + \sin ( \theta ) $$

روابط سینوس و کسینوس با دوره تناوب $$ ۲ \pi $$ یا ۳۶۰ درجه نیز به صورت زیر نوشته می‌شوند:

$$
\sin ( ۲ \pi - \theta ) = - \sin ( \theta )
$$

$$
\cos ( ۲ \pi - \theta ) = + \cos ( \theta )
$$

$$
\sin ( ۲ \pi + \theta ) = + \sin ( \theta )
$$

$$
\cos ( ۲ \pi + \theta ) = + \cos ( \theta )
$$

پس از دوران به اندازه $$ ۲ \pi $$ یا ۳۶۰ درجه، زاویه به محل اولیه خود در دایره مثلثاتی بازمی‌گردد. بنابراین، مقدار نسبت مثلثاتی، هیچ تغییری نمی‌کند. در صورت جمع زاویه با $$ ۲ \pi $$ یا مضرب زوج $$ ۲ \pi $$ (مانند $$ ۴ \pi $$، $$ ۶ \pi $$ و غیره) جمع شود، تغییری در مقدار نسبت مثلثاتی رخ نخواهد داد.

$$
\sin ( \theta \pm ۲ k \pi ) = \sin ( \theta )
$$

$$
\cos ( \theta \pm ۲ k \pi ) = \cos ( \theta )
$$

$$
\csc ( \theta \pm ۲ k \pi ) = \csc ( \theta )
$$

$$
\sec ( \theta \pm ۲ k \pi ) = \sec ( \theta )
$$

$$
\tan ( \theta \pm k \pi ) = \tan ( \theta )
$$

$$
\cot ( \theta \pm k \pi ) = \cot ( \theta )
$$

قوانین اتحادهای تناوبی مثلثات را با مقادیر نسبت‌های مثلثاتی زوایای معروف مقایسه کنید. پس از مقایسه، متوجه تکرار مقدار نسبت‌های مثلثاتی یک زاویه در بازه‌های مشخص خواهید شد.

مثال ۶: محاسبه توابع مثلثاتی با استفاده از اتحادهای تناوبی

عبارت زیر را ساده کنید:

$$
\frac { ۱ - \cos ^ ۲ ( ۷ \pi + \theta ) } { \cos ^ ۲ ( - ۸ \pi - \theta ) }
$$

برای ساده‌سازی عبارت بالا، هر یک از نسبت‌های مثلثاتی آن را به طور جداگانه در نظر بگیرید. بر اساس قوانین تناوب زاویه‌ها در مثلثات، اگر دوره تناوب یک نسبت مثلثاتی، مضربی از $$ ۲ \pi $$ باشد، می‌توان دوره تناوب را حذف کرد. نسبت مثلثاتی صورت کسر برابر است با:

$$
\cos ^ ۲ ( ۷ \pi + \theta )
$$

دوره تناوب زاویه θ در عبارت، مضرب فردی از $$ \pi $$ است. بنابراین، می‌توانیم کسینوس را به شکل زیر بازنویسی می‌کنیم:

$$
\cos ^ ۲ ( ۷ \pi + \theta ) = \cos ^ ۲ ( ۶ \pi + \pi + \theta )
$$

با توجه به توضیحات قبلی، داریم:

$$
\cos ^ ۲ ( ۶ \pi + \pi + \theta ) = \cos ^ ۲ ( \pi + \theta )
$$

بر اساس قوانین مثلثات، می‌دانیم:

$$
\cos ( \pi + \theta ) = - \cos ( \theta )
$$

بنابراین:

$$
\cos ( \pi + \theta ) \cdot \cos ( \pi + \theta ) = \left ( - \cos ( \theta ) \right ) \cdot \left ( - \cos ( \theta ) \right )
$$

$$
\cos ( \pi + \theta ) ^ ۲ = \cos ^ ۲ ( \theta )
$$

به این ترتیب، برای صورت کسر داریم:

$$
۱ - \cos ^ ۲ ( ۷ \pi + \theta ) = ۱ - \cos ^ ۲ ( \theta )
$$

اکنون به سراغ مخرج کسر می‌رویم. مخرج کسر عبارت است از:

$$
\cos ^ ۲ ( - ۸ \pi - \theta )
$$

این عبارت را به صورت زیر بازنویسی می‌کنیم:

$$
\cos ^ ۲ ( - ( ۸ \pi + \theta ))
$$

بر اساس قوانین مثلثات برای زوایای منفی، می‌دانیم که کسینوس یک زاویه منفی، با کسینوس مقدار مثبت همان زاویه برابری می‌کند. از این‌رو:

$$
\cos ^ ۲ ( - ( ۸ \pi + \theta )) = \cos ^ ۲ ( ۸ \pi + \theta )
$$

$$
\cos ^ ۲ ( - ۸ \pi - \theta ) = \cos ^ ۲ ( ۸ \pi + \theta )
$$

در عبارت بالا، زاویه θ با مضرب زوج $$ \pi $$‌ جمع شده است. بنابراین:

$$
\cos ^ ۲ ( ۸ \pi + \theta ) = \cos ^ ۲ ( \theta )
$$

$$
\cos ^ ۲ ( - ۸ \pi - \theta ) = \cos ^ ۲ ( \theta )
$$

اکنون، فرم ساده شده عبارت‌های مثلثاتی را در صورت و مخرج کسر قرار می‌دهیم:

$$
\frac { ۱ - \cos ^ ۲ ( ۷ \pi + \theta ) } { \cos ^ ۲ ( - ۸ \pi - \theta ) } = \frac { ۱ - \cos ^ ۲ ( \theta ) } { \cos ^ ۲ ( \theta ) }
$$

با توجه به قضیه فیثاغورس در مثلثات، داریم:

$$ \sin ^ ۲ ( \theta ) + \cos ^ ۲ ( \theta ) = ۱ $$

عبارت‌های این رابطه را به صورت زیر جابجا می‌کنیم:

$$
\sin ^ ۲ ( \theta ) = ۱ - \cos ^ ۲ ( \theta )
$$

با استفاده از رابطه بالا می‌توانیم صورت کسر را دوباره ساده کنیم:

$$
\frac { ۱ - \cos ^ ۲ ( \theta ) } { \cos ^ ۲ ( \theta ) } = \frac { \sin ^ ۲ ( \theta ) } { \cos ^ ۲ ( \theta ) }
$$

$$
\frac { ۱ - \cos ^ ۲ ( ۷ \pi + \theta ) } { \cos ^ ۲ ( - ۸ \pi - \theta ) } = \frac { \sin ^ ۲ ( \theta ) } { \cos ^ ۲ ( \theta ) }
$$

حاصل تقسیم سینوس بر کسینوس، برابر با تانژانت است. در نهایت به رابطه زیر می‌رسیم:

$$
\frac { ۱ - \cos ^ ۲ ( ۷ \pi + \theta ) } { \cos ^ ۲ ( - ۸ \pi - \theta ) } = \tan ^ ۲ ( \theta )
$$

در این مثال، با استفاده از قوانین مثلثات، یک رابطه به ظاهر پیچیده را به یک رابطه ساده تبدیل کردیم. این نوع ساده‌سازی‌ها، باعث بهبود عملکرد ابزارهای محاسباتی و افزایش سرعت آن‌ها می‌شود.

قوانین مثلثات برای زوایای متمم، مکمل و مقابل

به زوایایی که مجموع آن‌ها برابر با ۹۰ درجه شود، زوایای متمم می‌گویند. در یک مثلث قائم‌الزاویه، دو زاویه حاده، متمم یکدیگرند.

فیلم آموزش ریاضی پایه دانشگاهی

اگر یکی از این زاویه‌ها را برابر با θ در نظر بگیریم، خواهیم داشت:

۹۰° = متمم زاویه θ + زاویه θ

$$ ۹۰ ^ { \circ } - \theta $$ = متمم زاویه θ

قوانین مثلثات برای زوایای متمم عبارت هستند از:

$$
\sin { ( ۹۰ ^ { \circ } - \theta ) } = \cos { \theta }
$$

$$
\cos { ( ۹۰ ^ { \circ } - \theta ) } = \sin { \theta }
$$

$$
\tan { ( ۹۰ ^ { \circ } - \theta ) } = \cot { \theta }
$$

$$
\cot { ( ۹۰ ^ { \circ } - \theta ) } = \tan { \theta }
$$

$$
\csc { ( ۹۰ ^ { \circ } - \theta ) } = \sec { \theta }
$$

$$
\sec { ( ۹۰ ^ { \circ } - \theta ) } = \csc { \theta }
$$

قوانین متعددی را می‌توانیم از روابط بالا استخراج کنیم. به عنوان مثال، سینوس یکی از زوایای حاده مثلث قائم‌الزاویه با کسینوس دیگر زاویه حاده برابری می‌کند.

قوانین مثلثات برای زوایای مکمل

زوایایی که جمع آن‌ها برابر با ۱۸۰ درجه باشد نیز با عنوان زوایای مکمل شناخته می‌شوند. اگر جمع زاویه θ با زاویه دیگر برابر با ۱۸۰ درجه شود، رابطه مکمل آن به صورت زیر نوشته می‌شود:

۱۸۰° = مکمل زاویه θ + زاویه θ

$$ ۱۸۰ ^ { \circ } - \theta $$ = مکمل زاویه θ

قوانین مثلثات برای زوایای مکمل عبارت هستند از:

$$
\sin { ( ۱۸۰ ^ { \circ } - \theta ) } = \sin{ \theta }
$$

$$
\cos { ( ۱۸۰ ^ { \circ } - \theta ) } = - \cos{ \theta }
$$

$$
\tan { ( ۱۸۰ ^ { \circ } - \theta ) } = - \tan { \theta }
$$

$$
\cot { ( ۱۸۰ ^ { \circ } - \theta ) } = - \cot { \theta }
$$

$$
\csc { ( ۱۸۰ ^ { \circ } - \theta ) } = \csc{ \theta }
$$

$$
\sec { ( ۱۸۰ ^ { \circ } - \theta ) } = - \sec{ \theta }
$$

قوانین مثلثات برای زوایای مقابل

به زوایایی که مجموع آن‌ها برابر با ۳۶۰ درجه باشد، «زوایای مقابل» (Opposite Angles) می‌گویند. اگر جمع زاویه θ با زاویه دیگر برابر با ۳۶۰ درجه شود، برای رابطه مکمل آن خواهیم داشت:

۳۶۰° = مقابل زاویه θ + زاویه θ

$$ ۳۶۰ ^ { \circ } - \theta $$ = مقابل زاویه θ

قوانین مثلثات برای زوایای مقابل به صورت زیر نوشته می‌شوند:

$$ \sin { ( ۳۶۰ ^ { \circ } - \theta ) } = -\sin{ \theta } $$

$$ \cos { ( ۳۶۰ ^ { \circ } - \theta ) } = \cos{ \theta } $$

$$ \tan { ( ۳۶۰ ^ { \circ } - \theta ) } = - \tan { \theta } $$

$$ \cot { ( ۳۶۰ ^ { \circ } - \theta ) } = - \cot { \theta } $$

$$ \csc { ( ۳۶۰ ^ { \circ } - \theta ) } = - \csc{ \theta } $$

$$ \sec { ( ۳۶۰ ^ { \circ } - \theta ) } = \sec{ \theta } $$

مثال ۷: محاسبه کسینوس مکمل یک زاویه

کسینوس زاویه ۲۴۰ درجه را به دست بیاورید.

بهترین روش برای محاسبه کسینوس زاویه ۲۴۰ درجه، استفاده از قوانین مثلثات برای زوایای مکمل است. اختلاف زاویه ۲۴۰ درجه با زاویه ۶۰ درجه برابر با ۱۸۰ درجه می‌شود. بنابراین:

$$ ۲۴۰ ^ { \circ } - ۶۰ ^ { \circ } = ۱۸۰ ^ { \circ } $$

رابطه بالا را به صورت زیر بازنویسی می‌کنیم:

$$ ۲۴۰ ^ { \circ } + \left ( - ۶۰ ^ { \circ } \right ) = ۱۸۰ ^ { \circ } $$

در واقع، جمع زوایای ۶۰- و ۲۴۰ درجه برابر با ۱۸۰ درجه است. به عبارت دیگر، دو زاویه ۶۰- و ۲۴۰ درجه، مکمل یکدیگر هستند. بر اساس قوانین مثلثات برای زوایای مکمل، می‌دانیم:

$$
\cos { ( ۱۸۰ ^ { \circ } - \theta ) } = - \cos{ \theta }
$$

θ را برابر با ۶۰- درجه قرار می‌دهیم:

$$
\cos { ( ۱۸۰ ^ { \circ } - \left ( - ۶۰ ^ { \circ } \right ) ) } = - \cos{ \left ( - ۶۰ ^ { \circ } \right ) }
$$

$$
\cos { ( ۲۴۰ ^ { \circ } ) } = - \cos{ \left ( - ۶۰ ^ { \circ } \right ) }
$$

با توجه به قوانین مثلثات برای زاویه منفی، داریم:

$$ \cos ( { - \theta } ) = \cos { \theta } $$

$$
\cos{ \left ( - ۶۰ ^ { \circ } \right ) } = \cos{ \left ( ۶۰ ^ { \circ } \right ) }
$$

در نتیجه:

$$
\cos{ \left ( - ۶۰ ^ { \circ } \right ) } = \cos{ \left ( ۶۰ ^ { \circ } \right ) } = - \frac { ۱ } { ۲ }
$$

به این ترتیب، کسینوس ۲۴۰ درجه برابر با کسینوس ۶۰ درجه یا منفی یک‌دوم می‌شود.

قوانین جمع و تفریق زوایا در مثلثات

یکی دیگر از مهم‌ترین قوانین مثلثات، تابع جمع و تفریق دو زاویه است. روابط مرتبط با این نوع تابع، کاربرد زیادی در انجام محاسبات مثلثاتی دارند.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

مهم‌ترین قوانین جمع و تفریق زوایا در مثلثات عبارت هستند از:

$$
\sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta
$$

$$
\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta
$$

$$
\cos ( \alpha + \beta ) = \cos \alpha \cos \beta − \sin \alpha \sin \beta
$$

$$
\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta
$$

$$
\tan ( \alpha + \beta ) = \frac { \tan { \alpha } + \tan { \beta } } { ۱ - \tan { \alpha } \tan { \beta }}
$$

$$
\tan ( \alpha - \beta ) = \frac { \tan { \alpha } - \tan { \beta } } { ۱ + \tan { \alpha } \tan { \beta }}
$$

$$
\cot ( \alpha + \beta ) = \frac { \cot { \alpha } \cot { \beta } - ۱ } { \cot { \alpha } + \cot { \beta } }
$$

$$
\cot ( \alpha - \beta ) = \frac { \cot { \alpha } \cot { \beta } + ۱ } { \cot { \alpha } - \cot { \beta } }
$$

$$
\sec ( \alpha + \beta ) = \frac { \sec ( \alpha ) \sec ( \beta ) \csc ( \alpha ) \csc ( \beta ) } { \sec ( \alpha ) \sec ( \beta ) - \csc ( \alpha ) \csc ( \beta ) }
$$

$$
\sec ( \alpha - \beta ) = \frac { \sec ( \alpha ) \sec ( \beta ) \csc ( \alpha ) \csc ( \beta ) } { \sec ( \alpha ) \sec ( \beta ) + \csc ( \alpha ) \csc ( \beta ) }
$$

$$
\csc ( \alpha + \beta ) = \frac { \sec ( \alpha ) \sec ( \beta ) \csc ( \alpha ) \csc ( \beta ) } { \sec ( \alpha ) \sec ( \beta ) + \csc ( \alpha ) \csc ( \beta ) }
$$

$$
\csc ( \alpha +- \beta ) = \frac { \sec ( \alpha ) \sec ( \beta ) \csc ( \alpha ) \csc ( \beta ) } { \sec ( \alpha ) \sec ( \beta ) - \csc ( \alpha ) \csc ( \beta ) }
$$

مثال ۸: محاسبه تانژانت جمع دو زاویه

تانژانت زاویه $$ \frac { \pi } { ۶ } + \frac { \pi } { ۴ } $$ را به دست بیاورید.

تانژانت جمع دو زاویه، با استفاده از فرمول زیر به دست می‌آید:

$$
\tan ( \alpha + \beta ) = \frac { \tan \alpha + \tan \beta } { ۱ - \tan \alpha \tan \beta }
$$

فرض می‌کنیم:

$$ \frac { \pi } { ۶ } = \alpha $$

$$ \frac { \pi } { ۴ } = \beta $$

به این ترتیب داریم:

$$
\tan \left ( \frac { \pi } { ۶ } + \frac { \pi } { ۴ } \right ) = \frac { \tan \left ( \frac { \pi } { ۶ } \right ) + \tan \left ( \frac { \pi } { ۴ } \right ) } { ۱ - \left ( \tan \left ( \frac { \pi } { ۶ } \right ) \right ) \left ( \tan \left ( \frac { \pi } { ۴ } \right ) \right ) }
$$

برای دو زاویه $$ \frac { \pi } { ۶ } $$ و $$ \frac { \pi } { ۶ } $$، داریم:

$$ \tan ( \frac { \pi } { ۶ } ) = \frac { ۱ } { \sqrt { ۳ } } $$

$$ \tan ( \frac { \pi } { ۴ } ) = \frac { ۱ } { ۱ } $$

این مقادیر را در رابطه تانژانت جمع دو زاویه قرار می‌دهیم:

$$
\begin{aligned}
\tan \left ( \frac { \pi } { ۶ } + \frac { \pi } { ۴ } \right ) & = \frac { \frac { ۱ }{ \sqrt { ۳ } } + ۱ } { ۱ - \left ( \frac { ۱ } { \sqrt { ۳ } } \right ) ( ۱ ) } \\
& = \frac { \frac { ۱ + \sqrt { ۳ } } { \sqrt { ۳ } } } { \frac { \sqrt { ۳ } - ۱ } { \sqrt { ۳ } } } \\
& = \frac { ۱ + \sqrt { ۳ } } { \sqrt { ۳ } } \times \frac { \sqrt { ۳ } } { \sqrt { ۳ } - ۱ } \\
& = \frac { \sqrt { ۳ } + ۱ } { \sqrt { ۳ } - ۱ }
\end{aligned}
$$

مثال ۹: محاسبه سینوس جمع دو زاویه

حاصل عبارت $$ \sin \left ({ \cos } ^ { − ۱ } \frac { ۱ } { ۲ } + { \sin } ^ { −۱ } \frac { ۳ } { ۵ } \right ) $$ را به دستت بیاورید.

عبارت مورد سوال، با مسائلی که معمولا با آن‌ها مواجهه می‌شوید تفاوت دارد. در بخش زاویه سینوس، حاصل‌جمع دو تابع معکوس مثلثاتی آورده شده است. بر خلاف ظاهر مسئله، روش حل آن دشوار نیست. برای شروع حل، ابتدا هر یک از توابع معکوس را برابر با یک متغیر دلخواه قرار می‌دهیم. به منظور سادگی بیشتر، فرض می‌کنیم:

$$ { \cos } ^ { − ۱ } \frac { ۱ } { ۲ } = \alpha $$

$$ { \sin } ^ { −۱ } \frac { ۳ } { ۵ } = \beta $$

بر اساس قوانین مربوط به توابع معکوس مثلثاتی، می‌توان دریافت که کسینوس زاویه آلفا برابر با یک‌دوم است و در بازه ۰ تا π قرار دارد. سینوس زاویه بتا نیز برابر با سه‌پنجم است و در بازه π/۲- تا π/۲ قرار دارد. به عبارت دیگر:

$$
\begin{align*}
\cos \alpha & = \dfrac { ۱ } { ۲ } , \quad ۰ \leq \alpha \leq \pi \\[4pt] \sin \beta & = \dfrac { ۳ } { ۵ } , \quad - \dfrac { \pi } { ۲ } \leq \beta \leq \dfrac { \pi } { ۲ }\\[4pt] \end{align*}
$$

مطابق با قضیه فیثاغورس در مثلثات، برای سینوس و کسینوس زاویه آلفا داریم:

$$ \sin ^ ۲ ( \alpha ) + \cos ^ ۲ ( \alpha ) = ۱ $$

$$
\sin ^ ۲ ( \alpha ) = ۱ - \cos ^ ۲ ( \alpha )
$$

$$
\begin{align*}
\sin \alpha &= \sqrt{ ۱ - { \cos } ^ ۲ \alpha }\\[4pt] & = \sqrt { ۱ - \left ( \dfrac { ۱ } { ۲ } \right ) ^ ۲ }\\[4pt] & = \sqrt { ۱ - \dfrac {۱ } { ۴ } }\\[4pt] & = \sqrt { \dfrac { ۳ }{ ۴ } }\\[4pt] & = \dfrac { \sqrt {۳ } } { ۲ } \\[4pt] \end{align*}
$$

محاسبات بالا را برای سینوس و کسینوس زاویه بتا نیز تکرار می‌کنیم:

$$ \sin ^ ۲ ( \beta ) + \cos ^ ۲ ( \beta ) = ۱ $$

$$
\cos ^ ۲ ( \beta ) = ۱ - \sin ^ ۲ ( \beta )
$$

$$
\begin{align*}
\cos \beta &= \sqrt{ ۱ - { \sin } ^ ۲ \beta }\\[4pt] & = \sqrt { ۱ - \left ( \dfrac { ۳ } { ۵ } \right ) ^ ۲ }\\[4pt] & = \sqrt { ۱ - \dfrac { ۹ } { ۲۵ } }\\[4pt] & = \sqrt { \dfrac { ۱۶ }{ ۲۵ } }\\[4pt] & = \dfrac { ۴ } { ۵ } \\[4pt] \end{align*}
$$

با توجه به تغییر متغیر، عبارت مورد سوال را به صورت زیر بازنویسی می‌کنیم:

$$
\sin \left ({ \cos } ^ { − ۱ } \frac { ۱ } { ۲ } + { \sin } ^ { −۱ } \frac { ۳ } { ۵ } \right ) = \sin ( \alpha + \beta )
$$

می‌دانیم که سینوس جمع دو زاویه از رابطه زیر به دست می‌آید:

$$
\sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta
$$

تمام پارامترهای سمت راست رابطه بالا را داریم:

$$ \sin ( \alpha ) = \frac { \sqrt { ۳ } } { ۲ } $$

$$ \cos( \beta ) = \frac { ۴ } { ۵ } $$

$$ \cos( \alpha ) = \frac { ۱ } { ۲ } $$

$$ \sin ( \beta ) = \frac { \sqrt { ۳ } } { ۵ } $$

این مقادیر را در رابطه سینوس جمع دو زاویه قرار می‌دهیم:

$$
\begin{align*} \sin \left ( { \cos } ^ { - ۱ } \tfrac { ۱ } { ۲ } + { \sin } ^ { - ۱ }\tfrac { ۳ } { ۵ } \right ) & = \sin ( \alpha + \beta ) \\[4pt] & = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\[4pt] & = \left ( \dfrac { \sqrt { ۳ } } { ۲ } \times \dfrac { ۴ } { ۵ } \right ) + \left ( \dfrac { ۱ } { ۲ } \times \dfrac { ۳ } { ۵ } \right ) \\[4pt] & = \dfrac { ۴ \sqrt { ۳ } + ۳ } { ۱۰ } \\[4pt] & \approx ۰/۹۹۳ \end{align*}
$$

در نتیجه، $$ \sin \left ({ \cos } ^ { − ۱ } \frac { ۱ } { ۲ } + { \sin } ^ { −۱ } \frac { ۳ } { ۵ } \right ) $$، تقریبا برابر با ۰/۹۹۳ است.

قوانین مثلثات برای زوایای مضاعف

اگر اندازه زاویه‌ای را دو برابر کنیم، نسبت‌های مثلثاتی مرتبط با آن، بر اساس روابط مشخصی تغییر می‌کنند.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی

این روابط عبارت هستند از:

$$
\begin{align*} \sin ( ۲ \theta ) & = ۲ \sin ( \theta ) \cos ( \theta ) \\[4pt] & = \frac { ۲ \tan ( \theta ) } { ۱ + \tan ^ ۲ ( \theta ) } \end{align*}
$$

$$
\begin{align*} \cos ( ۲ \theta ) & = \cos ^ ۲ ( \theta ) - \sin ^ ۲ ( \theta ) \\[4pt] & = \frac { ۱ - \tan ^ ۲ ( \theta ) } { ۱ + \tan ^ ۲ ( \theta ) } \\[4pt] & =
۲ \cos ^ ۲ ( \theta ) - ۱ \\[4pt] & =
۱ - ۲ \sin ^ ۲ ( \theta ) \end{align*}
$$

$$
\begin{align*} \tan ( ۲ \theta ) & = \frac { ۲ \tan ^ ۲ ( \theta ) } { ۱ - \tan ^ ۲ ( \theta ) } \end{align*}
$$

$$
\begin{align*} \cot ( ۲ \theta ) & = \frac { \cot ^ ۲ ( \theta ) - ۱ } { ۲ \cot ( \theta )} \end{align*}
$$

$$
\sec ( ۲ \theta ) = \frac { \sec ^ { ۲ } ( \theta ) } { ۲ - \sec ^ { ۲ } ( \theta ) }
$$

$$
\csc ( ۲ \theta ) = \frac { \sec ( \theta ) \csc ( \theta ) } { ۲ }
$$

روابط بالا، برای مواقعی به کار می‌روند که نسبت‌های مثلثاتی یک زاویه را ندانیم اما بتوانیم آن زاویه را به صورت حاصل‌ضرب عدد ۲ در زاویه‌ای با نسبت‌های مثلثاتی معلوم بیان کنیم. در ادامه، این کاربرد را با حل یک مثال توضیح می‌دهیم.

مثال ۱۰: محاسبه توابع مثلثاتی با زاویه مضاعف

تانژانت زاویه‌ای برابر با $$ \theta = - \frac { ۳ } { ۴ } $$ است. اگر این زاویه در ربع دوم دایره مثلثاتی قرار داشته باشد، سینوس، کسینوس و تانژانت $$ ۲ \theta $$ چقدر است؟

بر اساس قوانین مثلثات می‌دانیم که تانژانت یک زاویه، نسبت ضلع مقابل به ضلع مجاور آن زاویه را نمایش می‌دهد. برای نشان دادن این نسبت، یک مثلث قائم‌الزاویه را در ربع دوم محورهای مختصات (در ربع قرارگیری زاویه تتا)، رسم می‌کنیم.

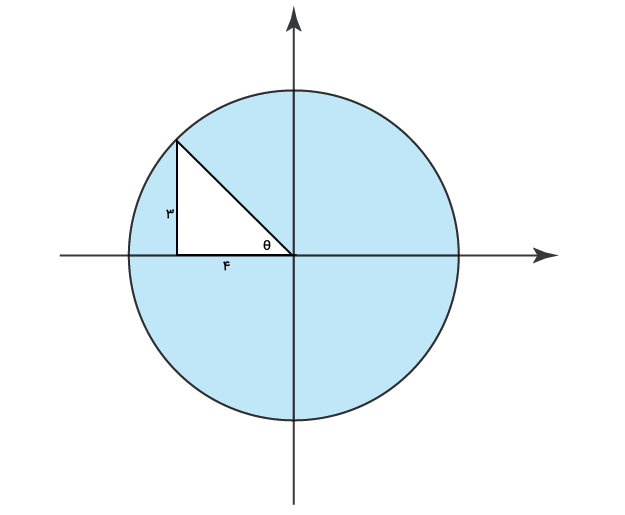
مثلث قائم الزاویه با زاویه θ و ضلع های 3 و 4

اندازه ضلع مقابل زاویه θ را برابر با ۳ و اندازه ضلع مجاور این زاویه را برابر با ۴ در نظر می‌گیریم. وتر مثلث قائم‌الزاویه، از قضیه فیثاغورس به دست می‌‌آید:

$$ c ^ ۲ = a ^ ۲ + b ^ ۲ $$

a و b، ساق‌های مثلث (ضلع‌های مقابل و مجاور θ) هستند. به این ترتیب:

$$ c ^ ۲ = ۳ ^ ۲ + ۴ ^ ۲ $$

$$ c ^ ۲ = ۹ + ۱۶ $$

$$ c ^ ۲ = ۲۵ $$

$$ c = ۵ $$

اکنون، اندازه تمام ضلع‌های مثلث قائم‌الزاویه را داریم. بنابراین، می‌توانیم به سراغ تعیین توابع مثلثاتی مورد سوال برویم. محاسبات خود را با تعیین سینوس زاویه مضاعف شروع می‌کنیم:

$$
\sin ( ۲ \theta ) = ۲ \sin ( \theta ) \cos ( \theta )
$$

بر اساس قوانین مثلثات، سینوس، نسبت ضلع مقابل (۳) به وتر (۵) و کسینوس، نسبت ضلع مجاور (۴)، به وتر (۵) است. از این‌رو، داریم:

$$ \sin ( \theta ) = \frac { ۳ } { ۵ } $$

$$ \cos ( \theta ) = - \frac { ۴ } { ۵ } $$

نکته مهم در نسبت‌های بالا، اضافه کردن علامت منفی به پشت مقدار کسینوس است. علامت منفی، به دلیل قرارگیری زاویه θ در ربع دوم به جواب کسینوس اضافه می‌شود. مقادیر بالا را در رابطه سینوس زاویه مضاعف قرار می‌دهیم:

$$
\sin ( ۲ \theta ) = ۲ ( \frac { ۳ }{ ۵ } ) ( - \frac { ۴ }{ ۵ } )
$$

$$
\sin ( ۲ \theta ) = - \frac { ۲ \times ۳ \times ۴ }{ ۵ \times ۵ }
$$

$$
\sin ( ۲ \theta ) = - \frac { ۲۴ }{ ۲۵ }
$$

رابطه کسینوس زاویه مضاعف عبارت است از:

$$
\cos ( ۲ \theta ) = { \cos } ^ ۲ ( \theta ) − { \sin } ^ ۲ ( \theta )
$$

مقادیر سینوس و کسینوس زاویه θ را در داخل این رابطه جایگذاری می‌کنیم:

$$
\cos ( ۲ \theta ) = ( - \frac { ۴ }{ ۵ } ) ^ ۲ − ( \frac { ۳ }{ ۵ } ) ^ ۲
$$

$$
\cos ( ۲ \theta ) = \frac { ۱۶ }{ ۲۵ } − \frac { ۹ }{ ۲۵ }
$$

$$
\cos ( ۲ \theta ) = \frac { ۱۶ - ۹ }{ ۲۵ }
$$

$$
\cos ( ۲ \theta ) = \frac { ۷ }{ ۲۵ }
$$

رابطه تانژانت زاویه مضاعف، به صورت زیر نوشته می‌شود:

$$
\tan ( ۲ \theta ) = \dfrac { ۲ \tan ( \theta ) } { ۱ − { \tan } ^ ۲ ( \theta ) }
$$

می‌دانیم که تانژانت یک زاویه، با نسبت سینوس به کسینوس آن زاویه برابر است. بنابراین:

$$ \tan ( \theta ) = \frac { \sin ( \theta ) }{ \cos ( \theta ) } $$

$$
\tan ( \theta ) = \frac { \frac { ۳ }{ ۵ } }{ - \frac { ۴ }{ ۵ } } = - \frac { ۳ }{ ۴ }
$$

این مقدار درون رابطه تانژانت زاویه مضاعف قرار می‌دهیم:

$$
\tan ( ۲ \theta ) = \dfrac { ۲ \left ( - \frac { ۳ }{ ۴ } \right ) } { ۱ − \left ( - \frac { ۳ }{ ۴ } \right ) ^ ۲ }
$$

$$
\tan ( ۲ \theta ) = \dfrac { - \frac { ۲ \times ۳ }{ ۴ }} { ۱ − \frac { ۹ }{ ۱۶ } }
$$

$$
\tan ( ۲ \theta ) = \dfrac { - \frac { ۶ }{ ۴ }} { \frac { ۷ }{ ۱۶ } }
$$

$$
\tan ( ۲ \theta ) = - \frac { ۶ \times ۱۶ }{ ۴ \times ۷}
$$

$$
\tan ( ۲ \theta ) = - \frac { ۶ \times ۴ }{ ۷}
$$

$$
\tan ( ۲ \theta ) = - \frac { ۲۴ }{ ۷}
$$

قوانین مثلثات برای سه برابر یک زاویه

روابط مثلثاتی برای سه برابر یک زاویه، به صورت زیر نوشته می‌شوند:

$$
\sin ( ۳ \theta ) = ۳ \sin ( \theta ) - ۴ \sin ^ ۳ ( \theta )
$$

$$
\cos ( ۳ \theta ) = ۴ \cos ^ ۳ ( \theta ) - ۳ \cos ( \theta )
$$

$$
\tan ( ۳ \theta ) = \frac { ۳ \tan ( \theta ) - \tan ^ ۳ ( \theta ) } { ۱ - ۳ \tan ^ ۲ ( \theta ) }
$$

$$
\cot ( ۳ \theta ) = \frac { ۳ \cot ( \theta ) - \cot ^ ۳ ( \theta ) } { ۱ - ۳ \cot ^ ۲ ( \theta ) }
$$

قوانین مثلثات برای نصف زاویه

مهم‌ترین روابط مثلثاتی مربوط به نصف یک زاویه عبارت هستند از:

$$
\sin ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ - \cos \theta } { ۲ } }
$$

$$
\cos ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ + \cos \theta } { ۲ } }
$$

$$
\tan ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ - \cos \theta } { ۱ + \cos \theta } }
$$

$$
\cot ( \frac { \theta } { ۲ } ) = \pm \sqrt { \frac { ۱ + \cos \theta } { ۱ - \cos \theta } }
$$

البته برای تانژانت نصف زاویه، رابطه زیر نیز وجود دارد:

$$
\tan ( \frac { \theta } { ۲ } ) = \frac { ۱ - \cos \theta } { \sin \theta }
$$

روابط زیر نیز به عنوان نسبت‌های پرکاربرد در مثلثات شناخته می‌شوند:

$$
\sin ( \theta ) = \frac { 2 \tan \left ( \frac { \theta } { 2 } \right ) } { 1 + \tan ^ 2 \left ( \frac { \theta }{ 2 } \right ) }
$$

$$
\cos ( \theta ) = \frac { 1 - \tan ^ 2 \left ( \frac { \theta } { 2 } \right ) } { 1 + \tan ^ 2 \left ( \frac { \theta }{ 2 } \right ) }
$$

در ادامه، کاربرد روابط بالا را با حل یک مثال آموزش می‌دهیم.

مثال ۱۱: محاسبه کسینوس نصف یک زاویه

کسینوس زاویه ۱۵ درجه را محاسبه کنید.

بسیاری از دانش‌آموزان و دانشجویان با مقدار کسینوس زاویه ۱۵ درجه آشنا نیستند. با این وجود، اگر کسینوس زاویه ۳۰ درجه را از آن‌ها بپرسیم، به احتمال زیاد جواب آن را می‌دانند. کسینوس زاویه ۳۰ درجه برابر است با:

$$ \cos ( ۳۰ ^ { \circ } ) = \frac { \sqrt { ۳ } } { ۲ } \approx ۰/۸۷ $$

با توجه به قوانین مثلثات برای نصف یک زاویه، داریم:

$$
\cos ( \frac { \theta } { ۲ } ) = \sqrt { \frac { ۱ + \cos \theta } { ۲ } }
$$

$$
\cos ( \frac { ۳۰ ^ { \circ } } { ۲ } ) = \sqrt { \frac { ۱ + \cos ۳۰ ^ { \circ } } { ۲ } }
$$

$$
\cos ۱۵ ^ { \circ } = \sqrt { \frac { ۱ + \cos ۳۰ ^ { \circ } } { ۲ } }
$$

$$
\cos ۱۵ ^ { \circ } = \sqrt { \frac { ۱ + ۰/۸۷ } { ۲ } }
$$

$$
\cos ۱۵ ^ { \circ } = \sqrt { \frac { ۱/۸۷ } { ۲ } }
$$

$$
\cos ۱۵ ^ { \circ } = \sqrt { ۰/۹۳۵ }
$$

$$
\cos ۱۵ ^ { \circ } \approx ۰/۹۶۶
$$

در نتیجه، کسینوس زاویه ۱۵ درجه، تقریبا برابر با ۰/۹۶۷ درجه است.

قوانین سینوس ها، کسینوس ها و تانژانت ها

یکی از معروف‌ترین و پرکاربردترین قوانین مثلثات، قانون سینوس‌ها است. بر اساس این قانون، نسبت سینوس زاویه هر راس مثلث به ضلع مقابل آن راس، مقدار ثابتی است.

مثلث زیر را در نظر بگیرید:

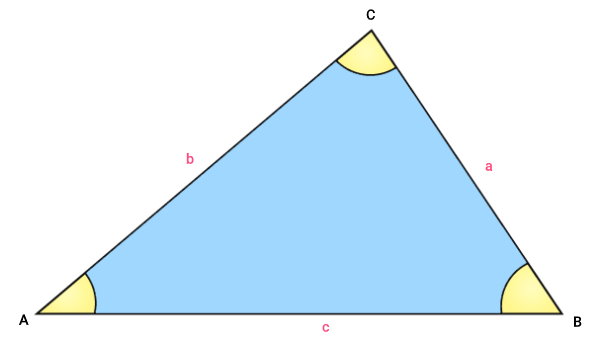
نمایش قانون سینوس ها در مثلث از قوانین مثلثات

قانون سینوس‌ها برای ضلع‌های این مثلث به صورت زیر نوشته می‌شود:

$$
\frac { \sin A }{ a } = \frac { \sin B }{ b } = \frac { \sin C }{ c }
$$

a: ضلع مقابل به راس A
b: ضلع مقابل به راس B
c: ضلع مقابل به راس C

قانون سینوس‌ ها (Law of Sines) — به زبان ساده

علاوه بر قانون سینوس‌ها، قانون دیگری با عنوان قانون کسینوس‌ها وجود دارد که رابطه بین ضلع‌ها و زاویه‌های داخلی مثلث را به کمک کسینوس زاویه رئوس بیان می‌کند. قانون کسینوس‌ها در مثلث ABC به صورت زیر نوشته می‌شود:

$$
a ^ ۲ = b ^ ۲ + c ^ ۲ - ۲ b c \cos A
$$

$$
b ^ ۲ = a ^ ۲ + c ^ ۲ - ۲ a c \cos B
$$

$$
c ^ ۲ = a ^ ۲ + b ^ ۲ - ۲ a b \cos C
$$

قانون کسینوس‌ ها — به زبان ساده

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی

قانون تانژانت‌ها نیز یکی دیگر از قوانین مثلثات است. این قانون، کاربرد کمتری نسبت به قوانین سینوس‌ها و کسینوس‌ها دارد. برای مثلث ABC، قانون تانژانت به صورت زیر نوشته می‌شود:

$$
\frac { a - b } { a + b } = \frac { \tan ( \frac { A - B } { ۲ } ) } { \tan ( \frac { A + B } { ۲ } ) }
$$

$$
\frac { b - c } { b + c } = \frac { \tan ( \frac { B - C } { ۲ } ) } { \tan ( \frac { B + C } { ۲ } ) }
$$

$$
\frac { c - a } { c + a } = \frac { \tan ( \frac { C - A } { ۲ } ) } { \tan ( \frac { C + A } { ۲ } ) }
$$

با توجه به برقرار بودن رابطه $$ \tan ( - \theta ) = - \tan ( \theta ) $$، می‌توانیم جای پارامترهای جمع و تفریق را در تمام روابط بالا تغییر دهیم. به عنوان مثال، از رابطه اول به رابطه زیر می‌رسیم:

$$
\frac { b - a } { b + a } = \frac { \tan ( \frac { B - A } { ۲ } ) } { \tan ( \frac { B + A } { ۲ } ) }
$$

مثال ۱۲: محاسبه زوایای مثلث از روی سه ضلع

مثلث مختلف‌الاضلاع زیر را در نظر بگیرید اندازه ضلع‌های این مثلث برابر با ۹، ۱۲ و ۱۸ واحد طول است. اندازه هر یک از زوایای مثلث را به دست بیاورید.

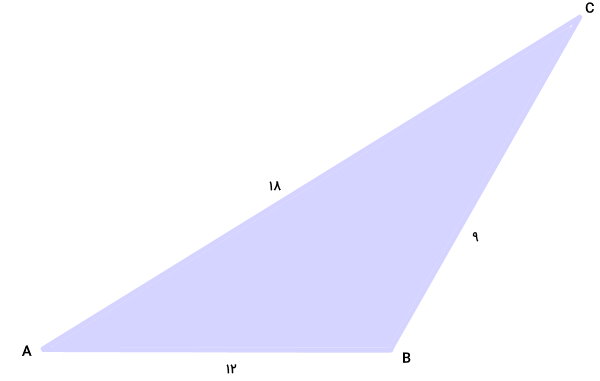
مثال قوانین مثلثات سینوس و کسینوس با مثلث مختلف الاضلاع

برای به دست آوردن اندازه زوایای راس مثلث ABC، کافی است یکی از زوایا را به کمک قانون کسینوس‌ها محاسبه کنیم. در اینجا، قانون کسینوس‌ها را برای زاویه راس C می‌نویسیم:

$$
AB ^ ۲ = BC ^ ۲ + AC ^ ۲ - ۲ BC \cdot AC \cos C
$$

AB: ضلع مقابل به راس C‌ برابر با ۱۲
AC: ضلع مقابل به راس B برابر با ۱۸
BC: ضلع مقابل به راس A برابر با ۹
C: زاویه راس C (پارامتر مجهول)

مقادیر معلوم ضلع‌ها را برای به دست آوردن زاویه راس C در رابطه بالا قرار می‌دهیم:

$$ ۱۲ ^ ۲ = ۹ ^ ۲ + ۱۸ ^ ۲ - ( ۲ \times ۹ \times ۱۸ \cos C ) $$

$$ ۱۴۴ = ۸۱ + ۳۲۴ - ۳۲۴ \cos C $$

$$ ۱۴۴ - ۸۱ - ۳۲۴ = - ۳۲۴ \cos C $$

$$ - ۲۶۱ = - ۳۲۴ \cos C $$C

$$
\cos C = \frac { - ۲۶۱ } { - ۳۲۴ }
$$

$$
\cos C \approx ۰/۸۰۶
$$

کسینوس زاویه راس C، تقریبا برابر با ۰/۸۰۶ است. در نتیجه زاویه راس C تقریبا برابر با ۳۶/۳ درجه است. اکنون، اندازه یکی از زوایای مثلث را داریم. بنابراین، برای به دست آوردن زوایای دیگر، قانون سینوس را می‌نویسیم:

$$
\frac { \sin A }{ BC } = \frac { \sin B }{ AC } = \frac { \sin C }{ AB }
$$

AB: ضلع مقابل به راس C‌ برابر با ۱۲
AC: ضلع مقابل به راس B برابر با ۱۸
BC: ضلع مقابل به راس A برابر با ۹
C: زاویه راس C برابر با ۳۶/۳ درجه
B: زاویه راس B (زاویه مجهول)
A: زاویه راس C (زاویه مجهول)

مقادیر معلوم را درون رابطه قرار می‌دهیم:

$$
\frac { \sin A }{ ۹ } = \frac { \sin B }{ ۱۸ } = \frac { \sin ۳۶ ^ { \circ } }{ ۱۲ }
$$

سینوس زاویه ۳۶/۳ درجه، تقریبا برابر با ۰/۵۹ است. به این ترتیب، با در نظر گرفتن نسبت‌ها به صورت دو به دو، خواهیم داشت:

$$
\frac { \sin B }{ ۱۸ } = \frac { \sin ۳۶ ^ { \circ } }{ ۱۲ }
$$

$$
\frac { \sin B }{ ۱۸ } = \frac { ۰/۵۹ }{ ۱۲ }
$$

$$
\sin B = \frac { ۱۸ \times ۰/۵۹ }{ ۱۲ }
$$

$$
\sin B = ۰/۸۸۵
$$

آرک‌سینوس ۰/۸۸۵ تقریبا برابر با ۶۲/۲۵ یا ۱۱۷/۷۵ درجه است. با توجه به شکل مثلث، زاویه راس B، تقریبا برابر با ۱۱۷/۷۵ درجه است. بر اساس قانون مجموع زوایای داخلی مثلث، داریم:

$$ A + B + C = ۱۸۰ ^ { \circ } $$

$$ A + ۱۱۷/۷۵ ^ { \circ } + ۳۶/۳۰ ^ { \circ } = ۱۸۰ ^ { \circ } $$

$$ A = ۲۵/۹۵ ^ { \circ } $$

در نتیجه، اندازه زاویه راس A تقریبا برابر با ۲۵/۹۵ درجه است. با توجه ابزار محاسباتی مورد استفاده و دقت محاسبات، امکان تفاوت بین زاویه‌ها در حد کم وجود دارد. با این وجود، زاویه راس‌ها را می‌توان نزدیک به مقادیر به دست آمده در نظر گرفت. اگر محاسبات را با دقت بالاتر انجام دهید، احتمالا به زوایای زیر می‌‌رسید:

$$
A = ۲۶/۳۸۴ ^ { \circ } , \;
B = ۱۱۷/۲۸۰ ^ { \circ } , \;
C = ۳۶/۳۳۶ ^ { \circ }
$$

قوانین تبدیل جمع به ضرب در مثلثات

از شناخته شده‌ترین قوانین مثلثات می‌توان به اتحادهای تبدیل جمع و تفریق به ضرب اشاره کرد.

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد

این روابط مثلثاتی به صورت زیر نوشته می‌شوند:

$$
\begin{aligned}
& \sin \alpha + \sin \beta = ۲ \sin \left ( \frac { \alpha + \beta } { ۲ }\right) \cos \left ( \frac { \alpha - \beta } { ۲ } \right) \\
& \sin \alpha - \sin \beta = ۲ \sin \left ( \frac { \alpha - \beta } { ۲ }\right) \cos \left ( \frac { \alpha + \beta } { ۲ } \right ) \\
& \cos \alpha + \cos \beta = ۲ \cos \left ( \frac { \alpha + \beta } { ۲ } \right ) \cos \left ( \frac { \alpha - \beta } { ۲ } \right ) \\
& \cos \alpha - \cos \beta = - ۲ \sin \left ( \frac { \alpha + \beta } { ۲ } \right) \sin \left ( \frac { \alpha - B } { ۲ } \right )
\end{aligned}
$$

با وجود معرفی روابط بالا در اغلب منابع، این قوانین مثلثاتی، کاربرد کمتری نسبت به دیگر قوانین دارند.

مثال ۱۳: محاسبه تفریق کسینوس های دو زاویه

حاصل تفریق زیر را به دست بیاورید:

$$
\cos ( ۱۵ ^ { \circ } ) - \cos ( ۷۵ ^ { \circ } )
$$

برای محاسبه تفریق بالا می‌توانیم از قوانین تبدیل جمع به ضرب در مثلثات استفاده کنیم. بر اساس قانون تبدیل تفریق کسینوس‌ها به ضرب، داریم:

$$
\cos \alpha - \cos \beta = - ۲ \sin \left ( \frac { \alpha + \beta } { ۲ } \right ) \sin \left ( \frac { \alpha - B } { ۲ } \right )
$$

مقادیر $$ \alpha = ۱۵ ^ { \circ } $$ و $$ \beta = ۷۵ ^ { \circ } $$ را درون رابطه بالا قرار می‌دهیم:

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = - ۲ \sin \left ( \frac { ۱۵ ^ { \circ } + ۷۵ ^ { \circ } } { ۲ } \right ) \sin \left ( \frac { ۱۵ ^ { \circ } - ۷۵ ^ { \circ } } { ۲ } \right )
$$

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = - ۲ \sin \left ( \frac { ۹۰ ^ { \circ } } { ۲ } \right ) \sin \left ( \frac { - ۶۰ ^ { \circ } } { ۲ } \right )
$$

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = - ۲ \sin \left ( ۴۵ ^ { \circ } \right ) \sin \left ( - ۳۰ ^ { \circ } \right )
$$

بر اساس قوانین مثلثات برای زوایای منفی، می‌دانیم:

$$
\sin ( { - \theta } ) = - \sin { \theta }
$$

به این ترتیب، داریم:

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = - ۲ \sin \left ( ۴۵ ^ { \circ } \right ) \times - \sin \left ( ۳۰ ^ { \circ } \right )
$$

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = ۲ \sin \left ( ۴۵ ^ { \circ } \right ) \times \sin \left ( ۳۰ ^ { \circ } \right )
$$

سینوس زاویه ۴۵ و ۳۰ درجه برابر است با:

$$
\sin ۴۵ ^ { \circ } = \frac { \sqrt { ۲ } } { ۲ }
$$

$$
\sin ۳۰ ^ { \circ } = \frac { ۱ } { ۲ }
$$

در نتیجه:

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = \frac { ۲ \sqrt { ۲ } } { ۲ } \times \frac { ۱ } { ۲ }
$$

$$
\cos ۱۵ ^ { \circ } - \cos ۷۵ ^ { \circ } = \frac { \sqrt { ۲ } } { ۲ }
$$

قوانین تبدیل ضرب به جمع مثلثات

با استفاده قوانین مثلثات می‌توانیم ضرب سینوس و کسینوس را به جمع این توابع تبدیل کنیم.

فیلم آموزش ریاضی پایه دانشگاهی

مهم‌ترین روابط تبدیل ضرب به جمع توابع مثلثاتی عبارت هستند از:

$$
\sin \alpha \cos \beta = \frac { ۱ }{ ۲ } [ \sin ( \alpha + \beta ) + \sin ( \alpha - \beta ) ] $$

$$
\cos \alpha \sin \beta = \frac { ۱ }{ ۲ } [ \sin ( \alpha + \beta ) - \sin ( \alpha - \beta ) ] $$

$$
\cos \alpha \cos \beta = \frac { ۱ }{ ۲ } [ \cos ( \alpha + \beta ) + \cos ( \alpha - \beta ) ] $$

$$
\sin \alpha \sin \beta = \frac { ۱ }{ ۲ } [ \cos ( \alpha - \beta ) - \cos ( \alpha + \beta ) ] $$

قوانین تبدیل ضرب به جمع مثلثات نیز مانند قوانین تبدیل جمع به ضرب، کاربرد کمی دارند. با این وجود، آشنایی با آن‌ها می‌تواند در حل برخی از مسائل کارگشا باشد.

مثال ۱۴: محاسبه ضرب سینوس های دو زاویه

حاصل عبارت زیر را به دست بیاورید:

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ }
$$

بر اساس اتحادهای تبدیل ضرب به جمع، داریم:

$$
\sin \alpha \sin \beta = \frac { ۱ }{ ۲ } [ \cos ( \alpha - \beta ) - \cos ( \alpha + \beta ) ] $$

یکی از زوایا را برابر با α و دیگری را برابر با β قرار می‌دهیم:

$$ \alpha = \dfrac { ۱۱ \pi } { ۱۲ } $$

$$ \beta = \dfrac { \pi } { ۱۲ } $$

به این ترتیب، داریم:

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } [ \cos ( \dfrac { ۱۱ \pi } { ۱۲ } - \dfrac { \pi } { ۱۲ } ) - \cos ( \dfrac { ۱۱ \pi } { ۱۲ } + \dfrac { \pi } { ۱۲ } ) ] $$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } [ \cos ( \dfrac { ۱۱ \pi - \pi } { ۱۲ } ) - \cos ( \dfrac { ۱۱ \pi + \pi } { ۱۲ } ) ] $$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } [ \cos ( \dfrac { ۱۰ \pi } { ۱۲ } ) - \cos ( \dfrac { ۱۲ \pi } { ۱۲ } ) ] $$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } [ \cos ( \dfrac { ۵ \pi } { ۶ } ) - \cos ( \pi ) ] $$

کسینوس زاویه π یا ۱۸۰ درجه برابر است با:

$$ \cos ( \pi ) = - ۱ $$

بر اساس قوانین مثلثات برای زوایای مکمل، کسینوس زاویه $$ \frac { ۵ \pi } { ۶ } $$ یا ۱۵۰ درجه نیز برابر است با:

$$ \cos ( \dfrac { ۵ \pi } { ۶ } ) = \cos ( ۱۵۰ ^ { \circ } ) $$

$$ = \cos ( ۱۸۰ ^ { \circ } - ۳۰ ^ { \circ } ) $$

$$ = - \cos ( ۳۰ ^ { \circ } ) $$

$$ = - \frac { \sqrt { ۳ } } { ۲ } $$

به این ترتیب داریم:

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } \left [ - \frac { \sqrt { ۳ } } { ۲ }- \left ( - ۱ \right ) \right ] $$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } \left [ - \frac { \sqrt { ۳ } } { ۲ } + ۱ \right ] $$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { ۱ }{ ۲ } \left ( \frac { - \sqrt { ۳ } + ۲ } { ۲ } \right )
$$

$$
\sin \dfrac { ۱۱ \pi } { ۱۲ } \sin \dfrac { \pi } { ۱۲ } = \frac { - \sqrt { ۳ } + ۲ } { ۴ }
$$

در نتیجه، حاصل‌ضرب دو تابع سینوسی را به دست آوردیم. مقدار عددی این ضرب، تقریبا برابر با ۰/۰۶۶۹۸ است.

جدول کامل مهمترین قوانین مثلثات

در این بخش، به معرفی مهم‌ترین قوانین مثلثات در قالب یک جدول می‌پردازیم.

عنوان قانون	رابطه ریاضی
رابطه کسری بین نسبت‌های مثلثاتی	$$ \tan ( \theta ) = \frac { \sin ( \theta ) } { \cos ( \theta ) } $$
	$$ \cot ( \theta ) = \frac { 1 } { \tan ( \theta ) } = \frac { \cos ( \theta ) } { \sin ( \theta ) } $$
	$$ \sec ( \theta ) = \frac { ۱ } { \cos ( \theta ) } $$
	$$ \csc ( \theta ) = \frac { ۱ } { \sin ( \theta ) } $$
فیثاغورس	$$ \sin ^ ۲ ( \theta ) + \cos ^ ۲ ( \theta ) = ۱ $$
رابطه بین سینوس و تانژانت نصف زاویه	$$ \sin ( \theta ) = \frac { 2 \tan \left ( \frac { \theta } { 2 } \right ) } { 1 + \tan ^ 2 \left ( \frac { \theta }{ 2 } \right ) } $$
رابطه بین کسینوس و تانژانت نصف زاویه	$$ \cos ( \theta ) = \frac { 1 - \tan ^ 2 \left ( \frac { \theta } { 2 } \right ) } { 1 + \tan ^ 2 \left ( \frac { \theta }{ 2 } \right ) } $$
زوایای متمم	$$ \sin { \beta } = \cos { \alpha} $$
	$$ \cos { \beta } = \sin { \alpha} $$
	$$ \tan { \beta } = \cot { \alpha} $$
	$$ \cot { \beta } = \tan { \alpha} $$
	$$ \csc { \beta } = \sec { \alpha} $$
	$$ \sec { \beta } = \csc { \alpha} $$
زوایای مکمل	$$ \sin { \beta } = \sin{ \alpha } $$
	$$ \cos { \beta } = - \cos{ \alpha } $$
	$$ \tan { \beta } = - \tan { \alpha } $$
	$$ \cot { \beta } = - \cot { \alpha } $$
	$$ \csc { \beta } = \csc{ \alpha } $$
	$$ \sec { \beta } = - \sec{ \alpha } $$
زوایای مضاعف	$$ \begin{align} \sin ( ۲ \theta ) & = ۲ \sin ( \theta ) \cos ( \theta ) \\[4pt] & = \frac { ۲ \tan ( \theta ) } { ۱ + \tan ^ ۲ ( \theta ) } \end{align} $$
زوایای مضاعف	$$ \begin{align} \cos ( ۲ \theta ) & = \cos ^ ۲ ( \theta ) - \sin ^ ۲ ( \theta ) \\[4pt] & = \frac { ۱ - \tan ^ ۲ ( \theta ) } { ۱ + \tan ^ ۲ ( \theta ) } \\[4pt] & = ۲ \cos ^ ۲ ( \theta ) - ۱ \\[4pt] & = ۱ - ۲ \sin ^ ۲ ( \theta ) \end{align} $$
زوایای تناوبی	$$ \sin ( \theta \pm ۲ k \pi ) = \sin ( \theta ) $$
	$$ \cos ( \theta \pm ۲ k \pi ) = \cos ( \theta ) $$
	$$ \tan ( \theta \pm k \pi ) = \tan ( \theta ) $$
زوایای قرینه	$$ \sin ( { - \theta } ) = - \sin { \theta } $$
	$$ \cos ( { - \theta } ) = \cos { \theta } $$
	$$ \tan ( { - \theta } ) = - \tan { \theta } $$
جمع زوایا	$$ \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $$
جمع زوایا	$$ \cos ( \alpha + \beta ) = \cos \alpha \cos \beta − \sin \alpha \sin \beta $$
تفریق زوایا	$$ \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $$
تفریق زوایا	$$ \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$

اثبات قوانین مثلثات

روش‌های مختلفی برای اثبات قوانین مثلثات وجود دارد. ساده‌ترین روش برای این کار، استفاده از مفاهیم مربوط به مثلث قائم‌الزاویه است. البته این روش به منظور اثبات قوانین ساده مورد استفاده قرار می‌گیرد. نسبت‌های مثلثاتی پیچیده، معمولا با کمک نسبت‌های ساده‌تر اثبات می‌شوند.

در مثال ۳ و ۵ مقاله، نحوه اثبات برخی از قوانین مثلثات را آموزش دادیم. در صورت تمایل به آشنایی با روش‌های اثبات روابط مهم مثلثاتی، مطالعه مطلب «اثبات روابط مثلثاتی – به زبان ساده» را به شما پیشنهاد می‌کنیم.

اثبات روابط مثلثاتی – به زبان ساده