اختلاف فاز — به زبان ساده
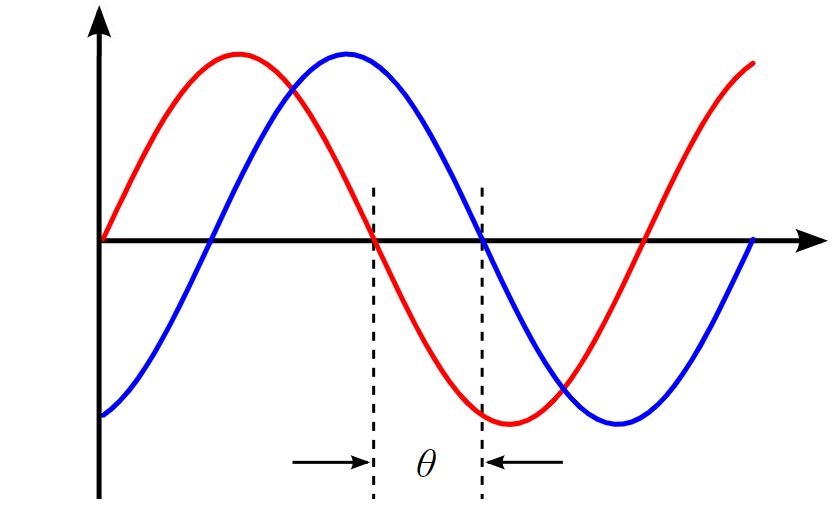
در آموزشهای قبلی مجله فرادرس، درباره شکل موج الکتریکی و سینوسی بحث کردیم. در این آموزش قصد داریم به بررسی مفاهیم اختلاف فاز و جابجایی فاز بپردازیم.
«اختلاف فاز» (Phase Difference)، اختلاف بین دو یا چند کمیت متناوب را بر حسب درجه یا رادیان توضیح میدهد.
همانطور که میدانیم، شکل موج سینوسی، یک کمیت متناوب است و میتوان آن را نسبت به محور افقی زمان رسم کرد. همچنین میدانیم که امواج سینوسی به عنوان یک کمیت متناوب، در لحظه $$\pi /2$$ پیک مثبت در لحظه $$3 \pi /2$$ پیک منفی دارند. موج سینوسی، در نقاط $$0$$ و $$\pi$$ و $$ 2 \pi$$ مقدار صفر دارد.
البته همه شکل موجهای سینوسی در یک لحظه از نقطه صفر عبور نمیکنند. ممکن است یک موج سینوسی نسبت به موج سینوسی دیگر، به چپ یا راست، جابجایی یا اختلاف فاز داشته باشد.
یک شکل موج جریان و یک شکل موج ولتاژ را در نظر بگیرید. بین این موج سینوسی، یک اختلاف فاز یا جابجایی زاویهای وجود دارد. هر شکل موج سینوسی، که در زمان $$t=0$$ از نقطه مبدأ عبور نکند، جابجایی فاز دارد.
تعریف اختلاف فاز
اختلاف فاز برای یک شکل موج سینوسی، مقدار جابجایی زاویهای شکل موج نسبت به نقطه مرجع معین در محور افقی است. این زاویه با نماد ($$\phi$$) نشان داده میشود و بر حسب درجه یا رادیان اندازهگیری میشود. به عبارت دیگر، اختلاف فاز بین دو موج، اختلاف بین دو شکل موج نسبت به یک محور مشترک است. طبق قرارداد، تنها شکل موجهای سینوسی با فرکانس یکسان میتوانند اختلاف فاز داشته باشند.
اختلاف فاز $$\phi$$ برای یک شکل موج متناوب میتواند از صفر تا مقدار ماکزیمم خود یعنی دوره تناوب موج سینوسی ($$T$$) متغیر باشد. بسته به واحد زاویه انتخاب شده، $$\phi$$ میتواند مقادیری از $$0$$ تا $$2\pi$$ یا از صفر تا $$360^\circ$$ داشته باشد.
اختلاف فاز را میتوان به صورت اختلاف زمانی $$t$$ نسبت به دوره تناوب $$T$$ یا کسری از دوره تناوب نیز نمایش داد. $$T$$ میتواند مقادیری مثل $$+10ms$$ یا $$-50 uS$$ داشته باشد. اما در حالت کلی بهتر است که اختلاف فاز به صورت اندازه زاویهای بیان شود.
به همین دلیل، معادله داده شده برای مقدار لحظهای شکل موج ولتاژ یا جریان سینوسی تغییر میکند تا زاویه فاز شکل موج را در بر گیرد. عبارت شکل موج لحظهای با احتساب فاز به صورت زیر نوشته میشود:
$$A_{(t)} = A_{max} \times sin (\omega t \pm \phi)$$
که در آن:
- $$A_m$$، دامنه شکل موج است.
- $$\omega t$$، فرکانس زاویهای شکل موج با واحد رادیان بر ثانیه (rad/s) است.
- $$\phi$$، زاویه فاز با واحد درجه یا رادیان است. این زاویه، نشاندهنده اختلاف فاز شکل موج نسبت به نقطه مرجع به چپ یا راست است.
فاز مثبت و فاز منفی در شکل موج سینوسی
اگر قسمتی از شکل موج سینوسی که شیب مثبت دارد، قبل از زمان $$t=0$$ از محور افقی عبور کند، گفته میشود که شکل موج به سمت چپ جابجا شده است. در این حالت، $$\phi>0$$ و زاویه فاز مثبت است. بنابراین در این حالت، فاز شکل موج نسبت به مرجع در حالت تقدم قرار میگیرد. به عبارت دیگر، به نظر میرسد این موج زودتر از زاویه $$0^ \circ$$ عبور کرده است. در این حالت بردار خلاف جهت عقربههای ساعت میچرخد.
به همین ترتیب، اگر قسمتی از شکل موج سینوسی که شیب مثبت دارد، بعد از زمان $$t=0$$ از محور افقی عبور کند، گفته میشود که شکل موج به سمت راست جابجا شده است. پس $$\phi<0$$ و زاویه فاز در این حالت منفی است. گفته میشود فاز شکل موج نسبت به مرجع در حالت تاخیر قرار میگیرد. به عبارت دیگر به نظر میرسد که این موج کمی کندتر از $$0^ \circ$$ عبور کرده است. در این حالت، بردار فازور در جهت عقربههای ساعت میچرخد.
این دو حالت در شکل زیر نشان داده شدهاند:
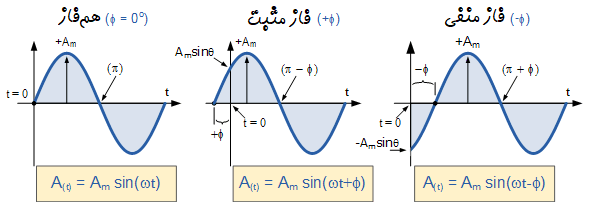
شکل موجهای همفاز و غیرهمفاز
دو کمیت متناوب مانند ولتاژ (v) و جریان (i) را با فرکانس یکسان f در نظر بگیرید. فرکانس زاویهای دو موج ($$\omega$$) برابر است، زیرا فرکانس این دو موج با هم برابر است. پس در هر لحظهای از زمان، میتوان گفت فاز ولتاژ (v) با فاز جریان (i) برابر است.
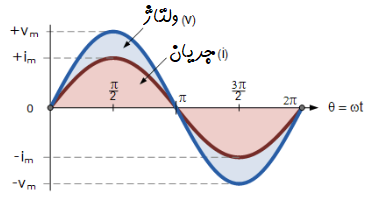
پس زاویه چرخش در یک محدوده مشخص زمانی، همواره برای این دو متغیر برابر خواهد بود. در این حالت اختلاف فاز بین دو کمیت v و i برابر صفر است ($$\phi=0$$). در یک دوره تناوب هر دو متغیر همزمان به مقادیر صفر، ماکزیمم و مینیمم خود میرسند، زیرا فرکانس شکل موج ولتاژ v و جریان i با هم برابر است. اگرچه ممکن است این دو شکل موج، دامنههای متفاوتی داشته باشند، اما باز هم همزمان به مقدارهای ماکزیمم، مینیمم و صفر خود میرسند. در این حالت، دو کمیت متناوب v و i را «همفاز» مینامند.در شکل زیر، دو موج همفاز نشان داده شدهاند:
حال فرض کنید که ولتاژ (v) و جریان (i)، اختلاف فازی به اندازه $$30^ \circ$$ دارند. پس میتوان گفت $$\phi = 30 ^ \circ$$ یا $$\phi = \pi / 6$$ رادیان است. هر دو کمیت متناوب به دلیل فرکانس یکسان، با سرعتی برابر میچرخند. به همین دلیل، اختلاف فاز بین دو موج در همه لحظات یکسان میماند. اختلاف فاز ۳۰ درجه بین دو کمیت با $$\phi$$ نمایش داده میشود. این اختلاف فاز در شکل زیر نشان داده شده است:
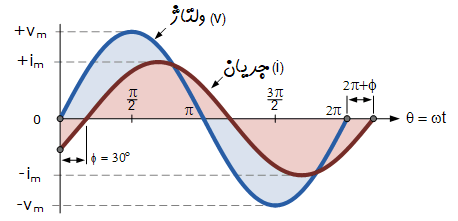
شکل موج ولتاژ در شکل بالا، از نقطه صفر محور مرجع افقی شروع میشود. اما در همین لحظه از زمان، شکل موج جریان مقداری منفی دارد و از محور مرجع، تا سی درجه جلوتر عبور نمیکند. پس یک اختلاف فاز بین دو شکل موج وجود دارد. همانطور که مشخص است، جریان پس از ولتاژ به مقدار ماکزیمم، مینیمم و صفر خود میرسد. یعنی ابتدا ولتاژ به ماکزیمم خود میرسد سپس بعد از سی درجه (واحد زمان در اینجا درجه است)، جریان به مقدار ماکزیمم خود میرسد. پس جریان دیرتر به ماکزیمم یا مینیمم خود میرسد.
در این حالت دو شکل موج، دیگر همفاز نیستند و غیر همفاز هستند. گفته میشود که دو موج به اندازه زاویه $$\phi$$ غیر همفاز هستند. در این مثال خاص $$\phi = 30 ^ \circ$$ است. پس میتوان گفت دو شکل موج به اندازه ۳۰ درجه غیرهمفاز هستند. در این مثال، موج جریان نسبت به ولتاژ، زاویه ۳۰ درجه تاخیر دارد. به طور معادل میتوان گفت شکل موج ولتاژ نسبت به جریان، به اندازه ۳۰ درجه تقدم فاز دارد. گفته میشود که «اختلاف فاز تاخیری» (Lagging Phase Difference) وجود دارد. پس میتوان برای شکل موج ولتاژ و جریان، عبارتهای زیر را نوشت:
$$Voltage , (V_t ) = V_m sin \omega t$$
$$Current , (i_t) = I_m sin (\omega t - \phi)$$
این معادله بیان میکند که i نسبت به v به اندازه زاویه $$\phi$$ عقب میافتد یا تاخیر دارد.
به صورت مشابه، اگر جریان i در زمان صفر مقدار مثبتی داشته باشد و زودتر از موج ولتاژ به ماکزیمم یا مینیمم یا نقطه صفر خود برسد، گفته میشود که جریان نسبت به ولتاژ به اندازه زاویه $$\phi$$ تقدم دارد. در این حالت گفته میشود که «اختلاف فاز تقدم» (Leading Phase Difference) وجود دارد. عبارت ولتاژ و جریان در این حالت به صورت زیر است:
$$Voltage , (V_t ) = V_m sin \omega t$$
$$Current , (i_t) = I_m sin (\omega t+\phi)$$
در این حالت، i نسبت به v با زاویه $$\phi$$ جلو میافتد.
از زاویه فاز یک موج سینوسی، میتوان برای تشریح رابطه بین دو موج سینوسی نسبت به هم با مفاهیم تقدم و تأخر استفاده کرد. این زاویه، برای دو شکل موج با فرکانس مشابه تعریف میشود. در مثال بالا، دو شکل موج نسبت به هم ۳۰ درجه اختلاف فاز دارند. پس بسته به اینکه کدام یک از بردارها به عنوان مرجع در نظر گرفته شود، میتوان گفت i نسبت به v به اندازه ۳۰ درجه تاخیر دارد یا v نسبت به i به اندازه ۳۰ درجه تقدم دارد.
رابطه بین دو شکل موج و اختلاف فاز آنها را میتوان با توجه به مرجع افقی صفر اندازهگیری کرد. در مدارهای توان AC، توضیح رابطه بین موج سینوسی ولتاژ و موج سینوسی جریان، بسیار مهم است و اساس تحلیل مدارهای AC را تشکیل میدهد.
شکل موج کسینوسی
اگر یک شکل موج در مقایسه با دیگر موجهای سینوسی به سمت راست یا چپ محور مرجع صفر جابجا شود، رابطه شکل موج به فرم زیر در میآید:
$$A_m sin( \omega t \pm \phi)$$
اما اگر شکل موج از محور صفر افقی با شیب مثبت عبور کند و زاویه آن $$90^ \circ$$ درجه یا $$\pi /2$$ رادیان قبل از شکل موج مرجع باشد، این موج را شکل موج کسینوسی مینامند. عبارت شکل موج کسینوسی به صورت زیر است:
$$sin (\omega t + 90^ \circ) = sin \large ( \omega t + \frac{\pi}{2} \large ) = cos (\omega t)$$
موج کسینوسی، به اندازه موج سینوسی در مهندسی برق حائز اهمیت است. موج کسینوسی شکلی مشابه موج سینوسی دارد اما به اندازه ۹۰ درجه یا یک چهارم تناوب، از شکل موج سینوسی جلوتر است.
شکل زیر، اختلاف فاز بین موج سینوسی و موج کسینوسی را نشان میدهد:
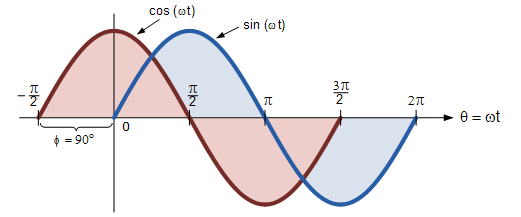
به طور مشابه میتوان گفت که موج سینوسی، یک موج کسینوسی است که به اندازه منهای ۹۰ درجه جابجایی فاز پیدا کرده است. در هر حالت، هنگامی که با امواج سینوسی و کسینوسی سروکار داریم، دانستن روابط بین موج سینوسی و موج کسینوسی بسیار مهم است.
روابط موج سینوسی و کسینوسی
$$cos (\omega t + \phi ) = sin (\omega t + \phi + 90 ^ \circ)$$
$$sin (\omega t + \phi ) = cos (\omega t + \phi -90^ \circ)$$
هنگام مقایسه دو شکل موج سینوسی، معمول است که شکل موج با دامنه مثبت بیان شود. روابط زیر برای تبدیل دامنه منفی به دامنه مثبت به کار میرود:
$$- sin (\omega t ) = sin (\omega t \pm 180^ \circ)$$
$$- cos (\omega t ) = cos (\omega t \pm 180^ \circ)$$
$$- cos (\omega t ) = sin (\omega t \pm 270^ \circ)$$
$$ \pm sin (\omega t ) = cos (\omega t \pm 90^ \circ)$$
$$ \pm cos (\omega t ) = sin (\omega t \pm 90^ \circ)$$
$$- sin (\omega t ) = sin (-\omega t)$$
$$ cos(\omega t ) = cos (-\omega t)$$
با استفاده از روابط بالا، میتوان هر شکل موج سینوسی را به شکل موج کسینوسی و بالعکس با اختلاف فاز یا بدون اختلاف فاز تبدیل کرد.










چیزی رو که ۲ ساله نمیفهمیدمش با این ویدیوی خوب تونستم بفهمم. دستتون درد نکنه سایتتون فوق العاده خوبه
امکان دارد متنی اموزشی درباره روشهای محاسبه اختلاف فاز بین دو سیگنال دیجیتال را هم قرار دهید.
سلام.
احتمالاً در آموزش «آشکارساز فاز — راهنمای جامع» به پاسخ پرسشتان خواهید رسید.
سالم و موفق باشید.
سلام
خیلی جامع و کامل و عالیییییییی
این الان به زبان ساده بود؟؟؟!!
:ا
عالی است دقیق روان