معادلات ساختاری PLS – مفاهیم و روش‌ها – به زبان ساده

ایجاد یا شناسایی متغیرهای مکنون یا پنهان از ترکیب متغیرهای قابل مشاهده، عملی است که توسط معادلات ساختاری PLS صورت می‌گیرد. اغلب چنین متغیرهایی را با نام عامل (Factor) می‌شناسیم. با تجزیه واریانس یا ماتریس کوواریانس و ایجاد مدل‌های رگرسیونی مناسب، رابطه بین عامل‌ها و متغیرها مستقل ساخته یا کشف می‌شود. در حقیقت می‌توان معادلات ساختاری PLS را به هدف پیش‌بینی ساختارهای نهفته یا پنهان به کار بست. به همین جهت در این متن به موضوع معادلات ساختاری به روش کمترین مربعات جزئی پرداخته‌ایم و ضمن معرفی مدل مربوطه، مفاهیم و روش‌های آن را نیز شرح خواهیم داد.

از آنجایی که معادلات ساختاری PLS که از تکنیک حداقل مربعات جزئی استفاده می‌کند باید مبنای مدل‌سازی باشد را باید بشناسید، بنابراین بهتر است نوشتار مدل معادلات ساختاری (Structural Equation Modeling) — مفاهیم، روش‌ها و کاربردها را مطالعه کنید. همچنین کسب اطلاع مفهوم ضریب همبستگی و همبستگی جزئی و کوواریانس که در مطلب ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده و ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده آمده است مناسب به نظر می‌رسد.

معادلات ساختاری PLS چیست؟

رگرسیون حداقل مربعات جزئی (رگرسیون PLS) یک روش آماری است که ارتباطی با «رگرسیون مولفه‌های اصلی» (Principle Component Regression) دارد. در این روش، به جای یافتن صفحه حداکثر واریانس بین متغیر پاسخ و متغیرهای مستقل، با ایجاد متغیرهای پیش‌بین جدید از روی متغیرهای مشاهده شده، به یک فضای جدید، یا یک مدل رگرسیون خطی تازه دست پیدا می‌کنیم.

معادلات ساختاری (SEM) الگویی برای پیدا کردن این متغیرهای پیش‌بین جدید ارائه می‌کند. از آنجا که هر دو سری داده‌های مربوط به متغیرهای $$X$$ و $$Y$$ در فضاهای جدید تصویر (Project) می‌شوند، خانواده روش PLS به عنوان «مدل عاملی دو خطی» (‌Bilinear Factor Model) شناخته می‌شوند. «تجزیه و تحلیل تشخیصی حداقل مربعات جزئی» (Partial least squares discriminant analysis) یا به اختصار PLS-DA نوعی از روش PLS محسوب می‌شود که برای طبقه بندی متغیر $$Y$$ مورد استفاده قرار می‌گیرد.

معادلات ساختاری PLS برای یافتن روابط اساسی و پایه، بین دو ماتریس ($$X$$ و $$Y$$) استفاده شده و به منظور مطالعه رابطه خطی بین آن‌ها به کار می‌رود. به این ترتیب PLS‌ را می‌توان یک رویکرد برای مدل سازی ساختارهای کوواریانس در این دو فضا توسط معادلات ساختاری موجود و ایجاد متغیرهای پنهان در نظر گرفت. یک مدل PLS سعی می‌کند جهتی چند بعدی را در فضای $$X$$ پیدا کند که حداکثر مقدار واریانس مشترک متغیرها را در فضای $$Y$$ توضیح دهد. رگرسیون PLS به ویژه هنگامی مناسب است که ماتریس متغیرهای پیش‌بین، ابعاد بیشتری نسبت به مشاهدات داشته باشند و هنگامی مورد استفاده قرار می‌گیرد که یا مشاهدات اندک باشند یا مشکل «هم خطی چندگانه» (Multicollinearity) بین مقادیر X وجود داشته باشد. در مقابل، رگرسیون استاندارد در این موارد شکست خواهد خورد و به نتایج مناسبی نخواهد رسید.

تکنیک حداقل مربعات جزئی، توسط آمارشناس نروژی «هرمان وُلد» (Herman O. A. Wold) معرفی شد، سپس آن را به همراه پسرش «سوانت وُلد» (Svante Wold) توسعه داد. یک اصطلاح جایگزین برای PLS که به نظر پسر او، صحیح‌تر به نظر می‌رسد، پیش بینی ساختارهای نهفته است، اما اصطلاح حداقل مربعات جزئی هنوز در بسیاری از حوزه‌های تحقیق و محاسبات آماری، غالب است.

اگر چه کاربردهای اصلی معادلات ساختاری PLS در حوزه‌های علوم اجتماعی و روان‌سنجی بود، اما رگرسیون PLS امروزه بیشترین کاربرد را در شیمی سنجی و موضوعات مرتبط دارد. این روش همچنین در بیوانفورماتیک (Bioinformatic)، «ارزیابی حسی» (Sensory analysis)، «علوم اعصاب» (Neuroscience) و «انسان شناسی» (Anthropology) استفاده می‌شود.

معادلات ساختاری PLS به بیان آماری

فرض کنید که ماتریس $$n \times m$$ شامل متغیرهای مستقل (پیش‌بین- Predictor) و $$Y$$ نیز ماتریس $$n \times p$$‌ از مقادیر متغیر پاسخ باشد. مدل عمومی در معادلات ساختاری با رویکرد PLS به صورت زیر نوشته می‌شود.

$$\large {\displaystyle X= T P^{ \mathrm {T} } +E}$$

$$\large {\displaystyle Y= U Q^{ \mathrm {T} } +F}$$

توجه داشته باشید که در رابطه‌های بالا، $$T$$ و $$U$$‌ ماتریس‌هایی با ابعاد $$n \times l$$‌ هستند که تصویر یا امتیاز $$X$$ ($$X$$- score) و تصویر یا امتیاز $$Y$$ ($$Y$$- score) را مشخص می‌کنند. همچنین $$P$$ یک ماتریس $$m \times l$$ و $$Q$$ نیز یک ماتریس $$p \times l$$ هستند که ماتریس‌های متعامد بارهای عامل‌ها را برای هر دو متغیر $$T$$‌ و $$U$$ نمایش می‌دهند. از طرفی ماتریس‌های $$E$$ و $$F$$ نیز عبارت خطای تصادفی بوده که فرض نرمال بودن و هم‌توزیعی نیز برایشان در نظر گرفته می‌شود.

تجزیه ماتریس‌های $$X$$ و $$Y$$ به شکلی صورت می‌گیرد که بیشینه‌سازی کوواریانس بین $$T$$ و $$U$$ محقق شود.

الگوریتم‌های حل معادلات ساختاری PLS

روش‌ها و تکنیک‌های مختلفی برای بدست آوردن عامل‌ها و ماتریس بارهای عاملی (ماتریس‌های $$T$$ ,$$U$$ ,$$P$$ و $$Q$$) وجود دارد. در اغلب موارد یک مدل رگرسیونی بین متغیرهای $$X$$‌ و $$Y$$ ساخته شده که به شکل زیر است.

$$\large Y = X \widetilde{ B} + \widetilde{ B}_0$$

فیلم آموزش آنالیز داده های چند متغیره با نرم افزار Unscrambler X در فرادرس

کلیک کنید

در بعضی از تکنیک‌های PLS، متغیر $$Y$$‌، باید یک بردار ستونی باشد که به آن حالت تک متغیره می‌گویند. البته الگوریتم‌هایی نیز وجود دارد که در آن‌ها ماتریس $$Y$$ مورد نظر است که وضعیت چند متغیره را نشان می‌دهد. تفاوت دیگر در بین الگوریتم‌های PLS، نحوه محاسبه ماتریس عامل‌ها ($$T$$) است که ممکن است با فرض «متعامد» (Orthogonal) یا «متعامد نرمال» (Orthonormal) همراه بوده یا چنین فرض‌هایی را در نظر نگرفته باشند.

نکته: توجه داشته باشید که با وجود یا عدم لحاظ کردن این فرض‌ها، پیش‌بینی نهایی برای گونه‌های مختلف PLS یکسان بوده ولی مولفه‌ها تفاوت خواهند داشت.

الگوریتم PLS1

یکی از محبوب‌ترین الگوریتم‌ها برای حل معادلات ساختاری PLS که کاربرد زیادی نیز دارد، الگوریتم PLS1 است. در این الگوریتم، متغیر $$Y$$ ‌به صورت یک بردار به کار می‌رود. همچنین ماتریس $$T$$ نیز با فرض اورتونرمال ساخته خواهد شد.

شبه کدی که در ادامه مشاهده می‌کنید، برای معرفی این الگوریتم نوشته شده است. سعی کردیم تا ساختاری که در بالا برای ماتریس‌ها مورد استفاده قرار دادیم، در شبه کد نیز لحاظ شود. حروف بزرگ لاتین، بیانگر ماتریس‌ها و حروف کوچک، بردارها را مشخص می‌کنند. البته برای روشن شدن نقش هر یک از ماتریس‌ها، بردار یا مقادیر عددی، در لابلای شبه کد، توضیحاتی نیز درج شده است. توجه داشته باشید که علامت $$^{\text{T}}$$‌ ترانهاده ماتریس مورد نظر است. همچنین اندیس بالا $$^{(k)}$$ نشانگر مقادیر در هر بار تکرار حلقه خواهد بود.

1- function PLS1 $${ \displaystyle (X, y, l)}$$

2- $${ \displaystyle X^{ (0) } \gets X}$$

3- $${ \displaystyle w^{( 0) } \gets X^{ \mathrm {T} } y / || X^{ \mathrm {T} } y || }$$, an initial estimate of w.

4- $${ \displaystyle \text{ for }k = 0 } \text{ to } { \displaystyle l - 1}$$

5- $${ \displaystyle t^{ (k) } \gets X^{ (k) } w^{ (k) }}$$

6- $${ \displaystyle t_{ k} \gets {t^{ (k) }}^{ \mathrm{ T} }t^{( k)} } \text{ (note this is a scalar) }$$

7- $${ \displaystyle t^{ (k)} \gets t^{( k) }/ t_{k} }t^{(k)}$$

8- $${ \displaystyle p^{( k)} \gets {X^{ (k) }}^{ \mathrm {T } }t^{ (k)}}$$

9- $${ \displaystyle q_{ k} \gets {y}^{ \mathrm {T} } t^{ (k)}} \text{(note this is a scalar)}$$

10- $${ \displaystyle \text{ if } q_{k} = 0 }$$

11- $${ \displaystyle l \gets k } \text{, break the for loop}$$

12- $${ \displaystyle \text{ if, } k < ( l - 1 )}$$

13- $${ \displaystyle X^{( k + 1 )} \gets X^{ ( k ) } - t_{k }t^{ (k) }{ p^{( k)}}^{ \mathrm {T} }}$$

14- $${ \displaystyle w^{( k + 1 )} \gets {X^{( k + 1)}}^{ \mathrm {T} } y}$$

15- end for

16- $${ \displaystyle \text{ define W to be the matrix with columns, } w^{(0)}, w^{( 1 )},...,w^{(l - 1 )}} \text{, Do the same to form the P matrix and q vector.}$$

17- $${ \displaystyle B \gets W {(P^{ \mathrm {T} }W )}^{ -1} q}$$

18- $${ \displaystyle B_{ 0 } \gets q_{ 0 } -{ P^{( 0 )}}^{ \mathrm {T} } B}$$

19- $${\displaystyle \text{ return } B ,B_{ 0 }}$$

این فرم از الگوریتم احتیاجی به تبدیل ورودی‌های $$X$$ و $$Y$$ به شکل مرکزی ندارد. این امر به این معنی است که می‌توان امید ریاضی یا میانگین این متغیرها را غیر صفر در نظر گرفت، زیرا تبدیل متغیرها به شکل مرکزی، درون الگوریتم و به شکل ضمنی صورت می‌گیرد. در نتیجه ورودی به همان صورتی که مقادیر اندازه‌گیری شده‌اند، در الگوریتم وارد می‌شوند. این الگوریتم ممکن است باعث تورم در ماتریس $$X$$ شود، زیرا تفاضل به صورت زیر تعریف و مورد استفاده قرار گرفته است.

$$\large X^{k + 1} \leftarrow X^{k} -\, t_{k} t^{( k)} p^{{( k)^{ \text{ T}}}}$$

اما تورم در بردار $$Y$$ صورت نخواهد گرفت. می‌توان ثابت کرد که تورم $$Y$$ همان نتایج را در صورت عدم تورم ایجاد خواهد کرد.

متغیر کمکی $$l$$ در الگوریتم بالا، محدودیت تعداد عامل‌ها یا متغیرهای پنهان را مدل رگرسیونی به همراه دارد. اگر مقدار $$l$$‌ برابر با رتبه یا مرتبه ماتریس $$X$$ باشد، الگوریتم برآورد مناسب برای پارامترهای مدل رگرسیونی کمترین مربعات یعنی $$B$$ و $$B_0$$‌ را ارائه خواهد کرد.

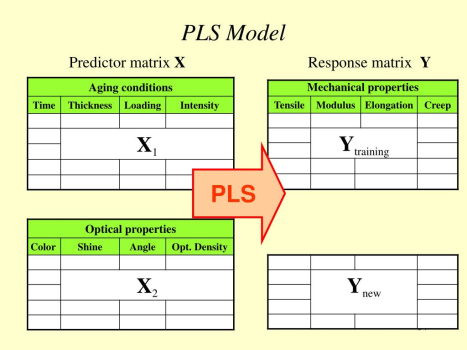
توسعه روش‌های حل معادلات ساختاری PLS

در سال 2002 روش جدیدی به نام «تصویر متعامد ساختارهای پنهان» (orthogonal projections to latent structures) منتشر شد که به اختصار OPLS نامیده می‌شود. در OPLS، داده‌های متغیر پیوسته به اطلاعات پیش‌بین و غیر همبسته تفکیک می‌شوند. این امر منجر به بهبود تشخیص و همچنین مصورسازی (Visualization) با تفسیر آسان‌تر می‌شود. البته باید توجه داشت که در مدل OPLS فقط تفسیر پذیری بهبود یافته ولی پیش بینی مدل‌های PLS را تغییر نمی‌دهد.

نوع دیگری از مدل PLS با نام L-PLS، رگرسیون PLS را به سه بلوک متصل از داده‌ها گسترش می‌دهد. به طور مشابه، هنگام کار با متغیرهای گسسته، مانند مطالعات طبقه بندی و «نشانگر زیستی» (Biomarker)، ممکن است از مدل‌های تجزیه و «تحلیل تشخیصی» (Discriminant Analysis) یا تحلیل افتراقی استفاده ‌شود که اغلب با نام خلاصه OPLS-DA مورد اشاره محققین قرار می‌گیرد.

در سال 2015 تکنیک حداقل مربعات جزئی با روش «فیلتر رگرسیون سه گام» (three-Pass Regression Filter) ‌به اختصار 3PRF، ادغام شد. با فرض اینکه تعداد مشاهدات و متغیرها زیاد باشد، مدل 3PRF و همچنین ترکیب آن با PLS به طور مجانبی نرمال بوده و برای بهترین پیش بینی یک مدل خطی از عامل‌های پنهان ارائه می‌کند. کاربرد چنین مدلی در داده‌های بازار سهام، نشانگر پیشگویی مناسب برای جریان نقدی توسط این مدل است.

یک نسخه PLS مبتنی بر «تجزیه مقادیر منفرد» (Singular Value Decomposition) یا SVD، پیاده سازی محاسبات با حافظه کمتر را میسر می‌سازد. به این ترتیب می‌توان از آن برای حل مسائل چند متغیره با ابعاد بالا بهره برد. برای مثال ارتباط میلیون‌ها نشانگر ژنتیکی با هزاران ویژگی تصویربرداری در ژنتیک را می‌توان روی سخت افزارهای ارزان قیمت و خانگی اجرا کرد.

«همبستگی معادلات ساختاری جزئی» (PLS correlation) که با حروف PLSC مشخص می‌شود،  یکی دیگر از روش‌های مربوط به رگرسیون PLS است که در تصویربرداری عصبی و اخیراً در علوم ورزشی نیز مورد استفاده قرار گرفته است. از این روش، برای تعیین کمیت قدرت و شدت رابطه بین بلوک‌هایی از مجموعه داده‌ها بهره می‌برند. PLSC داده‌ها را به دو بلوک (زیر گروه) تقسیم می‌کند که هر کدام شامل یک یا چند متغیر هستند. سپس با استفاده از تجزیه مقادیر منفرد (SVD) قدرت هر رابطه (یعنی مقدار اطلاعات مشترک) را اندازه‌گیری می‌کند که ممکن است بین دو زیر گروه از عامل‌ها وجود داشته باشد. در اینجا محاسبه SVD، برای تعیین مجموع مقادیر منفرد ماتریس کوواریانس گروه‌های فرعی لازم است.

کاربردهای مدل معادلات ساختاری PLS

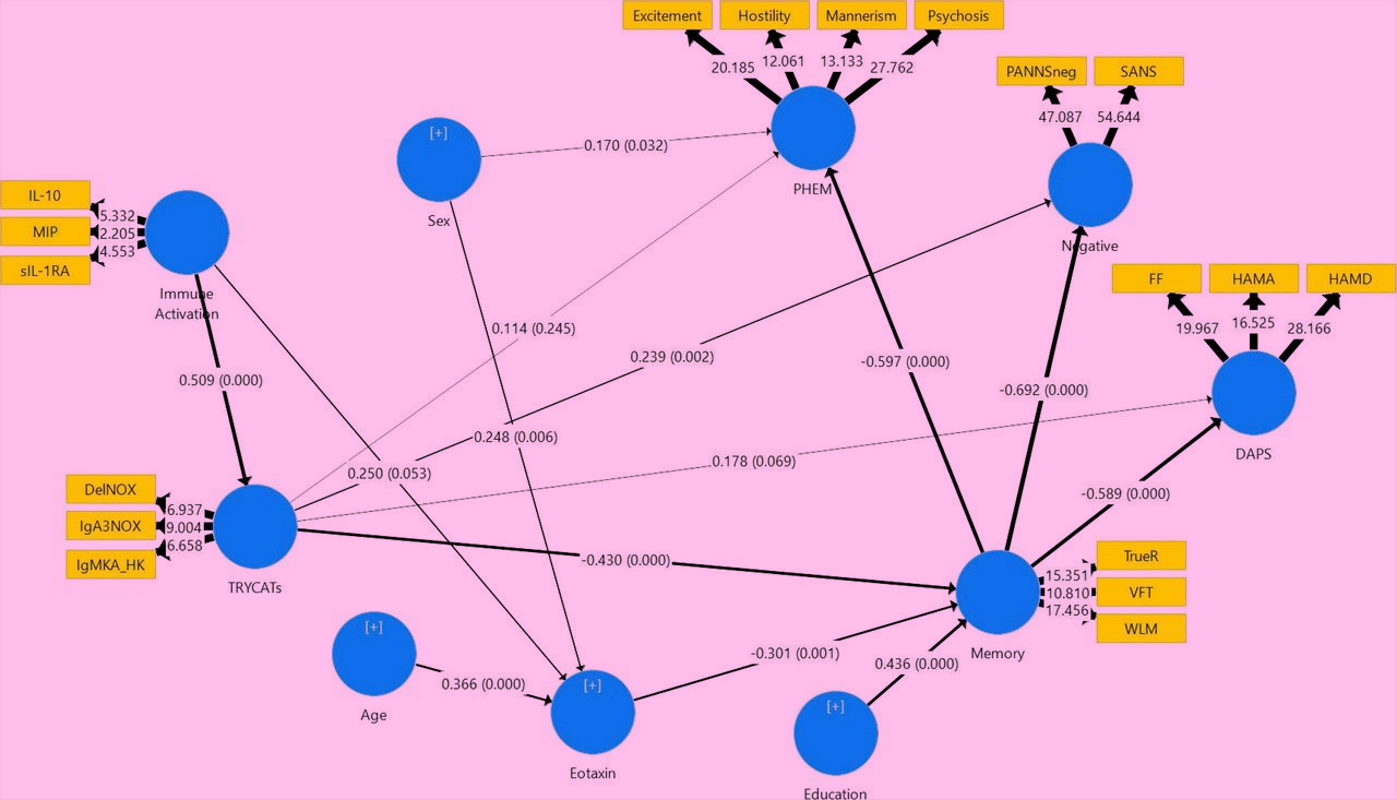
فرض کنید یک محقق می‌خواهد تاثیر رضایت شغلی بر دو عامل دیگر یعنی تعهد سازمانی و غرور سازمانی را مورد بررسی قرار داده و آن‌ها را اندازه‌گیری کند. متاسفانه روشی برای اندازه‌گیری این متغیرها وجود ندارد. ولی واضح است که رضایت شغلی یک متغیر مستقل و تعهد سازمان و غرور سازمانی، متغیرهای وابسته هستند. ولی به هر حال برای جمع‌آوری متغیرهای قابل مشاهده پرسشنامه‌ای به کار رفته است که سعی دارد این متغیرها را براساس گویه‌های دیگر قابل اندازه‌گیری کند.

به این ترتیب متغیرهای موجود در پرسشنامه که قابل اندازه‌گیری و محاسبه هستند، قرار است متغیرهای مکنون و پنهان را شناسایی کرده و از طرفی ارتباط بین این متغیرها را به کمک مدل برازش شده با الگوریتم PLS مشخص کرده و رابطه بین رضایت شغلی و تعهد سازمان و همچنین غرور سازمانی به صورت یک مدل خطی مشخص می‌شود.

به یاد دارید که در اینجا غرور سازمانی و تعهد سازمانی، قابل پیش بینی شده و براساس متغیرهای موجود در سوالات پرسشنامه، دو مدل ارائه و توسط PLS، آزمون‌های معنی‌داری پارامترها صورت خواهد گرفت.

به عنوان یک مثال دیگر به حوزه کسب و کار می‌پردازیم. می‌خواهیم به کمک یک طرح تحقیقی، وفاداری مشتریان یک محصول فرهنگی را مورد بررسی قرار دهیم. میزان فروش محصول فرهنگی یا قیمت آن با توجه به مسئولیت اجتماعی افراد به هنر ممکن است مورد نظر باشد. از طرفی برند ارائه کننده این محصول نیز در نزد مخاطبان اثرگذار است. مدل آماری برای نمایش رابطه بین وفاداری و مسئولیت اجتماعی را در نظر گرفتن تصویر ذهنی مخاطبان از شرکت ارائه دهنده، توسط مدل PLS سنجیده می‌شود. مشخص است که وفاداری و تصویر ذهنی و همچنین میزان مسئولیت اجتماعی افراد متغیرهای پنهان هستند و برای اندازه‌گیری آن‌ها باید از متغیرهای دیگری بهره برد که توسط پرسشنامه‌های استاندارد قابل استفاده است.

نرم‌افزارهای به کارگیری PLS

نرم‌افزارهای متعددی برای اجرای مدل معادلات ساختاری PLS‌ به کار می‌روند که البته از لحاظ محاسباتی شبیه یکدیگر بوده ولی امکانات و نحوه نمایش خروجی‌ها، متفاوت است. شکل نمایشی برای نمودارهای علت و معلولی یا ارتباط بین متغیرهای عامل (پنهان) با متغیرهای اصلی، همچنین بعضی از محاسبات جانبی و نحوه ارائه خروجی‌ها، این نرم‌افزارها را از یکدیگر متمایز می‌سازد. در ادامه بعضی از چنین برنامه‌هایی را معرفی کرده و به بعضی از خصوصیات و ویژگی‌های آن‌ها نیز اشاره خواهیم کرد.

نرم افزار SmartPLS

این نرم افزاری با رابط کاربری گرافیکی (GUI) برای «مدل سازی معادلات ساختاری» (Structural Equation Modeling) مبتنی بر واریانس با استفاده از روش مدل سازی حداقل مربعات جزئی (PLS) است.

فیلم آموزش اسمارت پی ال اس SmartPLS برای مدلسازی معادلات ساختاری و تحلیل آماری در مقاله و پایان نامه در فرادرس

کلیک کنید

به کمک SmartPLS برآورد پارامترهای مدل‌های مسیر با متغیرهای نهفته، با استفاده از الگوریتم PLS-SEM میسر شده، همچنین معیارهای ارزیابی نتایج استاندارد را نیز محاسبه می‌شود. به عنوان مثال، برای مدلهای اندازه‌گیری بازتابی معیاری برای ارزیابی مورد استفاده قرار می‌گیرد و از تجزیه و تحلیل آماری اضافی (به عنوان مثال، تحلیل عاملی تأییدی، تجزیه و تحلیل نقشه اهمیت عملکرد، تقسیم بندی، چند گروه، پشتیبانی می‌کند. از آنجا که SmartPLS به زبان برنامه‌نویسی جاوا تولید شده است، می‌توان آن را روی سیستم عامل‌های مختلف رایانه با سیستم عامل‌های «ویندوز» (Windows) و «مک» (Mac OS) اجرا کرد.

نرم افزار LISREL

نرم‌افزار لیزرل (LISREL)‌ که خلاصه‌ای از عبارت Linear Structural Relations یا «روابط ساختار خطی» است، در دانشگاه Uppsala سوئد، توسط «کارل یورسکوگ»‌ (Karl Jöreskog) توسعه یافت.

نسخه‌های اولیه، فقط به کمک خط فرمان امکان اجرای دستورات را به کاربران می‌داد ولی در نسخه‌های جدید به کمک نوار فهرست و رابط گرافیکی با کاربران در ارتباط است. این نرم‌افزار توسط شرکت «بین المللی نرم افزار علمی» (Scientific software international) در حال توسعه بوده و نسخه‌های جدید و به روز آن تولید می‌شود.

نرم افزار  Unscrambler X

به کمک نرم‌افزار Unscramber تحلیل‌های چند متغیره و رگرسیون چندگانه با تکنیک‌های PLS امکان‌پذیر است. Unscrambler X یک محصول نرم افزاری تجاری برای کالیبراسیون داده‌های چند متغیره محسوب می‌شود که اغلب در طیف سنجی مادون قرمز و توسعه مدل‌های پیش بینی کننده برای استفاده در تجزیه و تحلیل طیف سنجی در زمان واقعی، استفاده می‌شود. این نرم افزار در ابتدا توسط «هارالد مارتنز» (Harald Martens) و بعداً توسط شرکت نرم افزار CAMO توسعه یافته است.

فیلم آموزش آنالیز داده های چند متغیره با نرم افزار Unscrambler X در فرادرس

کلیک کنید

نرم افزار AMOS

AMOS یک نرم افزار آماری است که به ویژه برای مدل سازی معادلات ساختاری (SEM)، تجزیه و تحلیل مسیر و تحلیل عاملی تأییدی استفاده می‌شود. همچنین به عنوان تجزیه و تحلیل کوواریانس یا نرم افزار مدل‌سازی علت و معلولی مورد توجه محققین است.

AMOS یک برنامه تصویری برای مدل سازی معادلات ساختاری (SEM) نیز ارائه می‌دهد. در AMOS، کاربران می‌توانند با استفاده از ابزارهای ساده طراحی، مدل‌ها را به صورت گرافیکی و ارتباط بین نمادها، ترسیم کنیم. AMOS به سرعت محاسبات SEM را انجام می‌دهد و نتایج را به شکل زیبا و نموداری ظاهر می‌سازد.

خلاصه و جمع‌بندی

در این نوشتار با روش معادلات ساختاری PLS یا حداقل مربعات جزئی (پاره‌ای) آشنا شدید و کاربردهای آن را در برآورد مدل‌های رگرسیونی و پیش‌بینی فرا گرفتید. مشخص شد که شناسایی متغیرهای پنهان (مکنون) هدف اصلی به کارگیری معادلات ساختاری PLS است. باید توجه داشت که ایجاد چنین مدل‌های رگرسیونی، عامل‌های جدیدی را برای مدل پیش‌بین پیدا می‌کند که دارای مفهوم بوده و امکان کاهش تعداد متغیرها و کم کردن ابعاد مسئله را به تعداد عامل‌های جدید، به همراه دارند.

با توجه به بار محاسباتی زیاد در چنین مدل‌هایی، استفاده از نرم‌افزارهای محاسبات آماری مانند SmartPLS یا Unscrambler همچنین LISREL از ضروریات محسوب می‌شود. این نرم‌افزارها در حوزه تحقیقات علوم اجتماعی، مالی و کسب و کار همچنین روانشناسی و شیمی به کار می‌روند. در نوشتارهای دیگر از مجله فرادرس به این نرم‌افزارها خواهیم پرداخت و نحوه کار برای تحلیل مدل‌های خطی را فرا می‌گیریم.