فرآیند پواسون و توزیع آن – به زبان ساده + مفاهیم و کاربردها
فرآیند پواسون یکی از پرکاربردترین فرآیندهای شمارش است. به طور معمول از این فرآیند در رخدادهایی استفاده میشود که با آهنگی مشخص و کاملا تصادفی رخ میدهند. این رخدادهای تصادفی، هیچ ساختار مشخصی ندارند. به عنوان مثال، فرض کنید که با مراجعه به دادههای تاریخی میدانیم که زلزله در ناحیهای مشخص با آهنگ ۲ بار در ماه رخ میدهد. فرآیند پواسون، فرایندی مناسب برای مدلسازی وقوع زلزله در این ناحیه است. از توزیع پواسون برای مدلسازی اتفاقاتی مانند تعداد تصادفات جادهای در ناحیهای مشخص، تعداد مراجعه افراد به سایتهای اینترنتی و تعداد فوتونها روی فتودیود استفاده میشود.
از توزیع پواسون برای مدلسازی احتمال رخ دادن تعدادی اتفاق تکی یا گسسته در بازه زمانی مشخص، استفاده میشود. اتفاقات تکی، گسسته و مستقل از یکدیگر هستند و نمیتوانند در زمان یکسانی رخ دهند. بنابراین، سه شرط کلی گسسته بودن اتفاقات، همزمان نبودن و مستقل بودن اتفاقات از یکدیگر را میتوانیم برای توزیع پواسون در نظر بگیریم. توزیع پواسون را میتوانیم توسط پارامتری به نام $$\lambda$$ تعریف کنیم. $$\lambda$$ به صورت تعداد رخدادها در بازه زمانی تعیین شده تعریف میشود و نرخ یا آهنگ نام دارد. همچنین، $$\lambda$$ را میتوان برابر میانگین و واریانس توزیع موردنظر نیز در نظر گرفت. در این مطلب از مجله فرادرس، ابتدا فرآیند پواسون را به زبان ساده تعریف میکنیم. سپس، فرمول توزیع پوآسون را اثبات و با حل چند مثال، استفاده از آن را توضیح میدهیم. در پایان، توزیع پواسون را در اکسل و پایتون با یکدیگر بررسی میکنیم.
فرآیند پواسون چیست؟
فرآیند پوآسون، نام خود را از «سایمون دنیس پواسون» (Simeon Denis Poisson) گرفته است. از توزیع پواسون برای مدلسازی احتمال رخ دادن تعدادی اتفاق تکی یا گسسته در بازه زمانی مشخص، استفاده میشود. استفاده از این توزیع در صفهای انتظار یا نظریه صف، یکی از رایجترین کاربردهای آن است. توزیع پواسون تقریب بسیار خوبی برای تعداد افرادی است که در بازه زمانی داده شده به مکانی خاص میرسند. همچنین، از این توزیع میتوان برای تقریب تعداد تماسهای گرفته شده در طول روز یا تعیین تقریبی تعداد ورقههای پرینت گرفته در مدت یک دقیقه استفاده کرد.
اتفاقات تکی، گسسته و مستقل از یکدیگر هستند و نمیتوانند در زمان یکسانی رخ دهند. بنابراین، سه شرط کلی را میتوانیم برای توزیع پواسون در نظر بگیریم:
- اتفاقات گسسته هستند، بنابراین به راحتی شمرده میشوند.
- اتفاقات نمیتوانند همزمان رخ دهند.
- اتفاقات مستقل از یکدیگر هستند.
توزیع پواسون را میتوانیم توسط پارامتری به نام $$\lambda$$ تعریف کنیم. $$\lambda$$ به صورت تعداد رخدادها در بازه زمانی تعیین شده تعریف میشود و نرخ یا آهنگ نام دارد. همچنین، $$\lambda$$ را میتوان برابر میانگین و واریانس توزیع موردنظر نیز در نظر گرفت. انحراف معیار نیز برابر جذر $$\lambda$$ است. به این نکته توجه داشته باشید که از توزیع پواسون میتوانیم برای تعداد اتفاقات در بازههای دیگر مانند فاصله و مساحت نیز استفاده کنیم. برای درک بهتر توزیع پواسون مثال سادهای را با یکدیگر بررسی میکنیم.
مثال گربه و موش
فرض کنید گربهای دارید که علاقهمند به آوردن موشهای مرده برای شما است. گربه شما به طور متوسط یک موش را در هفته برای شما به ارمغان میآورد. با چه احتمالی گربه شما چهار موش در هفته به شما کادو میدهد؟

این مثال را میتوان به خوبی با توزیع پواسون شبیهسازی کرد. در این مثال، آوردن موش توسط گربه، اتفاق موردنظر است و بازه زمانی تعیین شده برابر یک هفته خواهد بود. مقدار $$\lambda$$ برابر یک است. با چه احتمالی گربه ۴ موش در هفته برای شما میآورد؟
$$P ( X = 4 ) = ? $$
برای بهدست آوردن احتمال موردنظر از اکسل و فرمول POISSON.DIST() استفاده میکنیم. این فرمول، سه ورودی دارد.
- $$x$$ تعداد پیروزیهای آزمایش موردنظر و در مثال گربه و موش مرده، مقدار $$x$$ برابر ۴ است.
- mean میانگین و در این مثال برابر یک، یک موش در هفته، است.
- $$cumulative$$ آخرین ورودی تابع POISSON.DIST() و میتواند True یا False باشد. اگر تمام احتمالات، شامل آوردن چهار موش مرده توسط گربه را بخواهیم، $$cumulative$$ را برابر True و اگر دقیقا احتمال آوردن چهار موش مرده توسط گربه را بخواهیم، $$cumulative$$ را برابر False قرار میدهیم.
اگر $$cumulative$$ را برابر False قرار دهیم، نتیجه بهدست آمده به ما میگوید که احتمال آوردن چهار موش توسط گربه در هفته برابر ۰/۰۱۵ خواهد بود. مقدار احتمال بهدست آمده بسیار کوچک است. این بدان معنا است که گربه ممکن است ۴ موش مرده در هفته برای شما بیاورد، اما احتمال آن بسیار کوچک است.
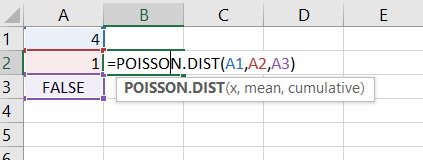
اگر احتمال آوردن یک، دو، سه و چهار موش توسط گربه را بخواهیم باید $$cumulative$$ را برابر True قرار دهیم. همانطور که در تصویر زیر دیده میشود، احتمال آنکه گربه در یک هقته موش مردهای نیاورد یا یک موش مرده برای شما بیاورد، برابر ۰/۳۶۸ است.
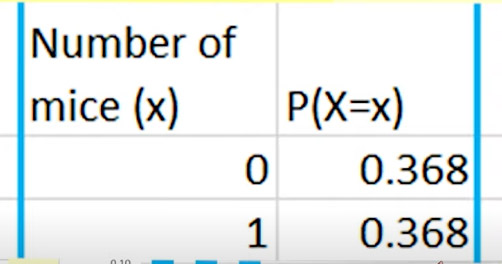
همچنین، احتمال آنکه گربه بیش از یک موش مرده در هفته برای شما بیاورد به شدت کاهش مییابد، به گونهای که احتمال آوردن هفت موش گربه در هفته برابر صفر میشود. در واقع با استفاده از این مدل، گربه ممکن است حتی شش موش مرده در یک هفته برای شما بیاورد، اما احتمال آن بسیار کوچک است.
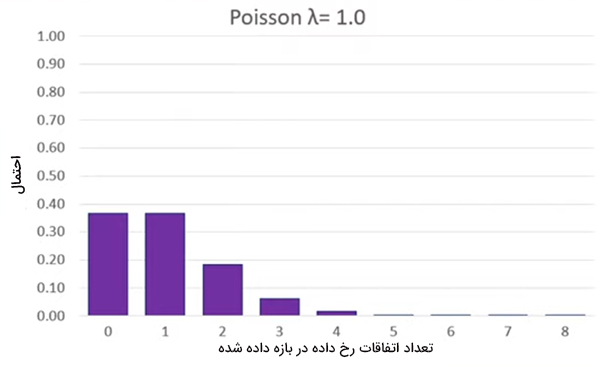
اکنون فرض کنید، گربه هر چهار هفته یک موش میآورد. در این حالت مقدار $$\lambda$$ برابر $$\frac { 1 } { 4 }$$ یا ۰/۲۵ است. اکنون، احتمال آنکه گربه در یک هفته هیچ موشی نیاورد بسیار بزرگتر از حالت قبل و برابر ۰/۷۹ خواهد بود. در ادامه اگر فرض کنیم گربه هر ده هفته یک موش میآورد، مقدار $$\lambda$$ برابر $$\frac { 1 } { 10 }$$ یا ۰/۱ است. در این حالت نیز احتمال آنکه گربه در یک هفته موش مردهای نیاورد به مقدار ۰/۹ افزایش مییابد. در مقابل، اگر مقدار $$\lambda$$ افزایش یابد، نمودار احتمال برحسب تعداد اتفاقات در بازه زمانی مشخص جالبتر میشود. با افرایش مقدار $$\lambda$$ نمودار احتمال برحسب تعداد اتفاقات حول مقدار احتمال، متقارنتر میشود.
مثال بستنی فروش
در ادامه، مثال دیگری را در رابطه با فرآیند پواسون با یکدیگر بررسی میکنیم. بستیفروشی را فرض کنید که در یکی از خیابانهای شلوغ تهران بستنی میفروشد. براساس تاریخچه فروش، بستنیفروش میداند که در روزهای آفتابی هر ساعت، ۳۰ نفر از او بستنی میخرند. از آنجا که بستنیفروش کمی با آمار و احتمال آشنایی دارد به این نتیجه رسیده که توزیع پواسون برای مدلسازی تعداد مشتریهای بستنی، بسیار مناسب است. در این حالت، مقدار $$\lambda$$ برابر ۳۰ مشتری بر ساعت است.
| تعداد اتفاقات گسسته | بازه زمانی داده شده |
| تعداد مشتریها | در یک ساعت |
| ۳۰ | یک ساعت |
بستنیفروش میخواهد بداند با چه احتمالی کمتر از سه مشتری در پنج دقیقه بعد از او بستنی میخرند. در واقع او میخواهد احتمال $$x < 3 $$ را بهدست آورد. از آنجا که بازه زمانی موردعلاقه بستنیفروش برابر ۵ دقیقه است، او باید تعداد مشتریها در یک ساعت را به تعداد مشتریها در ۵ دقیقه تبدیل کند.

بنابراین، به هنگام محاسبه احتمال پواسون باید به این نکته توجه داشته باشیم.
$$\lambda = 30 \enspace per \enspace hour \\ = 30 \times \frac { 5 } { 60 } = .5 \enspace per \enspace 5 \enspace minute \enspace interval$$
بر طبق رابطه بالا، ۳۰ مشتری در هر ساعت به ۲/۵ مشتری در ۵ دقیقه تبدیل شده و مقدار $$\lambda$$ برابر ۲/۵ است. توجه به این نکته مهم است که به هنگام صحبت در مورد متغیرهای تصادفی گسسته، $$ P ( X \leq 2 ) $$ مشابه $$ P ( X \leq 3 ) $$ خواهد بود. در واقع در عبارت $$ P ( X \leq 3 ) $$، تعداد ۳ در نظر گرفته نشده است. مقدار احتمال در اکسل برابر ۰/۵۴۳۸۱۳۱۲ بهدست میآید. بنابراین، با احتمال ۵۴ درصد در ۵ دقیقه بعد کمتر از ۳ مشتری از بستنیفروش بستنی خواهند خرید. با توجه به نمودار نشان داده شده در ادامه مشاهده میکنید که بستنیفروش با احتمال زیادی یک، دو یا سه مشتری در ۵ دقیقه بعد خواهد داشت. احتمال نداشتن مشتری در ۵ دقیقه بعد در حدود ۸ درصد است.
نیازها و فرضیات فرآیند پواسون چیست ؟
در فرآیند پواسون باید فرضیات زیر را در نظر بگیریم:
- اتفاقات تکی نمیتوانند همزمان رخ دهند.
- اتفاقات تکی مستقل از یکدیگر هستند و هیچ تاثیری روی یکدیگر ندارند.
- احتمال رخ دادن یک رویداد به مدت زمان وقوع آخرین رویداد وابسته نیست.
با در نظر گرفتن این سه فرضیه اینگونه به نظر میرسد که مدل ساخته شده با واقعیت متفاوت است. به هنگام استفاده از مدل پواسون باید به سه نکته اساسی و کلیدی توجه داشته باشیم:
- باید به طور دقیق بررسی کنیم که $$\lambda$$ با بازه زمانی استفاده شده در مدل مطابقت دارد (مثال بستنیفروش).
- باید دقت داشته باشیم که آیا احتمال اتفاقات تکی یا احتمال تعدادی از اتفاقات را میخواهیم بهدست آوریم. با تعیین این حالت میتوانیم $$cumulative$$ در فرمول تابع توزیع پواسون را برابر True یا False قرار دهیم.
- در آخر باید در نظر داشته باشیم که آیا احتمال ما مقدار داده شده را دارد یا خیر.
متغیر تصادفی چیست؟
در بخش قبل و در توضیح فرآیند پواسون با عبارتی به نام متغیر تصادفی آشنا شدیم. در این بخش کمی در مورد مفهوم این عبارت توضیح میدهیم. به زبان ساده، متغیر تصادفی نتیجه اتفاقی تصادفی است که میتواند اندازه گرفته یا شمارش شود.
در بخش قبل، مثال بستنیفروش را با یکدیگر بررسی کردیم. بستنیفروشی در یکی از خیابانهای شلوغ تهران، بستنی میفروشد و کمی با آمار و احتمال آشنا است. او میخواهد با تحلیل میزان فروش خود، دستیاری استخدام و کار خود را گسترش دهد. بستنیفروش دادههای فروش خود در ماه گذشته را جمعآوری کرده است. جدول زیر تعداد بستنیها و تعداد مشتریهایی که آن تعداد بستنی را خریدهاند، نشان میدهند.
| تعداد بستنی | تعداد مشتریها |
| ۱ | ۲۲۵ |
| ۲ | ۱۷۰ |
| ۳ | ۵۵ |
| ۴ | ۲۰ |
| ۵ | ۲۰ |
| ۶ | ۱۰ |
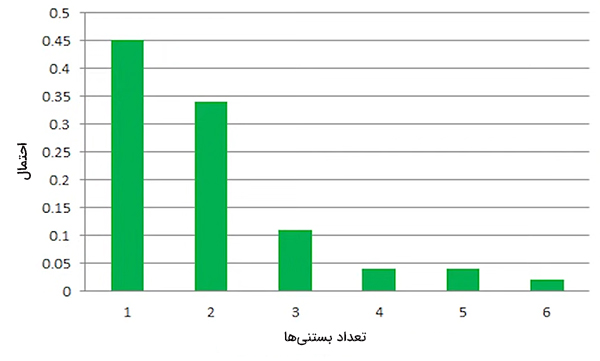
$$x$$ را به صورت تعداد بستنیهای سفارش داده شده توسط مشتری تعریف میکنیم. $$x$$ متغیری تصادفی است. چرا؟ زیرا میتواند متغیرهای متفاوتی داشته باشد و نتیجه اتفاقی تصادفی است. مقدار احتمال هر متغیر $$x$$ را میتوانیم بهدست آوریم. به عنوان مثال مقدار احتمال آنکه هر مشتری یک بستنی بخرد برابر نسبت تعداد مشتریهایی که این تعداد بستنی را خریدهاند، ۲۲۵، بر تعداد کل مشتریها، برابر ۰/۴۵ است. جدول زیر احتمال هر مقدار $$x$$ را نشان میدهد.
| تعداد بستنی | احتمال $$P ( X = x )$$ |
| ۱ | ۰/۴۵ |
| ۲ | ۰/۳۴ |
| ۳ | ۰/۱۱ |
| ۴ | ۰/۰۴ |
| ۵ | ۰/۰۴ |
| ۶ | ۰/۰۲ |
مقدار احتمال برحسب تعداد بستنی را میتوانیم به صورت نمودار میلهای زیر نشان دهیم.
با استفاده از نمودار رسم شده در بالا میتوانیم به سوالات زیر پاسخ دهیم:
- با چه احتمالی مشتری بعدی دقیقا یک بستنی میخرد؟ با توجه به نمودار بالا احتمال آنکه $$x$$ یک باشد، برابر ۰/۴۵ یا ۴۵ درصد است.
- از میان ۲۰۰ مشتری، چه تعداد افراد سه بستنی میخرند؟ برای پاسخ به این پرسش باید $$P ( X > 2 ) $$ را بهدست آوریم. بنابراین، از روی نمودار یا جدول، احتمالهای $$P ( X = 4 ) $$ و $$ P ( X = 5 ) $$ و $$ P ( X = 6 ) $$ را با یکدیگر جمع میکنیم.
$$ P ( X > 3 ) = P ( X = 4 ) + P ( X = 5 ) + P ( X = 6 ) = 0.04 + 0.04 +0.02 = 0.1$$
۲۰۰ مشتری داریم که ۰/۱ یا ۲۰ نفر از آنها احتمالا بیشتر از ۳ بستنی میخرند.
مثال بستنیفروش و تعداد بستنیهایی که میفروشد، مثالی در رابطه با توزیع گسسته است. همچنین، در بخش قبل دیدم که تعداد مشتریهایی که در یک ساعت بستنی میخرند را میتوان به عنوان مدل متغیرهای تصادفی گسسته در نظر گرفته شود. به این نکته توجه داشته باشید که متغیرهای تصادفی گسسته را میتوانیم به راحتی بشماریم. در حالت کلی، برخی متغیرها، متغیر تصادفی پیوسته با متغیر تصادفی گسسته هستند و یا متغیر تصادفی نیستند.
مثال ۱: وزن چمدان متغیری تصادفی و پوسته است.
مثال ۲: تعداد تلفنهای ضروری در هر ساعت متغیری تصادفی و گسسته است.
مثال ۳: وضعیت تاهل متغیری تصادفی نیست.
میتوانیم مقدار انتظاری متغیر $$x$$ یا جمعیت میانگین را بهدست آوریم.
$$E ( X ) = \Sigma x P ( x ) $$
فرمول پواسون و اثبات آن
برخی متغیرهای تصادفی، پیوسته هستند. متغیرهای تصادفی پیوسته میتوانند در محدوده تعییر شده هر مقداری، حتی کسری، داشته باشند. به طور مثال، اگر بخواهیم وزن بستنی را مدلسازی کنیم، محدودهای از متغیرهای برحسب گرم در نظر میگیریم. این حالت را میتوانیم به صورت متغیرهای تصادفی پیوسته مدلسازی کنیم. بستنیفروش دوست دارد بداند آمادهسازی بستنی و خدمت به مشتری چه مقدار طول میکشد. این دو حالت، متغیرهای تصادفی پیوسته هستند و برحسب دقیقه یا ثانیه اندازه گرفته میشوند.
پلیس راهنمایی و رانندگی را در نظر بگیرید که در خیابان ایستاده است و به این فکر میکند که چه تعداد اتومبیل از نقطه مشخصی در خیابان در مدت زمانی مشخص عبور میکنند. او علاقهمند است که بداند با چه احتمالی صد ماشین یا پنج ماشین در ساعت از نقطه مشخص شده عبور میکنند. برای پاسخ به این پرسش، ابتدا عددی تصادفی به نام $$X$$ را مشخص میکنیم. $$X$$ میتواند تعداد اتومبیلهایی باشند که در مدت زمان یک ساعت از نقطهای مشخص شده در خیابان عبور میکنند. توزیع تصادفی این عدد تصادفی را میخواهیم بهدست آوریم. با بهدست آوردن این توزیع، به راحتی میتوانیم احتمال عبور هر تعداد اتومبیل را در مدت زمان یک ساعت بهدست آوریم.

برای بهدست آوردن توزیع تصادفی $$X$$ دو فرضیه را باید در نظر بگیریم:
- هر ساعت در نقطه مشخص شده در خیابان با ساعتهای دیگر هیچ تفاوتی ندارد. این فرضیه میتواند اشتباه باشد. زیرا ساعتهای پرترافیک با ساعتهایی با ترافیک کمتر متفاوت هستند.
- اگر در ساعتی در روز تعداد زیادی اتومبیل از نقطه مشخص شده در خیابان بگذرند، این بدان معنا نیست که تعداد کمتری اتومبیل در ساعتهای بعدی از آن نقطه خواهند گذشت. به بیان دیگر، تعداد اتومبیلهای عبوری از نقطه مشخص شده بین ساعت ۱۰ تا ۱۱ هیچ تاثیر و ارتباطی با تعداد اتومبیلهای عبوری از آن نقطه بین ساعت ۱۱ تا ۱۲ ندارد. هر ساعت از روز مستقل از ساعت دیگر است.
با استفاده از این دو فرضیه توزیع تصادفی متغیر $$X$$ را بهدست میآوریم. نخستین کاری که انجام میدهیم بهدست آوردن مقدار میانگین به صورت تقریبی است. این کار را میتوانیم برای هر توزیعی انجام دهیم. برای انجام این کار روی نمودار مینشینیم و مقدار $$X$$ را در ساعتهای مختلف روز اندازه میگیریم و میانگین آن را بهدست میآوریم. این کار مقدار تقریبی خوبی از متغیر $$X$$ به ما میدهد. از آنجا که $$X$$ متغیری تصادفی است، با بهدست آوردن مقدار تقریبی میانگین میتوانیم مقدار انتظاری آن را بهدست آوریم. مقدار انتظاری متغیر $$X$$ را با $$ E ( X ) $$ نشان میدهیم. $$ E ( X ) $$ را میتوانیم به صورت زیر بنویسیم:
$$E ( X ) = \lambda$$
$$\lambda$$ میتواند برابر عبور نه ماشین در ساعت از نقطه مشخص شده باشد. برای بهدست آوردن این عدد، تعداد اتومبیلهای عبوری از نقطه مشخص شده را در ساعتهای مختلف روز میشماریم و با تقسیم تعداد کل اتومبیلهای عبوری و تقسیم آن بر تعداد ساعتهای مشاهده شده، میانگین تقریبی را بهدست میآوریم. برای بهدست آوردن فرمول ریاضی $$ E ( X ) $$ از توزیع دوجملهای استفاده میکنیم. تابع توزیع دوجملهای برای متغیر تصادفی $$X$$ به صورت زیر نوشته میشود:
$$P (X: n , p) = ^nC_X p^ X ( 1 - p ) ^ { n - X } \\ or \\ P ( X : n , p ) = ^ n C _ X p ^ X ( q ) ^ { n - X } $$

در رابطه فوق:
- n تعداد آزمایشهای انجام شده است.
- مقدار $$X$$ میتواند ۰، ۱، ۲، ۳ و ... باشد.
- p احتمال موفقیت در یک آزمایش است.
- q احتمال شکست در یک آزمایش و مقدار آن برابر $$1 - p$$ است.
فرمول توزیع دوجملهای همچنین میتواند به شکل زیر نیز نوشته شود:
$$P ( X : n , p ) = \frac { n ! } { x ! ( n - x ) ! } p ^ X ( q ) ^ { n - X }$$
همانطور که در رابطه نوشته شده برای توزیع دوجملهای مشاهده میکنید، مقدار انتظاری متغیر تصادفی $$X$$ با حاصلضرب تعداد آزمایشهای انجام شده و احتمال موفقیت متناسب است. در نتیجه، $$ E ( X ) $$ را میتوانیم به صورت زیر بنویسیم:
$$E ( X ) = \lambda = n \times p $$
$$\lambda$$ تعداد اتومبیلهایی است که هر ساعت از نقطه مشخص شده میگذرند. n را نیز به این صورت در نظر میگیریم که آیا در هر دقیقه اتومبیل از نقطه تعیین شده میگذرد یا خیر. بنابراین، مقدار n میتواند ۶۰ باشد، زیرا هر ساعت برابر ۶۰ دقیقه است. به بیان دیگر، تعداد آزمایشهای انجام شده برابر ۶۰ خواهد بود. همچنین، مقدار p، احتمال موفقیت یا احتمال عبور اتومبیل از نقطه مشخص شده در هر ساعت، برابر $$\frac { \lambda} { 60 } $$ است. بنابراین، $$\lambda$$ را میتوانیم به صورت زیر بنویسیم:
$$\lambda = \frac { cars } { hour } = 60 \ \frac { min } { hour } \times \frac { \lambda } { 60 } \ \frac { cars } { h } $$
اگر عبور اتومبیلها در هر ساعت را به صورت توزیع دوجملهای در نظر بگیریم، احتمال آنکه مقدار متغیر تصادفی $$X$$ برابر k باشد به صورت زیر نوشته میشود:
$$P ( X = k ) = \left(\begin{array}{c} 60\\ k \end{array}\right) \times ( \frac{ \lambda }{ 60 } ) ^ k ( 1 - \frac{ \lambda }{ 60 } ) ^ { 60 - k }$$

توزیع دوجملهای توزیع تقریبا مناسبی است و گاهی به ما نتایج قابلقبولی میدهد. اما مشکلی در این مدل وجود دارد. اگر بیشتر از یک اتومبیل در دقیقه از نقطه مشخص شده بگذرند چه اتفاقی رخ میدهد؟ با فرض عبور یک اتومبیل در هر دقیقه، تعداد موفقیت در هر دقیقه برابر یک است. اگر تعداد بیشتری اتومبیل در دقیقه از نقطه مشخص شده عبور کنند، به جای تقسیم بر دقیقه، بر تعداد ثانیه در یک ساعت تقسیم میکنیم:
$$P ( X = k ) = \left(\begin{array}{c} 3600\\ k \end{array}\right) \times ( \frac{ \lambda }{ 3600 } ) ^ k ( 1 - \frac{ \lambda }{ 3600 } ) ^ { 3600 - k }$$
رابطه بالا با این فرض نوشته شده است که در هر ثانیه یک اتومبیل از نقطه مشخص aده میگذرد. اما سوالی که ممکن است مطرح شود آن است که اگر دو اتومبیل در ثانیه از این نقطه عبور کنند، چه اتفاقی رخ میدهد. در این حالت باید عددی بزرگتر از ۳۶۰۰ انتخاب کنیم. به عنوان مثال، اگر در هر ثانیه دو اتومبیل از نقطه مشخص شده عبور کنند، مقدار ۳۶۰۰ باید در دو ضرب شود. با ادامه این کار به توزیع پواسون میرسیم. بنابراین، توجه به این نکته مهم است که توزیع پواسون از توزیع دوجملهای میآید. در واقع، بار بزرگتر شدن متغیر تصادفی $$X$$ و نزدیک شدن آن به بینهایت، توزیع دوجملهای به سمت توزیع پواسون میل میکند.
$$\lim_{X \rightarrow \infty} ( 1 + \frac{ a }{ X }) ^ X = e ^ a $$
با توجه به آنکه $$\frac { 1 } { n} = \frac { a } { X } $$ یا $$X = n a $$ است، با نزدیک شدن $$X$$ به سمت بینهایت، n نیز به سمت بینهایت میل میکند. رابطه $$\lim_{X \rightarrow \infty} ( 1 + \frac{ a }{ X }) ^ X = e ^ a $$ را میتوانیم به صورت زیر اثبات کنیم:
$$\lim_{n \rightarrow \infty} ( 1 + \frac{ 1 }{ n }) ^ { n a } = \lim_{n \rightarrow \infty} (( 1 + \frac{ 1 }{ n }) ^ { n } ) ^ a = ( \lim_{n \rightarrow \infty} ( 1 + \frac{ 1 }{ n })^ n) ^ { a } = e ^ a $$
توجه به این نکته مهم است که $$( \lim_{n \rightarrow \infty} ( 1 + \frac{ 1 }{ n })^ n) $$ برابر e است. کسر $$\frac { X ! } { ( X - k ) ! } $$ را میتوانیم به صورت زیر بنویسیم:
$$\frac{ X ! }{ ( X - k ) ! }= ( X ) ( X - 1 ) ( X - 2 ) ... ( X - k+1)$$
حاصل ضرب $$( X ) ( X - 1 ) ( X - 2 ) ... ( X - k+1)$$ از ضرب k عبارت تشکیل شده است. به عنوان مثال، مقدار عبارت $$\frac { 7 ! } { ( 7 - 2 ) ! } $$ برابر است با:
$$\frac{ 7 ! }{ ( 7 - 2 ) ! }= \frac { ( 7 ) ( 6 ) ( 5 ) ( 4 ) ( 3 ) ( 2 ) ( 1 ) } { ( 5 ) ( 4 ) ( 3 ) (2 ) ( 1 ) } = 7 \times 6 = 42$$
اکنون میتوانیم توزیع پواسون را بهدست آوریم. همانطور که در مطالب مشاهده کردید توزیع متغیر تصادفی $$X$$ را میتوانبه صورت زیر نوشت:
$$ E ( X ) = \lambda = n . p $$
در این فرمول، $$\lambda$$ تعداد کل موفقیتها بر ساعت، تعداد اتومبیل عبوری بر ساعت، را نشان میدهد. همچنین، n تعداد موفقیت در بازه زمانی کوچکتر و p احتمال موفقیت در بازه زمانی کوچکتر است. همچنین، با افزایش مقدار $$X$$ یا n رابطه فوق را به صورت حدی نوشتیم.
$$P( X = K ) = \lim_{n \rightarrow \infty} \left(\begin{array}{c}n\\ k\end{array}\right) (\frac { \lambda} { n } ) ^ k ( 1 - \frac { \lambda } { n } ) ^ { n - k } $$
سمت راست تساوری فوق را به صورت زیر مینویسیم:
$$\lim_{n \rightarrow \infty} \frac{ n ! }{ ( n - k ) ! k ! } \times \frac { \lambda ^ k } { n ^ k } \times ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - n } $$
همانطور که در مطالب بالاتر دیدم، کسر $$\frac{ n ! }{ ( n - k ) ! k ! }$$ برابر $$( n ) ( n -1 ) ( n - 2 ) ... ( n - k +1 )$$ است. در نتیجه، عبارت فوق را میتوانیم به صورت زیر بنویسیم:
$$\lim_{n \rightarrow \infty}\frac { ( n ) ( n -1 ) ( n - 2 ) ... ( n - k +1 ) }{ n ^ k } \times \frac { \lambda ^ k } { k ! } \times ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - n } $$
برای محاسبه حد فوق باید به ویژگی مهمی در محاسبه حد توجه کنیم:
$$\lim_{x \rightarrow a} f (x ) g ( x ) = \lim_{x \rightarrow a} f ( x ) \lim_{x \rightarrow a} g ( x )$$
از اینرو، حد $$\lim_{n \rightarrow \infty}\frac { ( n ) ( n -1 ) ( n - 2 ) ... ( n - k +1 ) }{ n ^ k } \times \frac { \lambda ^ k } { k ! } \times ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - n } $$ را میتوانیم به صورت زیر بنویسیم:
$$\lim_{n \rightarrow \infty} \frac { (n^ k + ... ) } { n ^ k } \times ( \frac { \lambda ^ k } { k ! } ) \times \lim_{n \rightarrow \infty} ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - k } $$
حاصل حد $$\lim_{n \rightarrow \infty} \frac { (n^ k + ... ) } { n ^ k }$$ برابر یک است. در نتیجه حاصل عبارت فوق را میتوانیم به صورت زیر بنویسیم:
$$1 \times ( \frac { \lambda ^ k } { k ! } ) \times \lim_{n \rightarrow \infty} ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - k } $$
در ادامه، حد $$\lim_{n \rightarrow \infty} ( 1 - \frac { \lambda } { n } ) ^ n \times ( 1 - \frac { \lambda } { n } ) ^ { - k } $$ را بهدست میآوریم. برای انجام این کار از حد زیر استفاده میکنیم:
$$\lim_{n \rightarrow \infty} ( 1 + \frac { a } { n } ) ^ n = e ^ a$$
در نتیجه حاصل حد $$\lim_{n \rightarrow \infty} ( 1 - \frac { \lambda } { n } ) ^ n$$ برابر $$ e ^ { - \lambda} $$ و حاصل حد $$\lim_{n \rightarrow \infty} ( 1 - \frac { \lambda } { n } ) ^ { - k } $$ برابر یک میشود. از اینرو، احتمال آنکه هر ساعت تعداد $$X$$ اتومبیل از نقطه مشخص شده در خیابان بگذرند را میتوانیم به صورت زیر بنویسیم:
$$P ( X = k ) = \lim_{n \rightarrow \infty} = \left(\begin{array}{c}n\\ k\end{array}\right) (\frac { \lambda } { n } ) ^ k ( 1- \frac { \lambda } { n } ) ^ { n - k } = \frac { \lambda ^ k } { k ! } e ^ { - \lambda } $$
فرآیند پواسون همگن چیست؟
فرآیند پوآسون همگن یکی از سادهترین مدلها برای الگوی نقطه مسطح است. میانگین در فرآیند پواسون همگن مستقل از زمان است. برای درک بهتر فرآیند پواسون همگن به تصویر زیر دقت کنید. ایده اصلی در این فرآیند آن است که اتفاقات نقطهای موردعلاقه به طور کاملا مستقل از یکدیگر رخ دادهاند و میدهند. به عدم برهمکنش بین نقطهها، مدل تصادفی فضایی کامل گفته میشود.
در بخش قبل فرمول توزیع پواسون با فرض مستقل بودن کمیت $$\lambda$$ از زمان بهدست آوردیم. اگر این کمیت به زمان وابسته باشد، فرآیند پواسون، ناهمگن خواهد بود.
فرآیند پواسون ناهمگن چیست؟
فرآیند پواسون ناهمگن (Non-homogenous Poisson process | NHPP) تعداد شکستها را تا زمان t نشان میدهد ($$ { N( t ) , t \geq 0 } $$). مشکل اصلی در فرآیند پواسون ناهمگن، تعیین تابع مقدار میانگین مناسب برای نشان داده تعداد شکستهای تجربه شده تا زمانی مشخص است.
با داشتن فرضیههای متفاوت، شکلهای تابعی متفاوتی از تابع مقدار میانگین خواهیم داشت. این دل بر فرضیههای زیر استوار است:
- تعداد شکستها در بازه زمانی t تا t+s به زمان t و بازه زمانی s وابسته و مستقل از گذشته فرآیند است.
- آهنگ شکست فرآیند با استفاده از رابطه زیر داده میشود:
$$ { exactly \enspace one \enspace failure \enspace in \enspace ( t , t + \triangle t ) } = P { N ( t , t + \triangle t ) - N ( t ) = } \lambda ( t ) \triangle t + o ( \triangle t )$$
$$\lambda$$ در رابطه فوق تابع شدت نام دارد.
- در بازه زمانی کوچک $$\triangle t$$، احتمال رخ دادن بیشتر یک شکست قابل چشمپوشی است.
- شرط اولیه برابر صفر است، $$ N ( 0 ) = 0$$.
براساس این مفروضات، احتمال رخ دادن n شکست در بازه زمانی سفر تا t در فرآیند پواسون ناهمگن به صورت زیر نوشته میشود:
$$Pr { N ( t ) = n } = \frac { ( m ( t) ) ^ n } { n ! } e ^ { - m ( t )}$$
$$ m ( t ) $$ به صورت زیر نوشته میشود:
$$Pr { N ( t ) = n } = \frac { ( m ( t) ) ^ n } { n ! } e ^ { - m ( t )}$$
$$\lambda ( t ) $$ تابع شدت نام دارد. به این نکته توجه داشته باشید که تابع مقدار میانگین، $$ m ( t ) $$، غیرکاهشی است.
نمونه سوال توزیع پواسون با جواب
تا اینجا میدانیم فرآیند پواسون و فرمول محاسبه آن چیست. در ادامه، دو مثال در رابطه با فرآیند پواسون با یکدیگر حل میکنیم.
حل مثال اول فرآیند پواسون
در مسابقات لیگ برتر بیسبال به طور متوسط هر ده دقیقه، پنج شرکتکننده به جایگاه ویژه میرسند:
- در بازه زمانی ده دقیقه، با چه احتمالی دقیقا سه شرکتکننده به جایگاه ویژه میرسند؟
- با چه احتمالی دقیقا سه شرکتکننده، در مدت زمان ۲۰ دقیقه به جایگاه ویژه میرسند؟
- با چه احتمالی سه شرکتکننده یا کمتر، مدت زمان ۲۰ دقیقه به جایگاه ویژه میرسند؟
- با چه احتمالی بیشتر از سه شرکتکننده در مدت زمان ۲۰ دقیقه به جایگاه ویژه میرسند؟

پاسخ
توزیع پواسون، توزیع مناسبی برای حل این مثال است، زیرا:
- تعداد افراد رسیده به جایگاه ویژه را میتوانیم به عنوان متغیر تصادفی گسسته در نظر بگیریم.
- مقدار میانگین در صورت مسئله داده شده است.
بنابراین، با توجه به دانستن مقدار میانگین در بازه زمانی داده شده و تصادفی و گسسته بودن متغیر، به راحتی میتوانیم این مثال را با استفاده از توزیع پواسون حل کنیم.
قسمت یکم
فرمول توزیع پواسون به صورت زیر نوشته میشود:
$$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x}
{ x ! }$$
$$\lambda$$ در رابطه فوق، میانگین یا آهنگ وقوع اتفاق در بازه زمانی دلخواه و t تعداد بازه زمانی داده شده است. بر طبق صورت مسئله، هر ده دقیقه ۵ شرکتکننده به جایگاه ويژه میرسند. بنابراین، بازه زمانی داده شده در این مثال برابر ده دقیقه و مقدار $$\lambda$$ در این مثال نیز برابر ۵ است. همچنین، بازه زمانی خواسته شده در قسمت یک برابر ده دقیقه و بنابراین مقدار t برابر یک ده دقیقه، یعنی یک داده شده است.
$$\lambda \times t = 5 \times 1 = 5$$
در نتیجه، با قرار دادن مقدار ۵ به جای $$\lambda t$$ و مقدار ۳ به جای $$x$$ در رابطه $$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x} { x ! }$$، احتمال آنکه در مدت زمان ده دقیقه دقیقا سه شرکتکننده به جایگاه ویژه برسند را بهدست میآوریم:
$$P ( X = 3 ) = P ( 3 ) = \frac { e ^ { - 5 } ( 5 ) ^ 3}{ 3! } \\ P ( 3 ) = 0.14 $$
قسمت دوم
بر طبق صورت مسئله، هر ده دقیقه ۵ شرکتکننده به جایگاه ويژه میرسند. بنابراین، بازه زمانی داده شده در این مثال برابر ده دقیقه و مقدار $$\lambda$$ در این مثال نیز برابر ۵ است. همچنین، بازه زمانی خواسته شده در قسمت دو برابر ۲۰ دقیقه و بنابراین مقدار t برابر دو تا ده دقیقه، یعنی دو داده شده است.
$$\lambda \times t = 5 \times 2 = 10 $$
در نتیجه، با قرار دادن مقدار ۱۰ به جای $$\lambda t$$ و مقدار ۳ به جای $$x$$ در رابطه $$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x} { x ! }$$، احتمال آنکه در مدت زمان ده دقیقه، دقیقا سه شرکتکننده به جایگاه ویژه برسند را بهدست میآوریم:
$$P ( X = 3 ) = P ( 3 ) = \frac { e ^ { - 10 } ( 10 ) ^ 3}{ 3! } \\ P ( 3 ) = 0.0076 $$
قسمت سوم
بازه زمانی خواسته شده در قسمت سه نیز برابر ۲۰ دقیقه و بنابراین مقدار t برابر دو تا ده دقیقه، یعنی دو است. در این قسمت میخواهیم بدانیم با چه احتمالی در مدت زمان بیست دقیقه، سه شرکتکننده یا کمتر به جایگاه ویژه میرسند. بنابراین، مقدار $$x$$ برابر سفر، یک، دو و سه خواهد بود. از اینرو باید، $$ P (0)$$ و $$ P ( 1)$$ و $$ P ( 2) $$ و $$ P ( 3 )$$ را بهدست آوریم. $$ P (0)$$ برابر است با:
$$P ( X = 0 ) = P ( 0 ) = \frac { e ^ { - 0 } ( 10 ) ^0}{ 0! } \\ P ( 3 ) = 4.5 \times 10^ { -5 } $$
به طور مشابه، $$ P (1)$$ برابر است با:
$$P ( X = 1 ) = P ( 1 ) = \frac { e ^ { - 10 } ( 10 ) ^1 }{ 1! } \\ P ( 3 ) = 4.5 \times 10^ { -4 } $$
$$ P (2)$$ برابر است با:
$$ P ( X = 2 ) = P ( 2 ) = \frac { e ^ { - 10 } ( 10 ) ^2 }{ 2! } \\ P ( 3 ) = 0.0023 $$
همچنین، $$P ( 3 ) $$ را نیز در قسمت دو برابر ۰/۰۰۷۶ بهدست آوردیم. در نتیجه، احتمال آنکه در مدت زمان ۲۰ دقیقه ۳ یا کمتر از ۳ شرکتکننده به جایگاه ویژه برسند برابر است با:
$$P ( X \leq 3 ) = P ( 0 ) + P ( 1 ) + P ( 2 ) + P ( 3 ) = 0.0103$$
قسمت چهارم
بازه زمانی خواسته شده در قسمت سه نیز برابر ۲۰ دقیقه و بنابراین مقدار t برابر دو تا ده دقیقه، یعنی دو است. در این قسمت میخواهیم بدانیم با چه احتمالی در مدت زمان بیست دقیقه، سه شرکتکننده یا بیشتر به جایگاه ویژه میرسند.
$$\lambda \times t = 5 \times 2 = 10 $$
احتمال آنکه بیشتر از سه شرکتکننده در مدت زمان بیست دقیقه به جایگاه ویژه برسند برابر است با:
$$P ( X > 3 ) = P ( 4 ) + P ( 5 ) + P ( 6 ) + ...$$
عبارت فوق را میتوان به صورت زیر نیز نوشت:
$$P ( x > 3 ) = 1 - P ( x \leq 3 ) $$
مقدار $$P ( x \leq 3 )$$ را در قسمت سوم بهدست آوردیم. با قرار دادن مقدار آن در رابطه فوق داریم:
$$P ( x > 3 ) = 1 - P ( x \leq 3 ) \\ P( X > 3 ) = 1 - 0.01 = 0.99 $$
بنابراین، با احتمال زیادی در ۲۰ دقیقه بیشتر از ۳ شرکتکننده به جایگاه ویژه میرسند.
مثال دوم توزیع پواسون
برنامهای کامپیوتری برای ترجمه به طور متوسط در هر ۴۰۰ کلمه، سه اشتباه دارد. فرض کنید به صورت تصادفی متنی ۱۲۰۰ کلمهای را انتخاب میکنیم. این متن توسط این برنامه ترجمه میشود.
- با چه احتمالی هیچ اشتباهی در متن ترجمه شده وجود ندارد؟
- با چه احتمالی در متن ترجمه شده بیش از ۱۴ اشتباه وجود دارند؟
- با چه احتمالی کمتر از ۹ اشتباه در متن ترجمه شده وجود دارند؟

پاسخ
توزیع پواسون، توزیع مناسبی برای حل این مثال است، زیرا:
- تعداد اشتباهات ایجاد شده توسط برنامه ترجمه متنی را میتوانیم به عنوان متغیر تصادفی گسسته در نظر بگیریم.
- مقدار میانگین در صورت مسئله داده شده است.
بنابراین، با توجه به دانستن مقدار میانگین در تعداد کلمات داده شده و تصادفی و گسسته بودن متغیر، به راحتی میتوانیم این مثال را با استفاده از توزیع پواسون حل کنیم. به این نکته توجه داشته باشید که بازه داده شده در این مثال، بازه زمانی نیست و تعداد کلمات ترجمه شده است.
قسمت یک
فرمول توزیع پواسون به صورت زیر نوشته میشود:
$$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x}
{ x ! }$$
مقدار $$\lambda$$ در هر ۴۰۰ کلمه برابر ۳ است. در صورت مسئله آمده است که متنی ۱۲۰۰ کلمهای به صورت تصادفی انتخاب و توسط برنامه کامپیوتری ترجمه میشود. از اینرو، باید مثال را در متنی ۲۰۰ کلمهای و نه ۴۰۰ کلمهای، حل کنیم. t تعداد بازه داده شده است. بر طبق صورت مسئله، در هر ۴۰۰ کلمه، ۳ اشتباه پیدا میشود. بنابراین، بازه زمانی داده شده در این مثال برابر ۴۰۰ کلمه و مقدار $$\lambda$$ در این مثال نیز برابر ۳ است. همچنین، بازه خواسته شده در قسمت یک برابر ۱۲۰۰ کلمه و بنابراین مقدار t برابر ۳ تا ۴۰۰ کلمه، یعنی سه داده شده است.
$$\lambda \times t = 3 \times 1 = 3$$
$$\lambda \times t = 3 \times 3 = 9 $$
در نتیجه، با قرار دادن مقدار ۹ به جای $$\lambda t$$ و مقدار ۳ به جای $$x$$ در رابطه $$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x} { x ! }$$، احتمال آنکه در متن ۱۲۰۰ کلمهای هیچ اشتباهی وجود نداشته باشد را بهدست میآوریم:
$$P ( X = 0 ) = P ( 0 ) = \frac { e ^ { - 9 } ( 9 ) ^ 0}{ 0! } \\ P ( 0 ) = 1.23 \times 10 ^ { - 4 } $$
قسمت دو
در این قسمت میخواهیم بدانیم با چه احتمالی در متن ۱۲۰۰ کلمهای انتخاب شده بیش از ۱۴ اشتباه وجود دارد. احتمال وجود بیش از ۱۴ اشتباه را میتوانیم به صورت زیر بهدست آوریم:
$$P ( X > 14 ) = 1 - P (X \leq 14 )$$
برای محاسبه $$P (X \leq 14 )$$ بهتر است از اکسل استفاده کنیم. چرا؟ زیرا برای محاسبه $$P (X \leq 14 )$$ باید احتمال $$P ( 0 )$$ و $$ P ( 1 ) $$ و ... تا $$ P ( 13 ) $$ را بهدست آوریم و با یکدیگر جمع کنیم که کاری وقتگیر و حوصلهسربر است. اکسل به راحتی و در کمترین زمان ممکن این کار را برای ما انجام میدهد.
$$$$P ( X > 14 ) = 1 - P (X \leq 14 )$$ = 1 - poisson.dist ( 14, 9 , 1)$$
در ادامه، در مورد توزیع پواسون در اکسل توضیح میدهیم و چگونگی محاسبه آن در اکسل را با یکدیگر بررسی میکنیم.
$$P ( X > 14 ) = 0.04145 $$
قسمت سه
در این قسمت میخواهیم بدانیم با چه احتمالی در متن ۱۲۰۰ کلمهای انتخاب شده، کمتر از ۹ اشتباه وجود دارد.
$$P ( X \leq 8 ) = P ( 0 ) + P ( 1 ) + P ( 2 ) + P ( 3 ) + P ( 4 ) + P ( 5 ) + P ( 6 ) + P ( 7 ) + P ( 8 )$$
بنابراین، برای بهدست آوردن احتمالِ کمتر از ۹ اشتباه در متن ۱۲۰۰ کلمهای انتخاب شده باید $$P ( 0 )$$ تا $$ P ( 8 ) $$ را محاسبه و با یکدیگر جمع کنیم. راه آسانتر و سریعتر برای محاسبه $$ P ( x \leq 8 ) $$ استفاده از اکسل و دستور poisson.dist(8,9,1) است. مقدار احتمال برابر ۰/۴۵۵۷ بهدست میآید.
توزیع پواسون در اکسل
در این بخش در مورد چگونگی محاسبه فرآیند پواسون در اکسل توضیح میدهیم. همانطور که در مطالب بالا اشاره شد از فرآیند پواسون برای تخمین تعداد اتفاقات در بازه زمانی یا فضایی مشخصی استفاده میشود. به عنوان مثال، در یک ساعت آینده چه تعداد اتومبیل وارد پارکینگ یک مرکز تجاری میشوند. در توزیع پواسون، احتمال وقوع هر اتفاقی در دو بازه زمانی یا فضایی با طول یکسان، برابر است. همچنین، اتفاقات تکی مستقل از یکدیگر هستند و هیچ تاثیری روی یکدیگر ندارند. توجه به این نکته مهم است که حد بالایی برای مقدار X وجود ندارد، اما با افزایش مقدار X، مقدار احتمال کاهش مییابد. به عنوان مثال، احتمال ورود یک تا ۴ اتومبیل به کارواش در مدت زمان ۱۵ دقیقه بسیار بزرگتر از احتمال ورود ۱۰۰ اتومبیل در این مدت زمان به کارواش است.

برای محاسبه پواسون در اکسل از تابع POISSON.DIST استفاده میکنیم. این تابع سه متغیر ورودی دارد:
- $$X$$ اولین متغیر ورودی تابع پواسون در اکسل است.
- Mean یا میانگین دومین متغیر ورودی این تابع در اکسل است.
- Cumulative آخرین متغیر ورودی این تابع است و میتواند دو مقدار صفر (False) یا یک (True) داشته باشد. اگر بخواهیم دقیقا احتمال وقوع n رویداد مشخص را محاسبه کنیم (احتمال ورود دو اتومبیل به کارواش در مدت ۱۵ دقیقه)، مقدار Cumulative را برابر صفر یا False قرار میدهیم. در این حالت، اکسل برای محاسبه $$P ( X )$$ از رابطه $$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x} { x ! }$$ استفاده میکند. اما اگر بخواهیم احتمال رخ دادن تعدادی اتفاق و کمتر از آن تعداد را بهدست آوریم (احتمال ورود دو اتومبیل یا کمتر به کارواش در مدت زمان ۱۵ دقیقه)، مقدار Cumulative را برابر یک یا True قرار میدهیم.
بنابراین، برای محاسبه توزیع پواسون در اکسل باید مقدار X و میانگین را بدانیم. در ادامه، حل مثالی را با استفاده از اکسل با یکدیگر بررسی میکنیم.
مثال اول فرآیند پواسون در اکسل
فرض کنید وبسایتی طراحی کردهاید و تعداد مراجعه به این وبسایت را میخواهید با استفاده از توزیع پواسون بررسی کنید. X برابر تعداد مراجعه به وبسایت شما با آهنگ ۷ مراجعه در دقیقه است. به بیان دیگر، وبسایت شما در هر دقیقه، ۷ بار دیده میشود. برای حل این مثال دو فرض را باید در نظر بگیریم:
- احتمال مراجعه به سایت در هر بازه زمانی یک دقیقهای، یکسان است.
- مراجعه با عدم مراجعه به سایت در هر یک دقیقه، مستقل از مراجعه یا عدم مراجعه به سایت در یک دقیقه دیگر است.
مقدار متوسط در این مثال برابر ۷ است. برای محاسبه احتمال مراجعه به سایت دو ستون در اکسل ایجاد میکنیم. در ستون اول مقدار X را مینویسیم و در ستون دوم مقدار $$ P ( x ) $$ را محاسبه میکنیم.
در ستون مربوط به $$ P ( x ) $$ تابع پواسون را به صورت نشان داده در تصویر زیر فرامیخوانیم.
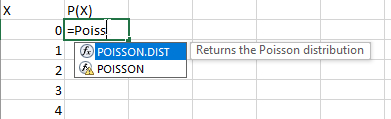
احتمال عدم مراجعه به سایت در هر دقیقه با نوشتن دستور =POISSON.DIST(0,7,0) محاسبه و مقدار ۰/۰۰۰۹۲ بهدست میآید. به این نکته توجه داشته باشید که مقدار Cumulative را برابر یک یا TRUE قرار دادیم، زیرا احتمال تعداد مشخصی مراجعه به سایت را میخواهیم بهدست آوریم.
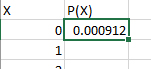
در ادامه $$ P ( x ) $$ را برای یک تا ۱۴ مراجعه به سایت در هر دقیقه، بهدست میآوریم. همانطور که در مقدارهای بهدست آمده برای $$ P ( x ) $$ مشاهده میکنید، احتمال مراجعه به سایت تا تعداد ۷، مقدار میانگین داده شده، به سایت افزایش و پس از آن کاهش مییابد.
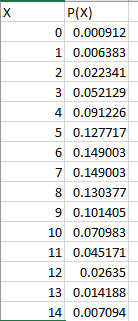
نمودار مقدار $$ P ( x ) $$ را میتوانیم برحسب تعداد مراجعه، X، به صورت زیر رسم کنیم. همانطور که در نمودار زیر نیز مشاهده میکنید، احتمال مراجعه به سایت برای اعداد ۶ و ۷ بیشترین مقدار را دارد و پس از آن، احتمال مراجعه به سایت کاهش مییابد، به گونهای که احتمال ۳۰ مراجعه در دقیقه به سایت تقریبا برابر صفر است.
نکته ۱:
برای محاسبه $$ P ( 0 ) $$ به صورت دستی از رابطه $$P ( X = x ) = P ( x ) = \frac { e ^ { - \lambda t} ( \lambda t) ^ x} { x ! }$$ استفاده میکنیم. در این مثال، X مقدار مراجعه به سایت در هر دقیقه، t بازه زمانی خواسته شده و $$\lambda$$ مقدار متوسط است. با قرار دادن این مقادیر در رابطه فرآیند پواسون، مقدار $$ P ( 0 ) $$ برابر ۰/۰۰۰۹۱ بهدست میآید که با مقدار محاسبه شده توسط اکسل، مطابقت دارد.
مثال دوم فرآیند پواسون در اکسل
فروشگاهی به طور میانگین، روزانه ۱۶ کنسرو تن ماهی میفروشد. احتمال فروش بیش از ۲۰ کنسرو تن ماهی در روز چه مقدار است؟
پاسخ
در این مثال، مقدارهای زیر را میتوانیم در تابع POISSON.DIST قرار دهیم:
- X مقدار اتفاقات رخ داده در بازه زمانی یا مکانی داده شده است.
- $$\lambda$$ مقدار میانگین در بازه داده شده و در این مثال مقدار آن برابر ۱۵ است.
- Cumulative در این مثال برابر یک است، زیرا احتمال فروش بیش از ۲۰ کنسرو تن ماهی در روز را میخواهیم بهدست آوریم.
برای پاسخ به این مثال، از تابع 1-POISSON.DIST(20,15,1) در اکسل استفاده میکنیم، چرا؟ زیرا برای محاسبه $$ P ( X \geq 20 ) $$، باید احتمال فروش ۲۱ تن ماهی، ۲۲ تن ماهی، ۲۳ تن ماهی و ... در روز را محاسبه و مقدارهای بهدست آمده را با یکدیگر جمع کنیم. از آنجا که حد بالایی برای تعداد فروش کنسرو تن ماهی در روز وجود ندارد، انجام این کار وقتگیر و بیهوده است و نتیجه درستی به ما نمیدهد. به جای این کار میتوان مقدار $$ P ( X < 20 ) $$ را محاسبه کنیم و عدد بهدست آمده را از یک کم کنیم. از اینرو، در اکسل از تابع 1-POISSON.DIST(20,15,1) استفاده میکنیم.
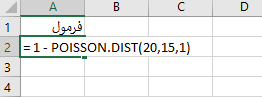
نکته: در این مثال، تابع POISSON.DIST(20, 15, 1) احتمال فروش ۲۰ یا کمتر از ۲۰ تن ماهی در روز را به ما میدهد.
پرسش: با چه احتمالی ۲۵ تا ۲۷ کنسرو ماهی در روز فروخته میشوند؟ برای پاسخ به این پرسش، از فرمول POISSON.DIST(27, 15, 1) – POISSON.DIST(25, 15, 1) در اکسل استفاده میکنیم.
توجه به این نکته مهم است که در نرمافزار اکسل ۲۰۰۷ از تابع POISSON برای محاسبه احتمال استفاده میشد، اما از نسخه ۲۰۰۸ و پس از آن از تابع POISSON.DIST برای محاسبه احتمال استفاده میشود که مقدار دقیقتری را میدهد.
توزیع پواسون در پایتون
در این بخش، در مورد فرآیند پواسون در پایتون صحبت میکنیم. بسیاری از تکنیکها و ابزارهای آماری در علم داده از احتمالات استفاده میکنند. مقدار احتمال وقوع هر رویدادی عددی بین صفر و یک، به گونهای که عدد صفر به معنای عدم وقوع آن رویداد و عدد یک به معنای وقوع حتمی آن رویداد است. همانطور که در بخشهای قبل اشاره شد، در توزیع پواسون از متغیرهای تصادفی استفاده میشود. توزیع احتمال به ما چگونگی توزیع متغیر تصادفی را میدهد.
شهری فرضی به نام پواسون را در نظر بگیرید. حرکت اتوبوسها در این شهر بسیار بینظم است. مدت زمانی که در ایستگاه اتوبوس منتظر ایستادهاید، مستقل از زمان رسیدن اتوبوس قبل است. به عنوان مثال، ممکن است اتوبوس بعدی بلافاصله پس اتوبوس قبلی به ایستگاه اتوبوس برسد. این امکان نیز وجود دارد که اتوبوس بعدی ساعتها پس از اتوبوس قبلی به ایستگاه برسد. به رسیدن اتوبوسها به ایستگاه اتوبوس در شهر پواسون، فرآیند پواسون گفته میشود. مدت زمان اتفاق بعدی به طور کامل مستقل از زمان رخ دادن اتفاق قبلی است.
بسیاری از اتفاقات در زدگی روزمره به صورت مشابهی رفتار میکنند. به عنوان مثال، تولد نوزادان در بیمارستان را میتوانیم به عنوان فرآیند پواسون در نظر بگیریم. زمان تولد هر نوزاد مستقل از زمان تولد نوزادی دیگر است. مثالهای زیاد دیگری مانند برخوردهای مولکولها داخل گاز را نیز میتوانیم به عنوان فرآیند پواسون در نظر بگیریم. به تعداد اتوبوسهای وارد شده به ایستگاه اتوبوس در شهر پواسون توزیع پواسون میگوییم.
همانطور که در مطالب بالا اشاره شد، تعداد متوسط اتوبوسهای وارد شده به ایستگاه اتوبوس در بازه زمانی داده شده یکی از پارامترهای مهم در توزیع پواسون است. با استفاده از توزیع پواسون میتوانیم:
- احتمال ورود X اتوبوس به ایستگاه را در بازه زمانی مشخص بهدست آوریم.
- احتمال ورود X اتوبوس بیشتر یا کمتر به ایستگاه را در بازه زمانی مشخص محاسبه کنیم.

تابع جرم احتمال
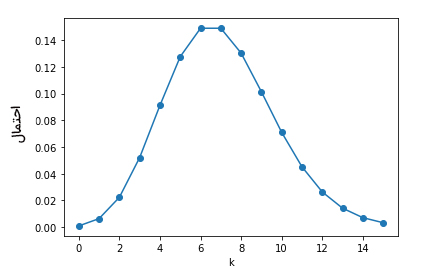
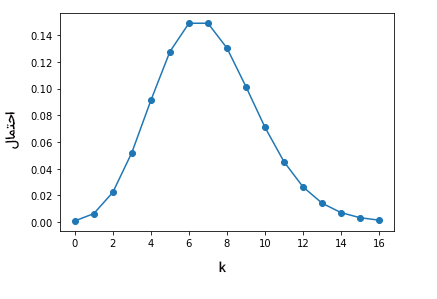
جدول زیر احتمال پواسون تعداد دفعاتی که اتوبوس به ایستگاه وارد میشود را با فرض ورود هر ساعت هفت اتوبوس به ایستگاه، را نشان میدهد.
| $$k$$ | $$P ( k , \lambda) $$ | % |
| ۰ | ۰/۰۰۰۹۱ | ۰/۰۹٪ |
| ۱ | ۰/۰۰۶۳۸ | ۰/۶۴٪ |
| ۲ | ۰/۰۲۲۳۴ | ۲/۲۳٪ |
| ۳ | ۰/۰۵۲۱۳ | ۵/۲۱٪ |
| ۴ | ۰/۰۹۱۲۳ | ۹/۱۲٪ |
| ۵ | ۰/۱۲۷۷۲ | ۱۲/۷۷٪ |
| ۶ | ۰/۱۴۹۰۰ | ۱۴/۹٪ |
| ۷ | ۰/۱۴۹۰۰ | ۱۴/۹٪ |
| ۸ | ۰/۱۳۰۳۸ | ۱۳/۰۴٪ |
| ۹ | ۰/۱۰۱۴۰ | ۱۰/۱۴٪ |
| ۱۰ | ۰/۰۷۰۹۸ | ۷/۰۱٪ |
| ۱۱ | ۰/۰۴۵۱۷ | ۴/۵۲٪ |
| ۱۲ | ۰/۰۲۶۳۵ | ۲/۶۴٪ |
| ۱۳ | ۰/۰۱۴۱۹ | ۱/۴۲٪ |
| ۱۴ | ۰/۰۰۷۰۹ | ۰/۷۱٪ |
| ۱۵ | ۰/۰۰۳۳۱ | ۰/۳۳٪ |
| ۱۶ | ۰/۰۰۱۴۵ | ۰/۱۵٪ |
با استفاده از دادههای نوشته شده در جدول فوق، نمودار تابع جرم احتمال پواسون را به صورت زیر رسم میکنیم.
تابع توزیع تجمعی
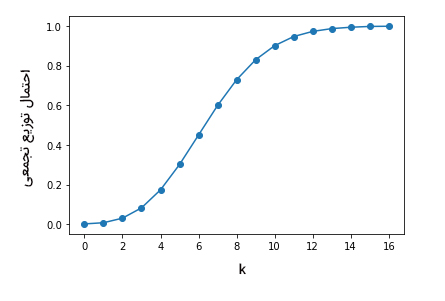
جدول زیر احتمال توزیع تجمعی پواسون، تعداد دفعاتی که اتوبوس به ایستگاه وارد میشود را با فرض ورود هر ساعت ۷ اتوبوس به ایستگاه، را نشان میدهد.
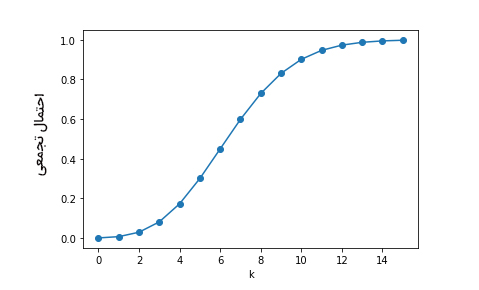
| $$k$$ | $$P ( k , \lambda) $$ | % |
| ۰ | ۰/۰۰۰۹۱ | ۰/۰۹٪ |
| ۱ | ۰/۰۰۷۳۰ | ۰/۷۳٪ |
| ۲ | ۰/۰۲۹۶۴ | ۲/۹۶٪ |
| ۳ | ۰/۰۸۱۷۷ | ۸/۱۸٪ |
| ۴ | ۰/۱۷۲۹۹ | ۱۷/۳٪ |
| ۵ | ۰/۳۰۰۷۱ | ۳۰/۰۷٪ |
| ۶ | ۰/۴۴۹۷۱ | ۴۴/۹۷٪ |
| ۷ | ۰/۵۹۸۷۱ | ۵۹/۸۷٪ |
| ۸ | ۰/۷۲۹۰۹ | ۷۲/۹۱٪ |
| ۹ | ۰/۸۳۰۵۰ | ۸۳/۰۵٪ |
| ۱۰ | ۰/۹۰۱۴۸ | ۹۰/۱۵٪ |
| ۱۱ | ۰/۹۴۶۶۵ | ۹۴/۶۷٪ |
| ۱۲ | ۰/۹۷۳۰۰ | ۹۷/۳٪ |
| ۱۳ | ۰/۹۸۷۱۹ | ۹۸/۷۲٪ |
| ۱۴ | ۰/۹۹۴۲۸ | ۹۹/۴۳٪ |
| ۱۵ | ۰/۹۹۷۵۹ | ۹۹/۷۶٪ |
| ۱۶ | ۰/۹۹۹۰۴ | ۹۹/۹٪ |
با استفاده از دادههای نوشته شده در جدول فوق، نمودار تابع توزیع تجمعی پواسون را به صورت زیر رسم میکنیم.
همانطور که میدانیم با استفاده از تابع جرم احتمال میتوانیم احتمال دقیق ورود X اتوبوس به ایستگاه و با استفاده از تابع توزیع تجمعی میتوانیم احتمال ورود کمتر یا بیشتر از X اتوبوس به ایستگاه را بهدست آوریم. پس از محاسبه تابع جرم احتمال و تابع توزیع تجمعی با استفاده از اکسل یا به صورت دستی، این توابع را با استفاده از پایتون نیز بهدست میآوریم.
مثال توزیع پواسون در پایتون
برای انجام این کار ابتدا کتابخانههای matplotlib و scipy.stat در پایتون را فرا میخوانیم.
1import numpy as np
2import matplotlib.pyplot as plt
3from scipy.stats import poissonدر ادامه، به آرایهای از مقدارهای k برای محاسبه تابع جرم احتمال پواسون نیاز داریم. در بخش قبل، این تابع را برای k از صفر تا ۱۶ بهدست آوردیم. بنابراین، پس از فراخوانی کتابخانههای لازم، آرایهای با مقدار ۰ تا ۱۶ ایجاد میکنیم.
1k = np.arange(0, 17)
2
3print(k)خروجی کد فوق به صورت زیر است:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16]
در ادامه، تابع جرم احتمال و تابع توزیع تجمعی پواسون را با نوشتن کد مناسب، محاسبه میکنیم.
تابع جرم احتمال پواسون در پایتون
برای محاسبه تابع جرم احتمال پواسون در پایتون از دستور .pmf() استفاده میکنیم. برای انجام این کار به دو پارامتر نیاز داریم:
- مقدار $$k$$: آرایه تولید شده از صفر تا ۱۶
- مقدار $$\lambda$$ یا میانگین: این مقدار در این مثال برابر ۷ است.
اکنون میتوانیم آرایهای با مقدارهای احتمالی پواسون ایجاد کنیم:
1pmf = poisson.pmf(k, mu=7)
2pmf = np.round(pmf, 5)
3
4print(pmf)خروجی کد فوق به صورت زیر است:
[0.00091 0.00638 0.02234 0.05213 0.09123 0.12772 0.149 0.149 0.13038 0.1014 0.07098 0.04517 0.02635 0.01419 0.00709 0.00331 0.00145]
اگر میخواهید خروجی کمی زیباتر و خواناتر نوشته شود و بدانید احتمال هر $$k$$ چه مقدار است میتوانید از دستور زیر استفاده کنید.
1for val, prob in zip(k,pmf):
2 print(f"k-value {val} has probability = {prob}")با اجرای این کد، نتایج به صورت زیر نوشته میشوند:
k-value 0 has probability = 0.00091 k-value 1 has probability = 0.00638 k-value 2 has probability = 0.02234 k-value 3 has probability = 0.05213 k-value 4 has probability = 0.09123 k-value 5 has probability = 0.12772 k-value 6 has probability = 0.149 k-value 7 has probability = 0.149 k-value 8 has probability = 0.13038 k-value 9 has probability = 0.1014 k-value 10 has probability = 0.07098 k-value 11 has probability = 0.04517 k-value 12 has probability = 0.02635 k-value 13 has probability = 0.01419 k-value 14 has probability = 0.00709 k-value 15 has probability = 0.00331 k-value 16 has probability = 0.00145
نتایج بهدست آمده مشابه نتایج محاسبه شده به صورت دستی و نوشته شده در جدول هستند. در ادامه، نمودار نتایج بهدست آمده را برحسب مقادیر مختلف $$k$$ رسم میکنیم.
1plt.plot(k, pmf, marker='o')
2plt.xlabel('k')
3plt.ylabel('Probability')
4
5plt.show()نمودار تابع جرم احتمال پواسون برحسب مقدارهای مختلف $$k$$ از صفر تا ۱۶ به صورت زیر رسم میشود.
تابع توزیع تجمعی پواسون در پایتون
برای محاسبه تابع توزیع تجمعی پواسون در پایتون از دستور .cdf() استفاده میکنیم. برای انجام این کار به دو پارامتر نیاز داریم:
- مقدار $$k$$: آرایه تولید شده از صفر تا ۱۶
- مقدار $$\lambda$$ یا میانگین: این مقدار در این مثال برابر ۷ است.
اکنون میتوانیم آرایهای با مقدارهای احتمال توزیعی پواسون ایجاد کنیم:
1cdf = poisson.cdf(k, mu=7)
2cdf = np.round(cdf, 3)
3
4print(cdf)خروجی کد فوق به صورت زیر است:
[0.001 0.007 0.03 0.082 0.173 0.301 0.45 0.599 0.729 0.83 0.901 0.947 0.973 0.987 0.994 0.998 0.999]
اگر میخواهید خروجی کمی زیباتر و خواناتر نوشته شود و بدانید احتمال هر $$k$$ چه مقدار است میتوانید از دستور زیر استفاده کنید.
1for val, prob in zip(k,cdf):
2 print(f"k-value {val} has probability = {prob}")با اجرای این کد، نتایج به صورت زیر نوشته میشوند:
k-value 0 has probability = 0.001 k-value 1 has probability = 0.007 k-value 2 has probability = 0.03 k-value 3 has probability = 0.082 k-value 4 has probability = 0.173 k-value 5 has probability = 0.301 k-value 6 has probability = 0.45 k-value 7 has probability = 0.599 k-value 8 has probability = 0.729 k-value 9 has probability = 0.83 k-value 10 has probability = 0.901 k-value 11 has probability = 0.947 k-value 12 has probability = 0.973 k-value 13 has probability = 0.987 k-value 14 has probability = 0.994 k-value 15 has probability = 0.998 k-value 16 has probability = 0.999
نتایج بهدست آمده مشابه نتایج محاسبه شده به صورت دستی و نوشته شده در جدول هستند. در ادامه، نمودار نتایج بهدست آمده را برحسب مقادیر مختلف $$k$$ رسم میکنیم. برای رسم نمودار در پایتون از کتابخانه matplotlib استفاده میکنیم.
1plt.plot(k, cdf, marker='o')
2plt.xlabel('k')
3plt.ylabel('Cumulative Probability')
4
5plt.show()نمودار تابع توزیع تجمعی پواسون برحسب مقدارهای مختلف $$k$$ از صفر تا ۱۶ به صورت زیر رسم میشود.
کاربردهای فرآیند پواسون چیست؟
در حالت کلی، فرآیند پواسون در رخدادهایی استفاده میشود که با آهنگی مشخص و کاملا تصادفی رخ میدهند. از این فرآیند میتوان برای توصیف پدیدههای فیزیکی استفاده کرد. به عنوان مثال، مادهای رادیواکتیو را در نظر بگیرید. این ماده با تابش ذرات مختلف در بازه زمانی کاملا تصادفی، دچار واپاشی میشود. از آنجا که ذرات مختلف در زمانها کاملا تصادفی از ماده خارج میشوند و از رفتار مشخصی پیروی نمیکنند، واپاشی ماده رادیواکتیو را میتوانیم با استفاده از فرآیند پواسون توصیف کنیم.
فرض کنید آشکارساز فوتونی دارید که منبعی نوری بسیار ضعیفی را بررسی میکند. فوتونها از منبع نور یکییکی خارج میشوند. زمان برخورد فوتونها با آشکارساز فوتونی را بررسی میکنیم. با بررسی زمان برخورد فوتونها میتوانیم آشکارسازی فوتونها را با استفاده از فرآیند پواسون مدلسازی کنیم. از این فرآیند نیز میتوان در بررسی بازارهای مالی استفاده کرد.
جمعبندی
در این مطلب از مجله فرادرس، در مورد فرآیند پواسون و کاربردهای این فرآیند صحبت کردیم. فرآیند پواسون یکی از پرکاربردترین فرآیندهای شمارش است. به طور معمول از این فرآیند در رخدادهایی استفاده میشود که با آهنگی مشخص و کاملا تصادفی رخ میدهند. پس از آشنایی با تعریف پواسون و چگونگی اثبات فرمول آن، در مورد چگونگی استفاده از اکسل و پایتون برای کار با دادههای تصادفی و کار با توزیع پواسون، آشنا شدیم.











سلام ممنون بابت آموزش
سوالی که داشتم این بوود که تابع احتمال پواسون چرا این شکلی می باشد؟؟ اثباتی داره ؟؟
سلام ممنون میشم با توجه به توضیحاتی که دادید لطف کنید پاسخ این سوال رو هم بدید، فرض کنید ورود مشتریان به یک سیستم بر اساس فرایند پواسون است. می دانیم که در فاصله صفر تا t یک مشتری وارد سیستم شده است ول زمان دقیق ورود معلوم نیست.تابع توزیع ورود او چیست؟
در توزیع های تصادفی گسسته،علاوه بر توزیع پواسون، توزیع هندسی هم بدون حافظه است
با سلام و سپاس از توجه شما به مطالب فرادرس
بله فرآیند پواسن یک فرآیند بدون حافظه است. در مورد توزیع هندسی نیز بهتر است به مطلب توزیع هندسی مراجعه فرمایید.
باز هم از این که همراه فرادرس هستید متشکریم.