تجزیه مقادیر منفرد (SVD) — به زبان ساده

روش تجزیه مقادیر منفرد یا SVD تاریخچه طولانی و البته جالبی دارد. این روش، در علوم اجتماعی و با تست هوش شروع شد. در گذشته، پژوهشگران آزمون‌هایی را برای اندازه‌گیری جنبه‌های مختلف هوش مانند هوش فضایی و هوش کلامی ارائه کردند که همبستگی زیادی با هم داشتند. آن‌ها بر این باور بودند که یک معیار عمومی مشترک برای هوش وجود دارد و آن را برای هوش کلی، $$g$$ نامیدند که امروزه بیشتر به عنوان آی کیو (IQ) شناخته می‌شود. بنابراین، پژوهشگران تصمیم گرفتند عوامل مختلف هوش را تجزیه و مهم‌ترین آن‌ها را انتخاب کنند. در ساده‌ترین حالت، تجزیه مقادیر منفرد به نوعی همین تجزیه و انتخاب مهم‌ترین عوامل یک ماتریس را انجام می‌دهد.

تجزیه مقادیر منفرد (Singular Value Decomposition) یا SVD با نام‌های مختلفی شناخته می‌شود. این روش، ابتدا به عنوان «تجزیه عامل» (Factor Analysis) نامیده می‌شد. تحلیل مؤلفه‌های اصلی (Principal Component) یا PC و تجزیه توابع متعامد تجربی (Empirical Orthogonal Function) یا EOF نیز از دیگر اصطلاحات نزدیک به این روش است. همه این‌ نام‌ها از نظر مفهوم ریاضی معادل هستند، هرچند در فرایند محاسبه آن‌ها تفاوت‌های زیادی وجود دارد.

امروزه، تجزیه مقادیر منفرد در بسیاری از شاخه‌های علوم و نجوم کاربرد دارد. این روش، در یادگیری ماشین و آمار توصیفی و مدل‌سازی آماری نیز بسیار مورد استفاده قرار می‌گیرد.

محاسبات تجزیه مقادیر منفرد

به طور خلاصه می‌توان گفت که تجزیه مقادیر منفرد روشی است که یک ماتریس را به سه ماتریس دیگر تجزیه می‌کند. برای مثال، ماتریس $$A$$ را می‌توان به صورت زیر نوشت:

فیلم آموزش مبانی آنالیز عددی – بخش یکم در فرادرس

کلیک کنید

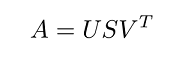
که در آن:

• $$A$$ یک ماتریس $$m \times n$$؛
• $$U$$ یک ماتریس متعامد $$m \times m$$؛
• $$S$$ یک ماتریس قطری $$m \times n$$
• و $$V$$ یک ماتریس متعامد $$n \times n$$ است.

شکل بصری ابعاد ماتریس‌ها به صورت زیر است:

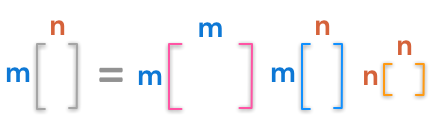
ماتریس قطری مقادیر منفرد مربعی نیست، اما شکل آن مشابه $$A$$ است.

شکل زیر نیز، یک نمایش بصری از تجزیه مقادیر منفرد را نشان می‌دهد.

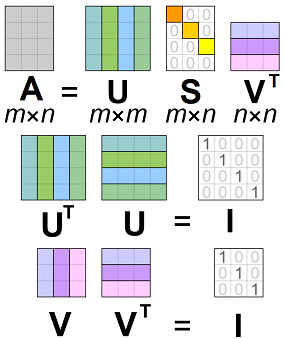
دلیل آنکه ماتریس آخر به صورت ترانهاده نوشته شده، در ادامه مشخص می‌شود. مفهوم عبارت «متعامد» و نیز دلیل متعامد بودن دو ماتریس کناری را نیز بیان خواهیم کرد.

فرض می‌کنیم $$m \ge n$$ باشد. رابطه ماتریسی (۱) را با استفاده از نمادگذاری سری‌ها بازنویسی می‌کنیم. با نوشتن رابطه ماتریسی به صورت یک سری، اگر هم فرایند محاسبات ساده نشود، همه چیز کاملاً صریح خواهد شد:

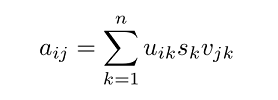
توجه کنید که چگونه ماتریس قطری $$S$$ را به یک بردار تبدیل کرده‌ایم و به صورت یک سری نوشته‌ایم. متغیرهای $$\{ s_{i}\}$$ مقادیر تکین یا منفرد نام دارند و معمولاً از بزرگترین به کوچکترین نوشته می‌شوند:‌

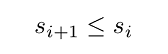
ستون‌های $$U$$، بردارهای منفرد چپ و ستون‌های $$V$$، بردارهای منفرد راست نامیده می‌شوند.

از جبر خطی می‌دانیم $$U$$ و $$V$$ وقتی متعامد هستند که رابطه زیر برقرار باشد:

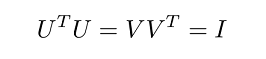
که در آن، $$I$$ ماتریس واحد یا همانی است. درایه‌های قطری ماتریس $$I$$، یک هستند و بقیه درایه‌های آن برابر با صفرند. ماتریس $$U$$ فقط در یک جهت متعامد است؛ یعنی نمی‌توان گفت $$UU^T=I$$.

با استفاده از ویژگی تعامد، می‌توانیم رابطه (۱) را به فرم دو معادله مقدار ویژه بنویسیم:

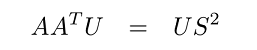
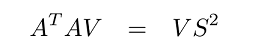
از آن‌جایی که تعداد سطر‌های $$A^TA$$ کوچکتر یا مساوی $$AA^T$$ است، یک روند متداول و با محاسبات کمتر، قرار دادن معادله (۳) در یک محاسبه‌گر مقدار ویژه برای یافتن $$V$$ و $$S^2$$ و در نتیجه، یافتن $$U$$ با تصویر کردن $$A$$ در $$V$$ است:

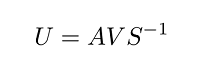
توجه کنید که وقتی $$A$$ ترانهاده شود، مکان $$U$$ و $$V$$ تغییر می‌کند:

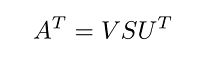
بنابراین، اگر $$m$$ باشد، می‌توانیم ترانهاده $$A$$ را محاسبه کرده، تجزیه را انجام داده، سپس نقش $$U$$ و $$V$$ را تغییر دهیم.

در این حاالت، $$U$$ یک ماتریس مربعی $$m \times m$$ است، زیرا حداکثر $$m$$ مقدار ویژه غیرصفر می‌تواند داشته باشد. در حالی که $$V$$ یک ماتریس $$n \times n$$ است.

مفهوم SVD چیست؟

در بخش قبل، ریاضیات مربوط به SVD را بیان کردیم. اما همان‌طور که متوجه شده‌اید، این ریاضیات درک شهودی از این روش به ما نمی‌دهد.

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

برای درک شهودی تجزیه مقادیر منفرد، می‌توان ماتریس $$A$$ را به عنوان یک تبدیل خطی در نظر گرفت. این تبدیل را نیز می‌توان به سه زیرتبدیل تجزیه کرد: ۱) چرخش یا دوران ۲) تغییر مقیاس ۳) چرخش. این سه گام متناظر با سه ماتریس $$U$$، $$S$$ و $$V$$ هستند. شکل زیر، این موضوع را به خوبی نشان می‌دهد.

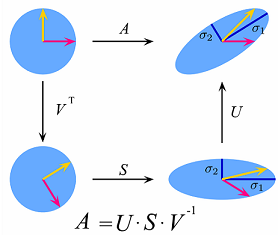
در ادامه، در قالب یک مثال ساده دو بعدی با SVD بیشتر آشنا می‌شویم. روندی که بررسی خواهیم کرد، قابل تعمیم به ابعاد بزرگتر است.

مثال عددی

دو بردار دو بعدی $$\mathbf {x}_1 =(x_1, y_1)$$ و $$\mathbf {x}_2 =(x_۲, y_۲)$$ را در نظر بگیرید. همان‌‌طور که در شکل زیر نشان داده شده است، می‌توانیم یک بیضی را با قطر بزرگ $$a$$ و قطر کوچک $$b$$ به این دو بردار منطبق کنیم. برای سادگی و کاهش محاسبات، معادلات را با استفاده از جبر ماتریسی می‌نویسیم.

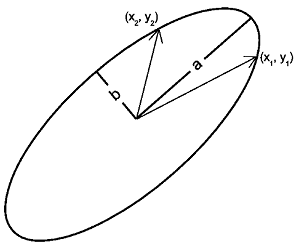
معادله بیضی را با اندازه و دوران دلخواه و با کش دادن و چرخش یک دایره واحد می‌نویسیم. فرض کنید $$\mathbf{x}' = ( x' , y' )$$ مختصات حاصل باشد که تحت تبدیل زیر قرار گرفته‌ است:

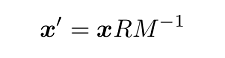
که در آن، $$R$$ ماتریس دوران است:‌

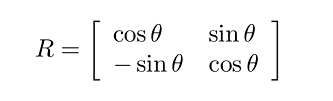
و $$M$$ یک ماتریس قطری است که شامل قطر‌های بزرگ و کوچک بیضی است:

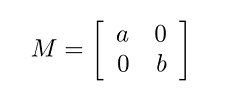
بردار را در حالت کلی و به صورت جمله به جمله می‌نویسیم:

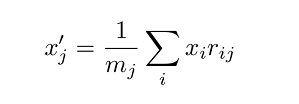
که در آن، $$m_i$$ برابر با $$i$$اُمین درایه قطری ماتریس $$M$$ است و برای حالت دو بعدی داریم:

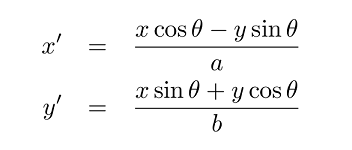
توجه کنید که دوران به صورت ساعتگرد است. زاویه‌ها نسبت به مرجع نیز به صورت پادساعتگرد تعیین می‌شوند.

معادله دایره واحد به صورت زیر است:

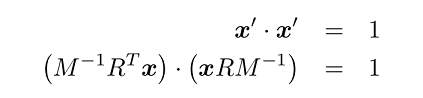
مجموعه‌ $$\mathbf{x}$$ها را در سطر‌های ماتریس $$X$$ قرار می‌دهیم:

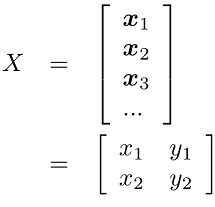
در نهایت، معادله ماتریسی به صورت زیر خواهد بود:

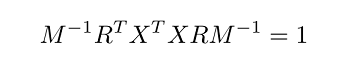
عبارت اخیر، در حقیقت، بازنویسی معادله (۳) است. اگر $$A$$ را به عنوان مجموعه‌ای از نقاط در نظر بگیریم، آن‌گاه مقادیر منفرد، محورهای یک بیضی برازش شده با کمترین مربعات هستند، در حالی که $$V$$ دوران آن است. ماتریس $$U$$ تصویر هر نقطه در $$A$$ روی محورها است.

کاربردها

مجموع مربعات مقادیر منفرد باید برابر با واریانس کلی در $$A$$ باشد. بنابراین، اندازه هر یک از این مقادیر بیان می‌کند که چه مقدار از واریانس کلی برای هر بردار منفرد محاسبه می‌شود.

فیلم آموزش جبر خطی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

به عنوان جایگزین، می‌توان یک SVD بریده را که شامل ۹۹ درصد واریانس است تشکیل داد:

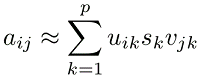
که در آن، $$p$$ تعداد مقادیر منفردی است که آن‌ها را نگه داشته‌ایم. معمولاً این تعداد کمتر از ۱۰ مقدار منفرد برجسته ($$p = 10$$) خواهد بود. این، یکی از قابلیت‌های تجزیه مقادیر منفرد برای استخراج حداقل مؤلفه‌ها است.

حل معادلات ماتریسی

با بازنویسی معادله (۱) می‌توانیم دستگاه معادلات خطی را حل کنیم:

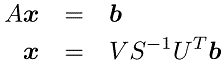
معادلات بالا را می‌توانیم به صورت مجموع سری زیر بنویسیم:

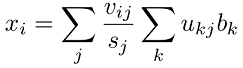
این معادلات را می‌توان به ماتریس‌های غیرمربعی تعمیم داد. از آن‌جایی که یک ماتریس $$m \times n$$ که در آن $$m>n$$ است، تنها $$n$$ مقدار منفرد خواهد داشت، در استفاده از تجزیه مقادیر منفرد، با حل یک ماتریس $$m \times m$$ معادل با $$n$$ مقدار منفرد مواجه خواهیم بود. برای ماتریس‌های غیرمربعی، معکوس ماتریس با استفاده از تجزیه مقادیر منفرد، برابر با حل معادله معمولی زیر خواهد بود:

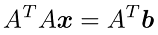
این معادله، جواب $$x$$ را که نزدیکترین به مبدأ است و کمترین فاصله را از آن دارد به دست می‌دهد. معادله معمولی، جواب مسئله کمینه‌سازی زیر است:

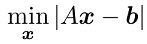
کاهش داده

یکی چالش‌های متداول در یادگیری ماشین، وجود چند صد متغیر است، در حالی که بسیاری از الگوریتم‌های یادگیری ماشین، اگر با تعدادی بیش از یک مقدار مشخص متغیر کار کنند، با شکست مواجه می‌شوند. این موضوع، استفاده از تجزیه مقادیر تکین را برای کاهش متغیر در یادگیری ماشین ضروری می‌کند.

اگر تعداد و انواع مناسبی از ویژگی‌ها برای حل یک مساله خاص به الگوریتم‌های یادگیری ماشین داده شود، این الگوریتم‌ها به خوبی کار می‌کنند. اما، در صورتی که تعداد ویژگی‌ها (متغیرها) بسیار زیاد باشد، اغلب الگوریتم‌های یادگیری ماشین در حل مسئله دچار مشکل می‌شوند، زیرا با مسئله «داده‌های ابعاد بالا» (High Dimensional Data) مواجه خواهیم بود. در اینجا است که بحث «کاهش ابعاد» (Dimensionality Reduction) مطرح می‌شود.

قبلاً در معادله (۶)، گفتیم که چگونه یک SVD با کاهش تعداد مقادیر تکین می‌تواند یک ماتریس را بسیار دقیق تقریب بزند. از این ویژگی می‌توان برای فشرده‌سازی داده‌ها با فرم‌های کوتاه شده $$U$$، $$S$$ و $$V$$ به جای $$A$$ و برای کاهش متغیر از جایگزینی $$A$$ با $$U$$ استفاده کرد. البته در پایان، بر اساس معادله (۴) باید با ضرب $$S$$ و $$V$$ نتایج را به دستگاه مختصات اصلی تبدیل کرد.

در ادامه، مثالی را درباره این موضوع بیان و برنامه کامپیوتری آن را نیز ارائه می‌کنیم.

مثال کاهش متغیر

فرض کنید ماتریس $$A$$ با ابعاد $$m \times n$$، مجموعه‌ای از داده‌های آموزش را با هر بردار آموزش در هر سطر رابطه (۵)‌ ذخیره می‌کند و $$n$$ طول هر بردار و عددی بسیار بزرگ است.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

می‌خواهیم $$A$$ را به الگوریتم خوشه‌بندی وارد کنیم که خروجی آن، یک عدد ثابت از مراکز خوشه است. از آن‌جایی که $$n$$ بسیار بزرگ است، اجرای الگوریتم بسیار طول خواهد کشید یا ناپایدار خواهد شد. بنابراین، تعداد متغیرها را با استفاده از SVD کاهش می‌دهیم. مراحل زیر، فرایند انجام این کار را نشان می‌دهند.

گام اول: خواندن داده‌ها

در ابتدا، باید داده‌ها را برای تکمیل ماتریس $$A$$ بخوانیم. برنامه $$\mathrm{C++}$$ مربوط به این گام از فرایند، به صورت زیر است:

1//subroutine header for performing cluster analysis:
2#include "cluster.h"
3//maximum number of clusters:
4#define MAX_CLUSTER 10
5int main(int argc, char **argv) {
6  char *infile;            //input file
7  char *outfile;           //output file
8  FILE *fs;                //file pointer
9  double **a;              //matrix of training data/U
10  int m;                   //number of rows in matrix
11  int n;                   //number of columns in matrix
12  int nsv;                 //number of singular values
13  if (argc!=4) {
14    printf("syntax: cluster_svd nsv train centers\n");
15    printf("  where:\n");
16    printf("nsv      = number of singular values (0 = use untransformed data)\n");
17    printf("infile   = ASCII input file containing training data\n");
18    printf("output   = ASCII output file containing cluster centers\n");
19    printf("\n");
20    printf("file format:\n");
21    printf("- one line header containing number of rows and number of columns\n");
22    printf("- row major list of each matrix element\n");
23    exit(1);
24  }
25  if (sscanf(argv[1], "%d", &nsv)!=1) {
26    fprintf(stderr, "Error parsing first command line argument\n");
27    exit(1);
28  }
29  infile=argv[2];
30  outfile=argv[3];
31  fs=fopen(infile, "r");
32  if (fs==NULL) {
33    fprintf(stderr, "Error opening input file, %s\n", infile);
34    exit(1);
35  }
36  if (fscanf(fs, "%d %d", &m, &n)!=2) {
37    fprintf(stderr, "Format error in input file: %s line 0", infile);
38    exit(1);
39  }
40  if (nsv>n) {
41    fprintf(stderr, "Command line parameter nsv=%d out of range\n", nsv);
42    exit(1);
43  }
44  a=new double *[m];
45  a[0]=new double[m*n];
46  for (int i=1; i<m; i++) a[i]=a[0]+i*n;
47  for (int i=0; i<m; i++) {
48    for (int j=0; j<n; j++) {
49      if (fscanf(fs, "%lg", a[i]+j)!=1) {
50        fprintf(stderr, "Format error in input file, %s, line %d\n", infile, i);
51        exit(1);
52      }
53    }
54  }
55  fclose(fs);

گام دوم:‌ تعریف SVD

از برنامه تجزیه مقدار تکین آماده در فایل هِدِر (header)، $$\mathrm{svd.h}$$ استفاده می‌کنیم:

1#ifndef SVD_H
2#define SVD_H
3//subroutine for singular value decomposition:
4int                       //returns an error code (0 for success)
5     svd (double **a,     //input matrix--replaced by U on output
6                int m,        //number of rows
7                int n,        //number of columns
8                double *s,    //singular values
9                double **vt); //V--right singular vectors
10#endif

معمولاً مقادیر تکین، با توجه به نوع ماتریس و بردار مورد استفاده، اغلب پیچیده‌تر از این است. البته این برنامه، برای قرار دادن همه موارد در یک تابع فشرده مناسب است. در ادامه بخش قبل، داریم:‌

1  double *ave;
2  double *s;               //singular values
3  double **vt;             //right singular vectors
4  //first we calculate and remove the arithmetic means:
5  ave=new double[n];
6  for (int i=0; i<n; i++) ave[i]=0;
7  for (int i=0; i<m; i++) {
8    for (int j=0; j<n; j++) {
9      ave[j]+=a[i][j];
10    }
11  }
12  for (int i=0; i<n; i++) ave[i]/=m;
13  for (int i=0; i<m; i++) {
14    for (int j=0; j<n; j++) {
15      a[i][j]-=ave[j];
16    }
17  }
18  if (nsv>0) {
19    //make space for singular values:
20    s=new double[n];
21    //make space for right singular vectors:
22    vt=new double *[n];
23    vt[0]=new double[n*n];
24    for (int i=1; i<n; i++) vt[i]=vt[0]+i*n;
25    //perform the decomposition:
26    int err=svd(a, m, n, s, vt);
27    if (err!=0) {
28      fprintf(stderr, "Error in svd subroutine\n");
29      exit(err);
30    }
31  }

گام سوم: تحلیل خوشه

الگوریتم خوشه‌بندی، یک مجموعه از مراکز خوشه $$c$$ را تولید می‌کند، به گونه‌ای که $$\{ \mu _i ; i \in [1,c] \}$$:

1#ifndef CLUSTER_H
2#define CLUSTER_H
3int                            //returns number of cluster centers
4    cluster (double ** x,      //training vectors
5                int m,         //number of training vectors
6                int n,         //dimension of each vector
7                int max_nc,    //maximum number of cluster centers
8                double **mu);  //returned cluster centers
9#endif

در ادامه، مراکز خوشه‌ها را تعیین می‌کنیم:

1double **mu_p;      //matrix of cluster centers
2  int nc;           //number of cluster centers
3  //make space for cluster centers:
4  mu_p=new double *[MAX_CLUSTER];
5  mu_p[0]=new double[MAX_CLUSTER*n];
6  for (int i=1; i<MAX_CLUSTER; i++) mu_p[i]=mu_p[0]+i*n;
7  if (nsv>0) {
8    //make space for cluster centers:
9    nc=cluster(a, m, nsv, MAX_CLUSTER, mu_p);
10  } else {
11    //make space for cluster centers:
12    nc=cluster(a, m, n, MAX_CLUSTER, mu_p);
13  }
14  if (nc <= 0) {
15    fprintf(stderr, "Cluster algorithm failed");
16    exit(-1);
17  }

از آن‌جایی که الگوریتم خوشه‌بندی از داده‌های آموزش جدید استفاده می‌کند، مراکز خوشه‌ها در سیستم جدید به صورت زیر محاسبه می‌شوند:‌

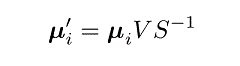
یا

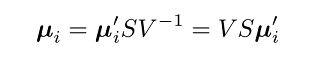
با نوشتن جزء به جزء جملات، داریم:

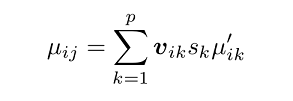
که در آن، $$p$$ تعداد مختصات‌ها در سیستم کاهش یافته است.

گام چهارم:

در این مرحله، مراکز خوشه را در دستگاه مختصات قبلی ذخیره کرده و سپس، معادله (۱۰) را اعمال می‌کنیم.

1  double **mu;        //cluster centers in un-transformed coords
2  //allocate space for the un-transformed cluster centers:
3  mu=new double *[nc];
4  mu[0]=new double[nc*n];
5  for (int i=1; i<nc; i++) mu[i]=mu[0]+i*n;
6  //perform the coordinate transformation:
7  for (int i=0; i<nc; i++) {
8    for (int j=0; j<n; j++) {
9      mu[i][j]=ave[j];
10      if (nsv>0) {
11        for (int k=0; k<nsv; k++) mu[i][j]+=vt[k][j]*s[k]*mu_p[i][k];
12      } else {
13        mu[i][j]+=mu_p[i][j];
14      }
15    }
16  }
17  //write the results to a file:
18  fs=fopen(outfile, "w");
19  if (fs==NULL) {
20    fprintf(stderr, "Error opening output file, %s\n", outfile);
21    exit(1);
22  }
23  fprintf(fs, "%d %d\n", nc, n);
24  for (int i=0; i<nc; i++) {
25    for (int j=0; j<n; j++) fprintf(fs, "%16.8lg", mu[i][j]);
26    fprintf(fs, "\n");
27  }
28  fclose(fs);
29  //clean up:
30  delete [] mu[0];
31  delete [] mu;
32  delete [] mu_p[0];
33  delete [] mu_p;
34  delete [] ave;
35  delete [] a[0];
36  delete [] a;
37  if (nsv>0) {
38    delete [] s;
39    delete [] vt[0];
40    delete [] vt;
41  }
42  return 0;
43}

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• بردار ویژه و مقدار ویژه — از صفر تا صد
• تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل
• تحلیل مولفه اساسی (PCA) در پایتون — راهنمای کاربردی

^^